Ben Wilbrink: Intellectuele capaciteiten in contexten

https://twitter.com/iQuirky_Teacher/status/721595015441551360 In 2012 publiceerde ik samen met Joost Hulshof en Henk Pfaltzgraff een artikel in Examens (zie hier voor de concept-versie), waarin de validiteit van de Cito-rekentoets-3F wordt betwist: de stelling is dat deze toets niet het rekenen toetst dat leerlingen bij de PPON in 2004 niet meer behoorlijk bleken te beheersen, dat het niet het rekenen toetst dat het hoger onderwijs verwacht dat aankomende studenten beheersen, en vooral dat de ‘toets’ test op verschillen in intellectuele capaciteiten. Ik heb geen aanwijzingen dat het Cito zal reageren op deze stelling. Het College voor Examens heeft wel gereageerd in het decembernummer van Examens, bij de pen van Jan Kastelein ophalen. Kastelein herhaalt nog eens de argumenten van de commissie-Schmidt, maar dat is precies de bureaucratische verdediging die in een eerder artikel in Examens pdf van hele nummer 3 door mij en Joost Hulshof al was bestreden (dit artikel speelde een rol bij het door OCW instellen van de commissie-Van de Craats om een rekentoets-3S (zie hier) voor te bereiden).

Dit maatschappelijke debat kan nu alleen verder komen door zelf dan maar de nodige onderzoekmatige en theoretische onderbouwing te geven bij de stelling dat de Cito-rekentoets-3F allereerst functioneert als een test op intellectuele capaciteiten, en pas veel later misschien ook nog iets heeft te maken met het toetsen op rekenvaardigheid. Die ‘intellectuele capaciteiten’ vat ik breed op. Het gaat om veel meer dan alleen het vermoeden dat ‘realistische contexten’ van de leerlingen vragen om abstract te redeneren; wat bedoel ik met dat abstract redeneren: de gegeven contexten zijn immers niet concreet, maar de leerlingen moeten zich die concreet voorstellen — het gaat om counterfactuals. Tot het bredere scala van intellectuele capaciteiten reken ik zaken als verschillen in capaciteit van het werkgeheugen (cognitive load theory), verschillen in kennis van de wereld (waaronder woordenkennis), verschillen in taalvaardigheid Nederlands (ook of juist in situaties waarin het Nederlands van de toetsvragen werkelijk beroerd is), verschillen in rekenvrees (math anxiety). Wat hoort hier niet tot verschillen in intellectuele capaciteiten: verschillen in rekenvaardigheid, bijvoorbeeld ontstaan doordat sommige leerlingen onvoldoende voorbereidingstijd hebben geïnvesteerd. Dit kan nog een knap lastig punt worden, zie ook het promotieonderzoek van Marian Hickendorf (2011), hoofdstuk 7, hierbeneden.

Waar in het nu volgende sprake is van de rekentoets-3F, kan gelezen worden: de voorbeeldrekentoets-3F, de eerste rekentoets-3F die door het Cito is vrijgegeven. Het Cito heeft ook een voorbeeldrekentoets-2F vrijgegeven. De verschillen tussen deze twee rekentoetsen zijn niet dusdanig groot, dat voor de onderstaande analyse een afzonderlijke behandeling van de rekentoets-2F nodig is. Dat neemt natuurlijk niet weg dat de examensituatie voor het vmbo een radicaal andere is dan voor havo/vwo.

Een specifiek onderdeel van de aan te snijden thematiek heb ik in behandeling op een andere webpagina, als mijn hypothese 4: Contextopgaven testen intelligentie, waarbij het vooral gaat om het fenomeen dat de contexten van deze rekenopgaven geen concrete contexten zijn, maar dat de leerling zich deze contexten moet voorstellen. Het gaat dus om abstract denken in counterfactuals. Laat dat nu precies een hoofdthema zijn in het werk van James Flynn (2007), over het Flynn-effect: dat deze vorm van abstract denken doorheen de laatste honderd jaar enorm sterk is ontwikkeld. Het gaat dus om een uitgesproken onderdeel van wat wij intelligentie plegen te noemen. Zie voor de specifieke literatuur op dit subthema dus deze webpagina.

Zie voor annotaties van Henk Pfaltzgraff en mij bij deze voorbeeldrekentoets deze pagina, idem voor de rekentoets-2F deze pagina.

Uitgangspunten - opzet artikel: Inleiding

Op alle punten is voldoende onderzoekliteratuur voorhanden om te kunnen scoren. Misschien is het laatste punt h) nog wel het eenvoudigst te onderbouwen, terwijl punt g) tamelijk complex kan blijken te zijn (zowel een directe aanval op de filosofie van het realistisch rekenen (constructivisme), als gebruikmaken van de stand van onze kennis over cognitief functioneren bij het aanpakken en oplossen van word problems)

Er zijn een aantal paradoxale fenomenen aan de orde. Zoals een rekentoets-3F die geen rekenvaardigheid toetst. En zoals de stelling dat aan het eind van het basisonderwijs iedereen rekenvaardig behoort te zijn, wat in flagrante strijd is met de empirische gegevens (zie o.a. Hickendorff, 2011 hoofdstuk 7, hierbeneden). Zoals de stelling dat iedereen bij eerste gelegenheid hoort te slagen voor de rekentoets die aan de eindexamens wordt toegevoegd: zo werken eindexamens toch niet? Punt g) stelt dat het rekenen in de rekentoets-3F ondergeschikt is, terwijl de data van Hickendorff (2011, hoofdstuk 7) juist laten zien dat er (bij 12-jarigen) een enorme spreiding is in basale rekenvaardigheid terwijl leerlingen geen moeite blijken te hebben met de ‘contexten’. Er valt dus het nodige uit te zoeken.

0. Inleiding

Leraren vragen mij hoe zij hun leerlingen het best kunnen voorbereiden op de rekentoets bij het eindexamen. Dat is een probleem van enorme omvang, maar er ligt geen helder antwoord op de plank. Er is dus een hoop spitwerk nodig om hier een begin van een goede analyse te geven. Het gaat in de kern van de zaak natuurlijk om de vraag of typische probleemstellingen in de rekentoets-3F een beroep doen op intellectuele capaciteiten waarop leerlingen verschillen van elkaar. De verwachting is immers dat, in de mate waarin die individuele verschillen op het moment van toetsing een rol spelen, het leraren niet is gegeven om in de jaren voorafgaand aan dit onderdeel van het eindexamen de leerlingen daar gericht op voor te bereiden. Het enige advies dat ik tot nu heb kunnen geven is gebaseerd op psychologische intuïtie en zich gestaag vermeerderende kennis over het fenomeen van contextrekenopgaven in het onderwijs en in toetsen van bijvoorbeeld het Cito. En dat advies komt hierop neer: breng/houd de rekenvaardigheid van de leerlingen op een hoog peil, en maak ze vertrouwd met het fenomeen van de contextrekenopgave. Verbied gebruik van de rekenmachine, ooit, op school of thuis, en leg uit waarom. Sta het gebruik van de QAMA-rekenmachine toe, voor wie echt een rekenmachine wil gebruiken. (zie rekenmachine.htm) Voorkom het ontstaan van reken- en wiskundeangst (math anxiety).

Herlezen van Hickendorff’s proefschrift hoofdstuk 7 levert een sterke ondersteuning van mijn ‘advies’ op, als het zou gaan om contextrekenopgaven voor 12-jarigen. Zij laat immers zien in de data van tabel 7.4, zoals hierbeneden nog te bespreken, dat voor deze leerlingen niet de contexten, maar de cijferopgaven een enorm probleem vormen. De meeste leerlingen kunnen niet rekenen. Wie niet kan rekenen, kan dat evenmin ‘in contexten’. Een eenvoudige ’logische’ fout in de realistische rekendidactiek is dat met het benadrukken van rekenen in contexten er voor dat rekenen zelf minder aandacht nodig zou zijn. De boodschap voor het basisonderwijs lijkt me glashelder: investeer in rekenvaardigheid van de leerlingen, vergeet al die contexten voorlopig maar.

Het valt nog niet mee om een begin van een goede analyse van het fenomeen ‘realistisch rekenen’ te krijgen. Alleen al het verhullend taalgebruik is een enorme belemmering. De term ‘realistisch’ is zelfs zo misleidend dat Adri Treffers er zijn spijt over heeft uitgesproken de term geïntroduceerd te hebben. In het jargon van de commissie-Meijerink gaat het dan om ‘functioneel rekenen’. Dat is allemaal tot je dienst, maar laten we gewoon kijken naar de contextopgaven zelf, zoals die in de eerste door het Cito vrijgegeven voorbeeldrekentoets-3F. Om greep te krijgen op deze malle toestanden is het allereerst nodig om afstand te nemen, om in het specifieke van die contextrekenopgaven het algemene te kunnen zien. Het gaat natuurlijk niet alleen om contextopgaven in de rekentoets-3F: heel het onderwijs vanaf groep een van de basisschool is doortrokken van dit contextrekenen. Het is dus in feite zoiets als een beroepspraktijk, waarin de leerlingen zich door eindeloze oefening doorheen hun schoolloopbaan moeten zien te bekwamen. Er dus een stevige beschrijving nodig van rekenvaardigheid, wat het is, wat het niet is, hoe die demarcatie valt te maken.

Het is absoluut noodzakelijk om scherp onderscheid te maken naar rekenvaardigheid, intelligentie, wereldkennis, en werkgeheugen, om maar even een paar belangrijke zaken te noemen, waarvan de rekenvaardigheid zelf de belangrijkste is. Een praktische definite van rekenvaardigheid is wat opleiders van achttienjarigen daaronder verstaan: Van de Craats & Bosch (2009) en Pfaltzgraff (2009).

Jan van de Craats & Rob Bosch (2009). Basisboek rekenen. Pearson Education Benelux. deels online

In een al wat ouder stuk pdf geeft Jan van de Craats een uitstekende uiteenzetting over de basisvaardigheden (hoofdrekenen), in contrast met het ‘handig rekenen’ in de realistische en staatsdidactiek. Ik noem het hier omdat het best eens zo kan zijn dat dit ‘handig rekenen’ in de rekentoets-3F eveneens zo is geïmplementeerd dat de intelligentere leerlingen in het voordeel zijn. Als dat niet al het geval is voor vwo-leerlingen, dan zal dat voor vmbo-ers ongetwijfeld wel zo werken. Want de rekentoets-3F begint met een reeks opgaven die ‘handig’ zijn op te lossen.

In het vervolg is onder rekenvaardigheid te verstaan het gewone rekenen, inclusief het rekenen met benoemde getallen, maten en gewichten: voor niveau 3S uitstekend aangegeven door de commissie-Van de Craats, voor het eerste deel van de rekentoets-3S (zie hier).

Naast het rekenen als zodanig zijn er nog onderwerpen als: het praten over rekenen, het lezen van teksten over rekenen, het opstellen van rekenmodellen, en probleemoplossen. Praten is niet aan de orde bij de schriftelijke rekentoets. Het lezen van tekst wel, maar als dat meer is dan alleen ‘bereken’ of ‘los op’ dan is het de vraag of dat strikt genomen nog rekenvaardigheid is, of iets anders. Het opstellen van rekenmodellen is een stap in een probleemoplos-cyclus; dan is de vraag of probleemoplossen thuishoort in een toets op rekenvaardigheid. Nee, dus. In zekere zin gaat dit hele stuk over deze kwestie, want in de rekentoets-3F en -3s zijn de contextrekenopgaven het omstreden deel. Het zijn deze opgaven die strikt genomen het domein van het rekenen oprekken tot dat van het probleemoplossen met hulp van rekenen. Van de gevaren die dit met zich meebrengt is de belangrijkste wel dat het een premie zet op slimheid, in vooroorlogse tijden minder respectloos ‘denkvermogen’ genoemd.

Marian Hickendorff (2013). The Effects of Presenting Multidigit Mathematics Problems in a Realistic Context on Sixth Graders' Problem Solving, Cognition and Instruction, 31:3, 314-344. abstract - pdf van hoofdstuk 7 van haar proefschrift

Op het eerste gezicht lijkt dit onderzoek belangrijke antwoorden te kunnen te geven op de probleemstelling dat de rekentoets-3F verschillen in intellectuele capaciteiten toetst, ook al heeft Marian Hickendorff dat niet in deze woorden als haar onderzoekhypothese geformuleerd. Dat het gaat om leerlingen in groep 8 mag nauwelijks een bezwaar zijn: de rekentoets-3F is verondersteld op het niveau te liggen van de betere leerlingen in groep 8. Op het tweede gezicht blijkt dit onderzoek toch slechts een begin van een antwoord op te leveren, maar heeft Hickendorff wel belangrijke werk gedaan in het verhelderen van de situatie waarin we ons bevinden met dit type rekentoetsen en het realistische rekenonderwijs waarop zij zijn geënt. Niet onbelangrijk is dat Hickendorff dit onderzoek in samenwerking met het Cito heeft kunnen doen: het is bepaald de inzet van het Cito geweest om stevig onderzoek (Hickendorff promoveerde cum laude) te zetten op kwesties die spelen in het Nederlandse rekenonderwijs, in het bijzonder zoals die blijken uit PPON-studies. Ik veronderstel de PPON als bekend (zie de website van het Cito voor de rapporten) en wel speciaal de uitkomsten van de PPON in 2004 afgenomen waarbij een dramatische terugval in basale rekenvaardigheid bleek. De PPON afgenomen in 2011 bevestigt dat beeld: de rekenvaardigheden liggen nu op hetzelfde niveau als in 2004.

Hickendorff stelt dat er weinig of geen onderzoek is gedaan op een directe vergelijking van het maken van redactieopgaven met het maken van alleen de rekensom zoals begrepen in de corresponderende redactieopgave. Ik stel er een eer in om te proberen toch iets van dat weinige onderzoek boven water te halen; of dat gaat lukken is geenszins zeker. Maar er is ongetwijfeld onderzoekliteratuur die, zij het zijdelings, wel degelijk antwoord op deze specifieke vergelijkingskwestie kan geven.

Het theoretisch kader dat Hickendorff in dit artikel (hoofdstuk 7) schetst, is direct relevant voor de thematiek die ik in dit werkdocument wil behandelen. Wie een goede inleiding zoekt die niet gekleurd is door mijn vooringenomenheden, kan die vinden in het theoretisch kader zoals Hickendorff dat schetst.

Dit onderzoek van Marian Hickendorff bestuderend, heb ik er een aantal opmerkingen en vragen bij, waarover ik met Marian van gedachten wil wisselen. Daarop vooruitlopend alvast de volgende aantekeningen.

Opmerkingen en vragen bij Marian Hickendoff (2011), hoofdstuk 7 (gepubliceerd: 2013).

Het hoofdstuk gelezen hebbend, lees ik opnieuw en nu met meer informatie het abstract. Ik vertaal en parafraseer.

Doel van dit onderzoek is om effecten van het geven van rekenopgaven in ‘realistische’ contexten t.o.v. diezelfde opgaven als cijferopgave vast te stellen, zowel op goedscore als op aanpakstrategie.

Pro memorie: Hickendorff gebruikt opgaven uit de PPON 2004; het is dan toch wel opmerkelijk dat die redactiesommen hier onverbloemd ‘realistische contextopgaven’ worden genoemd. Het is geen uitglijden met de pen: als relevante achtergrond geeft Hickendorff publicaties van Freudenthal en Treffers aan.

De term aanpakstrategie suggereert iets cognitief-psychologisch, maar daar blijkt het niet om te gaan. Ik werd erdoor op een verkeerd been gezet. Hickendorff bedoelt ermee dat er een grote verscheidenheid is in de manier waarop leerlingen bijvoorbeeld een vermenigvuldiging uitvoeren: netjes volgens het bekende algoritme, of minder strak volgens een ‘realistische’ aanpak (kolomrekenen), of op onbekende wijze uit het hoofd rekenend. Dit kennen we uit het onthullende onderzoek dat Kees van Putten voor het eerst heeft kunnen doen op gegevens van de PPON-2004 (ik veronderstel dat hier bekend; gepubliceerd als onderdeel van de rapportage over de PPON 2004 download ). Het heeft mij toch wel verrast, omdat de manier van uitrekenen op zichzelf niets heeft te maken met al dan niet in context gegeven zijn van de rekenopgave, en ik ook geen psychologische overwegingen kan zien waarom het al dan niet in context presenteren van rekenopgaven een effect zou moeten hebben (hypothetisch) op de keuze van de ene danwel een andere algoritmische benadering op papier, of uit het hoofd uitrekenen.

Pro memorie: een voor de hand liggende veronderstelling is hier toch dat de keuze voor een strategie vooral zal zijn bepaald door het onderwijs dat de betreffende leerling heeft gehad, maar daar maakt Hickendorff geen opmerking over, als ik dit hoofdstuk goed heb gelezen (er zou een effect van schoolklassen kunnen zijn op die strategiekeuze). En ik vermoed dat ook Kees van Putten er geen aandacht aan heeft geschonken. Ik ben benieuwd of daar in ander onderzoek misschien wel expliciet op is geanalyseerd. (Egbert Harskamp?)

Dat laatste pm-puntje is toch meteen al van belang voor een belangrijke nuancering die ik op dat ‘effect van contexten’ zou willen aanbrengen. Hickendorff weet heel goed, gaat daar ook expliciet op in, dat het rekenonderwijs dat haar proefleerlingen hebben gehad sterk is bepaald door het gedachtengoed van de ‘realistische’ rekendidactiek. Met andere woorden: dit onderzoek met een rekentoets vindt niet bepaald plaats onder omstandigheden die overigens neutraal zijn t.o.v. de vraagstelling. Naar mijn smaak zou dit onderzoek herhaald moeten worden met een groep leerlingen die het gebruikelijke rekenonderwijs hebben genoten, niet het ‘realistische’. Dat onderzoek hebben we niet voorhanden, maar het is natuurlijk mogelijk om het in gedachten te doen, en op die manier mee te nemen bij het lezen van het verslag van het onderzoek van Hickendorff.

Aan het onderzoek doen 685 leerlingen uit groep acht mee. Zij maken een toets die bestaat uit acht contextopgaven en acht cijferopgaven. Het gaat om telkens twee opgaven optellen, aftrekken, vermenigvuldigen en delen.

Dit lijkt een behoorlijk uitgebreide dataverzameling, bijna zevenhonderd leerlingen. Maar toch wel een beperkte rekentoets van slechts zestien opgaven. En die zestien opgaven moeten ook nog eens heel veel werk doen: wel of geen context, en zowel optellen, aftrekken, vermenigvuldigen als delen. Daar komen nog wat dingen bij: jongens versus meisjes, taalvaardigheid, en nog zo het een en ander. Bovendien worden er complexe statistische methodieken op losgelaten. De vraag is: heeft dit onderzoek in deze implementatie wel voldoende power om tot betekenisvolle uitkomsten te kunnen leiden? Ik heb niet gezien dat Hickendorff expliciet ingaat op deze bedenking (misschien heeft zij er tijdens de promotie iets over gezegd? Ik heb daar geen aantekeningen gemaakt). Toch lijkt het mij heel relevant, want zij spitst telkens het onderzoek toe op dat optellen, respectievelijk, aftrekken, vermenigvuldigen en delen. Maar dan gaat het telkens dus over twee contextopgaven versus twee cijferopgaven. Dat zijn wel heel korte toetsjes. En dat niet alleen: de resultaten zijn in onbekende mate afhankelijk van de contextopgaven die voor dit onderzoek zijn gekozen (de cijferopgaven zijn evident representatief, maar datzelfde kan van contextopgaven niet worden gezegd).

. . . dezelfde latente capaciteit was bepalend voor het oplossen van zowel contextopgaven als cijferopgaven . . .

Wat een ‘latente capaciteit’ (latent ability) is, dat veronderstelt Hickendorff bij de lezer bekend. Dat mag dan zo zijn, maar voor mij is hier sprake van een louter statistische constructie. Op zich had daar ook uit kunnen komen dat verschillen op itemscores niet allereerst op grond van een gemeenschappelijk kenmerk binnen leerlingen te verklaren zijn. Maar ook dat zegt me dan weinig. Ik ben hier niet uit, en moet nog eens nalezen hoe Hickendorff deze analyse koppelt aan haar theoretisch kader.

. . . de moeilijkheid van contextopgaven verschilt niet van die van de equivalente cijferopgaven . . .

Voor deze leerlingen in groep acht maakt het geen verschil bij deze opgavenset of ze in context zijn gegeven of niet. Dat is een behoorlijk sensationeel onderzoekresultaat. De eerste conclusie die ik zelf zou trekken is: gooi dan die contexten definitief de school uit, in ieder geval uit de rekentoetsen. Hickendorff komt mij halverwege tegemoet: gooi de helft eruit. Hoe verklaart Hickendorff dit onverwachte resultaat: kennelijk zijn deze leerlingen nu zo vertrouwd met contexten, anders dan leerlingen in groep 4 bijvoorbeeld, dat ze geen verschil meer maken in prestaties. Dat gaat mij te ver. Wat ik gemist heb in de data-analyse is of leerlingen uit de contextopgaven wel het juiste rekenmodel afleiden. Kennelijk is dat het geval. Zijn dit misschien contexten die volgens een bekend stramien gaan, waar leerlingen goed op zijn geoefend? Met andere woorden: zijn het wel contexten in de zin zoals Freudenthal en Treffers dat bedoelen? Een andere verklaring zou kunnen zijn dat deze leerlingen nog steeds zoveel moeite hebben met het eenvoudige rekenwerk zelf, dat probleempjes met contexten daarbij vergeleken in het niet zinken.

Als contexten aan het eind van het basisonderwijs geen verschil maken, doen ze dat dan in het voorafgaande traject wel? Anders gesteld: stel dat bij replicaties de conclusie blijft staan dat toevoegen van contexten toevoegen van dood gewicht is, dan gaat al die aandacht voor contexten toch direct ten koste van het verwerven van een behoorlijke rekenvaardigheid en het bijbehorende getalbegrip? Stel dat er in heel het basisonderwijs geen aandacht zou zijn voor het rekenen-in-contexten, en je zou in groep acht een test met contextopgaven afnemen, zouden de contextopgaven dan echt slechter worden gemaakt dan hun cijferequivalent? Waar is het onderzoek dat antwoord op deze vraag geeft? (Ik vermoed dat het er is)

Ik neem nu nog een keer het artikel door. En moet dan ook de expliciete verbinding maken met de situatie van de rekentoets-3F, want die is toch wel iets anders dan de toets bij Hickendorff. Hickendorff heeft niet onderzocht in hoeverre resultaten op deze rekenopgaven samenhangen met verschillen in taalvaardigheid, wél of taalvaardigheid een rol speelt bij contextopgaven versus cijferopgaven: niet in dit onderzoek in ieder geval. Intelligentie of de score op de Eindtoets Basisonderwijs is niet in dit onderzoek meegenomen.

de contextvragen

Kijk nog eens goed naar de gestelde contextvragen. Die zijn behoorlijk simpel. Het zijn eigenlijk geen contextvragen, en al helemaal geen ‘realistische’. Kijk mee:

Deze contextvraag noemt twee bedragen, met ‘en’ ertussen. Ergo: optellen die bedragen. De verdere tekst doet er helemaal niet toe. Dit is trouwens precies het trucje dat vanouds bekend is voor redactiesommen.
Deze contextvraag noemt vier bedragen. Wat kun je met vier bedragen doen? Precies. Deze contextvraag is goed te beantwoorden door de tekst de tekst te laten, en alleen de bedragen op te tellen. Eigenlijk helemaal geen context, dus.
Deze vraag noemt een bedrag, daar gaat een ander bedrag vanaf (het wordt opgenomen). Wat moeten er dus met die twee bedragen gebeuren? Precies. De leerling moet wel weten wat het is om een bedrag van je spaarrekening op te nemen, maar verder doet de tekst van de vraag er niet toe, die kan straffeloos worden verwaarloosd.
Ook hier twee bedragen op verschillende tijdstippen. Het zal dus wel om het verschil gaan, dus moet het kleine bedrag van het grote worden afgetrokken (negatieve getallen zijn niet aan de orde). Het is iets lastiger, maar geen context waar een leerling over na hoeft te denken, zou ik denken. De figuur zit wat onoverzichtelijk in elkaar, zie wat Berends & Van Lieshout (2009) hierover te melden hebben.
Hier is sprake van een getal en nog een getal waar ‘ieder’ bij staat. Het gaat niet om verdelen, dan is het dus vermenigvuldigen.
Hier moet de leerling iets uitzoeken: die 17 moet keer iets, maar wat? In de figuur staat het gezochte tweede getal, een bedrag.
De leerling moet hier even opletten, maar getal en bedrag wijzen vanzelf de goede weg: het is niet vermenigvuldigen, maar delen.
Dit is een vervelende context, want de suggestie is dat het om een meetkundesom gaat. Eenmaal over de verwarring heen, wijst het woord ‘ieder’ feilloos de weg: de beide getallen op elkaar delen. Het kleinere op het grotere. Daar komt een mooi getal uit, dat is altijd geruststellend. Is het een fout wanneer de leerling alleen het getal als antwoord geeft, zonder erbij aan te geven dat het om vierkante meters gaat? Want dat is dan wel een verschil met de cijferopgaven: die werken met onbenoemde getallen, de contextopgaven met benoemde getallen. Dat was ook al het geval met de eerder zes contextopgaven: het zijn allemaal benoemde getallen. Zijn daar antwoorden fout gerekend wanneer de benoeming achterwege bleef?

Hickendorff vermoedt dat het uitblijven van een verschillend resultaat van contextopgaven versus cijferopgaven komt omdat leerlingen met dit type contexten geen moeite meer hebben. Dat kan ik me wel voorstellen, al was die laatste deelsom even wat lastiger. Maar dan. Waarom alleen kijken naar wel of geen context? Ik zie dat deze leerlingen bij deze eenvoudige opgaven enorm veel fouten maken: gemiddeld maar circa 71% goed. Als dat zo beroerd is, dan zal er ook wel een behoorlijke spreiding zijn? Ja hoor. Met de natte vinger: tweederde van de leerlingen scoort tussen 50% en 90% van de opgaven goed. Tjonge. Deze leerlingen mogen dan hun contexten kennen, afgaande op de resultaten die Hickendorff presenteert, maar hun rekenwerk lijkt te vaak nergens op. Zal ik de acht cijfersommen eens netjes onder elkaar zetten?

677,50 + 975 =
19,95 + 198,50 + 129 + 8,80 =
4020 - 787 =
3618,88 - 2923,95 =
37 × 24 =
26 × 20,1 =
864 : 36 =
5880 : 14 =

Waarom zegt Marian Hickdorff hier niets over? Elders in haar proefschrift misschien?

Als de verschillen tussen leerlingen zo enorm zijn, dan kan het niet missen of die verschillen correleren zwaar met verschillen in intellectuele capaciteiten, waaronder in ieder geval verschillen in capaciteit van het werkgeheugen. Die belasting van het werkgeheugen zal voor zwakkere rekenaars bovendien al gauw groter zijn wanneer zij hun basiskennis onvoldoende hebben geautomatiseerd en bij wijze van spreken nog op de vingers rekenen.

Nu zou het in een ideale wereld zo moeten zijn dat alle leerlingen in ieder geval hun eenvoudige rekenvaardigheid op een behoorlijk peil hebben aan het eind van de basisschool, laten we zeggen dat iedereen op deze eenvoudige rekensommen toch tenminste 70% goed moet kunnen maken. Vergissinkjes zullen er altijd zijn, evenals toetszenuwen, maar de spreiding voor leerlingen van groep acht zou toch in het gebied tussen 70% en 100% moeten liggen, in plaats van tussen 0% en 100%. Faalt het onderwijs dan, wanneer dit niet gehaald blijkt? Is dat met taalvaardigheid misschien hetzelfde probleem? Mijn collega’s van de taalgroep in het SCO-Kohnstamm Instituut hebben daar toch vaak de stormbal over gehesen.

Paul Hager, Allison Lee & Ann Reich (Eds.) (2012). Practice, Learning and Change. Practice-Theory Perspectives on Professional Learning. Springer. preview

Het idee is om literatuur zoals dit boek te benutten omdat het leren maken van contextrekenopgaven is te zien als een speciaal geval van dit praktijkleren. Wat zijn dan de verschillen en overeenkomsten? Wat valt uit deze bredere literatuur op te maken over wat het beheersingsplafond zou kunnen zijn voor contextrekenopgaven, en hoe sterk de persoonlijke verschillen kunnen zijn in dat beheersingsplafond?

Een uitstekend onderzoek, waar OCW als de bliksem opdracht voor zou moeten geven: naast de rekentoets-3F ook een toets op louter rekenvaardigheid afnemen. Onderzoekhypothese: bij gelijke rekenvaardigheid zullen er toch belangrijke individuele verschillen op de rekentoets-3F blijken. Een stap in deze richting is al gezet met de uitwerking door de commissie-Van de Craats van een rekentoets-3F, die bestaat uit een deel rekenvaardigheid, een deel contextrekenopgaven zonder rekenmachine, en een deel contextrekenopgaven met beschikbaarheid van een rekenmachine (zie hier). De bewindslieden hebben nog geen besluit bekend gemaakt of deze rekentoets-3F de rekentoets voor het vwo gaat worden.

1. Toetsen zijn voorbereidbaar, tests niet

Een allesbepalend principieel punt is dat kandidaten zich op toetsen en examens gericht moeten kunnen voorbereiden, en dat dat bij psychologische tests juist niet mogelijk moet zijn. Nogal wiedes, zult u denken, maar zo wiedes blijkt dat in de praktijk toch niet te zijn.

Een interessant onderscheid valt dan te maken tussen het rekengedeelte van de Eindtoets Basisonderwijs, en de rekentoetsen die bij de eindexamens in het vo en (v)mbo worden afgenomen. Hoewel de Eindtoets Basisonderwijs een toets heet te zijn, is hij bedoeld als diagnostische test om bij te dragen aan de kwaliteit van de beslissing over het vervolgonderwijs van de betreffende leerlingen.

Voorjaar 2013 is met handjeklap tussen bewindspersonen en kamerleden in een paar dagen tijd de functie van de Eindtoets Basisonderwijs veranderd naar evaluatie van het basisonderwijs o.i.d.

De rekentoetsen bij eindexamens zijn puur afsluitende toetsen, waar kandidaten zich dus doeltreffend op moeten kunnen voorbereiden.

Ben Wilbrink (1986). Toetsen en testen in het onderwijs. In S.V.O. Jaarverslag / Jaarboek 1985. Den Haag: S.V.O., 275-288. html

Er zijn belangrijke verschillen tussen tests (psychologische diagnostiek) en toetsen (prestaties, certificering) die maken dat we voorzichtig moeten zijn met de technieken uit het ene domein ook te gebruiken in het andere. Die voorzichtigheid ontbreekt bij belangrijke institutionele actoren zoals het Cito en het CvE. En bij veel psychometrici in het veld van examinering, hoewel A. D. de Groot en Robert van Naerssen al in 1970 de weg aangaven om toetsen in het onderwijs op hun eigen kenmerken te behandelen.

A. D. de Groot (1970). Some badly needed non-statistical concepts in applied psychometrics. Nederlands Tijdschrift voor de Psychologie en haar Grensgebieden, 26, 360-376. Didakometrisch en Psychometrisch Onderzoek, juni 1970. html

Toetsen en examens moeten voor leerlingen en studenten doeltreffend zijn voor te bereiden. Dat adagium sluit uit dat er wordt getest op verschillen in intellectuele capaciteiten.

Verschillen in intellectuele capaciteiten zijn natuurlijk wel van belang, maar spelen uit in het onderwijstraject voorafgaand aan de afsluitende toets of examen. Leerlingen die om welke redenen dan ook relatief minder begaafd zijn met intellectuele capaciteiten, kunnen dat compenseren door meer inspanning te leveren dan anderen doen, en/of tevreden te zijn met een juist voldoende prestatie waar anderen misschien streven naar hoge cijfers. Hierbeneden komt het studieresultatenmodel nog expliciet aan de orde.

Waar het uiteindelijk om gaat is dat het intellectueel capabeler zijn dan anderen als zodanig op het moment van toetsing geen verschil moet maken in behaalde resultaten. Bijvoorbeeld: de beschikbare tijd voor een toets is juist om die reden altijd voldoende ruim zodat alle deelnemers hun werk binnen die tijd kunnen afronden. Zou dat anders zijn, dan komt er een premie te staan op intellectuele capaciteiten, maar dat willen we juist bij examens voorkomen.

Job Cohen herformuleerde het adagium van De Groot: wat er zal worden getoetst moet voor de student kenbaar zijn: het kenbaarheidsbeginsel. Dit beginsel impliceert dat een toets of examen binnen de opgegeven stof blijft. Naar mijn smaak sluit dat niet uit dat er bij toetsvragen van contexten gebruik wordt gemaakt, maar een voorwaarde is dan dat nieuwe contexten de kandidaten in gelijke mate goed bekend moeten zijn.

Voor contextrekenopgaven is dan een eis dat verschillend scoren op zo’n opgave niet een gevolg mag zijn van verschillende bekendheid met de gebruikte context. Taligheid speelt hier eveneens mogelijk een rol: de scriptie van Van der Weegh (2005) hier; een context kan op zich goed bekend zijn, maar de formulering kan dan nog een belemmerende rol spelen.

Contexten van buiten de opgegeven leerstof blijven natuurlijk altijd problematisch. Contrasteer dat met contexten die nadrukkelijk wél binnen de opgegeven leerstof liggen. Een voorbeeld uit de grafische opleiding in de zestiger jaren: Van der Hulst en Reens.

Robert F. van Naerssen (1970). Over optimaal studeren en tentamens combineren. Openbare les. Amsterdam: Swets en Zeitlinger. html

Waar De Groot en Cohen het beginsel van transparantie respectievelijk kenbaarheid formuleerden, gaf Van Naerssen met zijn tentamenmodel in feite een eerste operationele uitwerking van dat beginsel van transparantie. De eenvoudige gedachte, geïnspireerd op de eerdere besliskundige verkenning van Cronbach & Gleser (1957/1965), was dat het bij het inrichten van toetsen en examens van belang is om uit te gaan van de strategische positie waarin de student zich bevindt in de aanloop naar de toets of het examen. Een meer complete uitwerking heb ik zelf gegeven in het SPA-model (Strategic Preparation for Achievement Tests).

Lee J. Cronbach & Goldine C. Gleser, G. C. (1957/1965). Psychological tests and personnel decisions. University of Illinois Press.

Vrijwel iedere toets- en examensituatie laat zich vangen in een helder besliskundig model voor de strategische positie van de kandidaat op enig moment voorafgaand aan de toets. Dat maakt het model geschikt om te gebruiken bij het evalueren van de transparantie of kenbaarheid van toetsen en examens.

Jantine van der Weegh (2005). Schooltaalvaardigheid en realistisch rekenen: specifiek taalkundige moeilijkheden en de invloed op het begrijpen van realistische rekenopgaven. Doctoraalscriptie, Utrecht. [Geen online versie beschikbaar. Heeft waarschijnlijk iets te maken met dit NWO-project: abstract, maar het gaat bij Van der Weegh om een andere leeftijdscategorie dan 3- tot 6-jarigen. ]

Dit scriptieonderzoek, onder supervisie van Paul Leseman en Hans van Luit, laat zien dat taalproblemen de uitkomsten van rekentoetsen sterk kunnen beïnvloeden. Ondanks alle beperkingen van een enkel scriptieonderzoek — maar deze kreeg de NVO-scriptieprijs 2006 — zijn die uitkomsten verontrustend.

Zie ook deze powerpointtekst van Paul Leseman over schooltaalvaardigheid: html of html

Impliciet in het kenbaarheidsbeginsel besloten is uiteraard dat kenbaarheid een gradueel kenmerk is, en dat het niet zo mag dat zijn dat een toets voor de ene groep minder kenbaar is dan voor de andere. Dit is het algemeen geaccepteerde beginsel dat toetsvragen en toetsen niet partijdig mogen zijn (Engelse term: geen bias). De thematiek van deze webpagina draait dan ook rond de stelling dat voor toetsen in het onderwijs geldt dat er ook sprake is van partijdigheid wanneer verschillen in intelligentie bij het maken van de toets — bij de toetsafname — een rol spelen.

2. Rekenvaardigheid is voor iedere leerling bereikbaar

Het gaat hier om twee onderscheiden zaken: dat rekenvaardigheid een trainbare vaardigheid is, en dat rekenvaardigheid iets anders is dan denkvermogen. Ik begin hier met een historisch uitstapje naar de jaren waarin er een sterke koppeling werd gelegd tussen rekenen en denkvermogen, en er bijvoorbeeld voor de toelating tot het VHMO rekentests werden gebruikt om dat denkvermogen te testen. Ik verwacht aan de hand van het beschikbare materiaal (dat ik zal scannen en hier beschikbaar stellen) een glashelder contrast te kunnen maken tussen rekenen en denkvermogen. Tot de thematiek van deze paragraaf hoort dan ook dat dat denkvermogen niet iets is waar iedere leerling op kan excelleren, mits voldoende getraind. Er zijn enkele publicaties waarin dezelfde ‘denksommen’ zijn voorgelegd aan verschillende groepen leerlingen, of aan verschillende klassen, en waar dan prachtig een stijgende lijn is te zien die ongetwijfeld wel iets met het genoten onderwijs heeft te maken maar overigens toch vooral een kwestie van ontwikkeling is. Ik moet eraan denken hier een parallel te trekken met ‘echte’ inteligentietests, waar normtabellen op leeftijd worden gehanteerd, juist om die natuurlijke ontwikkeling eruit te filteren.

Om met het onderscheid tussen rekenvaardigheid en denkvermogen te beginnen: het psychologische onderscheid is dat tussen procedurele en declaratieve kennis. Rekenvaardigheid betreft procedurele kennis. Redeneervermogen gaat over declaratieve kennis. Dat laatste is nog tot daaraan toe als het kennis is die tot het vak hoort, maar vaak is met dat redeneervermogen iets bedoeld dat juist niet is gebonden aan vakinhoudelijke kennis. Merkwaardig is dat het werk van George Polya in deze context vaak wordt aangehaald; en dat is merkwaardig omdat het probleemoplossen van Polya bij uitstek gebruik maakt van vakinhoudelijke kennis, juist niet van contexten die uit het dagelijks leven zijn gegrepen.

Turkstra (1957) gaf in een artikel in Euclides in de vijftiger jaren al uitstekend het onderscheid aan, in de vorm van een onderscheiden toets op rekenvaardigheid en test op denkvermogen van eersteklassers, zie de annotaties bij zijn artikel. De betere denkertjes zouden het later op school ook beter blijken te doen. Dat laatste is een gevaarlijke uitspraak, Turkstra geeft geen emprische onderbouwing, maar er zal best wel iets van waar zijn. Het is ook gevaarlijk omdat er zoveel andere belangrijke factoren zijn die succes in schoolvakken mede bepalen. Hoe dat ook zij, Turkstra heeft een enorme ervaring met rekenopgaven die redeneervermogen enzovoort moeten testen, zie zijn zeer gedetailleerde rapporten 1940, 1942 en 1952 over toelatingstests met rekenopgaven.

Een toelatingstest is totaal iets anders dan een eindexamentoets zoals de rekentoets-3F. De werkgroep is daar waarschijnlijk heel helder over: de test Rekenen II moet de intellectuele capaciteiten van de kandidaten voor de H.B.S. op de proef stellen, niet hun technische rekenvaardigheid beproeven. Het interessante van dit materiaal is dat het laat zien wat in de overtuiging van deze werkgroep vragen zijn die testen op persoonlijke kenmerken, niet hoe de betreffende kandidaten in hun lager onderwijs hebben leren rekenen. Ik verwacht interessante overeenkomsten tussen tussen wat in deze toelatingstest van 12-jarigen wordt gevraagd, en wat in de Cito-voorbeeldtoets-3F wordt gevraagd van bijvoorbeeld 17-jarigen in havo en vwo. Ook wanneer zou blijken dat die overeenkomsten er niet zijn, valt er veel van te leren. Het jaar 1939 lijkt heel ver weg, maar dat is het natuurlijk niet: mijn eigen proefklas voor het gymnasium was in 1956 (een rekentestje werd individueel mondeling afgenomen door de rector); aan de toelating tot de Chr. HBS in Apeldoorn, deelnemer in het experiment van de werkgroep, hebben mogelijk familieleden deelgenomen. Het rekenonderwijs dat ik op de lagere school heb gehad, moet in hoge mate gelijk zijn geweest aan dat in de dertiger jaren (en werd in de derde en vierde klas door waarschijnlijk dezelfde onderwijzers verzorgd, Polman en De Boer).

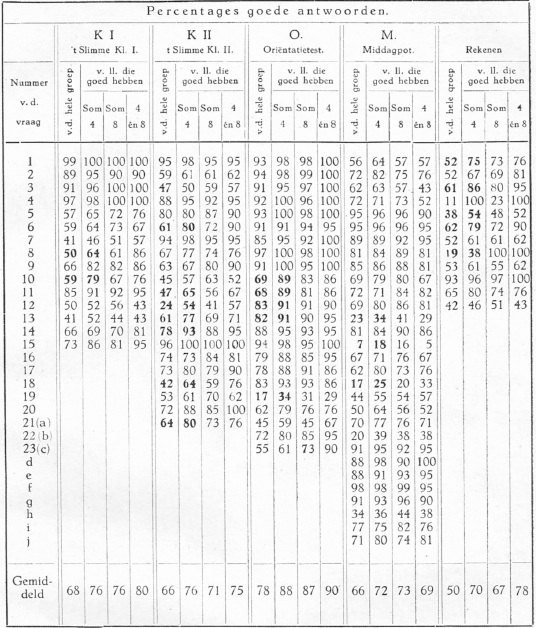
W. H. Brouwer, I. C. van Houte & P. Post (1948). Het meisje van 12 tot 14 jaar. Een onderzoek naar de prestaties van leerlingen der eerste klasse van de Primaire Opleiding aan Nijverheidsscholen voor Meisjes. Mededelingen van het Nutsseminarium voor Paedagogiek aan de Universiteit van Amsterdam No. 42. Wolters' Uitgeversmaatschappij. Vervolgonderzoek 1951, Mededelingen nr 51. scans blz. 1-102 en scans blz. 103-202

. In dit onderzoek een typische test-benadering, met onder andere rekenopgaven (zie de box). Over de beantwoording van deze vragen bevat de publicatie talrijke details, ook van groepen zesdeklassers. Met niet echt informatieve foutenanalyses.

Dit zijn natuurlijk extreme vragen die testen op nauwkeurig lezen en nog zo wat zaken. Er wordt nauwelijks getest op rekenvaardigheid als zodanig, en dat is ook niet de bedoeling. In de rekentoets-3F verwacht ik geen vragen zoals ze in bovenstaande box zijn te zien. Een vraag die veronderstelt dat de leerling weet dat augustus 31 dagen heeft, hoort in een rekentoets niet thuis; maar er is hier natuurlijk geen scherpe scheidslijn tussen wereldkennis die maar weinig leerlingen tot hun beschikking hebben, en wereldkennis die als algemeen aanwezig mag worden verondersteld. Zo is het ook met de leeftijd van de timmerman, een type vraag dat tegenwoordig vooral bekend is als die naar ‘de leeftijd van de kapiteit’, gegeven dat hij 27 schapen en een geit vervoert, o.i.d. Vraag 2, over Piet en zijn broers en zussen, zal in deze vorm niet in een rekentoets-3F voorkomen, maar een variant waarin leeg blijvende plaatsen in een bus toch moeten worden meegeteld (1128 leerlingen gaan op schoolreis . . . ) zou er zomaar tussendoor kunnen glippen. Vraag 4 lijkt een regelrechte rekenopgave, maar de resultaten laten zien dat het een strikvraag blijkt: percentages goed zijn schrikbarend laag, zie de bovenstaande figuur. Vraag 4 en 8 geven de onderzoekers aanleiding om te kijken hoe de groep leerlingen die 4 en/of 8 goed beantwoorden, het op de andere vragen in dit onderzoek doen, vergeleken met de totaalresultaten, zie de figuur hierbeneden. Een grappige manier van analyseren, maar wel behoorlijk omslachtig.

A. H. van der Hoeve, Ph. Kohnstamm & G. van Veen (1935). Stil-lees-stof als denk-materiaal en denk-maatstaf. Een onderzoek aangaande de vorming en toetsing van 'theoretische intelligentie'. J. B. Wolters' Uitgeversmaatschappij. Mededelingen van het Nutsseminarium voor Paedagogiek aan de Universiteit van Amsterdam No. 24. [aanwezig: KB; UB Leiden in de reeks Mededelingen van het Nutsseminarium] scan p. 0-57 22Mb - [geen scan van 58-107] - 208-245 - 246-261 - 262-288

Extreme denksommen (Bijlage VII), in dit onderzoek uit 1935 gebruikt. De onderzoekers noemen het rekenen, en relateren de resultaten op deze ‘rekenopgaven’ aan de resultaten op de taalopgaven (vooral tekstbegrip).

Met vaardigheden is het in het algemeen zo gesteld dat met adequate inspanningen daar altijd een voldoende hoog niveau in valt te bereiken. Heel hoge niveaus kosten buitenproportioneel veel inspanning; het zal dus zelden gaan om vaardigheidsniveaus van bijna 100% correct.

Geldt voor rekenvaardigheid hetzelfde als voor andere vaardigheden? Jazeker, waarom niet? Probleem is dat in de reformdidactiek wereldwijd aan rekenen en wiskunde surplus-betekenissen zijn toegekend die bepaald grensoverschrijdend zijn op het punt dat hier bijzondere taken voor het onderwijs zouden liggen. Zie bijvoorbeeld de inleidende alinea in de sectie ‘Wiskunde’ in het SLO-rapport (2011) over de PISA-test, bizar hoogdravend proza. Welke professionele wiskundige voldoet aan deze beschrijving? We hebben het over scholieren, pubers nog, van 15 jaar.

Wilmad Kuiper, Monique van der Hoeven, Elvira Folmer, Marja van Graft & Jan van den Akker (2010). Leerplankundige analyse van PISA-trends. SLO. pdf

Let op hoe in onderstaand citaat het zicht zoek is op het onderscheid tussen kennis en vaardigheden die het onderwijs kan bijbrengen, en verschillen in intellectuele capaciteiten waarbij het onderwijs geen of slechts een bescheiden rol heeft. Hier gaat het alleen om het voorbeeld van deze specifieke onderwijsideologie; in volgende secties zal een en ander nog uitgebreid aan de orde komen.

Ik worstel nu al een jaar met proza van dit type, dat ook kenmerkend is in promotie van ‘vaardigheden van de 21e eeuw’. Het gaat hier om een pseudopsychologie die nauwelijks enige relatie heeft met de actuele cognitieve psychologie (John Anderson en ACT-R; Stellan Ohlsson, 2011). Jan van den Akker, directeur SLO, weet dat ongetwijfeld goed.

Voor de helderheid is het goed om te beginnen met het onderscheid tussen het opstellen van rekenmodellen bij gegeven probleemsituaties, en het rekenen zelf. Moeten we het kunnen opstellen van rekenmodellen rekenen tot de vaardigheid zelf, of gaat dat (veel) te ver? Diverse auteurs, zoals ook de toetswijzercommissie-3F van OCW (commissie-Schmidt), gebruiken een technisch jargon dat verwijst naar probleemoplosschema’s zoals die vaak worden toegeschreven aan George Polya. Maar dan zijn we toch wel ver van huis, wat rekenen betreft. En dat blijkt ook wel: in de discussies over rekenonderwijs dreigt het rekenen zelf te worden overschaduwd door wenselijkheden op het punt van probleemoplossend rekenen in contexten, door sommigen ook wel functioneel rekenen genoemd (hoewel die term in het verleden ook voor andere zaken is gebruikt).

Ik wil in de cognitief-psychologische onderzoekliteratuur, dus op neutraal terrein wat de rekenoorlogen betreft, aanwijzingen zoeken over hoe het onderscheid valt te trekken tussen zoiets als rekenvaardigheid en de totaal andere vaardigheid van het opstellen van rekenmodellen bij gegeven probleemstelling. Laat ik het zo ook maar noemen: probleemstellingen, in plaats van contextrekenopgaven.

Dit is een spiegelpaleis. In zogenaamd realistische contexten (uit het dagelijks leven gegrepen: op vacantie, bij de kruidenier, in de uitverkoop; niet in de eigen beroepscontext of in de context van een zaakvak zoals natuurkunde) worden rekenproblemen gesteld. Daar zit dus een enorme spanning in. Op zijn minst moet de leerling als tussenstap een rekenmodel opstellen dat past bij het opgegeven probleem. Hoeveel vrijheid heeft de leerling eigenlijk om zo’n model op te stellen? Of is alleen het model goed zoals de ontwerper van de vraag dat heeft bedoeld?

Allen Newell and Paul S. Rosenbloom (1981). Mechanisms of skill acquisition and the law of practice. In John R. Anderson: Cognitive skills and their acquisition (1-56). Erlbaum. report pdf, zie ook leren.htm

David M. Neves and John R. Anderson (1981). Knowledge compilation: mechanisms for the automatization of cognitive skills In John R. Anderson: Cognitive skills and their acquisition (57-84). Erlbaum. pdf ophalen, zie ook leren.htm PM. Het voorgaande noemt wat oudere literatuur. Ik zal deze nog vervangen of aanvullen met recentere literatuur. De lezer die ongeduldig is, kan zelf googelen (Google Scholar) naar later onderzoek dat terugverwijst naar deze publicaties.

Een bijzondere complicatie bij woordproblemen is dat leerlingen vaak maar moeten gissen naar wat de bedoelingen van de vragensteller zijn. Een overbekend en berucht voorbeeld is het busprobleem: er moeten 1128 of zo supporters, leerlingen, whatever, worden vervoerd in bussen met plaats voor 60 passagiers. Hoeveel bussen zijn er nodig? Een variant op deze vraag is ooit eens afgenomen in de Amerikaans NAEP-test, met treurige resultaten wat betreft de juistheid van de geven antwoorden. Maar ja, wie bepaalt wat hier een correct antwoord is? Omdat er geen fracties van bussen bestaan waarmee passagiers zijn te vervoeren, worden niet naar boven op een heel aantal afgeronde antwoorden fout gerekend. Ik vind dat wel opmerkelijk. Leerlingen die in de veronderstelling zijn een rekentest af te leggen, zullen immers geneigd zijn het exacte resultaat van de gevraagde deling als antwoord te geven, de autobusdienstleider maakt daar wel netjes hele bussen van. De vragensteller gaat dan God spelen, en verordonneert dat een niet geheel getal geen juist antwoord kan zijn. Maar dit is een semantisch spel, en geen kwestie van rekenvaardigheid. Lieven Verschaffel c.s. (2000) bespreken dit casus eveneens, maar als ik mij goed herinner komen zij evenmin met een bevredigend antwoord. Zie ook mijn Toetsvragen ontwerpen, hoofdstuk twee, waar ik Millman citeer over dit casus.

Verschaffel, L., De Corte, E., & Lasure, S. (1994). Realistic considerations in mathematical modeling of school arithmetic word problems. Learning and Instruction, 4. 273-294. abstract

Carpenter, T. P., Lindquist, M. M., Matthews, W., & Silver, E. A. (1983) Results of the third NAEP mathematics assessment: Secondary school. Mathematics Teacher, 76,652-6.59. read online

De Corte, E., Greer, B., & Verschaffel, L. (1996). Mathematics teaching and learning. In D. Berliner & R. Calfee (Eds.), Handbook of educational psychology (491-549). New York: Macmillan. abstract “ . . . the conception of mathematics as a human activity embedded in historical, cultural, social, and experiential contexts . . . ” [Uitgesproken Freudenthal, dus; constructivistisch; ik heb deze tekst nog niet gezien?]

PM. Lieven Verschaffel en zijn collega’s hebben het nodige onderzoek naar woordproblemen gedaan, en in het bijzonder ook het opstellen van rekenmodellen als afzonderlijke stap bij het oplossen beschreven en onderzocht. Ik zal deze literatuur nog opzoeken. Zie anders het literatuurbestand wordproblems.htm op deze website.

Alan H. Schoenfeld (2006). Mathematics teaching and learning. In Patricia A. Alexander & Philip H. Winne : Handbook of Educational Psychology (479-511). second edition (reprint 2009). Routledge [als eBook te leen bij de KB]

Liping Ma (1999/2010). Knowing and teaching elementary mathematics: Teachers' understanding of fundamental mathematics in China and the United States. Erlbaum. [als eBook in KB te leen] reviewed door Roger Howe, 1999, in Notices of the AMS

3. Resultaat = combinatie van capaciteit en inspanning

Een voldoende prestatie is te bereiken door een geschikte combinatie van intellectuele capaciteiten en inspanning (=tijdbesteding).

Wanneer een toets zo is ingericht dat verschillen in capaciteiten mede bepalend zijn voor het resultaat, dan is dat een bewijs dat de toets niet transparant is: het kenbaarheidsbeginsel is geschonden.

Om het denken over verschillen in studieresultaten te ondersteunen gebruik ik grgaag de onderstaande figuur, oorspronkelijk gebruikt in een ORD-paper met Dick Tromp (1977) html.

De relatie tussen tijdbesteding en studieresultaten is natuurlijk dat leerlingen die meer tijd investeren een beter studieresultaat mogen verwachten (dan anderen, als andere omstandigheden gelijk zijn). Of leerlingen meer tijd willen besteden, hangt ervan af of hun actuele verwachting een lager cijfer is dan wat zij willen bereiken: het streefniveau speelt hier een rol. Wie gaat voor juist voldoende, wie voor een hoger cijfer? Het streefniveau van leerlingen zal mede afhangen van eigen talenten en voorkennis; omdat we die praktisch gesproken als een gegeven moeten zien, heten dit exogene variabelen. Voor transparante toetsing mag de eis dan zijn dat intellectuele capaciteit (een exogene variabele) wel van invloed is op het streefniveau en op de tijd die nodig is om dat streefniveau te realiseren, maar niet direct op het studieresultaat zelf. In termen van padanalyse: de pad-coëfficiënt van exogene variabelen naar studieresultaten moet nul zijn wil er sprake zijn van transparante toetsing.

Een eenvoudig padmodel zoals dit is met de hand uit te rekenen, als er geschikte empirische gegevens zijn. In het ORD-paper is dat beschreven en toegepast op een dataset van Everwijn en Willemsen, de uitkomst is als volgt:

In bovenstaande figuur hebben verschillen in intellectuele capaciteiten maar een geringe directe invloed op het toetsresultaat, en eveneens een geringe indirecte invloed via streefniveau en tijdbesteding. Het hele model is zwak: verschillen in studieresultaten worden hier vooral niet voorspeld uit verschillen in capaciteiten, streefniveau en tijdbesteding. Maar daar gaat het niet om; de dataset is alleen ter illustratie gebruikt.

Voor een rekentoets-3F bij het eindexamen-vwo mag op basis van het kenbaarheidsbeginsel verlangd worden dat verschillen in resultaat op de rekentoets niet direct samenhangen met verschillen in intellectuele capaciteiten. Er mag natuurlijk wel samenhang zijn via indirecte paden over streefniveau en tijdbesteding. Merk op dat de illustratieve analyse hierboven de invloed van verschillen in intellectuele capaciteiten op verschillen in tijdbesteding ongeveer nul is: het directe pad is -.05, het indirecte pad over verschillen in streefniveau is .17 × .27 is ongeveer .05. In het algemeen geldt voor onderzoek naar studieresultaten dat allerlei verbanden die men op basis van ervaring en gezond verstand zou verwachten, vaak maar zwak zijn of geheel afwezig. In dit geval gaat het om het eerste tentamen in de propedeuse, en dan is het voor veel studenten relatief lastig om in te schatten of ze voor het tentamen goed genoeg zijn voorbereid.

Gebruik dit eenvoudige modelletje om toch gestructureerd na te kunnen denken over toetssituaties. Bijvoorbeeld: wat gebeurt er wanneer het streefniveau van studenten erbuiten wordt gelaten? Waarschijnlijk zien we dan dat de directe samenhang tussen tijdbesteding en studieresultaat zwakkeer is. Dat betekent niet dat het er voor het studieresultaat niet toe doet of er wat langer wordt gestudeerd of niet! Maar wel dat begaafde studenten met een hoog streefniveau relatief weinig tijd nodig hebben om dat niveau te realiseren.

Er is een rijke literatuur over toetsmodellen en empirisch onderzoek daarover. Die literatuur zegt ons iets over de situatie die nu door de overheid en door het Cito is gecreëerd met de rekentoetsen in het vo, en de wijze waarop deze mede de eindexamenuitslag gaan bepalen.

Martin V. Covington (1992). Making the grade: a self-worth perspective on motivation and school reform. Cambridge University Press. info

Ondertussen gedateerd, ik zal dat nog actualiseren. Covington gaat het vooral om de motivatie van leerlingen, maar omdat hij daarbij onderscheid maakt naar talent en inspanning, leveren zijn onderzoeken daar interessante informatie over.

Martin V. Covington (2000). Goal Theory, Motivation, and School Achievement: An Integrative Review. Annual Review of Psychology, 51, 171-200. abstract

4. Iedereen moet kunnen slagen bij eerste gelegenheid

Meteen maar een onderzoek dat laat zien waar het om gaat. Dit is gedaan met kinderen in klas 2, 3 en 4, dat zijn jongere kinderen dan de 17- en 18-jarigen waar het bij de rekentoets-3F om gaat. Let erop dat het gaat over verschillen tussen leerlingen, zoals ook bij de problematiek van de rekentoets-3F juist de verschillen tussen leerlingen voortdurend aan de orde zijn.

Xinhua Zheng, H. Lee Swanson & George A. Marcoulides (2011). Working memory components as predictors of children's mathematical word problem solving. Journal of Experimental Child Psychology 110 (2011) 481-498 abstract

H. Lee Swanosn (2011). Working memory, attention, and mathematical problem solving: A longitudinal study of elementary school children. Journal of Educational Psychology, 103, 821-837. abstract

Voor de verschillende examens spelen onderscheiden problematieken. Zo zijn er binnen het vmbo enorme verschillen, waar het CvE in zijn wijsheid op heeft bedacht dat de beoordeling van de rekenprestaties voor vmbo-t strenger zal zijn dan voor voor de andere vmbo-opleidingen. Het CvE voelt nattigheid, weet niet precies wat nu eigenlijk het probleem is, en kiest een twijfelachtige oplossing door niet het onderliggende probleem weg te nemen — dat er wordt getest op verschillen in intellectuele capaciteiten — maar de gevolgen ervan met een kunstgreep te verdoezelen. [zie de WiskundE-brief voor details en bronnen]

Voor de helderheid spits ik de uiteenzetting toe op de situatie voor het eindexamen van het vwo. Zolang OCW nog geen beslissing heeft genomen over de rekentoets-3S, moeten we aannemen dat de rekentoets-3F gehandhaafd blijft. De wet verwijst voor een en ander naar de referentieniveaus (Nederlandse taal) en rekenen, zoals geformuleerd door de commissie-Meijerink. Dat mag zo zijn, maar commissies en wetgevers zijn niet feilloos. In de mate waarin die referentieniveaus grensoverschrijdend zijn wat rekenvaardigheid betreft, mogen ze natuurlijk niet bepalend zijn voor de inhoud van een eindexamen-rekentoets-3F. Bijvoorbeeld omdat wereldkennis, woordenschat, werkgeheugen en nog zo het een en ander aan verschillen in intellectuele capaciteiten verhinderen dat leerlingen zich het rekenen-volgens-Meijerink zo goed kunnen eigen maken dat zij met redelijke zekerheid bij eerste gelegenheid voor hun rekentoets kunnen slagen.

5. Pilots 2012 en 2013: het regent ‘onvoldoendes’

De uitslagen van de pilots 2013 zjn op de betreffende scholen natuurlijk al wel bekend, maar de landelijke cijfers heb ik nog niet gezien. Mogelijk moeten die eerst over de burelen van de bewindspersonen op OCW voordat ze voor publicatie vrij worden gegeven.

Hoe komt eigenlijk die grens tussen een vijf en een zes tot stand, voor de rekentoets-3F? De methode van het Cito, met instemming van het CvE, is om een aantal mensen tot ‘deskundigen’ te benoemen, ze het nodige nattevingerwerk te laten doen, en dan te redeneren dat die lammen en blinden elkaar gemiddeld genomen toch naar het bedoelde eindpunt kunnen leiden. Niet, dus, maar wie is daar verder nog in geïnteresseerd? Nou, veel leraren zijn waarschijnlijk toch wel benieuwd hoeveel vertrouwen ze in deze cijfer-alchemie kunnen stellen. Voor een kritische beschouwing zie de WiskundE-brief 621 en een uitvoeriger behandeling heb ik hier gegeven [het is nog ‘werk in uitvoering’, maar ja, de werkopdrachten buitelen nu wel heel erg over elkaar heen . . . . ]

Als hieruit het idee ontstaat dat het Cito en het CvE hier hun eigen ding doen, technocratisch en autoritair, vanuit een stevige kokervisie, zonder bekommernis om de samenleving of over wat eigenlijk de plaats van het onderwijs in die samenleving en in het leven van individuele leerlingen is, als dat het idee is dat uit het bovenstaande ontstaat, dan is dat terecht. We hebben hier te maken met een ethische problematiek van jewelste.

e) de pilots in 2012 en 2013 [de uitslagen 2013 zijn nog niet bekend, maar zullen weinig anders zijn dan in 2012] hebben laten zien dat er schrikbarende percentages onvoldoendes zijn, en grote systematische verschillen tussen bijv. havisten en vwo-ers (de bewindslieden zijn zich rot geschrokken en hebben het meetellen van de rekentoets voor de uitslag van het examen twee jaar uitgesteld)

6. Pilots 2012 en 2013 wijzen op karakter van intelligentietest

Wie tabellen ziet met gemiddelde resultaten in de verschillende schoolsoorten, kan niet anders dan vermoeden dat verschillen in intellectuele capaciteiten hier toch wel een stevige rol in moeten spelen.

Ik zal enige sleutelpublicaties toevoegen die laten zien hoe rekenopgaven aanspraak doen op de strikt beperkte capaciteit van het werkgeheugen (o.a. onderzoek in de lijn van Ashcraft) en daarmee dus al gauw als resultaat zullen laten zien dat leerlingen met een minder capaciteit om die reden slechter scoren dan leerlingen met meer capaciteit (span), als bijvoorbeeld op zich de rekenkennis en geoefendheid wel gelijk zijn.

Ook bij zeventien- en achttienjarigen hebben we nog te maken met verschillen in hersenontwikkeling. Bij contextrekenopgaven kunnen die verschillen gewicht in de schaal leggen. Er is ongetwijfeld in de cognitief-psychologisch onderzoekliteratuur materiaal voorhanden dat hier uitsluitsel over geeft. Als dat materiaal er is, dan valt er ook iets te zeggen over de eerlijkheid van de rekentoets-3F in dit licht.

Het algemene punt is dat een rekentoets-3F die zo zwaar is aangezet dat ze zelfs meegaat in de kernvakkenregel voor het eindexamen, niet mag discrimineren op intellectuele capaciteit of leeftijd/ontwikkeling.

f) de uitslagen van de pilots maken het aannemelijk dat de rekentoets inderdaad vooral op verschillen in intellectuele capaciteiten test (anders zouden havisten en vwo-ers vrijwel gelijk moeten kunnen presteren)

7. Rekentoets-3F: rekenvaardigheid is ondergeschikt gemaakt

In de tachtiger jaren deed Twijnstra Gudde een onderzoek voor de opleiding neerlandistiek in Leiden, naar de aansluiting op de arbeidsmarkt. Zij constateerden dat werkgevers belang hechtten aan schriftelijke en mondelinge uitdrukkingsvaardigheden, en adviseerden dat het ‘dus’ belangrijk was om in de opleiding neerlandistiek meer aandacht aan die uitdrukkingsvaardigheden te besteden. De opleiding neerlandistiek! Dat had de onderzoekers toch moeten waarschuwen voor een mogelijke begripsvernauwing. Denk er nog eens over na, lees het nog eens terug. In de box hierbeneden een verdere verduidelijking.

Hetzelfde mirakel hebben we aan de orde met rekenvaardigheid en ‘contexten’. In de reformrekendidactiek wordt het rekenen-in-contexten benadrukt, ten koste van het ontwikkelen van die rekenvaardigheid zelf. Het zou zomaar kunnen dat ‘functioneel rekenen in situaties in het dagelijks leven’ allereerst rekenvaardigheid betreft, en pas in tweede instantie allerlei andere factoren zoals verschillen in intellectuele capaciteiten van de actoren, maar ook verschillen in situaties in de mate waarin correct rekenen er werkelijk toe doet, enzovoort. Empirische kwesties. Daar moet onderzoek naar worden gedaan om te voorkomen dat een hoogdravende rekendidactiek het onderwijs kan misvormen. Dat onderzoek is destijds dus achterwege gelaten, en wel bewust achterwege gelaten (lees uitspraken van Hans Freudenthal, directeur IOWO in de zeventiger jaren).

De sleutel is getalbegrip. Onderzoeken waaruit blijkt dat gebrekkig getalbegrip diepe sporen in het menseleven kan trekken op het gebied van gezondheid en financiën. Onafhankelijk van (gecorrigeerd voor) verschillen in intellectuele capaciteiten en maatschappelijke achtergrond. Getalbegrip is natuurlijk basaler dan rekenvaardigheid zelf. Het onderwijs is allesbepalend voor dat getalbegrip, moet ik aannemen. In de mate waarin mensen in hun leven nadeel ondervinden van hun gebrekkige getalbegrip, zou het onderwijs hierin tekort kunnen zijn geschoten.

Dichter bij het onderwijs zelf blijft onderzoek zoals van Siegler c.s. (2011), dat laat zien dat de kwaliteit van het breukenonderwijs mede bepalend is voor latere prestaties van leerlingen in de wiskunde van het vo, maar ook voor de mate waarin zij later kiezen voor wiskundige schoolvakken.

Merk op dat in genoemde onderzoeken het gaat om tekorten in getalbegrip, niet om tekorten in zoiets als ‘functioneel getalbegrip in alledaagse situaties’. Een andere manier om hetzelfde uit te drukken is gewoon dat het gaat om kletspraat van reformdidactici. Kletspraat is wat wordt beweerd zonder enige feitelijke grond.

Onderzoek van Ashcraft en anderen doet mij vermoeden dat er een ernstig probleem kan schuilen in het gebruik van rekenmachinegetallen in de rekentoetsen-3F. En wel in deze zin dat zij leerlingen dwingen tot handelingen die een groot beslag doen op het werkgeheugen, waar het werken met eenvoudige getallen het juist mogelijk maakt dat leerlingen geautomatiseerde kennis kunnen gebruiken, dus met een gering beslag op het werkgeheugen. Dat beslag op het werkgeheugen is des te belangrijker wanneer het gaat om probleemstellingen (contextopgaven) in plaats van alleen maar rekenopgaven.

Een afzonderlijk punt van zorg is het toegestane gebruik van de rekenmachine. Dit probleem raakt niet direct aan de stelling dat deze rekentoets-3F vooral verschillen in intellectuele capaciteiten meet. Maar wel aan de keerzijde van die stelling: meet de rekentoets-3F eigenlijk wel rekenvaardigheid, als het gebruik van een rekenmachine is toegestaan en de getallen in de contextopgaven vaak zo zijn gekozen dat gebruik van die rekenmachine wel heel aantrekkelijk is? Dat kunnen we niet weten, tenzij de door het Cito gebruikte software registreert of en zo ja hoe die rekenmachine bij welke opgaven is gebruikt.

Is dit een belangrijke zaak? Dat zou ik wel denken. Bij de motie Dijkgraaf-Van der Ham in de Tweede Kamer heeft de minister zich laten adviseren door het CvE en de SLO. Het advies van het CvE blinkt uit door het ontbreken van enig besef dat een stevige stellingname wel enige onderbouwing behoeft die de toets van wetenschappelijkheid kan doorstaan. Het advies van de SLO doet daar weinig voor onder, maar heeft wel de verdienste dat er de commentaren van een reeks van deskundigen (standpunten zowel pro als contra!) aan zijn toegevoegd.

g) de opgaven in de rekentoets-3f zijn vooral ‘contextopgaven’, waarin het rekenen zelf eigenlijk ondergeschikt is, zeker waar dat met de rekenmachine gebeurt (en de getallen zijn vaak opzettelijk zo gekozen dat de leerlingen alleen al daarom zeker naar die rekenmachine zullen grijpen)

8. Technocratisch dictaat van de psychometrie

Is een verwijt aan de psychometrie wel terecht? Hierboven zijn toch voorbeelden gegeven van vooroorlogse rekentoetsen die onverbloemd pretenteerden te testen op denkvermogen of verschillen in intellectuele capaciteiten? Jazeker, maar hier was juist de psychometrie van de eerste decennia van de vorige eeuw het voorbeeld waarnaar werd gehandeld. Het opmerkelijke feit doet zich nu voor dat de psychometrische zienswijze op de onderwijswereld over de laatste eeuw in wezen niet meer is veranderd.

In de veldraadpleging voor de rekentoets-3S (commissie-Van de Craats zie hier) heb ik erop gewezen dat een geslaagde rekentoets een betrouwbaarheid van nul zou moeten hebben. Immers: voor de rekentoets volstaat het om te laten zien dat de leerlingen rekenvaardig zijn, ongeveer hetzelfde niveau hebben. Snelheid van werken mag geen invloed hebben op het resultaat op de rekentoets. Nauwkeurigheid van werken mag dat, binnen redelijke grenzen, ook niet. In deze situatie blijft er natuurlijk wel enige spreiding van scores, maar die spreiding moet vrijwel gelijk zijn aan wat verwacht mag worden bij een streekverdeling geconditioneerd op dezelfde mate van beheersing. In beginsel geldt dit ook voor een verschil tussen mbo-, havo- en vwo-kandidaten op de rekentoets-3F, en vmbo-kandidaten op de rekentoets-2F.

Het Cito gaat volkomen anders tewerk. In diverse reacties van het Ciito op kritiek uit de samenleving op bijvoorbeeld de spellingtoetsen voor het basisonderwijs (Bosman), wordt steevast benadrukt dat de toetsen heel betrouwbaar zijn en dat alles dus in orde is. Ik chargeer, maar het punt is dat in de Cito-ideologie evoor zal worden gezorgd dat de betrouwbaarheid van Cito-toetsen hoge waarden heeft. Daar is natuurlijk geen bezwaar tegen wanneer de aard van de toets en de toetssituatie dusdanig is dat een hoge betrouwbaarheid mag worden verlangd. Het springende punt is dat toetsen en toetssituaties niet vanzelfsprekend een dergelijk karakter hebben, en dat het Cito daar geen aandacht aan besteeedt. Met andere woorden: ook in situaties waarin het onderwijs ernaartoe heeft gewerkt dat alle leerlingen een behoorlijk niveau van rekenvaardigheid hebben behouden, zal het Cito met zijn rekentoetsen proberen om de verschillen tussen die leerlingen uit te vergroten. En dat gaat altijd lukken, want rekenopgaven kunnen zo worden ontworpen dat ze aanspraak doen op verschillen in capaciteit van het werkgeheugen, enzovoort enzoverder. Onderstaand onderzoek van Berends en Van Lieshout (2009) geeft een illustratie hoe gebruik van afbeeldingen bij opgaven kan leiden tot mentale overbelasting bij sommige leerlingen, waaruit mijns inziens mag worden geconcluderd dat toevoegen van afbeeldingen een techniek kan zijn waardoor rekenopgaven niet alleen moeilijker worden gemaakt, maar ook partijdiger voor leerlingen die kwetsbaarder zijn waar het gaat om mentale overbelasting.

Inez E. Berends & Ernest C.D.M. van Lieshout (2009). The effect of illustrations in arithmetic problem-solving: Effects of increased cognitive load. Learning and Instruction 19 (2009) 345-353. pdf

h) De professionele oogkleppen van het Cito zorgen ervoor dat de range van moeilijkheid van de toetsvragen zoiets als van .5 tot .8 zal zijn, meest keuzevragen bovendien. Dit is waarschijnlijk het belangrijkste mechanisme waardoor iets dat misschien nog te redden zou zijn als rekentoets, toch een test wordt op werkgeheugen, wereldkennis, logisch redeneren, taalvermogen, toetsslimheid, stressbestendigheid.

De contexten van Treffers

Het is nog verdraaid lastig om door te dringen in het denken van de ideologen van het realistisch rekenen, zoals Adri Treffers. Een bijzondere passage is dan waar hij uitlegt hoe het bus-probleem juist het uitgangspunt vormt in onderwijs van het delen. Alsof je water ziet branden. Nou zien we tegenwoordig vaak water branden, in gebieden in de VS waar schaliegas wordt gewonnen, maar toch. Want dit is een rekenopgave die typisch door hele volksstammen 14-jarigen fout wordt beantwoord. Treffers gebruikt hem om basisscholieren op weg te helpen met happend delen. Het moet dan mogelijk zijn, denk ik, om in cognitief-psychologisch onderzoek te laten zien hoe dat niet goed kan werken, omdat het probleem voor leerlingen waanzinnig complex is, laat staan voor leerlingen die aan het begin staan van het leren delen; bestaat dergelijk onderzoek?

“Waarom fungeert nu juist dit voorbeeld als paradigma voor het uitlijnen van leergangen. In traditionele methoden zal men zo’n probleem niet aantreffen. Maar zòu het erin staan, dan was het louter bedoeld als toepassing.

Hier echter staat de opgave juist aan de basis van een zelf te construeren algoritme. Het bijzondere eraan is namelijk dat de oplossingen van de leerlingen in feite al de hele toekomstige leergang weerspiegelen.

36/1128\             36/1128\        36/1128\               
    360  10 bussen       720  20        1080  30
    ———                  ———            ————
    768                  408              48
    360  10 bussen       360  10          36   1
    ———                  ———              ——
    408                   48              12  (1)  
    360  10 bussen        36   1   
    ———                   ——
     48                   12  (1)
     36   1 bus
     ——  (1 bus)

    (a.)                 (b.)            (c.)

Met andere woorden: in dit voorbeeld komt tot uitdrukking hoe elementaire contextproblemen als concrete oriënteringsbasis voor het verticale mathematiseren kunnen fungeren. Dus hoe kinderen zelf, zij het onder leiding, de standaardprocedure van de staartdeling kunnen construeren. Ze stellen zich zo bij het rekenen namelijk werkelijk iets voor: de rekenhandelingen krijgen door de vervoerscontext betekenis. Omgekeerd verleent die context zin om de betreffende rekenhandeling te verkorten en te schematiseren. Ook kale rekenopgaven over delen kunnen door middel van die betekenisverlening (in dit geval via een vervoersprobleem) opgelost worden.

Algemener geformuleerd laat dit voorbeeld zien op welke wijze een ideale leergang vanaf het informele contextgebonden rekenen naar het formele vakmatige opereren loopt, via het intermediair van een contextsituatie die als denk- en rekenmodel dienst kan doen. Nog algemener gesteld: in realistisch reken-wiskundeonderwijs zoeken we naar modelsituaties die als brug kunnen fungeren tussen het informele contextgebonden werken en het formele vakmatige opereren.”

A. Treffers (1992). Terug naar de toekomst. In F. Goffree; A. Treffers; J. de Lange (1992). Rekenen anno 2002. Toekomstverwachtingen van het reken-wiskundeonderwijs (11-34). NVORWO. Wie het in het Engels wil lezen: blz. 23 in A. Treffers: Realistic mathematics education in The Netherlands 1980-1990, in L. Streefland (Ed.) (1991). Realistic Mathematics Education in Primary School. On the occasion of the opening of the Freudenthal Institute. Freudenthal Institute. isbn 9073346118 Het Engels is verschrikkelijk, dus ik raad het niet aan. Dit is weer een voorbeeldje van de nooit aflatende stroom van niemendal-publicaties door de Freudenthal-groep, eeuwige herhaling, napraterij, nooit stevige bronnen aanvoeren voor dit didactisch gedachtengeod, laat staan er empirisch toetsend onderzoek naar doen. Voor dat laatste waren zeeën van tijd beschikbaar geweest wanneer deze mensen de zelfdiscipline hadden kunnen opbrengen om niet eidere scheet in druk te willen laten verschijnen.

Het gaat mij hier even niet om de volgorde van concreet naar abstract, waarvan Stellan Ohlsson stelt dat het leren juist plaatsvindt van algemeen (abstract) naar specifiek (concreet). Nee, het verbijsterende is hoe Treffers hier achter elkaar dingen beweert die op basis van psychologische theorie onwaarschijnlijk zijn, en die op zijn minst aan empirisch toetsend onderzoek onderworpen hadden moeten worden. Mogelijk is John Sweller’s theorie van mentale belasting al voldoende om aannemelijk te maken dat in deze didactiek de leerlingen bij voortduring met veel — te veeel — informatie worden belast, naast de belasting die het rekenen zelf al oplevert.

Exact hetzelfde numerieke voorbeeld kom ik dan tegen bij Koeno Gravemeijer, opgehangen aan de context dat 1128 supporters van Feyenoord een uitwedstrijd willen bezoeken, dat er bussen zijn met 36 passagiersplaatsen, en dat de penningmeester te horen krijgt dat er een korting op de prijs is voor iedere tien bussen. De korting is een hint dat met tientallen werken handig is. Hoe vaak zou ik die 1128 passagiers tegenkomen in de stortvloed van stukjes gepubliceerd door de freudenthal-groepers? En wat zegt dat? Waar het op wijst: dat de contextopgaven in de realistische rekendidactiek waarschijnlijk zijn terug te voeren tot een tiental basisvormen, ongeveer zoals voor de oorlog de hoofdonderwijzers heel goed wisten dat redactieopgaven — een werkman doet een klus in vijf dagen . . . . — in een stuk of vijf typen kwamen: volg dan het algoritme voor het betreffende type redactiesom.

K. Gravemeijer: Context Problems and Realistic Mathematics Instruction. In K. Gravemeijer, M. van den Heuvel & L. Streefland (1990). Contexts Free Productions. Tests and Geometry in Realistic Mathematics Education (10-3). OC & OW. geen isbn Ontleend aan:

class='bron'>K. Gravemeijer (Red.) (1983). Rekenen & Wiskunde. Bekadidact. [niet in mijn bezit]

Ook: Adri Treffers (1991, blz. 23) Algoritmen in didactisch perspectief. In H.G.B. Broekman, L.C. Spijkerboer & J.J.M. Terlingen (red.). Algoritmen en heuristieken in contextrijk reken-wiskundeonderwijs OW & OC. geen isbn zie hier Maar waar komt die bus-opgave met 1128 passagiers oorspronkelijk vandaan? Het is een NAEP-opgave (VS), maar ook dat zal een variant zijn op wat veel vaker eerder al is gebruikt; zie daarover: Toetsvragen ontwerpen hoofdstuk 2.

verder maar weer

De spagaat voor het basisonderwijs is dat goed rekenonderwijs en de rekentoetsen van het Cito (LVS, Eindtoets) in het geheel niet op elkaar aansluiten. Het Cito werkt uitsluitend met contextvragen, waarvan vermoed mag worden dat ze vooral verschillen in (analytische) intellectuele capaciteiten toetsen. Onderwijs geven met als doel ‘intelligentie’ te verhogen, is een ijdele onderneming. Dus ook: rekenonderwijs in de vorm van contextopgaven verspilt kostbare tijd van leerlingen. De beste voorbereiding op Cito-rekentoetsen bestaat waarschijnlijk uit het geven van goed rekenonderwijs, en de leerlingen vertrouwd maken met contextopgaven. Voor de scholen is het helemaal niet zo’n gek idee om naast de rekentoetsen in het LVS ook ‘gewone’ rekentoetsen af te nemen: die zijn eenvoudig op te stellen, in korte tjd door de leerlingen te maken, en eenvoudig te administreren. NB: in het aanbieden van echte rekentoetsen heeft het Cito geen verdienmodel; dat is ongetwijfeld een reden waarom ze zo ingewikkeld doen met contextopgaven/redactiesommen.

Een en ander sterkt mij in de gedachte dat het de hoogste tijd is om die contextopgaven-misstand aan te pakken. Het ligt nu voor de hand om voor ‘Examens’ een volgende artikel te schrijven, waarin de stelling dat rekenopgaven in de vorm van contextopgaven vooral verschillen in intelligentie testen, een uitwerking krijgen in de thematiek van de uitsplitsing van contexten en zuivere rekenopgaven. Dit is precies het thema dat Joost Hulshof aan de orde stelde in de expert-meeting van Victor Schmidt, april 2011, waar de aanwezige experts mee instemden, en waar de commissie-Schmidt vervolgens niets mee heeft gedaan.

In het laatste nummer van dit jaar zou zo’n artikel mee kunnen gaan in Examens. Het zal vooral een artikel met psychologische argumenten zijn, waarschijnlijk ga ik opnieuw medewerking zoeken van Denny Borsboom (zoals ook ook voor het artikel in 2011 over de rekentoetsen van de commissie-Schmidt). Maar eerst moet ik een voorlopige opzet van een dergelijk artikel formuleren, een opzet waaruit duidelijk moet zijn dat zo’n artikel mogelijk is en dat het als een bom zal inslaan in Arnhem. Nou ja, ik overdrijf, en ik mag niet onaardig zijn tegen het Cito. Tenslotte heeft Anton Béguin goed meegewerkt aan het promotieonderzoek van Marian Hickendorff. Wat me doet bedenken dat ik zou kunnen proberen het artikel (‘intellectuele capaciteiten in contexten’) zó te schrijven dat het een uitnodiging is om op het onderwerp een promotieonderzoek te laten doen (niet door mij).

Belangrijke achtergrondliteratuur is die betreffende het onderscheid tussen aptitude en achievement, zeg maar tussen intelligentietests en resultatentoetsen. Zoek op deze pagina op aptitude voor sleutelpublicaties op dit onderwerp.

Let ook op tekstbegrip als zodanig, zie daarvoor de literatuur ion tekstbegrip.htm

Dan is er nog de kwestie van scheefheid bij toetsen, door de buren bias genoemd, en in eigen land ook wel partijdigheid (Frank Kok). Ik zie een opvallende beschrijving in Bugel & Sanders (2006).

Ik was even heel verbaasd bij het lezen van de beschrijving van bias zoals hierbeneden geciteerd. Allereerst omdat de auteurs uitgaan van toetsen, daarmee suggererend dat belangrijke tests van het Cito, zoals de Eindtoets Basisonderwijs, studietoetsen zijn, en dus geen psychologische tests. Tests op individuele verschillen in analytische intellectuele capaciteiten, bijvoorbeeld. Een test ‘toets’ noemen, verhangt een bordje, maar doet niets af aan de onderliggende werkelijkheid. De vraag is natuurlijk: in de mate waarin toetsen van het Cito in feite psychologische tests zijn, kunnen zij uiteraard ook bias hebben, en hoe zouden Bugel en Sanders die bias dan beschrijven?

Het tweede opmerkelijke gemis dat mij van mijn stoel deed rollen: Bugel en Sanders veronderstellen stilzwijgend dat de bedoelde toets de bedoelde vaardigheid meet, al dan niet met enige bias. Maar de mate waarin de bedoelde toets de bedoelde vaardigheid niet adequaat meet is natuurlijk ook een vorm van bias! Bijvoorbeeld: rekenvaardigheid alleen met contextopgaven brengt op zich al een ongelooflijke bias in de toets aan. Brrrrrrrr.

Schema

‘reken’opgaven Citotoets

Het zou prachtig zijn wanneer ik een artikel kon schrijven waarin de context-hype scherp gekarakteriseerd wordt, maar dat is een veel te uitgebreid thema. Een interessante hypothese zou zijn: (1) Is het werken met contexten de opvolger van de opvatting dat het in het reken- en wiskundeonderwijs erom gaat dat de leerlingen leren denken? Een alternatieve hypothese, of misschien zijn zij beide waar: (2) Volgt het werken met contexten uit reformopvattingen dat het onderwijs ertoe dient dat leerlingen zich straks in het dagelijks leven kunnen redden? Ik ga het hier dus niet over hebben. Voor algemene literatuur die van belang is voor de thematiek van contexten in het onderwijs — en in de examens, hoewel het een zeker niet logisch uit het ander volgt — zie hier.

Het onderwerp moet dus ernstig worden ingeperkt, en de keuze die ik maak is (1) voor rekenen, en (2) voor de rekenopgaven in de Cito Eindtoets Basisonderwijs. Ad (1). De keuze voor rekenen ligt voor de hand, het is het terrein dat het meest overzichtelijk is, en tegelijk het ernstigst aangetast door de infusie van contexten. Verschillende opvattingen over het rekenonderwijs botsen heftig op elkaar, waar ook een compromissen-commissie van de KNAW niets aan heeft kunnen veranderen. De overheid neemt op dit terrein de ene ontwrichtende maatregel na de ander, de urgentie voor een rationele schoonmaak is dus groot. Ad (2). De keuze voor de rekenopgaven waar het Cito professionele verantwoordelijkheid voor neemt is eveneens een voor de hand liggende, omdat over de Citotoets (Cito Eindtoets Basisonderwijs) zeer veel empirische gegevens voorhanden zijn. Een belangrijke reden is natuurlijk ook dat deze Citotoets misbruikt wordt voor van alles en nog wat, en zodoende een sturende werking op de aard van de rekendidactiek heeft die zijn weerga in de Nederlandse onderwijsgeschiedenis niet kent. Klein probleem is dat het Cito geheimzinnig doet over de oetsvragen zelf, en die maar mondjesmaat af en toe vrijgeeft als voorlichtings- en oefenmateriaal. Voorlopig volstaat het om een vijftal typische rekenopgaven-in-context te kiezen als de casus aan de hand waarvan verder valt te analyseren.

het afzonderlijke item

Een goede beginvraag zou kunnen zijn: ‘Is het denkbaar dat ik zelf rekenvragen zou hebben ontworpen die in de buurt komen van de rekenopgaven die het Cito typisch in zijn toetsen stopt? Ik heb mij dat al vaak afgevraagd, n.a.v. mijn werk aan Toetsvragen ontwerpen (sinds eind zeventiger jaren), en ik was mij dan ook al aan het voorbereiden op de thematiek van het ontwerpen van toetsvragen voor rekenen en wiskunde. Ik was mij er tot 2008 niet van bewust dat het met het Nederlandse rekenonderwijs zo beroerd was gesteld als bleek bij de PPON-2004, en al helemaal niet van de achtergronden van deze nationale ramp.

de toets

Hoe het Cito denkt over de Eindtoets Basisonderwijs als juist niet een intelligentietest, is te lezen bij de toelichting op de Cito-intelligentietest voor groep 8, zie hier.

H. W. van Boxtel & B. T. Hemker (2009). Wetenschappelijke verantwoording van de Intelligentietest Eindtoets Basisonderwijs. Cito pdf

Hans Kuyper & Greetje van der Werf (14-6-2012). Excellente leerlingen in het voortgezet onderwijs. Schoolloopbanen, risicofactoren en keuzen. GION. pdf; Hans Kuyper schreef er een artikel over: Kwart excellente leerlingen ‘mislukt’ in het vo. In Didactief, juni 2012 blz. 48-49, hier te lezen. (zie ook mijn laatste blog op het forum van BON, voordat mijn account werd geblokkeerd: http://www.beteronderwijsnederland.nl/forum/excellente-leerlingen-het-vo )

Opmerkelijk is dat Kuyper en Van der Werf geen aarzeling hebben om de Cito Eindtoets Basisonderwijs een intellligentietest te noemen, zij het beperkt tot ‘gestolde’ intelligentie (Raymond B. Cattell). Maar juist het overdadige gebruik van contexten en het beroep doen op tekstbegrip, moet toch erin resulteren dat de Eindtoets ook ‘vloeiende’ intelligentie meemeet.

Waarom dit van belang is bij de vraag of de rekentoets-3F niet meer een intelligentietest dan een rekentoets is: de vragen in de rekentoets-3F verschillen wat het beroep op intelligentie betreft waarschijnlijk niet wezenlijk van die in de Eindtoets. Mijns inziens gaat de karakterisering van de Eindtoets als een intelligentietest (Kuyper en Van der Werf) om dezelfde redenen eveneens op voor de rekentoets-3F. Dat is een ernstige zaak, omdat het waarschijnlijk betekent dat de rekentoets-3F maar in beperkte mate goed is voor te bereiden in een oefenprogramma doorheen de jaren van het vo.

Voorzover de contextopgaven in Eindtoets en Rekentoetsen zich niet laten uitwerken langs schematische geoefende lijnen, doen ze mede een beroep op ‘fluid intelligence’. Anders dan Kuyper en Van der Werf vermoed ik dat Eindtoets en rekentoetsen-3F en -3S in hun contextopgaven ook vloeiende intelligentie meemeten. Is het bij gestolde intelligentie nog enigszins het geval dat goed onderwijs in voldoende omvang (bijvoorbeeld voor kinderen uit achterstandssituaties in de zomermaanden doorlopend) er positieve invloed op heeft (American Psychologist, begin 2012), voor vloeiende intelligentie is dat waarschijnlijk nauwelijks het geval (maar zie Sternberg, R. J. (2008). Increasing fluid intelligence is possible after all. Proceedings of the National Academy of Sciences, USA, 105, 6791- 6792. html [ik heb dit artikel nog niet ingezien; opmerkelijke titel]). Als dat laatste waar is, dan horen toetsen die aanspraak doen op vloeiende intelligentie niet thuis in afsluitende examens, maar op zijn best in testbatterijen voor selectieve toelating tot vervolgtrajecten.

De vraag is nu: wat laten de door Kuyper en Van der Werf gepresenteerde analyses zien over de samenhang van de Eindtoets met de NIO? De entreetoets is volgens Kuyper en Van der Werf te zien als een samenvatting van de Eindtoets, dus hier dezelfde vraag: de samenhang tussen de entreetoets en de NIO. Op zich bewijst een hoge samenhang nog niet dat de Eindtoets vooral een intelligentietest is, maar valt de stelling lastig te ontkennen. Kuyper en Van der Werf zijn niet echt geïnteresseerd in deze specifieke vraagstelling; de lezer moet dus goed opletten om niet uit tabel 2.1 en 2.2 verkeerde conclusies te trekken. Ik heb uit de gegevens van Kuyper en Van der Werf de volgende tabel geconstrueerd:

Bovenstaande tabel laat zien dat de entreetoets een iets betere voorspeller is van de ([sub-]excellente) resultaten op de een jaar eerder afgenomen Cito Eindtoets Basisonderwijs dan de NIO diezelfde resultaten voorspelt van de dan twee jaar eerder afgenomen Eindtoets. Ex-aequo, dus. Ik zie hier dat Eindtoets, entreetoets een jaar later, en NIO weer een jaar later, voor alle praktische doeleinden hetzelfde lijken te meten. Omdat de NIO een kwalitatief goede intelligentietest is, luidt de conclusie dat de Cito Eindtoets Basisonderwijs en de Cito entreetoets zich als intelligentiest gedragen (en niet alleen maar als een test op gestolde intelligentie, maar ook op vloeiende intelligentie). In tabel 3.6 van Kuyper en Van der Werf is te zien dat in de vwo-groep de gemiddelde scores op de wiskundetoets in het derde jaar voor de drie topgroepen gedefninieerd op respectievelijk de entreetoets, de NIO en de Eindtoets, vrijwel gelijk zijn.

Voor de rekentoetsen, voorzover zij contextopgaven bevatten van hetzelfde type als in de Eindtoets en de entreetoets, geldt derhalve waarschijnlijk dat ook deze toetsen verkapte intelligentietests zijn. Het is aan het Cito, die als ontwerper en uitgever tekent voor deze toetsen, om aannemelijk te maken dat deze conclusie onjuist moet zijn.

Sebrechts M. M., Enright M., Bennett R. E. & Martin K. (1996). Using algebra word problems to assess quantitative ability: Attributes, strategies, and errors. Cognition and Instruction, 14, 285-343.

Ramist L., Lewis C. & McCamley-Jenkins L. (2001). Using achievement tests/SAT ï Subject Tests to demonstrate achievement and predict college grades: Sex, language, ethnic, and parental education groups. (College Board Research Report No. 2001-5). New York: College Board.

Koedinger K. R. & Nathan M. J. (2004). The real story behind story problems: Effects of representation on quantitative reasoning. Journal of the Learning Sciences, 13, 129-164.

Koedinger K. R., Alibali M. W. & Nathan M. J. (2008). Trade-offs between grounded and abstract representations: Evidence from algebra problem solving. Cognitive Science, 32, 366-397. pdf

Kaminski J. A., Sloutsky V. M., Heckler A. F., (2008). The advantage of abstract examples in learning math. Science, 320, 454-455.

Gierl M. J., Tan X., Wang C., (2005). Identifying content and cognitive dimensions on the SAT (College Board Research Rep. No. 2005-11). New York, NY: College Board.

Dorans N. J., Lawrence I. M., (1987). The internal construct validity of the SAT (ETS Research Rep. RR 87-35). Princeton, NJ: Educational Testing Service.

Bridgeman B., (1992). A comparison of quantitative questions in open-ended and multiple-choice formats. Journal of Educational Measurement, 29, 253-271.

De nationale schande is dat die contextopgaven precies NIET doen waarvoor ze bedoeld zijn.

Het achterliggende probleem is immers het vermoeden bij vele rekendidactici dat leerlingen die goed hebben leren rekenen, hun vaardigheid in het dagelijks leven niet altijd blijken toe te passen. Dit is het probleem van de overdracht, vaak aangeduid met de Engelse term ‘transfer’. De volstrekt naïeve gedachte is dan, na de oorlog uitgedragen door de Freudenthal-groep, om dat probleem op te lossen door die situaties uit het dagelijks leven maar binnen het onderwijs zelf te behandelen.

En wat gaan zij dan doen bij de Eindtoets Basisonderwijs en bij de rekentoetsen bij de eindexamens: de leerlingen waarschuwen dat dit een rekentoets is, en ze dan de contextopgaven aanbieden. Terwijl het bij het transfer-probleem juist gaat om het rekenvaardig aanpakken van opgaven in het dagelijks leven ZONDER een waarschuwingssticker met de boodschap ‘hier moet je rekenen’.

Op basis van bovenstaand argument, ondersteund met empirisch onderzoek, moet de conclusie zijn dat contextopgaven in rekentoetsen bij eindexamens NIET valide zijn, en dus NIET in die rekentoetsen thuishoren.

Het voordeel van deze benadering vanuit wetenschappelijk onderzoek is dat het voldoende is om te weten dat de geheimgehouden toetsen vooral bestaan uit contextopgaven, om deze toetsen te kunnen diskwalificeren als REKENtoetsen.

Bijvangst: meteen ophouden met in de rekendidactiek te werken met contextopgaven.

Josetxu Orrantia, David Múñez (2013). Arithmetic word problem solving: evidence for a magnitude-based mental representation. Memory and Cognition, 14, 98-108.

http://link.springer.com/content/pdf/10.3758/s13421-012-0241-1 [button: Look inside voor de eerste twee pagina’s]

Lees hier een empirisch resultaat dat erop wijst dat een klungelige presentatie/formulering van een contextopgave de leerlingen op het verkeerde been zal zetten. Of ook hun leraar. In ieder geval mij. Dit gebeurt dus massaal (veel opgaven in een willekeurige rekentoets van het Cito; honderdduizenden leerlingen, zoniet veel meer).

manipulatives: zijn ook contexten, maar deze contexten moeten weer worden afgeleerd, vergeten.

Tracy Packiam Alloway & Ross G. Alloway (Eds.) (2013). Working Memory. The Connected Intelligence. Psychology Press. abstract

K. A. Ericsson, R. T. Krampe & C. Tesch-Römer (1993). The role of deliberate practice in the acquisition of expert performance. Psychological Review, 100, 363-406. pdf

Adrian Furnham, Jeremy Monsen and Gorkan Ahmetoglu (2009). Typical intellectual engagement, Big Five personality traits, approaches to learning and cognitive ability predictors of academic performance. British Journal of Educational Psychology 79, 769-782. abstract

Het is toch wel weer ontluisterend om te worden geconfronteerd met resultaten zoals in de box hierbeneden. Maar hoe zit dat dan" Zijn al deze leerlingen tot ongeveer hetzelfde niveau opgeleid, en zijn de examens ten onrechte onderscheidend gemaakt wat intellectuele capaciteiten betreft? Of zijn de inspanningen van deze leerlingen (time on task) niet echt verschillend geweest, zodat inhoudelijk goede examens juist de verschillen in intellectuele capaciteiten boven water halen? Vgl. het studieresultatenmodel Tromp & Wilbrink (1977) html. Opvallend is dan wel dat de auteurs ook in de discussion geen aandacht schenken aan tijdbesteding en streefniveau als mogelijke voorspellende variabelen voor studieresultaten. Ze zijn bovendien wat verward over de statistische techniek: aan de ene kant vertellen ze ons dat persoonlijkehidsvariabelen nauwelijks toegevoegde voorspellende waarde hebben bovenop intellectuele verschillen, en tegelijk houden ze ons in de laatste zin van het artikel voor dat persoonlijkheid 25% van de variantie van resultaten op kernvakken kan voorspellen. Het moet toch echt van tweeën een zijn. Het probleem is natuurlijk dat een ondergespecificeerd model voor studieresultaten altijd ook misleidend is.

Wei Wei, Hongbo Yuan, Chuansheng Chen & Xinlin Zhou (2012). Cognitive correlates of performance in advanced mathematics. British Journal of Educational Psychology, 82, 157-181. abstract

Terezinha Nunes, Peter Bryant, Rossana Barros & Kathy Sylva (2012). The relative importance of two different mathematical abilities to mathematical achievement. British Journal of Educational Psychology, 82, 136-156. abstract

Direct relevant onderzoek, zie het citaat. De conclusie van de auteurs volgt waarschijnlijk niet uit hun onderzoek, ik moet dat checken. Het punt is: wiskundig redeneren is een intelligente capaciteit, en daar valt met gericht onderwijs niet veel aan te doen. Ik ben benieuwd hoe deze auteurs dat probleempje oplossen. Snel doorbladerend zie ik dat zij er ruimschoots aandacht aan besteden. Het is bepaald geen kinderachtig onderzoek: longitudinaal over een zeer lange periode, grote aantallen kinderen, vele tests. Dit vergt zorgvuldige bestudering, temeer omdat de te voorspellen rekentoetsscores izijn afgenomen op 11-jarige resp. 14-jarige leeftijd, waarschijnlijk met rekentoetsen die zich goed laten vergelijken met wat het Cito onder rekentoetsopgane verstaat (in de Eindtoets Basisonderwijs).

Mark N. Bing, Susan M. Stewart and H. Kristl Davison (2009). An Investigation of Calculator Use on Employment Tests of Mathematical Ability. Effects on Reliability, Validity, Test Scores, and Speed of Completion. Educational and Psychological Measurement, 69, 322-350. abstract

Deze onderzoekers concluderen, voor de specifieke situatie in dit onderzoek, dat gebruik van de rekenmachine de nauwkeurigheid van de testscores niet verstoort. Let op de formulering: ik vermoed dat zij bedoelen dat de rangorde van de kandidaten (het gaat om personeelsselectie) niet wordt verstoord. Maar dat moet ik nog checken. Let op de precieze bewoordingen in de aanvang van dit artikel:

Walter N. Durost and George A. Prescott (1952). An Improved Method of Comparing a Capacity Measure With an Achievement Measure at the Elementary School Level. Educational and Psychological Measurement 1952 12: 741-755. preview

Een halve eeuw geleden kon een artikel op dit onderwerp nog glashelder worden geformuleerd. Lees het, geniet. Ik neem een uitvoerig citaat over, maar een enkel citaat doet geen recht aan dit artikel. Prescott heeft nog vervolgonderzoek gedaan; ik zal nog nagaan hoe dit balletje verder is gerold (Scholar levert niet direct geweldig bruikbare resultaten; beter lijkt om te zoeken op de aptitude-achievement thematiek) (niet genoemd in het mooie overzicht van Anne Anastasi 1984, zie hierbeneden).

Richard E. Snow (1992). Aptitude Theory: Yesterday, Today, and Tomorrow. Educational Psychologist, 27, 5-32. abstract

Lee J. Cronbach & Richard E. Snow (1977). Aptitudes and Instructional Methods. A Handbook for Research on Interactions. Irvington.

Donald Ross Green (Ed.) (1974). The aptitude-achievement distinction. Proceedings of the Second CTB/McGraw-Hill Conference on Issues in Educational Measurement. CTB/McGraw-Hill.

Anne Anastasi (1984). Aptitude and Achievement Tests: The Curious Case of the Indestructible Strawperson. Published in Social and Technical Issues in Testing: Implications for Test Construction and Usage, edited by Barbara S. Plake (Hillsdale, NJ: Lawrence Erlbaum Associates, 1984).pdf

Manfred Kochen, Albert N. Badre & Babara Badre (1976). On recognizing and formulating mathematical problems. Instructional Science, 5, 115-131. abstract

J. A. C. Sandberg & H. de Ruiter (1985). The solving of simple arithmetic story problems. Instructional Science, 14, 75-86. abstract

Randy Elliot Bennett, Marc M. Sebrechts and Donald A. Rock (1991). Expert-System Scores for Complex Constructed-Response Quantitative Items: A Study of Convergent Validity. Applied Psychological Measurement, 15, 227. abstract

Een mooie demonstratie van intelligentietesterij? Nou, nee hoor. Psychometrische oefeningen over het luchtledige. En dan ben ik nog te vriendelijk, want deze auteurs willen mee op de aankomende golf van meer toetsen in realistische contexten (p. 227 rechter kolom). Ze lijken niet geïnteresseerd in vervuiling van hun toetsen door gevoeligheid voor verschillen in intellectuele capaciteiten, tenslotte gaat het om het soort vragen dat in toelatingstests wordt gesteld, en dan is meetesten van verschillen op intellectuele capaciteiten mooie bijvangst. En zo kan het gebeuren dat de gemeenschap van psychometrici er niet in slaagt het constructivisme in het onderwijsveld te beteugelen: als men al iets in de gaten heeft, wordt het in dienstbaarheid omarmd.

Ross E. Traub and Charles W. Fisher (1977). On the Equivalence of Constructed- Response and Multiple-Choice Tests. Applied Psychological Measurement, 1, 355-369. abstract

Gebruikt tests voor wiskundig redeneren en voor taalbegrip. De auteurs geven geen voorbeelden van gebruikte items (daarvoor verwijzen ze naar bestaande tests waarvan gebruik is gemaakt).

Ulf Andersson (2008). Working memory as a predictor of written arithmetical skills in children: The importance of central executive functions. British Journal of Educational Psychology, 78, 181-203. abstract

Susan E. Whitely & René V. Dawis (1975). A model for psychometrically distinguishing aptitude from ability. Educational and Psychological Measurement, 35, 51-66. abstract

Dit gaat dus niet over het onderscheid tussen aptitude en achievement, maar dat tussen ability en aptitude. Het artikel zit daarmee middenin de controverse over nature en nurture. We mochten willen dat over aptitude en achievement er ook een stevig maatschappelijk debat zou zijn, maar dat is er merkwaardig genoeg dus niet (behalve misschien in de meer sociologische literatuur over meritocratie, dus verdienste versus afkomst als loopbaan-bepalende factor). Ik heb de indruk dat deze auteurs de begrippen ability en aptitude een betekenis geven die precies tegengesteld is aan wat ik verwachtte (p. 52). De theoretische uitwerking is vervolgens langs de lijn van toegevoegde waarde (dat stuit op het probleem van de gebrekkige betrouwbaarheid van verschilscores, zie bv Cronbach & Furby).

Han L. J. van der Maas, Dylan Molenaar, Gunter Maris, Rogier A. Kievit & Denny Borsboom (2011). Cognitive Psychology Meets Psychometric Theory: On the Relation Between Process Models for Decision Making and Latent Variable Models for Individual Differences. Psychological Review, 118, 339-356. abstract en pdf

Walter Kintsch & James G, Greeno (1985). Understanding and Solving Word Arithmetic Problems. Psychological Review, 92, 109-129. preview

Marcel V.J. Veenman & Jos J. Beishuizen (2007). Intellectual and metacognitive skills of novices while studying texts under conditions of text difficulty and time constraint. Learning and Instruction, 14, 621-640. abstract

Het is niet in een oogopslag af te lezen uit het abstract, maar dit artikel lijkt me belangrijke informatie te geven voor het theoretisch kader van mijn capaciteiten-in-contexten-project. Al was het maar omdat die contexten in Cito-rekentoetsen vaak situaties zijn waar de leerlingen als nieuweling (novice) tegenover staan. Een andere, grote, vraag is of het echt rekenvaardig zijn een zekere mate van bescherming oplevert tegen de verwarring die telkens nieuwe contexten opleveren. Met andere woorden: of rekenexpertise het mogelijk maakt om het nieuwelingschap wat de contexten betreft, in goede banen te leiden.

Hansjörg Hohr (2013). The Concept of Experience by John Dewey Revisited: Conceiving, Feeling and ‘‘Enliving’’Studies in Philosophy and Education, 32, 25-38 preview

Jan Bengtsson (2013). Embodied Experience in Educational Practice and Research. Studies in Philosophy and Education, 32, 39-53. preview

Gail Corrado (2012). Achievement is a Relation, Not a Trait: The Gravity of the SituationStudies in Philosophy and Education, 31, 587-601. abstract

Stuart J. Ritchie and Timothy C. Bates (2013 online first). Enduring Links From Childhood Mathematics and Reading Achievement to Adult Socioeconomic Status. Psychological Science, May 2, 2013 online first abstract

Neem de titel letterlijk: cohortstudie, taal en rekenen van zevenjarigen, hun inkomnespositie als 42-jarige. Een behoorlijk positief verband, gecorrigeerd voor sociale achtergronden, intelligentie, academische motivatie, lengte van onderwijsloopbanen. Fantastisch. Ik moet het nog wel en detail bestuderen. Het is geen experimenteel onderzoek, dus het betekent niet vanzelfsprekend dat betere of slechtere prestaties van 7-jarigen als gevolg van kwaliteitsverschillen van het onderwijs hetzelfde effect zullen hebben. Maar toch, het is niet onaannemelijk dat vroege resultaten in taal en rekenen, hoe dan ook verkregen, op de heel lange duur enorm belangrijk zijn. NB: als de schooljuffen die bang zijn voor rekenonderwijs dat dan juist in de groepen 1 t/m 4 moeten gaan geven, kan dat dus rampzalige gevolgen hebben.

Danny Beckers (2000): “My Little Arithmeticians!” Pedagogic Ideals in Dutch Mathematics Textbooks, 1790-1850. Paedagogica Historica: International Journal of the History of Education, 36, 978-1001. abstract

Opmerkelijk. Zou het kunnen dat het realistisch rekenen een terugkeer is naar het begin van de 19e eeuw?

Stephen G. Sireci and Polly Parker (2006). Validity on Trial: Psychometric and Legal Conceptualizations of Validity. Educational Measurement: Issues and Practice, fall, 27-34. abstract

Henny Uiterwijk & Ton Vallen (1996). Hoe worden toetsen minder partijdig voor allochtonen? MOER, 75-84. [het archief van MOER komt voorjaar 2013 beschikbaar op de website]

Ik neem een enkel voorbeeld-item volledig over. Het gaat mij niet om de vraagpartijdigheid (benadeeld zijn van een specifiek groep als gevolg van gebruikte taal) als zodanig. Belnagrijk is dat onderzoek zoals dit erop wijst dat waarschijnlijk ook zonder partijdigheid op groepsniveau er sprake zal zijn van gebruikte taal als stoorzender bij rekenopgaven. Omdat zoiets vermijdbaar is, is het een reden te meer om contextopgaven niet of slechts in speciale gevallen te gebruiken.

Jamal Abedi (2006). Language issues in item development. In Steven M. Downing and Thomas M. Haladyna (Eds) (2006). Handbook of test development. (377-398). Erlbaum. site [heel kostbaar] [Editie 2011, editors: Suzanne Lane, Mark Raymond, Steven M. Downing & Thomas S. Haladyna. eBook in KB]

S. E. Phillips (1996). Legal Defensibility of Standards: Issues and Policy Perspectives. Educational Measurement: Issues and Practice summer, 5-19 abstract

Morgan S. Polikoff (2010). Instructional Sensitivity as a Psychometric Property of Assessments. Educational Measurement: Issues and Practice, Winter , Vol. 29,, 3-14. abstract

Suzanne Lane (1993). The Conceptual Framework for the Development of a Mathematics Performance Assessment Instrument. Educational Measurement: Issues and Practice, Volume 12, Issue 2, 16-23 abstract

Ik ben wel benieuwd hoe zij dit uitwerkt, want het uitgangspunt dat instructie en toets in lijn moeten liggen, is voor discussie vatbaar. De discussie is deze: als de instructie berust op een bijzondere didactische filosofie, dan gaat het niet aan om de toetsing daarop aan te passen. Integendeel, zou ik denken. Met andere woorden: in een opavtting waarin het technisch rekenen niet meer van belang wordt gevonden, is het ongepast om een evaluerende toets af te nemen waar geen technisch rekenen meer wordt gevraagd (zoals het Cito dus doet met zijn Eindtoets Basisonderwijs, of met de rekentoets-3F om maar eens iets te noemen [daar is natuurlijk een smoes voor: de Wet op de referentieniveaus . . . . ]).

Gerhard Meisenberg & Michael A. Woodley (2013). Are cognitive differences between countries diminishing? Evidence from TIMSS and PISA. Intelligence online first.

Dit komt heel mooi van pas. Deze onderzoekers beschouwen TIMSS en PISA gewoon als intelligentietests, of tenminste als goede proxies daarvoor. Indachtig mijn lijfspreuk dat wat er uitziet als een intelligenitetest en zich blijkt te gedragen als een intelligentietest . . . .

Jinfa Cai (1997). Beyond Computation and Correctness: Contributions of OpenHEnded Tasks in Examining U. S. and Chinese Students' Mathematical Performance. Educational Measurement: Issues and Practice

M. Christina Schneider, Kristen L. Huff, Karla L. Egan, Margie L. Gaines & Steve Ferrara (2013). Relationships Among Item Cognitive Complexity, Contextual Demands, and Item Difficulty: Implications for Achievement-Level Descriptors. Educational Assessment, 18, 99-121. abstract

Dit lijkt me een sleutelpublicatie, althans wat betrfet aangeven van enkele belangerijke problemen.

Leanne R. Ketterlin-Geller, Paul Yovanoff, EunJu Jung, Kimy Liu & Josh Geller (2013). Construct Definition Using Cognitively Based Evidence: A Framework for Practice, Educational Assessment, 18, 122-146.abstract

John R. Anderson & Christian D. Schunn (2000). Implications of the ACT-R learning theory: No magic bullets. In R. Glaser (Ed.), Advances in instructional psychology: 5 (pp. 1-34). Mahwah, NJ: Lawrence Erlbaum Associates. pdf

Michelle L. Rizzella and Edward J. O'Brien (2002). Retrieval of concepts in script-based texts and narratives: The influence of general world knowledge. Journal of Experimental Psychology, 28, 780-790. abstract

Ook van belang voor tekstbegrip? Want wat mij triggerde is natuurlijk de general world knowledge: dat moet wel over contexten gaan, op een onbedoelde maar mogelijk niet minder interessante manier!

Arthur Glenberg , Jonathan Willford , Bryan Gibson , Andrew Goldberg & Xiaojin Zhu (2012): Improving Reading to Improve Math. Scientific Studies of Reading, 16, 316-340. To link to this article: http://dx.doi.org/10.1080/10888438.2011.564245 abstract

Het lijkt alleen maar grappig, maar pas op: wanneer een op beter lezen gerichte interventie zo’n grote verbetering bij het oplossen van woordproblemen oplevert, dan zegt dat ook iets over die woordproblemen. Leeftijdscategorie: groep 5 en 6. Verder lijkt het me niche-onderzoek, niet psychologisch onderbouwd, maar dat kan best verrassingen opleveren.

Marlene Schommer, Amy Crouse, and Nancy Rhodes (1992). Epistemological Beliefs and Mathematical Text Comprehension: Believing It Is Simple Does Not Make It So. Journal of Educational Psychology, 84, 435-443. abstract

Lynn S. Fuchs, Douglas Fuchs, Donald L. Compton, Sarah R. Powell, Pamela M. Seethaler, Andrea M. Capizzi, Christopher Schatschneider & Jack M. Fletcher (2006). The Cognitive Correlates of Third-Grade Skill in Arithmetic, Algorithmic Computation, and Arithmetic Word Problems. Journal of Educational Psychology, 98, 29-43. abstract and/or pdf

Elizabeth F. Loftus & Patrick Suppes (1972). Structural variables that determine probelm-solving difficulty in computer-assisted instruction. Journal of Educational Psychology, 63, 531-542. abstract en hele pdf (zoals alle publicaties van Suppes, trouwens)

Kohnstamm (1973). Geslachtsverschillen in prestaties op schoolvorderingentoetsen en enkele tests aan het einde van de basisschool. Nederlands Tijdschrift voor de Psychologie, 28, 351-367

Sandbergen e.a., Enkele relaties tussen een intelligentietest en een studietoets. NTvdPs 1972, 27, 509-529.

Schlesinger & Guttman (1969). Smallest Space Analysis of intelligence and achievement tests. Psychological Bulletin, 71, 95-100.

Bel, A., & Bloemers, W. (1992). Psychologen bij het Cito. De Psycholoog, 27, 302-307. (Ook over doelen van het Cito, onthullend in zekere zin, zonder dat de auteurs dat opmerken).

Blok, H. (1992). De grootte van het schooleffect in het basisonderwijs: een analyse op basis van vijf jaar Eindtoets Basisonderwijs. TOR, 17, 343-354.

Crano, W. D., Kenny, D. A., & Campbell, D. T. Does intelligence cause achievement? A crosslagged panel analysis. Journal of Educational Psychology, 1972, 63, 258-275.

Dalton (1976). A decline in the predictive validity of the SAT and high school achievement. EPM 36, 445-448.

Dekker,A.J.; Krieken,R.van. Algemene richtlijnen voor centrale eindexamenprogramma's. Arnhem: Cito;

Gustafsson, J-E., & Balke, G. (1993). General and specific abilities as predictors of school achievement. Multivariate Behavioral Research 28, 407-434. gezien, wel weer erg multivariaat.

Flood & Saggar (1968). Academic performance with, and without, knowledge of scores on tests of intelligence, aptitude and personality. JEP 59, 395-401.

Resnick, L. B., & Resnick, D. P. (1992). Assessing the thinking curriculum: New tools for educational reform. In B. R. Gifford & M. C. O'Connor (Eds.), Changing assessments. Alternative views of aptitude, achievement and instruction (p. 37-119). Dordrecht: Kluwer. [Bibl. POW 77.03 C1.]

Ellen M. Markman (1979). Realizing that you don’t understand: Elementary school children’s awareness of inconsistencies. Child Development, 50, 643-655. read online free

Het is maar een bescheiden onderzoekje, anders zou het een sleutelpublicatie zijn. Wat Markman laat liggen: het is te verwachten dat kinderen dezelfde problemen hebben met logisch consistente tektsten: daarvan moet je tenslotte de logica ook eerst nog maar eens expliciet in de gaten hebben? Het punt is natuurlijk dat teksten die in zekere zin oppervlakkig worden gelezen, op oneindig veel manieren een consistente interpretatie kunnen krijgen, waarvan de meeste dat dus fout zijn of in ieder geval net niet correct. Om deze reden zie ik onderzoek zoals dit, van Markman, als veelbelovende methodiek om de problemen bloot te leggen die inherent zijn aan contextopgaven zoals bijvoorbeeld door het Cito graag ingezet bij examens en toetsen. Zie verder ook Cain & Oakhill (2007) hier.

Ed de Moor (1994). Jan Versluys en het ontstaan van de vakdidactiek. Nieuwe Wiskrant, 14, 8-14 [nog niet online, 2013] annotatie

Martin Keune (1998). Naar de knoppen. Nieuw Wiskrant, 17 #4, 48-49. inaugurele rede

L. C. Spijkerboer (1994). Contexten in proefwerken. Nieuwe Wiskrant, 14, 17-22. [nog niet online beschikbaar, 2013] [Voor aantekeningen bij deze demonstratie van geloof in contexten, zie contexten.htm]

Richard J. Shavelson (2013). On an Approach to Testing and Modeling Competence. Educational Psychologist, 48, 73-86. abstract

Shavelson gaat uit van een definitie van competentie als capaciteit-in-context. Wat kan ik me nog beter wensen? Dit artikel — een voordracht, geen onderzoek — moet dus wel exact on topic zijn. Voorlopig citeer ik alleen een paar smaakmakers uit het abstract.

Karoline Koeppen, Johannes Hartig, Eckhard Klieme & Detlev Leutner (2008). Current Issues in Competence Modeling and Assessment. Zeitschrift für Psychologie / Journal of Psychology, 216, 61-73. abstract en ook pdf

Robert L. Goldstone & Samuel B. Day (2012): Introduction to “New Conceptualizations of Transfer of Learning”, Educational Psychologist, 47, 149-152. abstract

Dit is de introductie op het themanummer over transfer. Ik heb zo’n vermoeden dat Goldstone & Day een analyse geven die de voorstanders van het realistisch rekenen goed uitkomt. Daarom hier de (nog te maken) aantekeningen die voor capaciteiten-in-contexten van belang zijn.

Patrick Suppes (1957). Introduction to logic. Van Nostrand Reinhold, International Student Editions. integrale tekst

Neem bijvoorbeeld hoofdstuk 3 Symbolizing everyday language (43-57). Een goede demonstratie van de complexiteit van zoiets als ‘logisch denken in contexten’ waar de meeste realisch rekenaars weinig van willen weten.

Iets anders: ik zou eigenlijk een poging moeten doen om de eenvoudige rekencontexten in zoiets als de voorbeeldrekentoets-3F met het logische apparaat te lijf te gaan. Het moet immers mogelijk zijn om dubbelzinnigheden in contexten ondubbelzinnig duidelijk te maken. Zie ook Belnap & Steel.

Raymond S. Nickerson (1988). On improving thinking through instruction. Review of Research in Education, 15, 3-57. preview

Uit de achterliggende filosofie bij die contextopgaven is al snel duidelijk dat een grote gemene deler is dat de leerlingen veronderstel worden te hebben leren denken, zodat de contexten kunnen begrijpen en vertalen naar een rekenmodel. Welnu, over ‘leren denken’ is al heel wat onderzoek gedaan, zoals door Deanna Kuhn (Thinking Skills), en zoals hier door Nickerson in een overzicht samengevat.

Raymond S. Nickerson (2004). Teaching reasoning. In Jacqueline P. Leighton & Robert Sternberg (Eds) (2004). The nature of reasoning. Cambridge University Press. abstract

Raymond S. Nickerson (2010). Mathematical Reasoning. Patterns, Problems, Conjectures, and Proofs. Psychology Press. [verder nog niet gezien. In KB? Ik kan niet inloggen] book details

Nickerson is waarschijnlijk geen wiskundige, maar psycholoog. Dat vind ik best sympathiek, maar het is voor het onderwerp van zijn boek toch tricky. Ik ben wel benieuwd hoe hij zich hieruit heeft weten te redden.

J. M. Wijnstra (1984). Verantwoording Eindtoets Basisonderwijs 1981 (met een historisch overzicht over de periode 1966-1980). Specialistisch Bulletin Nr. 25. Cito. 144 blz. quarto offset

Samuel Messick (1984). Abilities and Knowledge in Educational Achievement Testing: The Assessment of Dynamic Cognitive Structures. pdf. In Barbara S. Plake (Ed.) . Social and Technical Issues in Testing. Implications for Test Construction and Usage. Erlbaum. pdf's

Lotte Schenk-Danzinger (1953). Entwicklungstests für das Schulalter. I. Teil Altersstufe 5-11 Jahre. Wien: Verlag für Jugend und Volk.

Ik ben altijd nieuwsgierig of er interessant materiaal in staat dat een vergelijking met meer dan een halve eeuw geleden mogelijk maakt. En dan vind ik een blokken-opgave die als twee druppels water lijkt op een opgave in de voorbeeldrekentoets-3F van het Cito, zij het dat het aantal blokjes dat de 17- of 18-jarigen moeten tellen, iets groter is.

Angeliki Kolovou (2011). Mathematical Problem Solving in Primary School. Proefschrift Universiteit Utrecht. Fisme. isbn 9789073346727 pdf

M. David Miller & Robert L. Linn (2005). Invariance of Item Characteristic Functions With Variations in Instructional Coverage. Journal of Educational Measurement, 25, 205-219. abstract

Bengt O. Muthén (1989). Using item-specific instructional information in achievement modeling Psychometrika, 54, 385-396. preview - concept

J. Roeleveld (2002). De kwaliteit van het basisonderwijs: dalen de Citoscores? Pedagogische Studiën, 79, 389- . samenvatting (.doc) Voor aantekeningen zie

Roeleveld analyseert trend in citoscores vergeleken met trends in PRIMA-resultaten taal, rekenen en abstract IQ.

L. Verschaffel, Br. Greer, & E. De Corte (2000). Making sense of word problems. Swets & Zeitlinger, review Christoph Selter;

Claire Stevenson (2012). Puzzling with potential. Dynamic testing of analogical reasoning in children. proefschrift Leiden. ophalen (deels nog embargo tot 2014)

Dynamic Testing: Measuring Inductive Reasoning in Children With Developmental Disabilities and Mild Cognitive Impairments. Journal of Cognitive Education and Psychology, 11, 159-178. [Springer-tijdschrift (sinds 2000); niet in UB VU] abstract

Robert J. Mislevy, Geneva Haertel, Britte H. Cheng, Liliana Ructtinger, Angela DeBarger, Elizabeth Murray, David Rose, Jenna Gravel, Alexis M. Colker, Daisy Rutstein & Terry Vendlinski (2013). A “conditional” sense of fairness in assessment. Educational Research and Evaluation, 19 121-140. abstract

Ik heb even oppervlakkig gekeken, en dan lijkt het mij dat dit een sleutelpublicatie is op de thematiek van capaciteiten-in-context. Mogelijk niet direct inhoudelijk (maar waarschijnlijk ook dat), maar indirect op de toetstechnische kwesties.

Dylan Molenaar & Denny Borsboom (2013) The formalization of fairness: issues in testing for measurement invariance using subtest scores, Educational Research and Evaluation, 19, 223-244. abstract

De auteurs gebruiken resultaten op subtests van een intelligentietest als casus. Waar ik benieuwd naar ben: welke raakvlakken heeft deze analyse met de thematiek van capaciteiten in contexten? Als die rakkvlakken er evident zijn, vraag ik Denny Borsboom om bij mij aan te schuiven in de analyse van de rekentoets-problematiek.

James A. Kuli, Robert L. Bangert-Drowns & Chen-Lin Kulik (1984). Effectiveness of Coaching for Aptitude Tests. Psychological Bulletin, 95, 179-188.

Sandra P. Marshall (1984). Sex Differences in Children's Mathematics Achievement: Solving Computations and Story Problems. Journal of Education Psychology, 76, ,194-204 abstract

K. Denise Muth (1984). Solving Arithmetic Word Problems: Role of Reading and Computational Skills. Journal of Education Psychology, 76, 205-210abstract

Zach Shipstead and Randall W. Engle (2013). Interference Within the Focus of Attention: Working Memory Tasks Reflect More Than Temporary Maintenance. Journal of Experimental Psychology: Learning, Memory, and Cognition, 39, 277-289 pdf

Adam Chuderski & Edward Neçka (2012). The Contribution of Working Memory to Fluid Reasoning: Capacity, Control, or Both? Journal of Experimental Psychology: Learning, Memory, and Cognition, 38, 1689-1710 abstract

Nash Unsworth & Randall W. Engle (2005). Working memory capacity and fluid abilities: Examining the correlation between Operation Span and Raven. Intelligence, 33, 67-81. pdf

Lyn English (Ed.) (2004). Mathematical and Analogical Reasoning of Young Learners. Erlbaum. [als eBook in KB] reviewed (preview blz. 1 en 2)

Is dit een aanwijzing dat redeneren in taal iets geheel anders is dan redeneren in wiskunde (rekenen), ook cognitief-psychologisch?

Stuart Shaw , Victoria Crisp & Nat Johnson (2012) A framework for evidencing assessment validity in large-scale, high-stakes international examinations, Assessment in Education: Principles, Policy & Practice, 19:2, 159-176. abstract

P.W. van Rijn, A.A. Béguin & H.H.F.M. Verstralen (2011): Educational measurement issues and implications of high stakes decision making in final examinations in secondary education in the Netherlands, Assessment in Education: Principles, Policy & Practice, 19:1, 117-136.abstract

Ik zou eigenlijk de tijd moeten nemen om op dit artikel een repliek te schrijven (ondertussen is het daar al weer te laat voor, natuurlijk). De filosofie van de auteurs is dat beslissingen juist of onjuist kunnen uitvallen, wat wel een begrijpelijk idee is, maar wie er langer over nadenkt zal ontdekken dat het vooral onzin is. Beleid voeren op basis van onzin is in het algemeen niet aan te raden. Ik zou dus graag een analyse maken waarin ik kan aantonen wat de ongewenste gevolgen zijn van de adviezen van het Cito die uit deze starre filosofie voortkomen. Ik heb er trouwens al een vruchteloos gebleken discussie met Anton Béguin over gevoerd, naar aanleiding van de reactie van hem en Zwitser op het artikel van Joost Hulshof en mij in Examens (september 2011).

Wat ik lees in de Discussie is nogal heftig probleemoplossen: intellectuele capaciteiten dus (al signaleren de auteurs dat zelf niet, maar het is verdraaid evident). Een interessante bespiegeling van de auteurs, aan het slot van hun artikel. Lees het maar alsof het over context-rekenen gaat.

Kinga Morsanyi, Amy Devine, Alison Nobes & Dénes Szucs (2013). The link between logic, mathematics and imagination: evidence from children with developmental dyscalculia and mathematically gifted children. Developmental Science, online first

H. Lee Swanson (2006). Cross-sectional and incremental changes in working memory and mathematical problems solving. Journal of Educational Psychology, 98, 265-281. abstract

James A. Holdnack (ca. 2001). Defining the role of intellectual and cognitive assessment in special education. The Psychological Corporation. pdf

Een heel andere doelgroep, maar dat maakt de analyse van testen op verschillen in intellectuele capaciteiten versus toetsen op prestaties nog niet meteen een heel andere. Uitvoerige literatuurlijst uit een andere dan de gebruikelijke gebieden.

Charles Clifton, Jr. and Susan A. Duffy (2001). Sentence and Text Comprehension: Roles of Linguistic Structure. Annual Review of Psychology, 52, 167-196. abstract

Arthur B. Markman & Dedre Gentner (2001). Thinking. Annual Review of Psychology, 52, 223-247. pdf

P. N. Johnson-Laird (1999). Deductive reasoning. Annual Review of Psychology, 50, 109-135. pdf

Mark H. Ashcraft & Jeremy A. Krause (2007). Working memory, math performance, and math anxiety. Psychonomic Bulletin & Review, 14. 243-248. pdf

Kerry Lee, Swee-Fong Ng, Ee-Lynn Ng & Zee-Ying Lim (2004). Working memory and literacy as predictors of performance on algebraic word problems. J. Experimental Child Psychology 89 (2004) 140-158. abstract

Daniel L. Shea, David Lubinsky & Camilla P. Benbow (2001). Importance of Assessing Spatial Ability in Intellectually Talented Young Adolescents: A 20-Year Longitudinal Study. Journal of Educational Psychology, 93, 604-614. pdf

Amélie Lubin, Julie Vidal, Céline Lanoë, Olivier Houdé, and Grégoire Borst (2013). Inhibitory Control Is Needed for the Resolution of Arithmetic Word Problems: A Developmental Negative Priming Study. Journal of Educational Psychology, 105, 701-708. abstract

Colleen M. Ganley & Marina Vasilyeva (2013). The Role of Anxiety and Working Memory in Gender Differences in Mathematics. Journal of Educational Psychology, 105, online first. abstract

Het belang van dit onderzoek voor de thematiek van capaciteiten in contexten is misschien niet meteen duidelijk uit de titel, maar als waar is wat de titel suggereert, dan laat dat zien hoe wiskundeopgaven onbedoeld kunnen testen op verschillen in intellectuele capaciteiten (al dan niet inclusief wiskundevrees). Belangrijker is of dit onderzoek iets laat zien van effecten van meer of minder capaciteit van werkgeheugen op prestaties op een reken- of wiskundetoets, en ook nog iets onthult over de kenmerken van de opgaven die daar dan mee hebben te maken: zijn dit wel opgaven waarop de kandidaten zich doeltreffend hadden kunnen voorbereiden, en zo ja, is er reden om aan te nemen dat sommige kandidaten zich dan toch niet voldoende hadden voorbereid?

Zhen Zhu (2007). Gender differences in mathematical problem solving patterns: A review of literature. International Education Journal, 2007, 8(2), 187-203. pdf

Daniel Voyer (1996). The Relation Between Mathematical Achievement and Gender Differences in Spatial Abilities: A Suppression Effect. Journal of Educational Psychology, 88, No. 3, 563-571 abstract

Richard Catrambone (1998). The subgoal learning model: Creating better examples so that students can solve novel problems. Journal of Experimental Psychology, 127, 355-376. abstract en/of pdf

Ik heb een strak model nodig om contextopgaven te kunnen analyseren. Catrambone geeft dat, althans voor bepaalde klassen van problemen. Hij begint met meteen twee voorbeelden die tevens duidelijk maken dat leerlingen een probleem hebben wanneer opgaven oppervlakkig gezien van hetzelfde type zijn, maar toch een andere oplossing vragen. In dit geval is het algebraïsch, maar dat doet aan het principe niet af. De insteek is een didactische, in zekere zin. Van de onderstaande voorbeelden begrijp ik overigens de uitwerking niet. Tom heeft nog maar ³⁄₄e van zijn grasveld te maaien, dus ³⁄₄ × 1,5 = 1,13 uur. De Bill & Fred-opgave is zo dubbelzinnig als wat: als samenwerken inhoudt dat zij afspreken ieder de helt te schilderen, zijn ze samen 1,5 + 2,5 = 4 uur. Kennelijk kan ‘samen’ ook twee radicaal verschillende betekenissen hebben! Het hier gekozen rekenmodel gaat uit van samen aan de slag totdat het werk klaar is. Ik moet het bij Reed, Ackinclose & Voss (1990) maar eens checken.

Alvin Vista (2013 online first). The role of reading comprehension in maths achievement growth: Investigating the magnitude and mechanism of the mediating effect on maths achievement in Australian classrooms. International Journal of Educational Research, 62, in progress/online first. abstract

Australië. Daar wordt sinds 2008 heftig getest, nationaal, een soort PPON. De rekentoetsen zijn bedoeld als intelligentietests, als ik het goed begrijp: het moet niet mogelijk zijn om erop te trainen. Interessant voor het huidige thema.

Theresa Richardson & Erwin V. Johanningmeier (1998). Intelligence testing: the legitimation of a meritocratic educational science. International Journal of Educational Research, 27, 699-714. abstract

Interessant. De titel is een contradictio-in-terminis, ik weet niet of de auteurs zich dat hebben gerealiseerd. Pro memorie. Ik moet tzt nog nagaan of er belangrijke kwesties in worden aangestipt.

Wim J. van der Linden (1998). A discussion of some methodological issues in international assessments. International Journal of Educational Research, 29, 569-577. abstract

Wim van der Linden spreekt niet direct over validiteit, maar indirect gaat vrijwel alles in dit opmerkelijk kritische artikel over validiteit van toetsen afgenomen in lastige situaties, in casu TIMSS. Bijvoorbeeld in sectie 3 Sampling of curricular content snijdt hij kwesties aan die makkelijk kunnen leiden tot aantasting van de validiteit van TIMSS zoals bedoeld. Wie die sectie leest met in het achterhoofd de stelling dat de rekentoets-3F verschillen in intellectuele capaciteiten meet, komt tot enkele mogelijke concrete uitwerkingen daarvan, zoals kwesties van transparantie (de mogelijkheid tot doeltreffende voorbereiding, in Grootiaanse zin).

B. G. Palland (1935). Een intelligentieonderzoek op een tiental Amsterdamse scholen. Mededelingen van het Nutsseminarium voor Paedagogiek aan de Universiteit van Amsterdam. No. 25. J. B. Wolters Uitgevers-Maatschappij. pdf 30Mb scan

Nutsseminarium (1938). Rapport van het Nutsseminarium aan de directeuren, vereniging van hogere burgerscholen in de voormalige 5e inspectie, naar aanleiding van de proef in September 1936 genomen met taal- en rekenwerk in den geest van het rapport-Bolkestein. Mededelingen van het Nutsseminarium voor Paedagogiek aan de Universiteit van Amsterdam. No. 32. J. B. Wolters Uitgevers-Maatschappij. pdf 13Mb scan

T. Kuiper (1929). De plaats van het testonderzoek in de aansluiting tussen lager- en middelbaar onderwijs. Mededelingen van het Nutsseminarium voor Paedagogiek aan de Universiteit van Amsterdam. No. 7. J. B. Wolters Uitgevers-Maatschappij. pdf 19Mb scan

Mark D. Leblanc & Sylvia Weber-Russell (1996). Text Integration and Mathematical Connections: A Computer Model of Arithmetic Word Problem Solving. Cognitive Science, 20, 357-407. pdf

M. Bartels, M. J. Rietveld, G. C. Van Baal & D. J. Boomsma (2002). Heritability of educational achievement in 12-year-olds and the overlap with cognitive ability. Twin Res., 5, 544-553. abstract en het hele artikel pdf

C. M. Haworth, K. Asbury, P. S. Dale & R. Plomin (2011). Added value measures in education show genetic as well as environmental influence. PLoS One. 2011 Feb 2;6(2):abstract

Het moet niet veel gekker worden. Als ik me niet vergis, is Plomin niet de eerste de beste onderzoeker van erfelijkheid van verschillen in gedrag. Ik vergis me niet. Het lijkt me, de discussie gelezen hebbend, prima onderzoek. Maar let wel op, want er zitten tegenintuïtieve verbanden in deze thematiek, en de auteurs geven dat in de discussie ook aan. Een onjuiste, romantische maar daarom nog wel onzinnige beschouwing in dezelfde discussie: de aansporing tot omhelzen van ‘het nieuwe leren’, gezien resultaten zoals uit dit onderzoek. Daar is geen splinter van empirisch bewijs voor aangedragen.

Arne Evers, Wouter Lucassen, Rob Meijer & Klaas Sijtsma (2010). COTAN Beoordelingssysteem voor de kwaliteit van tests. Nederlands Instituut van Psychologen (NIP). pdf

Evers, A., Caminada, H., Koning, R., Laak, J. ter, Maesen de Sombreff, P. van der, & Starren, J. (1988). Richtlijnen voor ontwikkeling en gebruik van psychologische tests en studietoetsen. Nederlands Instituut van Psychologen (NIP) [transcriptie van hoofdstuk 8 over toetsen

Means, M. L., & Voss, J. F. (1996). Who reasons well? Two studies of informal reasoning among children of different grade, ability, and knowledge levels. Cognition and Instruction, 14, 139-178. abstract

Richard Barwell (Ed.) (2009). Multilingualism in Mathematics Classrooms : Global Perspectives. Channel View Publications. [als eBook te leen van de KB] frontmatter

Pat Drake, Geoff Wake & Andrew Noyes (2012). Assessing 'functionality' in school mathematics examinations: what does being human have to do with it? Research in Mathematics Education, 14, 237-252 abstract [paywalled]

Daeun Park, Gerardo Ramirez & Sian L. Beilock (2014) The role of expressive writing in math anxiety. Journal of Experimental Psychology: Applied (online first) [I have no access to a pdf] abstract

This research shows that math anxiety impacts on capacity of short term memory available for problem solving. Math anxiety therefore will tend to lower achievement on math tests. The prevalence of math anxiety is a threat to the validity of math tests.

Jamie J. Jirout & Nora S. Newcombe (2015). Building Blocks for Developing Spatial Skills. Evidence From a Large, Representative U.S. Sample. Psychological Science abstract

Sean P. Yee & Jonathan D. Bostic (2014). Developing a contextualization of students' mathematical problem solving. The Journal of Mathematical Behavior, 36, 1-19. research.net

The theoretical framework definitely is constructivist, reason for me not to study the article yet in detail. The research itself is not quite interesting (interviews of six students), the theoretical framework might be, exactly because of its constructivist character. I am rather put off (Sorry, Sean) by statements like:

http://www.benwilbrink.nl/projecten/capaciteiten_in_contexten.htm http://goo.gl/ZLCMi

Intellectuele capaciteiten in contexten: rekenopgaven

werkdocument Ben Wilbrink