wetenschapsopvatting — debat
observeren
drogredenen
— sectarisme — napraten — public relations — Wiskrant
constructivisme — geen empirisch onderzoek doen — ontwikkelingsonderzoek
Ik ben nog niet goed op dreef met de drogredenen te noteren zoals ik ze tegenkom. Er zijn trouwens enkele bronnen waarin ze bij bossen te vinden zijn: de boeken van Hans Freudenthal over didactiek; de verdediging van het realistisch rekenen zoals ondernomen door Adri Treffers en door Marja van den Heuvel-Panhuizen.
Ik reken beweringen die niet worden gestaafd door behoorlijke data, niet als zodanig tot de drogredenen. Iedereen heeft recht op de eigen opvattingen. Pas wanneer er van een opvatting wordt geconcluderd tot een of andere didactische noodzaak, zijn de rapen gaar: uitgaan van een onjuiste premisse is weliswaar in de logica geen doodzonde, maar in de werkelijke wereld ligt dat bepaald anders. In de echte wereld kan niet worden volstaan met de aanname dat een preisse juist is, maar moet de juistheid theoretisch en empirisch onderbouwd kunnen worden. Zora een auteur dat kleine verschil prbeert weg te poetsen, is r sprake van een drogreden. Ik vind dit trouwens wel een heel interessante klasse van drogredenen, waar de publicaties uit de Freudenthal-groep goed mee gevuld zijn. Bijvoorbeeld stilzwijgend ervan uitgaan dat ‘handig rekenen’ een bewezen plaats heeft in het rekendidactische bouwwerk; idem dat het groot goed is om wendbaar van geest te zijn als het gaat om mogelijke uitwerkingen van rekenopgaven.
Delen uit deze webpagina zijn overgenomen in het tijdschrift bi-logical, de redacteur heeft er een wel een grappig stuk van gemaakt:
Ben Wilbrink (2012). Hebben er twee ruzie? Dan hebben ze beide een beetje gelijk . . . bi-logical, 4, juli, 33-34
Bijna oneindig veel interessanter in datzelfde nummer van bi-logical: Gravity demystified: Entropic force and the emergence of laws of Newton. Interview with Erik Verlinde. 9-13 (zie ook blz. 14).
Frans H. van Eemeren, Rob Grootendorst, & Tjark Kruiger (1987). Handbook of argumentation theory. A critical survey of classical backgrounds and modern studies. Pragmatics and discourse analysis. FORIS Publications.
Ron J. Oostdam (1991). Argumentatie in de peiling. Aanbod en prestatiepeiling van argumentatievaardigheden in het voortgezet onderwijs. Proefschrift UvA. Amsterdam: SCO.
Karel Lambert & William Ulrich (1980). The nature of argument. Macmillan.
Maurice A. Finocchiaro (2005). Arguments about arguments. Systematic, critical and historical essays in logical theory. Cambridge University Press.
Kuhn, Deanna Kuhn (1991). The skills of argument. Cambridge University Press.
Antoine Braet (2007). De redelijkheid van de klassieke retorica. Leiden University Press.
Het meest beruchte valse dilemma van de 21e eeuw is ongetwijfeld de uitspraak van George W. Bush: Wie niet met ons is, is tegen ons. Nu terug naar de discussie over het onderwijsonderwijs.
Er zijn twee mogelijkheden in de rekendidactiek: eerst oefenen, of eerst begrijpen. Eerst oefenen is mechanistisch, daar willen we juist vanaf, dus is de juiste volgorde: eerst begrijpen, dan oefenen.
Ik zal hiervoor de nodige vindplaatsen bijeenbrengen. Voor een review van de internationale literatuur zie alvast Rittle-Johnson & Siegler, 1998.
Bethany Rittle-Johnson & Robert S. Siegler (1998). The relation between conceptual and procedural knowledge in learning mathematics: A review. In Chris Donlan: The Development of Mathematical Skills. Psychology Press.
Voor annotaties bij dit hoofdstuk zie begrijpen_vs_oefenen.htm#R-JS
Een persoonlijke herinnering aan het mondeling eindexamen wiskunde mag hier dienen om te laten zien dat er een heel scala van mogelijkheden ligt tussen de extreme posities van eerst oefenen versus eerst begrijpen. Ik zie hier dus even af van de problemen die er zijn met vaststellen of een leerling iets aan het oefenen is, of aan het begrijpen: het zijn psychologische categorieën die niet behoorlijk door introspectie zijn te observeren.
Ik had in klas 5 en 6 moeite met analytische meetkunde, ik kon dat op de een of andere manier niet in mijn systeem krijgen: ik kon de opgaven redelijk maken, maar ik wist dat ik iets wezenlijks miste in mijn begrip van analytische meetkunde. Analytische meetkunde en gonio werden mondeling geëxamineerd, op de tweede examendag, de vrijdag na hemelvaart. De vrije dag benutte ik om de stof nog eens grondig door te nemen, en verdraaid, het kwartje viel! Ik begreep de stof, kon er alles mee doen wat maar te bedenken viel. Noel Entwistle noemt dit fenomeen een 'knowledge object', het is een opvallende variant op de algemene ervaring dat pas vlak voor het tentamen of examen een zo goed overzicht over de stof wordt bereikt, dat de stukken en stukjes op hun plek vallen.
Het gesprek met docent en gecommitteerde leverde mij een 10 op. Dat is een mooi resultaat, maar omdat ik geen wiskunde ben gaan studeren, is mijn inzicht in analytische meetkunde volkomen vervlogen. Alles is betrekkelijk. Het perfecte resultaat geeft aan dit hier inderdaad sprake moet zijn van plotseling en compleet inzicht, hoe kort dat misschien ook heeft bestaan, op basis van een grondige kennis van de stof die uiteraard niet verworven kon zijn zonder enig inzicht in de betreffende deelonderwerpen.
Ik heb dit voorbeeld gebruikt in een bijeenkomt van SLO, Enschede, 12-9-2011
Noel Entwistle (1995). Frameworks for understanding as experienced in essay writing and in preparing for examinations. Educational Psychologist, 30, 47-54.
Binnen de Freudenthal-groep wordt onderwijsontwikkeling stelselmatig ontwikkelingsonderzoek genoemd — meestal design research in engelstalige publicaties. Het is een misleiding die de groep geen windeieren heeft gelegd (zie ook pr.htm#stelling1): talloze publicaties, waaronder proefschriften, zijn onder deze valse vlag gepresenteerd als zou het gaan om wetenschappelijk onderzoek. Ik zou hier graag kritieken uit de wetenschappelijke literatuur bijeenbrengen, waarin de misleiding expliciet of in vriendelijke bewoordingen impliciet wordt aangekaart.
Een vroeg gebruik van de term, in de titel van een proefschrift, is Goffree (1979), in de interessante samenstelling: onderwijsontwikkelingsonderzoek. [Ik moet nog opslaan wat Goffree over deze term zegt: hij geeft ongetwijfeld een toelichting]
Fred Goffree (1979). Leren onderwijzen met Wiskobas. Onderwijsontwikkelingsonderzoek ‘Wiskunde en Didaktiek’ op de pedagogische akademie. Proefschrift Rijksuniversiteit Utrecht.
Het valt op dat er veel publicaties zijn die dat ontwikkelingsonderzoek zelf tot onderwerp hebben, om te rechtvaardigen dat het hier toch echt om heus onderzoek gaat, dat zich laat vergelijken met wat elders onder wetenschappelijk onderzoek wordt verstaan, maar dat veel beter past bij het goede werk dat onderwijsontwikkelaars in het onderwijsveld zelf verrichten. Ook in publicaties onder de vlag van ontwikkelingsonderzoek is er vaak een afzonderlijke paragraaf of een apart hoofdstuk waarin nut en noodzaak van het benoemen van onderwijsontwikkeing als ontwikkelingsonderzoek wordt beargumenteerd. Het meest saillante voorbeeld van een dergelijk afzonderlijk hoofdstuk is waarschijnlijk dat in het proefschrift van Koeno Gravemeijer (het zijn twee hoofdstukken): ‘4. Educational development and developmental research in mathematics education’, en ‘6. Developmental research revisited’.
Gravemeijer, K. P. E. (1994). Developing realistic mathematics education. Freudenthal Institute, CD β Press.
Ik geef meteen maar een voorbeeld: op je vingers rekenen, dat doen leerlingen later nooit meer. Betekent het dat het stadium van tellen op de vingers maar handiger kan worden overgeslagen?
Nu wordt in veel publicaties van de Freudenthal-groep beweerd dat volwassenen eigenlijk niet meer rekenen, anders dan met hulp van een rekenmachine, zodat het vaardig worden in cijfermatig rekenen geen doel meer dient. Zou het eerste deel van de voorgaande stelling juist zijn — wat mijns inziens niet het geval is maar hoe dan ook een empirische kwestie — dan volgt daar niet de juistheid van het tweede deel uit. Suggereren dat dat wel het geval, komt neer op het hanteren van een drogreden.
In deze paragraaf aandacht voor uitspraken van de president van de KNAW. Juist omdat Robbert Dijkgraaf geen voorvechter van de theorie van het realistisch rekenen is, is het verhelderend om te zien hoe hij positie kiest tegenover de rekendiscussie (niet ‘in’ de rekendiscussie, hoewel er redenen zijn waarom hij dat juist wèl zou moeten doen). Maar eerst even een anonieme bron.
Onlangs kwam ik als betiteling voor de discussie over het rekenonderwijs het woord ‘stammenstrijd’ tegen. Dat berust kennelijk op de gedachte dat er sprake is van twee stromingen die over het rekenonderwijs verschillend denken, en die ieder evenveel recht op hun standpunt hebben. Dat kan voor bepaalde discussies best het geval zijn, en zodra een discussie politiek wordt is het bijna per definitie zo.
In de wetenschap gaat dat toch anders. Daar speelt kracht van argumenten een rol, argumenten die berusten op theorie en dus op empirisch onderzoek. Dat wil niet zeggen dat ieder verschil van opvatting dan ook beslisbaar is, bijvoorbeeld door een cruciaal experiment uit voeren (W. K. B. Hofstee heeft dit uitgewerkt in zijn weddenschapsmodel: De empirische discussie. Boom, 1981), maar in veel gevallen is dat welk degelijk zo.
Robbert Dijkgraaf (2011). Over rekendidactiek en -vaardigheid, Wiskunde A of B en profielkeuze. bi logical, 3 nr 1, 33-35.
Met andere woorden, beweren dat er geen verschillen zijn tussen de effecten van de ene of de andere rekendidactiek is niet bepaald correct, maar het accentueren van de ene of de andere methode maakt de tweespalt alleen maar groter.
Wat Dijkgraaf hier schrijft zou betekenen dat iedere bijdrage aan de discussie, ook een zinvolle, het conflict alleen maar groter zou maken. Is Dijkgraaf, voorzitter van de KNAW, dan de grote conflictbedwinger? Door juist niet enig inhoudelijk argument te gebruiken? Hij heeft een eigen commissie gehad (de commissie-Lenstra), die hij ten onrechte citeert als zou de commissie een neutraal advies hebben gegeven. De commissie heeft immers de stormbal gehesen: Nederland heeft nu een vorm van rekenonderwijs die niet berust op enig deugdelijk wetenschappelijk fundament. Zeker, er dus ook geen bewijs dat het realistisch rekenen niet deugt, maar dat is niet het springende punt.
Er is een enorme polarisatie ontstaan waarbij de twee kampen vanuit de loopgraven elkaar bestoken.
Luister, Robbert, als je geen gelegenheid hebt om zelf de situatie te bestuderen, zie dan ook af van het doen van malle uitspraken zoals de geciteerde. Dat werpt immers olie op het vuur.
Door zichzelf toe te staan in termen van polarisatie en strijdkampen te denken, komt Dijkgraaf tot een onjuiste analyse van wat de commissie-Lenstra heeft opgeleverd.
Vanuit de academische wereld is scherp ingezet op bijzondere wiskundige vaardigheden die nodig zijn in de bèta-wetenschappen, zoals abstractie, conceptueel denken. Een ander gezichtspunt is een meer algemene ‘gecijferdheid’. Dit blijkt breed gedragen te worden.
p. 34 kolom 1 punt (1)
Wie dragen deze standpunten uit? Dit zijn karikaturen, tegenover elkaar gezet als zouden het elkaar uitsluitende posities zijn.
Dijkgraaf constateert terecht dat het grote gemis in deze kwestie het ontbreken van empirisch onderzoek is, maar doet toch zelf uitspraken die alleen zinvol zijn wanneer daar empirische ondersteuning is, quod non.
Nu we nog even bij het interview met Robbert Dijkgraaf zijn: hij geeft daarin eveneens een belangrijke misvatting over het matchen van leerlingen en onderwijsmethoden: de stilzwijgende vooronderstelling dat er een interactie zou zijn tussen methoden en talenten — een aptitude treatment interaction (ATI) (Cronbach & Snow, 1977). [Ik meen dat Tjeerd Plomp op dit onderwerp is gepromoveerd, eind zeventiger jaren; publicatie van het CDO]
Robbert Dijkgraaf (2011). Over rekendidactiek en -vaardigheid, Wiskunde A of B en profielkeuze. bi logical, 3 nr 1, 33-35.
De grote les is dat weinig onderzoek is verricht, veelal worden gezichtspunten verdedigd vanuit een introspectie (bijvoorbeeld directe ervaringen van docenten vanuit het realistisch rekenen, RR). Hierbij moet je volgens mij de vraag stellen: ‘voor welke scholieenpopulatie gebruik je welk didactisch vakmanschap en op welke manier?’. Sommige kinderen zijn bijvoorbeeld meer gebaat bij abstractere rekenmethodes. Kinderen die een hoger abstractieniveau aankunnen, haken af wanneer iets als te alledaags wordt voorgesteld.
p. 34 kolom 1 punt (3)
Het probleem met dit voor de hand liggende idee, zoals door Dijkgraaf verwoord, is dat zoiets in de werkelijkheid van het onderwijs meestal niet aantoonbaar is. En dat betekent eenvoudig het volgende: dat een methode die beter werkt voor groep A, dat ook doet voor groep B en C. Maar misschein is er voor rekenonderwijs wel eens iets opmerkelijks gevonden? Een snelle googel levert op:
Douglas B. McLeod & Verna M. Adams (1980). Aptitude-treatment interaction in mathematics instruction using expository and discovery methods. Journal for Research in Mathematics Education, 11, 225- . first page.

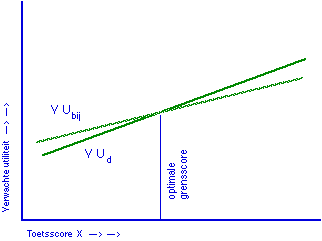
De afbeelding laat het principe van een ATI zien: er zijn twee behandelingen mogelijk, de verwachte effecten zijn door de twee regressielijnen aangegeven. Omdat de regressielijnen elkaar snijden, is er een interessante interactie (interacties zonder snijpunt in het relevante bereik, zijn er natuurlijk wel meer, maar die zijn niet van belang voor differentiëele behandelingsmogelijkheden): de ene behandeling is effectiever voor de groep die laag scoort, de andere voor de groep die hoog scoort. De afbeelding is niet die van een empirische situatie, maar geeft de ATI-veronderstelling weer. In dit geval zijn de twee behandelingen: leerlingen doorlaten of eerst laten bijspijkeren. Zie het artikel waar ik de afbeelding uit heb genomen:
Ben Wilbrink (1980). Enkele Radicale Oplossingen voor Criterium-Gerefereerde Grensscores. Tijdschrift voor Onderwijsresearch, 1980, 5 nr. 3, 112-125. html
Als wetenschappelijk onderzoek naar de doelmatigheid van methode A een negatief resultaat oplevert — de methode blijkt het voorspelde betere resultaat niet te leveren — dan is het een drogreden om daaruit te concluderen dat er wél een positieve uitkomst zal zijn wanneer de inspanningen maar worden vergroot, de kennis van de leraren beter is, er meer urem voor de methode beschikbaar komen, enzovoort.
Het lastige is natuurlijk dat het onderzoek methodologische tekorten kan hebben, zoals een veel te kleine steekproef, waardoor eenvoudig de power ontbreekt om een positief resultaat te kunnen laten zien wanneer dit er in werkelijkheid ook is. Interessant is om eens uit te zoeken of het gemiddelde ‘ontwikkelingsonderzoek’ precies dit gebrek heeft (een te kleine steekproef, of een niet random getrokken steekproef, of een combinatie van die twee), en dan te turven hoe de onderzoekers de resultaten van die ontwikkelingsonderzoeken inschatten: zijn ze positief, of niet? Bij onderzoeken met te weinig power is de verwachting immers dat de resultaten vooral toevallig verdeeld zullen zijn, en dus maar een fractie van die resultaat significant positief kan zijn. Maar ja, statistisch toetsend onderzoek en ontwikkelingsonderzoek gaan volgens de voorstanders van het laatste type onderzoek, niet samen. Hans Freudenthal was mordicus tegen al die statische toestanden.
Deze drogreden is gebrukt bij het wegredeneren van de slechte resultaten van de PPON 2004: als je de leerlingen maar dwingt om de opgaven op papier uit te rekenen, halen ze betere resutaten.
Deze drogreden is gebruikt in de rapportage van het MORE-onderzoek: als de leraren beter zijn opgeleid in de bedoelingen en de didactiek van het realistisch rekenen, dan zullen ze toch wel betere rekenresultaten boeken dan hun collega’s die gewoon rekenonderwijs geven.
De Freudenthal-groep heeft zich schuldig gemaakt en maakt zich schuldig aan het massaal stereotyperen van het gewone rekenonderwijs als zou dat mechanistisch zijn, trucjes-onderwijs, het onderwijs van opa. Een gevolg daarvan is dat er nogal wat leraren zijn die de standaard-rekenalgoritmen associëren met dat gewone onderwijs, en ze beschouwen als schadelijk voor de eigen leerlingen. Ook binnen de Freudenthal-groep komen extreme opvattingen voor over de standaard-rekenalgoritmen, zie de pagina over algoritmen (o.a. Uittenbogaard, 2008, in reactie op Van de Craats, 2007. Panama Post).
De betiteling van het gewone rekenonderwijs als mechanistisch, gaat terug op Adri Treffers, die vier typen van rekenonderwijs benoemde waarvan mechanistisch rekenonderwijs en realistsich rekenonderwijs de belangrijkste zijn. Deze karakteristiek en zijn streotyperende benadering is door Hans Freudenthal geaccepteerd.
Ik zal in deze paragraaf de nodige vindplaatsen bijeenbrengen.
Het gewone rekenonderwijs aangeduid als mechanistisch rekenonderwijs is te vinden in een van de weinig onderzoeken van de Freudenthal-groep die wetenschappelijk mogen heten: het MORE-onderzoek (Gravemeijer en anderen, 1993). De opdrachtgever van dit onderzoek, de Stichting voor Onderwijsonderzoek in DennHaag (de onderzoekmakelaar voor OCW), heeft de rapportage van dit onderzoek, inclusief deze stereotypering, geaccepteerd.
Ook het aanduiden van rekenonderwijs volgens Wiskobas als realistisch rekenen is tendentieus: een zelfgekozen stereotypering die de eigen methode op voorhand in een gunstig daglicht stelt, tegenover de mechanistische competitie. Zo worden in het MORE-onderzoek een ‘mechanistische’ rekenmethode tegenover een ‘realistische’ rekenmethode onderzocht. Zo’n onderzoek heeft het voordeel dat het de onderzoekers dwingt om te preciseren wat ze bedoelen met deze stereotyperende aanduidingen. Dan blijkt dat het, als puntje bij paaltje komt, gaat om specifieke opvattingen (van leraren), handelingen (te observeren in de klas), uitwerking (te analyseren in de methode-boekjes) en resultaten (op specifieke toetsvragen). Al deze zaken kunnen meer of minder kenmerken hebben van wat gewoon rekenonderwijs is, respectievelijk wiskobasonderwijs.
P. Woestenenk (1976). Rekenen/wiskunde op de basisschool. Tjeenk Willink/Noorduijn.
Typerend voor rekenonderwijs in oude stijl is het streven, zo spoedig mogelijk te komen tot het maken van ‘sommetjes’.
Woestenenk, eerst zin, blz. 11
Woestenenk behoort niet tot de Freudenthal-groep, voorzover mij bekend, maar hij is kennelijk gegrepen door hetzelfde gevoel dat het bestaande rekenonderwijs niet deugt, en nodig moet worden vernieuwd. De geciteerde zin krijgt zijn kwalijke lading door afkeuring die erin doorklinkt. Want laten we wel wezen: wat is er eigenlijk op tegen om zo spoedig mogelijk te komen tot het maken van sommetjes? Tja, als er een bullebak voor de klas staat, die er een lijdensweg van maakt .... Maar bullebakken zijn van alle tijden, dat fenomeen heeft niet cirect iets met rekendidactiek te maken. De drogreden is in dit geval dus niet dat er een stroman wordt opgericht, maar dat een met slechts enkele woorden aangeduide mogelijke praktijk zonder enige argumentatie wordt weggezet als afkeurenswaardig. Geloven wij deze boodschapper? Wil ik dit boek nog verder lezen, na deze openingszin? Jawel hoor. Ik laat me door zo’uitglijer daarvan niet weerhouden.
Anne K. Morris (2007). Factors affecting pre-service teachers’ evaluations of the validity of students’ mathematical arguments in classroom contexts. Cognition and Instruction, 25, 479-522. abstract
Ik noem dit onderzoek van Morris hier, omdat ik vermoed dat in de publicaties van de Freudenthal-groep nogal eens dezelfde logische misvattingen voorkomen als door Morris waargenomen in klassikale sitaties. Het lijkt alsof dit weer een geintje van mij is, maar ik meen het serieus: logisch correct argumenteren, bijvoorbeeld in de rekendiscussie, is niet het sterkste punt van de wiskundigen in de Freudenthal-groep. Het lijkt me verhelderend wanneer ik bijvoorbeeld in de oratie van Van den Heuvel-Panhuizen de logische argumenten inventariseer, en volgende de fouten-categorieën van Morris rangschik. Maar dat kost tijd, die tijd heb ik nog even niet.
![]() http://www.benwilbrink.nl/projecten/drogredenen.htm
http://www.benwilbrink.nl/projecten/drogredenen.htm