In Nederland heeft het probleem van het kiezen van grensscores altijd al in de belangstelling gestaan, omdat in ons onderwijs (helaas) nogal de nadruk wordt gelegd op voldoende - onvoldoende beoordelingen. In de Verenigde Staten heeft het grensscoreprobleem pas de laatste tien jaar sterk de belangstelling van voornamelijk theoretici getrokken, vanuit de wens om bij criteriumgerefereerde toetsen op verantwoorde wijze grensscores te bepalen. Een overzicht van de resultaten van dat theoretisch werk wordt gegeven door Hambleton et al. (1978), terwijl Glass (1978) verschillende benaderingen heeft gekritiseerd.
De meest belovende aanpak van het probleem hoe de grensscore in omschreven zin optimaal te kiezen is met gebruikmaking van de technieken uit de decisie-analyse (Raiffa en Schlaifer 1961, Raiffa 1968, Lindley 1971, Keeney en Raiffa 1976). Het is ook de enige benadering die in de ogen van Glass genade kan vinden. De moeilijkheid is echter dat tot nog toe alle auteurs die vanuit deze benadering optimale grensscores zoeken te bepalen daarbij wiskundige technieken nodig hebben die hen het contact met de mensen in het onderwijsveld hebben doen verliezen. Exponent bij uitstek hiervan is wel het werk van Huynh (1976, 1977). Is het nodig om ingewikkeld te doen over optimale grensscorebepaling? Ik dacht het niet, en zal in dit artikel een werkelijk eenvoudig alternatief aanreiken (Huynh noemde zijn methode al simpel, vandaar). Daarmee zijn we nog niet uit de problemen, omdat alle tot nu toe aangereikte methoden lijden aan een kwaal die ik in de discussie zal aanduiden, en waarvoor de medikatie in een tweede artikel zal worden aangereikt (Wilbrink, 1980).
Toetsen waarbij de behaalde score in de eerste plaats iets zegt over de mate waarin de getoetste leerstof beheerst wordt noemen we vandaag de dag criteriumgerefereerd (hoewel domeingerefereerd eigenlijk een betere term zou zijn, verwijzend naar het domein van toetsvragen waaruit de toets is samengesteld). Toetsen waarbij de score allereerst aan moet geven of de prestatie beter of slechter is dan die van andere leerlingen heten in dit jargon dan normgerefereerd.
Meestal wordt met de term 'criteriumgerefereerde toetsen' gedoeld op kleine voortgangstoetsen, zoals die bijvoorbeeld in individuele studiesystemen worden gebruikt. Maar het is ook niet ongebruikelijk om jaarlijks af te nemen diagnostische toetsen over een bepaald vak, meestal door bedrijven als CTB/McGraw-Hill geproduceerd, zo te noemen (Hambleton en Eignor, 1978). Op zich hoeft zo'n criteriumgerefereerde toets geen grensscore te hebben, als het gaat om toetsen van de mate van stofbeheersing. In de praktijk wordt op basis van de toetsscore beslist over de voortgang naar het volgende studieonderdeel, en dan ontstaat er wél een grensscoreprobleem. Er moet worden vastgesteld welke score tenminste behaald moet zijn om zonder bijspijkeren door te kunnen gaan met het verdere studieprogramma. Een stille omwenteling in de betekenis van criteriumgerefereerd toetsen, door meerdere auteurs gesignaleerd, en betreurd (laatstelijk door Glass).
Ervan uitgaande dat er een grensscore moet worden aangewezen, is de vraag hoe de beste grensscore kan worden gevonden. Een bijna traditioneel geworden eerste stap is de herformulering van het probleem: als ik zou weten wat de beste beslissing is ten aanzien van een enkele leerling (mits die leerling niet om een bijzondere reden is gekozen) dan kan ik daaruit afleiden welke toetsscore de leerling tenminste zou moeten hebben om doorgelaten te worden (voldoende beoordeeld), en dan zou dat ook de optimale grensscore voor de overige leerlingen zijn.
De juistheid van de beslissing doorlaten of bijspijkeren wordt beoordeeld op een geschikt gekozen criteriumvariabele. Dat kan de onderliggende ware beheersing zijn, gedefinieerd als de proportie gekende vragen in het domein van vragen waaruit de toets is samengesteld. Dat lijkt de vanzelfsprekende weg bij criteriumgerefereerd toetsen, maar zeker voor toetsen in een individueel studiesysteem is er een andere goed aansprekende mogelijkheid. Wanneer wordt aangenomen dat de ware beheersing op het ene onderdeel van de stof bevorderlijk is voor de bestudering van het volgende onderdeel, ligt het voor de hand de score op de vervolgtoets als criteriumvariabele te nemen. Deze tweede mogelijkheid leent zich beter voor illustratieve doeleinden omdat de analyse een wat minder abstract karakter kan hebben dan ware scoreanalyse. Er valt wel meer te zeggen over de keuze van de criteriumvariabele, maar dat wil ik doen aan de hand van de problematiek die ik in een vervolgartikel aansnijd (Wilbrink, 1980).
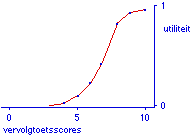
Aangenomen wordt dat er op de vervolgtoets een critische score, verder drempel te noemen, valt aan te wijzen. Het is gebruikelijk om daar letterlijk een drempel mee te bedoelen: er is een kwalitatief verschil tussen scores boven en scores beneden de drempel. In het leren-voor-beheersing jargon zou je zeggen dat scores beneden de drempel er op wijzen dat beheersing (nog) niet aanwezig is. Ik geloof niet dat het verstandig is om die drempel zo extreem op te vatten. Het is ook al prachtig wanneer de docent een streefniveau op de vervolgtoets kan aanwijzen, dat als drempel kan functioneren. In simpele gevallen zou de docent de overtuiging kunnen hebben dat goed kunnen beantwoorden van 8 uit 10 vragen het niveau is waar hij naar streeft en dat betere prestaties welkom zijn maar niet zo nodig hoeven. In minder eenvoudige gevallen kan de docent zijn streefniveau bepalen aan de hand van zijn utiliteitsfunctie over vervolgtoetsscores. Zo'n utiliteitsfunctie zou er uit kunnen zien als in figuur 1. Het gaat daarbij om de relatieve waardering die de docent voor de verschillende mogelijke toetsscores heeft. Voor het opstellen van dergelijke utiliteitsfuncties geven Keeney en Raiffa (1976) de technieken. Een iets andere benadering is te vinden bij Siegel (1957), zie ook Becker- en Siegel (1962), waarop misschien te verbeteren valt met een door Goode ontwikkelde methode (besproken in Van der Ven, 1977). Siegel zoekt alleen de verschillen in utilileit tussen verschillende mogelijke scores te bepalen. In de praktijk zou zijn techniek, die werkt met paarsgewijze vergelijkingen, daarom wel eens de eenvoudigst hanteerbare kunnen zijn.

Figuur 1. Mogelijke utiliteitsfunctie over scores op een vervolgtoets bestaande uit 10 vragen. Verkregen door ordered metric scaling.
In de definitie van Siegel (1957) is het streefniveau de hoogste van de twee scores waartussen de koorde het steilst is. In figuur 1 is de score 8 het streefniveau, en zou dan ook als drempel op de vervolgtoets gekozen kunnen worden.
De drempel op de vervolgtoets hoeft niet gelijk aan de op die vervolgtoets te hanteren grensscore te zijn, hoewel er geen al te groot verschil tussen beide zal bestaan. De drempel is het meest gewenste niveau van stofbeheersing, terwijl bij het bepalen van de grensscore rekening wordt gehouden met de gevolgen van ten onrechte door laten gaan of laten bijspijkeren.
Een verfijning die ik hier buiten beschouwing laat is dat de drempel eigenlijk aangewezen wordt op de onderliggende ware stofbeheersing, zodat je vervolgtoetsscores om precies te zijn zou moeten vervangen door de bijbehorende geschatte ware scores.
De onzekerheid bij het beslissen over een enkele leerling is of hij op de vervolgtoets de drempel zal halen. Zijn we nu zo gelukkig empirische gegevens ter beschikking te hebben over het verband tussen toetsscores en vervolgtoetsscores, dan is de oplossing al in zicht. Dan kunnen we immers een schatting maken van de waarschijnlijkheid dat een leerling i die een toetsscore Xi blijkt te hebben, op de vervolgtoets tenminste gelijk aan de drempel scoort.
Wie het van belang vindt of er meer of minder ver boven of onder de drempel wordt gescoord, kan beter niet met drempels werken. Ik verwijs naar Davis et al. (1973), v.d. Linden en Mellenbergh (1977), en Wilbrink (1980). Davis et al. (1973) laten zien dat bij lineaire en andere uitkomstutiliteitsfuncties het aanwijzen van een drempel niet nodig is. Ook bij v.d. Linden en Mellenbergh is dat dus niet nodig, hoewel zij de indruk wekken dat de plaats van een aangewezen drempel ook bij hanteren van lineaire verliesfuncties van belang zou zijn. Aangetoond kan worden dat bij de door hen gegeven oplossing voor de optimale grensscore deze aangewezen drempel geen rol speelt. Mijn verontschuldiging voor het gebruik van technische termen die ik pas later introduceer, ik dacht hier alternatieven voor drempelgebruik te moeten aangeven.
voetnoot 1. De drempel bij v.d. Linden en Mellenbergh (1977) wordt in hun model gebruikt als oorsprong waaraan de vergelijkingen voor de lineaire functies gerefereerd zijn. Maar de keuze van oorsprong is irrelevant voor de oplossing van het optimale grenscoreprobleem, want daarbij speelt slechts het snijpunt (als dat bestaat) van de utiliteits- of verliesfuncties een rol. Zie ook de opmerking van v.d. Linden en Mellenbergh (blz. 598) in geval beide constanten a(0) en a(1) in beide functies aan elkaar gelijk zijn, dat is: het snijpunt van beide functies ligt dan precies op de plaats waar de drempel is aangewezen. In dat geval is de optimale grensscore de waarde voor X waar het verschil tussen de verwachte score op de criteriumvariabele en de drempel voor de eerste keer positief wordt. Opmerkelijk is dat Glass o.c. als enige kritiek op deze benadering van v.d. Linden en Mellenbergh heeft dat deze aanpak nog steeds van het willekeurig aanwijzen van een drempel afhankelijk zou zijn. Het aardige is nu dat die drempel in dat model geen rol speelt.
Bij het werken met grensscores vallen er altijd foute beslissingen: sommige leerlingen scoren voldoende maar hebben eigenlijk bijspijkeractiviteiten nodig, anderen scoren onvoldoende en zouden het best zonder bijspijkeren kunnen doen. Zouden beide soorten foute beslissing even vervelend zijn, dan neem je ten aanzien van een enkele leerling de beslissing die de hoogste waarschijnlijkheid heeft de juiste te zijn, en ligt de optimale grensscore daar waar de waarschijnlijkheid van beide fouten gelijk 0,5 is.
Vind je het daarentegen vervelender een leerling ten onrechte te laten bijspijkeren dan het is om een (andere) leerling ten onrechte te laten doorgaan, of omgekeerd, dan wordt het ingewikkelder omdat nu de fouten als het ware moeten worden gewogen. Eén van de manieren waarop je dat kunt doen is met gebruik van de verworvenheden van de decisieanalyse (bijvoorbeeld Raiffa en Schlaifer, 1961). Ik zal hier een eenvoudige techniek bij wijze van voorbeeld geven, en in een vervolgartikel (Wilbrink, 1980) verder op deze decisie-analytische benadering ingaan, en er alternatieven voor geven (tenminste, waar het erom gaat optimale grensscores te bepalen).
Voor een enkele leerling heb je te maken met vier mogelijke uitkomsten, weergegeven in figuur 2: er zijn twee beslissingsalternatieven, en ieder kan achteraf juist of onjuist blijken te zijn.
| vervolgtoetsscore | Y < Drempel | Y ≥ Drempel | |
| beslissing | 'voldoende' ( X ≥ Grensscore ) | D ten onrechte voldoende | B terecht voldoende |
| 'onvoldoende' ( X < Grensscore ) | C terecht onvoldoende | A ten onrechte onvoldoende | |
| waarschijnlijkheid | 1 - P i | P i | |
Figuur 2. Het grensscoreprobleem met 4 mogelijke uitkomsten.
Je zou nu aan iedere uitkomst een waarde kunnen toekennen, de uitkomstutiliteit, af te leiden uit de utiliteitsfunctie over bestede tijd en opgedane kennis. Gelukkig is het niet altijd nodig deze omslachtige weg te bewandelen. Noem de uitkomsten die je verkregen zou hebben als je het wél deed A, B, C en D, algebraïsche labels (zie figuur 2) die niet hoeven te worden gekwantificeerd. Ik ben op zoek naar de wegingsfactoren voor de beide onjuiste uitkomsten. Voor ten onrechte bijspijkeren is dat het verschil in utiliteiten ( B - A ), voor ten onrechte doorgaan is dat het verschil ( C - D ). Bovendien blijkt voor dit soort probleem alleen de ratio van beide van belang te zijn. De technische term:
(1) verliesratio L = ( B - A ) / ( C - D ).
De verliesratio drukt uit hoeveel erger je het vindt dat een leerling ten onrechte bijspijkeronderwijs volgt, dan dat een leerling ten onrechte doorgaat met het vervolgonderwijs. Dit geraamte in het vlees zettend zou je bijvoorbeeld kunnen zeggen: ( B - A ), het verlies van ten onrechte bijspijkeren en eventueel hertoetsen, bestaat uit het tijdverlies daarbij opgelopen; ( C - D ), het verlies bij ten onrechte doorgaan, is wat moeizamer te omschrijven als het extra tijdverlies dat in de vervolgstudie ontstaat doordat niet tijdig is bijgespijkerd. Het laatste is dus niet gelijk aan de tijd die voor alsnog bijspijkeren in de vervolgstudie nodig is, want daar moet de tijd die anders aan tijdig bijspijkeren zou zijn besteed vanaf worden getrokken. Onderwijskundige ervaring doet vermoeden dat in reële onderwijssituaties ( C - D ) kleiner zal zijn dan ( B - A ), dus L groter dan 1.
Is voor die ene leerling de waarschijnlijkheid van beide verliezen (onjuiste uitkomsten) gelijk, dan beslis je voor het alternatief met het kleinere verlies. In alle andere gevallen vermenigvuldig je het verlies ( B - A ) met de kans Pi dat voor deze leerling i laten bijspijkeren de verkeerde beslissing zou zijn, en het verlies ( C - D ) met ( 1 - Pi ), de kans dat doorlaten de verkeerde beslissing is. Beide producten zijn verwachte verliezen. De Pi moet worden geschat uit beschikbare empirische gegevens over het verband tussen toets- en vervolgtoetsscores.
De optimale grensscore ligt bij de toetsscore waarbij de waarschijnlijkheid P hoort die beide verwachte verliezen aan elkaar gelijk maakt. De optimale grensscore moet het punt zijn waarbij het je onverschillig is of leerlingen met die score doorgaan dan wel bijspijkeren. Ofwel :
(2) P x ( B - A ) = ( 1 - P ) x ( C - D ) waar P uit op is te lossen:
(3) P = ( B - A ) / ( B - A + C - D ).
De selectieparameter P geeft de waarschijnlijkheid dat iemand die op de toets gelijk aan de optimale grensscore scoort op de vervolgtoets tenminste gelijk aan de drempel zal scoren, als scoring op de toets continu zou zijn.
Aangenomen dat bij hogere toetsscores Xj ook de Pj hoger worden (tenminste niet dalen), een niet onredelijke aanname in het onderwijs, is de optimale grensscore de toetsscore Xk waarvan de bijbehorende Pk het dichtst boven P ligt of daaraan gelijk is.
Welk vernuftig theoretisch model ook wordt gehanteerd bij het lokaliseren van optimale grensscores, altijd komt deze selectieparameter eruit (ik zal dat straks laten zien). Je hebt dan ook geen bijzondere modellen nodig om deze P te vinden, maar misschien zijn ze bruikbaar om tot verbeterde schattingen ^Pi te komen. Jammer is dat iedere auteur met veel moeite aantoont dat zijn model deze selectieparameter oplevert (wat niet meer is dan een check op de juistheid van het model), en expliciete formules voor ^Pi niet worden gegeven.
De verliezen gerefereerd aan een drempel worden veelal drempelverliezen genoemd, en worden meestal als voor alle leerlingen gelijk beschouwd. Deze aanname van constante verliezen is niet onredelijk wanneer bijspijkeren voor de onjuist beoordeelde leerlingen ieder van hen ongeveer evenveel tijd kost, respectievelijk niet bijspijkeren voor ten onrechte doorgelatenen ieder op ongeveer evenveel extra tijd komt te staan. Wanneer bijspijkeren klassikaal of groepsgewijs gebeurt, of daar een vaste individuele instructie voor wordt doorlopen, zul je daar zeker aan voldoen. Voor leerlingen die extreem ver van de grensscore af zitten is een en ander waarschijnlijk niet vol te houden, maar bedenk dat voor deze leerlingen geldt dat ten aanzien van hen altijd dezelfde beslissing zal worden genomen, hoe ook met de grensscore wordt geschoven: voor het vinden van de optimale grensscore leggen zij geen gewicht in de schaal.
Nu ik toch met aannamen bezig ben: ik heb er in het bovenstaande nog één verzwegen: ik heb verliezen gelijk gesteld aan tijdverliezen, wat een lineaire verliesfunctie over tijdverlies veronderstelt, althans in het tijdverlies-bereik dat wordt beschouwd. Mocht aan deze veronderstelling niet bij benadering zijn voldaan, dan moet met op de verliesfunctie gewaardeerde tijdverliezen worden gewerkt.
Figuur 3 geeft toets- en vervolgtoetsscores voor 200 leerlingen. De docent zou deze gegevens kunnen hebben verzameld over leerlingen die eerder dezelfde toets aflegden, en over wie hij ook scores op de vervolgtoets inmiddels heeft kunnen bepalen. Verondersteld is dat de gegevens over de vervolgtoetsscores betrekking hebben op leerlingen ten aanzien van wie op basis van de toetsscores geen speciale maatregelen genomen zijn: op de toets zijn voor deze leerlingen nog geen voldoende - onvoldoende beslissingen genomen, er zijn geen extra leertaken aan bepaalde leerlingen toegekend.
25 | | grensscore (=12)
24 | |
23 | | 1
22 | | 1 1 3 2 3 2
21 | | 2 1 6 1 1 1
20 | 2| 1 2 2 4 6 2 1
19 | | 2 2 2 1 2 1 1 1 1
18 | 1| 6 6 2 6 5 3 2 2 2
17 | Drempel 1| 4 5 4 6 1 2 4
vervolg- 16 | 1| 4 6 6 3 3 4
toets- 15 | 1 | 2 2 1 2 3 3 2
scores 14 | 1 | 3 3 4 3 1 1 2
13 | 1 3| 1 2 2 1
12 | 2| 1 2
11 | 1|
10 | 1| 1
|
.. 9 10 11|12 13 14 15 16 17 18 19 20 21 22 23 24 25
toetsscores → →
Figuur 3. Scores van 200 personen op toets en vervolgtoets.
Voor iedere toetsscore afzonderlijk wordt de proportie leerlingen bepaald die op de vervolgtoets tenminste de drempel (score 17) haalt. Tabel 1 geeft deze proporties in kolom 4. Deze proporties zijn te gebruiken als schatting voor de kans dat een willekeurige leerling met toetsscore Xj tenminste 17 punten op de vervolgtoets zal halen. Een ruwe werkwijze, toegegeven, maar goed genoeg voor het doel de optimale grensscore G(opt) te kunnen bepalen. Nu zullen de berekende proporties evenals in het onderhavige geval nogal eens grillig blijken uit te vallen. Grote uitschieters die zeer waarschijnlijk alleen aan dergelijke toevalsfluctuaties te wijten zijn, zou je graag willen verwijderen of vereffenen (smoothen). Een even simpele als bruikbare methode is voor ieder drietal proporties de mediane waarde te substitueren voor de middelste: bijv. 0,476, 0,583, 0,409, vervang 0,583 door 0,476. Kolom 5 in tabel 1 geeft de aldus vereffende proporties. Te zien is dat de proporties van boven naar beneden niet kleiner worden, in overeenstemming met de aanname uit de vorige paragraaf. Zou dit niet het geval zijn, dan kan nogmaals op dezelfde wijze worden vereffend =, en eventueel nogmaals totdat de nieuw verkregen proporties niet meer veranderen. Houd in deze reeks de bovenste en onderste proportie gelijk aan de beginwaarde; is het gewenst om ook deze mee te vereffenen, zie dan Tukey (1977, blz. 221) end value smoothing. Varianten op de hier gegeven eenvoudige methode van vereffenen worden in het opmerkelijke boek van Tukey gegeven. Een methode voor het direkt vereffenen van de data zoals in figuur 3 wordt o.a. door Novick en Jackson (1974, par. 10.9) gegeven, maar is verre van eenvoudig. Statistische vereffeningsmethoden zijn in talrijke vormen beschikbaar, maar ingewikkeld voor de docent, en kostbaar voor deze kleinere beslissingsproblemen; zie e.g. Kolen en Whitney (1978), Clark (1977), Hobson (1976).
Tabel 1
Ruwe en vereffende proporties Pi bij toetsscores Xi .
------------------------------------------------------------
toets- aantal totaal proportie vereffende
score ≥ Dr=17 aantal Pi proporties
------------------------------------------------------------
9 0 1 0 0
10 0 3 0 0
11 4 12 0,333 0,333
12 10 21 0,476 0,476
13 14 24 0,583 0,476
14 9 22 0,409 0,583
15 19 30 0,633 0,633
16 13 20 0,650 0,633
17 13 21 0,619 0,650
18 23 29 0,793 0,750
20 3 3 1 1
21 4 4 1 1
22 1 1 1 1
23 1 1 1 1
------------------------------------------------------------
Een illustratie
Zou de docent de verliesratio bepaald hebben op L = 1,5 dan is volgens Formule (3) de waarde van de selectieparameter P = 0,4. In kolom 5 van tabel 1 is te zien dat deze waarde ligt tussen die van de proporties horend bij de toetsscores 11 en 12, waarmee de optimale grensscore Gopt bepaald is op 12. Het voorbeeld laat zien dat de aanwijzing van Gopt een bruuske zaak is, een probleem dat sterker speelt naarmate het aantal vragen in de toetsjes kleiner is (Zie ook Novick en Lewis, 1974, blz. 142).
Het is leerzaam om na te gaan hoe ver de verliesratio zou moeten veranderen om tot een andere optimale grensscore te leiden. Wordt L kleiner dan 1,1 dan springt de grensscore van 12 op 14. Is L = 2, dan is 11 de optimale grensscore. Voor waarden van L tussen 1,1 en 2, een fors bereik, is Gopt = 12.
De gevoeligheid van Gopt voor de plaats waar de drempel gelegd wordt blijkt groot te zijn. Zou de drempel op 16 gekozen zijn dan is Gopt = 11 , bij drempel 18 blijkt Gopt = 15 te zijn. In dit scorebereik treft dat 79 van de 200 leerlingen!
Overigens is het hiermee ook duidelijk dat je bij het veranderen van drempels en grensscores rekening moet houden met terugkoppelingseffecten: leerlingen zullen hun gedrag aan veranderingen aanpassen, en daarmee bedoelde effecten gedeeltelijk teniet kunnen doen (zie ook Van Naerssen, 1976). Daardoor wordt het verzamelen van empirische valideringsgegevens een moeizame zaak, omdat het misschien een paar keer zal moeten gebeuren.
In gevallen waar de empirische proporties ook na herhaald vereffenen nog omkeringen in strijd met de aanname vertonen, waardoor misschien twee optimale grensscores zouden worden aangewezen, valt er weinig anders te doen dan de leerlingen het voordeel van de zwakte van de beschikbare empirische data te geven: neem van eventueel meerdere optimale grensscores degene waaraan de leerlingen de voorkeur geven.
Wat betreft het bepalen van de waarde van de selectieparameter P heb ik in het voorgaande een eenvoudige oplossing gegeven. Andere auteurs kiezen de moeilijker weg van het minimaliseren van het verwachte verlies over de hele groep leerlingen. Daarvoor is nodig de proportie a i van ten onrechte onvoldoende beoordeelde, en de proportie d i van ten onrechte voldoende beoordeelde leerlingen als X i als grensscore gekozen zou worden. Het verwachte verlies bij de keuze van X i als grensscore is
(4) V verlies (X i = G) = a i . ( B - A ) + d i . ( C - D )
Voor Gopt is dat verlies minimaal. Zonder enige aanname over de aard van de gezamenlijke verdeling van X en Y (toets- en vervolgtoetsscores) kan de selectieparameter P bepaald worden. Vastenhouw (1973) en Petersen (1976) hebben laten zien dat
(5) P = ( C - D ) / ( B - A + C - D ) = 1 / ( L + 1 )
een resultaat dat gelijk is aan formule (3).
Zij gaven het bewijs voor maximaliseren van de verwachte utiliteit, maar Raiffa en Schlaifer (1961) hebben laten zien dat het minimaliseren van het verwachte verlies dezelfde resultaten moet geven.
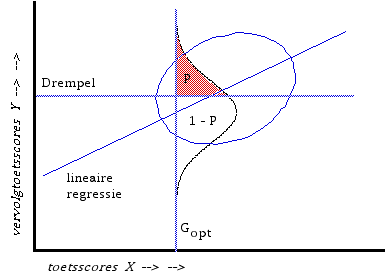
Figuur 4a. Model Alf en Dorfman. Zowel X als Y normaal verdeeld. De getekende verdeling f(Y|Gopt ) is ook normaal.
Anderen (Alf en Dorfman, 1967; Rorer et al., 1966; Huynh, 1976 om er enkele te noemen) stellen een model op voor de gezamenlijke verdeling van toets- en vervolgtoetsscores en leiden uit dat model de waarde van de selectieparameter P af. Ik verklap vast dat ze allen uitkomen op dezelfde waarde, zoals die in (3) en (5) al gegeven werd. Beschik je dan toch eenmaal over zo'n statistisch model, dan kun je dat ook gebruiken om empirische gegevens te fatsoeneren : in plaats van de ruwe data gebruik je een statistisch model dat in zijn parameters zo is gekozen dat het het best bij de data past. Je kunt dan voor iedere X i een schatting P i maken op basis van je model. Gegeven de eenmaal geschatte P i gaat het vinden van Gopt precies zoals we het eerder op de proporties uit tabel 1 hebben gedaan.
Alf en Dorfman veronderstellen zowel toets- als vervolgtoetsscores normaal verdeeld. De regressie van vervolgtoets op toets is dan lineair, de verdeling voor vervolgtoetsscore gegeven toetsscore is eveneens normaal (zie figuur 4a). Alf en Dorfman leiden dezelfde selectieparameter P = 1 / ( L + 1 ) af, in figuur 4a voorgesteld door het gearceerde gedeelte van de conditionele verdeling.
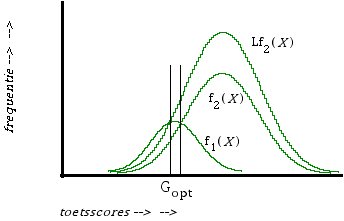
Figuur 4b. Model Rorer et al. (1966). Normaalverdelingen voor lager dan de drempel scorende personen f1 ( X ) en tenminste gelijk aan de drempel scorende personen f2 ( X ). L is de verliesratio.
Rorer et al. (1966a, b) veronderstellen een natuurlijke tweedeling als doelvariabele (man-vrouw, ziek-gezond, succes-falen bijv.), en dat de toets- en testsscores van personen uitdezelfde doelcategorie normaal verdeeld zijn (figuur 4b). Als L = 1 dan is Gopt grafisch te vinden als het punt (eventueel de twee punten!) waar deze normaalverdelingen elkaar snijden. Wanneer het aantal personen in de ene doelcategorie een stuk kleiner is dan dat in de andere categorie is het mogelijk dat er geen snijpunt is: dezelfde beslissing is ten aanzien van alle personen optimaal. In het algemeen echter zal de verliesratio L ≠ 1 zijn. Als f1 (X) de scoreverdeling is voor de groep die op de vervolgtoets beneden de drempel skoort, en f2 (X) de scoreverdeling voor de groep die tenminste gelijk aan de drempel scoort, dan is aan te tonen dat Gopt grafisch te bepalen is door f2 (X) te vermenigvuldigen met L, waarbij de snijpunten f1 (X) = L f2 (X) de optimale grensscores aangeven (zie figuur 4b).
Het is mogelijk om normaalverdelingen bij de ruwe empirische frequentieverdelingen te passen, maar het is natuurlijk ook mogelijk om beide empirische frequentieverdelingen met vereffeningstechnieken te bewerken.
Hoe zit dat nu met de selectieparameter P? Per definitie
(6) P i = f2 ( X i ) / ( f1 ( X i ) + f 2 ( X i )).
Omdat
(7) f1 ( Gopt ) = L f2 ( Gopt )
vinden we
(8) P = f2 ( Gopt ) / ( L f2 ( Gopt ) + f2 ( Gopt )) = 1 / ( L + 1 )
wat overeenstemt met formule (3).
Huynh (1976) behandelt verschillende modellen, waarbij het betabinomiale model een opvallende plaats inneemt. De toetsscore, gegeven ware beheersing t, is binomiaalverdeeld, de ware scoreverdeling is betaverdeeld. Op het ware scorebereik is de drempel t0 aangewezen. Ondanks de schijn van het tegendeel is het door Huynh hier gepresenteerde model een gewoon drempelverliesmodel (hij noemt het the beta-binomial model with constant losses and 0 - 1 referral success). Langs moeilijk navolgbare wegen bereikt hij de oplossing voor de optimale grensscore, bij hem c 0 geheten, gegeven in zijn formule (10). De vraag is of ook bij Huynh de optimale grensscore bepaald wordt door dezelfde waarde 1 / ( L + 1 ) voor de selectieparameter P. Dat kan worden aangetoond, gebruik makend van het feit dat in dit model de ware scoreverdeling voor gegeven toetsscore ook een betaverdeling is. De incomplete betafunctie-ratio in Huynh's formule (10) is precies het complement van de gezochte waarschijnlijkheid P. (Zijn verliesratio Q is gelijk aan mijn L). Ook Huynh komt zodoende uit op de selectieparameter P = ( 1 / (L + 1 )) [in TOR foutief, b.w.], zijn theoretisch model geeft de ^Pi als het complement van een incomplete betaverdeling, waarvan de parameters op basis van empirische gegevens te schatten zijn, of subjectief te bepalen wanneer het om het schatten van de ware scoreverdeling voor een enkele persoon gaat. Nog twee opmerkingen bij dit model. 'Constante verliezen' betekent zoals gezegd drempelverliezen. Huynh (1976, 1977) werkt in alle door hem gepresenteerde modellen met drempelverliezen. '0 - 1 Referral success' betekent dat gegeven de ware score succes op de vervolgtoets perfect voorspelbaar is (succes is het al dan niet beneden de drempel op de vervolgtoets scoren); bij deze aanname is de referral task van geen praktisch belang meer, het zijn alleen de ware scores op de toets die bij het vinden van de optimale grensscore van belang zijn.
Als afsluiting in deze rij het werk van Hambleton en Novick (1973), Swaminathan et al. (1975). Deze benadering is een oefening in betrouwbaarheid: gestreefd wordt naar zo goed mogelijke schatting van de ware beheersing per individuele leerling. Daartoe wordt een Bayesiaanse regressieanalytische benadering gebruikt, toegepast op getransformeerde data. Bijzonder knap, maar ook een bijzonder ondoorzichtige procedure. Het vinden van Gopt gaat, gegeven het voorgaande, langs de bekende weg van minimaliseren van het verlies over de hele groep leerlingen. Verder onderzoek langs deze lijn zal waarschijnlijk niet gebeuren, gezien de opmerking van Hambleton et al. (1978) dat de aanpak van Huynh (1976) eenvoudiger is.
In het dagelijks leven wordt op grote schaal met grensscores gewerkt, vaak in situaties en met tests die moeilijk of niet te standaardiseren zijn. De gebruiker van de test of toets, die vaak ook de maker ervan is, zal dan zelf een optimale grensscore moeten zien te vinden, en ook aan zijn leerlingen, cliënten, etc. duidelijk moeten kunnen maken op welke wijze die grensscore is bepaald. Dat alles vraagt om transparante, eenvoudige, praktische procedures. Ik heb laten zien dat een eenvoudige procedure kan worden gegeven. Wie toch reden heeft om met modellen over (onderliggende) scoreverdelingen te werken, bijvoorbeeld omdat de bijbehorende assumpties goed bij zijn specifieke situatie passen, kan zich in drie opzichten door de in het voorgaande gegeven methode gesteund weten: 1e hoeft niet vanuit het nieuwe model opnieuw bewezen te worden dat voor Gopt geldt dat de selectieparameter P = 1/ ( L + 1 ); 2e weet hij nu dat de functie van het nieuwe model moet zijn om tot verbeterde schattingen ^Pi te komen; 3e blijft het dan ook bij ingewikkelde modellen mogelijk om de wijze waar op Gopt bepaald is op begrijpelijke wijze uiteen te zetten aan betrokkenen. Ondanks de eenvoud van de gegeven aanpak zijn er nog problemen te over. Op een aantal daarvan wil ik hier kort ingaan. Ik begin met een citaat van Ebel, gebruikt door Hambleton (1978):
Het standpunt van Ebel is vandaag de dag nog steeds te beluisteren in kringen van meetspecialisten, ondanks de pogingen van De Groot (1970, 1972) om deze problematiek van differentiële rechtvaardigbaarheid op wat minder primitieve leest te schoeien. De Groot wijst er op dat de onderwijssituatie zo ingericht moet zijn dat de leerling het risico van pech in de grenszone zelf kan dragen. Dat vraagt om doorzichtige toetsing, waar de leerling zich effectief op kan voorbereiden (zie ook Wilbrink, 1978), het zakrisico kan beheersen. Zak-slaagbeoordelingen kunnen dan gezien worden als liggend binnen een afsprakensysteem met de leerlingen: je mag doorgaan met het vervolgonderwijs als je slaagt, maar je mag er niet op rekenen altijd te slagen wanneer je de stof ook voldoende beheerst; ten onrechte zakken is iets dat iedere leerling wel een paar keer zal overkomen, en inherent aan het gehanteerde beoordelingsstelsel. (Wat niet betekent dat er geen beter beoordelingsstelsel bedacht zou kunnen worden.)
Waarom breng ik dit alles ter sprake? Het heeft alles te maken met de nogal naïeve opvattingen die we er nog steeds op na houden waar het gaat om de vraag welke stofbeheersing van de leerling moet worden verlangd, welk niveau als mastery level kan worden aangeduid, etcetera. Welnu, dat zijn de verkeerde vragen. Zelden of nooit is er in het onderwijs sprake van een scherp afpaalbaar niveau van stofbeheersing dat als grens tussen voldoende en onvoldoende kan worden aangewezen. Het heeft er de schijn van dat het denken in termen van drempels e.d. ons de laatste tijd is opgedrongen vanuit de hoek van de meetspecialisten. Op zijn best kun je grensscore-procedures blijven hanteren om daarmee een omschreven, maar dan wel redelijk globaal, niveau van stofbeheersing voor de groep leerlingen te realiseren. Verhogen of verlagen van de grensscore zal effecten hebben op dat globaal gerealiseerde niveau, zodat de keuze van grensscore een effectief middel is om het onderwijs te sturen.
Werken met grensscores en drempels is prima, als we daar maar niet het idee bij hebben dat het zou gaan om duidelijk kwalitatieve grenzen in de aard van de stofbeheersing. Geen overdreven betekenis hechten aan het verschil tussen scores die net onder en net boven zo'n drempel liggen.
Ook binnen de boven geschetste toetsing-als-sturing-van-onderwijs opvatting is het van belang de resultaten van bijspijkeronderwijs voor een ongeselecteerde groep leerlingen te onderzoeken. Het opmerkelijke is nu dat bij alle eerder gegeven methoden (Hambleton et al. 1978), evenals bij de door mij geschetste eenvoudige methode overigens, van de docent wordt gevraagd om intuïtief deze alleen empirisch te achterhalen bijspijkereffecten mee te waarderen bij het kiezen van utiliteiten of het bepalen van de verliesratio L. Hoe je het ook bekijkt, dat is een weinig rationele procedure, en het siert onderzoekers van onderwijs niet van docenten een intuïtief oordeel te vragen waar zij zelf er in ieder ander geval op aan zouden dringen eerst maar eens valideringsgegevens te verzamelen. Het is niet onwaarschijnlijk dat bijspijkeren maar tot een kleine winst in termen van vervolgtoetsscores leidt, een winst die bij onderzoek wel eens ver beneden het niveau zou kunnen liggen at de docent met zijn ongewapend oog er altijd van heeft verwacht Ik werk dit uit in een vervolgartikel (Wilbrink, 1980).
Alf, E. F., Jr, and Dorfman, D. D. (1967). The classification of individuals into two criterion groups on the basis of a discontinuous payoff function. Psychometrika, 32, 115-123.
Becker, S. W., and Siegel, S. (1958). Utility of grades: level of aspiration in a decision theory context. Journal of Experimental Psychology, 55, 81-85.
Clark, R.M. (1977). Non-parametric estimation of a smooth regression function. Journal of the Royal StatisticalSociety, Series B,39, 107-113.
Davis, Ch. F., Hickman, J., & Novick, M. R. (1973). A primer on decision analysis for individually prescribed instruction. Iowa City, Iowa: The American College Testing Program. Technical Bulletin no. 17.
Glass, G. V. (1978). Standards and criteria. Journal of Educational Measurement, 15. 237-261 (Special issue on standard setting).
Groot, A. D. de (1970). Some badly needed non-statistical concepts in applied psychometrics. Nederlands Tijdschrift voor de Psychologie, 25, 360-376.
Groot, A. D. de (1972). Selectie voor en in het hoger onderwijs. Een probleemanalyse. Den Haag Staatsuitgeverij.
Hambleton, R. K., and Eignor, D. R. (1978). Guidelines for evaluating criterion referenced tests and test manuals. Journal of Educational Measurement, 15, 312-327.
Hambleton, R. K., and Novick, M. R. (1973). Toward an integration of theory and method for criterion-referenced tests. Journal of Educational Measurement, 10, 159-170.
Hambleton, R. K., Swaminathan, H., Algina, J., & Coulson, D. B. (1978). Criterion-referenced testing and measurement: a review of technical issues and developments. Review of Educational research, 48, 1-47. JSTOR read online free
Hobson, R. (1976). Properties preserved by some smoothing functions. Journal of the American Statistical Association, 71, 763-766.
Huynh (1976). Statistical consideration of mastery scores. Psychometrika, 41, 65-78.
Huynh, H. (1977). Two simple classes of mastery scores based on the beta-binomial model. Psychometrika, 42, 601.
Keeney, R. L., & Raiffa, H. (1976). Decisions with multiple objectives: preferences and value tradeoffs. New York: Wiley.
Kolen, M. J., and Whitney, D. R. (1978). Methods of smoothing double-entry expectancy tables applied to the prediction of success in college. Journal of Educational Measurement, 15, 201-211.
Linden, W. J. van der, and Mellenbergh, G. J. (1977). Optimal cutting scores using a linear loss function. Applied Psychological Measurement, 1, 593-599.
Lindley, D. (1971). Making decisions. London: Wiley.
Naerssen, R. F. van (1976). Het derde tentamenmodel met een toepassing. Tijdschrift voor Onderwijsresearch, 1, 161-171.
Novick, M. R., and Lewis, C. (1974). Prescribing test length for criterion-referenced measurement. In: Harris, Ch.E., Alkin, M.C., & Popham, W.J. (Eds). Problems in criterion referenced measurement. Los Angeles: Center for the study of evaluation, University of California.
Novick, M. R., and Jackson, P. H. (1974). Statistical methods for educational and psychological research. London: McGraw-Hill.
Novick, M. R., and Lindley, D. V. (1978). The use of more realistic utility functions in educational applications. Journal of Educational Measurement, 15, 181-191.
Petersen, N. S. (1976). An expected utility model for 'optimal' selection. Journal of Educational Statistics, 1, 333-358.
Raiffa, H. (1968). Decision analysis. Introductory lectures on choices under uncertainty. London: Addison-Wesley.
Raiffa, H., and Schlaifer, R. (1961). Applied statistical decision theory. London: The M.I.T. Press.
Rorer, L. G., Hoffman, G. E., LaForge, R., and Hsieh, K-Ch. (1966). Optimum cutting scores to discriminate groups of unequal size and variance. Journal of Applied Psychology, 50, 153-164.
Rorer, L. G., Hoffman, G. E., and Hsieh, K-Ch. (1966). Utilities as base-rate multipliers in the determination of optimum cutting scores for the discrimination of groups of unequal size and variance. Journal of Applied Psychology, 50, 364-368.
Siegel, S. (1957). Level of aspiration and decision making. Psychological Review, 64, 253-262.
Swaminathan, Hambleton & Algina (1975). A Bayesian decision-theoretic procedure for use with criterion-referenced tests. Journal of Educational Measurement, 12, 87-98.
Tukey, J. W. (1977). Exploratory data analysis. London: Addison-Wesley.
Vastenhouw, J. (1973). Optimale rationele selectie: een waardenprobleem. Onderzoek van Onderwijs, (4), 12-13.
Ven, H. G. S. van der (1977). Inleiding in de schaaltheorie. Deventer: Van Loghum Slaterus.
Wilbrink, B. (1978). Examenregeling deel A: Studiestrategieën. Amsterdam: COWO. html
Wilbrink, B. (1980). Enkele radicale oplossingen voor kriterium gerefereerde grensskores. Tijdschrift voor Onderwijsresearch, 5, 112-125. html
Manuscript ontvangen 2-5-'78
Definitieve versie ontvangen 26-6-'79
[om gebruik van lettertype Symbol te vermijden is in het volgende theta vervangen door p, alpha door a en beta door b. De integraal is niet de Symbol integraal. Het dakje voor een geschatte parameter staat er niet op, maar voor: ^p. Het archief bevat een klad- en een nette versie, die zijn identiek.]
17 juni 1979
Niet gepubliceerde noot, bewijsvoering ivm Huynh
Huynh's optimale grensscore (Huynh 1976) in zijn beta-binomiale model met drempelverliezen en '0-1 referral success.'
De ware scoreverdeling op de toets is de betaverdeling
f (q ) = B -1 ( a, b ) q a - 1 ( 1 - q ) b - 1.
De toetsscoreverdeling gegeven q is binomiaal:
f ( x | q ) = (n boven x ) q x ( 1 - q ) n - x
Dan:
f ( q | x ) = f ( q ) f ( x | q ) / f ( x ) =
B -1 ( a, b ) q a-1 ( 1 - q ) b-1 B ( a, b ) ( 1 / ( n boven x )) B -1 ( a + x, n - x + b ) ( n boven x ) q x ( 1 - q ) n-x =
B -1 ( a + x, n - x + b )
( q a + x - 1 ( 1 - q )b + n - x - 1 )
eveneens een betaverdeling.
Per definitie is de incomplete betafunctie ratio
It0 ( a + x, b + n - x ) =
∫
0t0
q a + x - 1 ( 1 - q ) b + n - x - 1
B -1 ( a + x, n - x + b ) dq =
∫
0t0
f ( q | x ) dq
t0 is de drempel op de onderliggende ware scoreverdeling.
c0 is de optimale grensscore.
Dan:
∫
t01
p ( q | c 0 ) dq = 1 - I t 0 ( a + c 0 , b + n - c 0 ) =
1 - Q / ( 1 + Q ) = 1 / ( 1 + Q ) = 1 / ( 1 + L ) = P.
Q is de verliesratio, en Q = L. P is de selectieparameter, zie de Discussie.
Maar zo mooi komt het natuurlijk niet uit; omdat de toetsscores discreet zijn wordt de kleinste score x i die voldoet aan
Pi ≥ P,
ofwel 1 - I t 0 ( a + x i, b + n - x i ) ≥ 1 - Q / ( 1 + Q ),
ofwel I t 0 ( a + x i, b + n - x i ) ≤ Q / ( 1 + Q )
tot optimale grensscore gepromoveerd,
De laatste formule is gelijk aan Huynh (1976) formule 10,
Q.E.D.
juni 1979
niet gepubliceerde voetnoot bij eerdere versie:
W = ( B - A ) / ( C - D ),
voor de optimale grensscore geldt dan
P = ( C - D ) / ( C - D + B - A ).
Rorer c.s. demonstreren dat de optimale grensscore afhangt van RW / ( 1 - R ), waarin de verhouding R = f2 (x) / (f1 (x) + f2 (x)).
Wanneer W ≠ 1 is er een S te vinden waarvoor geldt
S ( 1 - S ) = RW ( 1 - R).
Welnu, S is de nieuwe verhouding die ontstaat door f2 (x) met W te vermenigvuldigen:
S = W f2 (x) / (f1 (x) + f2 (x)).
S / ( 1 - S ) = { W f2 (x) / ( f1 (x) + W f2 (x)) } { ( f1 (x) + W f2 (x)) / f1 (x) }
= { f2 (x) / ( f1 (x) + f2 (x) ) } { ( f1 (x) + f2 (x) ) / f1 (x) }
= W R / ( 1 - R ).
Hiermee is ook een methode gegeven om de snijpunten op de ruwe scoreverdelingen (na vereffening) te vinden, na vermenigvuldiging van f2 (x) met W.
Bewijs voor de optimale grensscore:
Per definitie pc = f2 (x c ) / ( f1 (x c ) + f2 (x c )),
omdat f1 (x 0 ) = W f2 (x 0 ) is
p 0 = f2 ( x 0 ) / ( W f2 (x 0 ) + f2 (x 0 ) )) =
1 / ( W + 1 ) = ( C - D ) / ( C - D + B - A ).
In deze digitale versie is de tekst gelijk gehouden, maar is de spelling wel aangepast.
Noot: De niet vermelde vooronderstelling bij formule (2) is dat er een foute beslissing wordt genomen voor student i, de student voor wie de gegevens in Tabel 2 gelden. In dat geval geeft de kans dat de ware score beneden de drempel ligt de kans op ten onrechte doorlaten, de kans dat de ware score erboven ligt de kans op ten onrechte zakken. Je weet evenwel niet of de beslissing ten onrechte is of niet, al kun je wel de kans daarop bepalen. Ik vermoed dat ik in het tweede artikel daar wel op inga, want daar staat een uitgebreidere waaschijnlijkheidstabel in.
Erratum: Formule 3 was abusievelijk:
(3) P = ( B - A ) / ( B - A + C - D ),
is verbeterd, in overeenstemming overigens met formule (5), als:
(3) P = ( C - D ) / ( B - A + C - D ).
Checken: In de tabel is er een niet in de tekst toegelicht probleem met de aangegeven P en 1 - P. Ik heb dat in de Noot al vermeld. Ik moet dat natrekken, want in de verdere behandeling van de verliesratio ga ik er stilzwijgend vanuit dat de som van de beide kansen gelijk is aan die van de twee onterecht besliste quadranten, niet van alle vier. Daar wringt dus iets, waarvan ik nu vermoed dat het ook bij alle genoemde auteurs wringt, en waar ik in het tweede artikel op terugkom. Maar voordat ik het daar ga nakijken, zou ik het hier eerst zelf op willen lossen. Daarvoor heb ik denk ik de bewijsvoering voor Huynh nodig, die ik als appendix bij dit artikel had ingestuurd, maar die de redacteur niet wilde plaatsen. Ik heb die appendix nog niet terug kunnen vinden, maar vermoed dat hij ergens in de papierbakken zit.
verwachte verliezen (8 cellen)
| 0 | 0 | u 1 - u 0 + T | 0 |
| - T | u 1 - u 0 - T | 0 | - T |
Vi (Ld ) = Ri (1-pi ) (u1 +T-u0)
Vi (L bij ) = (1-pi ) (1-Ri ) (-T) + pi (1-Ri ) (u1 -u 0 -T) + pi Ri (-T)
gelijkstellen voor optimale grensscore
Ri (1-pi ) (u1 +T-u 0 ) = (1-pi ) (1-Ri ) (-T) + pi (1-Ri ) (u1 -u 0 -T) + pi Ri (-T)
Ri (u1 -u 0 +T) -Ri T - pi T - pi (u1 -u 0 -T) - pi Ri (u1+T-u 0 ) + 2pi Ri T + Ri pi (u1 -u 0 -T) = -T
Ri (u1 - u 0 ) - pi (u1 - u 0 ) + pi Ri (u1 -u 0 -T+ 2 T+ u1 - u 0 ) = -T
Ri (u1 - u 0 ) - pi (u1 - u 0 ) = -T
Ri - pi = -T / (u1 - u 0 )
Hetzelfde resultaat als bij verwachte utiliteiten.
Er is een ingrijpend geredigeerde versie van dit artikel, waarschijnlijk ergens in 1984 gemaakt, maar niet gepubliceerd.
Enrico Diecidue and Jeroen van de Ven (2006). Aspiration Level, Probability of Success and Failure, and Expected Utility. pdf
Chip Heath, Richard P. Larrick and George Wu (1999). Goals as reference points. Cognitive Psychology, 38, 79-101. pdf
James T. Austin and Jeffrey B. Vancouver (1996). Goal constructs in psychology: Structure, process, and content. Psychological Bulletin, 120, 338-375. pdf
R. Duncan Luce and Patrick Suppes (1965). Preference, utility, and subjective probability. In R. D. Luce, R. R. Bush and E. Galanter (Eds) (1965). Handbook of mathematical psychology. Vol. III 249-410.pdf
ben wilbrink, 25 juli 2022 - target='_blank'>twitterdraadje
Formatief toetsen is geen recent fenomeen. In een internationaal congres in 1973, in Leiden, was er uitvoerig aandacht voor. Ook criterium-gerefereerd toetsen hoort erbij. Mastery learning. Voor previews van de bijdragen in het congresboek zie onderaan de blz. de lijst hoofdstukken, doorklikken.
Hoewel ik erbij was, kan ik mij er nauwelijks meer iets van herinneren. Wel dat de vele Amerikaanse deelnemers in paniek waren: de dollar was plots sterk gedevalueerd. Maar dat terzijde.
Hoe interessant was dit congres voor huidige formatieve toetsers? Laten we eens kijken.
Ik citeer het begin van hoofdstuk 14, van Marshall N. Arlin, Jr, dat een indruk geeft van de thematiek van een belangrijk deel van dit congres:
Het idee van formatief toetsen is een halve eeuw geleden echt radicaal. Herken de visie van Benjamin Bloom en 'mastery learning' [denk aan het '2-sigma experiment']:
"Research studies have consistently found that formative evaluation can raise achievement level and minimize between-student achievement variance."
Hoe kan het dat dit Bloomiaanse doel in de jaren erna vrijwel geheel uit zicht is geraakt? Heeft dat misschien daarmee te maken dat het onderwijsveld afstand heeft genomen van psychologen, en onderwijskundigen heeft binnengehaald?
Waarschijnlijk hebben psychologen hun hand overspeeld door deze belangrijke thematiek vooral met statistische methoden te behandelen (literatuur over criterium-gerefereerd toetsen), in plaats van onderwijsexperimenten op te zetten zoals het 2-sigma experiment van Bloom, zie deze blog.
Dit heeft toch nog een (voor mij) onvermoed staartje. In de 2e helft van de 70er jaren was er een actieve werkgroep over criterium-gerefereerd toetsen, getrokken door Don Mellenbergh en Wim van der Linden. Ik deed daar ook vrolijk aan mee. Dat kwam overwaaien uit de VS. Niet alleen via dat Leidse congres in 1973, maar ook langs andere wegen, zoals een publicatie in 1974: Ch. E. Harris , M. C. Alkin & W. J. Popham (Eds): 'Problems in criterion referenced measurement'. Los Angeles: Center for the study of evaluation, University of California. Mogelijk heb ik het enige nog in Nederland beschikbare boekje. Het is niet online beschikbaar, wel een inhoudsopgave.
De schok was voor mij deze titel van de bijdragen van Chester Harris: '(Ch 9) Some Technical Characteristics of Mastery Tests, by Chester W. Harris.
Wait a sec, criterion =? mastery?
Wat ik mij nu pas (juli 2022) realiseer, veertig jaar te laat, is het volgende. In de meeste publicaties van de werkgroep Mellenbergh-van der Linden over criterium-gerefereerd toetsen is impliciet dat het criterium gelijk kan zijn aan de grens voldoende-onvoldoende uit de Nederlandse onderwijscultuur.
Maar de Amerikaanse publicaties slaan op de Amerikaanse onderwijscultuur waar pass-fail scoring niet algemeen is, en waar Bloom en anderen met het idee van mastery learning een forse steen in de vlakke onderwijsvijver hadden gegooid.
Bij mijn weten is die culturele kloof
tussen publicaties van Amerikaanse en van Nederlandse auteurs nooit expliciet benoemd. Maar die kloof is wel heel diep en breed, want aan het Nederlandse toetsen met criterium voldoende of onvoldoende is een cultuur gekoppeld van onderscheid maken tussen leerlingen, en dat is precies waer mastery learning een alternatief voor biedt dat verschillen juist kleiner maakt. Sterker contrast is moeilijk denkbaar, niet?
Mijn eigen bijdrage destijds (1980) bestaat uit twee artikelen in het Tijdschrift voor Onderwijsresearch, waarin het niet gaat om mastery, maar om onderscheid tussen wie slaagt, en wie vooralsnog niet slaagt. [deze webpagina geeft het eerste artikel uit dat tweeluik]. Best ernstig, ik overzie het nog niet.
Deze kleine bende psychometrici rond Don Mellenbergh en Wim van der Linden is wel mede bepalend geweest voor het denken over toetsen en selectie in Nederland. Hij bevestigde het denken in verschillen tussen leerlingen. En dat is een filosofie die schadelijk is voor onderwijs.
![]() http://www.benwilbrink.nl/publicaties/80aGrensscoresTOR.htm
http://www.benwilbrink.nl/publicaties/80aGrensscoresTOR.htm