In Scarvia B. Anderson and John S. Helmick (Eds) (1983). On educational testing. San Francisco: Jossey-Bass Publishers. p. 109-127.
The Case for Compromise in Educational Selection and Grading
Willem K. B. Hofstee
In 1975, the Dutch parliament invited the minister of education to propose a satisfactory solution to the problem of selection for "closed studies" such as medicine, dentistry, and veterinary science. The advisory committee established by the minister opened its first report by stating that a solution satisfactory to all persons involved does not exist and that the choice between alternatives is ultimately a political, not a scientific, matter. Decisions about grading or selection policies are, in fact, based on two classes of, premises, one political and the other cognitive. The term political does not here refer to national or party politics. It is used rather to denote actions that promote certain values at the expense of other values. In contrast to these political values, the validity of "cognitive" premises can be assessed analytically or empirically. What contributions can be expected from the educational researcher in this interplay of values and facts?
In many cases, there will be pressure on the researcher to provide "automatic" solutions in which the necessity of choosing between values is obscured. The researcher may be tempted to give in to this pressure, since doing so will enable him or her to make a personal choice between values and thus to exert power. The temptation should be resisted, however, because ignoring values or obscuring the distinction between values and facts is bad for both science and politics. Rather, the researcher should expose the value component of the problem so that it can be subjected to constructive political discourse. The selection and grading models to be discussed here attempt to do just that. They are called compromise models, in that seemingly opposing policies appear as special cases of the same model. More appropriately perhaps, the models may be described as generative or superordinate.
For purposes of illustration, let us say that a decision between two clearly opposed and mutually exclusive policies has to be taken. Each alternative has its partisans, and there is a certain balance of power between the two parties. The difference between the alternative policies is usually perceived as a difference of principle - in other words, a difference that touches on very fundamental values. Emotions may run high in the debate.
The contribution of a general model in this situation is as follows: First, it shows that the two alternatives may be thought of as special cases - usually, extreme cases - on a continuum of possible policies. The inescapable implication is that a difference of principle can be reduced to a difference of degree, which in turn may be solved through bargaining. The presentation of the general model is usually met with less than complete enthusiasm. It takes the sting out of the debate, to the disappointment of many. The presenter is usually accused of cynicism, and the model is found to be iconoclastic. Both parties will tend to focus on the fact that the other party's principle is incorporated in the model and will thus react negatively.
On second thought, however, both parties may come to realize that every conceivable solution to the debate amounts to choosing parameter values for the model and that a whole continuum of solutions exists - solutions that are at least preferable to the other party's proposals. Thus, sooner or later, depending on the pressure under which the debate takes place, the model may become a tool for finding a pragmatic solution to the conflict. The solution is going to make everybody unhappy, but the balance of unhappiness may be such that each party is satisfied with the other party's unhappiness. The sustained and clamorous proclamation of one's objections to the compromise therefore becomes a vital element in maintaining the balance.
Three such models, one pertaining to admission policies, a second to setting cutoff scores, and a third to the combination of grades, will be discussed. But certain reservations must first be made. The approach to applied problems through generative models has nothing to do with empirical science. Of course, one may use these models to find out how well they capture spontaneous choices between policies and to establish parameters in an empirical manner. But in the applications that I have in mind the models are simply put forward, and their parameters result from bargaining. In the bargaining, simulations of past decisions may provide an argument for one party or another, but it would be a grave mistake to believe that an objective empirical solution to the debate can be found. So the scientific contribution here is purely analytical. This is an unfamiliar situation in the behavioral sciences.
Another reservation is that the models to be discussed are very simple and unsophisticated. We all are familiar with far more elegant models. I even plead guilty to the charge that the models, in order to do their job, should be simple enough to be understood by the lay parties involved. But designing such models does require at least a touch of creativity.
A last reservation is that a plea for compromise models seems itself to be indicative of a particular system of values. Strictly speaking, that is not true. The models do not dictate a compromise; they just widen the scope of possible solutions and provide the tools for negotiating a solution. Psychologically, however, it is probably true that a person who believes in radical solutions would not ask that consideration be given to compromise models. That interpretation is not contested here. Compromises are obviously in the interest of the weaker party, which is why they agree very well with my definition of democracy.
Restricted Admission
The first example, which will be discussed at some length, is the weighted lottery model for admission of students to closed (numerus clausus) studies, such as medicine, dentistry, and veterinary science. One particular solution under this model was proposed by Vermaat, a Dutch professor of mathematics and member of parliament, and the general model is easily derived from that proposal. It states that in cases of restricted admission, an applicant's chances of being admitted - that is, the number of lottery tickets he or she receives - is a monotonically increasing function of his or her score (for example, a secondary school grade point average). Clearly, the model fills the gap between straight lottery selection and comparative selection.
The model may be formalized to a certain extent as follows: An applicant with score x receives a chance of admission f(x) where f is a monotonically increasing function such that
Σ f (x) p(x) = R
or
∫ f (x) p(x) dx = R,
with R the selection ratio and p(x) the empirical score distribution summing to 1.
In the special case of a straight lottery,
f (x) = R for all x,
whereas in the case of comparative selection,
f (x) = 1 for x > a
and f (x) = 0 for x < a
the cutoff point a being defined by
∫ axmax p(x) dx = R.
Figure 1 illustrates the model. Weighted lottery selection has been applied in The Netherlands on a national scale as an admission policy for studies such as medicine. In practice, applicants are classified according to grade point average, and ratio weights representing the relative proportion admitted to each class are established a priori.
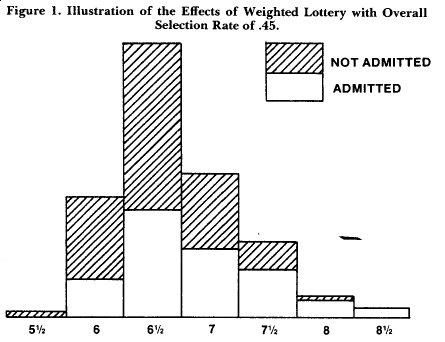
Weighted lottery selection has been discussed in other countries; the Germans have even coined their own term, Leistunggesteuertes Loßverfahren or performance-guided lottery procedure. But the compromise model does not seem to have caught on in countries other than The Netherlands, and even there it may have been abolished by the time this is printed. It may be questioned how useful the model is. In most countries there is ready acceptance of the notion of comparative selection. The problem arises, therefore, when the comparative selection procedure includes a lottery component that is unacceptable. There is little use for models that mediate between alternatives when one of the alternatives would generally be considered illegitimate or inappropriate.
The lottery alternative has been extensively debated in The Netherlands over the past few years. The arguments that have been brought forward may be classified according to the fourfold table containing false positive, false negative, valid positive, and valid negative arguments. An attempt will be made here to give a balanced, if incomplete, account of these discussions.
Advocates of admission by lottery have often stated that grade point averages are invalid predictors anyway. This is patently false. What is true is that because of favorable base rates and modest validities, the expected payoff of selection by grade point average rather than by random admission is not impressive. The more ultimate the criteria, the more "fleeting" (Humphreys, 1968) is the expected payoff. Finally, the distinction between expected payoff and observed payoff should be kept in mind. The institution may appear resistant to improvements because of adaptive processes on the part of both faculty and students that annihilate the effects of selection (Aiken, 1963).
As for the false negative argument, there is the highly sophisticated view that a probability has no meaning when applied to an individual. Theoretically, this argument is difficult to maintain since adequate rules have been proposed (Naerssen, 1961; Hofstee, 1979) to assess the validity of singular stochastic propositions. In the present context, the argument is as farfetched as it is sophisticated; for, if an individual probability had no meaning, the distinction between two tickets representing chances of admission of .99 and .01 would also be meaningless.
Probably the most important and valid negative argument against random admission pertains to what is sometimes called the immoral impact of the lottery method; that is, it does not reward achievement. The principle that achievement should be positively sanctioned is intuitively compelling. Selection by lottery undermines that principle. It should be noted, however, that the lottery rule is not unconditional. An applicant has to qualify himself or herself by demonstrating an appropriate level of performance in secondary school. For those who have little difficulty in fulfilling the minimum requirements, lottery admission is probably demotivating. However, comparative selection is probably demotivating to the majority of students - that is, average students - since it reduces their expected payoff relative to the random admission situation.
The prime valid positive argument for lottery admission is that it is the closest approximation to equal distribution of a scarce commodity. The right of admission to higher education is achieved through certain secondary school diplomas under Dutch law. In a restricted situation, equal probability of admission for qualified applicants may be found to be the most equitable policy.
There are secondary arguments in favor of the lottery method. One is that the intellectual pecking order among studies is disturbed by selection, not by lottery. Back in the 1960s, a colleague and I (Hofstee and Wijnen, 1968) compared intelligence scores with choice of study at Groningen University. The natural intellectual order was clearly visible, starting with mathematics and physics and ending with some of the more obscure studies. Psychology, I am happy to say, was above average. More to the point, the studies that became "closed" in the 1970s were not characterized by high intellectual status in the unrestricted situation. Medicine was above average but clearly below biology, and dentistry attracted quite mediocre students. Naturally, these professions will profit to some extent by comparative selection and even by the use of weighted lotteries. There is probably no such thing as being too intelligent to be a doctor. But from a societal point of view, one may have reservations about this redistribution of talent. It is difficult to see why the field of study that happens to have the most unfavorable selection rate - in The Netherlands, veterinarian studies - should consequently have the highest intellectual status. It may even be argued that problems of restricted admission are not likely to develop in studies requiring high intellectual ability and that the popularity of the restricted studies is caused in part by the restricted intellectual demands they impose upon students.
Another side effect of selection as opposed to the lottery method is that the former results in devaluation of secondary school diplomas. To the extent that one is satisfied with a secondary school system, the lottery method should be preferred, since it backfires least upon that system. Interestingly, however, secondary school teachers have been predominantly opposed to this method. One interpretation is that, in the discussions, numerus clausus and admission procedures were confused, and objections to admission restrictions were carried over to the weighted-lottery rule.
A final argument in favor of using lotteries is that they are more acceptable than comparative selection, at least to Dutch secondary school students. In a study by Hofstee and Trommar (1976), secondary school students in their last year were asked the following question: If you could advise the government on admission policies, which would you recommend? Since the investigation was carried out under the auspices of the advisory committee referred to earlier, our respondents were indeed indirectly advising the government. The straight lottery method received 40 percent of the votes, comparative selection only 10 percent; the remaining 50 percent went to weighted lottery. These results have been replicated in at least three other unpublished studies. One might hypothesize that the mediocre students were primarily responsible for the results. Figure 2, however, shows that this is only partially the case. The relationship between scholastic standing and preference is by no means perfect. Most notably, comparative selection received only some 25 percent of the votes even in the highest scholastic performance category.
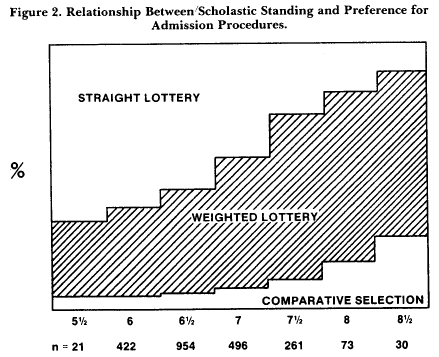
If we leave complications aside, the kernel of the discussion between the extremes of comparative selection and selection by straight lottery consists of two opposing political principles: rewarding achievement and providing equal opportunity. Many other political problems could be adequately captured in those terms, and many solutions consist of a weighted compromise between the two principles. Compromise models such as weighted lotteries may facilitate construction of the least unacceptable solution.
One feature of compromise models that was touched upon in the introduction has come up repeatedly in the discussion of admission policies. It is the "dirty hands" feature; that is, the very situation to which the compromise applies is found unacceptable by some. Any attempt to solve the problems created by numerus clausus can only prolong the existence of that undesirable state of affairs, according to this reasoning. I have little sympathy with the consequences that are usually drawn from this argument, but I think it should be acknowledged that compromises do compromise.
Cutoff Points
The second model (Hofstee, 1977) to be discussed here applies to the situation in which a cutoff score on an achievement test is set for the first time. The expression "for the first time" means that no agreed-upon prior or collateral information is available on the difficulty of the test, the quality of the course, or the amount of preparation by the students.
The following example illustrates the concept of setting a standard for the first time. In 1979, I gave a course on methodology to some 160 second-year psychology students. The passing score on the test had to be lowered to 45 percent mastery, and even then only 55 percent of the students passed. In 1980, the passing score was set at close to 60 percent, and over 90 percent of the students passed. The learning materials were essentially the same; the teachers and the test items were essentially the same; and in view of the large numbers it would be difficult to ascribe the discrepancy to a cohort effect. The discrepancy was probably caused by a shift in administrative regulations that enabled the students to spend more time on the subject. I know of no other standard-setting policy that could have handled these two testings in a coherent and still more or less acceptable way; the compromise model to be described did so, by treating both testings as "first tests."
The model is best explained by referring to Figure 3. The vertical axis there represents percentage of "knowledge" k - in the case of a multiple-choice test, it represents the percentage of right answers corrected for guessing. The horizontal axis represents percentage of failures (f) on the test, that is, the percentage of students scoring below the cutoff point.
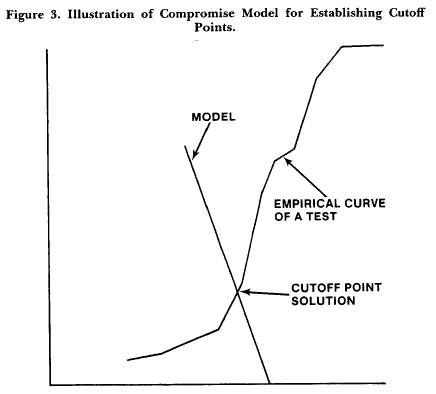
The model consists of the locus of admissible cutoff points and is represented by the straight line k + af = c. The parameters a and c may be established as follows: First, the maximum required percentage of mastery, kmax, is established. This may be defined as the cutoff score that would be satisfactory even if every student attained that score at the first trial. Second, the minimum acceptable percentage of mastery, kmin, is determined. This level may be defined as the cutoff score below which one would not go even if no student attained that score at the first trial. Third, the maximum acceptable percentage of failures, fmax, is established. Fourth, the minimum acceptable percentage of failures, fmin, is established. In our student-centered times, it may seem obvious to set this percentage at zero, but one might argue that this solution is unrealistic since the next cohort of students will quickly adapt to such a lenient state of affairs and will turn it into a self-defeating policy.
The points (fmin, kmax) and (fmax, kmin) are now considered admissible solutions and are substituted into the model to determine the model parameters. For example, if fmin, = 0, kmax = 70, fmax = 60, kmin = 40, the locus of admissible cut-off scores is k + .5 f = 70.
To find the actual cutoff score for a test, the empirical relation between k and f within the test is determined over all possible cutoff scores. An example is given by the curved line in Figure 3. The cutoff point is the point of intersection between the model and the empirical curve. Clearly, the model compromises between "absolute" and "relative" norms. Objections to the model are to be expected from the proponents of mastery learning and would run as follows: Norms should be absolute and should be set at about 85 percent; there is absolutely no need for compromise models; all they will do is take us back to the days when misguided psychometricians were busy mixing up selection and education.
In response, it should be noted that the 85 percent norm is not sacred. It is a compromise between the ideal of 100 percent and the realization of the old psychometric truth that item validities are usually somewhat less than perfect, so that even a "master" may choose an attractive distracter for his or her answer. So there seems to be room for bargaining within the mastery-learning philosophy.
There are, of course, some doubts about whether mastery learning is such a good idea after all (Crombag, 1979). I should like to submit that taking an achievement test score as a criterion or standard is to confuse learning for life with learning for school; that uniform high standards can usually only be met through capitalization on chance, outright coaching, and contempt for cost-benefit considerations; and that there is nothing very progressive about creating the false illusion of equal attainment. I should add that many school systems on the Continent have practiced mastery learning all along in the sense of having students repeat examinations that they fail, and little can be said in favor of that policy (Wilbrink, 1980). 1 could also make scathing remarks about other policies. But that would only support a plea for compromise models.
A second, more serious competitor to the present model is the decision-theoretic approach to establishing norms (Mellenbergh, 1979). In this approach, a loss function is defined on the discrepancy between observed score and criterion score. The criterion may be a true-score estimate or an external criterion. The cutoff score is the test score that minimizes the expected loss.
A minor criticism of the decision-theoretic approach is that so far too much attention has been given to linear and threshold loss functions. On the one hand, threshold or binary loss is realistic only if examination scores are combined in a strictly conjunctive, multiple-cutoff manner and if credits are the only thing that counts, not grades. My department experimented with such a system but abolished it, and I know of no other examples. Linear loss, on the other hand, is appropriate only when scores are combined in a strictly compensatory manner; that is, when there is no such thing as failing a course. Pure compensatory policies are probably even rarer than pure conjunctive policies. For most of the existing educational systems with their mixed policies, some S-shaped loss function is required, such as the normal or beta ogive or a polynomial function.
A more important source of uneasiness with the decision approach comes from the powerful nature of the assumptions that have to be made (Glass, 1978; Shepard, Chapter Four). In the first place, a cutoff score should be set on the criterion. Even if a certain level of required mastery can be agreed upon, this level cannot be directly translated into a required true-score level. There is simply no objective way to represent course objectives by test items, except in a trivial sense; and, in practice, the difficulty of a test is probably more indicative of the disposition of the item writer than of the difficulty of the course content. So it is always unreasonable to set standards in an a priori way without any regard for the number of passes and failures.
A second problem is the establishment of the utility parameters. It is customary to distinguish between direct assessment and indirect assessment of such parameters. Through use of indirect assessment, parameters are selected on the basis of tangible consequences. In many settings, and probably also in the educational setting, indirect assessment is a superior approach: If a discrepancy arises between directly chosen parameters and those that are indirectly derived, persons will change their direct utilities to avoid unacceptable consequences in terms of the proportion of knowledge and proportion of failures associated with the cutoff score. All this takes us back to my compromise model for setting cutoff scores. Whether the two approaches can to some extent be integrated, and especially whether the crudity of the compromise model could thus be alleviated, are open questions at this moment.
Before we leave the discussion of the decision-theoretic approach, a final comment on utilities should be made. In all applications to educational settings that I am aware of, policies are judged by their effects in the average individual case. No separate utility is placed on the global effect of a policy. There is some naiveté about this. If a norm is chosen that maximizes the utility with respect to the average individual, very high or very low percentages of failures may be the result. These extreme percentages may themselves have a negative utility. I am cynical enough to suspect that extremely low or extremely high failure rates may have a corrupting influence both on the next generation of students and on the instructional staff.
It should be stressed that the compromise model for establishing a first-generation cutoff score does not apply to subsequent occasions, that is, to situations in which no systematic differences are intended or expected. For the problem of equating or adapting norms, Gruyter (1978) has proposed very satisfactory solutions of a Bayesian type. His model, of which an earlier solution by Hofstee (1973) appears to be a degenerate case, compromises between maintaining a knowledge percentage and a failure percentage. Naerssen (1979) has shown that it makes little difference whether the equating of subsequent norms is carried out in a relative or absolute manner, that is, by maintaining a knowledge percentage or a failure percentage. His conclusion that there is little use for "hybrid models" needs to be qualified, however. By "little difference" Naerssen means difference in institutional utility. But if utility, as a function of cutoff score, has a flat optimum, a small shift may make a good deal of subjective difference to several students. Second, Naerssen uses linear utility. It remains to be seen what happens if this assumption is varied. Third, even if hybrid models are uncalled for in the context of equating norms, it would not follow that they can be dispensed with when the first standard is set in a situation where prior information is lacking.
Turning now to the compromise model itself, let us consider precisely what the compromise is about. A clue can be found in a study by Zegers, Hofstee, and Korbee (1978). We presented subjects with several frequency distributions of raw achievement test scores and asked them to establish a cutoff point. On the basis of these judgments, an attempt was made to capture their individual grading policies with the compromise model. The most relevant result was that students displayed more relative grading, whereas staff members tended to prefer absolute grading. This suggests that the model compromises between student-centered and staff-centered value systems. In fact, the model was derived to facilitate staff-student bargaining in educational policy committees, so the differences in strategy were not unexpected. In discussing I these differences, I shall not use the high-toned and idealistic arguments that make the reading of educational literature so pleasant, if not particularly rewarding. Instead, I will focus on the differential interests of students and staff. The offensive proposition that, compared to interests, ideals have little motivating power will serve as a guideline.
A priori or absolute standards are in the interest of the institution and its officials for obvious reasons. More status is associated with absolute than with relative norms, not only because in practice relative norms tend to come out lower but also because absolute norms have a sacrosanct quality that relative norms lack. Teaching is a secondary profession in the sense that it does not produce a tangible product, so the teacher is subject to feelings of unimportance. This may well be a reason why educational philosophies advocating absolute norms of 85 percent and higher have become so popular. Absolute norms also provide a more apt vehicle for acting out irritation with "ever duller" generations of students, upon whose performance the teacher depends - perhaps not materially but for his or her own sense of accomplishment.
The prime interest of the student, in contrast, is to obtain passing grades. Students are probably well aware of the virtual absence of correlation between educational and real-life criteria, so their interest is in obtaining a diploma rather than in mastering what is taught. Since at their age they have other interesting things to do, they will try to obtain the diploma with minimal effort. Thus, they may be expected to have little sympathy for the kind of surprises that result from absolute grading. They know where they stand relative to their group, so that with normal study effort they can predict their grades if relative norms are used. They are probably also aware that absolute grading is usually associated with a higher failure rate, which is directly against their interests.
Of course, there are exceptions to this picture. Some teachers are more student oriented than the students themselves, and some students have a keener interest in the learning material than the teacher has. But the student-oriented teacher is subject to collegial pressure, and the intrinsic motivation of a student can hardly extend to everything that he or she is taught. The mere proclamation that all interests are equal - usually followed by the corollary that staff interests are more equal than student interests - is not going to produce a healthy learning environment. The realization that there is an ongoing and structural conflict of interests and that bargaining and compromises are honorable facts of life may in the end lead to better solutions.
An interesting ramification of the cutting-score model was suggested by findings in the study by Zegers, Hofstee, and Korbee (1978) - findings that appeared anomalous at first. Some judges chose to set higher cutoffs for the more difficult tests and lower cutoffs for easier tests. An interpretation of this policy may be constructed by referring to cooperative grading systems (see, for example, Fraser and others, 1977; Beaman and others, 1977). With a relative policy, an individual's chances of passing are higher as the others perform worse; under a cooperative policy, his or her chances are higher as the others perform better. This interpretation of the grading behavior of the judges in the study by Zegers, Hofstee, and Korbee (1978) is a bit farfetched, since cooperative grading makes sense only when students are actually encouraged to cooperate, and the judges had no reason to suppose that this was the case. But the point is brought up because cooperative grading is an interesting possibility in itself, and because the compromise model can easily be extended to cover all intermediate policies between absolute and cooperative grading.
Combining Grades
Having discussed student admission and the grading of single tests, let us now turn to the topic of combining grades for an examination decision. A special case is the problem of setting standards for a single course when students who fail have to repeat the test until they reach a passing level. Some people may not think of this as a combination problem, but there are good reasons to do so.
The specific problem of setting a standard for a single course with repeated testings is almost invariably solved by a disjunctive policy; that is, the student passes as soon as a passing score is obtained on one out of two or more testings. In most cases there are no restrictions on the number of testings, though there may be restrictions on the intervals between testings. The disjunctive policy has at least two weaknesses. In the first place, it capitalizes on chance because of the unreliability of the tests. Naerssen (1976) calculated that inserting an extra testing per year would result in many false positives if the norm was not raised. Second, the disjunctive policy elicits a "reconnaissance effect" (Brink, 1977); since students can fail a test with impunity, some will take a test just to see what it looks like. This is a costly state of affairs, for several obvious reasons.
An alternative that would solve these problems is a compensatory policy in which the obtained grade for a single course is the average over repeated testings; a person passes as soon as his or her average is above the norm. Both capitalization on chance and reconnaissance strategy would be effectively counteracted by the averaging policy. Unfortunately, this policy is in conflict with most people's feelings (or sentiments) about justice. In the moral atmosphere that characterizes educational rhetoric, failing a test is a sin, so the student should be given the benefit of the doubt, even if that amounts to capitalization on chance.
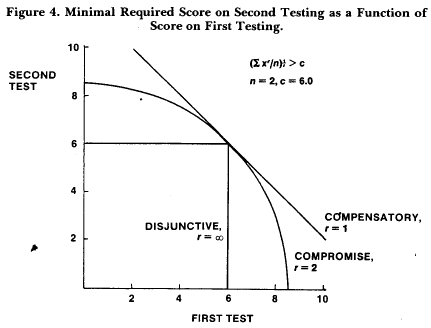
The compromise model for this dilemma is easily constructed through application of the Minkowski r metric (see, for example, Coombs, Dawes, and Tversky, 1970), as illustrated in Figure 4. The individual student is represented as a point in an n space; the coordinates of the point represent his or her scores on the n repeated testings. A student passes if the average distance between the point and the origin is greater than the norm distance. In general:
[ ( 1/n ) Σ xgr ]1/r ≥ c, r ≥ 1, g = 1, 2, .... , n,
where xg is the score on test g and c is the norm. Setting the Minkowski parameter r equal to infinity gives the disjunctive model; setting r = 1 gives the averaging model. An intuitively appealing compromise is the quadratic or Euclidian model, in which higher grades are given more weight than lower grades (Coombs, Dawes, and Tversky, 1970). 1 know of no present applications, but I hope that presentation of the compromise will lead to practical applications in the future.
With respect to the combination of scores for different courses, the debate is usually between conjunctive and compensatory policies. Compromise models between the two are easily constructed through a translation of axes in the Minkowski model. Here also, the compensatory policy deserves more attention for both psychometric and pedagogical reasons than it usually receives. The personal investment of the teacher in a particular course is probably the most serious obstacle to compensatory policies. To the marginal student, however, compensatory combination is threatening since, beyond a certain point, it may be practically impossible to attain a passing average. The interaction between these motives may form a powerful conspiracy against educational change.
Three compromise models have been discussed here in relative isolation: weighted lottery for the problem of student selection, a compromise model for setting a pass-fail standard on a single test, and a Minkowski solution for merging disjunctive, compensatory, and conjunctive combination policies. But the models and the problems may have more in common than their isolated treatment suggests. Formally, their main theme is the counterpoint between the relative and the absolute. It should be possible to find a superordinate, all encompassing compromise model; however, such integrative elegance was not attempted here.
An even greater challenge is offered by the heterogeneity of values and motives that dominate the discussion to which the models pertain. Would a global classification into absolutist versus relativist value systems make sense, or would it only obscure the substantive issues? Maybe the distinctions should be drawn along quite another dimension: between those favoring clear-cut solutions, either relative or absolute, and those who are looking for compromises.
References
Aiken, L. R. "The Grading Behavior of a College Faculty." Educational and Psychological Measurement, 1963, 23, 319 - 322.
Beaman, A. L., and others. "Effects of Voluntary and Semivoluntary Peer-Monitoring Programs on Academic Performance." Journal of Educational Psychology, 1977, 69, 109 - 114.
Brink, W. P. van den. "Het Verken-Effect." Tijdschrift voor Onderwijsresearch, 1977, 2, 253 - 261.
Coombs, C. H., Dawes, R. M., and Tversky, A. Mathematical Psychology. Englewood Cliffs, N.J.: Prentice-Hall, 1970.
Crombag, H. F. M. "ATI: Perhaps Not Such a Good Idea After All." Tijdschrift voor Onderwijsresearch, 1979, 4, 176 - 183.
Fraser, S. C., and others. "Two, Three, Four Heads Are Better than One: Modification of College Performance by Peer Monitoring." Journal of Educational Psychology, 1977, 69, 101 - 108.
Glass, G. V. "Standards and Criteria." Journal of Educational Measurement, 1978, 15, 237 - 261.
Gruyter, D. de. "A Bayesian Approach to the Passing Score Problem." Tijdschrift voor Onderwijsresearch, 1978, 3, 145 - 151.
Hofstee, W. K. B. "Een Alternatief voor Normhandhaving Bij Toetsen." Nederlands Tijdschrift voor de Psychologie, 1973, 28, 215 - 227.
Hofstee, W. K. B. "Caesuurprobleem Opgelost." Onderzoek van Onderwijs, 1977, 6, 6 - 7.
Hofstee, W. K. B. "'Jan Heeft een Kans van .70. Drogredenen met Betrekking Tot Individuele Kansuitspraken." Kennis en Methode, 1979, 3, 433 - 445.
Hofstee, W. K. B., and Trommar, P. M. "Selectie en Loting: Meningen van VWO-Eindexaminandi." Heymans Bulletin, No. 25 1, Department of Psychology, University of Groningen, 1976.
Hofstee, W. K. B., and Wijnen, W. H. F. W. "Intelligentieonderzoek Eerstejaars 1968." Mededelingenblad Rijks Universiteit Groningen, 1968, 2(8).
Humphreys, L. G. "The Fleeting Nature of the Prediction of College Academic Success." Journal of Educational Psychology, 1968, 59, 375 - 380.
Mellenbergh, G. J. "De Beslissing Gewogen." In G. J. Mellenbergh, R. F. van Naerssen, and H. Wesdorp (Eds.), Rede als Richtsnoer. The Hague: Mouton, 1979.
Naerssen, R. F. van. "A Scale for the Measurement of Subjective Probability." Acta Psychologica, 1961, 17, 159- 166.
Naerssen, R. F. van. "Het Derde Tentamenmodel, met een Toepassing." Tijdschrift voor Onderwijsresearch, 1976, 1, 161 - 170.
Naerssen, R. F. van. "Absolute of Relatieve Aftestgrens: Een Verkenning met Simulatie." Tijdschrift voor Onderwijsresearch, 1979, 4, 8-17.
Wilbrink, B. "Caesuurbepaling." COWO-Rapport, University of Amsterdam, 1980.
Zegers, F. E., Hofstee, W. K. B., and Korbee, C. J. M. "Een Beleidsinstrument m.b.t. Caesuurbepaling." Paper presented at Onderwijs Research Dagen, Utrecht, 1978.
Gregory J. Cizek and Michael B. Bunch (2007). Standard setting. A guide to establishing and evaluating performance standards on tests. Sage.
- Chapter 12: The Hofstee and Beuk methods.
 http://www.benwilbrink.nl/publicaties/83hofstee_compromise.htm
http://www.benwilbrink.nl/publicaties/83hofstee_compromise.htm



