
Inhoud.
0 Voorwoord
1 Beheersing van de leerstof: wat bedoelen we daarmee?
2 De toets als steekproef
3 Hoe schat ik mijn ware beheersing?
4 Schatting (voorspelling) van de te behalen toetsscore
5 Studiestrategie, RISICO beheersing, onderwijsbeleid
6 Studiestrategie onder HEx: hordenloop examenregelingen
7 HEx met beperkt aantal herkansingen
8 Studiestrategie onder CEx: compensatorische examenregelingen
9 Examenregelingen voor de propedeuse: een geval apart?
Bijlagen.
A Voorspellende kansverdeling voor de toetsscore van de student
B Studiestrategie onder hordenloop examenregelingen
C Studiestrategie onder compensatorische examenregelingen
D Verschillende leercurven als hulpmiddel bij de berekeningen
E Literatuur over subjectieve waarschijnlijkheid
F risico tabellen
Gerefereerde literatuur
Begrippenlijst
Symbolen en afkortingen
Een cursus over examenregelingen, wat houdt dat in? Voorop staat dat het examen op verschillende manieren geregeld kan zijn. Met regelen is dan vooral bedoeld de manier waarop studieresultaten voor afzonderlijke studieonderdelen gecombineerd worden. De cursus behandelt enkele mogelijkheden, voornamelijk twee vormen van examenregeling: de conjunctieve (dat is de regeling zoals we die vandaag de dag voornamelijk hanteren), en de compensatorische (het gemiddelde van de verschillende studieresultaten bepaalt het eindresultaat). De compensatorische regeling is ons allen erg vertrouwd, het is de manier waarop in lager en middelbaar onderwijs cijfers voor proefwerken en beurten binnen één vak tot eindcijfer voor dat vak gecombineerd worden. Het is ook de manier waarop resultaten voor verschillende vragen binnen één toets (of tentamen) gecombineerd (opgeteld in dit geval) worden tot het toetsresultaat. Wij zijn alleen niet gewend om het gemiddelde resultaat over verschillende studieonderdelen het examenresultaat te laten bepalen (zoals bijv. de Amerikanen dat weer wel gewend zijn).
De cursus is gericht op het onderwijsbeleid: wie de keuze moet maken tussen conjunctieve of compensatorische regeling van het examen, zal inzicht moeten hebben in de effecten die ieder van deze regelingen op de onderwijsresultaten heeft om een verantwoorde beslissing te kunnen nemen. Maar niet alleen de belangrijke keuze tussen deze beide vormen van examenregeling wordt aan de orde gesteld, ook allerlei kleinere variatie mogelijkheden binnen ieder van deze hoofdvormen kunnen op hun onderwijseffecten geëvalueerd worden, waartoe deze cursus de technieken hoopt aan te dragen.
Met één uitzondering: de problematiek van het bepalen van de zakslaag grens bij afzonderlijke studieonderdelen, een problematiek die zich alleen bij onze huidige conjunctieve, hordenloop, examenregeling voordoet, werd al eerder in een afzonderlijke cursus behandeld (Wilbrink, 1977 b). Waar mogelijk zal ik naar deze cursus verwijzen.
De cursist zal straks in staat zijn om een verantwoorde keuze te maken tussen verschillende voorgestelde varianten van examenregeling, door deze varianten te analyseren op hun verwachte onderwijseffecten, en deze varianten op hun effecten met elkaar te vergelijken.
In een meer actieve rol zal de cursist op basis van de informatie in deze cursus gegeven, beter in staat zijn om ook eigen voorstellen te ontwikkelen. Door het inbrengen van eigen (verdergaande) voorstellen, en van het resultaat van de analyse van te verwachten onderwijseffecten, kan de cursist de discussie in de eigen faculteit (vakgroep, onderwijscommissie) aanscherpen, zodat een meer verantwoord onderwijsbeleid kan ontstaan.
De meeste studenten zullen hun studiegedrag, de tijd die zij aan de studie besteden, de manier waarop zij de stof bestuderen, aanpassen aan de gestelde exameneisen. Het effect dat een examenregeling heeft op het rendement van het onderwijs, het niveau van het onderwijs, en de gemiddelde studieduur, heeft zij dan ook vooral via het gedrag van de studenten dat zij uitlokt, beloont, of bestraft. Wie de effecten van verschillende varianten van examenregeling met elkaar wil vergelijken, zal moeten weten hoe studenten in hun studiegedrag zullen verschillen. Vandaar dat ik de cursus begin met bespreking van studiestrategieën, dit hele deel A is er aan gewijd.
Afgezien van het feit dat dit deel een noodzakelijke voorbereiding vormt op het eigenlijke cursusdeel B (dat hopelijk eind 1979 kan verschijnen), wil ik als doelstelling voor dit deel noemen:
De cursist kan met behulp van de te presenteren technieken voor een gegeven examenregeling bepalen wat ongeveer optimale studiestrategieën voor de student zijn (voor afzonderlijke studieonderdelen, of voor het hele examen). Die informatie kan hij aan de studenten doorgeven, maar die informatie zou op zich ook aanleiding kunnen zijn om wijzigingen in de procedure (of in de cesuurbepaling) aan te brengen.
De student die op rationele wijze wil studeren, zijn kansen om te slagen in de hand wil houden, waar mogelijk en wenselijk tijd en moeite wil minimaliseren" zal in staat moeten zijn om een goede schatting te maken van de toetsscore die hij mag verwachten, gegeven de beheersing die hij over de leerstof denkt te hebben, of denkt te kunnen bereiken. Wat er zoal komt kijken bij het maken van dergelijke schattingen bespreek ik in de hoofdstukken 1 tot en met 4. Op basis van de dan verworven inzichten is het mogelijk om optimale studiestrategieën onder twee varianten van conjunctieve examenregeling (hoofdstuk 6 en 7), en onder compensatorische examenregelingen te vinden (hoofdstuk 8). Hoofdstuk 5 geeft hierop een introductie. Het bijzondere karakter van het propedeutisch examen vraagt om bespreking in een afzonderlijk hoofdstuk. Ook hier zijn uitsluitend studiestrategieën onder diverse soorten examenregeling aan de orde (hoofdstuk 9).
Het materiaal in dit cursusdeel is voor een behoorlijk deel resultaat van (modelmatige) berekeningen, waarvoor de technische verantwoording in de bijlagen gegeven wordt (bijlage A voor het materiaal gepresenteerd in de hoofdstukken 1 t/m 4, bijlage B bij hoofdstuk 6, en bijlage C bij hoofdstuk 7).
Er worden in deze cursus nogal wat nieuwe begrippen geïntroduceerd, waarvan achterin het cursusboek een lijst (met omschrijvingen) is opgenomen. Ook van veel voorkomende symbolen in de eigenlijke cursustekst is achterin een lijst voor naslagdoeleinden opgenomen.
De benadering van de beoordelingsproblematiek in het onderwijs zoals ik die in deze cursus presenteer, is tamelijk nieuw, en zal voor vele lezers de nodige verrassingen bevatten. Voorop staat dat de wijze van beoordelen van invloed is op het gedrag van de studenten, en daarmee ook op de beoordelingsresultaten (en de studieresultaten!), een standpunt dat nog door weinig onderwijskundigen wordt ingenomen. Een uitzondering is R. F. van Naerssen met zijn werk op het onderwerp tentamenmodellen (zie literatuurlijst, en bijlage B).
Deel A, over studiestrategieën, zou je kunnen zien als een cursus voor het kwantificeren van de doorzichtigheid (transparantie) van tentamens en examens (de wenselijkheid van doorzichtigheid van de toetsing werd door De Groot (1970) geponeerd).
Voor het leggen van de basis van dit werk over studiestrategieën heb ik gebruik kunnen maken van statistische technieken die van tamelijk recente datum zijn. De resultaten worden in deze cursus voor het eerst gepubliceerd, vandaar dat ik voor deze eerste editie graag enig voorbehoud ten aanzien van het gepresenteerde wil maken. Hier ligt de voornaamste reden voor het in het titelblad aangegeven voorlopige karakter. Daarnaast stelt de gepresenteerde stof nogal wat eisen aan de te gebruiken terminologie, en dat des te meer waar het hier een cursus voor docenten betreft, en niet direkt een verhandeling voor vakgenoten. Ik heb niet het idee alle presentatieproblemen in voldoende mate opgelost te hebben, en moet de lezer op sommige punten dan ook om begrip daarvoor vragen. Voor commentaren en kritiek sta ik open, maar vooral ontvang ik graag ervaringen die men opgedaan heeft in het toepassen van het in deze cursus gebodene.
Voor de cursist die een en ander in zijn eigen onderwijssituatie in toepassing wil brengen is het van belang te weten dat hij of zij zich voor verder advies altijd tot het COWO kan wenden (voor zover als docent verbonden aan of als student ingeschreven bij de U.v.A.).
B. W.
27 oktober 1978.
Wie gaat zoeken naar een definitie voor beheersing ontdekt al snel dat je daarbij nogal wat verschillende kanten uit kunt. Een in het oog springend probleem is bijvoorbeeld dat het er in de praktijk niet zozeer om lijkt te gaan dat de mate van stofbeheersing vastgesteld wordt, maar of de behaalde toetsresultaten aan een gestelde norm voldoen.
Gezocht wordt nu een definitie van beheersing van leerstof die een vruchtbare analyse mogelijk maakt van de effecten die het beoordelen in het onderwijs heeft. Daarom kan hier niet de makkelijke, maar o zo bedrieglijke weg gekozen worden waarbij beheersing van de stof gedefinieerd wordt als het resultaat dat de student op de toets weet te behalen. Het toetsresultaat als meting van de stofbeheersing is door allerlei fouten en toevalligheden beïnvloed: meetresultaat en hetgeen beoogd wordt te meten zijn niet hetzelfde!
Iedere docent heeft wel een voorstelling van het soort vragen dat relevant is voor wat hij met de geboden leerstof bij deze studenten heeft willen bereiken. Dat zijn de vragen die hij tot nu toe ook al gebruikte in de door hem afgenomen toetsen. Van belang is nu dat expliciet duidelijk gemaakt wordt welke vragen over de stof wel, en welke vragen niet in de toetsing zullen worden betrokken.
Mogelijke vragen over de stof, die niet in de toetsing opgenomen zullen worden, kunnen zijn:
Het zou erg mooi zijn wanneer een min of meer volledige verzameling aangelegd kan worden van alle vragen die wel van belang zijn. Dat is het meest concreet, en daarmee kun je het prettigst werken. Maar natuurlijk, meestal zal het aantal vragen dat over de geboden stof te bedenken valt en dat in overeenstemming is met de doelstellingen te groot zijn voor een dergelijke vorm van concrete opsomming.
Dan is het meestal toch wel mogelijk om een volledige opsomming te geven van alle soorten vraagstelling over ieder van de onderwerpen uit de leerstof. Mogelijkheden daarvoor werden beschreven in de cursus Cesuurbepaling (Wilbrink, 1977 b), paragrafen 4.5 en 4.6.
Wat de docent dan verstaat onder de beheersing van de stof, kan hij nu refereren aan deze verzameling van vragen. Dat kan dan een concrete, al dan niet uitputtende, verzameling zijn, of een omschreven verzameling van alle soorten van vragen die binnen de doelstellingen vallen, verder door mij aangeduid als een denkbare verzameling van vragen.
Het ligt dan voor de hand om de ware beheersing van de student te definiëren als de proportie vragen uit de (concrete of tenminste denkbare) verzameling van alle vragen over de stof die hij goed zou kunnen beantwoorden wanneer hem de vragen voorgelegd zouden worden. De verzameling verwijst in het vervolg naar de door de docent vastgestelde verzameling van vragen die voor opname in de toets in aanmerking komen.
Nu is het in de praktijk meestal niet mogelijk om de student alle vragen uit de verzameling metterdaad te laten beantwoorden, ook al zou de docent de beschikking hebben over een concrete verzameling. Dan is het ook niet mogelijk om de hierboven gedefinieerde ware beheersing exact vast te stellen. Het zal in het volgende nog blijken dat desondanks de gegeven definitie voor de ware beheersing het mogelijk maakt om belangrijke en concrete resultaten te boeken.
Maar, u wilt misschien tegenwerpen dat we toch in de vorm van de resultaten op de toets exacte gegevens over de ware beheersing van de studenten in handen krijgen? Ik zal in het volgende hoofdstuk laten zien dat het toetsresultaat weliswaar een aanwijzing geeft voor de mate van ware beheersing van de student, maar dat daarbij met bepaalde onzekerheden rekening gehouden moet worden.
Het is ondertussen niet alleen de docent die moet schatten wat de ware beheersing van de student is. Ook die student zelf heeft daarover niet meer dan een weinig precies idee. Hij heeft immers niet alle vragen over de stof gezien, en kan slechts een meer of minder goede schatting van zijn eigen ware beheersing maken. In hoofdstuk 3 komt de techniek voor het maken van die schatting aan de orde.
Bij het omschrijven van het begrip ware beheersing werd geen onderscheid gemaakt tussen open vragen en meerkeuze vragen. Omdat bij meerkeuze vragen sprake is van een aanzienlijke kans op goed raden bij het ontbreken van het juiste weten is een nadere toelichting hier op zijn plaats.
Om te beginnen: of men werkt met open vragen of met meerkeuze vragen maakt geen verschil zolang men in de definitie van ware beheersing en in de keuze van vraagvorm voor de toets maar consistent is. Met andere woorden: wie meerkeuzevragen gebruikt bij zijn toetsing, moet ook ware beheersing definiëren op de (denkbare) vraagverzameling waarin uitsluitend meerkeuzevragen opgenomen zijn.
Het zal alleen in de hoogte van de ware beheersing, in de proportie vragen die de student goed zou kunnen beantwoorden, enig verschil maken. Een ware beheersing van 0,6 gedefinieerd op open vragen over de stof is uiteraard iets anders dan de ware beheersing van 0,6 gedefinieerd op meerkeuze vragen over de stof. Men zal daar wel terdege rekening mee moeten houden.
Jammer genoeg is het niet mogelijk om een eenvoudige omzettingsregel te geven van ware beheersing op open vragen naar ware beheersing op meerkeuze vragen. Dat hangt van de kwaliteit van de vragen af, het aantal alternatieven dat bij de meerkeuzevragen gebruikt wordt, het soort scoringsregel dat voor de meerkeuzevragen gehanteerd wordt, etc.
De raadkans die zich bij meerkeuzevragen voordoet, over de exacte grootte waarvan meestal slechts gissingen zijn te doen, wordt dan ook eenvoudig geabsorbeerd in de definitie van ware beheersing.
Op deze wijze is al hetgeen verder in deze cursus gezegd wordt over toetsen, combinaties van toetsen, en studiestrategieën zonder meer ook van toepassing op meerkeuze toetsen. (Maar de in hoofdstuk 6 te behandelen leercurve moet wel aangepast worden, waarvoor in bijlage D aanwijzingen gegeven worden.)
Dat neemt niet weg dat aan meerkeuzetoetsen bepaalde nadelen verbonden zijn die open-vraag-toetsen niet kennen, terwijl het voordeel van de automatische scoorbaarheid voor de toch altijd nog kleine aantallen studenten waarvoor de docent zijn toetsen afneemt nauwelijks gewicht in de schaal legt. Voor bespreking van de nadelen van meerkeuze vragen bij eindtoetsen zie de cursus Cesuurbepaling, of Wilbrink (1977a).
Ik wil van deze gelegenheid nog wel gebruik maken om er op te wijzen dat voor veel vakgebieden het eenvoudiger is om goede open vragen over de leerstof te formuleren, dan goede meerkeuze vragen. Het bedenken van goede afleiders voor de meerkeuzevraag blijkt in de praktijk altijd weer bijzonder lastig te zijn, zodat zelfs het gevaar ontstaat dat docenten die voor de zoveelste keer een toets moeten samenstellen met meerkeuzevragen, daar steeds onwaarschijnlijker, steeds verder van de onderwijsdoelstellingen af staande vragen voor bedenken.
In het vorige hoofdstuk hebben we afgesproken onder de ware beheersing van de leerstof te verstaan de proportie vragen p uit de verzameling van alle (denkbare) vragen over de stof die de student goed zou beantwoorden wanneer ze hem voorgelegd zouden worden.
Dit is een hele mondvol, vandaar dat de volgende visuele voorstelling ons betere diensten kan bewijzen dan het bovenstaande verbale geweld:
FIGUUR 2.1 Ware beheersing als proportie geweten vragen p in de verzameling van alle (denkbare) vragen.
Om enige vooruitgang te kunnen boeken in ons inzicht over het functioneren van toetsen in het onderwijs, zullen we er vooral in het begin niet onderuit kunnen nogal sterke veronderstellingen te hanteren.
Zo zal in dit hoofdstuk de toets opgevat worden als bestaande uit vragen die op strikt toevallige wijze uit de verzameling van (denkbare) vragen getrokken zijn. In de praktijk zal het slechts zelden gebeuren dat de docent op die wijze zijn toets samenstelt, maar toch zal de veronderstelling van strikt toevallige samenstelling ons een eenvoudig model opleveren waarmee de praktijk aardig benaderd kan worden.
Wat houdt toevallig trekken in? In het geval dat er inderdaad een verzameling van vragen is aangelegd, waaruit voor iedere nieuwe toets de vragen gehaald worden, is daar een heel concrete voorstelling van te maken:
Veronderstel dat iedere vraag op een afzonderlijk kaartje is geschreven, dat alle kaartjes in een trommel gegooid worden, dat de trommel goed geschud wordt, en er telkens door een geblinddoekte persoon een kaartje uit getrokken wordt. De toets die samengesteld wordt uit vragen die op deze wijze strikt toevallig getrokken zijn, is een toevallige steekproef uit de verzameling van vragen.
Het wordt iets moeilijker in het geval er geen concrete verzameling vragen bestaat, maar slechts een denkbare verzameling van vragen: de docent formuleert in dat geval speciaal voor de af te nemen toets een aantal vragen over de leerstof. Een dergelijke toets is slechts onder speciale voorzorgen bij het kiezen van de vragen op te vatten als een steekproef uit de denkbare verzameling van vragen.
Vanuit het oogpunt van de student bezien kan een dergelijke toets meestal wel als een strikt toevallig getrokken steekproef van vragen gezien worden. De student heeft geen kennis van de wijze waarop de docent te werk gaat bij het samenstellen van de toets, zodat ook een niet strikt toevallig gekozen toets er voor de student wel als een strikt toevallig gekozen toets uitziet.
Zolang het gaat om inzicht in de slaagkans die de individuele student heeft voor een bepaalde toets, kunnen we de toets meestal wel opvatten als een strikt toevallig gekozen aantal vragen.
De kleinst denkbare toets bestaat uit één vraag. Wanneer deze ene vraag strikt toevallig uit de vragenverzameling gekozen wordt, of wanneer de student geen speciale voorkennis heeft over hoe de vraag gekozen is, kan de volgende analyse gemaakt worden:
De student die een toets gaat doen die bestaat uit één vraag, terwijl zijn ware beheersing gelijk is aan p = 0,70, heeft
Beide kansen samen vormen de kansverdeling voor zijn toetsscore. Ik zal direkt, bij het iets minder eenvoudige geval van een toets bestaande uit twee vragen, een tekening van zo'n kansverdeling geven. In de kansverdeling ligt alle relevante informatie over de te verwachten of de voorspelde toetsscore besloten, informatie op grond waarvan
de student bijvoorbeeld een weddenschap op zijn toetsresultaat zou kunnen afsluiten.
Voor een toets bestaande uit twee toevallig getrokken vragen is evenzo de kansverdeling voor de toetsscore te berekenen. De manier waarop dat gaat, is kort aangeduid in Bijlage A. Voor ons is slechts het resultaat van belang. In figuur 2.2 is de kansverdeling afgebeeld, de kans op een totaalscore van respectievelijk 0, 1 of 2 (dat zijn voor een toets van twee vragen alle mogelijkheden). In figuur 2.3 zijn de kansen afgebeeld op een totaalscore van tenminste 0, 1, of 2 respectievelijk. Het zijn juist deze kansen op tenminste een bepaalde toetsscore x die in het vervolg van deze cursus in het brandpunt van de belangstelling zullen staan (kans op voldoende score, bijv.!).
FIGUUR 2.2 kansverdeling. FIGUUR 2.3 kans op tenminste een score X.
Het hoeft geen verbazing te wekken dat op een toets bestaande uit maar twee vragen pech of geluk een grote rol kan spelen: hoewel de student een ware beheersing van 0,70 heeft, is zijn kans om tenminste één van de twee vragen goed te kunnen beantwoorden maar 0,91. In bijna één op de tien gevallen kan hij verwachten beide vragen niet te weten, een score 0 te behalen.
Dit kanselement, dat bij een toets van twee vragen een grote rol speelt, blijft ook bij toetsen van meer normale lengte een grote rol spelen. Het valt makkelijk in te zien dat de ware beheersing p op die kansen een sterke invloed heeft, immers: hoe hoger de ware beheersing, des te groter de kans op het behalen van tenminste een bepaalde toetsscore (zeg, een score x = 1). In dezelfde figuur kunnen deze kansen voor verschillende waarden voor de ware beheersing p afgebeeld worden, zie figuur 2.4.
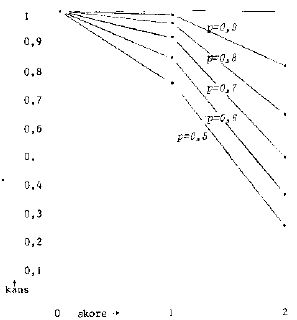
FIGUUR 2.4 Kans op tenminste score x = 0, 1 of 2.
Noot. Omdat in de reconstructie voor de manier van afbeelden is gekozen voor het staafdiagram, in plaats van voor het lijndiagram zoals in de publicatie van 1978, ziet de reeks voor beheersing van p = 0,5 tot p = 0,9 eruit als getrapt. De bovenste treden horen bij p = 0,9, de laagste bij p = 0,5. De 'hoekigheid' van deze plot beeldt overigens de 'hoekigheid' van zo'n kleine toets met maar twee vragen goed af. Het is niet echt subtiel om een toets maar uit twee vragen te laten bestaan. Uit hoeveel vragen een toets dan wel zou moeten bestaan, dat is een in het volgende nog te behandelen onderwerp. Daarop vooruitlopend in Figuur 2.5 de fijnere getraptheid die bij een toets met meer vragen hoort.
De dun getrokken lijnen in deze figuren hebben slechts de functie aan te geven welke punten bij elkaar horen, d.w.z. bij dezelfde waarde van p. De score op een toets die uit twee vragen bestaat kan maar drie verschillende waarden aannemen, en geen tussenliggende waarden.
Zoals uit figuur 2.4, en zeker ook uit figuur 2.5 blijkt, hebben de verdelingen voor verschillende waarden van p een regelmatigheid waarvan gebruik gemaakt kan worden bij het schatten van scorekansen voor waarden van p die in de figuur voor verschillende waarden van de niet ingetekend zijn: men kan op eenvoudige wijze interpoleren.
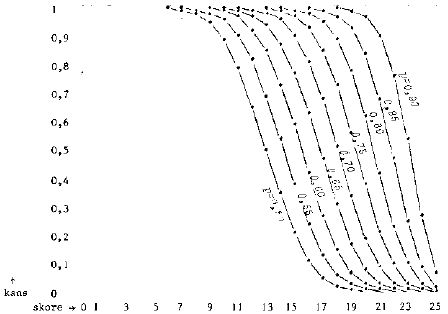
FIGUUR 2.5 Kans op tenminste een toetsscore x= 0, 1, 2, ... resp. 25 (voor een toets bestaande uit 25 vragen), voor verschillende waarden van de ware beheersing p.
In dit hoofdstuk gaat het alleen om het steekproef karakter van de toets, en hoe daaruit zelfs voor redelijk uitgebreide toetsen een forse marge van onzekerheid resulteert ten aanzien van de minimaal te verwachten toetsscore.
Om te beginnen is het zeker niet zo dat iemand met een ware beheersing p er op mag rekenen tenminste een score te behalen die daarmee in overeenstemming is. Kijk bijvoorbeeld naar het geval waar p=0,80. De statistische verwachting is dat iemand met deze ware beheersing ook 80 % van de toetsvragen zal weten te beantwoorden, dat is in het geval van een toets bestaande uit 25 vragen daar een score van 20 op zal boeken. Maar dat is niet meer dan het verwachte (gemiddelde) resultaat, en de kans daarop is maar 0,20. De kans op een score van 20 of meer valt af te lezen uit figuur 2.5, en is 0,62. Hoewel de student een redelijke kans heeft op een toetsscore die tenminste in overeenstemming is met zijn ware beheersing, is de kans toch erg groot, namelijk 0,38 bij een toets van 25 vragen, dat hij een lagere score behaalt.
Dit soort overwegingen laat zien dat er een forse onzekerheid kleeft aan het te verwachten toetsresultaat. In de praktijk is dat van groot belang voor de student. Denk bijvoorbeeld aan de situatie waarin hij kan zakken op de toets, en de student zich in de voorbereiding op de toets een zo hoge beheersing van de stof wil eigen maken dat de kans om te zakken een voor hem aanvaardbaar niveau bereikt.
Blijkt daarvan nu ook iets in de praktijk? Het voorgaande is een rijkelijk theoretisch verhaal, dat vraagt om aanvulling met empirische gegevens.
Uit figuur 2.5 valt af te lezen wat de kans is voor iemand met bijv. een ware beheersing van 0,60 om een score van tenminste 19 te boeken op een toets van 25 vragen. Die kans is niet zo groot, slechts 7 op 100. Deze student mag van iedere 100 toetsen die hij aflegt verwachten er op zeven meer dan 18 punten te scoren. In de praktijk wordt iedere toets één keer afgelegd, en is het kennelijk niet zonder meer mogelijk om gegevens over kansen te verzamelen. Een manier waarop daar tenminste een begin mee gemaakt kan worden, is door een afgenomen toets eenvoudig in tweeën te delen, en voor iedere toetshelft afzonderlijk de totaalscore te bepalen. Je mag aannemen dat voor iedere deelnemer geldt dat zijn ware beheersing gelijk is voor zowel de ene toets(helft) als de andere toets(helft). De verschillen in beide toetsscores zijn dan een aanwijzing voor het bestaan van het soort onzekerheden, voor het bestaan van de kansen die in dit hoofdstuk aan de orde zijn. In figuur 2.6 zijn de resultaten weergegeven van dit experiment: een werkelijk afgenomen toets bestaande uit 50 vragen werd naderhand gesplitst in twee toetsen van 25 vragen, waarvoor afzonderlijke totaalscores werden vastgesteld. De figuur laat zien dat voor veel studenten de scores op beide toets(helft)en nogal uiteenlopen, hoewel hun ware beheersing voor beide toetsen gelijk moet zijn (want gedefinieerd op dezelfde vragenverzameling waaruit ook beide toetshelften samengesteld zijn).
25 | | grensscore (=12)
24 | |
23 | | 1
22 | | 1 1 3 2 3 2
21 | | 2 1 6 1 1 1
20 | 2| 1 2 2 4 6 2 1
19 | | 2 2 2 1 2 1 1 1 1
18 | 1| 6 6 2 6 5 3 2 2 2
17 | Drempel 1| 4 5 4 6 1 2 4
vervolg- 16 | 1| 4 6 6 3 3 4
toets- 15 | 1 | 2 2 1 2 3 3 2
scores 14 | 1 | 3 3 4 3 1 1 2
13 | 1 3| 1 2 2 1
12 | 2| 1 2
11 | 1|
10 | 1| 1
|
.. 9 10 11|12 13 14 15 16 17 18 19 20 21 22 23
toetsscores → →
FIGUUR 2.6 Scores van 200 studenten op een in tweeën gedeelde toets van 50 vragen. (aantal keren dat iedere combinatie voorkomt)
Ondanks dezelfde ware beheersing blijken studenten zeer uiteenlopende scores te behalen. Zouden de scores op beide toetshelften exact in overeenstemming zijn met de (onbekende) ware beheersing van de student, dan zouden in figuur 6 alle studenten op de diagonaal ZW-NO liggen, omdat scores op beide toetsen aan elkaar gelijk zouden zijn. Welnu, er is in de verste verte geen sprake van dat de toetsscores op deze diagonaal liggen: ze liggen er rijkelijk rondom verspreid.
Hoe groter de steekproef is, d.w.z. hoe langer de toets gemaakt wordt, des te beter gelegenheid krijgt de student om zijn ware beheersing in de totaalscore van de toets tot uitdrukking te brengen. Maar helemaal precies zal dat nooit lukken, tenzij de toets zo lang gemaakt wordt dat alle vragen uit de verzameling er in opgenomen zijn. Maar het laatste is in vrijwel alle reële onderwijssituaties een onmogelijkheid.
Tot slot van dit hoofdstuk is het goed er op te wijzen dat, hoewel de toetsscore als steekproefresultaat een toevallig resultaat is, het toch een zaak is van beheerst toeval. Nog even teruggaand naar figuur 2.5 kunnen we daar uit aflezen dat het een heel stuk waarschijnlijker is dat iemand met een toetsscore van 15 een ware beheersing heeft van 0,65, dan van 0,90. Ja, het is zelfs vrijwel uitgesloten dat iemand met een ware beheersing van 0,90 op deze toets een score van 15 zou behalen. Het is ook bijzonder onwaarschijnlijk dat iemand met een ware beheersing van 0,75 een score van 15 zou behalen.
Omgekeerd mag een student die een beheersing van 0,90 heeft er, ondanks het steekproefkarakter van de toets, ook van deze relatief korte toets van 25 vragen, er vast en zeker op rekenen tenminste een score van 17 of 18 te zullen boeken. Het uitbuiten van dit soort zekerheden is het onderwerp van deze cursus!
In het vorige hoofdstuk hebben we bekeken wat de kans is om tenminste een bepaalde score op de toets te behalen, gegeven dat de ware beheersing bekend is. In werkelijkheid zal niemand ooit de ware beheersing van welke student dan ook, te weten komen.
Maar ook voor de student zelf geldt dat hij de eigen ware beheersing van de stof niet exact, maar slechts ten naaste bij kent. De student die denkt dat zijn ware beheersing 0,70 is, kan zich daarin vergissen. Het staat eigenlijk wel vast dat zijn ware beheersing daarvan af zal wijken, en de vraag is of die afwijking groot of klein is. In dit hoofdstuk wordt een kwantificerende uitwerking gegeven voor het schatten van de eigen ware beheersing.
Waarom is het schatten van de eigen beheersing van belang? Kan de student dan niet volstaan met de schatting achteraf die hem door het behaalde toetsresultaat gegeven wordt? Nee, dat kan hij niet, want die informatie komt voor hem te laat. Te laat om er gebruik van te kunnen maken.
Bij de beoordeling is het van groot belang dat de student op de hoogte is van de onderwijsdoelen, en hoe deze in de toets verwerkt zijn. Afgaande op die informatie zal hij zich op de toets voorbereiden, zodat ook afhankelijk van die informatie zijn voorbereiding goed of slecht kan zijn. De student die denkt de stof onvoldoende te kennen zal doorgaan met bestuderen van de leerstof totdat hij denkt een voldoende beheersing te hebben, totdat hij door tijdgebrek gedwongen is te stoppen, of totdat hij een stofbeheersing heeft die voldoet aan de wat hogere eisen die hij zichzelf stelt.
Kortom, de studie-inspanning van de student is afhankelijk van wat hij denkt dat zijn ware beheersing is (en of de 'slaagkans' die daaruit volgt niet te klein is, maar daarover meer in het volgende hoofdstuk). Het is daarom van enig belang om te weten hoe de eigen ware beheersing ingeschat moet of kan worden. Het zou ook aardig zijn om te weten hoe studenten de eigen ware beheersing plegen te schatten, maar dat verwijst naar empirisch onderzoek dat nog gedaan moet worden.
Hoe maak je nu zo'n schatting van de eigen ware beheersing? De idee is eenvoudig genoeg: teken op de schaal van ware beheersing van 0 tot 1 een kromme waarvan je denkt dat hij ongeveer wel weergeeft de waarschijnlijkheid dat de eigen ware beheersing bepaalde waarden aanneemt. Bijvoorbeeld: wanneer je denkt dat de waarschijnlijkheid dat de ware beheersing 0,70 is twee keer zo groot is als de waarschijnlijkheid dat hij 0,60 is, dan teken je de kromme zo dat hij bij 0,70 twee keer zo hoog is als bij 0,60.
Je hoeft natuurlijk niet in één keer de goede kromme te tekenen: begin met gewoon maar een kromme die misschien niet al te gek is, en breng daar correcties op aan totdat een kromme verkregen is waarmee je vrede kunt hebben. Ook het laatste, wat voor jou de beste kromme is, valt wel nader te specificeren, maar daarmee wil ik op dit moment de lezer niet belasten. In figuur 3.1 een voorbeeld van zo'n kromme met correcties.
FIGUUR 3.1. Impressionistische kromme voor de eigen ware beheersing, met correcties.
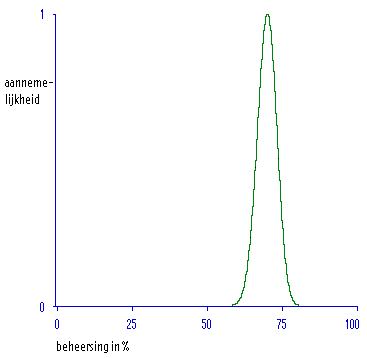
FIGUUR 3.2 Een te precieze schatting van de ware beheersing.
(noot: verdeling b(140, 60))
Merk op dat op de verticale as in figuur 3.1 geen schaalverdeling is aangebracht. De schaalverdeling wordt bepaald door de getekende kromme: de kromme is een waarschijnlijkheidsverdeling, wat betekent dat de oppervlakte onder de kromme gelijk moet zijn aan 1. Daardoor is dan ook de verticale schaal bepaald. Maar hiermee loop ik al vooruit op de kwantificering die straks gegeven zal worden.
Om een kromme zoals in figuur 1 te kunnen tekenen, moet de student over enige informatie beschikken. Dat kan zijn de complexe mengeling van vroegere toetservaring met de ervaringen opgedaan bij het doorwerken van de onderhavige leerstof, of ook informatie verkregen uit gesprekken met medestudenten over hoe zij de stof bestudeerd hebben. Allemaal nogal vaag dus, maar niet zo vaag dat geen redelijke schatting over de eigen ware beheersing gedaan zou kunnen worden.
De student die in de gelegenheid is om korte tijd voor het eigenlijke tentamen een proeftoets af te leggen, verkeert in de comfortabele situatie dat de score op deze proeftoets hem zonder verdere vaagheden een schatting voor de eigen ware beheersing verschaft. De score die hij op de proeftoets krijgt geeft de in zekere zin te verwachten score op het tentamen aan. Maar wat te verwachten is geeft in dit verband nog geen aanleiding om blind te gaan varen: een fors afwijkende score is weinig minder waarschijnlijk.
Nog even blijvend bij de schatting van de eigen ware beheersing: wanneer de student beschikt over de score die hij behaalde op een proeftoets, en alleen op dat gegeven wil koersen, kan hij daarvoor een bepaalde waarschijnlijkheidsverdeling kiezen, waarvan de waarden van de parameters bepaald worden door de behaalde score op de proeftoets, en het aantal vragen in die toets. Schrik niet van het jargon: misschien staat de gezochte kromme wel tussen de voorbeelden in figuur 3.3. op de volgende bladzijde.
Veronderstel dat de proeftoets bestaat uit 50 vragen, vragen die op dezelfde wijze als voor de eigenlijke toets gebeurt, op strikt toevallige wijze getrokken zijn uit de (denkbare) verzameling vragen over de stof, of tenminste als toevallig getrokken opgevat kunnen worden door de student. Het afleggen van de proeftoets geeft de student informatie over de eigen ware beheersing: hij krijgt als het ware een steekproef van 50 daaruit, of 50 waarnemingen. Dat aantal waarnemingen bepaalt de sterkte of de zwakte van de schatting van de ware beheersing die het proeftoetsresultaat toestaat.
Figuur 3.3 geeft voor een proeftoets bestaande uit 50 vragen, en voor de toetsscores 25, 30, 35, 40 en 45 daarop, de schattingen van de ware beheersing weer. Onmiddellijk is in te zien dat zo'n proeftoets resultaat geen scherpe conclusies over de eigen ware beheersing toestaat: gegeven een behaalde score van 35, ofwel 70 % van de vragen goed beantwoord, kan de ware beheersing nog overal tussen, zeg, 60 en 80 liggen, en dat is een fors verschil!
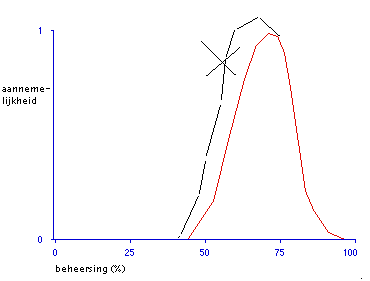
Het is in de praktijk te verwachten dat intuïtieve schattingen van de eigen beheersing, gezien het resultaat van de proeftoets, te sterk zullen zijn. Iemand die een score van 35 behaalde, zou bijvoorbeeld een kromme kunnen tekenen zoals in figuur 3.2 afgebeeld, aangevend dat hij er tamelijk zeker van is dat zijn ware beheersing ergens tussen 62 % en 78% in ligt. Maar de getekende curve veronderstelt als het ware 200 waarnemingen, ofwel vier keer zoveel als waarover de student in feite beschikte!
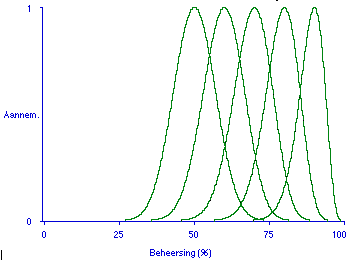
FIGUUR 3.3. Aannemelijkheidsverdelingen voor de ware beheersing gebaseerd op het verkregen proeftoetsresultaat (proeftoets bestaat uit 50 vragen).
(noot: de verdelingen zijn b(25, 25), b(30, 20), b(35, 15), b(40, 10), en b(45, 5) ).
Hier en in Figuur 3.4 heb ik in de reconstructie de oorspronkelijke kansverdelingen (dus curven met gelijke oppervlakte = 1) vervangen door aannemelijkheden met ieder hetzelfde maximum 1 en daarom ongelijke oppervlakken. Dat geeft een ander beeld, want de verschillen komen nu minder pregnant naar voren.
Merk op dat, hoe hoger de proeftoetsscore, des te scherper is de waarschijnlijkheidsverdeling voor de eigen ware beheersing. De reden daarvoor is simpelweg dat, hoe dichter de verkregen score bij de maximaal bereikbare score ligt, des te geringer wordt de mogelijkheid voor de ware beheersing om daarvan sterk af te wijken: afwijkingen naar boven zijn steeds beperkter mogelijk omdat de bovengrens van 1 zo dicht bij is! Dit is een merkwaardig verschijnsel, waar geen bijzondere betekenis aan te hechten valt, maar waar wel degelijk rekening mee gehouden moet worden.
Zo'n proeftoets wordt altijd enige tijd voor het eigenlijke tentamen afgenomen, tenslotte moet de student de gelegenheid hebben om zich te herstellen wanneer hij op grond van zijn proeftoetsscore zou ontdekken de stof niet goed genoeg te beheersen. Dat betekent dat de schatting van de eigen ware beheersing maar een beperkte waarde heeft:
Er is dus alle reden om het proeftoetsresultaat niet als zo'n sterke aanwijzing op te vatten als in de verdelingen in figuur 3.3 tot uitdrukking werd gebracht, er zijn eenvoudig nog te veel onzekerheden tussen proeftoets en het eigenlijke tentamen. Ook de voorzichtigheid gebiedt het iets bescheidener inschatten van de eigen ware beheersing: tenslotte zal de gemaakte schatting, zoals in het volgende hoofdstuk gedemonstreerd, gebruikt worden voor het schatten van bijvoorbeeld de slaagkans voor het tentamen. En daarbij is het beter om wat voorzichtiger te schatten.
Een mogelijkheid is om een proeftoets die in feite uit 50 vragen bestaat, voor het maken van de schatting van de eigen ware beheersing als niet sterker dan, zeg, 25 vragen te beschouwen. Dan worden de waarschijnlijkheidsverdelingen verkregen die in figuur 3.4 zijn afgebeeld, en die aanzienlijk minder scherp zijn dan de verdelingen in figuur 3.3.
Natuurlijk kan de student, afgaande op zijn vermoeden hoeveel hij zijn ware beheersing door verdere studie tussen proeftoets en tentamen heeft kunnen verbeteren, de verdeling voor zijn ware beheersing verder naar rechts schuiven dan zijn proeftoetsresultaat in eerste instantie rechtvaardigde.
Hoe in de direkte onderwijspraktijk met de hier gepresenteerde ideeën gewerkt kan worden, is in verschillende COWO cursussen aangegeven, en zal ook in deze cursus aan de orde komen. In het algemeen zal noch de docent, noch de student daarvoor meer dan de eenvoudigste statistische inzichten nodig hebben. Wie zich de theoretische achtergrond desondanks eigen wil maken, zij in eerste instantie verwezen naar Novick & Jackson (1974, vooral hoofdstuk 5 en 6), en de literatuur die in de bijlagen bij deze cursus genoemd wordt.
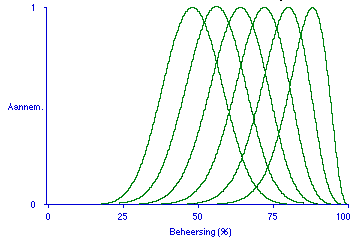
FIGUUR 3.4. Aannemelijkheidsverdelingen voor de ware beheersing alsof de proeftoets niet uit 50, maar uit 25 vragen bestond.
(noot: bètaverdelingen (12,13), (14,11), (16,9), (18,7), (20,5), (22,3))
Met behulp van de verdelingen zoals in bovenstaande figuren, die een precieze beschrijving geven van wat de student denkt dat zijn ware beheersing van de leerstof is, is het mogelijk om voor het afleggen van het tentamen een goede schatting te maken van de slaagkans, of de kans meer dan een bepaalde score te behalen. Nee, dat bekijken we in het volgende hoofdstuk.
Het zal duidelijk zijn dat op de een of andere wijze de onzekerheid die resulteert uit het steekproefkarakter van de toets, en de onzekerheid over wat de eigen ware beheersing van de stof is, gecombineerd moeten worden. Pas dan kan de student concreet aangeven wat volgens hem de kans is dat hij een toetsscore behaalt die groter is dan, bijvoorbeeld, de za k-slaag grens op de toets.
In figuur 4.1 is een illustratie van het resultaat gegeven. De meer ?steile curve geeft de kans op tenminste een score 32, 33, 34 etc. t/m 50 aan voor een student waarvan bekend zou zijn dat zijn ware beheersing 0,80 is. Door de onzekerheid over de eigen ware beheersing zal de uiteindelijke curve minder steil zijn: wanneer in dit concrete geval de student als waarschijnlijkheidsverdeling voor zijn eigen ware beheersing de curve 20 uit 25 heeft (figuur 3.4), staan zijn ingeschatte kansen voor de toets ervoor zoals door de minder steile curve in figuur 4.1 aangegeven.
FIGUUR 4.1. Kansen op tenminste een bepaalde score (horizontale as) op een toets van 100 vragen, voor en na incalculeren van de onzekerheden over de eigen ware beheersing.
Uit figuur 4.1 valt onmiddellijk af te lezen dat het van groot belang is om met de onzekerheden over de eigen ware beheersing rekening te houden. Neem bijvoorbeeld eens aan dat voor deze toets als zak-slaag grens de score 36 gehanteerd wordt (iemand met score 36 of hoger is geslaagd): zonder rekening te houden met onzekerheden over de ware beheersing zou de kans om te slagen ingeschat worden als 0,94, wel rekening houdend met de onzekerheden is de slaagkans 0,83. Het verschil is in alle praktische omstandigheden als zeer groot te kwalificeren. De student die nog wel bereid is om een zakrisico van 0,06 te aanvaarden, zal als dat enigszins mogelijk is een zakrisico van 0,17 liever vermijden (door bijvoorbeeld een intensievere voorbereiding op de toets).
De techniek die gebruikt wordt bij het combineren van beide soorten onzekerheden tot eindschattingen voor het te behalen toetsresultaat is een statistische, en is in bijlage A beschreven. De details daarvan hoeven ons in de dagelijkse onderwijspraktijk niet te hinderen. Wat we even moeten vasthouden is dat voor de onzekerheden inherent aan de toetsing vooral het aantal vragen dat in de toets opgenomen wordt van belang is, en voor de onzekerheden over de eigen ware beheersing het soort verdeling zoals in figuur 3.3 en 3.4 weergegeven. Deze laatste verdelingen, of we ze nu waarschijnlijkheids of geloofs verdelingen noemen mag daarbij van de eigen smaak afhangen, kunnen we karakteriseren als het aantal vragen goed op een proeftoets bestaande uit x aantal vragen (zoals bij de curven in figuur 3.4 aangegeven werd). Zoals besproken in hoofdstuk 3 hoeft dat niet per se een werkelijk verkregen score op een proeftoets met inderdaad x vragen te zijn, maar kan daarop een correctie aangebracht zijn die rekening houdt met bepaalde onzekerheden die tussen proeftoets en toets kunnen optreden.
Voor de waarschijnlijkheids of geloofs verdelingen in figuur 3.4 is uitgerekend tot welke scoringskansen zij leiden bij een toets die uit 50 vragen bestaat. In figuur 4.2 zijn de zes respectievelijke verdelingen afgebeeld, door ruimtegebrek aan de linkerzijde mogelijk iets ingekort. De bij elkaar horende punten zijn door gedachtenstreepjes verbonden: er worden tenslotte uitsluitend hele punten gegeven. Bij ieder curve is aangegeven op welke waarschijnlijkheidsverdeling (als schatting van de ware beheersing) zij is gebaseerd.
FIGUUR 4.2. Kans op tenminste een toetsscore x = 0 .... 100 (voor een toets bestaande uit 100 vragen), voor verschillende proeftoetsscores, resp. 12, 14, 16, 18, 20, 22 en 24 goed uit 25 vragen.
Voor de proeftoetsscore 20 uit 25 is ook het resultaat van een simulatie geplot, in rood. De simulatie gebruikt op geen enkele manier formules voor statistische verdelingen.
Voor de student die aan risico beheersing wil doen, die de kans om te zakken voor een toets binnen bepaalde marges wil houden, is vooral het linker deel van de curven in figuur 4.2 van belang. De informatie daaruit is in tabelvorm weer te geven als hieronder:
_____________________________________________________________________________ maximaal 12 uit 25 14 uit 25 16 uit 25 18 uit 25 20 uit 25 22 uit 25 risico _____________________________________________________________________________ .100 16 20 25 29 34 40 .075 15 19 23 28 33 39 .050 14 18 22 27 31 38 .025 12 16 20 25 29 37 .010 11 14 18 23 27 35 .005 9 13 17 22 26 33 .0025 8 11 15 20 24 31 .001 7 10 14 19 23 29 _____________________________________________________________________________
TABEL 4.1. Risico minder dan x aantal goed, toets van 50 vragen, bij verschillende inschattingen van de eigen ware beheersing.
Laten we eens kijken naar een toets waarop zak -slaag beslissingen genomen worden. Wanneer van te voren de grens zakken slagen bekend is. kan de student nagaan of zijn ingeschatte ware beheersing hem een voldoend hoge slaagkans geeft. Veronderstel dat om te slagen tenminste 27 uit de 50 vragen goed beantwoord moeten worden. De student die het zak risico tot maximaal 0,05 wil beperken, ziet uit tabel 4.1 op de rij van risico 0,050 dat hij dan de stof zo goed moet beheersen dat een geloofsverdeling van 18 uit 25 voor hem weergeeft wat de eigen ware beheersing is. Wanneer uit een afgelegde proeftoets blijkt dat hij daaraan niet voldoet, zal hij nog een extra studie-inspanning moeten plegen.
Ik hoop in dit en voorgaande hoofdstukken een beetje een idee gegeven te hebben van de mogelijkheden die er zijn om zaken te kwantificeren die de lezer misschien altijd onkwantificeerbaar hebben toegeschenen. Op welke wijze dergelijke technieken uitgebuit kunnen worden in de dagelijkse onderwijspraktijk, zowel door de student waar het gaat om het verstandig kiezen van zijn studiestrategie, als door de docent waar het gaat om het optimaliseren van zijn beoordelingsbeleid, is het onderwerp van deze cursus examenregeling (respectievelijk deel A en deel B).
De theorie die ik in de voorgaande hoofdstukken heb behandeld, is van essentieel belang om de plaats en de functie van de beoordeling in het onderwijs te kunnen begrijpen. zolang ware beheersing van de leerstof en het toetsresultaat voor de individuele student niet hetzelfde zijn, zal de docent daar in zijn onderwijsbeleid op de een of andere wijze rekening mee moeten houden.
Misschien hebt u ook wel eens het idee gekoesterd dat de goede of ideale student gewoon zijn best doet om de aangeboden leerstof zo goed mogelijk te verwerken, te leren, en dat het hem verder niet kan schelen hoe zijn kennis straks beoordeeld zal worden.
Iedere docent kent wel studenten die de indruk wekken dat ze inderdaad op die manier studeren: kennelijk zonder buitensporige moeite, maar wel heel gemotiveerd, behalen zij voor vrijwel alle vakken hoge cijfers, ook al vinden toetsingen onder heel uiteenlopende omstandigheden plaats. Ik wil hier niet ingaan op de vraag of dit waarnemingsfenomeen voldoende empirische basis heeft (bedenk slechts dat geniale studenten en geniale onderzoekers niet noodzakelijk dezelfde personen hoeven te zijn (geweest). Studenten die moeiteloos en probleemloos de studie doorkomen, stellen de docent ook geen problemen wat de inrichting van zijn onderwijs betreft, voor de opvang van deze studenten hoeft hij geen speciale onderwijskundige bagage te hebben.
In de onderwijspraktijk van alledag zien we dat grote aantallen studenten wel herkansingen nodig hebben om hun examens te behalen, dat voor de meeste studenten geldt dat zij in hun studie wel eens een of meer herkansingen hebben gedaan. Gemiddelde studieprestaties liggen niet rond de acht, maar veeleer net boven de zes. Bij meerkeuze studietoetsen zien we vaak p waarden van 0,5 of 0,6, wat betekent dat studenten gemiddeld slechts de helft van de vragen goed kunnen beantwoorden.
Nu is het probleem met die meerkeuze toetsen dat docenten soms menen dat toetsvragen moeilijk moeten zijn, terwijl het bovendien niet onwaarschijnlijk is (zie de cursus Cesuurbepaling) dat de meerkeuze vraagvorm op zich al aanleiding geeft tot te moeilijke vraagformulering. Zelfs hiermee rekening houdend, kun je toch moeilijk concluderen dat studenten pas opkomen voor het tentamen wanneer ze alles over de stof weten.
In de praktijk blijken studenten willens en wetens, of noodgedwongen, nogal wat risico's te nemen bij het afleggen van tentamens. Kennelijk volgen studenten een bepaalde, waarschijnlijk niet helder omschreven, studiestrategie. Eigenlijk zou je beter van studiegewoonten kunnen spreken: in de ervaring van lange jaren onderwijs gevormd, gebruik makend van gerucht achtige informatie (over de zwaarte van het tentamen, de aard van de te verwachten vragen), en zelden gebaseerd op rationele overwegingen en harde informatie over de toetsing.
Een voorbeeld van harde informatie is de voorspellende kansverdeling voor de toetsscore, die in de voorgaande hoofdstukken werd gegeven.
De manier waarop studieprestaties beoordeeld worden moet dan ook van invloed zijn op de studiestrategieën die studenten gebruiken. Dat zal in heel sterke mate gelden voor de plaats van de zak -slaag grens, dat geldt ook in sterke mate voor de aard van de examenregeling die gebruikt wordt. Er zijn verschillende soorten examenregeling denkbaar, en bruikbaar, waar geheel andere studiestrategieën bij gebruikt zullen worden.
Iedereen die onderwijsbeleid wil en moet voeren, zal daarom over de informatie moeten beschikken, welke gevolgen beleidsmaatregelen op beoordelingsgebied zullen hebben. Het gaat daarbij om gevolgen die direkt verband houden met de doelstellingen van het onderwijs, maar ook om algemene beleidsdoelstellingen die betrekking hebben op het bewaken van het onderwijs rendement, en het optimaal aanwenden van de (schaarse) beschikbare middelen.
Wie een bepaald minimum niveau van de afstudeerders wil bereiken, handhaven, of garanderen, zal dat dan ook moeten doen door maatregelen die de studiestrategie van de student zodanig beïnvloeden dat met een omschreven mate van waarschijnlijkheid dat niveau ook gerealiseerd wordt. Het spreekt vanzelf dat niveau hier opgevat moet worden in termen van ware beheersing en niet als (door het toeval beïnvloede) behaalde cijferresultaten.
Wil je iets zinnigs kunnen zeggen over de effecten van onderwijsbeleid op het gebied van beoordeling en examenregeling, dan zal een goed inzicht in de studiestrategieën die studenten onder verschillende omstandigheden volgen, onontbeerlijk zijn. Vandaar dat in deel B van deze cursus de beleidsmogelijkheden en hun consequenties behandeld zullen worden (deel B zal hopelijk eind 1979 beschikbaar zijn), en in dit deel A als voorbereiding daarop de problematiek van de strategiekeuze waar de student zich voor geplaatst ziet.
Het kiezen van een studiestrategie komt, zoals te begrijpen na het behandelde in voorgaande hoofdstukken, neer op het vaststellen van het niveau van stofbeheersing waarop in de voorbereiding op het tentamen gemikt zal worden.
In deze benadering van de beoordelingsproblematiek in het onderwijs wordt definitief gebroken met de overigens nog algemeen gevolgde zienswijze dat het afnemen van toetsen en examens betrekkelijk neutrale metingen zouden zijn, die weinig of geen invloed op het voorafgaande onderwijsgebeuren zouden hebben. Resultaten uit de psychometrie worden dan ook zonder kritische bedenkingen toegepast op het beoordelen in het onderwijs, en dat terwijl de vooronderstelling van deze psychometrie is dat mensen zich niet specifiek op de te geven tests hebben kunnen voorbereiden, en het in het onderwijs precies tegenovergesteld zo is dat de student zo optimaal mogelijk in de gelegenheid wordt gesteld om zich op de toetsing voor te bereiden. Daar is het immers onderwijs voor.
In de onderwijskundige literatuur, met name ook literatuur over het beoordelen in het onderwijs, is deze nieuwe benadering nog nauwelijks bespeurbaar, ook niet in de langzamerhand talrijke publikaties over criterium gerefereerde meting. Een uitzondering is het werk van Van Naerssen (1970, 1974, 1977) over tentamenmodellen.
In deze cursus zal ik twee soorten examenregeling bespreken, plus een aantal mengvormen van deze beide.
Je kunt van de student verlangen ieder studieonderdeel tenminste voldoende gemaakt te hebben. Dit heet de conjunctieve examenregeling, om niet geheel duidelijke redenen, maar het is ondertussen gevestigd spraakgebruik. Het spreekt misschien iets meer aan om te spreken van hordenloop: voor ieder studieonderdeel wordt een horde opgesteld, voorstellende de minimaal voldoende beoordeelde studieprestatie; om te slagen voor het examen moeten al deze horden zonder ongelukken gepasseerd worden. Dit soort regeling is ieder van ons van jongsaf aan bekend, het is de examenregeling waarvan Nederlanders wel eens ten onrechte denken dat het de enig mogelijke en zinnige vorm van examenregeling is.
Je zou echter best in plaats van deze hordenloop van de student kunnen verlangen om gemiddeld over alle studieonderdelen een bepaald minimum prestatie niveau te realiseren. Dat is een regeling die ieder van ons ook heel bekend is, maar niet als examenregeling. Het is de manier waarop cijfers binnen een vak gecombineerd plegen te worden tot een eindcijfer voor dat vak. Cijfers voor proefwerken en beurten worden, eventueel na gewogen te zijn zodat de proefwerken wat zwaarder meetellen dan de beurten, gemiddeld, en het gemiddelde is dan je rapportcijfer. Ook is het vanzelfsprekend dat de scores die voor verschillende vragen op het tentamen (de toets) behaald worden, bij elkaar opgeteld Worden om de eindscore, en daarmee het eindcijfer, voor het tentamen te bepalen. Binnen het tentamen kan de student het niet weten van bepaalde vragen compenseren door andere vragen wel goed te beantwoorden en zodoende nog aan een voldoende eindcijfer te komen. Hetzelfde middelen van cijfers toegepast op alle studieonderdelen die onder het examen vallen, levert een compensatorische examenregeling op.
Om te vermijden deze woordcombinaties nog een paar honderd keer uit te moeten schrijven, gebruik ik de volgende afkortingen:
HEx = Hordenloop Examenregeling
CEx = Compensatorische examenregeling.
In hoofdstuk 6 begin ik met HEx in zuivere vorm te bespreken, d.w.z. de studiestrategie keuze onder deze examenregeling. Er is een belangrijke variant op de zuivere vorm die afzonderlijke behandeling verdient: in hoofdstuk 7 komt de strategie keuze aan de orde wanneer voor ieder studieonderdeel een beperkt aantal herkansingen mogelijk dan wel toegestaan is. Door deze beperking blijken studenten in stress achtige situaties terecht te komen, terwijl daarvan bij een HEx zonder beperking geen sprake is.
In hoofdstuk 8 komt dan de studiestrategie onder CEx aan de orde.
Natuurlijk zijn er diverse uitzonderingen op ieder van deze examenregelingen denkbaar. Een groot aantal daarvan wordt besproken in hoofdstuk 9, waar speciaal aandacht wordt geschonken aan examenregelingen voor de propedeuse. De meeste uitzonderingen tasten het hordenloop of compensatorische karakter van de regeling niet ernstig aan.
In het begin van dit hoofdstuk heb ik al opgemerkt dat geniale en andere gelukkige studenten geen problemen zullen hebben met hun studiestrategie. Wat voor normale studenten optimaal is, dat zal hen een zorg zijn. Met name zal de geniale student strategieën volgen die hoger liggen dan de optimale, d.w.z.: die gericht zijn op een hoger niveau van stofbeheersing dan optimaal is.
En wat is optimaal? Het ligt voor de hand hierbij allereerst te denken aan het tijdbeslag. In de regel zal de student proberen in zo kort mogelijke tijd, of met zo weinig mogelijk studievertraging, af te studeren. Maar het hangt van het karakter van de examenregeling af of studietijd overwegingen bij het optimaliseren de belangrijkste rol moeten spelen. Bij CEx, evenals bij die vorm van HEx waarbij een beperkt aantal herkansingen per vak is toegestaan, is het veeleer van het grootste belang om je RISICO om voor het examen te zakken, te beheersen. De student moet dan voor zichzelf uitmaken welk zak RISICO voor hem nog juist aanvaardbaar is, en kan op basis van dat gegeven uitzoeken (berekenen) welke studiestrategie(ën) dan minimaal gevolgd moet worden om dat RISICO beneden deze grens te houden.
Voordat ik op beide criteria (tijd en RISICO beheersing) wat verder inga, wil ik een misverstand voorkomen waartoe het bovenstaande misschien aanleiding heeft gegeven. Het is niet zo dat optimale strategieën corresponderen aan studieresultaten die minimaal zijn.
Het minimaliseren van de studietijd is waarschijnlijk niet voor alle studenten een criterium, en voor de meeste studenten niet altijd een criterium. RISICO-beheersing leidt zeker niet tot minimum prestaties, maar tot prestaties die een veilig stuk boven het minimum niveau liggen. Tenslotte: wat minimaal aanvaardbare studieprestaties zijn wordt door de (sub)faculteit vastgesteld: het is niet zo dat de studiegewoonten van de studenten bepalen wat de studieresultaten zullen zijn, maar het beoordelings en examenbeleid bepalen welke strategieën door studenten gekozen zullen worden.
Het optimaliseren van benodigde studietijd is van belang bij de strategie keuze onder HEx, de huidige traditionele hordenloop examenregeling, waarbij het aantal toegestane herkansingen niet beperkt is. In deze situatie is het zo dat voor het merendeel van de studenten geldt dat zij zich niet tot zo'n hoog niveau van stofbeheersing willen of kunnen opwerken dat zij zeker zullen weten voor eerste opkomst ook meteen te slagen. De student moet rekening houden met een niet te verwaarlozen risico om voor het tentamen een onvoldoende te krijgen. Zoals in hoofdstuk 4 gedemonstreerd, is dat risico tamelijk nauwkeurig te schatten voor gegeven studiestrategieën. Omgekeerd kan de student dan ook, gegeven het risico dat hij bereid is te lopen om te zakken, vinden welke studiestrategie daar bij past. De vraag is dan, welk risico is een goed of optimaal risico? Welnu, dat is te beantwoorden wanneer de kosten die uit het moeten herkansen voortvloeien, bekend zijn. Die kosten zijn redelijk te schatten, en geven samen met de waarschijnlijkheid dat ze ook werkelijk gemaakt zullen worden (waarschijnlijkheid = risico) de sleutel tot het vinden van de strategie die in deze zin de kosten minimaliseert.
Kosten zijn: de studietijd die aan de herkansing te besteden is, maar ook de financiële offers die daarvoor gebracht moeten worden, het risico een toelage te verliezen, de psychische druk waaronder je toch weer komt te staan bij het herkansen, en dergelijke. Bij de bespreking van HEx strategieën in hoofdstuk 6 wordt gedetailleerd aandacht geschonken aan de vraag hoe deze kosten te minimaliseren.
Tijd overwegingen zijn op verschillende manieren belangrijk voor de student. Om te beginnen zal het voorbereiden van herkansingen nogal eens interfereren met de normale studieactiviteiten. Vooral studenten die wat ruimere voorbereidingstijd nodig hebben, en dat op kunnen brengen door een hoge studiemotivatie, kunnen in moeilijkheden komen wanneer zij naast deze normale studieactiviteit ook nog voorbereidingstijd moeten investeren voor herkansingen. De afweging studietijd vrije tijd zal iedere student moeten maken, en dan is de vraag hoe je die afweging op een verstandige manier kunt maken. Als het om grote studiebelangen gaat, zal er wat meer vrije tijd opgeofferd moeten worden. Is de vrije tijdbesteding belangrijk, dan zal daar studietijd aan opgeofferd worden (denk bijv. aan bestuurswerkzaamheden in de faculteit, of aan werkstudenten die een balans tussen studietijd en werktijd moeten zien te vinden). Studietijd is altijd een schaars goed, zij het dan ook wat minder schaars voor de student die daarnaast over veel vrije tijd kan beschikken, en wat schaarser voor de student die alle redelijkerwijs beschikbare tijd nodig heeft om aan de studie eisen te kunnen voldoen. Het is dan ook belangrijk voor de student om zijn tijd op evenwichtige wijze over de verschillende studieonderdelen te kunnen verdelen, en onder HEx-regelingen met name ook over toetsen bij eerste opkomst, en herkansingen. In deze cursus worden daar aanwijzingen voor gegeven die zeer veel verder gaan dan het soort globale richtlijn die ik hierboven noemde over de afweging tussen studietijd en vrije tijd.
Bij examenregelingen waar geen herkansingen zijn toegestaan, of slechts een beperkt aantal herkansingen, is het van belang om het RISICO om voor het examen te zakken in de hand te houden. Zoals ik in de hoofdstukken 7 en 8 zal laten zien, zijn er mogelijkheden om de keuze van studiestrategieën zo te doen, dat dit RISICO beneden een aanvaardbare grens zal blijven.
Wat een aanvaardbaar RISICO is, is een persoonlijke zaak, en zal bovendien afhangen van de ernst van de gevolgen van zakken voor het examen. Hoe ernstiger de gevolgen van zakken, des te kleiner zal het RISICO zijn dat de student aanvaardbaar vindt. De student die al zijn zinnen gezet heeft op deze studie (en geen alternatieven heeft die ook voor hem aanvaardbaar zouden kunnen zijn), zal een klein RISICO om te zakken kiezen. Etcetera.
Is het noodzakelijk om met dit RISICO te werken? De student kan toch gewoon zo studeren dat hij er zeker van kan zijn te slagen? Of toch niet?
Sommige statistici zijn gek op de uitspraak dat je nooit moet uitsluiten dat de achterkant van de maan uit groene kaas bestaat. Sinds die achterkant uitgebreid onderzocht is, zou je de uitspraak misschien wat moeten aanpassen. Het is natuurlijk overdreven geformuleerd, en dat is gedaan om in ieder geval het punt te scoren dat in het dagelijks leven allerlei eventualiteiten een niet verwaarloosbare waarschijnlijkheid van optreden hebben. Het is riskant om aan de overkant van de straat even een kop koffie te gaan drinken, er zijn mensen die bij zo'n oversteek aangereden worden.
Nu is bij het oversteken van een straat het aanrijdingsrisico misschien niet zo groot dat je het expliciet zou willen betrekken in je overweging of je die kop koffie wel zult gaan halen. Bij het afleggen van tentamens ligt dat even iets anders. In de eerste hoofdstukken heb ik laten zien dat de onnauwkeurigheden in de toetsing, en in het inzicht dat de student over de mate van zijn eigen stofbeheersing heeft, nogal omvangrijk zijn. Dat betekent dat voor de meeste studenten zekerheden niet kunnen bestaan.
Wie zich geen zekerheid kan verschaffen, kan er naar streven zo dicht mogelijk bij die zekerheid te komen, zijn RISICO om te zakken voor het examen zo klein mogelijk te maken. Maar dat is een onjuiste wijze van denken: dat zou betekenen dat je ieder beschikbaar kwartiertje aan de studie zou moeten besteden, ten koste van alles wat niet direct met die studie en met het in goede lichamelijke conditie blijven, te maken heeft. Nu is dat een strategie die iedereen wel eens volgt, zij het ook niet langer dan een paar dagen. Voor een langere termijn is iets dergelijks ondenkbaar. Ergens moet een grens getrokken worden. Er zal een bepaald RISICO zijn dat voor jou als student aanvaardbaar is, waar het geen extra opofferingen meer loont om het RISICO nog verder terug te dringen.
De student die voor zichzelf bepaalt welk RISICO om voor het examen te zakken voor hem aanvaardbaar is, zal daarbij een waardering maken van de gevolgen die het zakken voor hem zou hebben. Hij kan het examen dan opvatten als een weddenschap, waarbij het RISICO de kans is dat hij zijn inzet verliest, en de vervelende gevolgen van gezakt te zijn mag incasseren. Het maken van een ruwe schatting welk RISICO hij dan aanvaardbaar vindt, is voor de meeste doeleinden wel voldoende. Bijvoorbeeld een RISICO van 1/1000 voor de student die heel specifiek voor deze studie gekozen heeft, en wanneer de gevolgen van zakken zeer ernstig zijn. Een risico van 1/10e voor de student die zijn propedeuse jaar gebruikt om eens rustig te ervaren of deze studie hem voldoende ligt om toch niet liever één van de alternatieven die voor hem openstaan te gaan doen.
Het is duidelijk dat het RISICO om voor het examen te zakken, afhangt van strategieën voor afzonderlijke studieonderdelen gekozen, en de risico's die daarbij gelopen worden. De precieze aard van deze relaties is het onderwerp van de komende hoofdstukken. In die hoofdstukken wordt over verschillende risico's, RISICO's, Risico's gesproken, die de volgende betekenissen hebben:
geheugensteuntje: het examen is het belangrijkst, het grootst, daarom het RISICO met hoofdletters; de toets is het kleinste onderdeel waarop je het risico kunt lopen te zakken, te weinig punten te behalen, daarom risico met kleine letters; bij conjunctieve regelingen met een beperkt aantal toegestane herkansingen is er een Risico binnen dat aantal herkansingen niet te slagen, dit geval ligt a.h.w. tussen beide andere in, daarom Risico.
Wat ik in deze cursus aan studiestrategieën beschrijf, heeft meer te maken met hoe studenten het zouden moeten doen, dan met hun feitelijke studiegewoonten.
De pretentie van de in deze cursus gegeven aanpak is dat studenten zich zullen kunnen vinden in de gegeven argumentatie, en dan best bereid zullen zijn om van de gegeven informatie gebruik te maken bij het maken van hun strategie keuzen. Zouden er overwegingen zijn, op grond waarvan de student concludeert dat wat hier gepresenteerd wordt niet in zijn belang is, dan kan hij die extra overwegingen natuurlijk inbrengen, en proberen of die in de hier gegeven benadering op te nemen zijn.
Ook wanneer de docent alle relevante informatie over studiestrategieën verstrekt aan zijn studenten, zal deze doorgaans niet precies op de hier aangegeven wijze uitwerken, zullen andere studiegewoonten hun invloed in meerdere of mindere mate blijven doen gelden. Hier ligt dan ook een belangrijke opgave voor het evalueren van het functioneren van de examenregeling. Bij die evaluatie kun je speciale aandacht schenken aan de vraag of studenten doorgaans minder optimale strategieën gebruiken dan eigenlijk voor hen bereikbaar zijn. Zou dat het geval zijn, dan kan gezocht gaan worden naar de factoren die daarop mogelijk van invloed zijn, zodat misschien aanpassingen gemaakt kunnen worden in het onderwijs, de examenregeling, of de aard van de informatie die aan studenten verschaft wordt.
Wordt op deze wijze expliciet aandacht geschonken aan het studiegedrag van de studenten, dan is te verwachten dat het voorgeschreven gedrag steeds dichter benaderd zal worden door het feitelijke gedrag van de student. Ik heb er dus expliciet voor gekozen om te zoeken naar het optimale studiegedrag, gezien de aard van de gehanteerde examenregeling, en niet voor de heel andere mogelijkheid om door bestudering van het feitelijke studiegedrag, door beschrijving daarvan, mogelijk op het spoor te komen van ingangen om onderwijsprogrammering en dat feitelijk studiegedrag beter op elkaar af te stemmen. De beschikbare onderzoekliteratuur geeft voor deze laatste aanpak ook weinig motivatie: veel verder dan de constatering dat verschillende studenten op verschillende manieren studeren is het onderzoek niet gekomen, en aanwijzingen voor een verbeterde onderwijsaanpak of beoordelingsstructuur in het onderwijs zijn nauwelijks te vinden (maar zie Cronbach & Snow 1977 voor een bemoedigend begin van mogelijk wel vruchtbaar onderzoek in deze richting).
HEx, de hordenloop examenregeling, betekent in onverwaterde vorm dat voor ieder studieonderdeel tenminste een voldoende beoordeling behaald moet zijn. Omdat dit vrijwel ondoenlijk is wanneer er geen herkansingsmogelijkheden zijn, maken herkansingen integraal onderdeel van iedere HEx-regeling uit.
HEx is het soort examenregeling dat vrijwel zonder uitzondering op het ogenblik in het wetenschappelijk onderwijs gehanteerd wordt. Iedere student en iedere docent is daar, vanuit zijn ervaring, intensief mee vertrouwd, wat niet wil zeggen dat het karakter van HEx-regelingen voldoende doorgrond en bekend is om zonder blikken of blozen aan te kunnen geven wat een goede studiestrategie bij HEx inhoudt.
Talrijke varianten van HEx kunnen gevormd worden door uitzonderingsregelingen. Bekend, en tamelijk algemeen gehanteerd, is de uitzondering dat een bepaald aantal onvoldoendes mag blijven staan, wanneer ze aan bepaalde voorwaarden voldoen: bijv. dat er bepaalde goede andere studieprestaties tegenover moeten staan, dat bij 2 onvoldoendes dat een 5 en een 4 mogen zijn, maar niet lager, e.d. Een aantal van deze speciale regelingen zullen in hoofdstuk 9 aan de orde worden gesteld.
In het in 6.2 te presenteren tentamenmodel zal om te beginnen ook aangenomen worden dat aan het aantal herkansingen, noch aan de geldigheidsduur formele beperkingen gesteld zijn. In sommige studierichtingen is dat ook de feitelijk bestaande regeling, in de meeste (sub)faculteiten worden dit soort beperkingen in de één of andere vorm wel opgelegd.
Een HEx, hordenloop examenregeling, vereist in beginsel dat ieder studieonderdeel tenminste voldoende gemaakt (let op: niet beheerst) wordt. Evenzovele horden als er studieonderdelen zijn moeten gepasseerd worden. Het vervelende van zo'n soort regeling is dat zelfs bij hele kleine Risico's om te zakken het RISICO om voor alle studieonderdelen tezamen te zakken, omdat op tenminste één onderdeel een onvoldoende werd behaald. onaanvaardbaar groot wordt.
Bijvoorbeeld: reken eens uit wat de kans is om voor 10 studieonderdelen in één keer te slagen wanneer voor ieder van die studieonderdelen de slaagkans 0,95 is: dat levert de onthutsend lage slaagkans van 0,6 op. Slaagkans voor één onderdeel 0,9, voor 10 onderdelen 0,35. Slaagkans voor één onderdeel 0,8, voor 10 onderdelen 0,11.
De kans om voor 10 studieonderdelen te slagen is gelijk aan het product van de slaagkansen voor ieder studieonderdeel afzonderlijk.
In de praktijk zou een dergelijke regeling onmiddellijk tot absurde resultaten leiden, vandaar dat onder een HEx een uitgebreide herkansingsregeling voor ieder studieonderdeel afzonderlijk onontkoombaar is. Er moet, om te voorkomen dat bijna geen enkele loper de eindstreep haalt, gelegenheid gegeven worden voor herhaalde sprongen voor elke afzonderlijke horde. Herkansingen zijn een onontkoombaar compromis voor voorstanders van HEx-regelingen.
Ook met herkansingen blijft het heel moeilijk om reële schattingen te maken van het aantal herkansingen dat onder een bepaalde studiestrategie nodig zal zijn. Een goede beheersing van de stof, laten we zeggen 70 voor ieder afzonderlijk studieonderdeel, wekt al gauw de gedachte dat een student met deze stofbeheersing toch niet aan herkansingen onderworpen hoeft te worden. Maar hoe ver zitten we daarmee van de realiteit af! In dit hoofdstuk krijgen we daar de nodige voorbeelden van te zien.
Tversky (1974): "Onderzoek van waarschijnlijkheids schattingen, en keuzen tussen weddenschappen, wijst er op dat er een neiging bestaat de waarschijnlijkheid van conjunctieve gebeurtenissen te overschatten." Tversky geeft daar als verklaring voor dat de waarschijnlijkheid van één enkele gebeurtenis een te dominerende rol speelt bij het komen tot een schatting voor de waarschijnlijkheid van een aantal conjunctieve gebeurtenissen. Hij brengt het verschijnsel daarmee onder de bredere kategorie van het ankereffect: gegeven een bepaalde startwaarde, of ankerwaarde, blijken waarschijnlijkheids schattingen door die ankerwaarde sterk beïnvloed te worden, zelfs wanneer bekend is dat zo'n ankerwaarde strikt toevallig gekozen is.
Wat is de betekenis van dit verschijnsel voor examenregelingen? Tversky wijst er op dat deze algemene neiging tot overschatting van de waarschijnlijkheid van conjunctieve gebeurtenissen leidt tot ongerechtvaardigd optimisme bij het evalueren van de waarschijnlijkheid dat een bepaald plan zal slagen, dat een project op tijd afgesloten zal worden, e.d. Of, in onze context, tot optimistische schattingen over wat een reële studieduur is, wanneer het examen behaald zal zijn, of de kans om zonder herkansingen te hoeven doen voor het examen te slagen.
Het zou wel eens kunnen zijn dat wij sterk aan onze traditionele examenregelingen van het HEx-type blijven hangen omdat we voortdurend te optimistisch over deze examenregeling zijn, en niet door de empirie terecht gewezen worden.
Omdat uit onderzoek van Tversky en vele anderen blijkt dat subjectieve waarschijnlijkheden bijzonder vatbaar zijn voor over-optimisme, of andere stelselmatige mis-schattingen, is het streven in deze cursus er op gericht de student, en de docent, zo min mogelijk aan het eigen ongewapende oordeel over te laten waar het om het schatten van slaagkansen en dergelijke gaat. Er is alle reden (zie Tversky 1974) om te verwachten dat ook statistici, en ook onderwijskundigen, tot stelselmatig onjuiste schattingen komen wanneer zij zich op een subjectief oordeel verlaten. Het is te prefereren slaagkansen te evalueren via berekening, op grond van expliciete modelformulering, en uitgaande van harde gegevens als verkregen proeftoetsresultaten. Zelfs dan, wanneer de student de slaagkansen op een dienblad aangeboden krijgt, blijven er nog voldoende mogelijkheden voor het subjectieve oordeel over om op basis van deze informatie de verkeerde beslissingen te nemen. Bijvoorbeeld is het niet zo eenvoudig als het lijkt om een juiste interpretatie van waarschijnlijkheden te maken, we zijn dat eenvoudig niet gewend.
In bijlage E geef ik enige literatuur over de problematiek rond het schatten en interpreteren van kansen.
Wat is onder HEx een goede studiestrategie? Om enige greep op de problematiek te krijgen is het noodzakelijk eerst de studiestrategie te beschrijven zoals die onder een onverwaterde HEx er uit ziet, daarna is het eenvoudiger om na te gaan welke gevolgen bepaalde afwijkingen in de examenregeling kunnen hebben voor de studiestrategie.
In bijlage B is in precieze termen het zogenaamde tentamenmodel beschreven dat aan de hier te geven resultaten ten grondslag ligt. Globaal komt dit model op het volgende neer:
Aangenomen wordt dat er geen beperking is gesteld aan het aantal herkansingen. In theorie is het mogelijk om een zeer groot aantal herkansingen te benutten om met relatief lage stofbeheersing toch nog te slagen. In de praktijk zal het toch slechts zelden betekenen dat studenten meer dan gemiddeld één herkansing per studieonderdeel nodig hebben. Voor de student is het vrij zijn van het aantal herkansingen natuurlijk van belang: hij hoeft zich dan immers geen extra zorgen te maken over het RISICO om op een laatste herkansingsgelegenheid toch nog te zakken.
Wat bijzonder prettig voor de doorzichtigheid van de situatie is: door het onbeperkte aantal toegestane herkansingen is het mogelijk om een eenmaal (voor de eerste toetsgelegenheid) gekozen ongeveer optimale studiestrategie ook voor iedere eventueel daarop volgende herkansing te gebruiken.
Met studiestrategie wordt ook hier weer bedoeld: de mate van stofbeheersing waarop in de voorbereiding op de toets gemikt wordt
Voor een gekozen studiestrategie (mits deze ook reëel is, gehaald wordt) en gegeven het aantal vragen dat in de toets gesteld zal worden, is het mogelijk op de in hoofdstuk 4 geschetste wijze het risico te berekenen voor deze toets te zakken.
Bij dezelfde studiestrategie geldt dat ook voor herkansingen het risico gelijk blijft. Wie een goede of optimale studiestrategie voor de eerste toetsgelegenheid heeft gekozen, en gezakt is voor deze toets, zal ontdekken dat voor de herkansing de beste studiestrategie gelijk moet zijn aan de eerstgekozen strategie. Weliswaar ben je gezakt voor de eerste toets, maar wanneer herkansingstoetsen in alle opzichten gelijkwaardig zijn aan de eerst afgenomen toets, en aan het aantal toegestane herkansingen is geen beperking gesteld, dan zijn de omstandigheden precies gelijk aan de omstandigheden voor de eerste toetsgelegenheid. Daarom moet, wat toen een goede studiestrategie was, nu ook een goede studiestrategie zijn.
Een eenmaal voor een bepaald studieonderdeel gekozen optimale studiestrategie blijft ongewijzigd voor iedere eventueel af te leggen herkansing. Het risico blijft voor iedere herkansing dan ook gelijk,
en dat leidt. zoals in de bijlage te zien is, tot eenvoudige berekeningen voor wat de optimale strategie kan zijn.
Voor een gegeven risico is het mogelijk om uit te rekenen wat de kans is dat voor de eerste toets een voldoende gehaald wordt (vanzelfsprekend), maar ook kan de kans berekend worden dat een, twee, drie of meer herkansingen nodig zijn om te slagen voor dit studieonderdeel. Al die kansen zijn samen te vatten in het verwachte aantal benodigde herkansingen.
Studieonderdeel docimologie. De stof wordt telkens bestudeerd tot een niveau waarop het risico om te zakken op 0,40 geschat wordt. Dan:
Verwacht aantal benodigde herkansingen 0,40 / (1 - 0,40) = 213
(berekend volgens formule 7 in bijlage B)
VOORBEELD 6.1. Verband tussen risico en aantal herkansingen nodig om te slagen.
In voorbeeld 6.1 is het verwachte aantal benodigde herkansingen 2/3. Dat betekent dat bij vaak volgen van deze studiestrategie, bijvoorbeeld deze zelfde studiestrategie ook gehanteerd bij andere studieonderdelen, je mag verwachten ongeveer 2/3, zoveel herkansingen te moeten afleggen als er studieonderdelen zijn. Wordt deze strategie gevolgd voor 10 studieonderdelen, dan zul je door de bank genomen 7 keer een herkansing moeten doen (maar dat kunnen er ook best één of twee meer of minder zijn).
Nu zou je heel ruw en intuïtief kunnen vastleggen welk aantal herkansingen je aanvaardbaar vindt. Daarbij heb je dan op een of andere wijze rekening te houden met wat naar jouw idee de extra nodige tijd en inspanning voor zo'n herkansing is. Bovendien speelt daarin mee wat je denkt aan tijd en energie te moeten investeren om tot een bepaalde hogere stofbeheersing (kleiner risico) te komen. Je aanvaardbaar aantal herkansingen is de resultante van de intuïtieve afweging van deze kosten.
Beter is het om de factor benodigde studietijd etcetera te kwantificeren, vooral ook de tijd en energie die waarschijnlijk voor de voorbereiding op een herkansing nodig zijn. Dan kun je beter uitrekenen wat een goede studiestrategie onder HEx is. De eerste paar keer zal zo'n berekening niet al te precies uitkomen, maar met enige opgedane ervaring in het begin van de studie zal het zeker mogelijk zijn om voor benodigde studietijd etcetera nauwkeurige schattingen te geven.
Wie zichzelf langs deze weg, die in de volgende bladzijden verder uitgewerkt zal worden, inzicht verschaft in de verschillende mogelijke studiestrategieën, en waar die toe leiden in termen van studieresultaten en studietijd, is in staat om efficiënter te studeren dan hij misschien anders gedaan zou hebben, zal zijn eigen sucseskansen beter in kunnen schatten en minder gauw ten onrechte de studie staken.
Laten we om te beginnen eens proberen in te schatten wat een herkansing kost. Een inventarislijstje ziet er ongeveer als volgt uit:
Dit is een hele waslijst, en om die hanteerbaar te maken zal op één of andere wijze dit hele pakket van kosten en nadelen samengevat moeten worden. Handig zou zijn wanneer alle kosten in termen van studietijd worden uitgedrukt. Met andere woorden: studietijd is het wisselgeld waarin ook immateriële zaken als psychische spanning uitgedrukt worden. Om dat laatste als voorbeeld te nemen: je zou kunnen zeggen dat de psychische spanning waarmee het moeten doen van een herkansing gepaard gaat, best een extra studiedag waard is: om de extra psychische belasting van een herkansing te ontlopen zou je voor de voorbereiding op de eerste toetsgelegenheid wel een extra studiedag willen uittrekken.
In beginsel zou je verfijnde afwegingen als hier geschetst voor psychische belasting voor alle punten uit bovenstaande waslijst kunnen maken. Maar het is de vraag of al die moeite wel opweegt tegen de grotere nauwkeurigheid van de dan verkregen schatting, vergeleken met een ruwe bepaling van benodigde studietijd.
Zo'n ruwe bepaling zou kunnen zijn: studietijd voor een herkansing is de helft van de studietijd besteed voor de eerste toetsgelegenheid.
Door de eenvoud van deze aanname is er erg veel voor te zeggen deze schatting bij de berekeningen te gebruiken. Wie 0,5 te weinig vindt, kan natuurlijk een groter getal nemen, bijvoorbeeld 0,67. Is de ervaring na enkele studieonderdelen, en een enkele keer ook werkelijk een herkansing hebben moeten doen, dat de aanvankelijke schatting van een 0,5 bijgesteld moet worden, dan is dat heel eenvoudig mogelijk.
Bedenk dat in deze half zo grote studietijd ook alle andere nadelen van het moeten herkansen inbegrepen zijn. Ook studenten die voor het ophalen van de al eerder geleerde stof een stuk minder dan de helft van de tijd nodig hebben die zij in de voorbereiding op de eerste toets besteed hebben, kunnen tot de schatting van 0,5 komen wanneer zij rekening houden met de tijd nodig voor het afleggen van de herkansingstoets, financiële problemen die mogelijk voortvloeien uit het niet meteen slagen voor dit studieonderdeel, minder tijd kunnen besteden aan activiteiten buiten de studie, etcetera.
Ook voor iedere volgende herkansing wordt dezelfde kostenfactor 0,5 aangehouden. Dat lijkt reëel: weliswaar mag je verwachten steeds minder tijd nodig te hebben om de stof weer op te halen, maar iedere extra herkansing is op andere punten vervelender dan de vorige.
De berekening van de verwachte te besteden tijd om te slagen is dan heel eenvoudig. Als ut de benodigde tijd is om voor de eerste toetsgelegenheid een stofbeheersing te bereiken die een zak risico van r oplevert dan is:
(1) verwachte tijd nodig om te slagen = u t + 0,5 u t r /( 1 - r )
Formule (1) zit als volgt in elkaar: de tijd besteed aan de voorbereiding op de eerste toetsgelegenheid is ut, dat is een vast bestanddeel van de totaal benodigde tijd: of er één of meer herkansingen nodig zijn, of in het geheel geen herkansingen, een hoeveelheid tijd ut wordt altijd besteed.
Uit bijlage B weten we dat de formule voor het verwachte aantal herkansingen nodig om te slagen, r / ( 1 - r ) is. Voor iedere herkansing is een hoeveelheid tijd nodig van 0,5 ut. Wel, de tijd die nodig is voor het afleggen van het verwachte aantal herkansingen is het product van 0,5 ut en r / ( 1 - r ), de tweede term in formule (1).
Met concrete getallen ingevuld komt zoiets er als volgt uit te zien: Veronderstel dat de student 4 weken nodig heeft om de stof te beheersen op een niveau dat hem een zak risico van 0,40 oplevert. Dus:
ut = 4 r = 0,40 Ingevuld in (1):
verwachte tijd nodig om te slagen = 4 + 0,5 x 4 x 0,40 / ( 1 - 0,40 )
= 5,5 week.
Je kunt zo ook uitrekenen wat de verwachte tijd is bij een geringer inspanning (kleiner ut),en bij grotere inspanning (groter ut), waar natuurlijk een groter, respectievelijk kleiner, risico r bij hoort. De student die dat voor enkele mogelijkheden uitzoekt, wanneer de toetsen zullen bestaan uit 25 vragen, zou de resultaten in figuur 6.2 kunnen krijgen (zie volgende bladzijde).
De resultaten in deze figuur zijn niet verkregen door globale schatting van extra studietijd nodig om tot een bepaald hoger beheersingsniveau te komen, maar door een heel bepaald functioneel verband tussen studietijd ut en ware beheersing p te veronderstellen, zie figuur 6.1 :
-
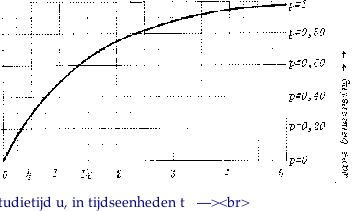
FIGUUR 6. 1. model-aanname verband tussen studietijd u en ware beheersing p, p = 1 - 2 -u.
Kort en bondig komt een curve zoals in figuur 6.1 er op neer dat, naarmate de stofbeheersing beter is, eenzelfde extra tijdbesteding minder extra stofbeheersing opbrengt. Ofwel: de laatste loodjes wegen het zwaarst. Het is vanzelfsprekend dat er een moment komt waar de ware beheersing p zo groot is, dat met een grote extra studie inspanning daar nauwelijks nog een verhoging in te bereiken is. Wanneer het studiedoel wat bescheidener gesteld is, bijvoorbeeld in de eerste plaats willen slagen voor een studieonderdeel met zo weinig mogelijk moeite, is al heel snel het punt bereikt waarop een extra studie-inspanning niet meer loont. (onder HEx, natuurlijk). Omdat uit de tabellen in bijlage F, of uit figuur 4.2 (maar dan moet het wel om een toets van 50 vragen gaan) is af te lezen welk risico bij iedere p hoort, kan op basis van figuur 6.1 de informatie in figuur 6.2 gevonden worden, voor verschillende mogelijke zak-slaag grenzen op de toets (of de herkansing).
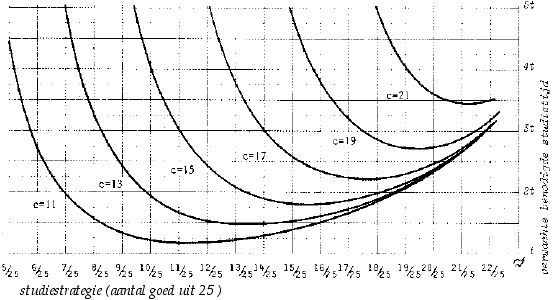
FIGUUR 6.2. Verwachte benodigde studietijd voor verschillende studiestrategieën, en verschillende zak-slaaggrenzen c bij toetsen van 25 vragen. Het laagste punt van iedere kromme correspondeert met de studiestrategie waarbij de studietijd om te slagen het kleinst is.
[Ik wil de ene al bestede episode aftrekken; een detaillering op de verticale schaal zou best nuttig zijn, is dat te doen? Of de gekozen range handig is, hangt af van de andere gevallen die ik in dezelfde figuur wil gaan plotten, dat zoek ik uit. Ik kan handwerk voorkomen door uit het array de historische posities te schrappen. Horizontaal: te investeren 1e opkomst; verticale schaal: naar verwachting te investeren om te slagen. Trek een referentielijn door de oorsprong naar verticaal zelfde aantal episodes als horizontaal.]
[nog niet beschikbaar]
FIGUUR 6.2. [Reconstructie 2002 mbv programma ATM] Verwachte benodigde studietijd voor verschillende studiestrategieën, en verschillende zak-slaaggrenzen c bij toetsen van 25 vragen. Het laagste punt van iedere kromme correspondeert met de studiestrategie waarbij de studietijd om te slagen het kleinst is.
In deze figuur 6.2 is de hele HEx-problematiek samengebald. Waar ook de zak-slaag grens getrokken wordt, er is altijd een uitgebreid scala van mogelijkheden voor de student die zijn totale studietijd zo klein mogelijk wil houden: duidelijk begrensde optimale studiestrategieën zijn uit figuur 6.2 niet af te lezen. Neem bijvoorbeeld de zak-slaag grens c=11: alle studiestrategieën tussen 8/25 en 16/25 zijn ongeveer even aantrekkelijk, vragen een ongeveer even groot tijdbeslag. Bij een strategie 8/25 zal de student weinig van de stof weten, een grote kans lopen voor herhalingen op te moeten; bij een strategie 16/25 weet de student meer van de stof, en heeft een klein risico. Het is gewenst dat de student de strategie 16/25 kiest, maar wat of wie kan verhinderen dat hij in plaats daarvan 8/25 kiest?
De student die verstandig is, kiest natuurlijk een studiestrategie die hem in zo kort mogelijke tijd doet slagen, maar dan wel met een zo groot mogelijke kennis van de stof. Dat betekent dat hij dan wel in de gelegenheid moet zijn om voor de eerste toetsgelegenheid die wat uitgebreidere voorbereidingstijd te gebruiken. De student die maar beperkt beschikbare tijd heeft, wordt daardoor gedrongen tot het volgen van een studiestrategie die leidt tot slagen, maar met geringer kennis van de stof.
Hoe zit dat dan met de strategie wanneer de zak-slaag grens nogal hoog gesteld is, zeg op c = 21 ? De curve in figuur 7.2 wijst toch op een duidelijk optimale studiestrategie van ongeveer 19/25 tot 22/25 of zelfs nog hoger? Maar ook dat is een heel uitgebreid gebied van mogelijkheden, zeker wanneer je dat afmeet tegen het verschil van c en de hoogst mogelijke score: 25 - 21 = 4. Het gebied van goede studiestrategieën is groter dan 4.
De conclusie voor de student is duidelijk: kies een goede studiestrategie zo ver mogelijk naar rechts.
Maar dan moet de student wel over zo'n strategie kunnen beschikken. Hoe de docent te werk kan gaan bij het opstellen van de curve die past bij de toetsen die hij afneemt, en de zak-slaag grens die hij daarbij zal hanteren, beschrijf ik nog eens voor een paar specifieke gevallen op de volgende bladzijden. Mocht de leercurve in figuur 6.1 niet van toepassing zijn, dan geeft bijlage D aanwijzingen voor het opstellen van een wel redelijk passende curve, waarop de berekeningen in tabellen 6.1 en 6.2 gebaseerd kunnen worden.
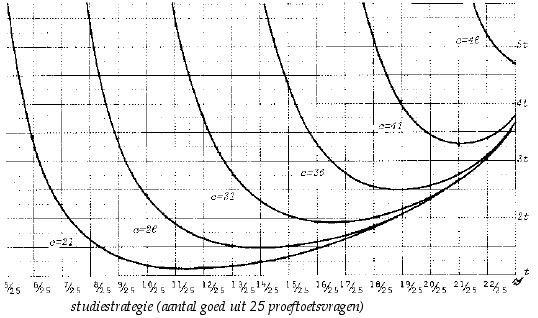
studiestrategie (aantal goed uit 25 proeftoetsvragen)
FIGUUR 6.3. Verwachte benodigde studietijd voor verschillende studiestrategieën, en verschillende zak-slaag grenzen c bij toetsen van 50 vragen.
_________________________________________________________________________________
gekozen beheersing risico studietijd om verwachte tijd verwacht aantal
strategie bijlage F p te bereiken om te slagen nodige herkansingen
________ _________________ _____________ ______________ ____________________
kans op 3
p 1-p r u = ln(1-p)/ln½ ½u(2-r)/(1-r) r/(1-r) of meer: r³
________ _________________ _____________ ______________ ____________________
9/25 0,36 0,64 0,900 0,64 3,52 9,0 0,729
10/25 0,40 0,60 0,824 0,74 2,47 4,7 0,559
11/25 0,44 0,56 0,721 0,84 1,90 2,6 0,375
12/25 0,48 0,52 0,595 0,94 1,63 1,5 0,211
13/25 0,52 0,48 0,459 1,06 1,51 0,85 0,097
14/25 0,56 0,44 0,327 1,18 1,47 0,49 0,035
15/25 0,60 0,40 0,214 1,32 1,50 0,27 0,0098
16/25 0,64 0,36 0,126 1,47 1,58 0,14 0,0020
17/25 0,68 0,32 0,066 1,64 1,70 0,07 0,0003
18/25 0,72 0,28 0,031 1,84 1,87 0,03 ...
19/25 0,76 0,24 0,012 2,06 2,07 0,012 ...
20/25 0,80 0,20 0,004 2,32 2,32 0,004 ...
21/25 0,84 0,16 0,001 2,64 2,64 0,001 ...
22/25 0,88 0,12 0,000 3,06 3,06 0,000 ...
_________________________________________________________________________________
TABEL 6.1. Berekening van studietijden bij verschillende studiestrategieën, voor toetsen van 60 vragen, en cesuur 31 (minimum aantal punten dat een voldoende oplevert is 31).
De toelichting op tabel 6.1 is eenvoudig. Bij iedere strategie hoort een beheersing die proportioneel gelijk is aan de strategie, dus bij strategie 9/25 een beheersing 36/100. Voor de volgende berekeningsstap is niet p, maar 1-p nodig, dat zet ik in kolom 3. Voor het risico dat de score kleiner dan de zak-slaag grens is, gebruiken we de tabel in bijlage F. Daaruit nemen we de tabel voor toetsen van 60 vragen, en lezen horizontaal de zak-slaag grens (=31), verticaal de studiestrategie. Bijvoorbeeld voor strategie 12/25 vinden we op de kruising van horizontaal 31 en verticaal 12/25 de risico-waarde (kans dat de toetsscore kleiner dan 31 is) 0,595. (Voor strategieën 11/25 en lagere maak je gebruik van de symmetrie-eigenschap van de getabelleerde functie: de kans dat bij strategie 11/25 het aantal goed kleiner is dan 31 is gelijk aan 1 - de kans dat onder strategie (25-11)/25 het aantal fout kleiner is dan 30; dat levert op 1 - 0,279 = 0,721 voor strategie 11/25.)
De berekeningsformule voor de overige kolommen is telkens in de tabel gegeven, en met een zakrekenmachine eenvoudig uit te voeren. Tenslotte zijn de gevonden waarden in de beide laatste kolommen grafisch uit te zetten (waarbij grafiek papier handig, maar niet noodzakelijk is), zoals in figuur 6.4 op de volgende bladzijde.
Het verwacht aantal benodigde herkansingen kan in dezelfde figuur uitgezet worden als de verwachte benodigde studietijden, maar bedenk dat bij beide een verschillende schaal hoort. Het snijpunt van beide curven heeft geen enkele speciale betekenis omdat de schaal van de ene curve, een tijdas, niets te maken heeft met de schaal van de andere curve, die gewoon het aantal herkansingen telt. Er is wel een relatie tussen de vorm van beide curven: bij geringe stofbeheersing zal een zeer groot aantal herkansingen nodig zijn, en al met al dus veel studietijd. Daarom verlopen beide curven links steil omhoog. Naar rechts geldt dat totale studietijd steeds meer gelijk wordt aan de tijd besteed aan voorbereiding op de eerste toetsgelegenheid.
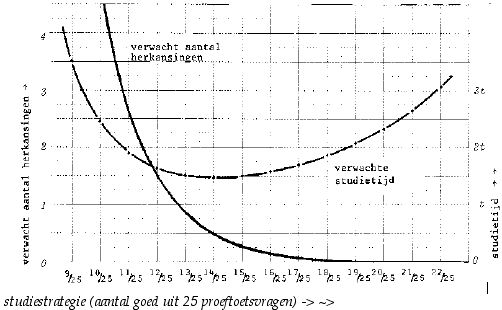
studiestrategie (aantal goed uit 25 proeftoetsvragen) -> ~>
FIGUUR 6.4. verwachte benodigde studietijd voor verschillende studiestrategieën, bij toetsen van 60 vragen met zak-slaag grens 31. (gebaseerd op de berekeningen in tabel 6.1). Ook is ingetekend het verwachte aantal benodigde herkansingen.
Uit figuur 6.4 is snel te concluderen dat wat benodigde studietijd betreft, alle strategieën van 12/25 tot en met 17/25 ongeveer optimaal zijn. De student die ook de vrijheid heeft om uit deze ongeveer optimale strategieën te kiezen, doet er goed aan de meest rechtse strategie aan te houden, omdat deze hem ook de hoogste stofbeheersing oplevert: strategie 16/25 of 17/25 dus. Bij deze laatste strategie hoort een verwachting voor het aantal benodigde herkansingen die heel erg klein is. In ieder geval voor de eerste toetsgelegenheid kan een strategie 16/25 of 17/25 dan ook gerust gevolgd worden. Is het aantal herkansingsmogelijkheden beperkt, maar groter dan twee, dan zal ook voor een eventueel nodige herkansing dezelfde strategie gehandhaafd kunnen blijven.
Dan hebben we nu nog te bekijken de strategie voor de student die om welke reden dan ook maar beperkte tijd heeft om zich voor de eerste toetsgelegenheid voor te bereiden: deze student kiest een ongeveer optimale strategie die links in de figuur zit: strategie 12/25 bijvoorbeeld. Het verwacht aantal benodigde herkansingen om te slagen is nu 1,5. Bij een beperkt aantal herkansingsmogelijkheden zou de student die hier strategie 12/25 kiest wel eens in moeilijkheden kunnen komen. Voor hem is de vraag: is een strategie 12/25 bij eerste opkomst een strategie die een te hoog Risico oplevert? Op welke wijze hangt de beantwoording van de eerste vraag af van de keuze van een hogere strategie voor de eerste herkansing?
Ook studenten die in deze situatie een strategie in de buurt van 15/25 kiezen zullen behoefte hebben aan een kwantificering van hun Risico om voor dit studieonderdeel niet binnen het toegestane aantal herkansingen te slagen. Voor verdere behandeling: zie hoofdstuk 7.
_________________________________________________________________________________
gekozen beheersing risico studietijd om verwachte tijd verwacht aantal
strategie bijlage F p te bereiken om te slagen nodige herkansingen
________ _________________ _____________ ______________ ____________________
kans op 3
p 1-p r u = ln(1-p)/ln½ ½u(2-r)/(1-r) r/(1-r) of meer: r³
________ _________________ _____________ ______________ ____________________
16/25 0,64 0,36 0,852 1,47 5,66 5,76 0,618
17/25 0,69 0,32 0,751 1,64 4,11 3,02 0,424
18/25 0,72 0,28 0,617 1,84 3,32 1,61 0,235
19/25 0,76 0,24 0,460 2,06 2,94 0,85 0,097
20/25 0,80 0,20 0,302 2,32 2,82 0,43 0,028
21/25 0,84 0,16 0,167 2,64 2,90 0,20 0,005
22/25 0,88 0,12 0,073 3,06 3,18 0,08 0,0004
_________________________________________________________________________________
TABEL 6.2. Berekening van studietijden bij verschillende studiestrategieën, voor toetsen van 60 vragen, en cesuur 46. Het verwacht aantal benodigde herkansingen is onder de veronderstelling dat voor iedere herkansing dezelfde strategie gebruikt wordt als bij de eerste opkomst (dat -geldt ook voor tabel 6. 1 ).
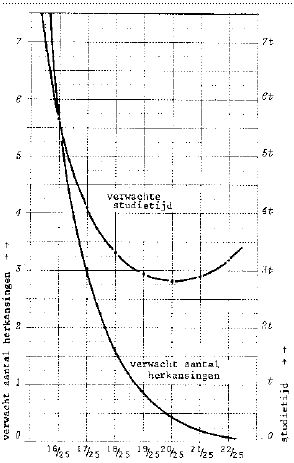
FIGUUR 6.5. Verwachte benodigde studietijd voor verschillende studiestrategieën, bij verwacht aantal toetsen van 60 vragen met herkansingen cesuur 46 (gebaseerd op resultaten van tabel 6.2). Het aantal nodige herkansingen om te slagen is onder de veronderstelling dat telkens dezelfde strategie gebruikt wordt.
Wanneer voor de toets meerkeuzevragen gebruikt worden moeten de figuren daaraan ook aangepast worden. De curven voor verwachte benodigde studietijd komen dan een stukje lager te liggen. Het is ook hier weer een taak voor de docent om rekening houdend met de raadkansen bij zijn meerkeuze vragen de juiste curven te construeren en deze de student aan te bieden. De student krijgt dan een curve voorgelegd die er ongeveer zo uit ziet als die in de figuren 6.2 en 6.3, en die op dezelfde manier gelezen kan worden.
Aanwijzingen voor de docent, hoe in het geval van meerkeuze vragen deze curve te construeren, worden in bijlage D gegeven.
Dan wordt het nu tijd om de veronderstelling van de mogelijkheid om een onbeperkt aantal keren te herkansen kritisch te bekijken. In de praktijk is het immers nogal eens het geval dat weliswaar een toets een onbeperkt aantal keren overgedaan mag worden, maar dat daardoor dan wel de studieduur erg sterk kan gaan uitlopen. Stel je voor dat slechts twee of drie toetsgelegenheden per jaar gegeven worden, dan kan de student in grote moeilijkheden geraken wanneer hij juist voor de laatste studieonderdelen van de herkansingsregeling gebruik moet maken. Hij kan niet afstuderen, of aan een volgende studiefase beginnen, voordat hij voor zijn examen geslaagd is. Dat betekent dat voor de laatste studieonderdelen een nogal hoge studiestrategie gekozen moet worden om het risico te zakken redelijk te houden. Het is niet direkt rampzalig om voor zo'n laatste toets te zakken, dus het risico hoeft niet erg klein gehouden te worden. Het risico, bij een gegeven studiestrategie (bij gegeven stofbeheersing) kan afgelezen worden uit de tabellen in bijlage F.
Wanneer de student het geluk heeft dat het toegestaan is al aan de volgende studiefase te beginnen wanneer nog niet alle studieonderdelen uit de vorige fase met een voldoende afgesloten zijn, verdwijnt de hier gesignaleerde problematiek natuurlijk. Maar wanneer het om een doctoraal examen gaat, is zo'n regeling moeilijk denkbaar.
Het is nog steeds ongebruikelijk, ook bij studietoetsen, om tevoren mee te delen hoeveel van de vragen goed beantwoord moeten zijn om tenminste een voldoende beoordeling te krijgen. Dat levert voor de student een extra stuk onzekerheid op, waar hij in zijn studiestrategie rekening mee zou kunnen houden. Bij doorrekenen, op de wijze als in bijlage B aangegeven, blijkt het echter dat onzekerheid over de precieze plaats van de zak-slaag grens weinig of geen gevolgen voor de strategie keuze heeft, wanneer er tenminste enige zekerheid bestaat over de plaats waar de zak-slaag grens ongeveer zal komen te liggen.
Studenten met een stofbeheersing beneden de verwachte zak-slaag grens hebben een iets grotere verwachte slaagkans dan bij zekerheid over de grens; studenten die een stofbeheersing hebben boven de verwachte zak-slaag grens moeten rekening houden met een iets groter risico om te zakken. Studenten in de laatste groep, die hun risico constant willen houden, moeten een grotere studie inspanning leveren wanneer er onzekerheid over de zak-slaag grens is.
Het gaat hier echter om effecten die voor één studieonderdeel klein zijn, maar over tien of twintig studieonderdelen wel tot een effect van enig belang kunnen cumuleren.
In dit hoofdstuk 6 is een serie oefeningen te vinden met een model dat direct is afgeleid van het tentamenmodel van Van Naerssen. Het is erg moeizaam allemaal, en er worden evenals in de andere hoofdstukken veel te veel minder belangrijke details besproken. In 1978 was geen programmatuur beschikbaar waarmee echt makkelijk situaties konden worden doorgerekend en al helemaal niet tevens grafisch worden afgebeeld; daardoor was de afhankelijkheid van tekst en in de tekst behandelde voorbeelden veel groter.
Wat in dit hoofdstuk wel van belang is, is het idee dat het in sommige (veel?) situaties wel eens zo kan zijn dat de student die erop uit is te besteden tijd te minimaliseren, de keuze heeft uit een breed scala van strategieën. Dat scala loopt evenwel van naar de toekomst toe ongunctige strategieën tot naar de toekomst toe gunstige. Dat is voor de programmering van het onderwijs voor individuele studenten van belang: immers, studenten die door welke oorzaak dan ook terechtkomen in een situatie van beperkt beschikbare tijd, kune zodoende de keuzemogelijkheid voor de naar de toekomst toe gunstige strategieën verliezen en gedwongen zijn de ongunstige strategieën te benutten. Hoe een en ander zich laat vertalen met gebruik van het latere algemene toetsmodel ligt dan voldoende voor de hand om dat niet uit te hoeven leggen, maar het gaat dan niet meer om een type strategie dat binnen het algemene toetsmodel valt te odnerscheiden, want het gaat om parameters die buiten het model zelf vallen.
Bij veel examenregelingen van het conjunctieve type is er een beperking gesteld aan het aantal keren dat er voor één bepaald studieonderdeel herkanst kan worden. In de propedeuse kan zich de situatie voordoen dat het aantal geboden gelegenheden beperkt is, in andere studiefasen kan er een formele beperking aangebracht zijn in het aantal herkansingen dat de student voor één studieonderdeel toegestaan wordt.
Dit zijn de beide varianten van strenge beperking van herkansingsmogelijkheden. Daarnaast zijn er situaties waarin er geen formele beperking hoeft te zijn, maar er vanuit de specifieke situatie van de student een groot belang bestaat om in niet meer dan één of twee keer een voldoende voor een bepaald vak te scoren (in de afsluiting van het vorige hoofdstuk werden een aantal mogelijkheden genoemd).
Door de beperking in het aantal herkansingsgelegenheden moet bij het zoeken naar een optimale studiestrategie nu rekening gehouden worden met het Risico om niet binnen dat aantal herkansingen te slagen.
Bij het zoeken naar de optimale studiestrategie kan in eerste instantie gekeken worden naar de strategieën die ongeveer optimaal zouden zijn zonder beperking in het aantal herkansingen. Berekening van het bijbehorend Risico om voor dit vak niet te slagen zal uit moeten wijzen of een in eerste instantie aantrekkelijke strategie ook aanvaardbaar is.
Wanneer het aantal herkansingsgelegenheden strikt beperkt is, ontstaat immers de mogelijkheid dat iemand voor een bepaald studieonderdeel geen voldoende kan behalen omdat hij in het toegestane aantal herkansingen telkens faalde.
Omdat het een HEx-regeling betreft, zou dat tevens betekenen dat hij voor het examen als geheel gezakt is.
De eerste stap in de analyse van deze HEx-variant bestaat er uit het RISICO te kiezen dat nog juist aanvaardbaar voor mij is, het RISICO om voor het examen te zakken. Laat ik bij wijze van voorbeeld ervan uit gaan dat een RISICO = 0,05 voor mij aanvaardbaar is (een kans van één op 20 om voor het examen te zakken, met alle gevolgen van dien).
De volgende stap is het vinden van het Risico voor ieder afzonderlijk studieonderdeel om voor dat onderdeel te zakken, zodanig dat ik voor alle studieonderdelen gezamenlijk uitkom op mijn aanvaardbaar RISICO.
De regel is: ieder studieonderdeel moet voldoende gemaakt zijn om te kunnen slagen voor het examen, of het nu een groot, dan wel een klein vak is doet niet ter zake. Dus: dan zal dat Risico voor afzonderlijke studieonderdelen ook hetzelfde moeten zijn.
Gelijk Risico impliceert gelijke slaagkans. Wel, de kans om onder HEx te slagen voor het examen, is gelijk aan het product van de slaagkansen voor de afzonderlijke studieonderdelen.
Als er nu 15 studieonderdelen zijn, en de slaagkans voor ieder studieonderdeel zou 0,995 zijn, dan is de slaagkans voor het examen
(1) slaagkans examen = 0,99515 = 0,928.
Het RISICO = ( 1 - slaagkans ) = 0,072 (ongeveer 1 op 14),
het Risico per vak = ( 1 - slaagkans per vak ) is dan ( 1 - 0,995 ) = 0,005.
De student kan zich niet veel Risico veroorloven, zelfs al zou een tamelijk fors examen RISICO van 0,07 voor hem aanvaardbaar zijn.
Een aantal andere voorbeelden in VOORBEELD 7.1:
________________________________________________________________
aantal studie- aanvaardbaar Risico per studieonderdeel wanneer het
onderdelen aanvaardbaar RISICO voor het examen gekozen is als
respectievelijk 0,10, 0,05, of 0,01
----------------------------------------------------------------
RISICO 0,10 RISICO 0,05 RISICO 0,01
----------- ----------- -----------
10 0,010 0,005 0,0010
15 0,007 0,003 0,0007
20 0,005 0,0026 0,0005
30 0,0035 0,0017 0,0003
________________________________________________________________
VOORBEELD 7.1. Verband tussen gekozen aanvaardbaar RISICO om voor het examen te zakken , en maximaal te nemen Risico per studieonderdeel om niet binnen het toegestane aantal herkansingen te slagen.
De algemene formule waarmee de Risico's in voorbeeld 7.1 berekend zijn ziet er als volgt uit
(2) Risico = 1 - ( 1 - RISICO )1/n n = aantal studieonderdelen
Hoe kom je als student onder deze omstandigheden tot een goede strategie keuze voor de eerste, tweede etc. toetsgelegenheid? Ik wil dat uiteenzetten aan de hand van een concreet voorbeeld. Ik veronderstel dat voor dit studieonderdeel de toets, ook een herkansingstoets, bestaat uit 60 vragen. Eerst bespreek ik de situatie voor het geval de zak slaag grens getrokken is bij 31 (31 is de minimum voldoende score). Straks geef ik ook nog de resultaten voor zak slaag grens 46.
Bij het nu te geven voorbeeld zal ik dan ook gebruik maken van de eerder gegeven berekeningen voor juist deze toetsingssituatie: zie tabel 6.1 en figuur 6.4 voor zak slaag grens 31, en tabel 6.2 en figuur 6.5 voor zak slaag grens 46.
De eenvoudigste situatie is die waarin maar één herkansing is toegestaan, die zal ik eerst behandelen. Daarna de situatie waarin het aantal toegestane herkansingen groter is dan één (maar wel beperkt).
De verschillende stappen in de overwegingen van de student zijn de volgende:
welk Risico om voor beide gelegenheden te zakken is voor mij aanvaardbaar? Het antwoord hangt af van het RISICO om voor het gehele examen te zakken dat voor mij nog juist aanvaardbaar is. Als ik RISICO gekozen heb, kan ik Risico berekenen uit de volgende formule, waarin n het aantal studieonderdelen voor dit examen is:
(3) Risico = 1 - ( 1 - RISICO )1/n.
Kies ik RISICO = 0,05, en zijn er 10 studieonderdelen die getoetst worden, dan vind ik:
(4) Risico = 1 - ( 1 - 0,05 )1/10 = 0,005.
Het Risico dat voor mij per studieonderdeel aanvaardbaar is, is erg klein. Maar dat wist ik al uit het eerder gegeven voorbeeld 7.1.
welk risico om voor de eerste keer te zakken is aanvaardbaar?
Het aanvaardbare risico voor de eerste toetsgelegenheid hangt af van de strategie die voor de eventuele herkansing gevolgd wordt, en het aanvaardbare Risico dat hierboven berekend is.
De algemene regel bij HEx is dat alleen het voldoende resultaat telt. Is de eerste toets voldoende, dan wordt geen herkansing gedaan. Is de eerste toets onvoldoende, dan telt het verkregen studieresultaat verder niet meer mee, begint de student voor de herkansing a.h.w. met een schone lei. Je slaagt dus of bij de eerste gelegenheid, of op de herkansing, of in het geheel niet. Er is geen sprake van dat je zou slagen wanneer een combinatie van de resultaten op eerste en tweede kans aan een minimum eis voldoet.
Als ik even aanneem dat ik ook aan de herkansing deel kan nemen wanneer bij eerste gelegenheid mijn resultaat al voldoende was (bij een onvoldoende op de herkansing blijft toch de voldoende van de eerste gelegenheid tellen), dan is de kans op tenminste één keer voldoende gelijk aan: 1 - de kans beide keren een onvoldoende te behalen. Dan is, als r1 het risico om bij de eerste gelegenheid te zakken voorstelt, en r2 het risico bij de tweede gelegenheid te zakken:
(5) Risico = r1 × r2
Maar dat is prachtig, want dat betekent dat ik een grote vrijheid in strategiekeuze heb, zolang ik er maar voor kan zorgen dat het product van de bijbehorende risico's kleiner of gelijk mijn aanvaardbare Risico van, in dit geval, 0,005 is! (zodra resultaten bekend zijn, is er een nieuwe situatie, zie 7,5). Laat ik daarom eens nagaan welke strategieën voor mij beschikbaar zijn. Wat is de hoogste strategie die ik, gezien het daarbij behorende tijdbeslag, kan volgen? Wat is de hoogste ongeveer optimale strategie?
Zou ik voor beide gelegenheden dezelfde strategie kiezen, dan moet dat de strategie zijn die een risico oplevert dat ongeveer gelijk is aan de wortel uit 0,005: de studiestrategie met risico 0,07.
Raadpleeg ik bijlage F of tabel 6.1, voor toetsen van 60 vragen en voor de zak slaag grens 31, dan zie ik dat studiestrategie 17/25 de geschikte studiestrategie is: het risico bij deze strategie is telkens 0,066.
In dezelfde kolom van tabel 6.1 (kolom 4) kan ik combinaties zoeken die samen een Risico kleiner of ongeveer gelijk aan 0,005 opleveren:
Voor de ene gelegenheid een studiestrategie van 16/25 en voor de andere gelegenheid een strategie van 18/25 leveren samen risico 0,126 maal risico 0,031 is ongeveer Risico 0,0039 op.
Andere mogelijke combinaties, wat aanvaardbaar Risico betreft:
15/25 en 19/25 : 0,214 maal 0,012 levert Risico ca. 0,0025
14/25 en 19/25 : 0,327 maal 0,012 levert Risico ca. 0,0035
13/25 en 19/25 : 0,459 maal 0,012 levert Risico ca. 0,005
12/25 en 20/25 : 0,595 maal 0,004 levert Risico ca 0,0025
11/25 en 20/25 : (1 - 0,279) maal 0,004 is Risico ca 0,003
Merk op dat het volgen van een studiestrategie voor de tweede en laatste toetsgelegenheid die een risico kleiner dan 0,005 kent, iedere strategie voor de eerste gelegenheid toelaat.
hoe kies ik uit de verschillende mogelijke combinaties de beste? De beste strategie keuze is die welke de minste kosten met zich mee brengt. Omdat alle kosten als benodigde studietijd uitgedrukt zijn (zie de paragraaf studiestrategie in hoofdstuk 6), is de beste strategiekeuze die welke de benodigde studietijd voor de combinatie van beide toetsgelegenheden zo klein mogelijk maakt. Dat alles alleen voor combinaties die een aanvaardbaar Risico opleveren. Het is best mogelijk dat ik nu ga ontdekken dat strategieën die een nog kleiner Risico opleveren binnen handbereik liggen, in welk geval ik mijn aanvaardbaar Risico wat lager kan kiezen.
Hoe bereken ik de benodigde studietijd? Omdat ik van tevoren niet kan weten of ik aan de herkansing moet meedoen, kan ik de studietijd niet recht toe recht aan berekenen. Maar als ik kan schatten wat de kans is dat ik zak voor de eerste gelegenheid, en dus aan de herkansing moet deelnemen, dan kan ik de verwachting van de totaal benodigde studietijd berekenen. De verwachting is het statistisch gemiddelde: zou je voor een groot aantal studieonderdelen dezelfde combinatie van strategieën, onder overigens ook dezelfde omstandigheden kiezen, dan mag je verwachten aan herkansingen voor al die verschillende studieonderdelen bij elkaar zoveel extra tijd kwijt te zijn dat het gemiddelde daarvan ongeveer gelijk is aan de verwachting van de benodigde tijd zoals ik die nu ga berekenen voor dit studieonderdeel.
Ik voer de berekening eerst uit voor het geval ik voor beide gelegenheden dezelfde strategie kies, en wel de strategie 17/25. Uit figuur 6.4 zie ik dat dit nog een redelijk optimale strategie is, zodat deze keus geen slechte hoeft te zijn. De pertinente gegevens, risico en tijdbesteding, staan in tabel 6.1.
De voorbereidingstijd voor de eerste gelegenheid is 1,64 tijdseenheden t, de voorbereidingstijd voor de herkansing, bij dezelfde strategie, is de helft daarvan, is 0,82 tijdseenheden t, en de kans dat ik inderdaad aan de herkansing moet deelnemen is gelijk aan het risico bij de eerste gelegenheid, en dat is volgens tabel 6.1 gelijk aan 0,066. Met deze gegevens kan ik de verwacht benodigde studietijd berekenen:
(6) V( u tot ) = 1,64 + 0,066 × 0,92 = 1,694 (in tijdseenheden t),
V( u tot ) = verwacht benodigde studietijd.
Een korte toelichting op het karakter van die tijdseenheid t: in principe zou iedere student voor zichzelf kunnen bepalen welke waarde t voor hem heeft bij dit bepaalde studieonderdeel, in termen van uren, dagen, of weken. Dat zou erg veel moeite kosten, en toch nog tot een nogal onnauwkeurige schatting kunnen leiden. Gelukkig is al die moeite niet nodig: ook zonder de omvang van t te weten, kan uit alle overwogen combinaties van strategieën die combinatie gekozen worden die het kortste tijdbeslag vraagt. Deze procedure is volkomen vergelijkbaar met het uitzoeken welk van een aantal pakjes het kleinste gewicht heeft, door op een balans de pakjes tegen elkaar af te wegen: zonder eerst van ieder pakje het gewicht bepaald te hebben, kan toch feilloos het lichtste pakje gevonden worden.
Het Risico van deze combinatie van 17/25 met 17/25 is 0,0662 = 0,0044.
Dit resultaat wil ik graag vergelijken met het tijdbeslag bij andere combinaties. Andere combinaties die in aanmerking komen zijn die combinaties waar de strategie voor de herkansing een hogere is dan de strategie voor de eerste gelegenheid. Bovendien moet dan de strategie voor de eerste gelegenheid een ongeveer optimale strategie zijn voor het geval waarin het aantal herkansingen onbeperkt is. Beide voorwaarden zijn eenvoudig op hun juistheid te controleren door een aantal combinaties door te rekenen die er niet aan voldoen.
Als voor de herkansing een hogere strategie wordt gekozen, dan is de voorbereidingstijd die voor deze herkansing nodig is te berekenen als de helft van de tijd nodig onder de strategie voor de eerste gelegenheid, plus de tijd nodig om de beheersing van het niveau onder de lagere strategie te brengen op het niveau horend bij de hogere strategie. In woorden klinkt dat heel wat ingewikkelder dan in symbolen:
(7) voorbereidingstijd herkansing = 0,5 u1+ ( u2 - u1 ) = u2 - 0,5 u1
uj = voorbereidingstijd nodig onder de strategie die gekozen wordt voor de j-de toetsgelegenheid.
Met de gegevens uit tabel 6.1 vind ik dan voor de combinatie van eerst strategie 16/25, en dan eventueel strategie 18/25 voor de herkansing als verwacht benodigde studietijd
(8) V( u tot ) = 1,47 + 0,126 × ( 1,84 1,5 × 1,47 ) = 1,609 ( eenheden t )
bij een Risico 0,126 maal 0,031 = 0,0039.
Vergelijking van beide combinaties leert dat de laatste combinatie een kleiner tijdbeslag vraagt, terwijl ook het Risico bij de laatste combinatie iets kleiner is dan bij de eerste. Tabel 7.1 op de volgende bladzijde geeft de resultaten voor andere combinaties.
_____________________________________________________________ strategiekeuze verwachte benodigde studietijd ------------------------------------------------------------------------ 17/25 & 17/25 (Risico 0,0044) 1,694 tijdseenheden t 16/25 & 18/25 ( ,, 0,0039) 1,609 ,, t 16/25 & 19/25 ( ,, 0,0015) 1,637 ,, t 15/25 & 19/25 ( ,, 0,0025) 1,620 ,, t 14/25 & 19/25 ( ,, 0,0035) 1,661 ,, t 13/25 & 19/25 ( ,, 0,005 ) 1,762 ,, t 13/25 & 20/25 ( ,, 0,0018) 1,882 ,, t 12/25 & 20/25 ( ,, 0,0025) 2,041 ,, t _____________________________________________________________
TABEL 7.1. Verwachte benodigde studietijden voor verschillende combinaties van studiestrategieën. Twee toetsgelegenheden, toetsen van 60 vragen, cesuur 31.
De conclusie uit de resultaten in tabel 7.1 gegeven, is duidelijk: de ongeveer optimale strategie keuze is voor de eerste gelegenheid strategie 15/25 of 16/25, met voor de tweede gelegenheid dan respectievelijk 19/25 en 18/25. Hoewel de combinatie 15/25 met 19/25 naar verwachting iets meer tijd kost, is het Risico weer iets kleiner dan voor de andere combinatie.
Een overweging die de keuze tussen de beide ongeveer optimale combinaties kan vergemakkelijken is de volgende:
Wanneer voor de voorbereiding op een herkansing maar weinig tijd beschikbaar is, verdient het de voorkeur om de combinatie te kiezen met de minder extreme strategieën, in dit geval de combinatie 16/25 met 18/25. De voorbereidingstijd voor de tweede gelegenheid is onder deze combinatie 1,06 tijdseenheden t. De voorbereidingstijd voor de tweede gelegenheid is bij de combinatie 15/25 met 19/25 daarentegen 1,40 tijdseenheden t.
WAARSCHUWING. Dit zijn strategieën die gekozen worden voorafgaand aan beide toetsgelegenheden. Zodra het resultaat van de eerste toetsgelegenheid bekend is verandert de situatie ingrijpend. Wie geslaagd is heeft geen verdere problemen meer. Wie gezakt is, zal aan de herkansing deel moeten nemen. Er is dan nog maar één kans om te slagen. Om het Risico op het gekozen niveau te houden moet een strategie gekozen worden waarvoor het risico daaraan gelijk (gelijk aan Risico) is. Dat zal in de regel een zeer hoge strategie zijn, en niet de strategie in het vooraf gekozen koppel van strategieën van het soort als in de tabel hierboven. Dit lijkt tegenstrijdig, maar is helaas volstrekt juist. Op deze verontrustende samenhang ga ik in paragraaf 7.5 verder in.
De verschillende stappen in de overwegingen van de student zijn in dit geval (en dit is tevens illustratief voor gevallen waarin drie, vier etc., herkansingsmogelijkheden zijn) de volgende:
Welk Risico om voor alle drie gelegenheden te zakken is voor mij aanvaardbaar? Dit is hetzelfde als wanneer er maar één herkansingsgelegenheid zou zijn. Dus de beantwoording gaat langs dezelfde weg als in de voorgaande paragraaf onder a. behandeld, en levert hetzelfde resultaat op: bij gekozen RISICO = 0,05, en wanneer het hele examen uit 10 studieonderdelen bestaat, is het aanvaardbaar Risico = 0,005.
welk risico om voor de eerste keer te zakken is aanvaardbaar?
Ik kan de strategieën voor de verschillende gelegenheden zo kiezen dat de bijbehorende risico's r1, r2, en r3 voldoen aan:
Risico = r1 r2 r3 = 0,005 (in dit voorbeeld).
Zou ik voor iedere gelegenheid dezelfde studiestrategie willen volgen, dan moet dat de strategie zijn waarbij een risico hoort dat gelijk is aan de derde machts wortel uit het Risico
( 0,005 )1/3 = 0,171.
Uit de tabel in bijlage F (voor toetsen van 60 vragen, cesuur 31) of uit tabel 6.1 kolom 4, zie ik dat strategie 16/25 een risico heeft van 0,126, terwijl strategie 15/25 een risico heeft van 0,214. Ik zou dus op een strategie daartussen kunnen gaan zitten, maar ik kan ook als compromis nemen: eerste twee gelegenheden strategie 15/25, laatste gelegenheid strategie 16/25. De berekening van de verwachte benodigde studietijd gaat met behulp van de volgende formule
(9) V( u tot ) = u1 + r1 (u2 - 0,5 u1 ) + r1 r2 (u3 - 0,5 u2 )
Uit figuur 6.4 lees ik af dat strategie 16/25 een ongeveer optimale strategie is, die een relatief hoge stofbeheersing geeft. Als ik de verwachte studietijd bereken voor telkens deze strategie bij alle gelegenheden: (gegevens tabel 6.1)
V( u tot ) = 1,47 + 0,126 × 0,735 + 0,126 2 × 0,735 = 1,574
(in tijdseenheden t) en Risico = 0,0020.
Omdat strategie 14/25 optimaal is wat tijdbeslag betreft, is te verwachten dat combinaties die beginnen met deze strategie een minimaal tijdbeslag vergen. Bijvoorbeeld 14/25, 15/25, 17/25:
V( u tot ) = 1,18 + 0,327 (1,32 0,59) + 0,327 × 0,214(1,64 0,66)
= 1.318 + 0,239 + 0,069 = 1,488 t, en Risico = 0,0046.
Een overzicht van deze en andere combinaties in tabel 7.2:
_____________________________________________________________ strategiecombinatie Risico verwachte benodigde studietijd ------------------------------------------------------------- 16/25 & 16/25 & 16/25 0,0020 1,574 tijdseenheden t 15/25 15/25 16/25 0,0058 1,498 ,, 15/25 16/25 16/25 0,0034 1,513 ,, 14/25 16/25 16/25 0,0052 1,498 ,, 14/25 15/25 17/25 0,0046 1,488 ,, 14/25 15/25 18/25 0,0022 1,502 ,, 14/25 14/25 18/25 0,0033 1,507 ,, _____________________________________________________________
TABEL 7.2 Verwachte benodigde studietijden voor verschillende combinaties van studiestrategieën. Drie toetsingsgelegenheden, toetsen van 60 vragen, cesuur 31.
WAARSCHUWING. Zodra bekend is dat het eerste toetsresultaat onvoldoende is, moet de nu ontstane situatie opnieuw geanalyseerd worden, maar nu uitgaande van nog slechts twee toetsgelegenheden om die voldoende te kunnen behalen. Dus wordt nu de analyse zoals gegeven in paragraaf 7.1 uitgevoerd. Zie ook paragraaf 7.5.
Voor drie toegestane herkansingen komt bij formule (9) nog een vierde, op te tellen term
r1r2r3 (u4 - u3)
en voor nog meer toets gelegenheden worden de extra termen op geheel analoge wijze gevonden.
In geval er maar één herkansings-gelegenheid is, en ik hanteer ook nu als aanvaardbaar Risico per studieonderdeel de waarde 0,005, dan vind ik dat de combinatie 22/25 & 22/25 een Risico = 0,00533 en verwacht tijdbeslag 3,06 + 0,073 × 1,53 = 3,17 t oplevert. Als ik kijk naar figuur 6.5, zou ik met een klein beetje moeite de strategie 22/25 als ongeveer optimaal kunnen beschouwen.
Zou ik als aanvaardbaar RISICO om voor het examen te zakken niet 0,05, maar 0,01 kiezen, en zou ik te maken hebben met een programma bestaande uit 15 studieonderdelen, dan is het aanvaardbaar Risico per studieonderdeel volgens Voorbeeld 7.1 nog maar 0,0007. Als er maar 2 toetsgelegenheden zijn, en ik zou voor beide gelegenheden dezelfde strategie willen kiezen, dan moet dat een strategie zijn die een risico heeft gelijk aan de wortel uit 0,0007 ofwel 0,026. Zoek ik in tabel 6.2 naar een strategie met ongeveer dit of een iets kleiner risico, dan is te vermoeden dat dat strategie 24/25 zal zijn! (de tabel geeft voor deze strategie geen gegevens, ook bijlage F niet, vandaar het vermoeden).
Het moet wel een heel bijzonder stukje onderwijs zijn, zeker in het w.o., waar dit beleidshalve te rechtvaardigen is.
Voor meerdere toetsgelegenheden, en andere aanvaardbare RISICO's, kunnen nog heel wat leuke berekeningen gemaakt worden. Wat ligt meer voor de hand dan dat de lezer voor zijn eigen onderwijssituatie eens een paar toepasselijke becijferingen langs de geschetste lijnen maakt?
Een enkele conjunctieve examenregeling kent de uitzondering dat één of twee onvoldoendes toegestaan zijn. Meestal met voorwaarden, bijvoorbeeld dat zo'n onvoldoende dan wel tenminste een vijf moet zijn, dat er tenminste voor een ander studieonderdeel een zeven tegenover moet staan, etcetera.
Het verwerken van dit soort uitzonderingen in de berekeningen over combinaties van strategieën voor afzonderlijke studieonderdelen wordt een heel erg vervelende zaak, waarbij bovendien de berekeningen herzien moeten worden na iedere bekend geworden toetsuitslag. Het lijkt dan ook het beste, hoewel niet optimaal, om de toegestane ruimte voor onvoldoendes te benutten door de laatste herkansing(en) niet af te leggen. Zeker in situaties waarin het moeten doen van een herkansing, nadat alle andere studieonderdelen al met een voldoende afgesloten zijn, leidt tot uitstel van het examen (afstuderen), levert deze aanpak de student tijdwinst op.
Een heel speciaal geval is natuurlijk het propedeutisch examen, waar genoemde uitzondering op de HEx regeling vaker voorkomt, en waar bovendien het aantal studieonderdelen (en het aantal herkansingsmogelijkheden) nogal beperkt pleegt te zijn. Aan deze bijzondere examensituatie in de propedeuse besteed ik een afzonderlijk hoofdstuk 9.
Aan het eind van dit hoofdstuk over beperkte herkansingsmogelijkheden komt er nog een heel vervelende aap uit de mouw.
Wat is het geval namelijk: alle strategie combinaties die in het voorgaande behandeld zijn hebben betrekking op de keuze die gedaan moet worden voordat aan de eerste toets begonnen wordt.
ZODRA DE UITSLAG VAN EEN TOETS BEKEND IS, EN HET RESULTAAT IS ONVOLDOENDE, VERANDERT DE SITUATIE VOOR DE STUDENT, EN ZAL HIJ ER VERSTANDIG AAN DOEN VOOR DE NOG RESTERENDE TOETSGELEGENHEID ( HEDEN) ZIJN STRATEGIE (COMBINATIE VAN STRATEGIEëN) TE HERZIEN.
Het probleem doet zich ook voor bij het aangaan van een weddenschap over de uitkomst van vier worpen met een muntstuk: wie een weddenschap afsluit op het tenminste één keer bovenkomen van munt, zal zijn weddenschap maar wat graag herzien zodra hij heeft gezien dat bijvoorbeeld de eerste twee worpen kop waren.
In het algemeen is het inderdaad zo, dat weddenschappen, studiestrategieën, e.d. herzien moeten worden wanneer meer informatie beschikbaar komt dan op het moment waarop de weddenschap aangegaan werd, de studiestrategieën gekozen werden, beschikbaar was.
Het is niet juist om, gegeven een al behaalde onvoldoende, voor de overige herkansingen toch de strategie te volgen die daarvoor in eerste instantie was uitgestippeld, daardoor wordt het Risico te groot om voor dit studieonderdeel, en daarmee voor het examen, te zakken.
Welke strategie voor de overige herkansingen te volgen is, wanneer bekend is dat voor de eerste gelegenheid een onvoldoende werd behaald, kan op dezelfde wijze onderzocht worden als in de voorgaande paragrafen beschreven werd. Het gevolg van deze strategie herziening zal vaak zijn dat op een hogere strategie voor de eerstvolgende herkansing overgeschakeld moet worden dan in eerste instantie voorzien was. Dat betekent ook een heel stuk extra tijdbesteding om de stofbeheersing op het verlangde niveau te brengen.
Vervelender wordt het, wanneer geen strategie beschikbaar is die een voldoend klein Risico oplevert. of wanneer de tijd niet voorhanden is om een dergelijke strategie te kunnen volgen. Vooral voor de laatste herkansingsgelegenheid kan de student zich zodoende in een situatie gemanoevreerd zien waarin hij geen greep meer heeft op het Risico om voor dit studieonderdeel te zakken. De beste aanpak die hem rest is om zo hard mogelijk te werken, daarmee het Risico zo klein mogelijk houdend, ook al is het Risico daarmee niet op een aanvaardbaar peil te brengen.
Voor de hand liggende suggestie: houd er van te voren rekening mee dat je wel eens in de situatie terecht kunt komen waarin je nog maar één of twee herkansingsmogelijkheden tot je beschikking hebt. Maar is dat wel zo'n goede suggestie? Vaak zal voor de laatste herkansing de strategie die een aanvaardbaar Risico oplevert niet bestaan, of qua tijdbeslag onhaalbaar zijn. Afgezien van dit praktische bezwaar is het in het algemeen onjuist om in de keuze van je strategie uit te gaan van de aller zwartgalligste van de gebeurtenissen die je eventueel zouden kunnen overkomen. Het zou bovendien betekenen dat ook voor de eerste toetsgelegenheden een veel hogere strategie gekozen zou worden, waardoor veel te veel studietijd per vak besteed zou worden, de studie vertraagd zou worden zonder misschien ooit werkelijk van een herkansing gebruik hebben hoeven te maken.
Al met al kan ik me voorstellen dat de situatie voor de lezer nog erg duister blijft. Ik zou er zelf, als ik weer als student mij in een dergelijke situatie zou bevinden, ook grote moeite mee hebben.
Het gaat hier om een heel wezenlijke tekortkoming van het beleid waarin herkansingsmogelijkheden per studieonderdeel beperkt zijn.
De HEx met beperking blijkt ingrijpend te verschillen van de HEx waarbij het aantal herkansingsmogelijkheden niet beperkt is. En dat terwijl de maatregel om het aantal herkansingen te beperken er zo onschuldig uitziet: het komt waarschijnlijk niet erg vaak voor dat studenten alle gelegenheden ook werkelijk nodig hebben om te slagen, en als het al voorkomt, gaat het misschien ook om studenten die bij meerdere studieonderdelen dezelfde moeilijkheden hebben, en die dan ook een studie gekozen hebben die hun krachten waarschijnlijk te boven gaat. Maar dan wordt vergeten dat eenmaal zo'n maatregel ingesteld, studenten daar in hun studiestrategie rekening mee zullen gaan houden (en moeten gaan houden), en dat dan de problemen ontstaan die ik hierboven geschetst heb.
Suggestie voor de faculteit die deze problemen wil vermijden, en tegelijkertijd wil voorkomen dat studenten door hei doen van vele herkansingen al te makkelijk (ten onrechte) hun examen behalen: beperkt niet het aantal herkansingen per vak, maar het aantal herkansingen over alle vakken gezamenlijk dat toegestaan is. Zie hoofdstuk 9.
Wat er ook aan het onderwijs gesleuteld mag worden, uiteindelijk zal de student zich door eigen inspanning de geboden leerstof eigen moeten maken. Het zoeken naar onderwijsmethoden die het beter doen is dan ook het zoeken naar methoden die het de student makkelijker, aantrekkelijker, eenvoudiger maken in zijn worsteling met de stof. De stelling dat het onderwijs erop gericht is de student te ondersteunen bij zijn zelfstudie laat zich, zeker waar het om wetenschappelijk onderwijs gaat, heel lang verdedigen.
Wat ligt nu meer voor de hand dan ook eens naar de examenregeling te kijken vanuit de vraagstelling in hoeverre zo'n regeling een stimulerende, faciliterende uitwerking heeft op de studieaanpak van de student?
De kern van een compensatorische examenregeling is dat goede en slechte studieresultaten elkaar mogen compenseren. Het gaat er om dat voor alle studieonderdelen tezamen een minimum aantal punten, de EIS, behaald wordt. De student is vrij om zijn studie inspanning gelijk, of juist ongelijk over alle vakken te verdelen.
Ik wijs er uitdrukkelijk op, en zal dat op vele plaatsen in deze cursus nog herhalen, dat behaalde resultaten bepalen of aan de EIS voldaan is of niet, en dat is wezenlijk iets anders dan de ware beheersing van de student voor de diverse studieonderdelen. In de inleidende hoofdstukken werd uitgebreid gedemonstreerd dat een toetsuitslag weliswaar verband houdt met de ware beheersing van de stof, maar daar geen al te nauwkeurige meting van is.
De student houdt zijn eigen vorderingen bij, en leidt uit het verschil tussen de al behaalde punten en de EIS af wat zijn studieïnspanning voor de nog resterende studieonderdelen moet zijn om met enige zekerheid te kunnen slagen voor het examen. In dit eenvoudige zinnetje liggen een aantal forse problemen besloten, die in dit hoofdstuk aangevat zullen worden.
Er wordt in het volgende van uitgegaan dat de EIS geformuleerd is als een tenminste te behalen aantal punten. Voor iedere afgelegde toets krijgt de student een aantal punten dat gelijk is aan het aantal goed beantwoorde vragen maal de voor dat vak vastgestelde wegingsfactor. De veronderstelling daarbij is natuurlijk dat beide, het aantal toetsvragen met de wegingsfactor, door het daartoe bevoegde orgaan, de (sub)faculteitsraad, worden vastgesteld in relatie tot elkaar. (omdat vergroting van het aantal vragen een groter gewicht aan het vak zou geven, waarvoor gecorrigeerd kan worden door de wegingsfactor te verkleinen). Voor de student die zijn studiestrategie moet bepalen is van belang dat hij tevoren voor alle vakken beide gegevens in zijn bezit heeft.
Laat ik als eenvoudige illustratie van de structuur van een compensatorische examenregeling het geval nemen waar het hele studieprogramma bestaat uit 10 studieonderdelen. Ik laat voor het moment nog buiten beschouwing of die studieonderdelen gelijkwaardig zijn, even moeilijk, even belangrijk, een even groot tijdbeslag van de student vragen, e.d.
De student legt over ieder studieonderdeel één keer de eindtoets af, er zijn geen herkansingen. De tien studieonderdelen worden dan ook zonder storende herkansingen voor eerder onvoldoende gemaakte toetsen achtereenvolgens door de student, hopelijk volgens het programma, afgewerkt. Iedere toets kan voorafgegaan worden door een proeftoets, bedoeld om de student informatie te geven over de mate waarin hij de stof beheerst. Schematisch ziet het activiteitenprogramma van de student er dan ook simpel uit, zoals in figuur 1 duidelijk is gemaakt.
_______________________________________________________ proeftoetsen 1 2 3 4 5 6 7 8 9 10 : : : : : : : : : : 1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7 -> 8 -> 9 -> 10 toetsen _______________________________________________________
FIGUUR 8.1. Het toetsprogramma voor de student onder CEx.
Het ontbreken van herkansingsgelegenheden vindt zijn reden in de aard van de compensatorische regeling, waar pech op een enkel studieonderdeel niet ingehaald wordt door datzelfde studieonderdeel nog eens te doen met hopelijk wat meer geluk, maar door voor de overige studieonderdelen een iets grotere inspanning te plegen. Het laatste is dan overigens alleen noodzakelijk voor die studenten die wat meer moeite hebben met voldoen aan de exameneisen, en hun RISICO om voor het examen uiteindelijk te zakken door verstandige strategie keuzen in de hand moeten houden (op een aanvaardbaar peil houden).
Hoewel het meer tot het onderwerp van deel B van deze cursus hoort, wil ik hier toch vast opmerken dat bijvoorbeeld voor het doctoraal examen de feitelijke situatie natuurlijk moet zijn dat studenten die tot deze onderwijsfase toegelaten zijn, ook het doctoraal moeten kunnen behalen binnen de randvoorwaarden (gebruik van onderwijsvoorzieningen bijvoorbeeld) die daarvoor gesteld zijn. Het voldoen aan de examen EIS zal voor doctoraal studenten ook geen ernstige problemen mogen opleveren. Voor het propedeutisch examen zal dat in de regel anders liggen, omdat daar een stuk selectieproblematiek aan de orde is, zoal geen selectie door de faculteit, dan toch de dringende vraag van de student aan zichzelf of dit nu wel de studie is die hij gezien zijn bewezen capaciteiten en toekomstkansen zou moeten volgen.
Hoewel voor examens aan het eind van de studie het zeldzaam behoort te zijn dat studenten alsnog niet aan de exameneisen kunnen voldoen, zal het voor grote groepen studenten toch belangrijk zijn er voortdurend voor te waken dat het RISICO om beneden de EIS uit te komen aanvaardbaar blijft.
Bij een CEx hoeft de student met gemiddeld goede beheersing van de stof zich weinig zorgen te maken over zijn RISICO te zakken voor het examen, niet aan de EIS te kunnen voldoen. Hij behaalt, bij een normale studie inspanning, gemiddeld goede resultaten, waarmee hij op een puntentotaal uitkomt dat redelijk ver boven de EIS ligt. Soms zal al aan de EIS voldaan zijn, wanneer de laatste toets nog afgelegd moet worden. Dan is de student zeker te zullen slagen, ongeacht het resultaat dat hij voor de laatste toets behaalt. Natuurlijk zal het voor hem wel van belang zijn om voor die laatste toets een behoorlijk resultaat te boeken, in lijn met de eerder door hem behaalde resultaten. Er zal immers aan zijn puntentotaal enig civiel effect verbonden zijn. (Zou er geen civiel effect aan het puntentotaal, dus aan de kwaliteit van de geleverde studieprestaties, verbonden zijn dan zou in de geschetste situatie dat laatste studieonderdeel in feite facultatief zijn, wat overigens niet altijd ongewenst hoeft te zijn).
Laat ik de strategische keuzen van deze student illustreren aan een concrete onderwijssituatie. Veronderstel dat gemiddeld goede stofbeheersing overeenkomt met het goed kunnen beantwoorden van 18 uit 25 vragen, dus met studiestrategie 18/25. De studiestrategie is het niveau van stofbeheersing waarop gemikt wordt, of ook, als blijk daarvan, het relatieve aantal goed beantwoorde vragen op toets of proeftoets.
Ik neem aan dat deze strategie 18/25, of een stofbeheersing van 72 %, voor deze student ook regel is, en dat hij bij een iets tegenvallend proeftoetsresultaat in de tijd die hem rest tussen proeftoets en eindtoets zijn beheersing kan ophalen tot ongeveer die 72 %.
Veronderstel dat iedere toets uit 50 vragen bestaat. Volgens de techniek beschreven in de inleidende hoofdstukken (en bijlage A), leidt dat tot een voorspellende kansverdeling voor de totaalscore zoals in figuur 4.2 afgebeeld (de curve 18/25).
Dezelfde voorspellende scoreverdeling geldt nu voor ieder van de, laten we zeggen 10 studieonderdelen, omdat telkens dezelfde strategie gebruikt wordt, iedere toets evenveel vragen heeft, en iedere toetsscore hetzelfde gewicht meekrijgt. Uit deze 10 voorspellende scoreverdelingen zou je eigenlijk één verdeling moeten construeren voor de somscore (de voorspellende kansverdeling voor de somscore over alle 10 toetsen), maar dat is een erg moeilijke zaak. In bijlage C laat ik zien dat het wel mogelijk is op eenvoudige wijze het gemiddelde en de variantie van deze voorspellende somscoreverdeling te berekenen (de term variantie zal ik straks bespreken). Met deze twee gegevens, het gemiddelde en de variantie, is het mogelijk om een nauwkeurige schatting van het RISICO te maken.
De variantie van een kansverdeling is een maat voor de gespreidheid van de verdeling, voor hoe ver verschillende waarden van het gemiddelde af kunnen liggen. In figuur 4.2 bijvoorbeeld zien we de linker curven als meer gespreid dan de curven aan de rechterkant. Het gaat hier om een technisch begrip, waarvan de precieze definitie voor het vervolg van deze cursus niet direkt van belang is. Symbolisch zal ik de variantie aanduiden met
s2 = variantie.
Terugkomend op mijn voorspellende somscoreverdeling, is het gemiddelde daarvan eenvoudig gelijk aan de som van de gemiddelden van de 10 afzonderlijke verdelingen, in dit geval
(1) m = 10 × 36 = 360 punten (36 is gemiddelde van iedere scoreverdeling).
De variantie voor de voorspellende somscoreverdeling is eveneens gelijk aan de som van de varianties van de afzonderlijke scoreverdelingen:
(2) s2 = 10 × 29,08 = 290,8 zodat s = √ 290,8 = 17,1
Als nu de EIS gesteld is op 300 punten, dan ligt het gemiddelde van 360 voor deze student daar een heel stuk boven. De vraag is, of die 60 punten verschil veel of weinig zijn, en welk RISICO daaraan vastzit.
De wortel uit de variantie, s dus, geeft de sleutel tot de interpretatie van het verschil van 60 punten. In dit geval is s = 17,1, het verschil bedraagt meer dan 3s. Een voorzichtige interpretatie daarvan op statistische gronden (zie technische voetnoot 1) is dat het RISICO kleiner dan 1 op 100 is.
1) technische voetnoot. Aangenomen dat de voorspellende kansverdeling voor de somscore niet al te veel afwijkt van een normaal verdeling, wat niet onredelijk lijkt voor de totaal 500 toetsvragen waar het hier om gaat. De overschrijdingskans bij 2,82 s is voor de normaalverdeling .0024. Een RISICO van 1 % is dan rijkelijke voorzichtig genoeg. In feite zou de aanname van normaal verdeeld zijn zelfs overschatting van het RISICO opleveren, zoals blijkt bij vergelijking met de gegevens in tabel 4.1 die exact zijn, en de overschrijdingskansen die de aanname van normaal verdeeld zijn voor deze verdelingen zou opleveren.
Maar dit is zeker nog niet het hele verhaal: dit is het RISICO zoals het aan het begin van de cursus ingeschat wordt, en aangenomen dat de strategieën ook tussentijds niet gewijzigd worden. Wijziging zou, gezien de dan al bekende studieresultaten, mogelijk of wenselijk kunnen zijn.
Het is een klein rekenkunstje om te laten zien dat het gemiddelde voor de voorspellende somscoreverdeling na negen toetsen gelijk is aan 324 punten, dat is al 24 punten meer dan de EIS! Het is dus te verwachten dat deze student na negen toetsen afgelegd te hebben al zeker is te zullen slagen.
Maar dat moet betekenen dat het te verwachten is dat voor een student die deze studiestrategieën kiest, het RISICO geleidelijk vermindert, naarmate hij meer toetsen al heeft afgelegd (en daar de resultaten van weet). Laat ik dat eens nagaan.
Veronderstel dat deze student voor de eerste toets zijn verwachte aantal van 36 punten behaalt. Voor de overige negen toetsen moet hij dan, om aan de EIS te voldoen, nog tenminste 264 punten scoren. Onder dezelfde studiestrategie is zijn gemiddelde van de voorspellende somscoreverdeling voor 9 toetsen gelijk aan 9 × 36 = 324 punten. Het verschil is nog steeds 60 punten, maar s blijkt nu een stukje kleiner te zijn, s = 16,2 punten. Hoe kleiner e, bij gelijkblijvend puntenverschil, hoe kleiner ook het RISICO wordt.
Het RISICO blijft op deze wijze afnemen naarmate meer toetsen al afgelegd zijn, en de student daarbij niet door pech achtervolgd is. Bij twee nog af te leggen toetsen, wanneer al 288 punten behaald zouden zijn, moeten nog 12 punten behaald worden, terwijl de te verwachten somscore over die twee toetsen op 72 punten staat. Het verschil is nog steeds 60 punten tussen het verwachte en het benodigde puntental, maar ondertussen is s = 7,6 punten. Statistisch gezien is het uitgesloten te achten dat een afstand van bijna 8 s door de pechduivel overbrugd zal worden.
De studiestrategie voor iedere nog af te leggen toets is het aantal vragen uit 25 die je goed wilt kunnen beantwoorden, de relatieve beheersing van de stof die je wilt bereiken. Wie reden heeft om erg zeker van zijn schatting van de eigen stofbeheersing te zijn, kan zijn strategie formuleren als het aantal vragen uit 50 dat hij goed denkt te kunnen of wil kunnen beantwoorden; dat leidt tot een kleiner RISICO, en dat kan gevaarlijk zijn wanneer er geen goede redenen waren om tot deze sterkere schatting over te gaan.
De strategie kan voor verschillende studieonderdelen natuurlijk verschillend gekozen worden. Bijvoorbeeld een hoge strategie voor vakken waartoe je je inhoudelijk voelt aangetrokken, of waar met wat minder inspanning meer punten te behalen zijn.
Een overwogen keuze van studiestrategieën berust uiteraard op ervaringen bij voorgaande studieonderdelen opgedaan. Daarnaast kunnen gegevens over wat de gemiddelde prestaties voor een bepaald vak voor vorige jaargroepen studenten bleken te zijn, behulpzaam zijn bij het maken van een overwogen keuze.
Bij de berekening van het RISICO over meerdere studieonderdelen is het handig om de benodigde gegevens en tussenresultaten in tabelvorm te zetten, zoals in voorbeeld 8.1 gedaan is. (volgende bladzijde).
Bereken voor ieder studieonderdeel de verwachte gewogen score wimi (het gemiddelde van de voorspellende scoreverdeling), waarbij mi het product is van de gekozen studiestrategie, uitgedrukt als quotiënt, met het aantal vragen in de toets, en waarbij wi de wegingsfactor of het gewicht voor studieonderdeel i is. Bijvoorbeeld: bij studiestrategie 18 uit 25, aantal vragen 50, en gewicht wi = 2
mi = (18/25) x 50 x 2 = 72.
Bepaal vervolgens voor ieder studieonderdeel si2, de bijdrage aan het kwadraat van de spreiding voor de somscore, door deze af te lezen uit tabel 8.1:
__________________________________________________________
aantal vragen in de toets i
25 40 50 60 75 100
________________________________________________________
Strategie ../25: 10 20 30 40 60 100
../50: 8 10 20 30 40 64
__________________________________________________________
TABEL 8.1. si2, de variantie van de nog ongewogen score. Bij interpoleren afronden naar boven, om geen te optimistische resultaten te krijgen. Tabel niet gebruiken bij studiestrategieën die op stofbeheersing van minder dan ongeveer 40 % mikken. (verantwoording: bijlage C.4).
Tel deze si2, na ze vermenigvuldigd te hebben met het kwadraat van het gewicht wi, bij elkaar op om de variantie s2 van de voorspellende somscoreverdeling te krijgen.
Voor de verwachte somscore m tellen we alle (wimi) bij elkaar op.
Tenslotte bepalen we het verschil tussen de voor het examen gestelde EIS en m, en delen dat door s. Voor het zo verkregen berekeningsresultaat geeft tabel 8.2 het bijbehorende RISICO.
Een concreet voorbeeld, voor studieonderdelen waarvoor een verschillende studiestrategie gekozen is, waar de toetsen uit verschillende aantallen vragen bestaan, en verschillend gewogen worden, hieronder:
______________________________________________________________
aantal gewicht verwachte
toets strategie vragen w(i) score s(i)² w(i)² w(i)²s(i)²
____________________________________________________________
1 18/25 50 2 72 30 4 120
2 16/25 50 1 32 30 1 30
3 16/25 75 1 48 60 1 60
4 16/25 50 3 96 30 9 270
5 18/25 100 2 144 100 4 400
6 18/25 50 1 36 30 1 30
7 35/50 25 3 52,5 8 9 72
8 18/25 25 1 18 10 1 10
9 16/25 50 3 96 30 9 270
10 16/25 50 3 96 30 9 270
_____ + _____ +
m = 690,5 s² = 1532
____________________________________________________________
Als EIS = 600, bereken (690,5 - 600) / √ 1532 = 2,312.
Uit tabel 8.2 lezen we af dat het RISICO < 0,012 is.
____________________________________________________________
VOORBEELD 8.1. Berekeningen bij 10 nog af te leggen toetsen.
_______________________________________________________________
berekeningsresultaat RISICO berekeningsresultaat RISICO
groter of gelijk aan: groter of gelijk aan:
_______________________________ _____________________________
4,00 < 0,0001 1,90 < 0,03
3,50 < 0,0002 1,80 < 0,04
3,25 < 0,0005 1,70 < 0,05
3,00 < 0,0015 1,60 < 0,06
2,75 < 0,003 1,50 < 0,07
2,50 < 0,006 1,40 < 0,08
2,25 < 0,012 1,30 < 0,10
2,00 < 0,023 1,20 < 0,12
______________________________________________________________
TABEL 8.2. RISICO's horend bij de berekeningsresultaten.
Ook onder CEx zullen er studenten zijn die met de nodige inspanning maar net komfortabel boven de EIS uit kunnen komen. Voor hen zal gelden dat zij bij een normale studie inspanning een verwachte somscore hebben, die maar een klein stukje boven de EIS zal liggen. Daar volgt uit dat voor hen het RISICO om te zakken erg groot zal zijn, wanneer zij niet af en toe een extra studie inspanning kunnen leveren.
De student die bij een normale studie inspanning een groot RISICO loopt, kan onder die omstandigheden gerust door studeren zolang de mogelijkheid bestaat om op latere studieonderdelen door het volgen van een hogere studiestrategie het RISICO wel aanvaardbaar te houden. Deze vorm van studiestrategie wordt in het vervolg de wisselstrategie genoemd: een normale studie inspanning wordt gepleegd, zolang tegenvallende toetsresultaten het niet nodig maken om op een hogere strategie over te stappen.
In plaats van nog eens in andere woorden te omschrijven hoe deze wisselstrategie functioneert, zal ik een concreet voorbeeld geven. Veronderstel eens dat bij de strategie uit voorbeeld 8.1 een EIS van 680 punten gesteld is. Dat betekent dat voor het afleggen van deze tien toetsen de verwachting is dat de somscore maar net boven de 680 punten uit zal komen, waarbij de kans groot is (het RISICO groot is) dat de 680 niet gehaald zal worden.
Maar veronderstel dat het mogelijk is, met enige opoffering, om een extra studie inspanning te leveren, die de studiestrategie voor de toetsen 4, 5, 7, 9 en 10 op het hogere niveau van respectievelijk 18/25, 20/25, 40/50, 18/25 en 18/25 brengt. De verwachte somscore wordt dan opgehoogd:
690,5 + 12 + 16 + 7,5 + 12 + 12 = 750 punten.
Hernieuwde berekening van het RISICO levert dan op:
(750-680) / √1523 = 1,79. Uit tabel 8.2 lezen we af: RISICO < 0,05.
Een RISICO van 1 op 20 om te zakken voor het examen lijkt aan het begin van de rit, althans wanneer nog tien studieonderdelen gedaan moeten worden, alleszins aanvaardbaar.
Zal het nu voor studenten die deze wisselstrategie volgen ook vaak nodig zijn om op de hogere (nood ) strategie over te schakelen? Wanneer gemiddelde of betere studieprestaties geboekt worden, gerefereerd aan de voorspellende scoreverdelingen die volgen uit de gekozen studiestrategieën, zal het voor één of twee toetsen nodig zijn een extra inspanning te plegen. Degenen die pech hebben, en het is inderdaad louter pech, aanvankelijk tegenvallende scores te krijgen, zullen wel vaker een extra inspanning moeten plegen, maar doorgaans ook snel weer terug kunnen vallen op hun normale studie inspanning.
Terug naar de gegevens van het voorbeeld: veronderstel eens dat de student de eerste vier toetsen heeft afgelegd met als resultaat 250 punten, dat is ongeveer gelijk aan het verwachte resultaat. Bij een EIS van 680 punten moet hij dan op de overige zes toetsen tenminste 430 punten verzamelen. De verwachte somscore is 442,5, zoals eenvoudig uit kolom 5 van voorbeeld 8.1 af te lezen. Bij het volgen van de hogere strategie voor toetsen 7, 9 en 10 is
(( 442,5 + 7,5 + 12 + 12 ) - 430 ) / √1052 = 1,36. Tabel 8.2 geeft RISICO < 0,10.
Dit is een fors RISICO, waardoor deze student genoodzaakt is om voor toets 5 een hogere studiestrategie te kiezen: 20/25. Dan is het RISICO < 0,04 geworden.
Nu zit in dit voorbeeld een eigenaardigheid ingebouwd die waarschijnlijk in de praktijk vaak te vinden zal zijn: toets 5 is een bijzonder zware toets, een toets bestaande uit 100 vragen, met een gewicht 2. Wanneer deze toets gesplitst zou worden in twee toetsen, met enige tijd daartussen waarin studenten in de gelegenheid zijn te studeren, worden de toetsresultaten voor de student minder grillig, beter voorspelbaar. Wanneer bijvoorbeeld twee keer een toets van 100 vragen afgenomen wordt, telkens met gewicht 1, vermindert de bijdrage van deze toets aan de s2 voor de somscore met 200. Bij een strategie van 18/25 voor beide deeltoetsen, en verhoogde strategie voor de toetsen 7, 9 en 10 wordt het RISICO niet < 0,10 zoals straks berekend, maar 44 / √852 = 1,51 levert dan een RISICO < 0,07 op, en bij eventueel op de tweede deeltoets de strategie 20/25 hanteren wordt het RISICO < 0,06.
Het principe van de wisselstrategie is dus eenvoudig: bereken het RISICO wanneer voor de eerstvolgende toets een normale studieïnspanning gepleegd wordt. Is dat RISICO te hoog, bereken dan het RISICO wanneer voor enkele nog volgende studieonderdelen een extra inspanning (die reëel binnen de mogelijkheden van de student moet liggen) gepleegd wordt. Is ook dát RISICO te hoog, dan moet op de eerst af te leggen toets al een extra inspanning gedaan worden, een hogere studiestrategie gevolgd worden.
Bij deze wisselstrategie wordt noodzakelijkerwijs gekapitaliseerd op pech of geluk bij de verkregen toetsscores: bij geluk is het mogelijk (veelal) om met een normale inspanning verder te studeren, bij pech zal een extra inspanning op een volgend studieonderdeel noodzakelijk worden. Door het maken van deze RISICO berekeningen wordt het voor de student mogelijk om een rationele studiestrategie te volgen, tot een goede verdeling van zijn krachten te komen.
De student die noodgedwongen van deze wisselstrategie gebruik maakt, beschikt over heel wat minder studievrijheden dan zijn kameraden die zich over het RISICO geen zorgen hoeven te maken. Het is bij een afgedwongen wisselstrategie in mindere mate mogelijk om de studieïnspanning over de verschillende vakken te verdelen naar de eigen belangstelling. Dat is te betreuren, het schept een stuk ongelijkheid, maar het lijkt onontkoombaar.
Een andere manier waarop de werking van de wisselstrategie gedemonstreerd kan worden, is door achteruit te redeneren.
Je kunt precies uitrekenen hoeveel punten je op de eerste negen toetsen verzameld moet hebben om te bereiken dat je voor toets 10 een aanvaardbaar RISICO hebt om het verEISte aantal punten niet te halen, zeg dat RISICO is < 0,012. Onder dat RISICO mag je verwachten bij de strategie van 16/25 tenminste 59 punten op toets 10 te scoren, dat wil zeggen dat op de voorgaande 9 toetsen bij elkaar tenminste 680 59 = 621 punten gescoord moeten zijn. Voor de strategie 18/20 op de laatste toets kan dat 609 punten zijn. Op dezelfde wijze kun je uitrekenen hoeveel punten tenminste na 8 toetsen behaald moeten zijn om een aanvaardbaar RISICO voor de laatste twee af te leggen toetsen te hebben. Voor de normale strategie op toets 9 en 10 moeten dat tenminste 680 139 = 541 punten zijn, voor de strategie 18/25 op toets 10 moeten dat 529 punten zijn, voor de strategie 18/25 op zowel toets 10 als toets 9 moeten dat 517 punten zijn. Heeft deze student 529 punten of meer, dan kan hij rustig de normale inspanning aan de voorbereiding van toets 9 geven. Dat laat de mogelijkheid open dat het resultaat van toets 9 tegenvalt, en een extra inspanning op de voorbereiding van toets 10 nodig is, maar daarbij zal het RISICO aanvaardbaar blijven ( < 0,012 ).
De student die ontdekt, laten we hopen in de loop van zijn eerste studiejaar, dat hij gezien zijn capaciteiten een hoog RISICO heeft om te zakken voor het examen, kan besluiten om dat RISICO te aanvaarden en door te studeren, ofwel om de studie te staken. Dit is een belangrijk beslissingsmoment, waarin de student ondersteuning van zijn studieadviseur hard nodig heeft. Hoe onder deze omstandigheden de beslissing voorbereid moet worden kan in deze cursus niet behandeld worden. Wel wil ik verwijzen naar enige (van de schaarse) literatuur op dit gebied, zoals Gelatt e.a. (1972, 1973).
Er zullen altijd studenten zijn die ook bij een nogal fors RISICO door willen studeren, omdat zij voor deze studie hoog gemotiveerd zijn, geen goede alternatieven hebben, of omdat zakken voor het examen geen ernstige gevolgen in de financiële sfeer voor hen hoeft te hebben. In de praktijk zal een CEx dan ook altijd wel voor een aantal studenten een teleurstelling opleveren, omdat zij ondanks een hoge studie inspanning niet konden slagen. Het streven moet er op gericht zijn dat deze studenten wel tijdig gewaarschuwd worden, zodat zij dit RISICO tevoren welbewust op zich nemen.
Bij bestudering van een concrete studiestrategie, zoals de strategie in voorbeeld 8.1 blijkt al snel dat het riskant is om een hoge studiestrategie te kiezen voor zwaar gewogen toetsen, dat het niet verstandig is om je voor sommige in het geheel niet voor te bereiden ook al verwacht je hoge scores voor ándere toetsen te behalen, e.d. De ervaring, en het maken van een enkele RISICO berekening, zullen de student hier de weg kunnen wijzen. In het algemeen is een gelijkmatige studie inspanning, in verhouding tot de zwaarte (door weging en het aantal toetsvragen) van de studieonderdelen, als richtlijn te nemen, en hopelijk is daar ook bij de programmering van de studie al rekening mee gehouden.
Voor propedeutische examens worden nog wel eens regels gehanteerd die afwijken van wat overigens gebruikelijk is. Het ligt voor de hand dat een propedeuse programma, vaak samengeperst in relatief kort tijdsbestek, zo zijn eigen problemen stelt voor studenten die een overwogen studiestrategie willen volgen. De beperktheid in tijd brengt al snel met zich mee dat voor sommige studieonderdelen maar één of hooguit twee herkansingsmogelijkheden bestaan: in het laatste deel van hoofdstuk 7 werd het problematische aspect daarvan al uit de doeken gedaan.
Propedeuseregelingen lenen zich bovendien uitstekend voor allerlei experimenten met de examenregeling, getuige de proliferatie van allerlei bijzondere regelingen. Daar zijn nogal wat varianten bij waarin in de richting van meer compensatorisch combineren van studieresultaten wordt gewerkt. Zo kom je terecht in het uitgestrekte gebied tussen zuiver compensatorische en zuiver conjunctieve regelingen: het laat zich denken dat het aantal mengvormen vrijwel onbeperkt is.
In dit hoofdstuk wil ik een aantal examenvarianten behandelen vanuit de vraag welke strategieën voor de student beschikbaar zijn, en op welke wijze hij daaruit zijn keuze kan maken.
Volledig conjunctief: ieder studieonderdeel moet voldoende gemaakt zijn. Aantal herkansingen onbeperkt: dat kan gerealiseerd worden door toe te staan dat de student al aan het 2e-jaarsprogramma begint, ook al zou hij nog één of twee herkansingen voor de propedeuse moeten afleggen.
Het is niet onwaarschijnlijk, dat de student aan herkansingen die nog plaats moeten vinden wanneer het 2e studiejaar al begonnen is, een hogere kostenfactor verbindt, dan aan herkansingen die nog tijdens het eerste jaar, of kort na de vakantie gedaan moeten worden. Het uitrekenen van verwachte studietijden onder een kostenfactor 1, in plaats van de factor 0,5, die ik doorgaans voor de voorbeelden gebruik, hoeft geen problemen op te leveren. In plaats van deze nieuwe berekeningen te maken, is het eenvoudiger ervan uit te gaan dat bij het hanteren van een hogere kostenfactor voor herkansingen in het tweede jaar, de ongeveer optimale studiestrategieën ongeveer 5% hoger moeten liggen (in termen van stofbeheersing), dus i.p.v. zeg 18/25 dan een strategie van 19/25 hanteren.
Een propedeuse programma verschilt nogal eens van de programmering van de overige studie, doordat het veel strakker is, alle studieonderdelen op daartoe vastgelegde tijdstippen doorlopen moeten worden, e.d. Er kan door de student niet zo gemakkelijk geschoven worden met de verschillende programmaonderdelen. Komt daar dan nog bij dat voor de gewone voorbereiding op de eerste toetsgelegenheden voor ieder vak eigenlijk al alle beschikbare tijd nodig is, dan zou het daar tussendoor nog moeten doen van herkansingen vervelende consequenties kunnen hebben. In dergelijke situaties is het van belang het moeten doen van herkansingen zoveel mogelijk te vermijden. Bij het zoeken naar goede studiestrategieën kun je dat gegeven verwerken in de kostenfactor voor herkansingen. In figuur 9.1 geef ik een voorbeeld van het effect van zo'n opwaardering van de kosten verbonden aan herkansingen. Wordt de kostenfactor in dit voorbeeld van 0,5 gebracht op 1, dan verschuiven de ongeveer optimale strategieën een stuk naar boven (naar rechts in de figuur dus).
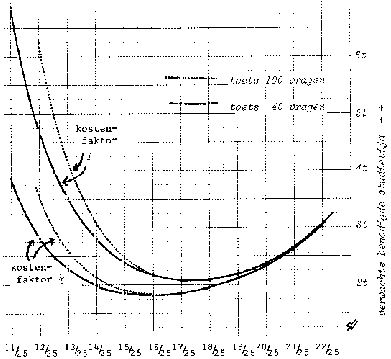
studiestrategie (aantal goed uit 25)
FIGUUR 9.1. Verschuiving van de strategiecurve wanneer de kostenfactor voor herkansingen van 0,5 opgehoogd wordt tot 1. Voor de toets van 40 vragen is de zak slaag grens in dit voorbeeld 24, voor de toets van 100 vragen is de zakslaag grens 60.
Zou de student voor herkansingen tijdens het 2e studiejaar de kostenfactor 1 nemen, en voor de overige de kostenfactor 0,5 , dan komt de strategiecurve tussen de beide curven in de figuur te liggen.
Dit heeft veel weg van het in de vorige paragraaf geschetste geval, het verschil is echter dat niet eerder aan de vervolgstudie begonnen mag worden of het propedeutisch examen moet ook volledig behaald zijn. Door deze regeling wordt het aantal toegestane herkansingen in theorie onbeperkt. De praktijk is echter dat het nog moeten herkansen van één enkel vak bijzonder vervelende gevolgen voor de student heeft wanneer hij daardoor nog niet aan het 2e jaars programma zou mogen beginnen. Kan hij zijn wachttijd niet op produktieve wijze gebruiken, dan moet de kostenfactor voor deze late herkansingen behoorlijk hoog gesteld worden. Dat betekent dat hogere strategieën gekozen moeten worden (ook al zijn de minimum eisen om een voldoende te krijgen lang niet zo hoog).
Deze regeling is niet zo ongunstig als een beperkt aantal herkansingsgelegenheden per studieonderdeel en gefixeerde examendatum, maar komt daar toch al dicht in de buurt.
Zou een enkele onvoldoende toegestaan worden, dan wordt de situatie voor de student veel beter: de laatste herkansing hoeft hij dan immers niet meer af te leggen, waardoor hij een stuk studievertraging ontloopt. Het is dan wel zaak om die toegestane onvoldoende dan ook in petto te houden voor laatst af te leggen toets(en). De student zal zo mogelijk zijn in een vroeg stadium behaalde onvoldoende in de herkansing tot een voldoende proberen om te zetten.
Bij deze regeling is het aantal herkansingsgelegenheden per studieonderdeel redelijk groot. Eventueel kan en mag de student deze ook alle benutten, zolang zijn totaal aantal herkansingen een aangegeven maximum niet overschrijdt. De student zou, in een extreem geval, bijvoorbeeld alle studieonderdelen behalve één direkt voldoende kunnen maken, en voor dat ene onvoldoende vak nog vier herkansingen gebruiken om het voldoende te scoren.
Wanneer het aantal studieonderdelen waarover een toets afgelegd moet worden klein is, is het doenlijk de mogelijkheden die deze regeling biedt te onderzoeken. Veronderstel dat er 5 studieonderdelen zijn" en er zijn in totaal 5 herkansingen toegestaan waarbij de student vrij is in de manier waarop herkansingen over studieonderdelen verdeeld worden. Om met een eenvoudig voorbeeld te kunnen beginnen veronderstel ik ook dat alle studieonderdelen toetsen met even groot aantal vragen gebruiken, waarbij bovendien de zak-slaag grens voor alle toetsen dezelfde is.
Als r het risico is om voor een toets te zakken wanneer een bepaalde strategie, zeg de strategie 18/25, voor alle toetsingen gebruikt wordt, is het RISICO om niet binnen het toegestane aantal herkansingen voor het examen te slagen gelijk aan de som van deze termen:
Deze termen zien er afschrikwekkend uit, maar blijken erg klein te zijn. Reken ik dit uit voor een paar uiteenlopende waarden van r dan zijn de resultaten
r = 0,1 RISICO = 0,00015
r = 0,2 RISICO = 0,0064
r = 0,3 RISICO = 0,047
Deze resultaten spreken duidelijke taal. De student die een strategie kiest met niet al te hoog risico zal de laatste herkansingsgelegenheid vrijwel zeker niet nodig hebben. Wie strategieën kiest met wat hoger risico zou zo'n laatste herkansingsgelegenheid (de 5e in dit voorbeeld) wel eens nodig kunnen hebben, en staat dan voor de vervelende situatie dat het RISICO om voor het examen te zakken gelijk is aan het risico om voor die laatste herkansing een onvoldoende te boeken. Zo hard mogelijk werken, is dan het devies.
Voor de volledigheid geef ik nog de algemene formule om het RISICO te berekenen wanneer het risico voor iedere afzonderlijke toetsgelegenheid bekend is (en voor alle gelegenheden gelijk gehouden wordt)
(1) RISICO = r h+1 {1 + ( h+1) (1-r) + [(h+2)!/(h! 2!)](1-r)2 + [(h+3)!/(h! 3!)](1-r)3 + ................... + [(h+n 1)!/(h! (n-1)!)] (1-r)n-1 }
waarbij h het aantal (nog vrije) herkansingen
n = het aantal studieonderdelen waarvoor nog een voldoende behaald moet worden
5! = 5 . 4 . 3 . 2 . 1 = 120
n! = n × (n-1) × (n-2) × ........... × 3 × 2 × 1
! spreek uit: faculteit, dus bijv. 'vijf faculteit' voor 5!
Wanneer één toets is afgelegd, en het resultaat daarvan is bekend gemaakt, verandert de situatie. Dan moet ook de berekening daaraan aangepast worden.
Werd de eerste toets voldoende gemaakt, dan is de examensituatie voor de student gunstiger geworden, er zijn dan, in dit voorbeeld, nog steeds vijf herkansingsgelegenheden beschikbaar, terwijl er nu nog maar vier studieonderdelen gedaan moeten worden. In formule (1) zou h gelijk blijven aan 5, en n zou verminderen tot 4.
Werd daarentegen een onvoldoende gehaald, dan is de situatie daarmee ongunstiger geworden, omdat voor de nog steeds vijf te behalen onvoldoendes nog maar 9 toetsgelegenheden beschikbaar zijn. Een herkansing moet nu gebruikt worden voor het inhalen van de al behaalde onvoldoende, er blijven dan nog vier vrije herkansingen over voor nog steeds vijf studieonderdelen. In formule (1) vermindert h tot 4, en blijft n gelijk aan 5.
De student die door het behalen van een voldoende in een gunstiger situatie terecht komt, zou daarvan gebruik kunnen maken door een wat lagere studiestrategie te kiezen voor de nog resterende studieonderdelen (wanneer een lagere strategie meer optimaal zou zijn).
De student die een onvoldoende heeft behaald, moet overwegen of voor volgende toetsgelegenheden door hem een hogere strategie gekozen moet worden om zijn RISICO aanvaardbaar te houden. De nodige berekeningen zijn snel uit te voeren op basis van formule (1).
Met het overgaan op een hogere strategie kan de student soms ook wel even wachten. Dat hangt ervan af of voor hem nog een reële strategie beschikbaar is (om het RISICO aanvaardbaar te houden) wanneer ook de volgende toetsgelegenheid onvoldoende uit zou vallen. De lezer kan hierin een variant op de wisselstrategie onder CEx herkennen.
Omdat de situatie waarin de student op de laatste herkansingsgelegenheid is aangewezen om te kunnen slagen zo buitengewoon onaantrekkelijk is, is het van belang de kans te kunnen berekenen dat dit inderdaad zal gebeuren, gegeven de strategie die voor iedere toetsgelegenheid gevolgd zal worden. Ik zal de berekening illustreren die antwoord geeft op de vraag naar de kans dat de student in twee nog resterende toetsgelegenheden één voldoende nog moet zien binnen te halen.
Dan heeft hij in de voorgaande 8 gelegenheden 4 voldoendes gehaald, en de kans daarop is:
r4 (1-r)4 8! / ( 4! × 4! ).
Daar komt uit, voor respectievelijk r = 0,1, 0,2, 0,3: 0,0046, 0,046, en 0,136.
De algemene formule voor de kans in twee resterende toetsgelegenheden nog één voldoende te moeten behalen is
(2) r h-1 (1-r) n-1 (h+n-2)! / {(h-1)! × (n-1)! }.
Voor de betekenis van de symbolen, zie formule (1).
Dan blijf ik nog zitten met het meer met de werkelijkheid overeenstemmende geval waarin toetsen voor verschillende studieonderdelen ook uit verschillend aantal vragen bestaan, andere zak slaag grenzen kennen. Dan kunnen dezelfde berekeningen gemaakt worden wanneer de student voor ieder studieonderdeel zijn strategie z(5 kiest dat deze telkens in een gelijk risico resulteert. De hierboven gegeven formules zijn immers alleen afhankelijk van dat risico.
Er zijn propedeuse regelingen waarin per studieonderdeel twee toetsgelegenheden zijn (maar één herkansing per studieonderdeel toegestaan wordt). Daaraan vallen de problemen van het beperkt zijn van het aantal herkansingen goed te illustreren.
Doorgaans zal een meerderheid van de studenten één of meer herkansingen moeten benutten om voor het examen te slagen. De dramatiek daarvan is dat zakken voor zo'n herkansing automatisch betekent dat je voor het examen in zijn geheel bent gezakt. Dit geldt voor de student die maar één onvoldoende hoeft in te halen!.
Studenten die meerdere herkansingen moeten afleggen, onder de voorwaarde dat per studieonderdeel maar één herkansing is toegestaan, hebben rekening te houden met het volgende verband tussen het RISICO om voor het examen te zakken, en het risico per toetsgelegenheid om een onvoldoende te krijgen:
(3) RISICO = 1 - (1 - risico) h
waarbij h het aantal af te leggen herkansingen is.
Omdat tegen deze tijd de student er al een jaar hard tegenaan is gegaan, zal hij maar een heel klein RISICO willen lopen tegen de finish nog voor het examen te zakken. Veronderstel dat een RISICO van 0,01 aanvaardbaar zou zijn, dan mag hij, als hij nog 2 herkansingen af te leggen heeft, voor iedere gelegenheid een risico lopen volgens formule (4) te berekenen, van 0,005.
(4) risico = 1 - ( 1 - RISICO) 1/h
Voor 3 herkansingen kun je met risico 0,003 het RISICO op 0,01 houden.
Doorgaans zullen bij dit soort kleine risico's nogal hoge strategieën behoren, die vaak ook niet bereikbaar zijn voor de student. Dat resulteert in de stressvolle situatie waarin er voor de student weinig anders op zit dan zo hard mogelijk te werken, in de wetenschap dat het niet genoeg zal zijn.
De stille veronderstelling bij het bovenstaande is dat de risico's telkens gelijk gehouden worden, zo nodig door er de geschikte strategie voor te kiezen (wanneer toetsen voor verschillende studieonderdelen uiteenlopen in aantal vragen, en zak slaag grens).
Sommige examenregelingen zijn ronduit schandelijk, zoals de variant waarbij voor herkansingen de zak slaag grens hoger gesteld wordt met het schertsargument dat zo voorkomen zou kunnen worden dat studenten met een ware beheersing die onvoldoende is, op den duur door geluk zouden kunnen slagen. Gaat het om een propedeuseregeling, dan zal het aantal herkansingen meestal ook strikt beperkt zijn. Dat heeft tot resultaat dat studenten niet alleen om hun RISICO aanvaardbaar te houden al de grootst mogelijke moeite met herkansingen zullen hebben, maar dat die moeite nog eens verdubbeld zou moeten worden om rekening houdend met de verhoogde cesuur het RISICO aanvaardbaar te houden. Een mijns inziens volstrekt onaanvaardbare regeling, waarvoor de beste strategie lijkt te zijn er tegen te protesteren.
De student die onder de volledig conjunctieve regeling met beperkte herkansing per vak maar één onvoldoende behaalt, kan en zal van de nu gegeven uitzonderingsmogelijkheid gebruik maken door deze onvoldoende niet in te halen.
De student die in eerste instantie meerdere onvoldoendes behaalde, kan van de geboden uitzonderingsmogelijkheid gebruik maken door de laatste van de herkansingen, gegeven dat hij de overige voldoende maakte, niet af te leggen. Maakte hij al een herkansing onvoldoende, en is meer dan één herkansing per studieonderdeel niet toegestaan, dan zal hij er voor de nog resterende herkansing(en) bijzonder hard tegenaan moeten om zijn RISICO zo klein mogelijk, zij het ook niet helemaal aanvaardbaar te houden.
De vraag die ik nu wil beantwoorden is hoe het RISICO voor het examen te zakken afhangt van het risico per toetsgelegenheid om daarvoor een onvoldoende te boeken. Ik neem weer het geval van 1 herkansingsmogelijkheid.
De kans om voor een studieonderdeel beide toetsgelegenheden onvoldoende te maken is het Risico, waarbij ik veronderstel dat de student dat Risico per studieonderdeel gelijk houdt (door een geschikte strategie keuze). R = Risico. De slaagkans is dan voor ieder studieonderdeel 1-R.
De student kan slagen voor het examen door alle onderdelen voldoende te maken. Veronderstel dat er 5 studieonderdelen zijn, dan is de kans daarop gelijk aan (1-R)5.
De uitzonderingsmogelijkheid betekent dat één studieonderdeel onvoldoende mag zijn. Wanneer dat het eerste studieonderdeel is, is de kans daarop R(1-R)4. Maar er zijn nog vier andere mogelijkheden, want die onvoldoende zou ook het 2e, 3e, 4e of 5e onderdeel kunnen zijn. De kans om met één onvoldoende te slagen is dan ook 5R(1-R)4.
Totale slaagkans is onder deze uitzonderingsregel
(1-R)5 + 5R(1-R)4 = 1 - RISICO.
En dit is dan de slaagkans zoals die vooraf berekend wordt, wanneer nog geen enkele toets is afgelegd. Is eenmaal een toets afgelegd, en het resultaat daarvan bekend, dan wordt voor de nieuwe situatie die nu ontstaan is opnieuw, nadat strategieën eventueel bijgesteld zijn, de slaagkans berekend. Mocht de slaagkans voor het examen te klein zijn, het RISICO te groot, dan moet zo mogelijk door de keuze van hogere strategieën aan die slaagkans gesleuteld worden.
Een wisselstrategie is voor dit soort examenregeling echter niet aan te raden, omdat het onverstandig is te gaan speculeren met die ene gelegenheid om een onvoldoende te laten staan.
Deze regeling is een versoepeling, maar laat alle nadelen van de regeling met beperkt aantal herkansingen per studieonderdeel verder intakt. De studiestrategie voor de student blijft moeilijk.
De student kan van deze regeling natuurlijk ook gebruik maken door één studieonderdeel in het geheel niet te doen (althans niet voor te bereiden). Dat kan extra riskant zijn, wanneer hij deze nul strategie kiest al voordat hij het vereiste aantal voldoendes heeft binnen gehaald.
Om te vermijden dat studenten van de mogelijkheid om één onvoldoende te hebben misbruik maken door één vak volstrekt te verwaarlozen, worden in sommige regelingen onvoldoendes (in beperkt aantal) toegestaan wanneer daarbij aan bepaalde voorwaarden is voldaan.
Bekend is natuurlijk het soort voorwaarde dat zo'n onvoldoende dan tenminste een vijf of een vier moet zijn. Wanneer de docent aangeeft welk aantal vragen goed beantwoord moet zijn om tenminste een vijf of een vier te krijgen, kan op de langzamerhand bekende wijze voor iedere toetssituatie en strategie de kans op tenminste leen vijf of een vier berekend worden (of uit de tabel in bijlage F afgelezen worden).
De voorwaarden plegen ook nogal eens compensatorisch gesteld te worden. Een voorbeeld daarvan is de regeling waarin een vijf wel toegelaten is mits daar voor één van de andere studieonderdelen tenminste een zeven tegenover staat. Ook hier weer: wanneer bekend is hoeveel vragen tenminste goed beantwoord moeten worden om een zeven te krijgen, kan de kans op zo'n zeven bepaald worden. De slaagkans voor het examen valt dan met enige moeite te berekenen, onder toepassing van de basisregels van de statistiek. Alle mogelijke combinaties, met hun waarschijnlijkheden, moeten daarvoor onderzocht worden. De situatie wordt er daarmee voor de student niet doorzichtiger op, en ik vind hier dan ook het punt wel gekomen waarop de student er voor het vaststellen van zijn studiestrategie beter maar vanuit kan gaan dat hij voor ieder studieonderdeel gewoon een voldoende moet zien te behalen. Wanneer daar, met het vorderen van de studie en het aantal bekende toetsresultaten, reden toe is, kan hij later natuurlijk zijn strategie daarbij aanpassen (door hogere, dan wel lagere strategieën te kiezen dan waar hij aanvankelijk op mocht rekenen).
Een opmerking over de aard van dit soort uitzonderingsbepalingen wil ik hier toch wel maken, hoewel ik daar op een andere plaats in deze cursus ook op in ben gegaan. En dat is dat uitzonderingen op de regel dat alles voldoende moet zijn er heel humaan uitzien, en ongetwijfeld goed bedoeld zijn. Het probleem is echter dat men ze schijnt te zien als een maatregel achteraf, waarmee schrijnende gevallen geholpen worden. Daarbij wordt er geheel aan voorbij gegaan dat dit soort maatregel nauwelijks iets kan verhelpen aan de problemen waar de student voor staat bij de voorbereiding op de tentamens. Deze uitzonderingsmaatregelen nemen van het stress-karakter van de examenregeling waarbij het aantal herkansingen per vak beperkt is, nauwelijks iets weg.
Wanneer het propedeuse examen uit maar een klein aantal te toetsen studieonderdelen bestaat, kan harde toepassing van de compensatorische regeling zonder uitlaatkleppen in de vorm van toegestane herkansingen, tot problemen voor de studenten leiden. Dat is ook goed in te voelen, wanneer we bedenken dat in het uiterste geval, wanneer de propedeuse uit maar één toets zou bestaan, er geen verschil meer kan zijn tussen een compensatorische regeling en een conjunctieve regeling (wanneer ook voor de conjunctieve regeling geen herkansing toegestaan zou zijn, of wanneer voor beide regelingen een gelijk aantal herkansingen toegestaan zou zijn).
Laat ik eerst eens in tabelvorm een voorbeeld geven, voor een programma bestaande uit 5 studieonderdelen, met verschillende toetslengten, en uiteenlopende gewichten.
___________________________________________________________
aantal gewicht verwachte
toets strategie vragen w(i) score s(i)² w(i)² w(i)²s(i)²
w(i)m(i)
-----------------------------------------------------------
1 18/25 50 2 72 30 4 120
2 20/25 50 1 40 30 1 30
3 18/25 60 2 86 40 4 160
4 16/25 40 3 77 20 9 180
5 16/25 100 1 64 100 1 100
____ + ____ +
m = 339 s² = 590
___________________________________________________________
VOORBEELD 9.1. Voorbereidende berekeningen voor het RISICO.
Nog even ter opfrissing: de waarden si2 zijn af te lezen uit tabel 8.1.
Met gebruik van tabel 8.2 is bij gegeven EIS het RISICO te berekenen (wanneer de studiestrategieën gevolgd worden op grond waarvan de berekeningen in het voorbeeld gemaakt zijn).
Als EIS = 300 berekenen we eerst (339 - 300) / √ 590 = 1,61. Uit de tabel is af te lezen dat bij deze uitkomst een RISICO van 0,06 hoort.
Dat is nogal een fors RISICO, maar hoeft ook voor de student die dit RISICO eigenlijk iets te hoog vindt, nog niet direkt te leiden tot de keuze van een hogere studiestrategie voor de eerste af te leggen toets, zolang een wisselstrategie beschikbaar is (d.w.z.: voor latere studieonderdelen eventueel een hogere studiestrategie beschikbaar is).
Kijk ik even speciaal naar de laatste af te leggen toets (laten we zeggen dat dat toets 5 uit mijn voorbeeld is), dan kan ik van de tabel in bijlage F gebruik maken om te kijken hoeveel punten voor de eerste vier studieonderdelen dan behaald moeten zijn om met een strategie 16/25 voor het laatste studieonderdeel een aanvaardbaar RISICO over te houden. Ik zoek dan bijvoorbeeld hoeveel punten ik met een waarschijnlijkheid van, zeg 0,025, voor de laatste toets zal behalen: 42 punten Voor de eerste vier vakken moet ik dan tenminste 300 - 42 = 258 punten al behaald hebben. Gezien de resultaten in voorbeeld 9.1 zit dat er wel in, maar het is ondertussen toch niet onwaarschijnlijk dat ik daar beneden uitkom,
Bij het overwegen van CEx regelingen voor de propedeuse, stuit je onvermijdelijk op het eigenaardige karakter van dit examen. Hoewel het meestal plaats vindt over het eerste studiejaar, heeft het sterk het karakter van een toelatingsexamen. Daarmee verschilt het wezenlijk van het doctoraalexamen, en ook van het kandidaatsexamen.
Mag je van studenten die zich voorbereiden op kandidaats of doctoraal stellen dat zij, door het feit dat zij tot deze examens toegelaten zijn, binnen redelijke grenzen mogen rekenen op alle steun en begeleiding die zij nodig mochten hebben om te kunnen slagen, dan is het voor studenten in de propedeuse veeleer het geval dat zij nog moeten tonen die ondersteuning straks waard te zijn. Ook in al die gevallen (vandaag de dag nog de regel) dat deze verhoudingen niet in studiecontracten zijn vastgelegd, heeft de onderwijspraktijk veelal wel het beschreven karakter.
De propedeuse heeft, hoe je het ook bekijkt, een sterk selectief karakter, terwijl examens onderweg, of aan het eind van de studie, dat niet hebben. Voor een doctoraalexamen kun je examenregelingen hanteren die het accent sterker leggen op de doctoraalbul als dossierdiploma. Bij HEx-regelingen is de idee dat het dosssier voor iedereen in principe gelijk zou moeten zijn, terwijl bij CEx-regelingen de fictie van die gelijkheid erkend wordt en ongelijke studieprestaties in het dossier tot uiting gebracht worden.
Nu is het niet eenvoudig om je het propedeutisch examen voor te stellen als bekroond met dossierdiploma's, het gaat immers slechts om het al dan niet toelaten, zonder verdere kwalificaties, tot de verdere studie. Het is dus te verwachten dat er weinig of geen civiel effect verbonden is aan prestaties die hoger liggen dan hetgeen vereist is om voor die propedeuse geslaagd te heten. Dat zal problemen op kunnen leveren bij pogingen om voor de propedeuse onverwaterde CEx-regelingen toe te passen. Studenten zijn geen heiligen, en zullen in de regel tevreden zijn met een puntenaantal dat hen ruim over de streep helpt.
Het is dan ook te verwachten dat bij CEx-regelingen voor de propedeuse ook goede studenten door onjuiste voorlichting, het helemaal ontbreken van voorlichting, of gewoon door het verkeerd interpreteren van hun slaagkansen, eigenlijk te grote RISICO's nemen om voor het examen te zakken. Je mag verwachten, gezien het onderzoek van Tversky (1974) dat ook in par. 6.1 besproken werd, dat studenten de neiging hebben om na een aantal goede studieprestaties behaald te hebben de kans op slechte prestaties voor komende studieonderdelen sterk te onderschatten (ankereffect van hoge cijfers: daardoor wordt de kans op eveneens hoge cijfers voor komende toetsen overschat).
Het selectieve karakter van de propedeuse, ook al zou het slechts om zelfselectie gaan (hoewel een dergelijke term meestal eufemistisch gebruikt wordt.), betekent dat noodzakelijkerwijs nogal wat studenten ondanks veel pijn en moeite niet aan de exameneisen zullen kunnen voldoen, ook niet aan de EIS zoals die bij CEx regelingen gesteld zou worden. Voor veel studenten is een strategie gericht op het aanvaardbaar houden van het RISICO om niet aan EIS te voldoen, dan ook in feite niet mogelijk. Voor hen gaat het er om dat bijtijds te signaleren, en daar de beslissing al of niet verder te studeren op te baseren.
Heel anders dan bij een doctoraalexamen, mag je dus van CEx-regelingen in de propedeuse verwachten dat veel studenten in de buurt van EIS zullen scoren, en velen ook daar beneden uit zullen komen (wanneer zij al niet eerder met de studie gestopt zouden zijn).
De faculteit die uitgaat van de gedachte dat de student in de propedeuse moet aantonen de studie aan te kunnen, zal als consequentie daarvan streven naar een examenregeling waarin de student ook zo goed mogelijk in de gelegenheid gesteld wordt om dat te laten zien (aan zichzelf, dan wel aan de faculteit). Een regeling die daar wel eens goed bij zou kunnen passen, is een CEx-regeling waarbij herkansingen op heel korte termijn gegeven worden. Te denken valt daarbij aan toetsen waarvan de uitslag binnen enkele dagen bekend is, en de herkansing dan over laten we zeggen een week plaats vindt. Dat geeft de student de mogelijkheid om zijn pech op de eerste toets weg te werken. Belangrijker is dat het de student in de gelegenheid stelt een onjuiste tentamenvoorbereiding nog te corrigeren in de week studietijd die hem in tweede instantie nog gegeven wordt. De eerste toets fungeert dan als een proeftoets, zou je kunnen zeggen. Een dergelijke regeling voor de propedeuse is aantrekkelijk, omdat juist in deze studiefase de student zich met enige moeite op de studie en de eisen die de studie hem stelt zal moeten oriënteren. Schat hij de eisen voor een tentamen verkeerd in, dan is een gelegenheid om daar correcties op aan te brengen, ook nadat de eerste toets al is afgelegd, misschien wenselijk. Merk op dat aan een dergelijke snelle herkansing niet het nadeel verbonden is dat eerder al eens bestudeerde stof gedeeltelijk weer opnieuw bestudeerd moet worden: de student kan verder gaan met studeren op het punt waar hij een paar dagen tevoren gebleven was.
Zoals ook bij de varianten in de volgende paragrafen het geval is, zijn hier verschillende mogelijkheden voor de puntentelling:
De student moet snel beslissen óf hij aan de herkansing deel zal nemen, of niet. Daarbij zal de aard van de regeling (a, b, of c hierboven) van invloed zijn. Om zijn beslissing een reële basis te geven, kan de student enkele berekeningen maken over RISICO's die uit wel/niet herkansen, bij enkele verschillende strategie mogelijkheden volgen. Ik zal geen voorbeeld geven, omdat de berekeningen afhankelijk zullen zijn van de gedetailleerde vorm die de examenregeling heeft, en overigens op dezelfde wijze uit te voeren zijn als eerder voor CEx-regelingen gedemonstreerd (hoofdstuk 8).
(technische kanttekening: de student mag zijn toetsresultaat, dat nu bekend is, opvatten als een proeftoetsresultaat, een goede schatting van de eigen beheersing. Dat moet met enige voorzichtigheid gebeuren, omdat er alleen reden is om herkansing te overwegen bij tegenvallende toetsresultaten. zodat de verwachting is dat zo'n toetsresultaat een te lage schatting van de ware beheersing zal opleveren. Een techniek om daarvoor te corrigeren, waarvan ik hier de details niet zal geven (zie bijv. Novick & Jackson 1974 daarvoor), is het toetsresultaat met de verwachting die de student had van zijn ware beheersing te combineren.)
Het is duidelijk dat het toegestaan zijn van herkansingen effect heeft op het RISICO dat volgt uit bepaalde strategie keuzen. Ik ben bang dat het een erg vervelende oefening is om RISICO's te berekenen, rekening houdend met deze herkansingsmogelijkheden. Ik wil dan ook slechts als algemene aanwijzing meegeven dat het bij deze herkansingsmogelijkheden past om in berekeningen waarin herkansingen niet voorkomen, een veel hoger RISICO als aanvaardbaar te hanteren.
Dit is een regeling waarin aan het eind van het studiejaar, of aan het begin van het tweede jaar, gelegenheid gegeven wordt om kort na elkaar herkansingen voor één of meer vakken af te leggen.
Ook hier heeft de student de vrije keuze welke, en hoeveel vakken hij zal herkansen. Om daarin een goede beslissing te maken, kan de student voor enkele voor de hand liggende mogelijkheden berekeningen van het RISICO maken, op de standaard manier. De student heeft daarbij de al behaalde studieresultaten als gegeven, en moet nagaan of hij door bepaalde vakken te herkansen, het ontbrekende aantal punten met een voor hem aanvaardbaar RISICO zal kunnen bereiken.
Ook hier geldt weer dat de regeling voor de puntentelling van de herkansing één van de vormen a, b, of c besproken in de vorige paragraaf, aan kan nemen. Daarmee is natuurlijk in de berekeningen rekening te houden.
Het open staan van deze herkansingmogelijkheid, betekent dat het RISICO zoals dat aan het begin van de studie berekend zou worden uitgaande van het niet beschikbaar zijn van herkansingen, nu aanzienlijk hoger gekozen mag worden. Maar let er op: wanneer de student zich moet gaan voorbereiden op de herkansingen moet hij daarbij met een regel aanvaardbaar RISICO rekenen! De reden om herkansingsmogelijkheden niet expliciet in de RISICO berekeningen aan het begin van de studie te betrekken is ook nu weer dat het aantal mogelijkheden dat doorgerekend zou moeten worden eenvoudig te groot is. Een grove schatting in de vorm van de verhoging van RISICO die je zou kunnen nemen bij hanteren van de standaardberekening uitgaande van geen herkansingen ligt dan meer voor de hand.
Bij de keuze van te herkansen vakken neemt de student allereerst die studieonderdelen waarvan hij aan mag nemen op de toets in eerste instantie door pech een te laag resultaat geboekt te hebben. Verder moet hij, zoals altijd bij CEx-regelingen, letten op de weging van de vakken, en de lengte van de toetsen. Daarnaast kan hij overwegen welke verdeling van zijn studietijd, rekening houdend met de moeilijkheid van de vakken voor hem persoonlijk, het meest economisch is in termen van te verwachten punten opbrengst.
Omdat herkansingen in tijd dicht bijeen geplaatst zijn, zal er geen gelegenheid zijn om tussentijds van studiestrategie te veranderen: er is eenvoudig geen of nauwelijks studietijd meer beschikbaar tussen deze herkansingen door. Bovendien zal de uitslag van afzonderlijke herkansingen vaak niet snel genoeg beschikbaar zijn om op basis van die gegevens tot strategie bijstelling te komen. Dit heeft geen gevolgen voor de aard van de RISICO berekening, omdat in de standaard RISICO berekening voor CEx geen rekening gehouden wordt met informatie die tussentijds beschikbaar komt. (wanneer tussentijdse studieresultaten bekend worden in het normale studieprogramma, moeten nieuwe berekeningen uitgevoerd worden om na te gaan welke gevolgen die resultaten hebben voor de strategie voor de overige nog af te leggen toetsen).
Hier geen snelle herkansing na een paar dagen, maar een gewone herkansing zoals die doorgaans na enkele maanden pas gedaan kan worden. Nadeel voor de student: voor deze herkansing moet hij tijd uit trekken om de stof weer op te halen. Voordeel: hij kan nu even aanzien welke studieresultaten voor ándere vakken behaald worden, zodat zijn beslissing om al dan niet te herkansen daarvan afhankelijk kan zijn.
Overigens gelden hier weer alle opmerkingen, die ik ook in de vorige paragrafen al maakte: over specifieke regelingen voor de punten telling (varianten a), b), en cÈ, over de berekening (niet proberen daarin expliciet de herkansingsmogelijkheden te verwerken, maar het RISICO een stuk groter nemen).
Strategiekeuze is nog steeds een zaak van RISICO-beheersing, en niet zozeer van kosten-minimalisering (zo kort mogelijke studietijd).
Kennelijk in de overweging dat het studenten niet toegestaan moet worden voor een enkel vak helemaal niets te doen, zijn er regelingen die in principe compensatorisch zijn. maar waar voor afzonderlijke studieonderdelen minimum prestaties vereist zijn. Ik neem aan dat het compensatorisch principe serieus is, en dat de minima aanzienlijk beneden de gemiddeld vereiste studieprestatie liggen (anders is er veeleer sprake van een recht toe recht aan conjunctieve regeling met een beetje compensatorische versiering).
Wie minumum eisen per studieonderdeel stelt, ontkomt er moeilijk aan om ook herkansingsgelegenheden te geven. Ik neem aan dat er inderdaad een herkansingsregeling (in één of andere vorm, de varianten zijn de lezer ondertussen wel bekend) bestaat.
Voor de student levert deze regeling geen bijzonderheden op: hij kan gewoon te werk gaan alsof het om een compensatorische regeling met-herkansingen gaat. Heeft de student voldoende punten verzameld, maar moet hij nog één of twee toetsen afleggen waarvoor minimum eisen gehaald moeten worden, dan gaat hij voor dit staartje van het examenprogramma te werk als was het een volledig conjunctieve regeling. Je mag aannemen dat studenten die al vroegtijdig aan de compensatorische verplichting voldaan hebben, met deze laatste conjunctieve verplichting geen moeite zullen hebben, mits zij hun RISICO niet onderschatten!
Overigens lijkt deze examenregeling inconsistent van karakter: de compensatorische EIS zal immers zo gesteld zijn, dat studenten die daar op welke wijze dan ook aan voldaan hebben, daarmee bewezen hebben dat zij het vervolg van de studie aan zullen kunnen. Welnu, dan is het een beetje kinderachtig om voor vakken waarover zij nog een toets af moeten leggen nog een keer minimumeisen te gaan stellen.
Voor de student die een efficiënte studiestrategie wil volgen, is het van belang dat hij tenminste enige tijd voor de toetsafname geïnformeerd is over de kansverdeling voor zijn toetsscore. Met name gaat het dan om de kans dat hij een score behaalt die boven de (tevoren bekend gemaakte) aftestgrens ligt, of om de kans dat hij tenminste een bepaalde score X = x behaalt; in welke kans hij geïnteresseerd is hangt van de gehanteerde examenregeling af.
Aangenomen wordt dat over de te toetsen leerstof een (denkbare) verzameling van toetsvragen bestaat, waaruit vragen random getrokken zijn voor opname in de af te nemen toets. Dat random trekken mag hier zo opgevat worden dat door de betreffende student de toets opgevat kan worden als een random getrokken steekproef, d.w.z. de student heeft geen enkele voorkennis over de precieze vragen die in de toets voor zullen komen.
De ware beheersing van deze student over de leerstof wordt gedefinieerd als de proportie p van de vragen in de verzameling die hij goed zou beantwoorden wanneer hij ze voorgelegd zou krijgen.
De kansverdeling voor de toetsscore, gegeven de ware beheersing p, is de binomiaalverdeling
(1)
f(x|p) = (n boven x) p x (1 - p) n-x
n = aantal toetsvragen
x = 0, 1, 2, ....... , n
0 ≤ p ≤ 1.
Het is echter niet de verdeling f(x|p), maar f(x) die we zoeken. Wanneer de verdeling f(p) gespecificeerd kan worden, is f(x) te vinden. De functie f(p) is de uitdrukking van de idee die de student heeft over zijn ware beheersing: wat hij denkt dat de meest waarschijnlijke waarde voor zijn p is, en hoe ver hij denkt dat hij er met die schatting wel eens naast zou kunnen zitten. In de Bayesiaanse statistiek zou f(p) een prior distribution genoemd worden, en hoewel het hier niet gaat om een stukje toegepaste Bayesiaanse statistiek kan wel gebruik gemaakt worden van de methoden voor het specificeren van priors. Daarvoor verwijs ik naar Novick & Jackson (1974); de daar besproken interactieve programmatuur (CADA) zal op de meeste rekencentra in ons land beschikbaar zijn. Wordt inderdaad de weg van specificatie van een prior gekozen, dan moet de bètaverdeling daarvoor gekozen worden, omdat dit de natural conjugate is voor de verdeling f(x | p).
Wanneer kort voor het eigenlijke tentamen een proeftoets wordt gegeven, die in alle relevante opzichten gelijkwaardig is aan de definitieve toets, kan de subjectiviteit van het specificeren van een prior met behulp van CADA of de nomogrammen gegeven in Novick & Jackson (1974) vermeden worden: kies dan voor f(p) de bètaverdeling met parameter a gelijk aan het aantal vragen goed + 1 op de proeftoets, en b het aantal vragen fout + 1, waarbij n = aantal vragen in de proeftoets.
Deze parameters zijn een voortdurende bron van verwarring, omdat de notatie van de bèta-verdeling op historische gronden berust, en zodoende ligt de natuurlijke interpretatie niet in lijn met de notatie. Als de formules opgesteld worden zoals hier formules (2) en (3), dan is a-1 = aantal goed, niet a = aantal goed zoals in 1978 foutief geschreven op p. 77; idem b-1 ipv. b. Deze fout heeft evenwel, voorzover ik al heb kunnen nagaan, niet doorgewerkt in latere formules of berekeningen in het 1978 boek. Zie voor de details spa_likelihood.htm, gebaseerd op Novick and Jackson (1974, p. 109).
(2) f(p) = B-1(a, b) p a-1 (1-p) b-1 , waar
B(a, b) = (a-1)! (b-1)! / (a+b-1)! a,b < 0.
(3) f(x, p) = f(x|p) f(p) = B-1(a, b) (n boven x) p a+x-1 (1-p) b+n-x-1
kan de marginale kansverdeling f(x) voor de toetsscore verkregen worden door f(x, p) te integreren over alle waarden van p:
(4) f(x) = ∫01 f(x, p) dp
= B-1(a, b) ( n boven x ) ∫01 p a+x-1 (1-p) b+n-x-1 dp.
De integraal in het uiterste rechterlid van (3) is gelijk aan de incomplete bèta
B(a+x, b+n-x) = ∫01 p a+x-1 (1-p) b+n-x-1 dp,
zodat
(5) f(x) =( n boven x ) B-1 (a, b) B(a+x, b+n-x).
De verdeling (5) staat in de literatuur onder uiteenlopende benamingen bekend, en onder uiteenlopende wiskundige schrijfwijzen. In het algemeen wordt (5) de negatief hypergeometrische verdeling genoemd. Bij Bosch (1963) heet het de Pólya verdeling, bij Johnson & Kotz (1977) de Pólya Eggenberger. Raiffa & Schlaifer (1961, blz. 237 e.v.) noemen het de bèta binomiaal verdeling. Omdat deze auteurs slecht of in het geheel niet naar elkaar verwijzen, vraagt het enig puzzelwerk om achter deze identiteiten te komen. Daarom in tabel 1 een vergelijkend overzicht van de notatie bij deze verschillende bronnen, en bij Lord & Novick (1968).
_________________________________________________________________
Raiffa and Bosch Johnson Lord and
Schlaifer and Kotz Novick
-----------------------------------------------------------------
toetsscore r x k x
toetslengte n n n n
bèta param. a r' r α a
bèta param. b n'- r' s β b+n-1
_________________________________________________________________
Tabel 1. Vergelijkende nomenclatuur.
Bij de alternatieve schrijfwijzen voor de verdeling (zie voor een goed overzicht daarvan Bosch, 1963), doet zich bovendien een hinderlijk inconsistente notatie voor, waarop men wel bedacht moet zijn:
De cumulatieve verdeling F(x) is eenvoudig, zij het ook moeizaam te berekenen. Omdat de negatief hypergeometrische verdeling drie parameters heeft is het niet doenlijk de cumulatieve verdeling uitgebreid te tabelleren, en zal men voor de eigen praktijk zélf de cumulatieve verdelingen die daar relevant zijn moeten opstellen. (Voor een aantal gangbare gevallen zijn de cumulatieve verdelingen gegeven in bij lage F).
Wil men de kans dat x tenminste gelijk aan een bepaalde waarde v zal zijn, waarbij v kan variëren van 0 tot n, dan kan men de berekening beginnen met f(x=n) te berekenen, vervolgens f(x=n-1), etcetera. Voorwaarde bij deze aanpak van de berekeningen is dat men een kalkulator gebruikt die een groot aantal decimalen in de berekening meeneemt.
(6) f(x=n) = (n boven x) B-1 (a, b) B (a+x, b+n-x) = (a+n 1)! (a+b 1)! /{(a+b+n 1)! (a 1)!}
(7) f(x=v-1) = { ((n+1)/(n-v+1)) - 1} (b+n-v) (a-v+1) f(x=v) + Σnx=v f(x).
Met behulp van (7) zijn, uitgaande van (6), alle termen van de verlangde cumulatieve verdeling te berekenen. Wie beschikt over een programeerbare kalkulator heeft het nog makkelijker. Een geschikt programma voor de Texas Instruments 58 of 59 is:
voorbereiding: bereken f(x=n) en STORE in R 01 en in R 02,
(n+l) STO 04, (b 1)STO 05, (n+a)STO 06, 0 STO 03.
(8) programma: LBL A OP 23 ((RCL 4 / RCL 3 1) x (RCL 5 + RCL 3)
(RCL 6 RCL 3)) PRD 2 RCL 2 SUM 1 RCL 1 R/S
berekening: intoetsen van A berekent telkens de volgende term van de cumulatieve verdeling, te beginnen met (omdat de eerste term f(x=n) al berekend is)
9) Σnx=n-1 f(x),, vervolgens Σnx=n-2 f(x), etcetera
Voor deze berekeningsmethoden is het wel noodzakelijk dat de parameters a en b gehele getallen groter dan 0 zijn. In de praktijk levert dat geen problemen op.
Raiffa & Schlaifer (1961) geven benaderingsformules voor de cumulatieve verdeling F(x): onder bepaalde voorwaarden is deze te benaderen door een cumulatieve binomiaalverdeling of een cumulatieve bètaverdeling (Raiffa & Schlaifer blz. 241).
Wanneer x<<n, a+x << max {n,a+b} beide gelden, is F(x) goed te benaderen door de cumulatieve binomiaal met parameters p=n/(n+a+b 1) en n=x+a 1 n<a+b 1 , of, voor het geval n≥a+b 1, door 1 min de cumulatieve binomiaal van a met parameters p=(a+b 1)/(n+a+b 1) en n=x+a 1.
Een meer volledige benadering zou volgens deze lijn gaan (zie ook Aitchison en Dunsmore ,1975, hoofdstuk 2):
Van Naerssen (1974, appendix) pdf geeft geen expliciete voorspellende kansverdeling, maar wel gemiddelde en variantie. Een vergelijking met de door mij gepresenteerde voorspellende verdeling leidt tot de volgende resultaten:
n1 = a + b = aantal vragen in de proeftoets.
n2 = aantal vragen in de toets
m = gemiddelde voorspellende verdeling
s2 = variantie ,, ,,
p = 1-q = ware beheersing = a (a+b)
negatief hypergeometrische voorspellende kansverdeling:
(11) m = n2a /(a+b)
(12) s2 = n2ab (n1+n2)/{n12 (n1+1)}
Van Naerssen's model (noot: De notatie bij Van Naerssen is afwijkend. Omdat Van Naerssen toetsscores omzet tot proportionele scores moeten zijn formules voor variantie met n22 vermenigvuldigd worden om varianties in termen van ruwe scores te krijgen.):
(13) m = n2a /(a+b)
(14) s2 = (n1+n2) pq = (n1+n2) ab / (a+b)2 = ab (n1+n2) / n12
In gevallen waarin n1+1 n2 komt Van Naerssen tot onderschatting (als n1+1 groter dan n2) respectievelijk overschatting (als n1+1 kleiner dan n2) van de nauwkeurigheid van de voorspelling. In de praktijk zal zich voornamelijk het laatste geval voordoen. Van Naerssen heeft dan ook een te optimistische kijk op de transparantie van het toetsgebeuren.
In het wetenschappelijk onderwijs is de stof voor een enkel tentamen meestal nogal heterogeen. Sommige delen van de stof zijn makkelijker dan andere, zonder noodzakelijk ook minder belangrijk te zijn. Vragen over de stof zijn ook te onderscheiden naar het niveau van complexiteit. Wanneer dan de ware beheersing van de stof nog steeds gedefininiëerd wordt over een dergelijke heterogene verzameling van (denkbare) vragen, is het op zijn plaats om de zin daarvan te onderzoeken.
Om te beginnen is er in principe natuurlijk niets op tegen om de verzameling van vragen op te splitsen in homogene deelverzamelingen, en bij het begrip ware beheersing ook de specif ikatie van de bijbehorende deelverzameling van vragen te geven. Een andere mogelijkheid is om de homogene deelverzamelingen in omvang aan elkaar te relateren, ook in de toets vragen uit de deelverzamelingen op te nemen in dezelfde verhouding, en dan te blijven spreken van één ware beheersing over deze gestratificeerde verzameling van vragen. Een variant op het laatste zou nog kunnen zijn dat aan bepaalde deelverzamelingen een groter gewicht wordt toegekend, dat ook in de scoring van de toetsvragen tot uitdrukking gebracht wordt (een soort compensatorische combinatie van deelscores op de toets).
Een en ander kreëert dan wel grotere rekenproblemen, en problemen van statistische aard. Zolang het gaat om de individuele student die een schatting moet maken van de toetsscore die hij mag verwachten, en die deze schatting gebruikt om zijn studiestrategie eventueel bij te sturen, zou overwogen kunnen worden om de toets niet streng te stratificeren, maar op probabilistische wijze vragen telkens uit de hele gestratificeerde verzameling te trekken (zie hoofdstuk 2), waardoor schattingstechnieken die in deze cursus gepresenteerd worden ook bruikbaar blijven voor toetsen die heterogene stof bestrijken.
Het laatste geldt ook waar we te maken hebben met vragen die weliswaar niet op heterogene onderwerpen betrekking hebben, maar die uiteenlopen in moeilijkheid. Zolang de toets door de student maar opgevat kan worden als een strikt toevallige keuze uit de beschikbare verzameling van vragen, zijn de hier te presenteren schattingstechnieken van toepassing.
Het moet natuurlijk ook niet te gek worden: wanneer men in één en hetzelfde tentamen eenvoudige kennisvragen in de vorm van meerkeuzevragen wil opnemen, én uitgebreide essayvragen die van de student een zeer eigen beantwoording vragen, is het toch wel verstandig om van twee gescheiden vraagverzamelingen te spreken, en twee soorten van stofbeheersing die in dit stukje onderwijs relevant zijn. Analyse van deze toets als bestond hij uit twee afzonderlijke deeltoetsen hoeft dan geen bijzondere extra problemen op te leveren.
De benaming tentamenmodel is ingevoerd door Van Naerssen (1970), voor modelmatige beschrijvingen van optimaal studeergedrag in de voorbereiding op tentamens. Dat is hetzelfde streven als in dit hoofdstuk studiestrategie onder HEx, en veel elementen uit Van Naerssen's tentamenmodellen (laatste versie: 1976), komen in het hier te ontwikkelen model terug.
aanname 1
om te slagen voor het examen moet de student voor ieder afzonderlijk studieonderdeel tenminste een voldoende behaald hebben.
aanname 2
het aantal toegestane herkansingen is onbeperkt.
aanname 3
de score behaald op de laatst afgelegde herkansingstoets is bepalend of voor dit studieonderdeel een voldoende behaald is of niet.
aanname 4
de student volgt een ongeveer optimale studiestrategie.
aanname 5
Als de bestede tijd, moeite, geld voor de eerste gelegenheid u is, is die voor iedere herkansing 0,5 u .
Aanname 3: het ligt niet helemaal voor de hand om eerder behaalde resultaten niet meer mee te laten tellen, of om geen rekening te houden met het aantal benodigde herkansingen. Toch is de regel in het algemeen konform deze aanname: het laatste resultaat telt.
Aanname 4: de student volgt een ongeveer optimale studïës trategie. Dat betekent dat hij de totale hoeveelheid tijd, moeite, en geld, nodig om voor een studieonderdeel te slagen, minimaliseert. Het bijvoegsel ongeveer verwijst naar studiestrategieën in de buurt van het wiskundig optimum, die weinig meer tijd etc. kosten.
Het feit dat eerder al een x aantal herkansingen voor een bepaald studieonderdeel werd afgelegd, is niet van invloed op de strategie voor de x+1 ste herkansing: omdat een onbeperkt aantal herkansingen is toegestaan, is de optimale strategie voor de x+1 ste herkansing gelijk aan de optimale strategie voor de voorgaande herkansing, en die optimale strategie is gelijk aan de optimale strategie voor de eerste toetsgelegenheid. Dat wil zeggen dat de bestudering van de stof telkens doorgaat totdat hetzelfde (geschatte) niveau van beheersing dat aan de optimale strategie beantwoordt, bereikt is.
Het tweede deel van aanname 5 kan dan zo geïnterpreteerd worden dat voor iedere herkansing half zo veel tijd, moeite etc. nodig is als voor de eerste toetsgelegenheid. In werkelijkheid mag je verwachten dat bij iedere volgende herkansing de voorbereidingstijd iets minder mag zijn, maar rekening houdend met andere vervelende gevolgen van het nog eens, en nog eens moeten herkansen (toenemende psychische druk, toenemende interferentie met andere studieverplichtingen, toenemend financieel risico), is het om te beginnen niet onredelijk om de totale hoeveelheid tijd, moeite, en geld nodig voor iedere herkansing constante nemen.
De keuze voor de faktor 0,5 is natuurlijk willekeurig, maar lijkt voor de meeste feitelijke situaties niet onredelijk. In het model zijn andere waarden makkelijk hiervoor te substitueren. Het is echter wél zo dat een forse waarde als 1 impliceert dat er nogal wat tijd verloopt tussen iedere toetsgelegenheid, m.a.w. dat herkansingen niet onmiddellijk, of korte tijd, na de eerste toetsgelegenheid worden gegeven. In het laatste geval hebben we met een geheel andere situatie te maken, van verlengde toetsing, en eigenlijk niet van herkansing.
Bij het kiezen van de studiestrategie gaat het ook hier weer om het specificeren van een waarschijnlijkheidsverdeling voor de eigen ware beheersing, waar de student naar toe werkt, en waarbij proeftoetsresultaten hem informatie verschaffen over het gerealiseerd hebben van de gewenste mate van stofbeheersing.
Als u de hoeveelheid voorbereidingstijd voor de eerste gelegenheid is, en 0,5 u de voorbereidingstijd voor iedere herkansing, en het risico r om te zakken voor eerste toets of een herkansing is bekend, dan is de hoeveelheid tijd die je verwacht nodig te hebben om te slagen voor dit studieonderdeel E (u tot) gelijk
(2) E (u tot) = u + 0,5 ur + 0,5 ur2 + 0,5 ur3 + .......... .
Uit de eigenschappen van meetkundige somreeksen volgt dan dat
(3) E (u tot) = 0,5 u + 0,5 u / (1 r).
Formule (3) maakt de keuze van een optimale strategie mogelijk: de student gaat door met studeren zolang zijn extra tijdbesteding Δu resulteert in een vermindering van het risico Δr die beide per saldo E (utot) verminderen. Daarvoor is nodig dat hij schat wat de verhoging van zijn ware beheersing zal zijn, om de vermindering van het risico te kunnen berekenen.
Wanneer een functioneel verband tussen tijdbesteding en ware beheersing gespecificeerd wordt, kan de optimale strategie (en strategieën daar in de buurt) bepaald worden.
Een geschikte aanpak daarvoor ligt in het hanteren van de volgende aanname:
Aanname 6
Wanneer t de hoeveelheid tijd is die nodig is om een geschatte ware beheersing van 0,50 te bereiken, is ut de hoeveelheid tijd die nodig is om een geschatte ware beheersing
(4) p = 1 - (0,5) ut u ≥ 0
te bereiken.
Om een geschatte ware beheersing van 0,875 te bereiken is t nodig om 0,50 te bereiken, nog een keer t om 0,75 te bereiken, en nogmaals t om de laatste proportie onkunde te halveren.
Of aanname 6 een beetje in overeenstemming met de empirie is, hangt van die empirie af. Bijvoorbeeld mag je verwachten dat de mate van heterogeniteit in de moeilijkheid van de vragen van belang is: hoe heterogener, hoe makkelijker het is om die eerste 50% beheersing te bereiken, hoe moeilijker het is om een hoge mate van stofbeheersing daarna te bereiken.
Wie voor t graag de hoeveelheid tijd neemt die één keer doornemen van de leerstof vraagt, kan dat ook doen, maar moet in plaats van de factor 0,5 in (4) nemen (1 - v), waar v is: de proportie van de nog niet gekende vragen die na een extra keer doornemen van de stof wél gekend wordt.
Aangenomen dat v constant is, ook voor de u de keer dat de stof doorgenomen wordt, kan dan
(5) p = 1 - (1 -v) u, en u = ln(1- p)/ln(1- v)
gebruikt worden.
Voor een gegeven cesuur, en een gespecificeerde bètaverdeling voor de waarschijnlijkheid van de eigen ware beheersing, is het in beginsel mogelijk om de optimale u te bepalen. Eenvoudiger is het om voor een aantal waarden van u, met gebruikmaking van de figuren in hoofdstuk 6, de verwachte totale studietijd te berekenen. De range voor ongeveer optimale strategieën is dan snel gevonden.
Er wordt niet aangenomen dat eenmaal gekende vragen niet meer vergeten worden. Het enige dat aangenomen wordt, is dat de ware beheersing, na nog een keer doorwerken van de stof, of na een extra studietijd t, een specifieke (hogere) waarde heeft bereikt, waarbij ware beheersing gedefineerd is aan de (denkbare) verzameling van vragen over de stof (zie hoofdstuk l).
De waarschijnlijkheidsverdeling voor het aantal herkansingen h nodig om te slagen voor een studieonderdeel is de meetkundige verdeling (een speciaal geval van de wachttijdverdeling, de negatieve binomiaal).
Als r de kans om te zakken is, is (1-r) de kans om te slagen. De kans om precies h herkansingen nodig te hebben om een voldoende te behalen is dan, wanneer telkens dezelfde strategie gevolgd wordt:
(6) f(h) = r × rh-1 × (1-r) = rh (1-r)
Gemiddelde en variantie van de meetkundige verdeling zijn (Kendall & Stuart volume 1, 1969):
(7) E(h) = r/(1-r) sh2 = r / (1-r)2.
Is de cesuur tevoren niet bekend gemaakt, dan kan de student een waarschijnlijkheidsverdeling daarvoor specificeren. Het ligt voor de hand daar een bètaverdeling voor te kiezen. In veel gevallen zal een β(a, b; c) met a+b = 100 wel ongeveer geschikt kunnen zijn.
Wanneer n het aantal toetsvragen is, kan de slaagkans berekend worden
(1) ∫01 β(a,b;c) P(x/n ≥ c) dc.
Een benadering in n+1 stappen wordt verkregen door als benadering voor P{(x-½)/n < c < (x+½)/n} de waarde van β(a,b;c=x/n) te nemen.
Bij een onvermengde compensatorische examenregeling moet de student een minimum aantal punten scoren voor alle studieonderdelen tezamen om te slagen. Onder punten kunnen we eenvoudigheidshalve de gewogen ruwe scores voor ieder van de afzonderlijke toetsen verstaan: het aantal vragen goed, eventueel vermenigvuldigd met een wegingsfaktor voor deze specifieke toets vastgesteld, is het aantal punten dat voor dat studieonderdeel behaald is.
Onder een compensatorische examenregeling is het kennelijk van groot belang voor de student om zich door een juiste studiestrategie te verzekeren van een goede kans om inderdaad het minimum aantal punten .(tenminste) binnen te halen. De consekwenties van zakken voor het examen kunnen immers ernstig zijn (afhankelijk van de specifieke regeling daarvoor binnen de (sub )fakulteit opgezet): overdoen van het hele studieprogramma, of definitief uitgesloten worden van de verdere studie. Afhankelijk van de consekwenties van zakken zullen in de praktijk waarschijnlijk herkansingsmogelijkheden geboden moeten worden voor studenten die blijk hebben gegeven een juiste studiestrategie te volgen, maar mogelijk door pech op de laatste studieonderdelen gestruikeld zijn. In het volgende wordt ervan uit gegaan dat de student het voor hem nog juist aanvaardbare RISICO om te zakken aangeeft: de kans om het mini maal vereiste aantal punten niet te halen. Bij de keuze van dat RISICO kan rekening gehouden worden met de mogelijkheid of onmogelijkheid van herkansingen.
Wanneer nog één toets af te leggen is kan, gegeven de plausibiliteit voor zijn ware beheersing, gerepresenteerd door een bètaverdeling f(p) (zie bijlage A), de kans om minder dan een bepaald aantal punten te scoren berekend worden op de wijze als in bijlage A aangegeven. Dat levert het RISICO op, gegeven de plausibiliteit voor de ware beheersing. Het is natuurlijk ook mogelijk om te berekenen bij welke f(p) het RISICO een tevoren gespecificeerde waarde heeft.
De studiestrategie voor de student ziet er dan als volgt uit: bestudeer de stof totdat de beheersing zo goed is dat de plausibiliteit f(p) het gespecificeerde RISICO oplevert.
Het kan dan zijn, dat in de hand houden van het RISICO niet meer mogelijk blijkt te zijn, omdat op de voorgaande studieonderdelen te weinig punten werden behaald. Laten we daarom eens één stap terug doen:
Wanneer nog twee toetsen afgelegd moeten worden, is de vraag hoe het RISICo dat de somscore beneden het minimaal te behalen aantal punten blijft, in de hand gehouden kan worden. Of: welke mate van stofbeheersing voor iedere afzonderlijke toets is nodig om dat RISICO op een aanvaardbaar peil te brengen? De mate van stofbeheersing refereert aan de plausibiliteit, de prior, voor de ware beheersing f(p). Die stofbeheersing hoeft niet voor beide toetsen op hetzelfde niveau te liggen.
Is het zinvol om al over de plausibiliteit voor de stofbeheersing voor toets 2 te spreken wanneer toets 1 nog niet afgelegd is? Voor de student is dat zinvol, zolang het gaat om een beheersingsniveau dat naar zijn schatting vooraf binnen het bereik van zijn capaciteiten (en beschikbare tijd) ligt.
In de bètaverdeling f(p) voor de ware beheersing van de stof voor toets 1 ligt alle informatie besloten die de student heeft met betrek~ king tot de toetsscore x die hij mag verwachten (kan voorspellen). Evenzo ligt in de bètaverdeling f(q) voor de ware beheersing van de stof voor toets 2 alle informatie besloten die de student op het moment waarop hij de stof op het door f(q) gespecificeerde niveau beheerst, heeft over de toetsscore y die hij voor toets 2 mag verwachten (kan voorspellen).
Het laatste impliceert f(y|x) = f(y), de voorspellende kansverdeling voor toets 2 is onafhankelijk van de voorspellende kansverdeling voor toets 1:
(1) f(x, y) = f(x) f(y).
De voorspellende kansverdeling voor de somscore s = x + y is
(2) f(s) = Σ f(x) f(y),
waarbij de sommering is over alle x en y zodanig dat x + y = s.
Het RISICO dat de somscore s kleiner is dan het minimaal nog te behalen aantal punten t
(3) R(s<t) = Σt-1s=0
Σmx=0
(m boven x)(n boven s-x) B(a+x, b+m-x) B(c+s-x, d+n-s+x) / (B(a, b) B(c, d)),
waarbij a en b de parameters van f(p), c en d de parameters van f(q), m het aantal vragen in toets 1, n het aantal vragen in toets 2. (gebruik makend van formule (5), bijlage A).
Het is mogelijk om (3) voor gekozen parameterwaarden te berekenen, zij het ook moeizaam. Eenvoudiger wordt het, wanneer we ermee tevreden zijn om het RISICO uit te drukken in standaarddeviaties. Gebruik makend van (1) vinden we immers dat de verwachting van de somscore gelijk is aan de som van de verwachtingen van de afzonderlijke toetsscores, en de variantie van de somscore gelijk is aan de som van de varianties van de afzonderlijke toetsscores:
(4) μ = E(s) = E(x + y) = E(x) + E(y) = μx+ μy.
(5) σ2 =E{(s - μ)2}= E{(x)2}+E{(y)2}+ 2E(xy) 2μ E(s) + μ2
= σx2 + μx2 + σy2 + μy2 + 2μxμy - μ2 = σx2 + σy2 .
Gemiddelde en variantie voor een voorspellende kansverdeling voor de toetsscore, een negatief hypergeometrische verdeling met parameters a, b, en m, zijn
(6) gemiddelde ma /(a+b)
(7) variantie mab (a+b+m)/(a+b)2 (a+b+1).
De student kan nu eenvoudig berekenen wat het effect van een verandering van studiestrategie voor toets 1, dan wel voor toets 2 is. De student die niet gedwongen is tot een maximale inspanning voor beide toetsen heeft de keuze tussen
noot: Lord en Novick (1968) laten voor twee parallel toetsen, voor gegeven ware beheersing onafhankelijk van elkaar, zien dat de somscore eveneens de negatief hypergeometrische verdeling heeft (althans, dat volgt onmiddellijk uit hun resultaat 23.6.19). Hun resultaat heeft betrekking op parallel toetsen met een gelijk aantal vragen
Omdat Σsx=0 (m boven x)(n boven s-x) = (m + n boven s), wanneer (m boven x) gedefineerd is voor x > m, geldt ook voor paralleltoetsen van ongelijke lengte m en n dat de somscore negatief-hypergeometrisch verdeeld is
(8) f(s) = (m + n boven s) B-l(a, b) B(a+s, b+m+n-s).
Waar zit nu het verschil met de door mij gegeven benadering in? Dat zij voor f(p) de verdeling van ware beheersing in de populatie van personen nemen is geen essentieel verschil met de door mij gekozen benadering: zij hadden evengoed de f(p) als de verdeling voor de ware beheersing voor een gegeven persoon op kunnen vatten. Nee, het verschil zit hierin, dat zij veronderstellen dat tussen beide parallel toetsingen de ware beheersing niet verandert. Sta je toe dat de ware beheersing wèl verandert, bijvoorbeeld door verg eten en opnieuw leren tussen beide parallelafnamen, dan komen we terecht bij het op de beide vorige bladzijden geschetste model. Zou voor beide toetsen dezelfde f(p) gespecificeerd zijn, dan vinden we dat de variantie voor de somscore in dit geval kleiner is dan voor de somscore bij twee prallel toetsen die onmiddellijk na elkaar afgenomen worden. (doordat nu twee keer getrokken wordt uit f(p) is de variantie van de som kleiner).
Bij uitbreiding naar meer dan twee toetsen ontstaan geen extra problemen. Worden toetsscores gewogen, dan blijft gelden dat de verwachting voor de somscore gelijk is aan de som van de gewogen verwachtingen voor de afzonderlijke toetsscores, en dat de variantie voor de somscore gelijk is aan de som van de afzonderlijke varianties telkens vermenigvuldigd met het kwadraat van hun wegingsfaktor:
(9) μ = Σ wi μi sommering over alle toetsen i.
(10) σ2 = Σ wi2 σi2 ,, ,, ,, ,, ,,
Is bij een gekozen studiestrategie het RISICO te groot, dan wordt nagegaan of bij ggn of meerdere studieonderdelen (maar niet voor het eerste af te leggen tentamen) de studiestrategie hoger gekozen kan worden (eventueel met opoffering van vrije weekeinden of een stuk vakantie), en wordt doorgerekend of daaruit wél een aanvaardbaar RISICO resulteert. Is dat inderdaad het geval, dan wordt de eerste toets volgens de eerstgekozen strategie voorbereid en afgelegd, en worden nieuwe berekeningen van het RISICO, maar nu met dit toetsresultaat als gegeven, uitgevoerd. In de meeste gevallen zal de hogere studiestrategie niet metterdaad gevolgd hoeven te worden, maar blijft voor toekomstige studieonderdelen als noodmaatregel achter de hand. Dit is te betitelen als een wisaelstrategie.
Levert een wisselstrategie geen aanvaardbaar RISICO op, dan zal op de eerstvolgende toets een hogere strategie, een intensievere voorbereiding, gekozen moeten worden.
In tabel 8.1 wordt voor verschillende toetslengten voor de variantie van de prediktieve scoreverdeling égn waarde opgegeven, onafhankelijk van de gekozen prior (studiestrategie). Dat is in afwijking van de exacte variantie voor de negatief hypergeometrische verdeling die door formule (7) in bijlage A gegeven wordt. De waarden in tabel 8.1 zijn zo gekozen dat de uitkomst van de berekeningsprocedure in hoofdstuk 8 gegeven, opgevat als σ voor de standaard normaal verdeling het RISICO oplevert als kleinste oppervlak onder de normaalverdeling in tweeën gedeeld bij deze σ.
Belangrijke reden voor deze handelwijze is de eenvoud van de tabel, vergeleken met tabellering van varianties voor verschillende studiestrategieën. De rechtvaardiging is dat tabel 8.1 een voorzichtige (dus: over )schatting van het RISICO geeft. Voor de meer symmetrische negatief hypergeometrische verdelingen is het risico kleiner dan dat bij de normaalverdeling met gelijk gemiddelde en variantie; voor de scheve verdelingen die resulteren bij hogere studiestrategieën is het risico groter dan wat resulteert bij normaalverdeling met gelijk gemiddelde en variantie. Ergens daartussenin liggen de waarden gegeven in tabel 8.1 die voor alle strategieen een goede (over ) schatting van het RISICO geven. Bij strategie~n die op een beheersing van minder dan zeg 40 % mikken geeft de tabel echter onaanvaardbaar té hoge schattingen van het RISICO.
Voor het RISICO over een aantal studieonderdelen geldt dat bij gebruikmaking van de waarden uit tabel 8.1, die ieder voor zich voorzichtige schattingen van de variantie zijn, ook voor de voorspellende somscore verdeling het RISICO op voorzichtige wijze geschat wordt (eveneens refererend aan de tabel voor de normaalverdeling).
Vergelijking van het RISICO bij een toets van 50 vragen, onder de benaderende berekening en de exacte berekening, laat zien dat bij een strategie van 22 uit 25 (prior bèta(22, 3)), het RISICO twee keer te hoog geschat wordt als het bij exacte berekening blijkt te zijn, bij een studiestrategie van 12 uit 25 (prior bèta (12, 13)) ongeveer 1,5 keer te hoog.
Het verband tussen studietijd en stofbeheersing zal niet altijd zo fraai zijn als in figuur 6.1. Vele varianten zijn daarop denkbaar, afhankelijk van de aard van de leerstof, het soort toetsvragen dat gebruikt wordt, voorkennis die studenten hebben, en dergelijke. In onderstaande figuur zijn een aantal van dergelijke curven bijeengebracht, die in deze bijlage verder besproken zullen worden. Ik zal laten zien dat het meestal mogelijk zal zijn een bepaalde variant terug te brengen tot een curve van het soort als in figuur 6.1 gegeven werd (in onderstaande figuur is dat curve A).
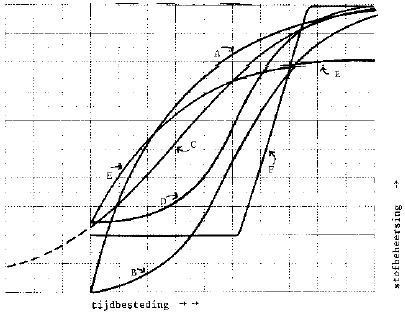
FIGUUR D.1 Verschillende voorbeelden van mogelijke leercurven.
Een korte toelichting, voordat ik dieper op de afzonderlijke mogelijkheden inga:
Curve A is dezelfde als afgebeeld werd in figuur 6.1. Bedenk bij al deze curven dat de tijdas niet gespecificeerd is, wat de mogelijkheid openlaat dat verschillende studenten in verschillend tempo studeren terwijl toch hetzelfde soort verband tussen studietijd en stofbeheersing kan gelden (de tijdas is voor de ene student meer samengedrukt dan voor de andere; wat de ene student in tien dagen kan, daar doet een ander misschien twee keer zo lang over).
Bij curve B is er sprake van wat je een aanloopperiode zou kunnen noemen, waarin aanvankelijk de stofbeheersing weinig aangroeit. Hetzelfde is het geval bij curven C en D, maar bovendien is er bij curve C sprake van enige voorkennis, bij curve D is het effect geïllustreerd van raadkansen zoals die zeker bij meerkeuze vragen voorkomen.
Door de mogelijkheid meerkeuzevragen door raden goed te maken, zal ook de student die nog geen enkele kennis van de stof heeft behoorlijk wat vragen uit de vragenverzameling goed beantwoorden, en dus beginnen op een niveau van stofbeheersing dat hoger is dan nul. Ook curven E en F hebben betrekking op stofbeheersing die gedefinieerd is op meerkeuzevragen. Curve E is overigens van dezelfde soort als curve A. Curve F is waarschijnlijk zelden of nooit van toepassing waar het gaat om de grote stukken leerstof in het wetenschappelijk onderwijs die gelijktijdig getoetst worden. Bij kleine partjes leerstof kan het zijn dat bij begrijpen van de stof de beheersing plotseling van nul tot bijna perfect stijgt, zoals curve F laat zien.
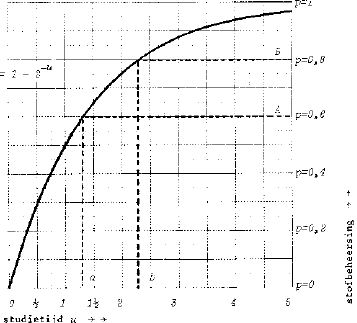
FIGUUR D.2 . Aflezen van de studietijd die nodig is om van stofbeheersing A te komen tot stofbeheersing B. u = aantal tijdsperioden t
Welk gebruik willen we maken van de leercurve? Het belangrijkste gebruik is het schatten van de studietijd die nodig is om van het ene niveau van stofbeheersing tot het andere te komen. Figuur D.2 illustreert dat: uit de figuur kan afgelezen worden hoeveel studietijd nodig is om van niveau A tot niveau B te komen: trek vanuit A en vanuit B horizontale lijnen, totdat de leercurve gesneden wordt, trek dan vanuit de snijpunten vertikale lijnen. De gevraagde studietijd nodig om van niveau A tot niveau B te komen is dan gelijk aan het verschil van de u waarden op de punten a en b, of, als a en b de betreffende t waarden voorstellen, is de gezochte studietijd gelijk aan b -a.
In het volgende zal ik demonstreren dat voor praktisch gebruik van de leercurve, de verschillende curve varianten herleidbaar zijn tot de curve in figuur D.2 (die gelijk is aan de curve in figuur 6.1).
Het aflezen van benodigde studietijd voor verhoogde stofbeheersing uit de gegeven figuur is voor de meeste toepassingen nauwkeurig genoeg. Voor precieze tijden kan natuurlijk ook van de formule voor deze leercurve gebruik gemaakt worden. De tijd die nodig is voor een bepaalde niveauverbetering (van niveau A naar niveau B) is:
(1) b a = ln(1 B)/ln(0,5) ln(1 A) ln(0,5)
Met hulp van een wetenschappelijke zakrekenmachine is dit snel en simpel te berekenen, wanneer voor A en B de respectievelijke proporties ingevuld worden. ('ln' staat voor de natuurlijke logaritme, ofwel de logaritme voor het grondtal e; i.p.v. ln kan ook log gebruikt worden, de logaritme voor het grondtal 10).
De student die voordat hij met de studie voor dit vak begonnen is een bepaalde proportie vragen al goed kan beantwoorden (zonder dat daarbij van raden sprake is), heeft voorkennis. Zijn leercurve vangt dan ook op dat niveau van voorkennis aan, en niet bij een stofbeheersing van nul. Welke gevolgen heeft dat voor de studietijd berekeningen?
Voor het berekenen van de tijd die nodig is om van beheersing A te komen tot beheersing B heeft dit geen gevolg: zowel aflezen uit de figuur als berekenen volgens formule (1) kan op de eerder gegeven manier gebeuren.
Voor het berekenen van de tijd nodig om voor een herkansing weer op het niveau van stofbeheersing te komen dat bij de laatste toets werd bereikt ligt de situatie nu iets anders. Het zal meestal redelijk zijn te veronderstellen dat de voorkennis die aan het begin van de studie bestaat, ook bij de aanvang van de voorbereiding op de herkansing bestaat. Als dat aangenomen kan worden, kan figuur C.2 toch gebruikt worden voor alle berekeningen wanneer de vertikale schaal voor de mate van stofbeheersing aangepast wordt. De schaal voor p begint dan niet bij p = 0, maar bij p = voorkennis, de schaalwaarden worden als het ware opgerekt. Voor enkele voorkennis niveaus geeft tabel D.1 aan welke schaalwaarden te substitueren zijn in figuur D.2
______________________________________________________
mate van voorkennis
0% 10% 20% 30% 40%
------------------------------------------------------
1 1 1 1 1
0,80 0,82 0,84 0,86 0,88
0,60 0,64 0,68 0,72 0,76
0,40 0,46 0,52 0,58 0,64
0,20 0,28 0,30 0,44 0,52
0 0,10 0,20 0,30 0,40
______________________________________________________
TABEL D.1. Gewijzigde schaalwaarden voor figuur D.2 bij
voorkennis van 10, 20, 30 en 40 %.
Wie liever rekent kan gebruik maken van de aangepaste formule voor de leercurve. De leercurve zonder voorkennis is
(2) p = 1 - 2 -u
u = aantal tijdsperioden t
t = tijd nodig om de proportie niet geweten vragen te halveren
p = stofbeheersing (proportie geweten vragen in de vragen verzameling)
De leercurve met voorkennis v is
(3) p = v + (1 - v) (1 - 2-u )= 1 - 2-u (1 - v )
v = voorkennis (proportie vragen die bij begin van het onderwijs al geweten wordt)
De tijd (uitgedrukt in aantal perioden t) nodig om van p = A tot p = B te komen is b a, en is te berekenen als:
(4) b - a = ln (1 - B) / ln½ - ln (1 - A) / ln½.
De mate van voorkennis kan voor verschillende studenten uiteenlopen. Wanneer alle studenten ongeveer evenveel voorkennis blijken te hebben, is er alle aanleiding om het vragenbestand te herzien. Een aantal vragen kan waarschijnlijk door het grootste deel van de studenten al beantwoord worden voordat er enig onderwijs is gevolgd; die vragen zijn niet specifiek voor het gegeven onderwijs, en horen in geen enkele toetsing thuis, en zeker niet in de eindtoets. Deze vragen geven immers geen informatie over de kwaliteit van het gegeven onderwijs, en geven de student geen informatie over zijn studievorderingen.
Soms is het mogelijk, ook bij open eind vragen, dat de student een goed antwoord raadt. Voorbeeld: "Noem de hoofdstad van Nederland. Het aantal voor de hand liggende mogelijkheden is beperkt, er is een aanzienlijke kans dat leerlingen die het antwoord niet weten een goede gok maken. Bij zogenaamde objectieve vraagvormen is de raadkans ingebouwd. Raadkansen zijn op dezelfde wijze op te vangen als voorkennis. Eerst de formules maar, die zijn gelijk aan form. (3) en (4) hierboven, maar nu met r van raadkans i.p.v. v van voorkennis.
(5) p = 1 - 2-u (1 - r) r = raadkans
(6) b - a = ln (1 - B) / ln&½ - ln (1 - A) / ln&½.
Merk op dat zowel in formule (4) als formule (6) de parameter v, respectievelijk r, weggevallen is. Daardoor zijn de formules (4) en (6) identiek aan elkaar, én aan formule (1).
Over de omvang van de raadkans bij objectieve vragen valt heel wat te filosoferen. Dat neemt niet weg dat in de praktijk heel goed te werken valt met een raadkans die geschat wordt als de reciproke van het aantal antwoordalternatieven, of iets groter wanneer uit toetsresultaten blijkt dat studenten vrijwel altijd in staat zijn om tenminste één van de alternatieven als onjuist af te strepen. Dus, als k het aantal alternatieven is waaruit de student die het antwoord niet weet een keuze maakt, is de raadkans r = 1/k.
Wie graag figuur D.2 gebruikt om de gevraagde studietijden af te lezen, kan de vertikale schaalwaarden voor stofbeheersing aanpassen aan de raadkans, door de betreffende waarden uit tabel D.2 over te nemen.
________________________________________________________
raadkans
0 1/10 1/5 1/4 1/3 1/2
---------------------------------------------------
p = 1 1 1 1 7 1
p = 0,80 0,82 0,84 0,85 0,87 0,90
p = 0,60 0,64 0,68 0,70 0,73 0,80
p = 0,40 0,46 0,52 0,55 0,60 0,70
p = 0,20 0,28 0,36 0,40 0,46 0,60
p = 0 0,10 0,20 0,25 0,33 0,50
________________________________________________________
TABEL D.2 Gewijzigde schaalwaarden voor figuur D.2 bij raadkans van 1/10, 1/5, 1/4, 1/3, of 1/2.
In veel onderwijssituaties zal de student aanvankelijk weinig of geen vorderingen maken. Daar zijn verschillende redenen voor aan te wijzen. De eerste introductie tot de stof vraagt een stukje gewenning, je vertrouwd maken met een aantal grondbegrippen, e.d. Dat kost relatief veel tijd, en brengt weinig op in termen van eindtoetsvragen die je leert beheersen. Een andere voor de hand liggende reden is dat de meeste leerstof, hoewel niet streng hiërarchisch opgebouwd, toch een bepaalde progressie zal kennen van eenvoudig basis materiaal tot de wat moeilijker leerstof die daarop voortbouwt. In de eindtoetsing zal aan de eenvoudige basis begrippen weinig of geen aandacht besteed worden, hoewel beheersing daarvan een voorwaarde is voor het kunnen maken van de meeste toetsvragen.
Omdat stofbeheersing gedefiniëerd is op de vragenverzameling waaruit eindtoetsen worden samengesteld, zal de student in het begin van zijn studie weinig vordering maken in deze stofbeheersing, hoewel hij best in hoog tempo zich de grondbeginselen eigen kan maken.
Hoe dat ook zij, een leercurve, gedefinieerd aan de vragenverzameling waaruit eindtoetsen worden samengesteld, zal in het begin wel eens tamelijk horizontaal of langzaam stijgend kunnen zijn, waarna er een periode van grote vorderingen komt, met daarna een verder afvlakken van de curve tegen het plafond van de perfecte stofbeheersing.
Voorbeelden van dergelijke leercurven zijn gegeven in figuur D.I, de curven B, C, en D.
Een redelijke veronderstelling die we hier kunnen maken is: de tijd besteed aan de aanloop is voor herkansingen niet meer nodig. De aanloop tijdbesteding is éénmalig. Waar precies de grens getrokken wordt tussen wat nog als aanloop beschouwd kan worden, en wat niet meer, is niet zo geweldig belangrijk.
Wanneer dat niet met de ervaring in strijd is, zou je de grens ongeveer in het midden van het rechte stuk van de S vormige curve kunnen trekken.
Nu is er op voorhand niets tegen om voor het rechter gedeelte van zo'n S vormige curve (boven het juist genoemde grenspunt), de curve te hanteren die als formule heeft:
(7) 1 - (1 - v ) × 2-u
waar v het niveau van stofbeheersing is dat, evenals dat bij onze veronderstelling over voorkennis het geval was, van de ene toetsgelegenheid tot de andere blijft bestaan. Anders gezegd: v is het niveau van voorkennis dat aanwezig is op het moment dat met de voorbereiding op een herkansing begonnen gaat worden.
technische voetnoot. Het gaat bij het zoeken naar optimale studiestrategieën niet om het ontwikkelen van een leertheorie. De precieze aard van de leercurve is niet van bijzonder belang, het gaat er immers slechts om dat we een leercurve gebruiken die geschikt is voor het opsporen van optimale leerstrategieën. Daar komt bij dat het bijzonder moeilijk zou zijn om empirische ondersteuning voor de juistheid? van deze leercurven te verzamelen. Laten we afspreken dat het ontbreken van dergelijke empirische ondersteuning ons niet zal verhinderen deze leercurven te gebruiken zolang:
De logistische functie g/(h+e-u) is een mogelijke kandidaat voor formele beschrijving van S vormige leercurven. Kies bijvoorbeeld g=l en h=1, dan is voor u groter dan ½ een redelijke overeenstemming te vinden tussen deze logistische functie en de curve in formule (7) wanneer daarin v = ½ gekozen wordt. Voor het gebruik dat in dit cursusdeel van leercurven gemaakt wordt, leiden beide formules tot ongeveer dezelfde resultaten.
Overigens is er natuurlijk ook niets op tegen om op basis van eigen ervaring een leercurve te schetsen zoals men denkt dat die in algemene vorm voor iedere student ongeveer zal gelden, en alle berekeningen uit te voeren door direkt met de getekende functie te werken, zonder eerst te proberen een wiskundige formule als benadering van de curve te vinden.
Alle tot nu toe besproken leercurven hebben de mogelijkheid in zich dat de student bij voldoende tijdbesteding een vrijwel perfecte stofbeheersing p = 1 bereikt. Het is niet vanzelfsprekend dat dat altijd mogelijk is.
Wanneer er vragen in de verzameling voorkomen waarop de student zich niet door oefening kan voorbereiden, zal bijna perfecte stofbeheersing voor deze student niet mogelijk zijn.
Op triviale wijze kan zoiets gebeuren wanneer per vergissing in het vragenbestand vragen voorkomen ever leerstof die inmiddels uit het onderwijspakket verwijderd is.
Minder onschuldig zijn vragen die op een niveau mikken dat hoger ligt dan dat waarop het onderwijs gegeven is. Een eufemistische omschrijving van dit soort vragen is dat ze een beroep doen op probleem oplossende kapaciteiten van de studenten. Voorzover het daarbij echter gaat om oplossingsstrategieën die niet expliciet onderwerp van onderwijs geweest zijn, is het uiterst dubieus of dergelijke vragen wel in de eindtoetsing opgenomen mogen worden. Worden ze namelijk daarin opgenomen, dan zal voor de meeste studenten het kennis plafond lager dan 1 komen te liggen, en wel voor de ene student wat lager dan voor de andere (persoonlijke verschillen kunnen daarbij aanzienlijk zijn).
Ook wagen waarbij minder van belang is of het onderwijs gevolgd is, maar wel of de student intelligent is of niet, zullen tot gevolg hebben dat voor veel studenten het kennis plafond lager dan 1 is, met alle gevolgen van dien voor hun leercurve. Het is hier niet de plaats om een diskussie te beginnen over de gewenstheid van vragen die mede een beroep doen op de intelligentie van de student. Ik wil er slechts op wijzen dat in het algemeen voor dergelijke vragen geldt dat zij weinig specifiek zijn voor het gegeven onderwijs, en alleen dáárom al uit de vragenverzameling verwijderd zouden moeten worden. Informatie over de intelligentie van studenten, wanneer men daarin geïnteresseerd zou zijn, behoort niet op sluikse wijze via toetsing van studieprestaties verkregen te worden, De toets is een evaluatie instrument, voor zowel docent als student, en kan gebruikt worden om de studieaktiviteiten van de student te sturen, maar is zeker geen intelligentie test.
Wanneer er een situatie is waarin een kennisplafond in de leercurve verdisconteerd moet worden, dan is dat eenvoudig te doen. Laat f het het niveau van stofbeheersing zijn dat bij zeer lange studietijd maximaal bereikbaar is. Dan wordt de leercurve:
(8) p = f(1 - 2-u)
De leercurve wordt op gelijkmatige wijze verticaal samengedrukt.
Is er gelijkertijd sprake van raadkansen (raadkans r), of voorkennis, dan wordt de leercurve
(9) p = r + f (1 - r)(1 - 2-u)
in welk geval de tijd nodig am van niveau A tot niveau B te komen is
(10) b - a = ln{f(1-r)-(B-r)}/lnfrac12; - In{f(1-r)-(A-r)}/1nfrac12;.
Is er geen raadkans (resp. voorkennis), dan in (10) gewoon r=0 nemen.
COHEN, J. Psychological probability, op The Art of Doubt. London: Allen and Unwin, 1972.
HAMPTON, J. M., MOORE, P. G., and THOMAS, H. Subjective probability and its measurement. Journal of the Royal Statistical Society, Series A, 1973, 136, 21 42.
HOGARTH, R. M. Cognitive processes and the assessment of subjective probability distributions. Journal of the American Statistical Association, 1975, 70, 271 289.
JUNGERMANN, H. Rationale Entscheidungen. Stuttgart: Huber, 1976.
NOVICK, M. R., and JACKSON, P. H. Statistical methods for educational and psychological research. London: McGraw Hill, 1974.
SCHAEFER, R. E. Probabilistische Informationsverarbeitung. Stuttgart: Huber, 1976.
STAëL VON HOLSTEIN, C. A. S. (Ed.) The concept of probability in psychological experiments. Dordrecht: Reidel, 1974.
TVERSKY, A. Assessing uncertainty. Journal of the Royal Statisticoal Society, Series B, 1974, 36, 148-159.
WENDT, D., and VLEK, Ch. (Editors) Utility, probability, and human decision making. Dordrecht: Reidel, 1975.
De ZEEUW, G., VLEK, C. A. J., and WAGENAAR, W. A. (Editors) Proceedings of the second research conference on subjective probability. Acta Psychologica, 1970, 34.
Twee inleidingen tot het soort besliskunde waar het hier om gaat zijn:
VLEK, C. A. J., en WAGENAAR, W. A. Oordelen en beslissen in onzekerheid, in MICHON, J. A., EIJKMAN, E. G. J., en De KLERK, L. F. W. L. F. W. (Redaktie) Handboek der psychonomie. Deventer: Van Loghum Slaterus, 1976.
WAGENAAR, W. A. De beste stuurlui dempen de put. Baarn: Ambo, 1977.
Cumulatieve voorspellende kansverdelingen voor de score op toetsen van verschillende lengte, en voor verschillende studiestrategieën.
Wanneer β(a,b) de schatting van de eigen ware stofbeheersing representeert (bijvoorbeeld op grond van een behaald proeftoets resultaat), waarbij a + b = 25, en c is de zak slaag grens (of iedere andere mogelijke toetsscore waarin men geïnteresseerd is), dan geeft de tabel
(7) Σc-1x=0 (n boven x) B-1 (a, b) × B (a+x, b+n-x)
x = toetsscore
n = aantal toetsvragen
c = zak-slaaggrens (passing score)
B(a,b) = (a-1)! (b-1)! /(a+b 1)!
a + b = 25
(vergelijk formule (5) in bijlage A). Er is symmetrie in de tabel voor wat betreft de waarden van de parameters a en b. In de tabellen is dat te zien door de kolommen 12/25 en 13/25 met elkaar te vergelijken. Wie belangstelling heeft voor de cumulatieve verdelingen voor lagere studiestrategieën dan in de tabel opgenomen, kan op eenvoudige wijze uit de cumulatieve verdeling voor b/25 die voor a/25 construeren. De berekeningsmethode voor deze cumulatieve verdelingen werd in bijlage A beschreven. (zie in die bijlage (6), (7), (8) en (9).)
Iedere tabel geeft voor verschillende studiestrategiegn het risico dat de score lager uitvalt dan de zak-slaaggrens (of lager dan een aantal goed gelijk aan wat in de tabel de zak-slaag grens genoemd wordt).
______________________________________________________________________________________________________
studiestrategie studiestrategie
zak zak-
slaag 12 13 14 15 16 17 18 19 20 21 22 slaag 12 13 14 15 16 17 18 19 20 21 22
grens 25 25 25 25 25 25 25 25 25 25 25 grens 25 25 25 25 25 25 25 25 25 25 25
------------------------------------------------- --------------------------------------------------
100 999 993 75 999 997 997
99 toets met 100 vragen 999 995 977 74 toets met 75 vragen 999 997 988 957
98 999 997 987 952 73 999 998 991 971 910
97 998 993 974 914 72 998 994 981 943 849
96 999 996 987 955 869 71 999 996 988 964 905 778
95 999 993 977 930 817 70 999 998 992 978 941 858 701
94 999 997 988 963 899 760 69 999 995 986 963 910 803 623
93 998 994 981 945 863 701 68 999 997 992 977 943 872 743 546
92 999 997 990 971 923 821 640 67 999 995 986 965 918 827 678 472
91 999 995 985 958 897 776 579 66 999 997 992 978 948 886 777 612 403
90 999 998 992 978 942 866 728 520 65 998 995 987 968 926 949 723 545 340
89 999 996 989 969 923 831 677 464 64 999 997 993 980 954 900 807 665 481 284
88 998 994 983 957 900 793 626 411 63 999 996 988 971 936 869 760 606 419 235
87 999 997 992 977 942 873 752 574 361 62 929 998 993 983 960 914 833 710 546 362 193
86 999 996 988 968 925 844 709 524 315 61 999 996 990 975 945 897 793 657 488 309 157
85 999 998 994 983 958 905 811 664 474 274 60 998 994 985 965 926 857 749 603 431 262 126
84 999 997 991 977 945 882 775 619 426 236 59 997 992 979 953 904 822 702 548 378 220 100
83 999 996 988 969 930 857 738 573 381 203 58 995 988 971 938 878 784 653 494 328 192 79
82 909 998 994 984 960 913 828 698 527 339 173 57 993 983 961 919 848 742 602 441 282 150 62
81 999 997 992 978 949 892 797 657 482 299 147 56 990 976 948 897 815 698 550 390 240 122 48
80 999 996 989 972 936 870 763 615 438 263 124 55 986 968 932 871 778 651 499 342 202 99 37
79 998 994 985 963 920 845 728 572 396 229 104 54 981 957 914 642 736 602 448 297 169 79 29
78 997 992 980 954 903 817 691 530 356 199 87 53 974 945 892 810 695 553 399 255 140 63 22
77 996 990 974 942 883 787 652 488 318 172 72 52 966 929 867 774 650 504 353 218 115 50 16
76 995 986 967 929 861 756 613 447 282 148 60 51 955 911 839 735 603 455 309 184 93 39 12
75 993 982 959 913 836 722 573 407 249 126 49 50 943 889 807 694 556 407 269 154 75 30 9
74 991 977 949 896 810 687 533 368 219 107 40 49 927 865 772 650 508 362 230 128 60 23 7
73 988 971 937 876 781 650 493 332 191 90 33 48 909 837 734 605 461 318 196 105 48 17 5
72 985 964 924 855 750 613 454 297 166 76 27 47 888 806 694 559 414 278 165 85 37 13 4
71 981 955 908 831 718 575 416 265 144 64 21 46 864 772 652 512 369 240 138 69 29 10 3
70 975 945 891 805 684 536 379 235 124 53 17 45 837 735 608 466 326 206 114 55 22 7 2
69 969 934 872 777 649 498 343 207 106 44 14 44 807 696 562 420 286 175 94 44 17 5 1
68 962 920 851 748 613 460 304 181 90 36 11 43 773 654 516 376 248 147 76 34 13 4 1
67 953 905 827 716 577 423 277 158 76 29 9 42 737 611 471 333 213 122 61 26 10 3 1
66 943 888 802 684 540 387 247 137 64 24 7 41 699 566 425 292 182 101 49 20 7 2
65 932 869 775 650 503 352 219 118 53 19 5 40 657 521 381 254 153 82 38 15 5 1
64 919 849 746 615 466 319 193 101 44 16 4 39 615 475 338 219 128 66 30 12 4 1
63 904 826 716 579 430 287 169 86 37 13 3 38 570 430 298 187 106 53 23 9 3 1
62 887 801 684 543 394 257 148 73 30 10 2 37 525 385 259 158 86 42 19 6 2
61 869 775 651 507 360 229 128 62 25 8 2 36 479 343 224 132 70 33 13 5 1
60 848 747 617 471 327 203 111 52 20 6 1 35 434 301 191 109 56 25 10 3 1
59 826 717 582 435 295 179 95 43 16 5 1 34 389 263 161 89 44 19 7 2 1
58 802 686 547 400 265 157 81 36 13 4 1 33 346 227 135 72 34 15 5 2
57 776 654 511 366 237 136 69 29 10 3 1 32 304 193 111 58 27 11 4 1
56 749 620 476 333 211 118 58 24 8 2 31 265 163 91 45 20 8 3 1
55 720 586 440 302 186 101 48 20 7 2 30 228 136 73 35 15 6 2 1
54 689 551 406 272 163 87 40 16 5 1 29 194 112 58 27 11 4 1
53 657 516 372 243 143 74 33 13 4 1 28 163 91 46 21 8 3 1
52 624 480 339 216 124 62 27 10 3 1 27 135 73 35 15 6 2 1
51 590 445 307 192 107 52 22 8 2 1 26 111 57 27 11 4 1
50 555 410 277 168 91 44 18 6 2 25 89 45 20 8 3 1
49 520 376 248 147 78 36 14 5 1 24 71 34 15 6 2 1
48 484 343 221 128 66 30 12 4 1 23 55 26 11 4 1
47 449 311 195 110 55 24 9 3 1 22 43 19 8 3 1
46 414 280 172 94 46 20 7 2 1 21 32 14 5 2 1
45 390 251 150 80 38 16 6 2 20 24 10 4 1
44 346 224 130 68 31 13 4 1 19 17 7 2 1
43 314 199 112 57 26 10 3 1 18 12 5 2
42 283 174 96 47 21 8 3 1 17 8 3 1
41 253 152 82 39 17 6 2 1 16 6 2 1
40 225 131 69 32 13 5 1 15 4 1
39 199 113 57 26 10 4 1 14 2 1
38 174 96 48 21 8 3 1 13 1
37 151 81 39 17 6 2 1 12 1
36 131 68 32 13 5 2 11
35 112 57 26 10 4 1 10
34 95 47 21 8 3 1
33 80 38 16 6 2 1
32 66 31 13 5 2
31 55 25 10 4 1 TABEL Risico op score kleiner dan de zak slaag
30 45 19 8 3 1 grens, voor verschillende studiestrategieën
29 36 15 6 2 1 en toetsen met verschillende aantallen
28 29 12 4 1 vragen. (in duizendsten).
27 23 9 3 1
26 18 7 2 1
25 14 5 2
24 10 4 1
23 8 3 1
22 6 2 1
21 4 1
20 3 1
______________________________________________________________________________________________________
-------------------------------------------------------------------------------------------------------------
studiestrategie studiestrategie
zak zak-
slaag 12 13 14 15 16 17 18 19 20 21 22 slaag 12 13 14 15 16 17 18 19 20 21 22 23 24
grens 25 25 25 25 25 25 25 25 25 25 25 grens 25 25 25 25 25 25 25 25 25 25 25 25 25
------------------------------------------------ ---------------------------------------------------------
60 toets 60 vragen 999 994 979 50 toets 50 vragen 999 997 991 969 898 676
59 998 993 978 932 49 999 996 988 964 903 756 454
58 999 998 994 982 947 862 48 999 996 988 967 918 810 609 302
57 999 995 986 961 901 777 47 999 996 989 9?2 933 851 703 475 200
56 999 996 989 971 929 842 683 46 999 997 991 977 946 883 770 592 360 132
55 999 997 992 980 950 887 772 588 45 999 997 993 982 958 909 821 680 486 267 86
54 999 998 995 986 965 920 835 695 497 44 999 998 994 986 967 929 860 747 586 389 195 56
53 999 996 990 976 944 882 775 614 412 43 999 996 989 975 946 891 801 667 493 304 139 36
52 999 998 994 983 961 916 835 708 534 336 42 999 997 992 981 959 916 844 733 583 407 233 98 23
51 999 996 989 973 941 881 781 637 457 269 41 998 994 986 969 936 879 787 659 499 328 176 68 14
50 999 997 993 982 959 915 839 722 565 385 213 40 996 990 978 952 907 832 724 582 420 260 130 46 9
49 998 995 988 972 940 883 790 658 494 319 166 39 993 984 965 929 869 778 654 505 346 202 94 31 6
48 997 993 982 959 916 844 736 592 425 261 128 38 989 975 947 900 824 718 582 430 280 154 67 21 3
47 995 988 972 942 887 800 678 526 361 210 97 37 982 961 924 863 772 652 509 359 222 115 47 14 2
46 993 982 960 919 852 751 617 460 302 167 73 36 973 944 895 819 714 583 438 295 173 85 33 9 1
45 989 973 944 892 811 697 554 398 250 131 54 35 959 921 859 769 651 514 370 238 132 61 22 6 1
44 983 962 924 660 765 640 492 339 204 102 40 34 942 892 816 713 585 445 307 188 100 44 15 4
43 975 947 899 823 715 591 431 295 164 78 29 33 919 857 767 652 518 379 250 146 73 30 10 2
42 965 929 869 780 662 521 373 237 130 59 21 32 891 815 712 588 451 317 200 112 53 21 6 1
41 952 906 835 733 605 461 318 194 102 44 15 31 856 767 653 522 386 260 157 84 38 14 4 1
40 935 879 795 683 548 404 268 157 78 32 10 30 815 714 590 456 325 210 121 61 26 9 3
39 914 847 751 623 490 349 223 125 60 23 7 29 769 656 526 392 268 166 92 44 18 6 2
38 889 811 704 574 433 298 183 98 45 17 5 28 716 594 461 331 218 129 68 31 12 4 1
37 860 769 652 517 378 250 148 76 33 12 3 27 659 530 397 275 173 99 50 22 8 2 1
36 826 724 599 461 326 208 118 58 24 8 2 26 598 466 337 224 135 74 35 15 5 1
35 788 675 544 406 277 170 93 44 18 6 1 25 534 402 280 179 104 54 25 10 3 1
34 745 623 488 353 232 138 72 33 13 4 1 24 470 341 228 140 77 38 17 6 2 1
33 698 579 433 302 192 110 55 24 9 3 1 23 406 284 182 107 57 27 11 4 1
32 648 514 379 256 157 86 42 17 6 2 22 344 231 143 80 41 18 7 2 1
31 595 459 327 214 126 66 31 12 4 1 21 286 185 109 58 28 12 5 2
30 541 405 279 176 100 51 22 9 3 1 20 233 144 81 42 19 8 3 1
29 486 352 235 142 78 38 16 6 2 19 185 109 59 29 13 5 2 1
28 431 302 194 113 60 28 11 4 1 18 143 81 42 19 8 3 1
27 377 255 158 89 45 20 8 3 1 17 108 58 29 13 5 2 1
26 325 212 127 69 33 14 5 2 16 79 41 19 8 3 1
25 276 174 100 52 24 10 4 1 15 56 27 12 5 2 1
24 231 140 77 39 17 7 2 1 14 39 18 8 3 1
23 189 111 59 28 12 5 2 13 25 11 4 2 1
22 153 86 44 20 8 3 1 12 16 7 3 1
21 121 65 32 14 5 2 1 11 10 4 1 16 17 18 19 20 21 22
20 94 48 23 10 4 1 10 6 2 1 25 25 25 25 25 25 25
19 71 35 16 6 2 1 ------------------------------------------------
18 53 25 11 4 1 40 toets 40 vragen 999 998 994 983 951
17 38 17 7 3 1 39 999 997 991 976 939 856
16 27 11 4 2 38 999 996 989 972 937 865 732
15 18 7 3 1 37 999 998 996 989 973 941 878 768 598
14 12 5 2 1 36 999 999 996 989 975 946 992 900 659 471
13 7 3 1 35 999 999 996 990 978 952 906 827 707 546 358
12 5 2 1 34 999 997 992 981 959 919 851 748 608 438 264
11 3 1 15 16 17 18 19 20 21 22 33 997 993 984 965 931 873 784 660 507 341 189
10 1 25 25 25 25 25 25 25 25 32 994 987 971 942 892 815 706 568 411 258 132
------------------------------------------------ 31 989 976 952 909 843 746 621 475 325 190 90
25 toets 25 vragen 999 998 996 990 979 950 890 30 981 961 925 967 782 669 534 388 249 137 60
24 999 998 996 990 979 957 914 838 711 29 969 939 889 815 713 587 447 308 187 95 39
23 999 999 997 993 985 969 940 890 808 686 520 28 951 908 843 753 637 504 366 239 136 65 25
22 998 996 990 980 960 927 872 789 673 524 354 27 926 869 789 683 557 422 291 180 97 43 15
21 994 988 976 953 917 859 776 665 527 375 222 26 893 821 725 607 476 344 226 132 67 28 9
20 986 972 948 909 851 768 660 531 390 253 136 25 851 764 654 528 397 274 171 94 45 18 5
19 970 945 904 845 762 658 534 402 273 161 78 24 800 699 579 449 323 213 126 66 29 11 3
18 942 901 841 759 657 538 411 288 180 97 43 23 741 628 501 373 257 161 90 45 19 7 2
17 900 839 758 657 542 419 300 196 113 56 22 22 674 552 424 302 198 118 63 29 12 4 1
16 839 758 659 545 426 310 208 126 67 30 11 21 602 475 350 238 149 84 42 19 7 2 1
15 760 661 549 432 319 218 136 77 38 16 5 20 525 398 281 183 109 58 28 12 4 1
14 665 553 437 325 226 145 84 44 20 8 2 19 448 326 219 136 77 39 18 7 2 1
13 558 442 331 232 151 91 49 24 10 4 1 18 372 259 166 98 53 25 11 4 1
12 447 335 237 156 95 53 27 12 5 2 17 301 200 122 68 35 16 6 2 1
11 339 240 159 98 56 29 14 6 2 1 16 236 149 87 46 22 10 4 1
10 242 161 100 58 31 15 7 3 1 15 179 107 59 30 14 6 2 1
9 165 100 58 31 16 7 3 1 14 131 74 39 19 8 3 1
8 99 58 31 16 7 3 1 13 92 49 24 11 5 2 1
7 55 30 15 7 3 1 12 61 31 15 6 2 1
6 28 14 7 3 1 11 39 19 8 3 1
5 12 6 2 1 10 24 11 4 2 1
4 4 2 1 9 13 6 2 1
3 1 1 8 7 3 1
-------------------------------------------------------------------------------------------------------------
AITCHISON, J., and DUNSMORE, I. R. Statistical prediction analysis. Cambridge: Cambridge University Press, 1975.
BOSCH, A. J. The Pó1ya distribution. Statistica Neerlandica, 1963, 17, 201 213.
CRONBACH, L. J., and SNOW, R. E. Aptitudes and instructional methode. A handbook for research on interactions. New York: Irvington, 1977.
GELATT, H. B., VARENHORST, B., & CAREY, R. Deciding. New York: College Entrance Examination Board, 1972.
GELATT, H. B., VARENHORST, B., & CAREY, R. Deciding: a leader's guide. New York: College Entrance Examination Board, 1972.
GELATT, H. B., VARENHORST, B., CAREY, R., & MILLER, G. P. Decisions and outcomes. New York: College Entrance Examination Board, 1973.
GELATT, H. B., VARENHORST, B., CAREY, R., & MILLER, G. P. Decisions and outcomes: a leader's guide. New York: College Entrance Examination Board, 1973.
De GROOT, A. D. Some badly needed non statistical concepts in applied Psychometries. Nederlands Tijdschrift voor de Psychologie, 1970, 25, 360-376.
JOHNSON, N. L., and KOTZ, S. Urn models and their application; an approach to modern discrete probability theory. London: Wiley, 1977.
KENDALL, M. G., and STUART, A. The advanced theory of statistics, volume 1. London: Griffin, 1969.
LORD, F. M., and NOVICK, M. R. Statistical theories of mental test scores. London: Addison Wesley, 1968.
Van NAERSSEN, R. F. Over optimaal studeren en tentamens combineren. Openbare les. Amsterdam: Swets & Zeitlinger, 1970. html
Van NAERSSEN, R. F. Een model voor tentamens. Nederlands Tijdschrift voor de Psychologie. 1971, 26, 121-132 en 551-559.
Van NAERSSEN, R. F. A mathematical model for the optimal use of criterion referenced tests. Nederlands Tijdschrift voor de Psychologie, 1974, 29, 431 445. pdf
Van NAERSSEN, R. F. Het derde tentamenmodel met een toepassing. Tijdschrift voor Onderwijsresearch, 1976, 1, 161-171.
Van NAERSSEN, R. F. Over het nut van een tentamenmodel. Tijdschrift voor Onderwijsresearch, 1976, 1, 278-280.
NOVICK, M. R., and JACKSON, P. H. Statistical methods for educational and psychological research. Düsseldorf: McGraw Hill, 1974.
RAIFFA, H., and SCHLAIFER, R. Applied statistical decision theory. London: Massachusetts Institute of Technology Press, 1961.
TVERSKY, A. Assessing uncertainty. Journal of the Royal Statistical Society, Series B, 1974, 36, 148-159.
WILBRINK, B. Het verborgen vooroordeel tegen andere dan meerkeuze vraagvormen. ORD Congresboek, 1977a. html
WILBRINK, B. Cesuurbepaling. Methoden voor het bepalen van de grene zakken slagen bij studieonderdelen. Docentencursus 6. Amsterdam: COWO, Oude Turfmarkt 149, 1977b. html
aanvaardbaar
gebruikt in samenhang met risico. Een aanvaardbaar risico voor de student is een risico op dusdanig niveau dat de tijd en moeite die het nog verder verlagen van het risico zou kosten, voor deze student niet meer tegen het voordeel van het lagere risico opwegen. Hetzelfde natuurlijk wanneer het gaat om het RISICO voor het examen te zakken. (zie 5.2 & 5.4). Merk op dat aanvaardbaar in samenhang met RISICO te zakken voor het examen niet betekent dat bij onbereikbaar blijken van een aanvaardbaar RISICO niveau de student de studie zou staken (zie 8.5).
beheersing
niet de behaalde toetsprestatie, maar de (niet direkt waarneembare) ware beheersing van de leerstof, dat is de proportie vragen uit de (conkrete of tenminste denkbare) verzameling van alle vragen over de leerstof die hij goed zou kunnen beantwoorden wanneer hem de vragen voorgelegd zouden worden. (zie hoofdstuk l).
geloofsverdeling
de waarschijnlijkheidsverdeling (zie daar) waarvan de student denkt dat die zijn ware beheersing van de leerstof goed weergeeft (zie hoofdstuk 3).
kansverdeling
zie 'voorspellende kansverdeling'.
leercurve
curve die het verband aangeeft tussen bestede tijd en bereikte ware beheersing van de leerstof. In de cursus gebruikt als hulpmiddel voor het opsporen van ongeveer optimale studiestrategieën (zie 6.2 en
bijlage D).
psychometrie
statistische theorie van het meten met behulp van psychologische tests (zie bijv. Lord & Novick 1968); als zodanig niet zonder meer toepasbaar op toetsing in het onderwijs.
punten
ruwe score (bijvoorbeeld het aantal vragen goed) behaald op een toets (tentamen), eventueel gewogen met de aan die toets toegekende wegingsfaktor (zie daar). Het is natuurlijk mogelijk om punten om te zetten tot cijfers op de in nederland gebruikelijke schaal van 1 tot 10, maar daarmee wordt niets gewonnen aan doorzichtigheid.
risico
(geschatte) kans om een minimaal benodigd aantal punten niet te halen (een onvoldoende te halen, het examen niet te halen, e.d.).
tentamenmodel modelmatige beschrijving van optimaal studeergedrag in de voorbereiding op tentamens. (zie bijlage B).
toets
gebruikt als verzamelnaam voor iedere vorm van beoordeling (met name eindbeoordeling) in het onderwijs. Dus niet alleen de meerkeuze toets, maar evenzeer schriftelijke toetsing (essay, open eind), mondelinge ondervraging, of praktijktoetsing (het maken van werkstukken als proeve van bekwaamheid).
variantie
technische term voor de mate van gevarieerdheid in scores, of in de voorspellende kansverdeling (zie daar) voor de toetsscore. Zie voor behandeling van dit begrip teksten statistiek.
verwachting of verwachte waarde zijn technische termen voor wat in de wandeling het gemiddelde heet. Omdat een voorspellende kansverdeling geen waarneembare verdeling is waar je over de waarnemingen het gemiddelde kunt berekenen, spreken we daar bij voorkeur over de verwachting, en niet over het gemiddelde.
verzameling
de verzameling van alle relevante vragen over de leerstof die in aanmerking komen voor opname in de toets. Deze verzameling kan in conkrete vorm bestaan (een boek met alle vragen), of slechts omschreven zijn (zodat duidelijk is welke vragen er wel, en welke er niet toe behoren). Deze omschreven verzamelingen worden in de tekst denkbare verzamelingen genoemd.
voorspellende kansverdeling voor de toetsscore
Geeft voor iedere mogelijke score op de toets de kans dat die score behaald zal worden. gegeven het aantal vragen dat de toets zal bevatten, en gegeven dat de student een waarschijnlijkheidsverdeling (zie daar) heeft op gesteld voor de mate waarin hij denkt de stof te beheersen. (zie hoofdstuk 4).
waarschijnlijkheid
is gewoon een ander woord voor kans; in de cursustekst wordt de term waarschijnlijkheid bij voorkeur gebruikt waar het gaat om het schatten van de eigen ware beheersing, en wordt over kans gesproken waar het gaat om de te behalen score op de toets.
waarschijnlijkheidsverdeling
een technische term uit de statistische literatuur, waarvan in de cursustekst op enigszins intuitieve wijze gebruik gemaakt wordt. Zie hoofdstuk 3. Het oppervlak onder een waarschijnlijkheidsverdeling moet altijd gelijk aan 1 zijn, omdat waarschijnlijkheden altijd tot 1 moeten sommeren.
wegingsfaktor getal waarmee de toetsscore vermenigvuldigd wordt, om zodoende het aantal punten te verkrijgen dat in de telling voor het compensatorisch examen van belang is.
wisselstrategie
bepaalde strategie bij de planning van de studie inspanning onder een compensatorische examenregeling, zie paragraaf 8.4.
102
symbolen en afkortingen gebruikt in hoofdstukken 1 t/m 9.
c cesuur, minimum aantal punten dat nog een voldoende oplevert.
i index, bijv. r. is het risico voor toets i; i kan 1, 2, 3, etc. zijn, zoveel toetsen er te onderscheiden zijn.
m gemiddelde (of preciezer: de verwachte waarde).
p ware beheersing van de stof.
r risico (minder dan een aangegeven aantal punten x te scoren).
R RISICO (voor het examen te zakken), een enkele keer ook voor Risico (een studieonderdeel onvoldoende te maken), duidelijk uit de contekst.
s2 de variantie; s is de wortel uit de variantie, ook standaard afwijking genoemd.
t tijdseenheid (bijv. een aantal dagen), is persoonsgebonden. in het tentamenmodel: tijd nodig om de proportie niet geweten vragen te halveren.
u aantal tijdseenheden t. (soms ook als ut geschreven).
V de verwachting van hetgeen er tussen haakjes achter staat.
w gewicht, of wegingsfaktor.
x score op de toets.
HEx conjnctieve (hordenloop ) examenregeling.
CEx compensatorische examenregeling.
EIS aantal minstens te behalen punten om voor CEx te slagen.
RISICO kans om voor het examen te zakken.
Risico kans om niet binnen het toegestane aantal herkansingen voor een studieonderdeel te slagen.
risico kans om een onvoldoende te scoren op de toets, of kans om op de toets minder dan x punten te scoren.
Hoewel dit cursusboek destijds in onwaarschijnlijk korte tijd in elkaar is gezet, is het anno 2007 nog steeds de basis voor modellen voor toetsen, zoals het algemene toetsmodel, Strategic Preparation for Achievement tests, kortweg het SPA-model. De ingangspagina's voor publicaties, resp. huidige projecten zijn publicaties/model.htm en projecten/spa_project.htm.
www.benwilbrink.nl/78StudiestrategieCOWO.htm