Literatuur over decision-making
Ben Wilbrink
Gerd Gigerenzer, Ralph Hertwig & Thorsten Pachur (Eds.) (2011). Heuristics. The foundations of adaptive behavior. Oxford University Press. [niet als eBook in KB] info, & contents & abstract to every chapter available.
Gerd Gigerenzer and Wolfgang Gaissmaier (2011). Heuristic Decision Making. Annual Review of Psychology, 62, 451-482. abstract
Kris N. Kirby (2011). An empirical assessment of the form of utility functions. Journal of Experimental Psychology: Learning, Memory, and Cognition, 37, 461-476. abstract
James K. Rilling & Alan G. Sanfey (2011). The Neuroscience of Social Decision-Making. Annual Review of Psychology, 62, 23-48.
abstract
Robert Axelrod (1997). The complexity of cooperation. Agent-based models of competition and collaboration. Princeton University Press. isbn 0691015678
C. Emdad Haque 1987). Hazards in a fickle environment: Bangladesh. Kluwer Academic Publishers. isbn 0792348699
ao: Hazardous environment and disastrous impact - Human coping responses to natural hazards- Social class formation and vulnerability of the population: a historical account of human occupance and land resource management - Impacts of riverbank erosion disaster - Toward a sustainable floodplain development strategy
Daniel Kahneman & Amos Tversky (Eds.) (2000). Choices, values, and frames. Cambridge University Press. info
1. Choices, values, and frames [Kahneman, D., & Tversky, A. (1984). Choices, values, and frames. American Psychologist, 39, 341-350]; Part I. Prospect Theory and Extensions: 2. Prospect theory: an analysis of decision under risk; [Kahneman, D., & Tversky, A. (1979). Prospect theory: an analysis of decision under risk. Econometrica, 47: 263.] 3. Advances in prospect theory: cumulative representation of uncertainty [Tversky, A., and D. Kahneman (1992): “Advances in prospect theory: Cumulative representation of uncertainty,” Journal of Risk and Uncertainty, 5, 297-323.
pdf]; Part II. The Certainty Effect and the Weighting Function: 4. Compound invariant weighting function in prospect theory, paper by Drazen Prelec; 5. Weighing risk and uncertainty [Tversky, A., & Fox, C. R. (1995). Weighing risk and uncertainty. Psychological Review, 102, 269-283]; 6. A belief-based account of decision under uncertainty [Craig R. Fox & Amos Tversky (1998). in Management Science, 44.]; Part III. Loss Aversion and the Value Function: 7. Loss aversion in riskless choice: a reference-dependent model [Amos Tversky and Daniel Kahneman (1991). The Quarterly Journal of Economics, 106, 1039-1061]; 8. Anomalies: the endowment effect, loss aversion, and status quo bias [Daniel Kahneman, Jack L. Knetsch and Richard H. Thaler (1991). In Journal of Economic Perspectives, 5, 193-206]; 9. The endowment effect and evidence of nonreversible indifference curves [Jack L. Knetsch, in The American Economic Review, 79, 1277-1284]; 10. A test of the theory of reference-dependent preferences [Ian Bateman, Alistair Munro, Bruce Rhodes, Chris Starmer, and Robert Sugden, in The Quarterly Journal of Economics, 112, 479-506]; Part IV. Framing and Mental Accounting: 11. Rational choice and the framing of decisions [Amos Tversky and Daniel Kahneman (1986). Journal of Business, 59, 5251-78]; 12. Framing, probability distortions, and insurance decisions [Eric J. Johnson, John Hershey, Jacqueline Meszaros, and Howard Kunreuther (1993). In Journal of Risk and Uncertainty, 7, 35-51.]; 13. Mental accounting matters [Richard H. Thaler (1999). In Journal of Behavioral Decision Making, 12, 183-206]; Part V. Applications: 14. Toward a positive theory of consumer choice [o.a. over sunk costs] [Richard H. Thaler (1980). In Journal of Economic Behavior and Organization, 1, 39-60]; 15. Prospect theory in the wild: evidence from the field; 16. Myopic loss aversion and the equity premium puzzle; 17. Fairness as a constraint on profit seeking: entitlements in the market; 18. Money illusion; 19. Labor supply of New York City cab drivers: one day at a time; 20. Are investors reluctant to realize their losses?; 21. Timid choices and bold forecasts: a cognitive perspective on risk taking; 22. Overconfidence and excess entry: an experimental approach; 23. Judicial choice and disparities between measures of economic values; 24. Contrasting rational and psychological analyses of political choice; 25. Conflict resolution: a cognitive perspective; Part VI. The Multiplicity of Value: Reversals of Preference: 26. The construction of preference; 27. Contingent weighting in judgment and choice; 28. Context-dependent preferences; 29. Ambiguity aversion and comparative ignorance; 30. The evaluability hypothesis: explaining joint-separate preference reversals and beyond; Part VII. Choice over Time: 31. Preferences for sequences of outcomes; 32. Anomalies in intertemporal choice: evidence and an interpretation; Part VIII. Alternative Conceptions of Value: 33. Reason-based choice; 34. Value elicitation: is there anything in there?; 35. Economists have preferences, psychologists have attitudes: an analysis of dollar responses to public issues; Part IX. Experienced Utility: 36. Endowments and contrast in judgments of well-being; 37. A bias in the prediction of tastes; 38. The effect of purchase quantity and timing on variety-seeking behavior; 39. Back to Bentham? Explorations of expereiences utility; 40. New challenges to the rationality assumption.
Jerad H. Moxley, K. Anders Ericsson, Neil Charness, Ralf T. Krampe (2013). The role of intuition and deliberative thinking in experts' superior
tactical decision-making. Cognition, 124, 72-78.
abstract
Lichtenstein, Sarah Lichtenstein & Paul Slovic (Eds) (2006). The construction of preference. Cambridge University Press. isbn 0521542200
G. J. Mellenbergh (1979). De beslissing gewogen. In A. D. Groot. Rede als richtsnoer. Mouton: 's-Gravenhage. 183-196. Liber amicorum.
Vaithilingam Jeyakumar and Alexander Rubinov (Eds) (2004). Continuous optimization. Current trends and modern applications. Springer.
Wim J. van der Linden & Gideon J. Mellenbergh (1978). Coefficients for Tests from a Decision Theoretic Point of View. Applied Psychological Measurement 2, 119-134. abstract
Wim J. van der Linden & Gideon J. Mellenbergh (1977). Optimal Cutting Scores Using A Linear Loss Function. Applied Psychological Measurement 2, 593-599. abstract
Ariel Rubinstein (1998). Modeling bounded rationality. MIT Press. isbn 0262681005
pdf (whole book)
'bounded rationality' is een term van Herb Simon, die ook een kritiek geeft in het laatste hoofdstuk van dit boek.
Gerd Gigerenzer (2007). Gut feelings. The intelligence of the unconscious. Penguin. isbn 9780713997514
Ralph L. Keeney and Howard Raiffa (1976). Decisions with multiple objectives. Preferences and value tradeoffs. Cambridge University Press. isbn 0471465100
Hooker, C. A. Hooker, J. J. Leach & E. F. McClennen (Eds) (1978). Foundations and applications of decision theory. Volume I: Theoretical foundations. Volume II: Epistemic and social applications. Reidel. isbn 9027708428 (I) 9027708444 (II)
- ao: I:
- Dreyfus & Dreyfus: Inadequacies in the Decision Analysis Model of Rationality 115 [o.a. het Newcomb probleem]
- Nigel Howard: A Piagetian Approach to Decision and Game Theory 205
- R. Duncan Luce: Conjoint Measurement: A Brief Survey 311
- Isaac Levi: Newcomb's Many Problems 369
- Doris Olin: Newcomb's Problem, Dominance and Expected Utility 385
- R. D. Rosenkrantz: The Copernican Revelation 399
- VOLUME II
- Leon Ellsworth: Decision-Theoretic Analysis of Rawls' Original Position 29
- David Gauthier: The Social Contract: Individual Decision or Coflective Bargain? 47
- Alfred Kuhn: On Relating Individual and Social Decisions 69
- R. D. Rosenkrantz: Distributive Justice 91
Elke U. Weber (1994). From Subjective Probabilities to Decision Weights: The Effect of Asymmetric Loss Functions on the Evaluation of Uncertain Outcomes and Events. Psychological Bulletin, 115, No. 2, 228-242. pdf
p. 228: With this interpretative review, I attempt to present these often technical results and theories in an integrative and more accessible way. I argue that people's behavior in the judgment and decision situations discussed can be seen as responsive to self- or outwardly imposed constraints in their environment rather than as the result of perceptual or cognitive errors. In particular, I suggest that in situations in which an uncertain quantity needs to be assessed, for example, the probability with which some event will occur or the value of some object, people will be sensitive to the consequences of misjudging this quantity and that consequences are often asymmetric for over- as opposed to underassessments. As a result, judgments and choices that incorporate such considerations win often deviate from normative models, which ignore these consequences of misjudgments to which people are sensitive. In this article, I review more general theories in several different domains that capture these deviations, and I point out the common psychological intuition behind the better descriptive fit of these models.
Hillel J. Einhorn & Robin M. Hogarth (1978). Confidence in judgment: persistence of the illusion of validity. Psychological Review, 85, 395-416. )
. . . people have great confidence in their fallible judgment. This article examines how this contradiction can be resolved and, in so doing, discusses the relationship between learning and experience.(...) A model for learning and maintaining confidence in one's own judgment is developed that includes the effects of experience and both the frequency and importance of positive and negative feedback.
H. Swaminathan, Ronald K. Hambleton & James Algina (1975). A Bayesian decision-theoretic procedure for use with criterion-referenced tests. Journal of Educational Measurement, 12, 87-98.
preview
Gebruikt in 1980-artikelen.
Lord, F. M. (1985). Estimating the imputed social cost of errors of measurement. Psychometrika, 50, 57-68.
Fredric M. Lord (1980). Applications of item response theory to practical testing problems. Erlbaum. Ch. 11: Mastery testing.
P. van Rijn, A. Béguin & H. Verstralen (2009). Zakken of slagen? De nauwkeurigheid van examenuitslagen in het voortgezet onderwijs. Pedagogische Studiën, 86, 185-195.
abstract
Bastiaan J. Vrijhof, Gideon J. Mellenbergh & Wulfert P. van den Brink (1983). Assessing and Studying Utility Functions in Psychometric Decision Theory. Applied Psychological Measurement, 7, 341-357. abstract
- Onbegrijpelijk is waarom in een evident institutioneel model aan studenten wordt gevraagd nutsfuncties te specificeren bij het probleem van de docent. Natuurlijk komt er wat uit, dergelijk onderzoek levert altijd iets op. Maar wat? Dit is een geschikt artikel om naar te verwijzen waar het gaat om de theorie van utiliteitsfuncties zoals op dit moment gehanteerd. Ik zal tzt het laatste door Wim van der Linden geschreven overzicht checken en daar ook naar verwijzen om duidelijk te maken dat de opvattingen anno 1983 ook in 1994/1995 nog opgeld doen. p. 342: An essential point in decision-theoretic procedures is the specification of a loss or, equivalently, a utility function. Suppose an observed, discrete variable X (X = 0, 1, ..... , n) is used for making decisions on a continuous true state-of-nature variable Z. The general structure of a decision-theoretic procedure is the maximization of the expected utility, where the expectation is taken with respect to both X and Z (see, e.g., Ferguson, 1967, chap. 1): Dit is de kern van de vigerendede theorie, en het verbazingwekkende is dat de evidente problemen in deze conceptualisering niet zijn gesignaleerd (maar zie Novick et al 1976; Wilbrink 1980 TOR 2e artikel). 1) Om welke beslissingen gaat het? Hier is zonder omhaal van woorden aangenomen dat het toekennen van een ware score de beslissing is. In het onderwijs gaat het, behalve bij evaluatie van dat onderwijs, om de resultaten zelf, niet om de onderliggende ware scores: de ruwe scores / cijfers hebben betekenis, niet welk onderliggend construct dan ook, al moet hier bij worden aangetekend dat de toetsen waarop die cijfers behaald worden natuurlijk inhoudelijk verantwoord moeten zijn. 2) Een andere vooronderstelling is dat de docent de beslissing neemt. Dat gaat voorbij aan een aantal andere actoren in het onderwijs, waarvan de leerlingen / studenten niet de meest onbelangrijke zijn. 3) Een sterke vooronderstelling is dat de beslissing geen neveneffecten oproept: er zijn in deze theorie geen backwash effecten, maar er wordt evenmin gebruik gemaakt van de mogelijkheden (zoals door Van Naerssen wel verkend) om gewenste backwash effecten te verkrijgen. 4) nutsfuncties en verliesfuncties zijn niet equivalent, maar ik neem aan dat in het volgende alleen met nutsfuncties wordt gewerkt. Dan de formule, die is kenmerkend voor een volgende trits van problemen die in de literatuur op vele plaatsen zijn te vinden: 1) Onnauwkeurigheid: het gaat niet om het verwachte nut in het algemeen, maar voor een gegeven beslissing: E (U) gegeven dat de cesuur wordt gelegd bij X=x ;2) Vermijdbare ingewikkeldheid: de formule gaat uit van normal form analysis, terwijl de equivalente extensive form analysis zeer veel eenvoudiger is. Eenvoudig geformuleerd: voor het bepalen van de optimale cesuur is het voldoende voor iedere gegeven x de verdeling voor Z te hebben (de likelihood!), er is dus geen gezamenlijke verdeling voor X en Z nodig. 3) Er is stilzwijgend een verandering in de definitie van de te nemen beslissing opgetreden: er wordt geen beslissing over Z genomen, maar er wordt een dichotomie opgesteld, een heel ander soort beslissingsprobleem, waarvoor de analyse ontbreekt. De formule komt hier dus uit de blauwe lucht vallen. 4) De begrippen ’nut’ en ’verwacht nut’ lopen onontwarbaar door elkaar heen. Nut is de waardetoekenning aan mogelijke uitkomsten, terwijl verwacht nut een kenmerk is dat hoort bij een beslissingsalternatief. Alleen wanneer er geen onzekerheid is, vallen nut en verwacht nut samen. Over Z gespecificeerd kan er alleen sprake zijn van een nutsfunctie, omdat contingent op Z geen beslissingen kunnen worden genomen. Over X gespecificeerd, kan er in de conceptie van Vrijhof et al. alleen sprake zijn van verwacht nut, omdat omdat X zelf geen nut heeft maar de onderliggende Z wel. Vooral het laatste punt is erg belangrijk, ook voor dit onderzoek van Vrijhof et al.: zij hebben geen nutsfuncties laten specificeren, maar functies voor verwacht nut, en die zijn inclusief de stochastische structuur van de aa de proefpersonen voorgelegde probleemsituaties.
Donald A. Rock, John L. Barone and Robert F. Boldt (1972). A two-stage decision approach to the selection problem. British Journal of Mathematical and Statistical Psychology, 25, 274-282. abstract "Theoretical solutions developed on the computer suggest that a considerable amount of testing time may be saved with little or no decrease in the validity of the selection procedure for all values of the selection ratios."
Hans J. Vos (1997). Adapting the amount of instruction to individual student needs. Educational Research and Evaluation, 3, 79-97. abstract
The three-action problem - The linear utility model - Binomial distribution as psychometric model - Optimal number of interrogatory examples - An empirical example
Henk de Vos (1989). A rational-choice explanation of composition effects in educational research. Rationality and Society, 1, 220-239. (genoemd en gebruikt door Bosker & Guldemond, 1994 abstract
frog-pond effect
Pratt, J. W. (1964). Risk aversion in the small and in the large. Econometrica, 32, 122-136. (genoemd door vd Gaag par 2.3). Reprinted in Tummala, V. M. R, & Henshaw, R. C. (Eds.) (1976). Concepts and applications of modern decision models. Division of Research, Graduate School of Business Administration, Michigan State University, East Lansing, Michigan.
Pratt, J. W., Raiffa, H., & Schlaifer, R. (1964). The foundations of decision under uncertainty: an elementary exposition. Journal of the American Statistical Association, 59, 353-375. Tummala, V. M. R, & Henshaw, R. C. (Eds.) (1976). Concepts and applications of modern decision models. Division of Research, Graduate School of Business Administration, Michigan State University, East Lansing, Michigan.
Gideon J. Mellenbergh & Wim J. van der Linden (1978). Decisions based on tests: Some results with a linear loss function. Paper presented at the European Meeting on Psychometrics and Mathematical Psychology, University of Uppsala, Uppsala, Sweden, June 15-17, 1978. Kwantitatieve Methoden, 4, 51-61.
Two questions, reading the abstract: 1) is the resit properly modelled in decision-theoretic terms? 2) Is it really the case that personnel selection is an analogue?
Abstract An important problem in education is determining cutting scores on educational tests consisting of items that can be answered right or wrong. Students with the number of items answered correctly that is equal to or greater than the cutting score pass the test. The others must study the subject again and take a new test later. This problem is comparable to determining the cuttinq score on a selection test in applied psychology, for instance accepting people for a job, psychotherapy, treatment, and so on. An extra requirement that cutting scores for these procedures should meet, is that they should be fair with respect to the various categories represented amonq the applicants. A decision theoretic approach with a linear loss function, which results in a simple procedure for determining optimal scores, is dscussed.
Ad 1.1: the intention is to predict on the basis of the raw test scores.
Ad 1.2. No, correction. The to be ‘predicted’ scores turn out to be true scores of a variable ‘suitable’. How is it possible to predict platonic scores?
Ad 1.3 Introduces a linear loss function, following Mellenbergh & Van der Linden (1977). I will first annotate that one!
Mellenbergh, G.J., & Van der Linden, W.J. (1981). The linear utility model for optimal selection. Psychometrika, 46, 283 - 293.
Wim J. van der Linden & Gideon J. Mellenbergh (1977). Optimal cutting scores using a linear loss function. Applied Psychological Measurement, 1, 593-599.pdf
This is an exercise in reliability, as Wim van der Linden will call it later (1980, Applied Psychological Measurement). Does finding ‘optimal’ cutting scores, given one has ‘fixed in advance’ a latent cutting score solve any real problem? The article might present some useful techniques, or demonstrate some techniques to be not useful at all. Let’s see.
References: Hambleton & Novick (1973); Meskauskas (1976); Huynh (1976).
The analysis will be over the total group of testees. This particular choice is not discussed by the authors. An alternative analysis is to consider only the testees scoring x = c, c being the particular cutting score considered for analysis. Would that model choice have made a difference? Sure: an order of magnitude, much and much simpler, better transparency. See my 1980 in Tijdschrift voor Onderwijsresearch.
Specifying loss functions is a somewhat forced approach. Why not specify utility funtions?
One may wonder how it is possible and why it could be useful to specify utility on a variable that is latent. This is a serious objection; especially so where experimental subjects are being asked to specify their utilities. They will do so, of course, obligingly. (see dissertation Van der Gaag on this issue)
Reference to Huynh (1976) & Mellenbergh, Koppelaar & Van der Linden (1976) for threshold loss analysis: minimizing the risk. I will have to annotate these articles, too: searching for the ancestry of the concepts of loss and risc as used by Mellenbergh & Van der Linden. A shorcut: Mellenbergh & Gode 2005, last chapter on decision-theoretic analysis.
G. J. Mellenbergh & M. Gode (2006). Beslissend testgebruik. In W. P. van den Brink & G. J. Mellenbergh: Testleer en testconstructie (399-427). Boom. isbn 9053522395
info boek
I will comment in English, even though the book is in Dutch. The reason is that I expect the problematic aspects in this chapter to be typical of the decision-theoretic literature in the field of educational measurement.
The chapter identifies Cronbach & Gleser’s classification, allocation and selection, as well as Van der Linden’s (1985) mastery. In the latter case the prediction is of the latent trait or true score. Wow! This is 1977. Totally unacceptable, because is does not offer any practical solution? Let’s see. Mellenbergh & Gode here define allocation as classification; classification with Cronbach & Gleser is categorical (with the testee, not with the treatment): man/woman; healthy/cancer. I really am disappointed, already on the first page of the chapter. Will have to talk to Don about this, I suppose. The Van der Linden ‘mastery’ category is phoney and therefore superfluous (I have shown as much in my 1980 articles). The chapter does not treat the mastery decision at all; why then introduce this dubious distinction?
Utility functions get introduced on p. 405. Regrettably, this introduction is faulty. The text states: “A utility function represents what the ‘results’ are of the selection procedure’ [my translation, b.w.]. Expected utility gets mistaken voor utility. These concepts are categorically different! This is the kind of mistake that is rather typical of the literature on decision making in testing situations, regrettably.
The next problem is dat suitability is declared to be absolute: either the employee turns out to be suitable, or not. This kind of rationalizing is not unusual in selection psychology, yet it is very clumsy and above all it is unnecessary. It is also unnecessary if one has to take pass-fail decisions, as will be the case in, f.e., the situation depicted in Figure 12.1.
Here threshold loss gets introduced. The reference is Hambleton & Novick 1973. I will now annotate that one, it is pretty basic to pretty much all that has been published later on utility models for achievement tests.
Wim J. van der Linden (1985). Decision theory in educational research and testing. In T. Husen & T. N. Postlethwaite (Eds.), International encyclopedia of education: Research and studies (pp. 1328-1333). Oxford: Pergamon Press.
Lee J. Cronbach & Goldine C. Gleser (1957/1965 ). Psychological tests and personnel decisions. University of Illinois Press.
Ronald K. Hambleton & Melvin R. Novick (1972). Toward an integration of theory and method for criterion-referenced tests. ACT Research Report 53. Journal of Educational Measurement, 1973, 10, 159-170.
pdf
The basic paradigm, believe or not, is sketched verbally in the following citation. It has been followed stubbornly by many researchers not asking some critical but simple questions. The formal apparatus follows the next description (see the report).
The primary problem in the new instructional models, such as individually prescribed instruction, is one of determining, if
πi, the student's mastery level, is greater than a specified standard
πo. Here,
πi is the ‘true’ score for an individual i in some particularly well-specified content domain. It
may represent the proportion of items in the domain he could answer successfully. Since we cannot administer all items in the domain, we sample some small number to obtain an estimate of
πi, represented as E(
πi). The value of
πo is the somewhat arbitrary threshold score used to divide individuals into the two categories described earlier, i.e., Masters and Nonmasters.
Basically then, the examiner's problem is to locate each examinee in the correct category. There are two kinds of errors that occur in this classification problem: false positives and false negatives. A false-positive error occurs when the examiner estimates an examinee's ability to be above the cutting score when, in fact, it is not. A false-negative error occurs when the examiner estimates an examinee's ability to be below the cutting score when the reverse is true. The seriousness of making a false-positive error depends to some extent on the structure of the instructional objectives. It would seem that this kind of error has the most serious effect on program efficiency when the instructional objectives are hierarchical in nature. On the other hand, the seriousness of making a false-negative error would seem to depend on the length of time a student would be assigned to a remedial program because of his low test performance. (Other factors would be the cost of materials, teacher time, facilities, etc.) The minimization of expected loss would then depend, in the usual way, on the specified losses and the probabilities of incorrect classification. This is then a straightforward exercise in the minimization of what we would call threshold loss.
p. 4
The formal model then gets presented in a formalistic way that makes it rather difficult to understand. Let me therefore first report in my own words what the authors propose here, and the extensions of the model that in my opinion are necessary to avoid any fuzziness..
-
The situation to be modeled is that of pass-fail scoring, failed students will have to resit the test after some extra preparation time.
-
The goal variable is mastery, the latent trait or true score that is.
-
The utility function on mastery is a threshold funtion, f.e. it is zero below the point of sufficient mastery, one above it.
-
The exact ‘point of sufficient mastery’ is assumed to be known! This is unacceptable, but at this point I will go along with this assumption. A complete decision theoretic approach, of course, should not hinge on this kind fuzziness, but instead resolve it. For example, by using a utility function that is derived from or identical with the learning curve for mastery.
-
Somehow costs are relevant too according to the authors; they do not explicitly model it, however. Fuzziness again. I will leave costs out of the model altogether.
-
The model may be applied in the case there is only one student, as well as in the case of groups (in the latter case some Bayesian statistics might be used forfine tuning)
-
The question then is: given the individual’s test score X=x, should she be passed, or failed?
-
Some mapping of observed score on the mastery variable is needed. I prefer using a binomial model here, so there is a definite likelihood function on the mastery variable (SPA-model)
-
Expected utility for the pass decision under threshold utility E(u1) then simply is the probability this individual is a master.
-
Now the question is: what is the expected utility of the fail-decision? The Hambleton-Novick model is thoroughly fuzzy on this point. Let me try to be specific, then
-
Assume there is only one resit (it is always possible to extend the model to more resits, see, f.e., Van Naerssen’s tentamenmodel)
-
After the resit, given de raw score on the resit, the expected utility E(u2) is, again, the probability of mastery.
-
The problem then becomes: what is the prediction of the score on the resit, given de score on the first test? For an immediate resit the prediction function is the betabinomial function. The situation is more complicated than that, however: the student will spend time learning, heightening her mastery score. This will soon get way too complicated to model abstractly, however.
- Assume empirical data to be available — as they should be, of course (a validation study) (otherwise: do the experiment to obtain them) — on the resit-scores given the score on the first test.
-
Assume a betabinomial distribution (n, a, b) fitted to the resit-score distribution given the score of our individual student X = x. The density function on mastery then is a beta function on parameters a and b, the expected utility E(U2) under threshold utility then is the probability of mastery.
-
The expected utility of the fail decision given X = x now is E(u2), and that value, of course, is always higher than E(u1) barring extreme contingencies. Therefore: always fail all students, unless X = n.
-
Wow. How further? Is there only fuzziness?
-
Plot E(u2) - E(u1) for X = 0, 1 .. n. For an impression of this kind of plot, see the figure.
-

-
A good criterion now might be to set the cutting/passing score X=c at the score c where the difference in expected utilities E(u2) - E(u1) is smaller than the corresponding difference for X = c-1. Assume the plot of differences to be decelerating in the range of interest, and deceleration first to increase and then to decrease. The optimum passing score then is the score corresponding to the inflection point: the number correct at the righ end of the steepest strech. Is this a procedure resulting in the optimal cutting score, within the restrictions of the situation as given? No, but it obviates fuzzy talk about costs. Call this solution ‘satisficing’ (Herbert A. Simon): it is evidently the case ‘better’ models can be developed, but this solution in many cases will do perfectly.
- Simon introduced the distinction maximizers - satisficers in 'Rational choice and the structure of the environment. Psychological Review, 1956, 63, 129-138 (repr in his Models of thought as well as in his Models of man, social and rational. Wiley, 1957.
-
Observe that in the above exposition there is no need for talk about ‘false negatives’ or ‘false positives’, or ‘incorrect decisions’. Also this kind of terminology does not belong in science: it is value-laden, better get rid of it.
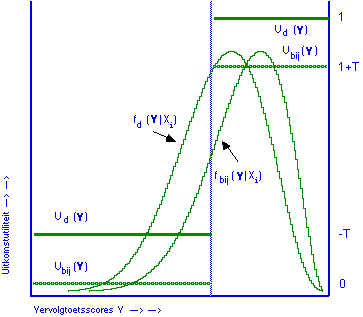 The figure is from Wilbrink 1980b, Figure 3. It illustrates the situation pretty well. I did not succeed in 1980 to get rid of the fuzzy ‘costs’ of the resit, however ;-)
The figure is from Wilbrink 1980b, Figure 3. It illustrates the situation pretty well. I did not succeed in 1980 to get rid of the fuzzy ‘costs’ of the resit, however ;-)
The test supposedly is a rather short one, the authors never suggest a specific number of items, however. Yet the model has been used in later years for more serious testing in, for example, higher education. Will that make a difference? Supposedly so, but I do not know of any analyses on the subject (they should be available in the literature, I suppose).
Let me first take a look at the following: “Basically then, the examiner's problem is to locate each examinee in the correct category.” This is problematic, it runs counter to the intention to find an acceptable utility function on the goal variable that is relevant to the situation. The goal variable is not correct classification, it is mastery. The problem then is to optimize the level of mastery, using the instrument of extended instruction/learning and a second test., implying a cutoff score on the first test.
Another problem here is the decision to reduce the criterium variable ‘mastery’ to a dichotomy, for no good reason whatsoever. In fact, no reason is given at all, except implicitly that the talk of the town has it that there should be a very special point on the dimension of mastery: so special, in fact, that we speak of masters for those above this magical point, and non-masters for those still below it. I ridicule the thinking of Hambleton and Novick here, because they are smuggling in threshold utility. A mortgage on the house of decision theoretic test psychology. Categories are, f.e., man-woman; cancer yes-no; cat or dog. What Hambleton and Novick are doing is introducing a pseudo category that seems to come in handy in a situation where pass-fail decisions have to be taken.
See here above also the already familiar mistake of calling an expected utility (or loss) simply utility (or loss). Yet these are fundamentally different. Utility is a function over the goal variable, in this case the goal variable is mastery. Expected utility is what obtains for the options in your decision problem, in this case passing or retaining students with a score X=c. In fact it is really simple: whether the decision is to pass or fail this person, her mastery π stays the same and has one definite utility. Meaning also: there is no way to construct a loss here, there are no differences in utility at all, for this person. Therefore the decision model needs to be developed further: failing the student means she has to sit the test again, after some extra time spent in preparation and thus ameliorating her mastery π. The loss in passing this student is then the absolute difference between the utilities of both levels of mastery.
Allow me one more comment on the sentence cited above. The authors have it that (some) decisions are ‘incorrect’. How can that be? Should other decisions have been taken? This is all very clumsy. If decisions have been taken reckoning with the information available, how is it that they can be ‘incorrect’? Herbert Simon was quite explicit on this point: if two alternatives have expected utilities near each other, choose the one with the somewhat higher expected utility. It might turn out that the outcome is disappointing; does that make the decision ‘incorrect’? I don’t think so.
There is quite another problem yet with this decision model: the decision maker is not the student. Yet students will adapt their preparation strategies contingent on where the cutting score will be placed (assuming the difficulty of the test will remain the same). See Van Naerssen (1970), or on this website my SPA-model. For the student as decision maker, the model is also one of threshold utility; assuming a pass will have utility 1, a fail utility 0, expected utility for the student is simply the probability to pass. That probability depends on her mastery. For the institution or the teacher the optimalization problem therefore is quite another one than Hamilton and Novick try to let us believe: it is to find that threshold on the test as well as the retest that will result in the highest mastery (for individuals or for the group of testees) in some sense (expected utility that is).
Naerssen, R. F. van (1965). Enkele eenvoudige besliskundige toepassingen bij test en selectie. Nederlands Tijdschrift voor de Psychologie, 20, 365-380. fc
Hunter, J. E. , & Schmidt, F. L. (1980?). Fitting people to jobs: the impact of personnel selection on national productivity. In Fleishman, E. A. (Ed. ), Human performance and productivity. (COWO?). fc selectie
Chen, J.J., & M.R. Novick (1982) On the use of a cumulative distribution as a utility function in educational or employment selection. Journal of Educational Statistics, 7, 19-35. fc uit het abtract: A least-squares procedure, developed by Lindley and Novick for fitting a utility function, is applied to truncated normal and extended beta distribution functions. The truncated normal and beta distributions avoid the symmetry and infinite range restrictions of the normal distribution and can provide fits in some cases in which the normal functional forms cannot provide a reasonable fit.
Novick & Grizzle (1965). A Bayesian analysis of data from clinical trials. JASA. (fc)
Novick (1980). Statistics as psychometrics. Pm, 45: 411. (fc)
Melvin R. Novick and D. V. Lindley (1979). Fixed-state assessment of utility functions. Journal of the American Statistical Association, 74, 306-310. (fc) preview
This approach may be a useful alternatiev to fixed probability methods, but only in an interactive environment in which the resolution of incoherence is encouraged and facilitated.
Melvin R. Novick and D. V. Lindley (1978). The use of more realistic utility functions in educational applications. Journal of Educational Measurement, 15, 181-191. fc preview
Sluit aan bij de manier waarop Pratt, en ook Schlaifer, nutsfuncties opstellen. De summary:
"The use of distribution functions has been shown to provide a more flexible approach to utility analysis than previous methods used in educational decisionmaking (sic). Our expectation is that a variety of forms will be studied to determine those most appropriate in particular educational applications. A variety of such forms is now available on the Computer Assisted Data Analysis monitor, distributed by the University of Iowa."
Michael T. Kane & Robert L. Brennan (1980). Agreement coefficients as indices of dependability for domain-referenced tests. APM, 4, 105-126. (loss functions)
pdf
Julius Kuhl (1978). Standard setting and risk preference: an elaboration of the theory of achievement motivation and an empirical test. Psychological Review, 85, 239-248. abstract
It should be noted that personal standards for self-evaluation are not identical with level of aspiration, which has been studied extensively as a result rather than as a determinant of achievement motivation (Atkinson & Litwin, Heckhausen).
N. v.d. Gaag (1990). Empirische utiliteiten voor psychometrische beslissingen. Proefschrift UvA 22 november 1990 (promotor: Don Mellenbergh).
mijn notitie d.d. 4-2002: Dan blijkt dat van proefpersonen heel vreemde dingen worden gevraagd, en dat ze keurige antwoorden geven die bij benadering lineaire nutsfucnties (inderdaad: twee, over ware beheersing) opleveren. Dit zijn experimenten die heel bruikbaar zijn om te illustreren hoe volgzaam proefpersonen zijn (niet alle proefpersonen, trouwens, er is wel een enkele opstandige proefpersoon geweest). Bijzonder problematisch, maar dat gaat al terug tot op het onderzoek van Vrijhof (1981) (zie Psychon aanvraag, 1986, van Mellenbergh), is dat studenten, als student, en docenten, als docent, tot dezelfde nutsfuncties komen. Dat suggereert dat de resultaten van deze onderzoeken artefactueel kunnen zijn
par 2.3: ‘De houding ten opzichte van risico heeft zijn weerslag op de utiliteiten. Er zijn verscheidene maten ontwikkeld om deze risicohouding te meten. De Pratt-Arrow maat geniet hiervan de meeste bekendheid. (zie o.a. Pratt, 1964; Krzysztofowicz, 1983 en Pope, 1983).’
Dit moet ik uitzoeken, want risico is nu juist inbegrepen in de nutsfunctie (Keeney & Raiffa! Bv. risicomijdende, risicozoekende functies). vd Gaag gaat uit van de misvatting dat voor besliskundige cesuurbepaling de cesuur op de onderliggende trek to al bekend moet zijn. Hfdst. 3:
‘Met behulp van de psychometrische besliskunde kan een waarde voor c worden bepaald die optimaal is, gegeven de gekozen waarde voor to.’
vd Gaag gaat ook uit van de bijzondere opvatting over wat utiliteit is (einde par. 3.1):
‘Voorwaarde hierbij is dat utiliteiten worden gespecificeerd als functie van de behandeling en het criterium.’
vd Gaag behandelt in par. 3.2 kort en m.i. onvolledig het verschil tussen extensive forms [sic] analysis en normal forms analysis. vd Gaag vermengt in par. 3.3 het nut over de onderliggende trek met een soort verliesfunctie gegeven de genomen beslissing. Dat is één van de fundamentele problemen in de literatuur in de school van van der Linden, als ik dat zo even mag aanduiden (de misvatting komt in de literatuur al eerder voor, ik zal een onderzoekje doen wie ermee is begonnen). vd Gaag haalt in 4.1 een platonische misvatting binnen: ‘De criteriumscore op zich is echter een vaststaand gegeven.’
Dat is beggging the question. In par. 4.5 weer verwoord dat de ware cesuur al bekend moet zijn:
‘Voor het bepalen van de optimale cesuur op de test is het van belang dat het punt op he criterium waarbij de utiliteitsfuncties voor beide beslissingen (slagen en zakken, dan wel aannemen en afwijzen) elkaar snijden (‘het snijpunt’), bekend is. Als de beslisser zelf de standaard to op het criterium heeft vastgesteld, dan is het aannemelijk dat de functies elkaar in dit punt snijden. Als dit niet het geval is, dan is het mogelijk dat het snijpunt niet samenvalt met de standaard to. De exacte waarde van het snijpunt kan worden bepaald door rechtsstreeks te vragen naar het punt op het criterium waarbij beide beslissingen hetzelfde worden gewaarderrd.’
Nou ja.
éénmaal fout gestart, blijft het behelpen. par. 4.6:
‘Om tot één unieke optimale waarde voor de cesuur te komen is het noodzakelijk dat de utiliteitsfuncties voor de beslissingen slagen en aannemen monotoon niet-dalende functies zijn, en de utiliteitsfuncties voor de beslissingen zakken en afwijzen monotoon niet-stijgende functies.’
Hfdst. 5: het is mij een raadsel wat de rechtvaardiging is om studenten te vragen nutsfuncties te specificeren voor beslissingen die zij zelf niet nemen of hoeven te nemen. Ook heel wonderlijk is dat bij de vage opdrachten die de proefpersonen voorgelegd krijgen, in het merendeel van de gevallen keurige functies verschijnen die in overeenstemming zijn met de foute theorie (geven eerdere publicaties over dit type experimentjes misschien een aanwijzing of er uiteindelijk methoden gekozen zijn die opleveren wat ervan werd verwacht?). p. 66 onderaan: ik begrijp niets van het makkelijke switchen van testscores naar onderliggende trek. Leuke opmerking is hier:
‘Twee personen hebben aangegeven dat de functies voor slagen en zakken elkaar niet behoren te snijden. Zij waarderen de beslising slagen altijd meer dan de beslissing zakken, onafhankelijk van de criteriumscore.’
Hier zit misschien ook een aanwijzing voor wat de manco is in de methode: de proefpersonen waarderen de mogelijke uitkomst van de beslissing. Je hebt dat hele gedoe met nutsfuncties nu juist nodig om die beslissing te kunnen nemen. par. 5.2.4 vd Gaag voelt nattigheid:
‘Het is immers voor de meeste studenten altijd aantrekkelijker om te slagen dan om te zakken, onafhankelijk va de hoeveelheid kennis die zij hebben.’
Ze zegt daarmee in het tweede vooronderzoek rekening gehouden te hebben, maar dat ontgaat mij toch. Ik denk dat de ‘methode Direct’ gewoon niet deugt:
‘Voor de methode Direct krijgen de beslissingen slagen en zakken bij een gegeven kennisniveau altijd dezelfde utiliteitswaarde met een tegengesteld teken toegewezen (bijvoorbeeld +3 voor slagen en -3 voor zakken).’
Ik vind dit wonderlijk, en enkele proefpersonen ook:
‘Niet alle personen konden op deze manier hun mening goed tot uiting brengen. In het tweede vooronderzoek werd dit probleem verholpen door beide beslissingen in één opgave apart te laten beoordelen.’
par. 5.3.1 De methode Bechtel leidt dan tot de volgende vraag aan proefpersonen:
‘U BENT GESLAAGD. Geef aan in welke mate u meer waarde aan deze beslissing hecht bij het ene kennisniveau dan bij het andere kennisniveau: 40% 9 8 7 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 9 70 %.’
Dat is een merkwaardige vraagstelling. Er is immers maar één waar kennisniveau, en dat is onbekend. Wat zou er omgaan in de grijze hersencellen van deze proefpersonen? par. 9.2, p. 122:
‘Van den Brink (1982) verdedigt het individuele standpunt, waarbij de prestaties van de groep geen invloed hebben op de beslissing voor een gegeven persoon.’
par. 9.4, p. 125:
‘Een serieuze belemmering bij de toepassing wordt gevormd door het feit dat de beslissingen voor individuele personen afhankelijk zijn van de prestaties van de groep waartoe zij behoren. Voor selectiebeslissingen valt dit vanuit het instituut gezien nog wel te verdedigen, maar voor beheersingsbeslissingen is dit op zijn minst een aanvechtbare strategie.’
Jammer dat dit opmerkingen na afloop van het onderzoek zijn. Ik heb onvrede met het soort beslissingen waar dit type onderzoek over gaat: dat zijn guillotine-beslissngen, keuzen tussen dood of leven: eenmaal dood, altijd dood. Dat is niet realistisch genoeg, het tentamenmodel van Van Naerssen is dan toch een heel eind verder op de goede weg.
-
G. J. Mellenbergh, W. P. van den Brink, & N. van der Gaag (1986). Utiliteitsfuncties voor psychometrische beslissingen. Psychon-aanvraag (promotieonderzoek van der Gaag). Bij deze aanvraag de volgende aantekeningen Op p. 2 wordt verwezen naar een overzichtsartikel van Wim van der Linden (1984). Decision theory in educational research and testing. In T. Husen & T. N. Postlethwaite (Eds) International ecyclopedia of education: research and studies. Oxford: Pergamon Press. Hij onderscheidt daarin vier typen psychometrische beslissingssituaties: classificatie, plaatsing, selectie, en beheersing, waarbij er bij de laatste een ‘intern criterium’ is, de mate van ‘ware’ kennis van de stof. Het probleem dat ik met deze formulering heb is dat de actor hier de psychometricus is, niet degene over wie wordt beslist. That goes against the grain of decision theory, al kun je er natuurlijk expliciet voor kiezen te optimaliseren vanuit de optiek van de docent. De grote vraag is dan wat voor zin het heeft studenten nutsfuncties te laten aangeven, zoals zowel in de onderzoeken van Vrijhof als van Van der Gaag gebeurt (naast docenten als proefpersonen). Op p. 3 blijkt dat Don Mellenbergh zich wel van het onderscheid bewust is, maar er geen consequenties uit trekt:
‘Een alternatief is degenen, die beslissingen nemen of ondergaan, zelf hun utiliteitsfunctie te laten specificeren.’ (mijn cursivering).
Deze uitspraak getuigt ook overigens van een hoog ivoren toren gehalte, wat juist voor besliskundige analyses niet nodig is.
In deze aanvraag wordt op p. 3 kort het onderzoek van Vrijhof weergegeven, waarbij studenten nutsfuncties moeten specificeren voor een kunstmatige situatie van geslaagd of gezakt te zijn (vignet-methode), waarvan ik de zin niet kan inzien. Bijzonder probleem is voor de beslissing gezakt en ook voor de beslissing geslaagd (alsof het om twee verschillende beslissingen zou gaan!) een nutsfunctie wordt aangegeven (maar het APM-artikel 1983 laat zien wat daar de voorgeschiedenis van is). Boeiend is de samenvatting bovenaan blz. 4 van de onderzoeken van Vrijhof en van der Gaag (scripties): (1) nutsfuncties specificeren kan betrouwbaar gebeuren (maar wat is de zin daarvan, wat is de validiteit?), (2) er zijn geen systematische verschillen tussen de nutsfuncties van docenten en leerlingen (dat verbaast mij; waarom zou je verwachten dat deze actoren identieke nutsfuncties hebben?; (3) minstens 70% van de empirisch bepaalde utiliteitsfuncties kan redelijk benaderd worden met een lineaire functie (dat is unbelievable).
= Gruijter Dato N.M. de Ronald K. Hambleton (1984) On Problems Encountered Using Decision Theory to Set Cutoff Scores APPLIED PSYCHOLOGICAL MEASUREMENT Vol. 8, No. 1, Winter 1984, pp. 1-8 In the decision-theoretic approach to determining a cutoff score, the cutoff score chosen is that which maximizes expected utility of pass/fail decisions. This approach is not without its problems. In this paper several of these problems are considered: inaccurate parameter estimates, choice of test model and consequences, choice of subpopulations, optimal cutoff scores on various occasions, and cutoff scores as targets. It is suggested that these problems will need to be overcome and/or understood more thoroughly before the full potential of1the decision-theoretic approach can be realized in practice. Linden Wim J. van der Some Thoughts on the Use of Decision Theory to Set Cutoff Scores: Comment on de Gruijter and Hambleton APPLIED PSYCHOLOGICAL MEASUREMENT Vol. 8, No. 1, Winter 1984, pp. 9-17 In response to an article by de Gruijter and Hambleton (1984), some thoughts on the use of decision theory for setting cutoff scores on mastery tests are presented. This paper argues that decision theory offers much more than suggested by de Gruijter and Hambleton and that an attempt at evaluating its potentials for mastery testing should address the full scale of possibilities. As for the problems de Gruijter and Hambleton have raised, some of them disappear if proper choices from decision theory are made, while others are inherent in mastery testing and will be encountered by any method of setting cutoff scores. Further, this paper points at the development of new technology to assist the mastery tester in the application of decision theory. From this an optimistic attitude towards the potentials of decision theory for mastery testing is concluded. Dato N. M. de Gruijter Ronald K. Hambleton Reply to van der Linden's "Thoughts on the Use of Decision Theory to Set Cutoff Scores"
Ronald K. Hambleton, Hariharan Swaminathan, James Algina& Douglas Bill Coulson (1978). Criterion-referenced testing and measurement: a review of technical issues and developments. Review of Educational research, 48, 1-47.
JSTOR read online free
Authors think in terms of classification. Philosophers would call this an category mistake. The better approach: decision-theoretic without artificial classificatory cutting scores.
Vos, H. J. (1990). Simultaneous optimization of decisions using a linear utility function. Journal of Educational Statistics, 15, 309-340. preview: http://www.jstor.org/discover/10.2307/1165091
W. J. van der Linden (1987). The use of test scores for classification decisions with threshold utility. Journal of Educational Statistics, 12, 62-75. open access
p. 62: Obviously, the classification problem is a decision problem, and as such it has definite relationships to other decision problems in educational and psychological testing. Elsewhere, the author has proposed a typology of test-based decisionmaking that, in addition to the classification decision, has the selection, mastery, and placement decisions as basic types of decisionmaking (van der Linden, 1985). Selection and mastery decisions differ from classification and placement decisions by the presence of only one treatment. In these decisions, it is the decisionmaker's task to decide whether or not to accept subjects for a certain treatment, whether or not they have profited enough from a treatment to be dismissed. The four basic types of decisions briefly defined here can be met both in their pure forms or in combination with each other. The latter is the case, for instance, in decisionmaking in individualized study systems that can be conceived of as networks consisting of these various types of decisions as nodes (van der Linden & Vos, 1986). Also, further refinements within each type are possible, for instance, by imposing quota restrictions or distinguishing between subpopulations varying on a relevant attribute (cf. van der Linden, 1985). An appropriate framework for dealing with decision problems such as the above is (empirical) Bayesian decision theory (e.g., Raiffa, 1968). Applications of Bayesian decision theory to selection (e.g., Chuang, Chen, & Novick, 1981; Cronbach & Gleser, 1965; Novick & Lindley, 1979), mastery (e.g., Hambleton & Novick, 1973; Huynh, 1976; van der Linden, 1980; van der Linden & Mellenbergh, 1977), and placement decision problems (e.g., Cronbach & Gleser, 1965; van der Linden, 1981) are amply available now, whereas Bayesian theory has also been used to deal with the problem of selection from different subpopulations (e.g., Mellenbergh & van der Linden, 1981; Petersen, 1976; Petersen & Novick, 1976). To date, however, the classification problem has been devoid of a decision-theoretic analysis [my emphasis, b.w.]. ] . . . The purpose of this paper is to demonstrate how the classification problem can be formalized as a problem of Bayesian decisionmaking. In particular, the case of classification with a threshold utility function is analyzed, and for this case it is indicated how optimal rules can be found for a variety of conditions. p. 73: Concluding Remarks TWo further comments are necessary. First, it is noted that the decisionmaker's task of specifying his or her utility parameter values, usually a delicate matter, is a somewhat simpler one in the present case of a threshold utility function. The decisionmaker only needs to provide values for the parameters wj and vi. In practical applications, this task can easily be performed using a lottery method well-known in this area (e.g., Luce & Raiffa, 1957, chap. 2) or via direct scaling of preferences (Vrijhof, Mellenbergh, & van den Brink, 1983 ). If it is believed that the final exam is not the ultimate criterion but that this lies in its civil effects, psychological well being, and so on, Keeney and Raiffa's handling of proxy attributes may be useful (Keeney & Raiffa, 1976, sect. 2.5). . . . The purpose of this paper was to give the reader the flavor of such differences between the traditional linear regression and a Bayesian approach to the classification problem.
Huynh Huynh (1977). Two simple classes of mastery scores based on the beta-binomial model. Psychometrika, 42, 601-608. !--hardcopy bak dm-->
preview
See Huynh (1976) on the idea of the referral task.
Huynh Huynh (1980). A non-randomized minimax solution for passing scores in the binomial error model. Pm, 45, 167.
abstract
Huynh Huynh (1982). Assessing efficiency of decisions in mastery testing. JESt, 7, 47-63.
preview
False positive error, false negative error.
Huynh Huynh (1976). On the reliability of decisions in domain referenced testing. JEM , 13, 265-276.
preview
bivariate beta-binmial model. In fact, an exercise in threshold loss with criterion referenced tests.
Daniel Gigone & Reid Hastie (1997). Proper analysis of the accuracy of group judgments. sychological Bulletin, 123, 149-167.
abstract
George K. Chacko (1971). Applied statistics in decision-making. American Elsevier. 0444001093
Conditions for Intuitive Expertise. A Failure to Disagree. Daniel Kahneman & Gary Klein (2009). American Psychologist pdf
Ben R. Newell, David A. Lagnado, David R. Shanks (2015 2nd). Straight choices. The psychology of decision making. Psychology Press. 9781848722835 info [UBL wassweg aanwezig] [Hoewel op een breder publiek gericht, is het wel up to date wat ontwikkelingen betreft]
Hal R. Arkes and Kennth R. Hammond (Eds.) (1986). Judgment and decision making. London: Cambridge University Press. isbn 0521339146 [er is in 1999 een 2e editie verschenen]
- a.o.
-
Multiattribute evaluation 13 W Ward Edwards & J Robert Newman 9uniek in deze bundel) (taken from their 1982 book under the same title)
-
Judgment under uncertainty: Heuristics and biases 38 Amos Tversky and Daniel Kahneman. Originally: Science 1974, 185, 1124-1131
-
Alternative visions of rationality 97 Herbert A. Simon (on bounded rationality etcetera) (taken from Simon's 1983 'Reason in human affairs') (also in Moser, 1990)
-
Science, values, and human judgment 127 Kenneth R. Hammond and Leonard Adelman. Science, 1976, 194, 389-396.
-
Choices, values, and frames 194 Daniel Kahneman and Amos Tversky. American Psychologist, 1984, 39, 341-350. Ook in Kahneman & Tversky (2000)
-
The Camp David negotiations 322 Howard Raiffa
- 24
Knowing with certainty: The appropriateness of extreme confidence 397 Baruch Fischhoff, Paul Slovic, and Sarah Lichtenstein
-
Cultural variation in probabilistic thinking: Alternative ways of dealing with uncertainty 417 George N. Wright and Lawrence D. Phillips
-
Reducing the influence of irrelevant information on experienced decision makers 449 Gary J. Gaeth and James Shanteau
-
Improving scientists' judgments of risk 466 Kenneth R. Hammond, Barry F. Anderson, Jeff-rey Sutherland, and Barbara Marvin
- 29
Expert judgment: Some necessary conditions and an example 480 Hillel J. Einhorn
-
Social Judgment Theory: Teacher expectations concerning children's early reading potential 523 Ray W. Cooksey, Peter Freebody, and Graham R. Davidson
-
An analysis-of-variance model for the assessment of configural cue utilization in clinical judgment 568 Paul J. Hoffman, Paul Slovic, and Leonard G. Rorer
- 37
Discretionary aspects of jury decision making 593 John C. Mowen and Darwyn E. Linder
-
Measuring the relative importance of utilitarian and egalitarian values: A study of individual differences about fair distribution 613 John Rohrbaugh, Gary McClelland, and Robert Quinn
-
The two camps on rationality 627 Helmut Jungermann
-
On cognitive illusions and their implications 642 Ward Edwards and Detlof von Winterfeldt
-
Beyond discrete biases; Functional and dysfunctional aspects of judgmental heuristics 680 Robin M. Hogarth
-
In one word: Not from experience 705 Berndt Brehmer
Kenneth R. Hammond (2000). Judgments under stress. Oxford University Press. isbn 0195131436 info
Judgments under stress are the kind of decisions leading to disasters such as with the Challenger
C. R. Bell (Ed.) (1979). Uncertain outcomes. MTP Press. isbn 0852001037
- ao.: Decision-making as a discourse J. S. Bruner 93-115
W. M. Goldstein & R. M. Hogarth (Eds) (1997). Research on judgment and decision making. Currents, connections, and controversies. Cambridge University Press. isbn 0521483344 info
- a.o.
- Eldar Shafir, Itamar Simonson, & Amos Tversky (1993): Reason-based choice. Cognition, 49, 11-36.
- Gerd Gigerenzer, Ulrich Hoffrage, & Heinz Kleinbölting (1991): Probabilistic mental models: A Brunswikian theory of confidence. Psychological Review, 89, 506-528.
- Kenneth R. Hammond, Robert M. Hamm, Janet Grassia, and Tamra Pearson: Direct comparison of the efficacy of intuitive and analytical cognition in expert judgment. abstract
- John W. Payne, James R. Bettman, & Eric J. Johnson: The adaptive decision maker: effort and accuracy in choice. (chapter in Hogarth, 1990)
- Joshua Klayman & Young-Won Ha: Confirmation, disconfirmation, and information in hypothesis testing. pdf
-
Robin M. Hogarth, Brian J. Gibbs, Craig R. M. MKenzie, & Margaret A. Marquis (1991): Learning from feedback: Exactingness and incentives. Journal of Exprimental Psychology: Learning, Memory, and Cognition, 17, 734-752.
-
Patricia W. Cheng & Laura R. Novick: Covariation in natural causal induction. pdf
-
Daniel Kahneman & Carol A. Varey: Propensities and counterfactuals: The loser that almost won. Journal of Personality and Social Psychology 59, 1101-1110. abstract
-
Colin F. Camerer & Eric J. Johnson: The process-performance paradox in expert judgment: How can experts know so much and predict so badly? pdf
-
Michael E. Doherty & Berndt Brehmer: The paramorphic representation of clinical judgment: A thirty-year retrospective. abstract
- Willem A. Wagenaar, Gideon Keren, & Sarah Lichtenstein: Islanders and hostages: Deep and surface structures of decision problems. Acta Psychlogica, 67, 175-189 (1988). abstract
- William M. Goldstein & Elke U. Weber: Content and discontent: Indications and inplications of domain specificity in preferential decison making. Psychology of Learning and Motivation 1995, vol 32, 83-136
- Lola L. Lopes: Between hope and fear: The psychology of risk.
Robin M. Hogarth (2001). Educating intuition. Chicago: The University of Chicago Press. isbn 0226348601
David T. Chuang, James J. Chen & Melvin R. Novick (1981). Theory and practice for the use of cut-scores for personnel decisions. JESt, 6, 129-152. abstract
James J. Chen & Melvin R. Novick (1982). On the use of a cumulative distribution as a utility function in educational or employment selection. JESt, 7, 19-35. abstract & https://sci-hub.st/10.2307/1165026
Coleman, J. S. (1986). Individual interests and collective action. Selected essays. London: Cambridge UP. UBL: 3594 C12
Cooper, W.S., Decision theory as a branch of evolutionary theory: a biological derivation of the Savage axioms. PR 1987, 94, 395-411.
Charles E. Davis, James Hickman and Melvin R. Novick (1973). A primer on decision analysis for individually prescribed instruction. Iowa City, Iowa: The Research and Development Division / The American College Testing Program. ACT Technical Bulletin no. 17. Not available on the ACT website (Research Reports are, Technical Bulletins not).
The decision maker can make one of the two types of errors. If he retains the student at the current level when, in fact, the student is a master, the student will probably repeat the current unit with only minimal gain. On the other hand, if the student is advanced when he has not mastered the topics on the current level, ultimately he may have to repeat both the current level and the one to which he had prematurely been advanced.
p. 6
Jon Elster & Nicolas Herpin (Eds.) (1994). The ethics of medical choice. London: Pinter. isbn 1855672111
Ferguson, T. S. (1967). Mathematical statistics. A decision theoretic approach. London: Academic Press.
Freeman, A. M., III (1993). The measurement of environmental and resource values. Theory and methods. Washington, D.C.: Resources for the Future. isbn 0915707691
Shaun P. Hargreaves Heap and Yanis Varoufakis (1995). Game theory. A critical introduction. London: Routledge. isbn 0415094038
Ben R. Newell, David A. Lagnado, David R. Shanks (2015 2nd). Straight choices. The psychology of decision making. Psychology Press. 9781848722835 info
Raab, M., & Gigerenzer, G. (2005). Intelligence as smart heuristics. In R. J. Sternberg & J. E. Pretz (Eds.), Cognition and intelligence: Identifying the mechanisms of the mind (pp. 188-207). Cambridge: Cambridge University Press.
pdf
McElreath, R., Boyd, R., Gigerenzer, G., Glöckner, A., Hammerstein, P., Kurzban, R., et al. (2008). Individual decision making and the evolutionary roots of institutions. In C. Engel & W. Singer (Eds.), Better than conscious? Decision making, the human mind, and implications for institutions (pp. 325-342). Cambridge, Mass.: MIT Press. pdf
Marsh, B., Todd, P. M., & Gigerenzer, G. (2004). Cognitive heuristics: Reasoning the fast and frugal way. In J. P. Leighton & R. J. Sternberg (Eds.), The nature of reasoning (pp. 273-287). Cambridge: Cambridge University Press.pdf
McGuire, C. B. McGuire & R. Radner (Eds) (1972). Decision and organization. A volume in honor of Jacob Marschak. North-Holland. isbn 0720433134 0444101209
(ao.: Roy Radner: Normative theory of individual decision: an introduction - Kenneth J. Arrow: Exposition of the theory of choice under uncertainty - Tjalling C. Koopmans: Representattion of preference orderings with independent components of consumption; Representation of preference orderings over time - Kenneth J. Arrow: The value of and demand for information - Martin J. Beckman: Decisions over time - Herbert A. Simon: Theories of bounded rationality 161-176)
Daniel Kahneman , Paul Slovic & Amos Tversky (Eds) (1982). Judgment under uncertainty: heuristics and biases. Cambridge University Press.
- Part I: Introduction Judgment under uncertainty: Heuristics and biases 3 Amos Tversky and Daniel Kahneman
- Belief in the law of small numbers 23 Amos Tversky and Daniel Kahneman
- Subjective probability: A judgment of representativeness 32 Daniel Kahneman and Amos Tversky
- On the psychology of prediction 48 Daniel Kahneman and Amos Tversky
- Studies of representativeness 69 Maya Bar-Hillel
- Judgments of and by representativeness 84 Amos Tversky and Daniel Kahneman
- Popular induction: Information is not necessarily informative 101 Richard E. Nisbett, Eugene Borgida, Rick Crandall, and Harvey Reed
- Causal schemas in judgments under uncertainty 117 Amos Tversky and Daniel Kahneman
- Shortcomings in the attribution process: On the origins and maintenance of erroneous social assessments 129 Lee Ross and Craig A. Anderson
- Evidential impact of base rates 153 Amos Tversky and Daniel Kahneman
- Availability: A heuristic for judging frequency and probability 163 Amos Tversky and Daniel Kahneman
- Egocentric biases in availability and attribution 179 Michael Ross and Fiore Sicoly
- The availability bias in social perception and interaction 190 Shelley E. Taylor
- The simulation heuristic 201 Daniel Kahneman and Amos Tversky
- Informal covariation assessment: Data-based versus theory-based judgments 211 Dennis L. Jennings, Teresa M. A mabile, and Lee Ross
- The illusion of control 231 Ellen J. Langer
- Test results are what you think they are 239 Loren J. Chapman and jean Chapinan
- Probabilistic reasoning in clinical medicine: Problems and opportunities 249 David M. Eddy
- Learning from experience and suboptimal rules in decision making 268 Hillel J. Einhorn
- Overconfidence in case-study judgments 287 Stuart Oskamp
- A progress report on the training of probability assessors 294 Marc Alpert and Howard Raiffa
- Calibration of probabilities: The state of the art to 1980 306 Sarah Lichtenstein, Baruch Fischhoff, and Lawrence 1). Phillips
- For those condemned to study the past: Heuristicsand biases in hindsight 335 Baruch Fischhoff
- Evaluation of compound probabilities in sequential choice 355 John Cohen, E, I. Chesnick, and D. Haran
- Conservatism in human information processing 359 Ward Edwards
- The best-guess hypothesis in multistage inference 370 Charles F. Gettys, Clinton Kelly III, and Cameron R. Peterson
- Inferences of personal characteristics on the basis of information retrieved from one's memory 378 Yaacov Trope Part VIII: Corrective procedures
- The robust beauty of improper linear models in decision making 391 Robyn M. Dawes
- The vitality of mythical numbers 408 Max Singer
- Intuitive prediction: Biases and corrective procedures 414 Daniel Kahneman and Amos Tversky
- Debiasing 422 Baruch Fischhoff
- Improving inductive inference 445 Richard E. Nisbett, David H. Krantz, Christopher Jepson, and Geoffrey T. Fong
- Facts versus fears: Understanding perceived risk 463 Paul Slovic, Baruch Fischhoff, and Sarah Lichtenstein
- On the study of statistical intuitions 493 Daniel Kahneman and Amos Tversky
- Variants of uncertainty 509 Daniel Kahneman and Amos Tversky
Hogarth, R. M. Hogarth (Ed. 1990). Insights in decision making. A tribute to Hillel J. Einhorn. University of Chicago Press. isbn 0226348563 — 356 pp. paperback near mint
met oorspronkelijke bijdragen, dus geen reader
- o.a. Thomas S. Wallsten: The costs and benefits of vague information 28-43
- Maya Bar-Hillel: Back to base rates 200-216
- Daniel Kahneman and Jackie Snell: Predicting utility.
- Colin F. Camerer: Behavioral game theory
Lichtenstein, Sarah Lichtenstein & Paul Slovic (Eds) (2006). The construction of preference. Cambridge University Press. isbn 0521542200
Original contributions!
- a.o.:
- 15 When Web Pages Influence Choice: Effects of Visual Primes on Experts and Novices 282 Naomi Mandel and Eric J. Johnson
-
16 When Choice Is Demotivating: Can One Desire Too Much of a Good Thing? 300 Sheena S. Iyengar and Mark R. Lepper
-
17 Constructive Consumer Choice Processes 323 James R. Bettman, Mary Frances Luce, and John W. Payne
-
18 Decision Making and Action: The Search for a Dominance Structure 342 Henry Montgomery
-
21 Constructing Preferences From Memory 397 Elke U. Weber and Eric J. Johnson
-
22 Reason-Based Choice 411 Eldar Shafir, Itamar Simonson, and Amos Tversky
-
23 The Affect Heuristic 434 Paul Slovic, Melissa L. Finucane, Ellen Peters, and Donald G. MacGregor
-
24 The Functions of Affect in the Construction of Preferences 454 Ellen Peters
-
27 New Challenges to the Rationality Assumption 487 Daniel Kahneman
-
29 Lay Rationalism and Inconsistency Between Predicted Experience and Decision 532 Christopher K. Hsee, Jiao Zhang, Frank Yu, and Yiheng Xi
-
30 Miswanting: Some Problems in the Forecasting of Future Affective States 550 Daniel T. Gilbert and Timothy D. Wilson
-
31 Economic Preferences or Attitude Expressions? An Analysis of Dollar Responses to Public Issues Daniel Kahneman, Ilana Ritov, and David A. Schkade
-
32 Music, Pandas, and Muggers: On the Affective Psychology of Value 594 Christopher K. Hsee and Yuval Rottenstreich
-
33 Valuing Environmental Resources: A Constructive Approach 609 Robin Gregory, Sarah Lichtenstein, and Paul Slovic
-
36 Informed Consent and the Construction of Values 668 Douglas MacLean
-
37 Do Defaults Save Lives? 682 Eric J. Johnson and Daniel G. Goldstein
Paul K. Moser (Ed.) (1990). Rationality in action. Contemporary approaches. Cambridge University Press. isbn 0521385989
- a.o.:
- Savage, L. J. (19**). Historical and critical comments on utility. Uit The foundations of statistics, 91-104.
- Ellsberg, D. (1961). Risk, ambiguity, and the Savage axioms. Quarterly Journal of Economics, 75, 643-669.
- Allais, M. (1979), de pp 67-95 uit The foundations of a positive theory of choice involving risk and a criticism of the postulates and axioms of the American school. In Allais, M., & Hagen, O. (Eds.) Expected utility and the Allais paradox. Dordrecht: Reidel. 27-145. This is the direct English translation of 'Fondements d'une théorie positive des choix comportant un risque et critique des postulats et axiomes de l'école americaine.'
- Kahneman, D., & Tversky, A. (1979). Prospect theory: an analysis of decision under risk. Econometrica, 47: 263.
- Tversky, A., & D. Kahneman (1974). Judgment under uncertainty: heuristics and biases. Science, 185: 1124-1131.
- Simon, H. A. (1983). Alternative visions of rationality. Reprinted from Reason in human affairs. Stanford university Press.
- Nozick, R. (1970). Newcomb's problem and two principles of choice. Reprinted from N. Rescher (Ed.), Essays in honor of Carl G. Hempel. Dordrecht: Reidel.
- Lewis, D. (1981). Causal decision theory. Australasian Journal of philosophy, 59, 5-30.
- Harsanyi, J. C. (1977). Advances in understanding rational behavior. In R. E. Butts & J. Hintikka (Eds.), Foundational problems in the special sciences (p. 315-343). Dordrecht: Reidel.
- Axelrod, R. (1981). The emergence of cooperation among egoists. American Political Science Review, 75, 306-318.
- Gauthier, D. (1986). Maximization constrained: the rationality of cooperation. Uit zijn Morals by agreement. Oxford University Press.
- Arrow, K. J. (1967). Values and collective decision making. In P. Laslett & W. G. Runciman (Eds.) Philosophy, politics, and society. Oxford: Basil Blackwell.
Daniel Kahneman & Amos Tversky (Eds.) (2000). Choices, values, and frames. Cambridge University Press. isbn 9780521627498 info
Ariel Rubinstein (1998). Modeling bounded rationality. MIT Press. isbn 0262681005 pdf (whole book)
Roger J. Bowden (1989). Statistical games and human affairs; the view from within. Cambridge: Cambridge University Press. isbn 0521361788.
Een interessante analye van het probleem van nonrespons (hfdst 2 en 3), en van het eerder al eens door Hofstee aangekaarte probleem van respondenten die de doelen van de onderzoeker anticiperen. Een razend belangrijk onderwerp is dat van de predictive games, waar de statisticus publieke voorspellingen doet. Dat associeert onmiddellijk met Pygmalion-effecten, self-fulfilling prophecies, en in het algemeen de onverantwoordelijk grote sturingskracht die leraren in het onderwijs hebben mbt loopbanen van leerlingen, juist ook langs deze weg van predictive games. Je zou van mijn ATM kunnen zeggen dat het juist de aardige eigenschap heeft deze voorspellingen te doorbreken, door er de neutrale voorspellingen op basis van proeftoetsen voor in de plaats te zetten.
Kenneth R. Hammond (1996). Human judgment and social policy. Irreducible uncertainty, inevitable error, unavoidable injustice. Oxford University Press. isbn 0195097343
Charles Vlek (1973). Notes on the integration of decisionmaking and problem-solving research. Charles Vlek (1973). Psychological studies in probability and decision makin (210-226). dissertation Leiden.
Richard Nisbett and Lee Ross (1980). Human inference: Strategies and shortcomings of social judgment. Prentice-Hall. [decision making]
Gigerenzer G, Gaissmaier W, Kurz-Milcke E, Schwartz LM, Woloshin S: Helping doctors and patients make sense of health statistics.
Psychol Sci Public Interest 2008, 8:53-96. OpenURL
#false_positives
Dimov, C.M., Marewski, J. N., & Schooler, L. J. (2017). Architectural process models of decision making: Towards a model database. In G. Gunzelmann, A. Howes, T. Tenbrink, & E. J. Davelaar (Eds.), Proceedings of the 39th Annual Conference of the Cognitive Science Society (pp. 1931-1936). Austin, TX: Cognitive Science Society. download
Kenneth J. Arrow (1984). Individual choice under certainty and uncertainty. Collected papers of Kenneth J. Arrow, volume 3. The Belknap Press of Harvard University Press. 0674137620 (ao.: Utilities, attitudes, choices: A review note, 55-84. Utility and expectation in economic behavior, 117-146. The theory of risk aversion, 147-171. Exposition of the theory of choice under uncertainty, 172-208. Risk perception in psychology and economics, 261-270.)
Judgment and Decision Making
Baruch Fischhoff and Stephen B. Broomell
Vol. 71, 2020, pp. 331–355 free
Schmidt, F. L. , Hunter, J. E. , McKenzie, R. C. , & Muldrow, T. W. (1979). Impact of valid selection procedures on work-force productivity. Journal of Applied Psychology, 64, 609-626. researchgate.net
- (p. 624:) "Finally, we note by way of caution that productivity gains in individual jobs cannot be extrapolated in a simple way to productivity gains in the composite of all jobs making up the national economy. (. . . ) Since the total talent pool is not unlimited, gains due to selection in one job are partially offset by losses in other jobs. (. . . ) Nevertheless, potential net gains for the economy as a whole are large. The impact of selection procedures on the economy as a whole is explored in detail in Hunter and Schmidt (in press). "
Hunter, John E., and Frank L. Schmidt (1982). Fitting people to jobs: The impact of personnel selection on national productivity. In Marvin D. Dunnette and Edwin A. Fleishman (Eds): Human performance and productivity: Human capability assessment (p. 233-284). Hillsdale, New Jersey: Lawrence Erlbaum Ass. researchgate.net (scan)
- p. 271: “ . . . the way in which talent is allocated to jobs in the economy does have a significant impact on national productivity. This finding contrasts with the dominant emphasis in economics on technological improvements as essentially the sole route to increased productivity. The wise use of human resources does lead to significant productivity payoffs. ” De fantastische claim van Hunter & Schmidt, die veronachtzamen dat bedrijven vaak uit dezelfde pool van sollicitanten moeten putten [maar zie hun 1979 hierboven], staat op p. 267-8: “To provide a more accurate, though still conservative, estimate of the impact of selection, let us set SDy at 40% of mean salary and adjust all incomes upward by 10% to allow for underreporting and by 20% to allow for inflation since 1976. (. . ) Under these assumptions the average productivity difference between random selection and univariate selection is approximately $423 per worker per year ($10,832 - 10,409), or 44. 1 billion dollars per year for the labor force as a whole. Similarly, the difference between random and multivariate selecton is $839 per worker per year ($11,248-10,409), or $87. 5 billion per year economy wide. ”
Schmidt, F. L. , Hunter, J. E. , Outerbridge, A. N. , & Trattner, M. H. (1986). The economic impact of job selection methods on size, productivity, and payroll costs of the federal work force: an empirically based demonstration. Personnel Psychology, 39, 1-29. researchgate.net
- Dit is een becijfering van met selectie te behalen macro-verdiensten. p. 1: In this study, job performance increases resulting from improved selection validity were measured empirically rather than estimated from the standard liinear regression utility equations. Selection utility analyses based on these empirical measurements were carried out for most white-collar jobs in the federal government. Results indicate that selection of a one-year cohort based on valid measures of cognitive ability, rather than on non-test procedures (mostly evaluations of education and experience), produces increases in output worth up to ¢600 million for each year that the new employees remain employed by the government. . . . This gain represents a 9. 7% increase in output among new hires. If total output is held constant rather than increased, new hiring can be reduced by up to 20,044 per year (a 9% decrease), resulting in payroll savings of $272 million for every year the new cohort of employees remains on the job. selectie
Novick, M. R. (1980). Statistics as psychometrics. Psychometrika, 45, 411- 424.
abstract
- Uitgebreid over nut. Bv. p. 420:
It is evident that utility assessment is difficult and that there are many biases to be avoided. My only surprise is that there was ever any belief that simple methods would be adequate. Surely fifty years of work in opinion polling should have made us more sophisticated.
Nancy S. Petersen (1976). An expected utility model for 'optimal' selection. Journal of Educational Statistics, 1, 333-358. 10.2307/1164987 preview
Raju, N.S., M.J. Burke, & J. Normand (1990). A new approach for utility analysis. Journal of Applied Psychology, 75, 3-12. researchgate.net
Daniel Kahneman. A perspective on judgment and choice: Mapping bounded rationality. Or his December 8 2002 Nobel prize lecture: Maps of bounded rationality: A perspective on intuitive judgment and choice. pdf. Daniel Kahneman (2003). Experiences of collaborative research. American Psychologist. 58, 723-730. Zie ook zijn 2002 autobiografische artikel (een korte versie van het AP-artikel?):
Daniel Kahnman (2003). A perspective on judgment and choice: Mapping bounded rationality. American Psychologist, 58, 697-720 10.1037/0003-066X.58.9.697 abstract
Leonard Green & Joel Meyerson (2003). A discounting framework for choice with delaed and probabilistic rewards. PB, 130, 769-792. abstract
E. Brandstätter, Gerd Gigerenzer, Ralph Hertwig (2006). The priority heuristic: Making choices without trade-offs. Ps. Rev., 113,409-432 researchgate.net
F. J. Anscombe & R. J. Aumann (1963). A definition of subjective probability. AnnMathStat 34: 199.
open
Arkes, H.R. (1991). Costs and benefits of judgment errors: implications for debiasing. PB, 110, 486-498.
researchgate.net
O.a. over de werkelijkheidswaarde van laboratoriumstudies.
Hal R. Arkes & Laura Hutzel (2000). The role of probability of success estimates in the sunk cost effect. Journal of Behavioral Decision Making, 13, 295-306. abstract
The sunk cost effect is manifested in a greater tendency to continue an endeavor once an investment in money, effort. or time has been made (Arkes and Blumer, 1985). Such a tendency can lead to suboptimal economic decisions, because such decisions sh-ould be based-solely on future costs and benefits, jot---onesw-hich have already occurred. Unfortunately the sunk cost effect has been found to be relatively robust, having been demonstrated in such diverse fields as professional sports (Staw and Hoang, 1995), venture capital investment (McCarthy et al., 1993), and theater attendance (Arkes and Blumer, 1985 'The psycholofy of sunk cost' Organizational behavior abd human decision processes, 35, 124-140). The purpose of this paper will be to investigate a possible cause of the sunk cost effect, namely, the unjustified inflation of the probability that an investment will succeed following an initial investment of money, effort, or time.
Jonathan Baron (1997). Biases in the quantitative measurement of values for public decisions. Psychological Bulletin, 122, 72-88. utility text
DeFinetti (1970). Logical foundations and measurement of subjective probability. Acta Ps, 129-145. 10.1016/0001-6918(70)90012-0
abstract
Hillel J. Einhorn & Robin M. Hogarth (1981). Behavioral decision theory: processes of judgment and choice. AnnRevPs 32, 53-88. 10.1017/CBO9780511598951.008 abstract
. Deze tekst is best de moeite waard om even door te nemen, omdat de auteurs zich voor de taak gesteld zagen in het kort uit te leggen waar deze belsiskunde over gaat, wat het belang is, welke de filosofische en andere vooronderstellingen.
"recently, Simon (1978) has argued for different types of rationality, distinguishing between the narrow economic menaing (i.e. maximizing behavior) and its more general dictionary definition of 'being sensible, agreeable to reason, intelligent'. Moreover, the broader definition itself rests on the assumption that behavior is functional. That is, "Behaviors are functional if they contribute to certain goals, where these goals may be the pleasure or satisfaction of an individual or the guarantee of food or shelter for the members of society... It is not necessary or implied that the adaptation of institutions or behavior patterns of goals be conscious or intended... As in economics, evolutionary arguments are often adduced to explain the persistence and survival of functional patterns and to avoid assumptions of deliberate calculation in explaining them. (pP3-4)" Accordingly, Simon's concept of 'bounded rationality', which has provided the conceptual foundation for much behavioral decision research, is itself based on functional and evolutionary arguments. However, although one may agree that evolution is nature's way of doing cost/benefit analysis, it does not follow that all behavior is cost/benefit efficient in some way. We discuss this later with regard to misconceptions of evolution, but note that this view: (a) is unfalsifiable (see Lewontin, 1979, om 'imaginative reconstructions'); (b) renders the concept of'error' vacuous; (c) obviates the distinction between normative and descriptive theories. Thus, while it has been argued that the difference between bounded and economic rationality is one of degree, not kind, we disagree." Simon, H.A. "Rationality as a proces and as product of thought.' Am. Econ. Rev., 1978, 68, 1-16.
Berg, N., & Gigerenzer, G. (2007). Psychology implies paternalism? Bounded rationality may reduce the rationale to regulate risk-taking. Social Choice and Welfare, 28, 337-359. http://dx.doi.org/10.1007/s00355-006-0169-0
Goldstein, D. G., & Gigerenzer, G. (1999). The recognition heuristic: How ignorance makes us smart. In G. Gigerenzer, P. M. Todd, & the ABC Research Group., Simple heuristics that make us smart (pp. 37-58). New York: Oxford University Press. http://library.mpib-berlin.mpg.de/ft/gg/GG_The_Recognition_1999.pdf
Goldstein, D. G., & Gigerenzer, G. (2002). Models of ecological rationality: The recognition heuristic. Psychological Review, 109, 75-90. http://library.mpib-berlin.mpg.de/ft/gg/GG_Models_2002.pdf
Hertwig, R., & Gigerenzer, G. (1999). The "conjunction fallacy" revisited: How intelligent inferences look like reasoning errors. Journal of Behavioral Decision Making, 12, 275-305. http://www.mpib-berlin.mpg.de/en/institut/dok/full/hertwig/hrtcfjoba/hrtcfjoba.html
Chase, V. M., Hertwig, R., & Gigerenzer, G. (1998). Visions of rationality. Trends in Cognitive Sciences, 2, 206-214. http://www.mpib-berlin.mpg.de/en/institut/dok/full/hertwig/cvvortics/cvvortics.html
Gigerenzer, G., & Todd, P. M. (1999). Fast and frugal heuristics: The adaptive toolbox. In G. Gigerenzer, P. M. Todd, & the ABC Research Group., Simple heuristics that make us smart (pp. 3-34). New York: Oxford University Press. http://library.mpib-berlin.mpg.de/ft/gg/GG_Fast_1999.pdf
Gigerenzer, G., & Selten, R. (2001). Rethinking rationality. In G. Gigerenzer, & R. Selten (Eds.), Bounded rationality: The adaptive toolbox. Dahlem Workshop Report (pp. 1-12). Cambridge, Mass.: MIT Press. http://library.mpib-berlin.mpg.de/ft/gg/GG_Rethinking_2001.pdf
Gigerenzer, G., & Kurzenhäuser, S. (2005). Fast and frugal heuristics in medical decision making. In R. Bibace, J. D. Laird, K. L. Noller, & J. Valsiner (Eds.), Science and medicine in dialogue: Thinking through particulars and universals (pp. 3-15). Westport, CT: Praeger. http://library.mpib-berlin.mpg.de/ft/gg/GG_Fast_2005.pdf
Gigerenzer, G., Krauss, S., & Vitouch, O. (2004). The null ritual: What you always wanted to know about significance testing but were afraid to ask. In D. Kaplan (Ed.), The Sage handbook of quantitative methodology for the social sciences (pp. 391-408). Thousand Oaks: Sage. http://library.mpib-berlin.mpg.de/ft/gg/GG_Null_2004.pdf
Gigerenzer, G., & Goldstein, D. G. (1999). Betting on one good reason: The Take The Best heuristic. In G. Gigerenzer, P. M. Todd, & the ABC Research Group., Simple heuristics that make us smart (pp. 75-95). New York: Oxford University Press. http://library.mpib-berlin.mpg.de/ft/gg/GG_Betting_1999.pdf
Gigerenzer, G., & Edwards, A. (2003). Simple tools for understanding risks: From innumeracy to insight. British Medical Journal, 327, 741-744. http://library.mpib-berlin.mpg.de/ft/gg/GG_Simple_2003.pdf
Gigerenzer, G., Czerlinski, J., & Martignon, L. (1999). How good are fast and frugal heuristics? In J. Shanteau, B. Mellers, & D. Schum (Eds.), Decision science and technology: Reflections on the contributions of Ward Edwards (pp. 81-103). Boston: Kluwer. http://www.mpib-berlin.mpg.de/en/institut/dok/full/gg/gghgadsat/gghgadsat.html
Gigerenzer, G. (2006). Heuristics. In G. Gigerenzer & C. Engel (Eds.), Heuristics and the law (pp. 17-44). Cambridge, Mass.: MIT Press.
http://library.mpib-berlin.mpg.de/ft/gg/GG_Heuristics_2006.pdf
Gigerenzer, G. (2006). Bounded and rational. In R. J. Stainton (Ed.), Contemporary debates in cognitive science (Contemporary Debates in Philosophy No. 7) (pp. 115-133). Oxford, UK: Blackwell. http://library.mpib-berlin.mpg.de/ft/gg/GG_Bounded_2006.pdf
Gigerenzer, G. (2005). I think, therefore I err. Social Research, 72, 195-218.
http://library.mpib-berlin.mpg.de/ft/GG/GG_I_think_2005.pdf
Gigerenzer, G. (2004). Striking a blow for sanity in theories of rationality. In M. Augier & J. G. March (Eds.), Models of a man: Essays in memory of Herbert A. Simon (pp. 389-409). Cambridge, Mass.: MIT Press.
http://library.mpib-berlin.mpg.de/ft/gg/GG_Striking_2004.pdf
Gigerenzer, G. (2004). Mindless statistics. The Journal of Socio-Economics, 33, 587-606. http://library.mpib-berlin.mpg.de/ft/gg/GG_Mindless_2004.pdf
Gigerenzer, G. (2004). Fast and frugal heuristics: The tools of bounded rationality. In D. Koehler & N. Harvey (Eds.), Blackwell handbook of judgment and decision making (pp. 62-88). Malden: Blackwell. http://library.mpib-berlin.mpg.de/ft/gg/GG_Fast_2004.pdf
Gigerenzer, G. (2003). Where do new ideas come from? A heuristics of discovery in the cognitive sciences. In M. C. Galavotti (Ed.), Observation and experiment in the natural and social sciences (Boston Studies in the Philosophy of Science No. 232) (pp. 99-139). Dordrecht: Kluwer.
http://library.mpib-berlin.mpg.de/ft/gg/GG_Where_2003.pdf
Gigerenzer, G. (2002). In the year 2054: Innumeracy defeated. In P. Sedlmeier & T. Betsch (Eds.), Etc.: Frequency processing and cognition (pp. 55-66). Oxford: Oxford University Press. http://library.mpib-berlin.mpg.de/ft/gg/GG_In_2002.pdf
Gigerenzer, G. (2001). The adaptive toolbox: Toward a Darwinian rationality. In J. A. French, A. C. Kamil, & D. W. Leger (Eds.), Nebraska Symposium on Motivation: Vol. 47. Evolutionary psychology and motivation (Current theory and research in motivation No. 47) (pp. 113-143). Lincoln: University of Nebraska Press. http://library.mpib-berlin.mpg.de/ft/gg/GG_Adaptive_2001.pdf
Scheibehenne, B. (2008). The effect of having too much choice. Doctoral dissertation, Humboldt-Universität zu Berlin, Germany. http://edoc.hu-berlin.de/dissertationen/scheibehenne-benjamin-2008-01-21/PDF/scheibehenne.pdf
Sedlmeier, P., & Gigerenzer, G. (2000). Was Bernoulli wrong? On intuitions about sample size. Journal of Behavioral Decision Making, 13, 133-139. http://www3.interscience.wiley.com/cgi-bin/fulltext?ID=68504727&PLACEBO=IE.pdf
v Sedlmeier, P., & Gigerenzer, G. (2001). Teaching Bayesian reasoning in less than two hours. Journal of Experimental Psychology: General, 130, 380-400. http://library.mpib-berlin.mpg.de/ft/gg/GG_Teaching_2001.pdf
Todd, P. M., & Gigerenzer, G. (2007). Mechanisms of ecological rationality: Heuristics and environments that make us smart. In R. I. M. Dunbar & L. Barrett (Eds.), The Oxford handbook of evolutionary psychology (pp. 197-210). Oxford: Oxford University Press. http://library.mpib-berlin.mpg.de/ft/gg/GG_Mechanisms_2007.pdf
Zhu, L., & Gigerenzer, G. (2006). Children can solve Bayesian problems: The role of representation in mental computation. Cognition, 98, 287-308. http://library.mpib-berlin.mpg.de/ft/gg/GG_Child_2006.pdf
Hull, J., P. G. Moore & H. Thomas (1973). Utility and its measurement. JRStSoc A, 136, 226-247. 10.2307/2345110 JSTOR
Tversky, A., and D. Kahneman (1992): “Advances in prospect theory: Cumulative representation of uncertainty,” Journal of Risk and Uncertainty, 5, 297-323. pdf Ook in Kahneman & Tversky (2000)
Kahneman, D. (1992). Reference points, ancjors, norms and mixed feelings. Organizational behavior and decision processes, 51, 296.
Kahneman, D., & Tversky, A. (197?). The psychology of preferences. Scientific American? 136-149.
Kahneman, D., & Tversky, A. (1973). On the psychology of prediction. PR.
Kahneman, D., & Tversky, A. (1979). Prospect theory: an analysis of decision under risk. Econometrica, 47: 263. (fc) prospect theory is een alternatief voor expected utility theory. Ook in Kahneman & Tversky 2000. Ook in Moder (1990).
Kahneman, D., & Tversky, A. (1982). On the study of statistical intuitions. Cogn., 11, 123-141. (fc)
Kahneman, D., & Tversky, A. (1982). Variants of uncertainty. Cogn. 11. 143-157. (fc)
Liberman, V., & Tversky, A. (1993). On the evaluation of probability judgments: calibration, resolution, and monotonicity. PB, 114, 162-173.
Lindley, Tversky & Brown (1979). On the reconciliation of probability assessments. JRStSoc A, 142:,146-180.
Shaver, G., & A. Tversky (1985). Languages and designs for probability judgment. CognSc, 9, 309-339
Amos Tversky and Daniel Kahneman (1971). Belief in the law of small numbers. Psychological Bulletin, 76, 105-110. html
- abstract People have erroneous intuitions about the laws of chance. In particular, they regard a sample randomly drawn from a population as highly representative, that is, similar to the population in all essential characteristics. The prevalence of the belief and its unfortunate consequences for psychological research are illustrated by the responses of professional psychologists to a questionnaire concerning research decisions.
(fc)
Tversky, A., & D. Kahneman (1980). Causal schemas in judgments. In Progress in Soc Ps vol. 1 (E-12)
Tversky, A., & Koehler, D. J. (1994). Support theory: a nonextensional representation of subjective probability. PsRev, 101, 547-567.
Tversky, A., S. Sattath, & P. Slovic, Contingent weighting in judgment and choice. PR 1988, 95, 385-316
Amos Tversky & Daniel Kahneman (1983). Extensional versus intuitive reasoning: the conjunction fallacy in probability judgment. PR, 90, 293. 10.1037/0033-295X.90.4.293 abstract
Van belang voor thematiek van combineren van slaagkansen.
Tversky, A., & Fox, C. R. (1995). Weighing risk and uncertainty. Psychological Review, 102, 269-283. fc Ook in Kahneman & Tversky (2000). researchgate.net
ATM: Zou het kunnen dat ik met mijn model de risks evaluaeer zodat de student die zou kunnen gebruiken, terwijl in dezelfde bslissingssituatie zonder het model de student op basis van uncertainty moet opereren? Dat zou een zinvol discussiepunt opleveren, zij het ook theoretisch omdat het ATM in de praktijk immers niet door studdenten zal worden gebruikt. Dan blijft staan dat in de praktijk voor de studenten dus de onzekerheidssituatie zal blijven gelden, met de consequenties die de onderzoekliteratuur daaraan lijkt te verbinden:
p. 282: The experiments reported in this article demonsrate SA [subadditivity] for both risk and uncertainty. They also show that this effect is more pronounced for uncertainty than for risk. The latter finding suggests the more general hypothesis that SA, and hence the departure from expected utility theory, is amplified by vagueness or ambiguity. Ofwel door ondoorzichtigheid.
TVERSKY, Amos Tversky & Daniel Kahneman (1977). Causal thinking in judgment under uncertainty. In R. E. Butts & J. Hintikka (Eds.), Foundational problems in the special sciences (p. 315-343). Dordrecht: Reidel (download http://library.lol/main/DB36580CB2BED4168A6878F7EA6DF85B ). 10.1007/978-94-017-0837-1_11 abstract
- p. 167: Many of the decisions we make, in trivial as well as in crucial matters. depend on the apparent likelihood of events such as the keeping of a promise, the success of an enterprise, or the response to an action. In general, we do not have adequate formal models to compute the probabilities of such events. Consequently, most evaluations of likelihood are subjective and intuitive. The manner in which people evaluate evidence to assess probabilities has aroused much research interest in recent years, e.g. Edwards (1968), Slovic (1972). Slovic. Fischhoff, and Lichtenstein (1975), Kahneman and Tverskv (1973). and Tversky and Kahnernan (1974). This research has identified different heuristics of intuitive thinking and uncovered characteristic errors and biases associated with them. The present paper is concerned with the role of causal thinking in the evaluation of evidence and in the judgment of probability. Students of modern decision theory are taught to interpret subjective probability as degree of belief, i.e. as a summary of one's state of information about an uncertain event, This concept does not coincide with the lay interpretation of probability. People generally think of the probability of an event as a measure of the propensity of some causal process to produce that event, rather than as a summary of their state of belief. The tendency to regard probabilities as properties of the external world rather than of our state of information characterizes much of our perception. We normally regard colors as properties of objects, not of our visual system, and we treat sounds as external rather than internal events. In a similar vein, people commonly interpret the assertion 'the probability of heads on the next toss of this coin is 1/2' as a statement about the propensity of the coin to show heads. rather than as a statement about our ignorance regarding the outcome of the next toss. The main exceptions to this tendency are assertions of complete ignorance, e.g. J haven't the faintest idea what will happen in the coming election'.
= Tversky (1972). Elimination by aspects: a theory of choice. PR, 79, 281-29. (fc) abstr: Most probabilistic analyses of choice are based oil theassumption of simple scalability which is ail ordinal formulation of the principle of independence from irrelevant alternatives. This assumption, however, is shown to be illadequate on both theoretical and experimental grounds. To resolve this problem, a more general theory of choice ba5ed oil a covert elimination process isdeveloped. In this theory, each alternative is viewed asa set ofaspects. At each stage ill tile process, an aspect is selected (with probability proportional to its weight), and all the alternatives that do not include the selected aspect are eliminated. The process continues until all alternatives but one are eliminated, It isshown (a) that this model is expremible purely in terms, of the choice alternatives without any reference to specific aspects, (b) that it can be tested using observable choice probabilities, and (c) that it generalizes the choice models of R. D. Luce and of F. Restle. Empirical support from a study of psychophysical and preferential judgments is presented. The strategic implications of the present development are sketched, and the logic of elinliflation by aspects is discussed from both psychological and decision- theoretical viewpoints.
Tversky, A. (1974). Assessing uncertainty. JRoyalStatSoc Series B 148-159. 10.1111/j.2517-6161.1974.tb00996.x JSTOR
SUMMARY Intultiva judgments of probability are based on a limited number of heuristics that are usually effective but sometimes lead to severe and syste- matic errors. Research shows, for example, that peoplejudge the probability of a hypothesis by the degree to which it represents the evidence, with little or no regard for its prior probability. Other heuristics lead to an overestimation of tbe probabilities of highly available or salient events, and to overconfidence in the assessment of subjective probability distributions. These biases are not readily corrected, and they are shared by both naive and statistically sophisticated subjects. The implications of the psychology of judgment to the analysis of-rational behaviour are explored. Keywords: ANCHORING; AVAILABILITY; COHERENCE; hEURISTICS; POSTERIOR probability; PRIOR PROBABILITY; REPRESENTATIVENESS; SUBJECTIVE PROBABILITY
Tversky, A., & S. Sattath (1979). Preference trees. PR, 86, 542-573. researchgate.net
The analysis of choice behavior has concerned many students of social science. Choices- among political candidates, market products, investment plans, transportation modes, and professional careers have been investigated by economists, political scientists, and psychologists using a variety of empirical and theoretical methods. An examination of the empirical litemture indicates that choice behavior is often inconsistent, hierarchical, and context dependent. Inconsistency refers to the observation that people sometimes make different choices under seemingly identical conditions. Although inconsistency can be explained as the result of learning, satiation, or change in taste, it tends to persist even when the effects of these factors are controlled or minimized. Furthermore, even in an essentially unique choice situation that cannot be replicated, people often experience doubt regarding their decisions and feel that in a different state of mind, they might have made a different choice. The observed inconsistency and the experienced uncertainty associated with choice behavior have led several investigators to conceptualize choice as a probabilistic process and to use the concept of choice probability as a basis for the measurement of strength of preference CLuce, 1959; Marsdmk, 1960; Thurstone, 1927).
Griffin, D., & Tversky, A. (1992). The weighing of evidence and the determinants of confidence. CognPs, 24, 411-435.
Elster, J. (Ed.) (1986). Rational choice. Cambridge: Cambridge University Press. D. Parfit, Prudence, morality, and the prisoner’s dilemma. A. Sen, Behaviour ad the concept of preference [Economica, 1973, 40, 241-59]. J. C. Harsanyi, Advances in understanding rational behavior in R. E. Butts and J. Hintikka (ed), Foundational problems in the special sciences (Dordrecht 1977), pp. 315-343.]. G. Becker, The economic approach to human behavior [G. Becker, The economic approach to human behavior (Chicago University Press, 1976), 3-14.]. A. Tversky & D. Kahneman, The framing of decisions and the psychology of choice [Science 211 (1981), pp. 453-8]. J. G. March, Bounded rationality, ambiguity, and the engineering of choice [Bell Journal of Economics, 9 (1978), 587-608]. R. Boudon, The logic of relative dfrustration [The unintended consequences of social action. Presses Universitaires de France 1981]. S. Popkin, The political economy of peasant society [S. popkin, The rational peasant. University of California Press, 1979, 35-72.]. D. North, A neoclassical theory of the state [D. C. North, Structure and change in economic history. Norton.] Aardig allemaal, maar ik heb geen materiaal gevonden waarover ik aantekeningen had te maken. Er is een paperback-editie van ca ƒ40, gezien bij Kooyker.
Janoff-Bulman, R., & Brickman, Ph. (1982). Expectations and what people learn from failure. In Feather, N. T. (Ed.). Expectations and actions: expectancy-value models in psychology (p. 207-237). Hillsdale, New Jersey: Lawrence Erlbaum. p. 220: Somewhat surprisingly, there is actually no consensus in the psychologival literature on how important it is for individuals to be able to distinguish between controllable and uncontrollable outcomes, and no general theory which makes this ability its central feauture. Wortman and Brehm (1975) suggest that when outcomes are truly uncontrollable, the most adaptive response may be to give up or not to try to exert control in the first place. [Wortman, C. B., and Brehm, J. W. (1975). Responses to uncontrollable outcomes: An integration of reactance theory and the learned helplessness model. In L. Berkowitz (Ed.). Advances in experimental social psycholoy. Vol. 8, New York: Academic Press] But these authors, as well as Wortman (1976), also cite reports that victims of natural disasters or diseases blame themselves or others for these events as evidence of an understandable and healthy tendency for people to believe that these events are controllable rather than random and uncontrollable. [Wortman, C. B. (1976). Causal attributions and personal control. In J. H. Harvey, W. J. Ickes, & R. F. Kidd (Eds.), New directions in attribution research. Vol 1. Hillsdale, New Jersey: Lawrence Erlbaum Associates.] Likewise, Janoff-Bulman (1979) interprets self-blame by rape victims as healthy effort by victims to believe that they can, by their own careful and responsible behavior, prevent the recurrence of the trauma of rape, though rape episodes may in fact be essentially independent of victim behavior. [Janoff-Bulman,R. (1979). Characterological versus behavioral self-blame: Inquiries into depression and rape. Journal of Personality and Social psychology, 37, 1789-1809.] Langer (1975) and Seligman (1975) are unequivocal in taking the position that it is valuable for individuals to believe that they have control when in fact they do not and this belief is an illusion. [Langer, E. J. (1975). The illusion of control. Journal of Personality and Social psychology, 32, 311-328.] [SeligmanM. E. P. (1975). Helplessness. San Francisco: Freeman.] Furby (1979) surveys the psychological literaure on perceived control and finds a general bas toward the belief that that one has control is good. [Furby, L. (1979). Individualistic bias in studies of locus of control. In A. R. Buss (Ed.), Psychology in social context. New York: Halsted.] It is really quite remakrable that the literature has been zo sensitive tot the consequences of people's mistakenly assuming that they do not have control and so insensitive to the consequences of people's mistakenly assuming that they do have control. p. 220: The belief that people are personally resposible for their own successes and failures, that they are in control of their own fates, rconciles people towards accepting their own lot and the lot of others as fair and just (Lerner, 1975). [Lerner,M. J. (1975). The justice motive in social behavior. Journal of Social issues, 31, 1-20.] I this domain, as in others, the culture appears to have two messages, one of them widely publicized and available to all and the other largely hidden and available only to the elect or the elite. The public message is that one should persist and persevere no matter how discouraging things appear, that good things will eventually follow if one only stays on the job, that th only real failure is to stop trying. people who follow orders need not be socialized to decide for themselves when to start and whe to stop, but only to persist at whatever tasks they are assigned. Theirs not to reason why, theirs just to do or die. For the managerial elite, however, discretion rather than blind perseverance is the requisite social virtue. People responsible for making decisions and committing social resources to the realizations of these decisions must, in theory at least, learn how to quit, how to call off disastrous enterprises, how to avoid being trapped in unpromising situations. Children of workers must learn to persist because changing careers, exploring alternatives, and failing are luxuries they cannot afford. Children of the elite not only have the cushion of parental resources that enable them to fail, but have access through these resources to a kind of learning - the ability to discriminate among tasks - that is vital to future success and not available to their less fortunate peers.
Krzysztofowicz, R. (1983). Risk attitude hypotheses of utility theory. In B. P. Stigum & F. Wenstop, Foundations of utility and risk theory with applications. Dordrecht: Reidel. 201-216.
- (ivm risico; genoemd door vd Gaag par. 2.3) Is een korte versie van 1982 artikel. p. 213:
The results of our experiments reinforce earlier opinions and experimental findings that a value function (compatible with the theory of ordereed value differences) and a utility function (compatible with the expected utility theory) are distinct constructs not only theoretically but also behaviorally. A behavioral hypothesis explaining the difference is that a value function encodes the strength of preference while a utility function encodes the strength of preference and risk attitude. In light of this, the classical interpretation of a von Neamann-Morgenstern utility function must be re-examined. What has been traditionally termed ‘risk attitude’ is a joint effect of the strength of preference and risk attitude, and what has been labelled herein ‘relative risk attitude’ is, from a behavioral standpoint, risk attitude in the absolute sense.
Krzysztofowicz, R. (1983). Strength of preference and risk attitude in utility measurement. Organizational Behavior and Human Performance, 30, 88-113.
- Eerder heb ik dit artikel terzijde gelegd als 'gezien.' Maar het gaat over een thematiek waarover ik klaarheid moet scheppen in mijn proefschrift: het verschil of de overeenkomst tussen waardefuncties en nutsfuncties, en i.h.b. de stelling dat nutsfuncties gelijk zijn aan waardefuncties + risicohouding. Ik heb die waarde- of voorkeursfunctie de laatste tijd verwaarloosd: in 1980 maakte ik er juist een belangrijk punt van! Dit artikel is uuberhaupt erg interessant omdat het een reeks voorbeelden van waarde- en nutsfuncties bevat! Dat moet dus goed passen bij de behandeling van nutsfuncties die ik zelf geef. Nu bedenk ik bij dit artikel dat ik van meet af aan duidelijk moet maken dat ik weliswaar werk met nutsfuncties over scores of cijfers, maar dat dat niet betekent dat ik de intrinsieke didactische betekenis van scores en cijfers hoog inschat! Integendeel, ik moet hier verwijzen naar het algemene inzicht dat scores en cijfers geen betekenisvolle terugkoppeling vormen. Nee, waar het mij om gaat is louter de formele betekenis in termen van behalen van examens. In ieder geval zorgvuldig bestuderen dit artikel!
Jon Elster (1989). Solomonic judgements. Studies in the limitations of rationality. Cambridge: Cambridge University Press. loten p. 1: My concern here is ... with failures in rational choice theory. p. 2: in this book ... the emphasis is on the indeterminacy of rational vhoice theory. p. 37 I shall argue that we have a strong reluctance to admit uncertainty and indeterminacy in human affairs. Rather than accept the limits of reason, we prefer rituals of reason. p. 114; Using a weighted lottery (or multiple queues) could increase everybody’s chance of getting the scarce good, if the inequality created opportunities or incentives that in the end would make the good less scarce. The regulation of access to medical or technical education by a weighted lottery could be justified by this argument. Ik kan deze gedachte van Elster niet volgen. p. 121; The basic rreason for using lotteries to make decisions is honesty. [Leuk: dat onderscheid tussen fairness en honesty!) Honesty requires us to recognize the pervasiveness of uncertainty and incommensurability, rather than deny or avoid it. Some decisions are going to be arbitrary and epistemically random no matter what we do, no matter how hard we try to base them on reasons. Chance will regulate a large part of our lives, no matter how hard we try to avoid it. By taming chance we can bring the randomness of the universe under our control as far as possible and keep free of self-deception as well. The requirements of personal causation [De Charms (1968)] and autonomy [Elster (1983a), ch. 3] are reconciled by the conscious use of chance to make decisions when rational argument fails. Although the bleakness of this vision may disturb us, it is preferable to a life built on the comforting falsehood that we can always know what to do. Otto Neurath characterizes the belief that we can always have good reasons for our decisions as pseudorationalism. Whereas Cartesian ‘rationalism sees its chief triumph in the clear recognition of the limits of actual insight’, pseudorationalism ‘leads partly to self-deception, partly to hypocrisy’. To conclude the present chapter I can do no better than to quote his further comments on this distinction: [ik neem alleen het tweede deel van het citaat over] “Let us go back to the parable of Descartes. For the wanderers lost in the forest, who have no indication at all as to which direction to follow, it is most important to march on energetically. One of them is driven in some direction by instinct, another by an omen; a third will carefully consider all eventualities, weigh all arguments and counter-arguments and, on the basis of inadequate premises of whose deficiencies he is unaware, take one definitte direction which he considers the correct one. The fourth, finally, will think as well as he can, but not refrain from admitting that his insight is too weak, and quietly allow himself to decide by lot. Let us assume that the chances of getting out of the forest are the same for the four wanderers; nevertheless there will be people whose judgment of the behaviour of the four is very different. To the seeker after truth whose esteem of insight is hghest, the behaviour of the last wandere will be congenial, and that of the pseudorationalist most repellent. In these four kinds of behaviour we can perhaps see four stages of development of mankind without exactly claiming that each one of them has come into full existence. (Neurath, 1913, 9-11).
Ranald R. Macdonald (1986). Credible conceptions and implausible probabilities. BrJMStPsychol, 39, 15-27.
McKenzie, C. R. M. (1994). The accuracy of intuitive judgment strategies: covariation assessment and Bayesian inferene. Cognitive Psychology, 26, 209-239.
Onderzoek in de Kahneman & Tversky lijn, zou je kunnenz zeggen. De taak is schatten van de correlatie in een twee-bij-twee tabel.
MORGENSTERN, OSKAR (1979). SOME REFLECTIONS ON UTILITY. In M. Allais & O. Hagen (eds.). Expected Utility and the Allais Paradox, 175-183. D. Reidel Publishing Company. abstract he whole book: download
p. 175: It is natural that the 'expected utility hypothesis' as presented in Chapter I of Theory of Games and Economic Behavior (von Neumann, Morgenstern, 1944) would have been challenged. After all, the theory goes a significant step beyond the thus far accepted version of a theory of utility which deals only with sure prospects and yields a number for utility only up to monotone transformations. What von Neumann and I have done is: (a) we recognize the undeniable fact that in our world some prospects are uncertain and that probabilities must be attached to them. This is clearly an empirical observation or assertion. (b) We have established a set of axioms expressing precisely the assertions. For these axioms, we have carefully shown that they are free of contradictions and have all the properties a true axiomatic system has to exhibit.
M. Allais & O. Hagen (eds.) (1979). Expected Utility Hypotheses and the Allais Paradox: Contemporary Discussions of the Decisions under Uncertainty with Allais’ Rejoinder
download
Robert E. Nisbett, David H. Krantz, Christopher Jepson & Ziva Kunda (1983). The use of statistical heuristics in everyday inductive reasoning. Psychological Review, 90, 339-363. 10.1037/0033-295X.90.4.339 abstract
- p. 339; It can be argued that inductive reasoning is our most important and ubiquitous problem-solving activity. Concept formation, generalization from instances, and prediction are all examples of inductive reasoning, that is, of passing from particular propositions to more general ones or of passing from particular propositions to other particular propositions via more general ones. Inductive reasoning, to be correct, must satisfy certain statistical principles. Concepts should be discerned and applied with more confidence when they apply to a narrow range of clearly defined objects than when they apply to a broad range of diverse and loosely defined objects that can be confused with objects to which the concept does not apply. Generalizations should be more confident when they are based on a larger number of instances, when the instances are an unbiased sample, and when the instances in question concern events of low variability rather than high variability. Predictions should be more confident when there is high correlation between the dimensions for which information is available and the dimensions about which the prediction is made, and, failing such a correlation, predictions should rely on the base rate or prior distribution for the entits to be predicted. Because inductive reasoning tasks are so basic, it is disturbing to learn that the heuristics people use in such tasks do not respect the required statistical principles. The seminal work of Kahneman and Tversky has shown that this is so and, also, that people consequently overlook statistical variables such as sample size, correlation, and base rate when they solve inductive reasoning problems. (See surveys by Einhorn & Hogarth, 198 1; Hogarth, 1980; Kahneman, Slovic, & Tversky, 1982; Nisbett & Ross, 1980.) The above research on nonswistical heuristics has been criticized on several grounds. p. 346 een verdraaid leuke opmerking over het interview; Daniel Kahneman (personal communication, 1982) has suggested to us that the “interview illusion” exists in part because we expect that brief encounters with a living, breathing person ought to provide a “hologram” of that person rather than merely a sample of the person’s attributes and behaviors. In most situations, cues as to the fact that an interview ought to be regarded as a sample from a population, rather than a portrait in miniature, are missing.
Roskam, E. E. Ch. I. (1985). Formele benaderingen van keuze- en beslissingsgedrag. NTvdPs 1985, 40, 321-347. [ik heb een kopie]
Leonard J. Savage (1971). Elicitation of personal probabilities and expectations. JASA, 68, 783-800. pdf
Becker, S. W., & S. Siegel (1962). Utility and level of aspiration. American Journal of Psychology, 75, 115-120.
Bepaalt nutsfuncties van studenten voor grades.
: In a recent theoretical formulation, it was suggested that the setting of a level of aspiration should be viewed as making a decision. Level of aspiration was defined as a point on an individual's scale of the utility of his goals.' It was also asserted that when the goals form a discrete set on a scale of achievement, then at least an ordered-mctric measurement of the individual's utility of those goals is necessary to identify his level of aspiration. Furthermore, the level of aspiration is associated with the goal that bounds the top of the largest distance, i.e. the largest difference in utility between adjacent goals. This formulation was based on the proposition that, for an individual, there is some utility, positive or negative, associated with obtaining any goal on a scale of achievement. Becker and Siegel supported this formulation empirically by correlating an ordered metric measure of the level of aspiration with an independent measure of the level of aspiration.2 To supplement this correlational evidence the present paper offers an experitnental test of the thcory. The most general conclusion that may be drawn from previous research on the level of aspiration is that success generally leads to a raising of aspiration, and failure to a lowering, but that the effects of failure are more variable.3 For this reason, the study reported in this paper was designed to apply the proposed measure of the level of aspiration to the prediction of changes in the level of aspiration folllowing induced success or failure.
p. 115 gescand
Becker, S. W., and Siegel, S. (1958). Utility of grades: level of aspiration in a decision theory context. Journal of Experimental Psychology, 55, 81-85.
The level of aspiration of an individual is a point in the positive region of his utility scale of an achievement variable; it is at the least upper bound of that chord (connecting two goals) which has maximum slope, i.e., the level of aspiration is associated with the higher of two goals between which the rate of change of the utility function is a maximum. uit de methode: Each S was given a booklet containing a series of alternative gambles ... . bijv. Would you prefer a 50-50 chance of an A or an F, or would you prefer a B or a D? Interessant is ook nog p. 83: From the verbatim account of each interview, four sorts of information were abstracted for each S: (a) his desired grade, (b) his expected grade, (c) the lowest grade which would be satisfactory to him, and (d) the number of hours he was willing to work at clerical tasks in order to effect a one-level raise in grade. Using this information the two Es independently estimated each S's level of aspiration. They did this prior to examining any S's test booklet. Inderdaad is er een probleem door de investering die voor presteren nodig is. Ook is een probleem wat het cijfer wordt bedoeld, hier is het evident het voor het betreffende onderdeel te halen cijfer, maar later (in 1962), gaat het om gpa als doel, en hoe dat doel verandert met een tegenvallend of meevallend cijfer.
p. 81
Sidney Siegel (1957). Level of aspiration and decision making. Psychologicl Review, 64, 253-262. 10.1037/h0049247 abstract
- Hier komt het idee vandaan om nutsfunctie en streefniveau te combineren, zoals ik dat in 1980 heb gebruikt.
p. 253: The purpose of this paper is to discuss two related topics: (a) the role of a person's level of aspiration in his decision making, and (b) the measurement of level of aspiration in a decision-theory context. The discussion of the second topic will include a brief summary of some experimental evidence which lends support to the methodological stand taken here. - The notion of level of aspiration is invoked in reference to the goal-striving behavior of an individual when he is presented with a task whose outcome can be measured on an achievement scale. Level of aspiration refers to the particular achievement goal for which the person strives. The concept of level of aspiration was introduced by Dembo (8), and the first experiment in the area was conducted by Hoppe (14). It is a familiar concept to psychologists and others, having been the topic of extensive discussion and experimentation in the last quarter of a century. An early review of the literature is given by Frank (13). Rotter has offered a critical review of-the methodological aspects of level of aspiration studies (19). An exceptionally important theoretical article, by Lewin, Dembo, Festinger, and Sears, appeared in 1944 (16). DEcisioN THEORY AND LEVEL OF AsPIRATioN THEORY It is the contention of the present writer that the psychological situation established in level of aspiration experiments may profitably be characterized as a decision situation, for from the alternative possible goals the individual must decide for which goal he will strive. It is a remarkable fact that, by a simple change in nomenclature, the theoretical model used by Lewin et al. (16) in the prediction of the choices (deci' sions) of individuals in a goal-strivina situation-a model based on the work of Escalona (11) and Festinger (12)may be rendered fundamentally equivalent to the theoretical model employed by decision and game tbeoriSts. This latter theory, first advanced by Bernoulli (2), discussed by Ramsey (18), and formalized by Von Neumann and Morgenstern (28) and by Savage (20), states that under conditions of uncertainty individuals behave as if they were attempting to maximize expected utility. According to these and other decision theorists, an individual's decisions underlying his choices among ahernatives involving uncertain outcomes (outcomes with stated probabilities of attainment) are based on the utilities of the entities (objects, actions, goals, etc.) and on the probabilities (subjective probabilities, for most decision theorists) associated with attainment of the entities. The decisions are a function of these two variables (utility and subjective probability) in that the individual seeks by his choices to maximize the sum of the products of probability and utility, i.e., (....) p. 261: p. 261: SUMMARY AND CONCLUSIONS This paper suggests that Lewinian theory concerning level of aspiration may be integrated with certain parts of decision theory. An achievement scale where may be viewed as a scale of utility of the achievement goals. A formal definition of level of aspiration in terms of utility is offered. The problem of ascertaining a person's level of aspiration reduces to the problem of measuring his utility of the achievement goals. It is hypothesized that level of aspiration is associated with the largest distance on an individual's utility scale. If this is so, with a discrete set of goals, ordered metric measurement is sufficient for identifying a person's level of aspiration, since an ordered metric scale contains"J~ not only a ranking of the entities (achievement goals) but also a ranking of the'distances between them. Certain experimental evidence which supports, the hypothesis is summarized. Suggestions for future research are presented; these draw upon the ideas presented here, together with those of other workers in the fields of level of aspiration and decision theory. In conclusion, it would seem that a useful behavioral model of decision making should include not only the concepts of utility and subjective probability, as do the present models, but should also include a formulation of the effects of level of aspiration and reinforcement on utility. That is, the model should include recognition that utility has a model in its own right, in which the main concepts are level of aspiration (LA) and reinforcement effects (R). In terms of such an extended model, it may be said that if various alternatives are available to an individual, he will choose from among these alternatives, toward each of which lie has a subjective probability of attainment and a utility, so as to maximize subjectively expected utility, SEU. That is, the individual will choose so as to maximize SEU= som van pi ui over i ... (...).
Slovic, Fischhoff, Lichtenstein (1977). Behavioral decision theory. AnnRevPsychol, 28, 1019. fc
Paul Slovic (1995). The construction of preference. American Psychologist, 50, 364-371. pdf
"People’s preferences and how they report them are remarkably labile. They are exquisitely sensitive to how questions are asked and to the mode of response allowed."
Patrick Suppes (1979). The logic of clinical judgment: Bayesian and other approaches. In H. T. Engelhart, Jr., S. F. Spicker, and B. Towers (eds). Clinical judgment: a critical appraisal. 145-159. Dordrecht: Reidel (download: http://library.lol/main/B68B5206870F2049BE0BB5ADACFCFDAA) . [ik heb een fc]. Met repliek van Martin E. Lean p. 161-166.
preview
 http://www.benwilbrink.nl/literature/decision-making.htm
http://goo.gl/aq6uH0
http://www.benwilbrink.nl/literature/decision-making.htm
http://goo.gl/aq6uH0

 The figure is from Wilbrink 1980b, Figure 3. It illustrates the situation pretty well. I did not succeed in 1980 to get rid of the fuzzy ‘costs’ of the resit, however ;-)
The figure is from Wilbrink 1980b, Figure 3. It illustrates the situation pretty well. I did not succeed in 1980 to get rid of the fuzzy ‘costs’ of the resit, however ;-)