Sorry, I will do my annotations in Dutch. The subject is rather difficult, and too subtle to risk wasting it in an attempt to write in English. I will refer frequently to publications of mine written in Dutch. However, if you happen to be interested in a particular topic, let me know, and I will probably be able to translate it for you (and add the translation to this page).
Borsboom, Romeijn en Wicherts bouwen voort op het werk van Millsap en Kwok (2004). Voor de annotatie van op Borsboom e.a., zie hier.
Denny Borsboom, Jan-Willem Romeijn and Jelte M. Wicherts (2008). Measurement invariance versus selection invariance: Is fair selection possible? Psychological Methods, 13, 75-98 pdf
De upshot is dat Millsap en Kwok (M&K) helemaal de mist in gaan met hun succesrato, sensitiviteit en specificitit genomen over scorebereik boven de aftestgrens, in plaats van conditioneel op die aftestgrens. Dat is precies het duistere vermoeden dat ik kreeg bij eerste kennisname met jullie 2008-artikel, destijds reden om er in discussie stevig in te duiken.
Al doende ben ik het artikel van Cronbach (1976, JEM) hooglijk gaan waarderen, en heb ik ontdekt dat ik Einhorn en Bass 91971) ook nog een goed moet doornemen. Mogelijk maak ik een annotatie op Cronbach (1976), omdat ik voor mezelf helder wil krijgen wat hij heeft geanalyseerd, om mijn werk dat raakt aan deze thematiek er achteraf mee te kunnen vergelijken.
De commentaar op M&K puntsgewijs.
1. Het factor-model leidt alleen maar af van waar het M&K om te doen is; gevolgen van schending van meetinvariantie op kwaliteiten van beslissingen (wat zij 'selectie' noemen).
2. p. 95: "In this article, we consider the use of a measure as a basis for selecting individuals. This selection seeks to use the measure to identify individuals who are in a desired range on the construct being measured."
Hier vallen M&K in de val waar ook Wim van der Linden en na hem Henk Vos eerder al intuinden: dat voor optimale beslissingen het nodig is te evalueren (vd Linden: Bayes Risk) over de HELE groep (M&K: populatie). Dat zorgt voor wiskundige ingewikkeldheden, en analytische mist.
In de geciteerde passage is het toch evident dat het gaat om een grensscore die een range van hogere, resp. lagere scores begrenst. Ik laat even open of dat een grensscore op de test, of op de trek kan zijn.
M&K kiezen voor een grensscore op de trek (het construct). Ik kan daarmee leven, er is immers een uitstekend model voor: het binomiaalmodel, zoals in tentamenmodellen als bouwsteen gebruikt. Dta lijkt M&K overigens te zijn ontgaan.
Het vinden van een grensscore is alleen zinvol wanneer er iets valt te optimaliseren. Ook M&K moeten iets te optimaliseren hebben, zou je zeggen. Neem even aan dat dat het geval is.
Dan is per definitie de optimale grensscore die grensscore waarvoor de beslisser het om het even is of de betreffende kandidaten/testees 'geselecteerd' worden, of niet.
Denk even over die definitie na, en je ziet dat het een ingeklede vergelijking is: het verwachte nut van afwijzen is gelijk aan het verwachte nut van toelaten van de kandidaten met deze score. In mijn TOR-artikelen uit 1980 is dit allemaal tot in detail uitgespeld, maar niet in termen van meetinvariantie (of referentie- versus focale groep).
3. p. 96: "Selection on Z(ik) proceeds in a top-down fashion, taking the top of the scores on Z(ik) (as an example)."
Met alle respect, maar dit is een dwaas casus. De impliciete gedachte is dat ergens is besloten dat de top 25% van de zich aanmeldende groep wordt geselecteerd. Dat gaat eraan voorbij dat de omvang van de zich aanmeldende groep niet is gespecificeerd, dat kan van alles zijn, wat de 25%-regel tot een onzin-regel maakt.
Dit dwaze casus verduistert onmiddellijk de belangrijkste vraag: wat is de optimale aftestgrens? Zijn M&K daar eigenlijk wel in geïnteresseerd? Maar als ze dat niet zijn, waar gaat dit artikel dan over? Ik begrijp dit niet.
Ik moet hier iets uitleggen. In algemene zin gaat het bij het vinden van een optimale aftestgrens om een probleem dat met de mate van absolute geschiktheid van kandidaten heeft te maken: iedere kandidaat die in absolute zin voldoende geschikt is, wordt ook toegelaten.
M&K lijken iets heel anders te gaan doen: zij willen de 25% meest geschikten hebben, uit een groep die in zijn geheel bestaat uit geschikte/gekwalificeerde kandidaten. Ik vind dat een heel vreemde strategie (van een werkgever? van een selecterende onderwijsinstelling?).
Minder vreemd zou zijn: er zijn 25 openingen, vind de 25 best gekwalificeerde kandidaten in een grotere groep gekwalificeerde kandidaten. Quota-selectie, numerus clausus, of Nederland potjeslatijn: numerus fixus.
M&K hebben zichzelf met de keuze voor dit casus geen dienst bewezen: ze staan vanaf hier voortdurend op het verkeerde been.
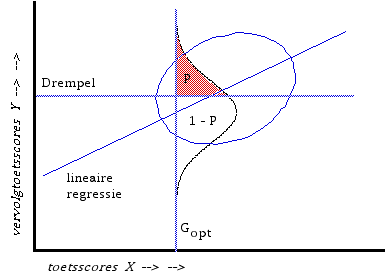
4. p. 97: Figuur 1. De val sluit zich hier. De figuur laat schematisch een bivariaat-normale verdeling zien, opgesplits in vier volume-delen, waarmee de hele populatie is gekenmerkt. OK, je kunt dit zo doen, zeker. Maar waarom zou je?
Het ligt op dit moment dan toch verschrikkelijk voor de hand om over te gaan op de conditionele verdeling, gegeven Z(c)? Dat is overigens een normaalverdeling. Kennen we die figuur? Jazeker, Alf en Dorfman, bijvoorbeeld.

Dit is Figuur 4a uit mijn 1980a http://www.benwilbrink.nl/publicaties/80aGrensscoresTOR.htm. Let maar niet op de verkeerd ingetekende regressielijn (die is te stijl). Lees i.p.v. vervolgtoetsscores Y de M&K situatie: onderliggende trek (Factor score).
Alf, E. F., Jr, and Dorfman, D. D. (1967). The classification of individuals into two criterion groups on the basis of a discontinuous payoff function. Psychometrika, 32, 115-123.
By the way: Cronbach (1976) legt ook nog eens uit dat het gaat om het 'marginale' casus, dus de situatie precies op de grensscore, een puntje meer, of een puntje minder.
Einhorn and Bass, the Equal Risk model, gebruikt dit eveneens, zie de heldere figuren in Petersen & Novick's bespreking van dit model , samen met dat van Cleary (1968) het enige coherente model voor eerlijk beslissen.
5. p. 97 "We can measure the impact of the failure of invariance by studying group differences in the resulting quadrant proportions and by comparing these differences to those found under the invariant case."
Dat kan, zeker, maar dan moet de lezer wel voortdurend zijn hersenen in nieuwe kronkels leggen. Want wat betekenen die verschillen dan eigenlijk? Ik ben niet de enige die dergelijke getallen niet kan interpreteren:. Cronbach (1976, p. 36) kan dat ook niet: "I say no more about the [overall risk] because I have found no rationale to justify equalizing it." M&K kennen deze uitspraak van Cronbach niet: heel hun artikel druist er tegenin, zonder dit feit te signaleren.
Kortom, de geciteerde passage uit M&K hebben de auteurs alleen op kunnen schrijven omdat zij niet op de hoogte waren van het bestaan van relevante literatuur in het veld van psychometrie (zij noemen wel literatuur uit de wereld van signaaldetectie, bijvoorbeeld, maar ik heb geen flauw idee of zinvolle toepassingen in die wereld een analogon hebben in educational measurement).
Kan het anders? Ja, natuurlijk kun je conditioneel op de gekozen grensscore voor selectie een twee-bij-twee tabel construeren met proporties afgewezen maar op de trek boven de cesuur, etcetera. Die twee-bij-twee tabel bevat dan maar twee verschillende waarden voor de kansen. Maar dat hoeft natuurlijk niet te gelden voor het toegekende nut aan de mogelijke uitkomsten. Sterker: dat geldt sowieso niet voor toegekend nut voor de vier mogelijke uitkomsten per testee.
Als je wilt conditioneren op de cesuur in de onderliggende trek, OK, doe dan een simulatie.
6. p. 98. De overall succes ratio (formule 8).
Deze 'index' is in het maatschappelijk debat aanwezig in bepaalde opvattingen over eerlijkheid.
Maar de oefeningen die M&K ermee doen, trekt hen zonder dat zij zich daarvan bewust lijken, in het kleine kamp van degenen met deze extreme opvatting over eerlijkheid.
Dit is dus bepaald geen zinvolle index. Heel anders is dat voor de success ratio gegeven dat de testscore gelijk is aan de aftestgrens. (Of aan een score die als aftestgrens kan worden gekozen). Dat is de kans op succes bij Alf en Dorfman, bij Einhorn en Bass, en bij Cronbach.
7. p. 98 p. de sensitivity (formule 9).
Hier hetzelfde probleem: de index is geconditioneerd op de range boven de cesuur op de onderliggende trek.
Conditioneer op de cesuur zelf.
8. p. 98 specificity. Idem.
Conditioneer op de cesuur zelf. Dan krijg je, als ik het goed zie, het complement van de sensivity.
Waarom is het een blunder van M&K om niet te conditioneren op de grensscore? Denk jezelf in de schoenen van een belanghebbende: Cronbach's Applicant, of zijn Employer. De kandidaat heeft geen grensscore te kiezen, dus hier gaat het om de werkgever, de selecterende instelling, of maatschappelijk belang zoals behartigd door de politiek en politieke lichamen: die hebben allemaal wat te kiezen. En wat ze kiezen is niet een range boven een aftestgrens, maar die aftestgrens zelf. Een keuze komt dan neer op al dan niet verplaatsen van die aftestgrens. De data en de analyse die je dan nodig hebt zijn beide conditioneel op de specifieke aftestgrens in deze overweging.
9. De rest van het artikel, die mega-tabellen, de discussie: het is allemaal overbodig, omdat de onderliggende concpetie gewoon niet deugt.
10. p. 98. M&K beroepen zich dan op anderen, van wie ze hun indices hebben overgenomen. Ik ken die literatuur niet, maar als ik de stukken op mijn bureau had liggen, zou ik checken of daar de indices conditioneel op gegeven X=x zijn, of op de range boven/beneden die x.
Een andere mogelijkheid is dat de auteurs op wie M&K zich beroepen, ook in de war zijn. Helemaal onmogelijk is dat niet, omdat in de literatuur over criterium-gerefereerd toetsen precies die verwarring voorkomt. Maar het lijkt me onwaarschijnlijk.
11. p. 102. Hier beginnen die mega-tabellen. Daar kun je van zeggen dat het verdraaid weinig zinvol is om ze te berekenen, laat staan te publiceren, omdat alles afhangt van nogal specifieke parameterwaarden. Cronbach (1976), toen al een oude rot in het vak, zag er om die reden vanaf om getallenvoorbeelden uit te werken: de juiste begripsmatige analyse is belangrijk, vervolgens kan een ieder zijn eigen toepassing berekenen. Als ik een oud werkstuk van mezelf opsla, Cesuurbepaling uit 1977, dan zie ik dat ik daar ook een reeks gedetailleerde tabellen geef. Dat had ik beter na kunnen laten, ik geloof niet dat iemand ooit iets zinnigs met die tabellen heeft kunnen doen.
p. 110: "The examples presented here represent only a small fraction of the many possible parameterizations that could have been explored." Hadden M&K even iets mager bij dit inzicht stilgestaan, dan hadden ze mogelijk ook ingezien dat het enorme verspilling is om al die tabellen in dit arikel op te nemen.
12. Nee, de Discussie levert werkelijk geen enkel inzicht op waar ik een mooie uitroepteken bij heb kunnen zetten. Wat een overbodigheid.
Vergelijk dat eens met het artikel van Cronbach (1976) dat ik je eerder toestuurde, uit het themanummer van het JEM: moeilijk leesbaar door zijn algebraïsche notatie, maar wat een rijkdom van inzicht en overzicht!
Gebruik Cronbach (1976) als toetssteen voor volgende publicaties over eerlijkheid!
In een discussie met Bob van Naerssen heeft hij zich eens verontschuldigd dat de dingen die hij leuk vond om eens uit te zoeken, haaks kunnen staan op wat er nodig is in de praktijk van alledag, bij toetsen in het onderwijs bijvoorbeeld. Er zit een zekere spanning tussen het stellen van fundamentele kwesties, en het oplossen van praktische problemen. M&K benadrukken nogal dat ze dingen aandragen die voor het oplossen van praktische problemen nodig zijn.
Het is ook niet zo dat M&K evidente fouten maken, en alles wat ze berekenen zal best zo te berekenen zijn. Het probleem met M&K is meer dat ze de weg kwijt zijn (geraakt). Dat was te voorkomen geweest door wel degelijk tot een uiteenzetting met Petersen & Novick (1976) te komen. Nu heeft het er veel van weg dat zij meetvariantie hebben opgevat als iets zo wezenlijk verschillend van predictie-invariantie, dat ze de geschiedenis van de testpsychologie en i.h.b. die van predictie-invariantie meenden te kunnen passeren.
Conditioneren op trekgrens of op trekrange, that is the question. Met een enkel goed uitgewerkt kwantitatief contrast zou het duidelijk gemaakt moeten kunnen worden. Ik vermoed dat bij Cronbach (1976) de kiem daarvoor wel is te vinden. Kijk, het ligt natuurlijk helemaal niet voor de hand, anders zouden M&K zelf al wel nattigheid hebben gevoeld, of referenten. Neem maar even als houvast de opmerking, een beetje verborgen, van Lee Cronbach dat hij indices zoals van M&K over hele populaties niet kan interpreteren.
Over het vinden van optimale aftestgrenzen. Als het artikel van M&K daar niets over te zeggen zou hebben, of er geen betekenis voor zou hebben, dan lijkt me dat een goede reden om een verdwijntruc op dat artikel toe te passen. Selecteren gaat over het kiezen van aftestgrenzen. Ik breng het onderwerp te berde, omdat althans de besliskundige literatuur op dat thema direct relevant is voor M&K (niet de flauwekul van methoden zoals die van Angoff, etcetera).
Die 25% beste kandidaten willen hebben ..... . Het is zo gemakzuchtig om op zoiets een casus te bouwen. Nee, ik kan het anders zeggen: als je al weet dat je de beste 25% van de kandidaten wilt hebben, waarom ben je dan nog geïnteresseerd in analyses zals die van M&K? Het veronderstelt het selectieprobleem al als opgelost.
OK, ook bij opgeloste selectieproblemen kun je nog analyses-achteraf doen. Maar ik denk hier toch meer als een ingenieur: ik wil goede selectieprocedures ontwerpen, onder beperkingen die de samenleving, het recht, of gewoon een opdrachtgever oplegt. Dan kom ik nooit op die 25% toelaten als premisse uit.
De kunst is nu om de vingen precies op de zere plek te krijgen. Pas als dat lukt (mijn commentaar doet dat nog te intuïtief), komt mogelijk in beeld dat er een alternatief op de door M&K gekozen benadering valt uit te werken, voor publicatie. Ik denk dat het echt nodig is om M&K te corrigeren, of op zijn minst aan te vullen. Er zit een enorm gat in hun theoretisch kader, zeg maar. Dat gat moet worden gedicht.
Lastig is even dat ik die verwijzingen naar signaal-detectie en zo na moet trekken. Ik ben toevallig bezig een boek over waarschijnlijkheidsleer en modellen voor MC-toetsen, geschreven door iemand in die hoek, te reviewen, ik zal eens kijken of hij vergelijkbare dingen doet als M&K doen.
Als je even terugdenkt aan het Petersen en Novick (1976) artikel, waarin al die modellen voor predictie de revue passeren, dan zie je een tweedeling tussen coherente modellen die conditioneel op een (grens)score werken (Cleary, Einhorn en Bass, Cronbach in zijn reactie op Peteresen en Novick), en incoherente modellen die met indices zoals die van M&K werken. Althans, ik vermoed dat die tweedeling is te construeren. Als dat mogelijk blijkt, ligt het voor de hand dat aan te tonen is dat de indices van M&K incoherent zijn. Ik ben benieuwd of dit een goede hunch is.
 uitstapje: selectieverhoudngen en gewogen loting
uitstapje: selectieverhoudngen en gewogen loting
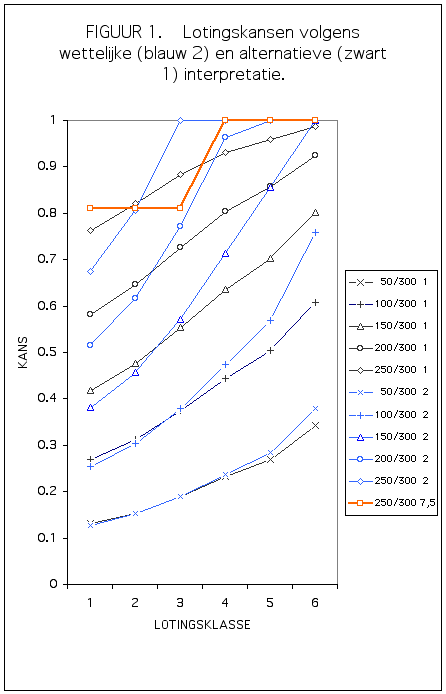
Ik heb in 1975 wat berekeningen/simulaties gedaan op de gewogen loting: al naar gelang de verhouding van aantal gegadigden tot aantal plaatsen, gebeuren er in de verhoudingen van inlotingskansen voor kandidaten in verschillende cijferklassen opmerkelijke verschuivingen.
De verhoudingen tussen INlotingskansen zijn scherp afhankelijk van de selectieverhouding, dus heel anders bij tandheelkunde dan bij geneeskunde, en alleen in de verte lijkend op de wegingsgetallen in het amendement Vermaat, en kamerbreed gesteund.
Het punt is, voor de UITlotingskansen liggen de verhoudingen werkelijk absurd anders dan je logischerwijs zou willen dat het geval was, gegeven de verhoudingen van de INlotingskansen.
Zo is het nog maar de vraag of het de bedoeling van de indieners van het nu in de wet opgenomen amendement Vermaat geweest kan zijn dat in de situatie waarin de toelatingskansen voor twee kandidaten resp. 0,30 en 0,90 zijn (volgens interpretatie 2 mogelijk), de uitlotingskansen voor beide kandidaten resp. 0,70 en 0,10 zijn. Dus een factor zeven verschillen als we in de geest van interpretatie 2 redeneren, en aanzienlijk veel meer wanneer we de situatie behoorlijk in termen van de voor beide kandidaten bestaande kansen analyseren."
Uit mijn Gewogen loting (1975) http://www.benwilbrink.nl/publicaties/75GewogenLotingCOWO.htm:
Dit is precies de methode die Petersen en Novick gebruiken om de coherentie van de *group parity models* van Thorndike en Cole te onderzoeken, evenals het bij wijze van academische oefening door Linn voorgestelde Equal Probability Model (ook een *group parity model*, zie Petersen en Novick p. 9-10 waar ze deze term introduceren).
Dan terug naar M&K.
Het is voldoende om aan te tonen dat hun *success ratio* incoherent is. Lukt dat, dan volgt immers dat ook de *sensitivity* en *predictivity* incoherent moeten zijn.
Als het M&K artikel over klassieke predictie zou gaan, dan is eenvoudig te constateren dat die *success ratio* niets anders is dan het *Equal Probability Model* van Linn, zoals door Petersen en Novick besproken. En dat model is incoherent, zoals Petersen en Novick hebben bewezen door tegenspraak aan te tonen met het logischerwijs equivalente Converse Equal Probability Model (ik moet dat bewijs nog bestuderen, maar het volgt dezelfde logica als het bewijs voor het Thorndike Constant Ratio en Converse Constant Ratio Model).
Als ik het goed zie, dan is de *sensitivity* van M&K gelijk aan het Conditional Probability Model van Cole; en de *specificity* van M&K is het Converse Conditional Probability Model (zie het staatje in Petersen en Novick p. 18).
Petersen en Novick doen over die incoherentie wat besmuikt, geven als het ware ruimte om ondanks die incoherentie toch voor zo'n model te kiezen. Ik vermoed toch dat het zo is dat voor een incoheent model het niet mogelijk is om verstandige interpretaties te geven aan de betreffende proporties. Het standpunt van Cronbach 1976 dus.
De vraag is dan: maakt het werkelijk verschil dat M&K niet een toekomstig criterium, maar een onderliggende trek voorspellen? Ik dacht het niet: de woorden mogen verschillen, maar het casus is wiskundig analoog op te zetten. Toch? (Dat verschillen op een onderliggende trek perfect betrouwbaar zijn, is bijzaak.)
Het laatste laat onverlet dat er een interessant en belangrijk probleem is zodra (schending van) meetinvariantie in een predictor wordt gecombineerd met de kwestie van eerlijke predictie van een toekomstig criterium, het onderwerp van jullie artikel.
![]() http://www.benwilbrink.nl/literature/millsap.kwok.2004.htm
http://www.benwilbrink.nl/literature/millsap.kwok.2004.htm