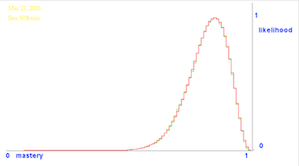
concept
Presentatie op de FBE/HvA Studiedag Nominaal = Normaal, 14 december 2017
11 december
De powerpoint is op mijn website geplaatst: powerpoint
De beschikbare tijd is kort, ik spits mijn uitleg toe op het in de greep krijgen van wat er gebeurt bij iedere afzonderlijke toets. Want daar gebeurt het telkens, daar ligt de weerstand die verbeteraars moeten overwinnen. Vrijwel iedere discussielijn over meer of minder compenseren komt uit op de situatie van de afzonderlijke toetsen. Ik ga in kort bestek het basismodel presenteren.
- Ik begin met een simpel feit: een toets is geen meting maar een steekproef. BEen meting kan meer of minder nauwkeurig zijn, maar gaat wel over dezelfde gemeten zaak. Bij een toets is dat totaa anders: iedere opgave is een nieuwe zaak, om het zo maar te zeggen.
- Nog een feit: er zijn meerdere actoren in het spel betrokken, op zijn minst zijn dat studeten en docenten.
- Aanname: alles draait in eerste aanleg om de studenten, welke strategische keuzen maken zij in de voorbereiding op de toets. Hoeveel tijd willen ze investeren? Hoe zijn examencondities daarop van invloed?
- Handig om te weten is dan dat een toets dus geen psychologische test is, want voor die test kun je je niet gericht voorbereiden. Toch gaan veel denkers over toetsen en examens uit van methodologie uit het rijk van de psychologische test. Dat is oppassen geblazen.
- Een belangrijke aanname om een toetsmodel op te kunnen stellen: voor de student ziet de toets eruit als een willekeurige steekproef uit alle examenwaardige opgaven.
- Oké, aan de slag. Kort voor de toetsafname is er gelegenheid om een proeftoets af te leggen, in alle opzichten vergelijkbaar met de toets zelf. Toets en proeftoets tellen ieder 20 opgaven, dat is niet al te veel voor een toets, maar zijn niet al te eenvoudige opgaven.
- Neem nu in gedachten een student die op die proeftoets 17 goed scoort, van de 20. Wat weet die student dan over de eigen beheersing van de stof? Iemand een idee?
- Die beheersing is verborgen, niemand kent hem, het is een platonisch begrip. Toch kunnen we er heel goed mee werken, ik zal dat laten zien. Ik definieer die beheersing als de proportie van alle denkbare opgaven die deze student goed zou maken, als daar de gelegenheid voor was. Die gelegenheid is er niet, maar dat deert osn niet.
- Want we kunnen nu zeggen dat voor iedere opgave de kans dat de student hem goed kan maken gelijk is aan die beheersing van de stof. En dat is een heel nuttig.
- Gegeven is nog steeds: 17 goed uit 20 opgaven van de proeftoets. Kunnen we dan een gebied bepalen waarbinnen die beheersing ligt? Ja, dat kan. Hier is dat gebied:
- Hoe is dit geconstrueerd? We kennen die beheersing niet, maar we kunnen wel voor een aantal mogelijke waarden van die beheersing bepalen hoe aannemelijk het is dat die waarde de score 17 uit 20 oplevert. Als we dat doen door te simuleren, telkens 1000 toetsen simuleren en bepalen welke proportie van de scores precies 17 is, dan krijgen we deze plot, ik geloof de groene. De rode lijn is de theoretische functie, details daarover laat ik hier achterwege.
- Een beetje zorgwekkend is dat een proeftoetsscore van 17 uit 20 de student, maar ook de docent, zo weinig informatie geeft over de hoogte van de beheersing van de stof. De plot is nauwkeurig genoeg, daar niet van, maar het bereik van mogelijke waarden voor die beheersing is erg breed. Veel breder dan beleidsmakers, u dus, denken.
De volgende stap is dan: gegeven deze aannemelijkheid, een voorspelling voor de toetsscore opstellen. Dat kan bijvoorbeeld weer door simulatie: trek 1000 keer een random waarde uit de oppervlakte onder de aannemelijkheid, en simuleer een toetsscore op basis van de zo gevonden mogeijke beheersing. Een raagje vooraf, voordat ik die concrete voorspelling laat zien: wat denkt u dat de spreiding voor die voorspelling is? De standaard deviatie dus. Is die ongeveer 0,5 punt, 1 punt, 1, 5 punt, 2 punt, of nog hoger?
- Laat deze plot maar even indalen. Stel een score van 16 is vereist voor een voldoende: behoorlijke kans dat de toets 'onvoldoende' blijkt. Maar wat betekent dat? Hebben we absolute maatstaven voor zo’n oordeel? Kunnen we weten of onvoldoendes of voldoendes terecht of onterecht zijn gegeven?
- Het ziet er allemaal best simpel uit, maar toch zien we hier de kern van de eeuwige problematiek van rendementen, vertraging, en staken van studies. Dat gedoe met onvoldoendes en zo’n vak dan moeten herkansen.
- Met dit basale modelletje gewapend is onmiddellijkte zien aan de data in het Risbo-rapport over Nomiaal = normaal aan de EUR dat er toch welheel weinig wordt gecompenseerd, en dan alleen nog vijfjes. Er moeten dus nog heel veel herkansingen gedaan zijn. Alles wijst erop dat ze bij de EUR de toetssituatie voor de studenten verkeerd inschatten: stdenten kunnen veel minder goed voorspellen dan waar de gedetailleerde examenregelingen van uitgaan.
- Verrassing. Wat er gebeurt bij iedere toets: studenten investeren hun tijd, docenten geven hun schaarse budget aan cijfers uit. [model James Coleman, mijn papers in 1992} Het si een markt, een impliciete onderhandeling. En zie de zwakte van deze uitwisseling van tijd en cijfers: studenten hebben niet echt een scherp idee of wel voldoende zijn voorbereid, docenten geven dan wel cijfers maar weten ook niet voor welke beheersing van de stof dat is.
- Ik heb met dit model wat kunnen stoeien aan de hand van data uit de propedeuse rechten in de tachtiger jaren. Ik heb bovendien de laatste dagen nog honderden bladzijden rapporten doorgewerkt en kwam daar vaak zaken tegen die ineens begrijpelijk worden als toetsen en examens als onderhandeling tussen studenten en docenten worden gezien. Want dat is het systeem, een systeem dat door individuele studenten en docenten nauwelijks, zeg maar helemaal niet valt te veranderen.
Ik heb 17 goed uit 20 gekozen, maar had natuurlijk ook iets traditioneler kunnen kiezen voor bijvoorbeeld 14 goed 14, 12 als minimaal voldoende. Dat maakt voor onze analyse geen wezenlijk verschil, maar ik laat toch maar even een afbeelding zien. De voorspelling bij 14 goed uit 20:
- Hoe eenvoudig ons model ook is, het leidt tot boeiende nieuwe inzichten:
- Toetsen worden betrouwbaarder door ze te verlengen. Laten we de toets, maar niet de proeftoets, eens verlengen tot een heel examen: 200 opgaven. Heeft onze student met 17 goed uit 20 er iets aan?
- Nee dus. Verlengen van de toets leidt niet per se tot betere voorspelbaarheid. Daar zit een waarschuwing in: one-issue benaderingen om examenproblemen op te lossen zijn riskant. In dit geval sneuvelt een gouden stelregel uit de testpsychologie, en dat is niet niks.
De student is buitengewoon goed geïnformeerd: zij heeft zojuist een proeftoets van 200 opgaven afgelegd, en er 170 van goed gemaakt. Al die informatie heeft wel invloed op de kwaliteit van de voorspelling, maar als de toets gewoon uit 20 opgaven bestaat is de voorspelling niet spectaculair beter dan op grond van de eerdere 17 goed uit 20. De conclusie lijkt te zijn dat bij een onbalans tussen informatie die de student op voorhand heeft, en de lengte van de toets , we iets niet goed doen.
- En dat blijkt wanneer zowel informatie vooraf, als de lengte van de toets, op 200 worden gezet. Wederom, het is geen relistische situatie, het is een gedachte-experimentje:
Hier is de zaak weer in balans, de goede informatie van de student matcht de stevige omvang van de steekproef. Wat wil je, het is een heel examen! Levert dit dan niet het idee dat weliswaar afzonderlijke toetsen zwak zijn in de uitwisseling van studietijd en cijfers, maar dat hun combinatie in het examen juist krachtig is? Dit zouden we toch graag willen? De vraag is dan, en die leg ik maar neer zonder hem te beantwoorden: maakt volledige compensatie dat ideaal tot werkelijkheid?
- Als er tijd voor is: ons model kunnen we ook gebruiken voor voldoendes en onvoldoendes. Een examen met 10 onderdelen is dan als het ware een steekproef van 10. Stel, in een virtuele wereld, dat onze student een proefexamen heeft afgelegd en 6 voldoendes heeft gescoord. Dan ziet de voorspellende verdeling voor zijn voldoendes op het examen er zo uit (2 figuren achter elkaar)
- Vergelijk die uitkomst met wat we eerder zagen bij de compensatoire optelling van 10 examenonderdelen
Bij wijze van afsluiting, een concept map om discussies over toetsen en examens binnen de lijntjes te kunnen houden
Benadrukken: is op verschillende manieren te gebruiken. Voor de individuele student: meer tijd investeren levert hogere verwachting voor studieresultaten op, etcetera. Maar vooral voor groepen: dan gaat het om verschillen in studieprestaties, en hoe die afhangen van verschillen tussen studenten, op de andere variabelen. Het is onmiddellijk te zien dat studieprestaties geen goed criterium zijn voor effecten van verbeteringen in het onderwijs: als verbeteringen het mogelijk maken om dezelfde resultaten te bereiken in minder tijd, wat denkt u dat studenten dan doen?
- Dank u.
========================================
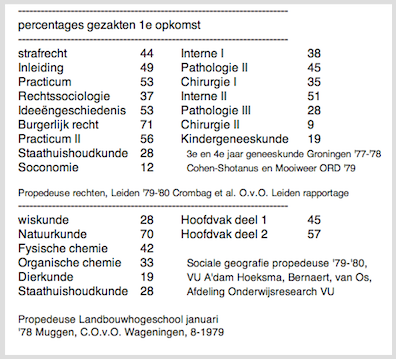
Figuur 1. De feiten
Bovenstaande rampzalige slaagcijfers voor tentamens in de 70er jaren waren een belangrijke aansporing om de mogelijkheden van meer compensatoir examineren te onderzoeken. Zou de situatie nu echt anders zijn? Een eigen overzicht over propedeuserendementen, in opdracht van OCW, dateert van 1987.
Recent publiceerden Smits, Kelderman en Hoeksma (2015) een overzicht van voor- en nadelen. Helaas kan ik het met deze analyse niet eens zijn. Gelukkig zijn hun laatste zinnen, in een paragraaf over wenselijkheid van meer onderzoek naar beslisregels: “Ten tweede kan het simulatieonderzoek sterk verbeterd worden door niet aan te nemen dat studenten zich onder alle toetssystemen hetzelfde gedragen, maar juist per systeem verschillen in hun gedrag en dit expliciet te modelleren. Het werk van Wilbrink (1995) lijkt daarvoor een goed beginpunt.” En dat is inderdaad het springende punt: het strategische gedrag van studenten. We zullen zien. Ik presenteer nu een aantal grondgedachten die nodig zijn om orde in het denken over compenseren te scheppen. Ik zal de verschillen met Smits c.s. laten voor wat ze zijn, op een enkele uitzondering na. Zo’n uitzondering is dat het startpunt de strategische positie van de studenten moet zijn; kies je, zoals Smits c.s., een testpsychologisch uitgangspunt dan redeneren we ons helemaal vast met platonische beschouwingen over terechte en onterechte beslisisngen.
Niels Smits, Henk Kelderman & Jan Hoeksma (2015). Een vergelijking van compensatoir en conjunctief toetsen in het hoger onderwijs. Pedagogische Studiën, 92, 275-285. open access
Marjon Voorthuis & Ben Wilbrink (1987). Studielast, rendement en functies propedeuse. Relaties tussen wetgeving, theorie en empirie. Deelrapport 2: Evaluatie-onderzoek Wet Twee-fasenstructuur. Amsterdam: SCO-rapport 112. ISBN 90-6813-135-4. pagina
Ben Wilbrink (1995). Studiestrategieën die voor studenten en docenten optimaal zijn: het sturen van investeringen in de studie. ORD. pagina
Ieder examen is sterk contingent, dat wil zeggen: bepaald door locale omstandigheden. Ook voor het meer compensatoir maken van een examen is in die zin sterk contingent: er is geen recept voor, al zijn er wel inspirerende voorbeelden. Dat neemt niet weg dat er algemene inzichten zijn die in vrijwel alle situaties van belang zijn. Er zijn fundamentele inzichten, en er zijn praktische toepassingen. Zonder inzicht aan examens gaan sleutelen kan ik niemand aanraden. Dat inzicht is een noodzakelijke voorwaarde, zij het geen voldoende voorwaarde, voor constructieve verbetering van examens. Aan de slag dus.
Stel u voor, een student heeft op haar toets 17 van de 20 opgaven goed gemaakt. Het mag ook een proeftoets zijn. Laten we het op een proeftoets houden. De toets heeft maar 20 vragen, maar het zijn wel complexe vragen (complexe vragen: Wilbrink, 1998). Als dit het enige is dat u van die student weet, en u zou moeten voorspellen wat haar score zal zijn op de echte toets, hoe pakt u dat aan?
Oké, ik zal een hint geven. Verplaats u in die student, en realiseer u dat voor die student de afgelegde en de komende toets zich in alle opzichten gedragen als random steekproeven uit alle mogelijke vragen over de stof. Sterker nog, iedere volgende opgave is een random trekking. Hebben we daar een handig modelletje voor?
Ja, een binomiaalmodel [info]. Voor iedere opgave is de kans dat de studente de opgave goed maakt gelijk p, haar ware beheersing van de stof, waarvan we helaas de waarde niet kennen. Maar daarom niet getreurd, gegeven die score van 17 goed uit 20, kunnen we voor alle mogelijke waarden van p de waarschijnlijkheid bepalen dat deze de score 17 uit 20 oplevert. Dat levert de volgende aannemelijkheid op. Het meest aannemelijk is dat p = 0,85, en dat verbaast ons niets. Toch? [zie hier over aannemelijkheid]
binomiaalverdeling als model: The Generator. Module one of the SPA model: Scores. pagina
Aannemelijkheid (betaverdeling): The mastery envelope: The likelihood of it all. Module two of the SPA model: Mastery. pagina
Ben Wilbrink (1998). Inzicht doorzichtig toetsen. In Theo H. Joostens en Gerard W. H. Heijnen (Red.). Beoordelen, toetsen en studeergedrag. Groningen: Rijksuniversiteit, GION - Afdeling COWOG Centrum voor Onderzoek en Ontwikkeling van Hoger Onderwijs, 13-29. webpagina
Figuur 2. Aannemeijkheid voor de beheersing, gegeven 17 goed uit 20
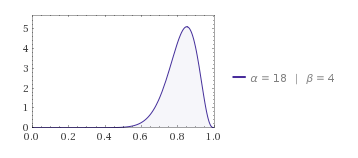
Gegeven die 17 opgaven goed uit 20, kan de ware beheersing van deze student zich overal onder de bovenstaande curve bevinden. Is dat even schrikken? Of kijkt u er helemaal niet van op? Laten we dan de volgende stap nemen, en op basis van deze informatie over de ware beheersing een voorspelling opstellen voor de toetsscore, toets van 20 opgaven getrokken uit hetzelfde domein van vragen over de stof:
Figuur 3. Voorspellende toetsscoreverdeling, gegeven 17 goed uit 20.
Hoe komen we aan deze voorspelling: 1000 keer trekken uit aannemelijkheid die we hierboven zagen, en telkens op basis van de getrokken p-waarde 20 keer een opgave trekken, de groene verdeling. Theoretisch levert dat een betabinomiaalverdeling op, de zwarte lijn.
Je doet als student dan zo’n proeftoets, scoort 17 goed uit 20, en mag dan beslissen om onmiddellijk ook voor de echte toets te gaan, die eveneens 20 vragen heeft. Als de score 16 of hoger een ‘voldoende’ oplevert, dan geeft ons eenvoudige model aan dat de kans daarop 0,68 is. Zou u het doen? En zo ja, waarom dan?
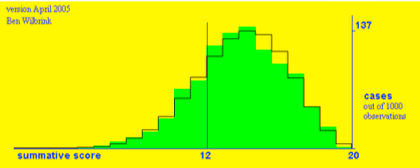
Figuur 3a. Idem, nu gegeven 14 goed uit proeftoets van 20 opgaven, referentie 12.
Vat het allemaal maar op als een gedachte-experiment. De logica ervan is onontkoombaar, bijt er uw tanden maar op stuk. Toetsen zijn voor studenten niet echt goed voorspelbaar. De tragiek daarvan is dat studenten zich niet echt doeltreffend kunnen voorbereiden, en als je er niet van overtuigd bent dat extra investeren van tijd iets gaat opleveren, investeer je dan nog? Ik kom er straks op terug, want alles draait om de tijd die studenten willen investeren.
In een heel ander model functioneert de toets als het wisselkantoor waar studenten hun beloning voor hun inspanningen halen, en docenten die beloning geven. Het is een raar wisselkantoor, want je krijgt er soms veel meer dan je verwacht, soms veel minder. Dat geeft aan dat examens vaak een beroerde economie kennen, waarin partijen (studenten versus docenten) elkaar niet echt vertrouwen. Het is een bijzonder model, voor kostelijke info en empirische data zie Wilbrink 1992.
Ben Wilbrink (1992a). Modeling the connection between individual behaviour and macro-level outputs. In Tj. Plomp, J. M. Pieters & A. Feteris (Eds.), European Conference on Educational Research (pp. pp. 701-704.). Enschede: University of Twente. pagina
Maakt het verschil wanneer we die toets heel, heel veel betrouwbaarder maken door hem 10 keer zo lang te maken? Onze student weet nog steeds niet meer dan zij 17 goed uit 20 heeft gescoord.
Het maakt verdraaid weinig verschil! Hier gaat een niet onbelangrijk geloofsartikel van de psychometrie het raam uit! Laten we het eens omdraaien: heel, heel veel informatie vooraf hebben, door 170 goed uit 200 te hebben, maar de toets die je moet afleggen is gewoon 20 vragen:
Ik geef toe, de voorspelling is wel scherper, maar veel vertrouwen in een goede afloop kan ik het niet noemen: verwacte slaagkans is 0,81.
Wnneer de informatie vooraf in balans is met de lengte van de toets, dan breekt het zonnetje door de wolken. Kunnen we hiermee aan de slag in een discussie over examens? Want 200 opgaven is ongeveer de omvang van een heel examen over het eerste studiejaar.
Stel dat ons examen bestaat uit 10 onderdelen van ieder 20 vragen. Telkens komt onze willekeurig gekozen student op in de wetenschap kort tevoren 17 goed uit 20 proeftoetsopgaven goed te hebben. Dan kunnen we een Mandelbrotje doen: het hiervoor summier gepresenteerde toetsmodel is ook toepasbaar op een examen dat uit 10 onderdelen bestaat, onderdelen die ieder ofwel voldoende (kans 0,68), ofwel onvoloende worden gemaakt: binomiaalmodel met parameters 0,68 en 10. In een gedachte-experiment kunnen we onze student een proefexamen laten afleggen, stel dat ze 6 onderdelen voldoende maakt:
Voor het echte af teleggen examen is dan de aannemelijkheid voor het aantal voldoendes:
En de voorspellende verdeling:
Dat is toch om wanhopig van te worden? Ook al weten we dat we verondersteld hebben dat onze student voor iedere toets dezelfde strategie blijft volgen; in de werkelijke wereld zetten studenten die aanvankelijk onverwacht laag scoren waarschijnlijk toch wel een paar tandjes bij.
Groter contrast is moeilijk denkbaar, toch? We hebben hier een student die voor iedere toets behoorlijk is voorbereid, die ongetwijfeld meteen zou slagen voor alle 10 toetsen gezamenlijk (rechts), maar die bij de middeleeuwse gewoonte van ‘onvoldoendes moeten over’ op verliestijden voor herkansen, en dus op studievertraging wordt gezet (links). (Geschiedenis van beoordelen in onderwijs: Wilbrink, 1997). Onnodige studievertraging: want wie twijfelt eraan dat deze student vlot het tweede jaar zal kunnen doen? En dat moet toch echt het criterium zijn voor een tussentijds examen.
Een tussentijdse conclusie kan eenvoudig zijn dat enige compensatie toestaan een win-winsituatie oplevert: waarschijnlijk veel minder herkansingen, minder verstoring van de studievoortgang (Wilbrink, 1980c), mogelijk betere prestaties.
Over herkansingen gesproken: wie zegt dat die positieve resultaten opleveren? (Wilbrink 1980a) Als een herkansing zinvol is voor wie een ‘onvoldoende’ haalde, waarom niet even zinvol voor wie een ‘voldoende’ haalde? Herhaald toetsen van dezelfde stof is best een goed idee, het is zelfs een uitstekende studiemethode! (Kirschner & Neelen, 2017) Maak er gebruik van bij het ontwerpen van betere examenregelingen.
Ik heb in 2001 al eens een overzicht gemaakt van bekende mogelijkheden (en resultaten) om verliestijden te vermijden voorzover deze voortvloeien uit de examenregeling en de kwaliteit van de toetsen. Ik verwijs u daarnaar, maar zal hierbeneden wel enkele punten aanstippen.
Paul A. Kirschner & Mirjam Neelen (October 31, 2017). Tips and Tricks for Spaced Learning blog
(1980). Ben Wilbrink (1980). Enkele radicale oplossingen voor kriterium gerefereerde grensskores. Tijdschrift voor Onderwijsresearch, 5, 112-125. html
Ben Wilbrink (1980c). Toetsen, herkansen, studievertraging: achterliggende mechanismen. Onderzoek van Onderwijs, 9 nr. 2, 7-11. html
Ben Wilbrink (1997). Assessment in historical perspective. Studies in Educational Evaluation, 23, 31-48. html
Ben Wilbrink (2001). Examens doeltreffend regelen. Ongepubliceerd. pagina
Wat is ons houvast om ons hieraan te ontworstelen? In het onderwijs kennen we geen absolute normen: alle normen zijn relatief. Alleen sleutelen aan de normen is een favoriet spel voor politici, maar dat gaat niet zomaar resultaat opleveren. Daarom is het nodig om door studenten te investeren tijd erbij te betrekken.
Het is een volledig recursief structural equations model, met een geschikte dataset is je het model uit te rekenen (Tromp & Wilbrink 1977). Maar dat terzijde, want het gaat nu vooral om houvast bij de discussie over het examen. De resultaten hangen af van tal van factoren, waarvan de tijdbesteding van studenten de meest interessante is: als we betere resultaten willen, zullen we studenten moeten verleiden of nudgen om meer tijd te investeren. Eens? Kan dat door te spelen met compensatie? Laten we even in de wacht zetten dat we studenten ook kunnen helpen hun tijdinvestering op orde te krijgen door de kwaliteit van de toets te verhogen (Schotanus, 2015), door verliestijden te minimaliseren (Vos & van dr Drift 1987) en/of door de kwaliteit van de tijdbesteding te verhogen (Wieman, 2014).
Let ook even op dat streefniveau: als studenten in het duister tasten over wat er precies van ze gevraagd gaat worden, is het toch raar om ze te vragen om de lat voor zichzelf hoog te leggen. Als niet duidelijk is wat ‘hoog’ is, is dat op voorhand al een verloren zaak. Adriaan de Groot waarschuwde er al voor in 1970.
Janke Cohen-Schotanus (19 juni 2015). Maatregelen ter verbetering van het rendement in het Hoger Onderwijs: waar is de evidentie? Keynote OnderwijsResearchDagen 2015 Leiden. keynote en powerpoint
Koen D. J. M. van der Drift en Peter Vos (1987). Anatomie van een leeromgeving. Een onderwijseconomische analyse van universitair onderwijs. Lisse: Swets en Zeitlinger. Proefschrift Rijksuniversiteit Leiden.
Adriaan D. de Groot (1970). Some badly needed non-statistical concepts in applied psychometrics. Nederlands Tijdschrift voor de Psychologie pagina
Dick Tromp & Ben Wilbrink (1977). Het meten van studietijd. Paper ORD. html Carl Wieman (2014). Large-scale comparison of science teaching methods sends clear message. open access
![]() http://www.benwilbrink.nl/publicaties/17compenserenFBE
http://www.benwilbrink.nl/publicaties/17compenserenFBE