Simon introduced the distinction maximizers - satisficers in 'Rational choice and the structure of the environment. Psychological Review, 1956, 63, 129-138 (repr in his Models of thought as well as in his Models of man, social and rational. Wiley, 1957.
Andere keuzen voor de utiliteitsfunctie
Drempelutiliteit of drempelverlies is wel een erg eenvoudige functie, maar in situaties waar geen duidelijke drempel aan te wijzen is op de criterium- of doelvariabele van een wat hinderlijke eenvoud. Er is niets dat de keuze van een beter passende utiliteitsfunctie over de doelvariabele Y in de weg staat. Figuur 4 laat een ogief zien, de functie Ud(Y), die bij criteriumgerefereerde toetsing goed bruikbaar lijkt. Wie niet aan nauwkeurigheid hecht zou zo'n utiliteitsfunctie zelfs grafisch kunnen bepalen. Wie enige zorg aan het bepalen van zijn utiliteitsfunctie over Y wil besteden kan gebruik maken van technieken zoals gegeven door Siegel (1957), Becker en Siegel (1962), Keeney en Raiffa (1976), en Novick en Lindley (1978), om maar drie verschillende benaderingen te noemen. Voor gedetailleerde toepassingen van dergelijke utfliteitsfuncties verwijs ik naar Davis, Hickman en Novick (1973), hoewel aan hun behandeling het bezwaar kleeft waartegen ik mij in dit artikel richt, dat impliciet in de uitkomstutiliteitsfunctie voor de behandeling bijspijkeren het effekt is opgenomen dat bijspijkeren heeft op de voorspellende kansverdeling over de doelvariabele Y. Van der Linden en Mellenbergh (1977) werken met lineaire uitkomstutiliteitsfuncties, met hetzelfde bezwaar.
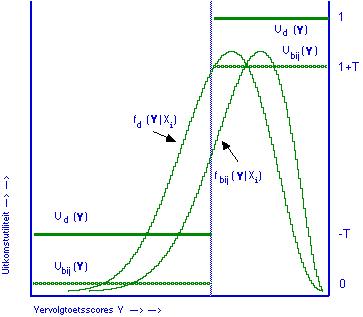
Figuur 4. Best passende uitkomstutiliteitsfuncties (Ud | y) voor doorlaten en Ubij | Y) voor bijspijkeren, met beide voorspellende kansverdelingen fd en fbij , gegeven Xi.
Voor de behandeling doorlaten hebben we dan als uitkomstutiliteitsfunctie weer de functie die gelijk is aan de utiliteitsfunctie over de criterium- of doelvariabele Y, vervolgtoetsscores, in figuur 4 aangegeven door Ud(Y). Voor de behandeling bijspijkeren hebben we te maken met dezelfde utiliteitsfunctie over Y, en moet deze gecombineerd worden met de negatieve utiliteit ofwel de kosten van bijspijkeren, dat levert Ubij(Y).
In figuur 4 zijn alle functies continu getekend, om illustratieve redenen: in de praktijk nemen ze discrete waarden aan. Verwachte utiliteit van ieder beslissingsalternatief gegeven dat Xi waargenomen wordt, is dan weer volgens formule (4) te berekenen.
Een bijzonderheid van figuur 4 lijkt ook te zijn dat beide uitkomstutiliteitsfuncties elkaar niet snijden. Dat volgt direct uit de aard van de gekozen doelvariabelen, en houdt geenszins als vanzelfsprekend in dat de behandeling doorgaan altijd de betere zou zijn. In een volgende paragraaf zal ik, in figuur 5, verwachte utiliteiten over toetsscores X bespreken, en voor deze functies geldt uiteraard wél dat er een snijpunt in het bereik van de toetsscores moet zijn wil niet één van beide behandelingen altijd beter zijn ongeacht de waargenomen toetsscore.
Ik wil toch iets langer bij het verschijnsel van elkaar niet snijdende uitkomstutiliteitsfuncties stil blijven staan, omdat Davis et al. (1973), en van der Linden en Mellenbergh (1977, 1979) ervan uitgaan dat er wel een snijpunt moet zijn wil er een optimale grensscore bestaan. Deze auteurs modelleren het beslissingsprobleem als een selectieprobleem in deze zin dat effecten van bijspijkeren uitsluitend tot uitdrukking gebracht worden in de te kiezen uitkomstutiliteiten, zodat er (stilzwijgend) vervolgens vanuit gegaan kan worden dat over de criterium- of doelvariabele onder beide behandelingen de conditionele kansverdelingen identiek zijn. Welnu, weeg je twee uitkomstutiliteitsfuncties met dezelfde kansverdeling bij het berekenen van verwachte utiliteiten, dan kun je alleen een niet-triviale optimale grensscore vinden wanneer beide uitkomstutiliteitsfuncties elkaar ook snijden.
Weeg je ze met verschillende kansverdelingen, dan is elkaar snijden geen voorwaarde voor het bestaan van een optimale grensscore.
Dat beide functies Ud(Y) en Ubij(Y) elkaar niet snijden volgt direct uit de utiliteitsanalyse voor het onderhavige probleem. Bijspijkeren heeft zeker effect op de waarde van de doelvariabele, maar alleen via de voorspellende kansverdeling onder de behandeling bijspijkeren: de utiliteit van de waarde van Y die bereikt wordt is niet afhankelijk van de gevolgde behandeling. (Zou je van mening zijn dat een hoge score op de criteriumvariabele Y iets anders waard is wanneer ze na bijspijkeren verkregen is, dan is er kennelijk nog een andere doelvariabele in het spel, bijvoorbeeld de snelheid waarmee het eenmaal geleerde weer vergeten wordt, die hoger zou kunnen liggen voor bijgespijkerde leerlingen dan voor de anderen met dezelfde Y score). Voor beide behandelingen hebben we te maken met dezelfde utiliteitsfunctie over vervolgtoetsscores, en alleen voor bijspijkeren moet daar een correktie op gepleegd worden door er de kosten van bijspijkeren af te trekken om de uitkomstutiliteitsfunctie Ubij(Y) te krijgen.
Voor alle duidelijkheid: bijspijkeren zal doorgaans natuurlijk effekt hebben op de vervolgtoetsscore, maar in de zin van een hogere verwachte score, dus via de kansverdeling over Y voor bijgespijkerde leerlingen.
Extensive en normal form analysis
Voor een goede vergelijkbaarheid van het in dit artikel gepresenteerde en oudere literatuur is het goed om te weten dat er twee nogal verschillende mogelijkheden voor het decisie-analytisch benaderen van het grensscore-probleem zijn, in de literatuur (bijv. Raiffa 1968) bekend als de normal form en de extensive form analysis. Beide methoden geven dezelfde resultaten, de ene doet dat alleen op omslachtiger wijze dan de andere. Het vervelende is dat overeenkomsten tussen beide niet eenvoudig te vinden zijn, zodat de indruk kan ontstaan dat het om wezenlijk verschillende methoden gaat. Davis et al. (1973, blz. 17 e.v., 43) bespreken verschillen en overeenkomst op verhelderende wijze.
Extensive form analyse kiest de beslissingsregel die het verwachte verlies minimaliseert voor de waargenomen waarde van X. Daarentegen kiest de normal form analyse de beslissingsregel die het gemiddelde van de verwachte verliezen voor alle mogelijke waarden van X minimaliseert. (Davis et al., 1973 blz. 18).
In dit en in het voorgaande artikel hanteer ik de extensive form analyse, zoals ook Novick en Jackson (1974) doen, terwijl Davis et al. (1973) beide naast elkaar gebruiken (om didaktische redenen zoals zij zeggen). De normal form analyse is gebruikt door Petersen (1976), Huynh (1976), en Van der Linden en Mellenbergh (1977, 1979). In het voorgaande artikel heb ik een poging gedaan dit op verschillende benaderingen gebaseerde werk aan elkaar te relateren.
Verbinding met het werk van Cronbach en Snow (1977)
Verwachte utiliteit onder beide behandelingen kun je berekenen volgens formule (4) voor iedere observeerbare toetsscore X. Daar kun je dan een mooi plaatje van maken, zoals figuur 5. De gelijkenis met de gebruikelijke afbeelding van aptitude treatment interactions is niet alleen een oppervlakkige. De aptitude is in dit geval de stofbeheersing zoals die in de toetsscore tot uiting komt, een nogal ruime opvatting van aptitude die Cronbach en Snow (blz. 6) uitdrukkelijk toelaten. Hetzelfde geldt voor de treatment, die er in dit geval uit bestaat of de leerling bijspijkeronderwijs volgt of niet. De interaction is gedefinieerd op de op een utiliteitsschaal geëvalueerde uitkomstvariabele, en daar zijn Cronbach en Snow helaas wat minder duidelijk over (zie bijv. blz. 32).
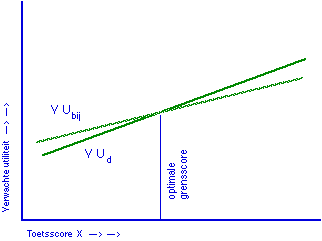
Figuur 5. Verwachte utiliteiten als functie van toetsscore X. Het snijpunt van beide functies bepaalt de optimale grensscore. Rechte lijnen zijn louter illustratief, al was het alleen maar omdat X in de praktijk diskreet is.
In figuur 5 heb ik verticaal de verwachte utiliteit afgezet, omdat dat ook is wat de beide getekende functies voorstellen. Ik kan even goed verticaal de utiliteit van de bereikte uitkomst, dat is de utiliteit van de behaalde vervolgtoetsscore Y na al dan niet bijgespijkerd te zijn, noemen, zoals Cronbach en Snow (fig. 2.6a) doen, dat blijft hetzelfde. De methodologie voor ATI onderzoek kan van belang zijn voor degenen die met grensscores willen werken op criteriumgerefereerde toetsen. Dan zijn er echter nog wel enige problemen op te lossen. Zo zal in het algemeen de decisie-analyse niet leiden tot lineaire regressie van uitkomstutiliteit op toetsscore, zoals ik gemakshalve in figuur 5 nog wel getekend heb. Ook is de relatie tussen toetsing van de ATI veronderstelling, en het aanwijzen van de optimale grensscore niet zonder meer duidelijk, al lijkt het dat je het laatste best kunt doen zonder het eerste.
Een eenvoudiger aanpak om optimale grensscores te bepalen
Terugblikkend op de geschetste volledige decisie-analytische methode voor het bepalen van optimale grensscores bij criteriumgerefereerde toetsjes lijken we in de situatie geraakt te zijn dat er weliswaar een goede methode beschikbaar is, maar dat deze praktisch vrijwel onhanteerbaar is. Het is eenvoudig ondenkbaar om voor ieder toetsje een volledig valideringsonderzoek te doen, en vervolgens een utiliteits- en decisie-analyse. Dergelijke toetsjes zijn kort, en talrijk: ze plegen maar een handvol vragen te bevatten, 10 of zelfs minder, en iedere cursus bevat een reeks van dergelijke toetsjes als afsluiting van ieder onderdeel. Ook waar het gaat om landelijk gebruikt toetsmateriaal is in principe lokaal valideringsonderzoek als aanvulling op de algemene gegevens over toetsen en grensscores noodzakelijk.
Om aan deze praktische bezwaren het hoofd te kunnen bieden zou je kunnen proberen om niet voor ieder toetsje afzonderlijk, maar voor de hele reeks toetsjes per cursus tegelijk de optimale grensscores te bepalen. Zeker wanneer die toetsjes qua opzet en karakter niet veel van elkaar verschillen is zoiets mogelijk door te experimenteren Met de plaats van de grensscore op alle toetsjes tegelijk, en de onderwijsresultaten en benodigde tijdbesteding als afhankelijke variabelen te registreren. Iets wat daarop lijkt is bijvoorbeeld door Barkmeier, Duncan en Johnston (1978) gedaan: zij onderzochten niet het effect van verschillende hoogte van de grensscore, maar van verschillend aantal herkansingsgelegenheden op bestede tijd en behaald resultaat over een cursus met negen criteriumgerefereerde toetsjes.
Wanneer het niet mogelijk is om in dezelfde cursusperiode met verschillende experimentele groepen te werken, kan de grensscore voor iedere nieuwe cursus stelselmatig voor alle toetsjes veranderd worden (telkens een punt hoger of lager gelegd).
Misschien zijn de resultaten niet makkelijk te interpreteren: het kan zijn dat de docent de tradeoff tussen stofbeheersing en studietijd moet bepalen (Keeney en Raiffa (1976) geven technieken). Het kan zijn dat randvoorwaarden (tijd, te lage stofbeheersing, te veel herhalingen) overschreden worden, waardoor het pleit ten gunste van een bepaalde grensscore beslecht kan worden. Hebben leerlingen bij de optimale grensscore veel herhalingen nodig, dan kan de docent overwegen of dit concept van criteriumgerefereerd toetsen voor hem wel bruikbaar is. Een alternatief zou zijn dat niet ieder onvoldoende toetsje bijspijkeren en herhalen vraagt, maar dat pas na een aantal opeenvolgende onvoldoendes de docent speciale aandacht aan de leerling schenkt. Een flexibele aanpak van het grensscore probleem is hiermee weer mogelijk, de situatie blijft doorzichtig voor de docent, het onderwijs is eenvoudig te evalueren. Statistische en psychometrische technieken die je hierbij zou kunnen gebruiken zullen het in deze termen geformuleerde probleem niet zo makkelijk nog kunnen versluieren.
Ook een grensscoreprobleem: zakken - slagen voor tentamens
Wie niet bezwijkt voor de verleiding om een model zoals dat van Huynh (1976) op de zak-slaag problematiek bij tentamens in het wetenschappelijk onderwijs toe te passen, zou de volgende oplossing kunnen vinden (zie Wilbrink (in voorbereiding) voor een gedetailleerde uitwerking).
Voor tentamens geldt, zeker voor studenten die niet tot de hoogvliegers behoren, dat de hoogte van de gestelde cis (grensscore) de mate van voorbereiding op het tentamen beïnvloedt. Dat is uit te werken tot een tentamenmodel, waaruit optimale studiestrategieën bij gegeven grensscores te bepalen zijn (Van Naerssen, 1976; Wilbrink, 1978). De student die zakt legt opnieuw tentamen af, totdat hij slaagt. Het zit ingebakken in deze conjunctieve examenregeling dat de student zo af en toe, en vaak eigenlijk ten onrechte, tentamens zal moeten overdoen ook wanneer hij een verstandige studiestrategie hanteert. Voor de student ligt het voor de hand om zijn studiestrategie dan ook mede op het aantal te verwachten herkansingen af te stemmen.
De grensscore moet kennelijk zo gekozen worden dat studenten studiestrategieën kiezen die in de beschikbare tijd tot maximale stofbeheersing leiden. Ik zeg met opzet de beschikbare tijd, dat is de tijd die volgens het studieprogramma voor dit studieonderdeel uitgetrokken is. In die beschikbare tijd moeten ook de herkansingen gedaan kunnen worden, voorzover het gaat om herkansingen die volgen uit optimale studiestrategieën. (Tijd nodig voor deze herkansingen moet dan opgevat worden als gemiddeld over deze deelgroep studenten). Een belangrijke doelvariabele, tijdbesteding, is hiermee gefixeerd. Dan is voor de doelvariabele stofbeheersing het maximum te zoeken door uit het tentamenmodel voor verschillende grensscores en toetslengten de verwachte mate van stofbeheersing te schatten.
Zonder utiliteitsanalyse is de optimale grensscore te vinden. Dit is een compromisloze aanpak voor het vinden van optimale grensscores bij tentamens. Daarin zijn heel wat details in te vullen, maar de grondgedachte is in het bovenstaande tamelijk volledig weergegeven. Overigens betekent het hanteren van optimale grensscores niet dat het beoordelingsstelsel daarmee ook optimaal zou zijn: bij een ideale examenregeling zou je dezelfde stofbeheersing kunnen bereiken zonder dat er tijd en kosten verloren gaan aan herkansingen. Het is niet uitgesloten dat een compensatorische examenregeling, waarin geen herhalingen van tentamens voorkomen, waarin het over-all gemiddeld (gewogen) studieresultaat bepalend is voor het slagen voor het examen in zijn geheel, dicht in de buurt van zo'n ideale regeling komt.
19 november 2015. Waarom herschrijf ik dit artikel niet voor een Engels tijdschrift? Ik heb de indruk dat ik het nu allemaal scherper en korter kan opschrijven, en op een enkel onderdeel (die rare ‘kosten’) het model kan verbeteren. Het enige probleem lijkt het updaten van de literatuur te zijn, maar dat is een klusje dat ik toch eens een keer moet gaan doen.
LITERATUUR
Barkmeier, D. R., Duncan, Ph. K., and Johnston, J. M. (1978). Effects of opportunity for retest on study behavior and academic performance. Journal of Personalized Instruction, 3, 89-92.
Becker, S. W., and Siegel, S. (1958). Utility of grades: level of aspiration in a decision theory context. Journal of Experimental Psychology, 55, 81-85.
Cronbach, L. J., and Snow, R. E. (1977). Aptitudes and instructional methods. A handbook for research on interactions. New York: Wiley.
Davis, Ch. F., Hickman, J., & Novick, M. R. (1973). A primer on decision analysis for individually prescribed instruction. Iowa City, Iowa: The American College Testing Program. Technical Bulletin no. 17.
Huynh (1976). Statistical consideration of mastery scores. Psychometrika, 41, 65-78.
Keeney, R. L., & Raiffa, H. (1976). Decisions with multiple objectives: preferences and value tradeoffs. New York: Wiley.
Linden, W. J. van der, and Mellenbergh, G. J. (1977). Optimal cutting scores using a linear loss function. Applied Psychological Measurement, 1, 593-599.
Linden, W. J. van der (1981). Using aptitude measurements for the optimal assignment of subjects to treatments with and without mastery scores. Psychometrika, 46, 257.
Mellenbergh, G. J., & van der Linden, W. J. (1979). The internal and external optimality of decisions based on tests. Applied Psychological Measurement, 3, 257-273.
Naerssen, R. F. van (1976). Het derde tentamenmodel met een toepassing. Tijdschrift voor Onderwijsresearch, 1, 161-171.
Novick, M. R., and Jackson, P. H. (1974). Statistical methods for educational and psychological research. London: McGraw-Hill.
Novick, M. R., and Lindley, D. V. (1978). The use of more realistic utility functions in educational applications. Journal of Educational Measurement, 15, 181-191.
Petersen, N. S. (1976). An expected utility model for 'optimal' selection. Journal of Educational Statistics, 1, 333-358.
Raiffa, H. (1968). Decision analysis. Introductory lectures on choices under unvertainty. London: Addison-Wesley.
Raiffa, H., and Schlaifer, R. (1961). Applied statistical decision theory. London: The M.I.T. Press.
Wilbrink, B. (1978). Examenregeling deel A: Studiestrategieën. Amsterdam: COWO
Wilbrink, B. (1980). Optimale kriterium gerefereerde grensscores zijn eenvoudig te vinden. Tijdschrift voor Onderwijsresearch, 5, 49-62. html
Manuscript ontvangen 9-3-'79
Definitieve versie ontvangen 3-10-'79
13-9-80
Beide TOR-artikelen besproken in de NSP [Psychometrie] bijeenkomst, Arnhem, Cito, 11 september.
Concept-versies zijn besproken in de werkgroep criterium-gerefereerd toetsen onder voorzitterschap van Wim van der Linden, mijn dank voor de ontvangen aandacht en opmerkingen.
Nabeschouwing 2007
Deze TOR-artikelen zijn een poging helderheid te scheppen in een overigens nogal warrige theorie over het bepalen van de grenzen voor slagen en zakken bij toetsen door daar de besliskundige theorie bij te gebruiken. Die verdwaalde theorie staat op het conto van een kleine groep onderzoekers in de VS en in Nederland, en de dwaling zit, zoals in de TOR-artikelen aangegeven, in de begripsvorming over wat nutsfuncties zijn. In het huidige SPA-project html is in het moduul over nutsfuncties html een gedetailleerde uitwerking te vinden over wat in het allereerste artikel in die lijn van onderzoek al helemaal misging, en in feite door latere auteurs klakkeloos is overgenomen. Sorry lui, maar zo is het toch?
Maar eerst even die bepaling van de grens slagen-zakken, een probleem dat docenten regelmatig slapeloze nachten kan bezorgen, en waar ze echt geen besliskunde voor hoeven studeren om het praktisch aan te pakken. Het bijzondere kenmerk van onderwijs is dat studenten er zijn om iets op te steken, en daar moeten ze hun tijd dan ook verstandig aan besteden. De grondgedachte is nu een groep studenten die gemiddeld te weinig tijd aan de studie besteedt, daarvoor niet met een 'voldoende' resultaat te belonen. Toch? Daar kan niemand het mee oneens zijn, gegeven de beoordelingstraditie die niet even helemaal opzij is te zetten. Heel precies is het niet te steken, want op zijn best is het mogelijk een globaal idee te hebben over die hoeveelheid bestede tijd. Is die bestede tijd, bijvoorbeeld voor de groep in de gevarenzone van vijven en zessen, te laag, dan gaat de lat voor deze toets omhoog. Zo simpel is dat. Lees evenwel De Groot (1966) Vijven en zessen voor het gedoe dat dan op de loer ligt. Of mijn 1992 ECER-artikelen html over de impliciete onderhandeling tussen studenten die de lijn trekken, en docenten die er als het even kan toch iets meer uit willen halen. Of het nawoord bij mijn Cesuurbepaling uit 1977 html.
Deze beide TOR-artikelen laten zien wat er nodig is om de begrippen 'nut' en 'nutsfunctie' een goede uitwerking te geven. Op dat punt is de impact, bijvoorbeeld bij de Nederlandse onderzoekgroep waar ik destijds ook in deelnam, nul komma nul geweest. In een bepaalde opvatting is het zo dat ik gewoon een of twee jaar te laat was met deze theoretische bijdrage, ook al circuleerden eerdere versies al een jaar eerder. Te laat, omdat andere onderzoekers al tot over hun oren in het moeras van een onhandige analogie uit de besliskundige statistiek waren gezonken; zij konden weliswaar niet aangeven waar in deze TOR-artikelen fouten of verkeerde concepties zaten, maar waren ook niet in staat de theoretische ontwikkeling te begrijpen en op eigen werk toe te passen. Omdat het paradigma van onderzoekers als Hambleton, Van der Linden, en Mellenbergh omstreeks 1980 naar hun eigen opvatting was vastgelopen, zie het overzichtsartikel van Wim van der Linden in Applied Psychological Measurement's themanummer van 1980, droogde het onderzoek op. Dat neemt niet weg dat er veel later toch weer proefschriften verschenen die de draad van het oude paradigma weer oppakten: Van der Gaag (Amsterdam), en Vos (Enschede). Zij bouwen hun onderzoek op een visie over nut en nutsfuncties waarvan ik nu juist in deze TOR-artikelen 1980 laat zien dat ze inconsistent is.
In mijn eigen onderzoek heb ik natuurlijk wel verder gebouwd op de fundamenten die hier, in 1980, zijn gelegd. Omdat ik begin 80-er jaren terecht kwam in een zichzelf voortdurend vernieuwende reorganisatie, was het niet mogelijk om er rechtlijnig aan door te werken. Recent zijn er evenwel belangrijke doorbraken geweest, in het kader van mijn project over tentamenmodellen. In de module over nut en nutsfuncties is een paragraaf project history html opgenomen over de belangrijke theoretische ontwikkelingen. Inderdaad, de theoretische oefeningen in 1980 zijn cruciaal geweest voor mijn eigen verdere werk. Achteraf is het duidelijk dat er in 1980 belangrijke problemen zijn blijven liggen of niet zijn opgemerkt. Zo is de gedachte om docenten 'hun' nutsfunctie over mate van beheersing van de stof te laten construeren, onhelder, to say the least. Het springende punt was natuurlijk hoe het mogelijk te maken om de stelling van Van Naerssen concreet uit te werken: het gaat om de strategie van de individuele student, en daar is die van haar docent een afgeleide van. Een belangrijke misser, bijvoorbeeld in het onderzoek van Van der Gaag, is om net te doen alsof die strategisch opererende studenten, met dus hun eigen opvattingen over het nut van dat alles, er niet toe doen. Mogelijk kon zij, evenmin als haar begeleider Don Mellenbergh, die misser te pakken krijgen omdat het project scharnierde om een foutieve opvatting van verwacht-nutsfuncties voor docenten - precies waar dit 1980 TOR-artikel over gaat - in combinatie met een onderzoekopzet waarin deze docenten gewoon gevraagd werd hun nutsfuncties te schetsen en zij daar - met twee of drie veelbetekenende uitzonderingen - daar welwillend aan voldeden door iets onmogelijks te schetsen. Maar die welwillendheid is proefpersonen eigen.
Gaag, N. van de (1990). Empirische utiliteiten voor psychometrische beslissingen. Proefschrift Universiteit van Amsterdam. [Zie voor annotaties toetsen.htm#Gaag_1990]
Groot, A. D. de (1966). Vijven en zessen. Groningen: Wolters Noordhoff.
Linden, W. J. van der (1980). Decision models for use with criterion-referenced tests. Applied Psychological Measurement, 5, 469-492.
Vos, H. J. (1994). Simultaneous optimization of test-based decisions in education. Proefschrift Universiteit Twente.
Wilbrink, Ben (1977). Methoden voor het bepalen van de grens zakken/slagen voor studieonderdelen.Amsterdam: COWO (docentenkursusboek 6). html
Wilbrink, Ben (1992). The first year examination as negotiation; an application of Coleman's social system theory to law education data. In Tj. Plomp, J. M. Pieters & A. Feteris (Eds.), European Conference on Educational Research (pp. 1149-1152). Enschede: University of Twente. Paper: auteur. html
Wilbrink, Ben (2007, in ontwikkeling). The Ruling html. Onderdeel van A general model of achievement testing. html
Uit correspondentie met Wim van der Linden over normal form versus extensive form: 3-10-1977
Allereerst de relatie van de door jullie gepresenteerde optimalisering [in 1977 gepubliceerd artikel], en wat ik in hoofdstuk 7 van mijn Cecuurbepaling beschrijf. In bijgaand stukje laat ik zien dat beide procedures tot hetzelfde resultaat leiden. Het voordeel van het werken met de selectieparameter p = (C - d) / (C - D - A + B) is dat dudielijk wordt dat de verdeling van y (of van tau in jullie art.) slechts van invloed is op de cutting score voorzover p er door beënvloed wordt. Mijns inziens is het laatste een belangrijke kwalificatie die je zou kunnen aanbrengen op jullie uitspraak (blz. 13) "... and this principle takes into account the entire distribution of values of tau for the given population of students."
Overigens ben ik erg blij met deze opmerking, omdat ik langs andere weg tot mijn verrassing gevonden had dat de slaagkans van de student met voldoende beheersing van de stof ongunstig beïnvloed wordt door aanwezigheid van grotere aantallen studenten met onvoldoende beheersing van de stof (opmerking in Cesuurbepaling, blz. 83 bovenaan). In mijn benadering van de beoordelingsproblematiek zal ik aan dit verband argumenten ontlenen om de onderwijs- en beoordelingssituatie zó in te richten dat een minimum aantal studenten met onvoldoende voorbereiding aan tentamens deelneemt (althans, onder conjunctieve examenregelingen).
Met de boven gegeven afzwakking van jullie uitspraak over de invloed van de hele verdeling van tau is het duidelijk te maken dat optimaliseren van payoff functies (minimaliseren van risico functies) géén 'relatieve beoordeling' is.
OPTIMAL CLASSIFICATION OF INDIVIDUALS INTO TWO CRITERION GROUPS UNDER THRESHOLD UTILITY: CASE Il.
Ben Wilbrink
3-10-1977.
lt will be shown that optimal classification of individuals into
two criterion groups only depends on the proportion p of individuals in the group with testscore xc that is estimated to have a criterion score or true score y above the cutting point ycon that variable. 'Optimal classfication' is defined on the expected total utility function U under threshold utility.
Assumptions.
The criterion score or true score variable y is dichotomized by yc; the proportion g of individuals with y≥ycis a constant (and need not be known).
The estimated proportion of individuals with both y≥ycand x≥xcis b;
The estimated proportion of individuals with both y≥ycand x<xcis a;
The estimated proportion of individuals with both y<ycand x<xcis c;
The estimated proportion of individuals with both y<ycand x≥xcis d.
The proportion of individuals with x≥xcis t = b + d.
The proportion b is a differentiable function of t.
Parameters a, b, c, and d correspond to the four possible outcomes resulting from pass-fail scoring on testvariable x with cutting score xc; the utility of individual cases is correspondingly A, B, C, or D. Total expected payoff of pass-fail scoring is
(1) U = aA + bB + cC + dD.
The particular assumption in pass-fail scoring is that B>A and C>D; Those preferring a loss function could use the expected risk
(2) R = a(B-A) + b(B-B) + c(C-C) + d(C-D) = a(B-A) + d(C-D).
The optimal cutting score xc maximizes U (minimizes R).
Optimal classification.
There is a monotonically decreasing functional relationship
between t and xc, enabling us to find the value to that maximizes R by differentiating R to t, and setting the differential quotient equal to zero.
U = aA + bB + cC + dD
= bB + (g-b)A + (1-g+b-t)C + (t-b)D
= b(B-A+C-D) + g(A-C) + t(D-C) + C.
(3) dU/dt = (B-A+C-D) db/dt + (D-C) = 0.
(4) db/dt = (C-D) / (C-D-A+B)
The cutting score xo is optimal for that value t = to that is the solution to (4).
Or, equivalently, the cutting score xo is optimal if in the group of students with observed xo the proportion p with y>yc is equal to (C-D)/(C-D-A+B).
This follows from the definition of the differential quotient, and is perhaps easier to understand if the argument is given in terms of numbers of individuals instead of in terms of proportions of individuals. The differential quotient:
(5) (db/dt)t=to = d f(to)/dt = limt to to (f(t) - f(to))/(t - to).
The decisionmaker is indifferent between passing or failing the group scoring exactly xo on the test. In this subgroup:
(6) p = (C-D) / (C-D-A+B)
The expected payoff passing these individuals is
pB + (1-p)D,
the expected payoff failing these individuals is
pA + (1-p)C,
the identity between these payoffs is easily established in using (6).
The argument as presented here is a slight revision of Vastenhouw 1973 (Onderzoek van Onderwijs, 1973, volume 2, no 4, 8-10.), and a generalization of Alf and Dorfman 1967 (Psychometrika, 1967, volume 32, 115-123). Alf and Dorfman proved (6) for optimal classification, under the assumption of bivariate normal distrubition of test en criterion variable, an assumption that is not needed, as shown above.
Artikelen die ik in 1984/1985 heb gemist omdat er even een paar andere problemen (UvA) langs kwamen. Ik moet er toch nog eens een keer voor gaan zitten, en de vraag beantwoorden waarom deze geachte collega’s niet de moeite hebben genomen om in te gaan op de besliskundige methodiek die ik in de beide TOR-artikelen heb uiteengezet. Het had mijn loopbaan kunnen veranderen. Op zijn minst had ik een dergelijke steun in de rug op zo’n moeilijk moment in mijn loopbaan goed kunnen gebruiken, om mentaal op de been te blijven.
Dato N. M. de Gruijter & Ronald K. Hambleton (1984). On problems encountered using decision theory to set cutoff scores. Applied Psychological Measurement, 8, 1-8.abstract
Wim J. van der Linden (1984). Some Thoughts on the Use of Decision Theory to Set Cutoff Scores: Comment on de Gruijter and Hambleton. Applied Psychological Measurement, 8, 9-17.abstract
Dato N. M. de Gruijter & Ronald K. Hambleton (1984). Reply to van der Linden's "Thoughts on the Use of Decision Theory to Set Cutoff Scores". Applied Psychological Measurement, 8, 18-20.abstract
Katy Murphy (October 9, 2016). Grim dropout stats force California colleges to rethink remedial education
The Mercury News blog
Placement tests that misplace students. It’s a classic methodological point that anything intended to be remedial has to be evaluated for its working correctly. Think decision-theoretically. For the methodology. see my 1980 articles (in Dutch) in Tijdschrift voor Onderwijsresearch.
 http://www.benwilbrink.nl/publicaties/80bGrensscoresTOR.htm
http://goo.gl/aXwKx
http://www.benwilbrink.nl/publicaties/80bGrensscoresTOR.htm
http://goo.gl/aXwKx