The analysis of student outcomes in school is typically done in a way that completely bypasses the subjective orientation of the student. Typically, the background characteristics and school characteristics are the regressors, with achievement, behavior, post-secondary plans, etc. as the dependent variables. But there is another way of proceeding. This is to assume that students (assume for concreteness high school students) are engaged in a production process (alternatively describable as an investment process), in which they are attempting to produce rewards.
I started, a couple of years ago, to develop ideas in this fashion, and made a presentation at OSC. However, I never pursued this. The current presentation will be an extension of the work I began and abandoned two years ago.
The general idea is that each student in school is attempting to maximize utility (i.e., to maximize realization of interests), and that student's interest is in respect or status from others. The question of which others will depend on the student's background and immediate environment. And what he will do will depend on the resources he believes he has, and the achievements for which status or respect is awarded. For example, in my high school, football brought highest status. There were 166 graduating seniors in that year. The initial drawing power of each of the four school sports, their retention rate after the first year, the drawing power for the second year among those who had not gone out the first year, and the total who went out for the sport at some time during high school, were:
| First Year Drawing | Retention Rate | 2nd Year Drawing | Total Anytime | |
| Football | 12.1 | 75.0 | 11.5 | 24.7 |
| Basketball | 12.1 | 40.0 | 4.1 | 13.3 |
| Baseball | 8.1 | 81.3 | 0.7 | 10.7 |
| Track | 9.6 | 68.8 | 6.7 | 16.3 |
This table shows the greater ability of football to attract players, with a quarter of the total cohort having gone out for football at some time during high school, and a much higher drawing power than the other sports in the second year, after the boys had been in the school environment for a year.
For predicting how each student would invest his time, what one would want to have, then, are:
1) The degree to which the student is oriented to particular others, whose status rewards are of interest to him. For students in school, I think the principal parties to which a student is oriented are parents, particular groups of students, the opposite sex, coaches, teachers. The last of these probably depends on the degree to which the student is known by teachers, which in turn depends on the number of students in the school, and whether the student is seen as outstanding in any way.
In school, this information could be obtained from the student simply by asking questions that would elicit the importance of different potentially significant others for his own self-perception. This would include questions about which other students' opinions matter most to him.
(In a more complex model, the degree to which a student is oriented to particular others is not exogenous, but depends on the respect he gets from those others, which in turn depends on how well he does in the things those others give rewards for.)
2) The areas of performance for which each of the 'significant others' gives rewards. This would be obtained from each of those significant others. In the case of other students, one can get this by questions to the students, together with the information from (1) above about which students opinions matter to him most. In the case of parents, questioning would also be necessary. In the case of teachers and coaches, one can infer the performance area as the area for which that teacher or coach has responsibility.
3) The potential that each student has for each activity. Such information could be obtained (with some reporting error) by asking each to rank himself in terms of his abilities in particular areas, or his potential in particular areas, relative to others in his grade.
What we are interested in, then, is the following: a) How a student in a particular environment allocates his time in such a way as to maximize his utility (the environment consisting both of other students competing for rewards from significant others, and the significant others); b) how changes in the rewards given by significant others can change the profile of time allocation.
Consider the following framework, based on what is described above.
1) Let xki be the proportion of student i's interests in the rewards from other k. (This was described under (1) earlier, with the significant others being other students, considered individually, parents, coaches, teachers.)
2) Let djk be the proportion of significant other k's rewards that are given for achievement in activity j. (This is what was described earlier under (2) above.)
3) Let sij be the potential of i for activity j. The data can be obtained in any units; they are best measured in whatever way that students are best able to answer them. They may, but need not, be measured relative to other students in the system. They are then scaled so that the sum of sij for activity j is 1.0.
Then we think of the situation in the following way:
a) Each student i invests time in producing achievement in different activities. The amount of achievement produced depends on his investment of time in the activity, and on his potential in the activity, according to a production function specified below. Let tij be the fraction of total time (total time is the 'budget constraint') student i invests in the activity. The time is assumed equal for all. The sum tij for actor i is 1.0.
The production function for achievement of student i in activity j is Cobb-Douglas, with the time he has invested in the activity as one factor input, and his potential for that activity as the other. Arbitrarily, each is taken to the .5 power.
(1) pij = tij.5 sij.5
The total amount of production in activity j is
(2)
pj = Σ i
tij.5 sij.5
[summation is over i, in html the summing variable can not be placed directly below the summation sign; b.w.]
and the proportion of the total production of j that is produced by i is
(3)
cij = pij / pj
If we let 1/pj = cj, then
(4)
cij = cj pij
Expressed in terms of his and others' time investments and potential in the activity, this is
| tij.5 sij.5 | |||
| (5) | cij | = | —————— |
| Σ k tkj.5 skj.5 |
Student i's derived interest in activity j, yij, is his interest in the rewards from different significant others, each multiplied by the fraction of rewards which that significant other gives for achievement in various activities. For student i this is
(6)
yji = Σ k
djk xki
Then if students have Cobb-Douglas utility functions, and if their rewards depend on achievement relative to other students, they will allocate their time so as to maximize
(7)
Ui = Π j
cij yji
If D, X, S, are exogenous, and if rewards depend on relative achievement, then student i will maximize Ui by allocating time such that cij* is his equilibrium fraction of achievement in activity j.
The competitive equilibrium in this production process must be conceived somewhat differently from that in a system of exchange in a perfect market. In a perfect-market exchange system, all transactions involving good j take place at the same price, vj. Here, however, there are no transactions. Each person (tentatively) invests time according to his potential and his derived interests in activities, given the 'price' of relative achievement in each activity. One can conceive of a competitive system arising out of tentative transactions which finally settle down to a single price for for each good. Here, each person in the system adjusts his tentative investments until the ratio of the marginal utilities of each pair of investments is equal to the ratio of the prices of achievement in those two activities.
A student's equilibrium achievement levels in each activity result from the time investments which maximize utility subject to his resource constraint. The resource with which each begins is his total time, assumed to be equal for all students, and arbitrarily set to 1.0.
The optimal time investment in each activity may be found by use of Lagrange multipliers. The Lagrange function is
L = Ui + λ ( 1 - [ti1 + ... + tij + ... + tim])
and using eq. (7)
(8)
L = Π j
cij yji + λ ( 1 - [ti1 + ... + tij + ... + tim])
Expressing cij in terms of time investments and setting the partial derivative of L with respect to tij equal to zero,
| ∂L | ∂ | (tij.5 sij.5)yji | ||||
| (9) | —— | = | —— | Π j | ———————— | + λ ( 1 - [ti1 + ... + tij + ... + tim]) = 0 |
| ∂tij | ∂tij | (Σ k tkj.5 skj.5)yji |
| ∂L | yji Ui | |||
| (10) | —— | = | ———— | (1 - cij) - λ = 0 |
| ∂tij | tij |
The partial derivatives for activities j and k, each equal to zero, can be set equal to each other, and λ and Ui eliminated from the resulting equation
| yji (1 - cij) | yki (1 - cik) | |||
| (11) | ————— | = | ————— | |
| tij | tik |
Since Σk tik = 1.0, summing over k after multiplying through by tij and tik gives
(12)
tij Σk yki (1 - cik) = yji (1 - cij)
and solving for tti
| yji (1 - cij) | ||||
| (13) | t*ij | = | ————— | |
| Σk yki (1 - cik) |
If one were to begin with the three exogenous quantities, the matrix of interests in other persons' esteem or respect, X; the matrix of rewards (esteem, respect) given by each significant other for achievement in each activity, D; and the potential for achievement of each student in each activity, S, it would be possible to solve for optimal time investments by use of eq. (5) and eq. (13) iteratively, until equilibrium levels of relative achievement and time investment are reached.
It is also possible to define three system-level quantities characterizing the power of each student through achievements, the value or price of achievement in each activity, and the importance of esteem from each significant other. The three definitions are:
1. The power of an actor through achievements is the sum of amounts of achievement in each activity, with each activity's achievement weighted by the price or value of achievement in that activity.
(14)
ri = Σj c*ij vj (Σi ri = 1.0, Σi c*ij = 1.0, Σj vj = 1.0)
2. The price of achievement in an activity j is the sum of the respect or esteem accorded accorded to achievement in activity j, with each actor's esteem weighted by the importance of his esteem.
(15)
vj = Σk djk wk (Σj djk = 1.0, Σk wk = 1.0)
3. The importance of an actor's esteem is the interest that others have in receiving respect or esteem from him, each actor's interest weighted by the power of that actor.
(16)
wk = Σk xkh rh (Σk xkh = 1.0)
With information on the exogenous variables, D, X, S, as well as the equilibrium distribution of time activities, it is possible to solve for ri, vj, and wk. From eq. (14), (15), and (16), we can write:
(17)
ri = Σj c*ij Σk djk Σh xkh rh
(18)
vj = Σk djk Σi xki Σh c*ih vh
(19)
wk = Σi xki Σj c*ij Σh djh wh
The quantity c*ij (student i's relative achievement in activity j) may be directly measured, or derived from i's equilibrium distribution of time in activity j, by use of eq. (5).
To solve for the vector of achievement power, r, eq. (17) may be written as:
(20)
r = CDXr
An n×n matrix En with elements 1/n may be defined, and an n×1 vector en1. Since the n elements of r sum to 1, en1=Enr. Then subtracting r from both sides of eq. (20) and adding eni to the left side and Enr to the right gives
en1 = CDXr - r + Enr
Factoring out r and left-dividing by CDXr - r + En gives
(CDX - I + En)-1 en1 = r
The vector of prices or values of achievement, v, and the vector of actors' esteem importance, w, can be found in a similar way, by first defining em1, Em (where there are m activities) and eu1, Eu, where there are u significant others whose esteem or respect is of interest to students in the school.
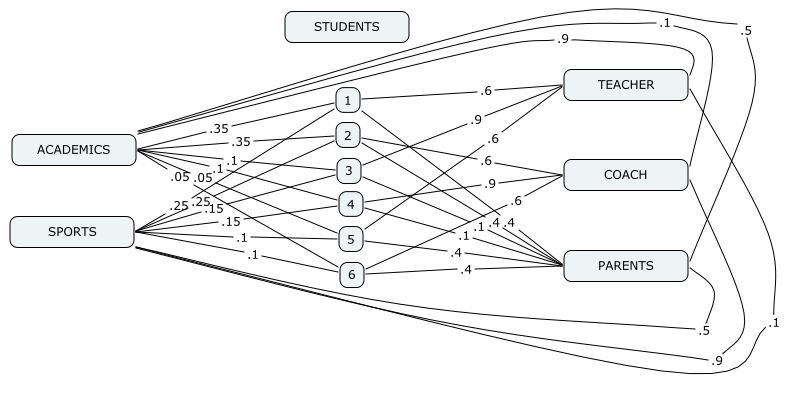
Suppose there is a school with six students, two activities (academics and sports) and three significant others. For the six students, the relative potential (sij) for academics and sports is distributed as follows:
| student | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | |
| academics | .35 | .35 | .10 | .10 | .05 | .05 |
| sports | .25 | .25 | .15 | .15 | .10 | .10 |
The three significant others are teacher, coach, and parents, and their esteem is awarded for achievement as indicated below. All parents are assumed alike, so they are treated as a single significant other. The teacher awards esteem, primarily for achievement in academics, and the coach primarily for achievement in sports, while all parents are balanced in the esteem they award.
| academics | sports | |
| teacher | .9 | .1 |
| coach | .1 | .9 |
| parents | .5 | .5 |
Students' interest in esteem or respect from teacher, coach, and parent are as follows:
| teacher | coach | parent | |
| student 1 | .6 | 0 | .4 |
| student 2 | 0 | .6 | .4 |
| student 3 | .9 | 0 | .1 |
| student 4 | 0 | .9 | .1 |
| student 5 | .6 | 0 | .4 |
| student 6 | 0 | .6 | .4 |

Using the above values of D, X, and S in eq (15) and (13) until equilibrium is reached gives the following equilibrium values.
| Time investments | Relative achievement | |||
| academics | sports | academics | sports | |
| student 1 | .70 | .30 | .32 | .17 |
| student 2 | .28 | .72 | .20 | .26 |
| student 3 | .85 | .15 | .19 | .09 |
| student 4 | .16 | .84 | .08 | .22 |
| student 5 | .73 | .27 | .13 | .10 |
| student 6 | .28 | .72 | .08 | .16 |
| power of students | values of activities | importance of significant other | |
| 1 | .25 | academics .50 | teacher .34 |
| 2 | .23 | sports .50 | coach .35 |
| 3 | .14 | parents .31 | |
| 4 | .15 | ||
| 5 | .11 | ||
| 6 | .12 |
These results show some interesting points. As expected, students invest their time in those activities in which achievement is rewarded by the persons whose esteem they want. Students 1, 3, and 5 invest time in academics, while 2, 4, and 6 invest their time in sports. But their relative success in achievement differs very much, as a result of their differences in potential. Students 2 and 3 provide a useful comparison in their academic achievement.
These numbers show that students 1 and 2 have greatest potential in both academics and sports, though somewhat more in academics than in sports. They differ sharply, however, in the persons who are important significant others to them. Student 1 pays no attention to the coach's esteem, and somewhat more to teacher's than to parents [sic]. Student 2 is oblivious to esteem from the teacher, and pays somewhat more attention to the coach's esteem than that of parents. Students 3 and 4 are like 1 and 2 respectively in whose esteem they are interested in, except more extreme, each having little interests in parents' esteem. Students 5 and 6, with lowest potential in both academics and sports, are just like students 1 and 2 respectively in their interests in esteem from others.
This configuration will show the effect of different potentials and of different patterns of interest in significant others.
The tabulations below show the equilibrium time investments, relative achievement of different students in the two activities at equilibrium, and the relative power of each student, the relative value of the two activities, and the relative importance of the thee significant others.
At about the same level, but student 2 achieves that level through ability combined with little time investment, while student 3 achieves the same level with lower ability but greater investment of time. Students 1 and 5 provide an interesting comparison as well. Student 5 spends even slightly more time in academics than does student 1, but achieves at a much lower level because of his lower ability.
In addition to these calculations, it is possible to calculate the utility levels of each student that came about when each maximizes utility. As a result of differing potentials, and of the match between potentials and the rewards provided by others whose esteem he is interested in, different students attain different levels of utility. The relative levels of utility, setting student #1's utility at 1.0 are
| Student | 1 | 2 | 3 | 4 | 5 | 6 |
| Utility | 1.00 | .89 | .63 | .70 | .45 | .49 |
Note that this also provides a means by which the student can maximize utility, given his potential and given the reward schedules of significant others, by modifying his interest in esteem from others. One can see how this can have an effect by comparing the utility levels of students 1 and 2, students 3 and 4, and students 5 and 6. Despite the fact that the two members of each of these pairs has the same potential, one has a higher attained utility than the other. This is because the two members of the pair have different interests in significant others.
I have raised questions about the effects of changes in various factors on the optimal allocation of time. If we shift back to a data analysis mode, we can treat students' allocation of time as a dependent variable, or we can take relative achievement in particular activities, cij, as dependent variables.
Thus what we could do is attempt to measure what I have described as exogenous, that is interests of i in rewards from persons k, xki, the rewards from person k for achievement in activity j, dkj and i's potential for achievement in activity j, sij. The interests depend very much on i's immediate environment, and will differ among students in the same school. Similarly with potential. These would be measured for each individual. The rewards given by each significant other would tend to be very much affected by the milieu of the school or the community.
If these quantities were measured, then the predicted time investments and achievement levels could be calculated as indicated in the preceding example. The predictions could be tested against observed time investments and achievements.
This remains somewhat short of what we usually think of in data analysis. It constitutes a start, possibly, for work in a direction in which the student's own interests in significant others, and the rewards given by those significant others, play an explicit role in analyzing what goes on in school.
Note that in this production process, there is no exchange. The fraction of achievement in activity j that student i ends up with, cij*, is determined in competition others for achievement in those activities he has most derived interest (yji) in. Unlike a pure exchange process, in which he begins with control of certain resources, which he can exchange for others, here he begins with potential sij for achievement in particular activities, in competition with others, and with a time budget, which he invests to maximize utility, given his potential, the rewards from significant others, and the competition from others.
It may be useful to make a few more comments on the kind of production process assumed here. In a system of social exchange, each actor uses the resources with which he begins to realize his interests, with the freedom to exchange any resource for any other, subject to relative values of resources. Here, however, the 'resources' with which he begins are not only time, which is fungible across activities, but also potential, sij, which is specific to activity j. This can constrain the student, for it may well be that the activities for which his significant others give rewards are not those in which he has a high potential. This constitutes a limitation on the utility he can realize in this system, and can be the cause of low self esteem.
There appear to be several ways in which this limitation can be overcome. One is a change in D. For example, the principal of a school which is highly sports oriented (that is, dkj is high where j is sports and k covers students and others in the school, resulting in a high vj for sports) may attempt to draw attention to students who have achieved academic success. Or a principal in a school where any one activity has a very high value vj may attempt to generate new activities, such as debate, drama, music, chess club, subject matter clubs (such as Future Teachers of America), and focus attention on achievers in these activities, so as to expand the set of potentials (sij) which will bring utility (and self esteem) to students.
A second way in which this limitation can be overcome is for the student to attempt to increase his potential in those activities for which his significant other provide high rewards. For example, in my high school, one friend showed some improvement in football the first year, even though he was on the junior varsity team, and still was on the JV team in the second year, but still improving. He worked hard and made the varsity team and his letter in football in his senior year. Achievement in football had the potential for producing a lot of rewards for him, and his improving ability made this potential a likelihood, so by working hard he increased the potential, finally getting the achievement and the rewards, There were a lot of others in the same boat: For others, either the lack of improvement or the lack of potential rewards (small yij) made them quit after a first try.
A third way in which the limitation on realization of utility can be overcome is by the student's changing the persons whose rewards of status or respect are of interest to him. This can happen through abandoning one set of friends and taking on a new set; or it sometimes happens through a sharp reduction of interests in rewards from parents.
Both of these latter kinds of change (in sij or xki) are internal changes on the part of the student, ordinarily in search for ways to increase his esteem in the eyes of others, or his self-esteem. Both come at a cost, of course; if we knew more about the nature of these costs, they could be incorporated in the model, and both S and X could be endogenized.
At this point, however, I must admit that as things stand, this approach remains a long way from being competitive with the usual approach in the analysis of student outcomes, based on background and school characteristics. However, it does something which the usual approach does not do, that is, it shows how interests of individuals and their abilities can determine the value of different activities in a school, and the status or power of different students in the school.
Comment by Ben Wilbrink
The paper does not refer to the relevant literature. I do not know how or where James Coleman intended the paper to be published, possibly in a context relating papers to his (1990) book. This book gives the theory, and its backgrounds, that the paper uses. The rather peculiar terminology of the article is typical for the theory and methodology developed in the earlier book.
Of course, the (1990) book contains some examples—one using a small data set on time spent in homework—resembling the one worked out in the paper.
I am not aware of any recent research using the Coleman methodology, yet there should be at least some publications. Please inform me, or send me pdf-files of resarch reports. Benjamin Zablocki (1996) reviewed James Coleman's work on this particular point.
James S. Coleman (1990). Foundations of social theory. Cambridge, Massachusetts: The Belknap Press of Harvard University Press.
class='lit'> Benjamin Zablocki (1996). Methodological individualism and collective behavior. In Jon Clark: James S. Coleman pp. 147-160. Falmer Press.
class='lit'> J. Donald Moon (1991). Review: Foundations of Social Theory by James S. Coleman. The American Political Science Review, 85, pp. 263-265. jstor
Ben Wilbrink
SCO-Kohnstamm Educational Research Center
Grote Bickersstraat 72
1013 KS Amsterdam
The Netherlands
tel. 020 5550363
To Mr. James D. Coleman
Amsterdam, May 17th 1994
Dear Mr. Coleman,
Your 1990 Foundations of Social Theory has proven [sic] to be a tremendous help in solving problems of interpretation that haunted me for years. In the 1980's I collected a highly interesting set of data consisting of grades obtained, grades expected, en time spent by first year law students at the University of Amsterdam. Correlational studies of this kind of data typically lead to nonsens results, because of compensating mechanisms between these variables and exogeneous variables like intelligence and level of aspiration. Competition between students is also part of the problem.
I applied your model to these data, and reported this exercise in two papers at the European Conference on Educational Research in 1992. I'll use the papers in a (late-career) dissertation on educational assessment. It was my intention to send you the papers immediately after the conference ... Well, better late than never.
The results are quite spectacular, and definitely show that the social system theory constructs are valid descriptors of this particular educational setting.
Yours sincerely,
Ben Wilbrink.
Ben Wilbrink (1992). Modelling the connection between individual behaviour and macro-level outputs. Understanding grade retention, drop-out and study-delays as system rigidities. In Tj. Plomp, J. M. Pieters & A. Feteris (Eds.), European Conference on Educational Research (pp. 701-704.). Enschede: University of Twente. Paper: auteur.
http://www.benwilbrink.nl/publicaties/92ColemanModelingECER.htm
Ben Wilbrink (1992). The first year examination as negotiation; an application of Coleman's social system theory to law education data. In Tj. Plomp, J. M. Pieters & A. Feteris (Eds.), European Conference on Educational Research (pp. 1149-1152). Enschede: University of Twente. Paper: auteur.
http://www.benwilbrink.nl/publicaties/92ColemanApplicationECER.htm
THE UNIVERSITY OF CHICAGO
DEPARTMENT OF SOCIOLOGY
1126 EAST 59TH STREET
CHICAGO - ILLINOIS 60637
James S. Coleman
(312) 702-8696 - FAX: (312) 702-9529
E-mail: mill.kicero.spcmehicago.edu
June 1, 1994
Ben Wilbrink
SCO-Kohnstamm Educational Research Center
Grote Bickersstraat 72
1013 KS Amsterdam
The Netherlands
Dear Mr. Wilbrink:
Thanks very much for your papers. I read them with interest. I think you interpret the results quite well, and I thought the results are very instructive about the relative values of different areas of law in the Department of Law. The relative power of students and teachers (or the relative value of marks and time) for the overall system are less meaningful because (as in my example in the 1990 book), the true minimum for marks may not be 1, but something higher. The mark of 4 was the lowest average in your Figure 2.
I'm enclosing a paper I just finished using a different conceptualization of what goes on in school, though the same formal model, somewhat elaborated. Reading your papers, having just finished the one I'm enclosing, has led me to reflect upon whether the two processes (competition among students for achievement in various activities, and exchange with teachers) do in fact coexist, and if so, how the combination of these two processes can be modelled. I think one way of doing so is to assume that (to use the terminology of the new model) teachers award esteem only for the subject matter they teach, and that grades in a subject measure the achievement which is an argument in the student's utility function. The student, in maximizing utility (which in the new model is a Cobb-Douglas function of relative achievement in various activities) is both in competition with other students and in an exchange relation with all those who award him esteem for achievement in the same activity. Those persons, in turn, at least in the case of teachers, may be in competition with each other for the time of students. So I think a general equilibrium model could be specified, and with the right data, estimated.
If you have data on some measure of ability of students, you might be able to estimate such a model, by first estimating the coefficients in the production function for each subject (referring to the new model) instead of assuming them to be .5 as I have done in the paper, and assuming the ability measure is the potential in each subject, though with different coefficients in different subjects.
If you have any additional ideas about these things after reading the enclosed paper, I would be interested in hearing them.
Sincerely,
James S. Coleman
University Professor
JSC:dm
![]() http://www.benwilbrink.nl/publicaties/94coleman.htm
http://www.benwilbrink.nl/publicaties/94coleman.htm