ORD 1995 tekst in congresboek + paper
In B. Creemers e.a. (Red.), Onderwijsonderzoek in Nederland en Vlaanderen 1995. Proceedings van de Onderwijs Research Dagen 1995 te Groningen (218-220). Groningen: GION.
Studiestrategieën die voor studenten èn docenten optimaal zijn: het sturen van investeringen in de studie
Ben Wilbrink
SCO-Kohnstamm Instituut van de Universiteit van Amsterdam
In het hoger onderwijs hebben studenten een relatief grote vrijheid hun tijd zelf in te delen. Onder de toenemende druk van tempobeurs en (volgend studiejaar) prestatiebeurs wordt die vrijheid minder vrijblijvend. De vraag is wat de instellingen (examencommissies, raden, docenten) kunnen doen om ervoor te zorgen dat studenten zo weinig mogelijk vertraging oplopen, en zo weinig mogelijk gelegenheid krijgen onnodig dingen uit te stellen. De instellingen hebben daar zelf ook belang bij, omdat uitstelgedrag en overmatig herkansen leiden tot een groot en ondoelmatig beslag op tijd van docenten.
model & programmatuur
Het zou mooi zijn wanneer er een theorie voorhanden is die beschrijft wat onder de vigerende examenregeling voor studenten een optimale studiestrategie is. Immers, dan is het ook mogelijk na te gaan onder welke varianten op die examenregeling de optimale strategie voor studenten ze minder tijd kost, of eerder het examen laat behalen, of in dezelfde tijd tot een hoger kwalificatieniveau brengt. In 1970 presenteerde Van Naerssen de kern van zo'n theorie, zijn tentamenmodel. Het is mogelijk dat tentamenmodel een meer algemene vorm te geven, zodat in beginsel alle denkbare varianten van examenregeling ermee zijn te analyseren. Zo'n algemeen toetsmodel (ATM) is beschikbaar (zie het parallelpaper in het thema Methodologie en Evaluatie), en wel in de vorm van een computerprogramma waarmee tal van examen- toetsvarianten op hun mogelijke effecten zijn door te rekenen of na te bootsen. Als besliskundig model berust het op zowel de specificatie van nutsfuncties van de student over tentamenresultaten, als op voorspellingen van die resultaten (en op de mate van doorzichtigheid van de tentamens).
analyse
Het ATM is te gebruiken om te analyseren welke effecten zijn te verwachten van veranderingen in toetsen of in examenregelingen. Voor examenregelingen is de eeuwige vraag of en zo ja in welke mate kan worden toegestaan dat prestaties voor het ene onderdeel die op een ander onderdeel compenseren. Hofstee heeft daarover opgemerkt (in Rekveld & Starren, 1994) dat deze problemen pas goed zijn aan te pakken met een theoretisch verantwoord wiskundig instrumentarium voor analyse. Zonder compensatie zijn de nutsfuncties voor veel studenten drempelfuncties, kansen op een hoger cijfer door een extra inspanning zijn dan maximaal onaantrekkelijk; het ATM kan het contrast tussen wel of geen compensatie doorrekenen en zichtbaar maken.
Voor toetsen zijn de vragen eenvoudiger: hoe lang moet een toets bij voorkeur zijn, hoe doorzichtig moet de toets zijn? Maar vooral: hoe sturen de kwaliteit en de moeilijkheid van de toets de investering in de voorbereiding erop? Het paper geeft enkele voorbeelden van dergelijke analyses. Het ATM kan zo bijdragen aan de verklaring van bekend probleemgedrag van studenten (uitstelgedrag, Schouwenburg 1993), of voorspellingen opleveren hoe studenten zich zullen gedragen na wijzigingen in toets of examen. Het ATM genereert hypothesen over studentengedrag, en kan daarmee richting geven aan het beleid, maar bij de eerste gelegenheid moeten deze hypothesen natuurlijk met empirische gegevens worden vergeleken.
empirie
Voor een deel berust het ATM op economische theorie waarvan de empirische basis niet echt ter discussie staat. Een interessante vraag is of economische theorie voor kleinschalige situaties in het onderwijs toepasbaar is: resultaten uit de experimentele economie bevestigen die vraag (Davis & Holt, 1993). Voor tal van specifieke toepassingen in het onderwijs blijft het altijd de vraag of het model daar, gezien de empirische gegevens, wel bij past. Het paper zal enkele analyses geven waarin het model is afgezet tegen empirische gegevens, of omgekeerd. In 1992 heb ik een toepassing van Coleman's (1990) sociale theorie op tijdbesteding en studieresultaten in een propedeutische studie gepresenteerd; deze dataset en de resultaten van de Coleman-analyse maken het in beginsel mogelijk na te gaan wat de vorm van de nutsfuncties is op basis waarvan studenten hun tijd verdelen tussen vakken, en tussen studie en vrije tijd. Geprobeerd zal worden om het ATM toe te passen op data van Van Naerssen, van Cohen-Schotanus (1994), of van Schouwenburg.
belang
Het belang van het ATM ligt in de toepassing op diverse probleemgebieden. Studievertraging is zo'n probleem waarin studeergedrag, examenregeling, en beoordelingsgewoonten (Wetmatigheid van Posthumus) resulteren in het overdoen van examenonderdelen en daardoor ook weer in nieuwe vertraging. In beginsel is het mogelijk met modellen zoals dit ATM het onderwijs zo af te regelen dat dergelijke verliestijden worden vermeden of geminimaliseerd. Voor alle betrokken partijen zijn daar grote financiële belangen mee gemoeid.
Voor de kwaliteitsbewaking van toetsen en examens kan het ATM een aantal kritische vragen genereren, waardoor de kwaliteitszorg richting of 'smoel' kan krijgen, en men vragen van visitatiecommissies voor kan zijn.
gerefereerde literatuur
Cohen-Schotanus, J. (1994). Effecten van curriculumveranderingen. Studiewaardering, studeergedrag, kennis, studiedoorstroom in een veranderend medisch curriculum. Proefschrift Rijksuniversiteit Groningen.
Coleman, J. S. (1990). Foundations of social theory. London: Belknap.
Davis, D. D., & Holt, C. A. (1993). Experimental economics. Princeton, New Jersey: Princeton University Press.
Naerssen, R. F. van (1970). Over optimaal studeren en tentamens combineren. Openbare les. Amsterdam: Swets & Zeitlinger.
Rekveld, I. J., & Starren, J. (1994). Een examenregeling zonder compensatie in het Nederlandse Hoger Onderwijs? Een vergelijking tussen compensatie en conjunctie. [Heymans Bulletins, HB-94-1150-SW, met bijlagen, o.a. opmerkingen van expert-panelleden Hofstee, de Gruijter, Cohen-Schotnus en Wilbrink] Tijdschrift voor Hoger Onderwijs, 12, 210-219.
Schouwenburg, H. (1993): Uitstelgedrag bij studenten. Proefschrift Rijksuniversiteit Groningen.
Wilbrink, B. (1992). The first year examination as negotiation; an application of Coleman's social system theory to law education data. In Plomp, Tj., Pieters, J. M., & Feteris, A. European Conference on Educational Research. Enschede: University of Twente. pp. 1149-1152. paper: auteur.
paper
Studiestrategieën die voor studenten èn docenten optimaal zijn: het sturen van investeringen in de studie
Ben Wilbrink
SCO-Kohnstamm Instituut van de Universiteit van Amsterdam
De inrichting van toetsen en examens heeft ongetwijfeld belangrijke effecten op de doelmatigheid van het onderwijs, zoals studievertraging en numeriek rendement. Waar de wetgever zijn best heeft gedaan examens en studieduren te regelen, is er waarschijnlijk zelfs sprake van majeure ondoelmatigheden die door wet- en regelgeving zijn geïntroduceerd. Wat hier ontbreekt is een analytisch instrumentarium waarmee ondoelmatigheden in examens zijn te traceren en te kwantificeren. Van Naerssen (1970) heeft met zijn tentamenmodel zo'n instrument willen aanreiken, als basis voor een examenkunde. Op basis van de beginselen achter dat tentamenmodel is het mogelijk gebleken een Algemeen Toetsmodel (ATM) te ontwikkelen waarmee ook complexere examenregelingen zijn te analyseren (dit ATM is beschreven in een parallel-paper in de sectie methodologie). Een interessant casus voor zo'n analyse is de ontwikkeling in de numerieke rendementen van de propedeuse geneeskunde in Groningen, zoals beschreven door Janke Cohen-Schotanus een (1994). Zij presenteert voor de propedeuse een reeks rendementsgegevens met een breuk in het jaar 1987-88, waar een gestaag neergaande lijn is omgebogen naar een sterk opgaande. In dat jaar zijn twee belangrijke veranderingen doorgevoerd: de examenregeling is ingrijpend gewijzigd, en er is toezicht uitgeoefend op de kwaliteit van toetsen met slaagpercentages beneden 70%. Beide ingrepen laten zich op hun mogelijke effecten analyseren met een algemeen model voor toetsen, waarvan de methodologische principes in een parallel-paper in de sectie Methodologie zijn gepresenteerd.
In 2005 is een serie instrumenten gereed gekomen die over het internet zijn te gebruiken binnen de eigen browser. Analyses zoals in dit paper beschreven komen met deze applets in het publieke domein nu binnen ieders handbereik. Zie onderaan deze webpagina, en/of het actuele project.
Kwaliteit van toetsen: voorspelbaarheid en studiestrategie
Anders dan bij psychologische tests is voor toetsen de voorspelbaarheid van wezenlijk belang. De student die niet in staat is een redelijke voorspelling voor het te behalen toetsresultaat op te stellen, zal er niet aan denken zelfs maar te beginnen met het bestuderen van de stof voor die toets: dat vereist immers de overtuiging dat ieder geïnvesteerd uur bijdraagt aan de verhoging van de op de toets verwachte score. Het idee is dat mindere kwaliteit van de toets samengaat met verminderde voorspelbaarheid, en daarom ook met verminderde investering van studietijd. Een aantal van de maatregelen die volgden uit toepassing van de 70% regel bij geneeskunde in Groningen (Cohen par. 5.4.2) laten zich analyseren naar hun effecten op geïnvesteerde studietijd, en op de doelmatigheid van die investering. De analyse is te zien als een oefening in het operationaliseren van het begrip 'doorzichtigheid' zoals door De Groot (1970) geïntroduceerd.
Het ATM is een instrument dat is ontstaan uit de poging om een exact model op te stellen voor wat optimale studiestrategieën zijn. Een exact model is een wiskundig model, of een voor simulatie op de computer geïmplementeerd model. De poging tot het opstellen van zo'n model dwingt om allerlei globale noties over studeren precies te maken, en te operationaliseren. Zo zijn er voor de voorspelbaarheid van toetsresultaten een aantal belangrijke begrippen die met elkaar een operationalisatie vormen voor De Groot's beginsel van doorzichtigheid:
- inzicht in de eigen stofbeheersing,
- inzicht in de eigen leercapaciteit, en
- inzicht in het toevalskarakter van toetsen als steekproeven uit de stof.
Doorzichtigheid is een sleutelbegrip voor studiestrategieën. Verder gaat het bij studiestrategieën vooral om keuzen, zoals de verdeling van de studietijd over meerdere vakken, en de verdeling van de tijd over de studie en over andere belangrijke bezigheden. Voor die keuzen is inzicht nodig in het nut van de af te wegen alternatieven. Dat is bij het verdelen van tijd nog een lastige opgave, want het nut staat tevoren niet vast en is dus slechts een verwachting. De student moet impliciet enig idee hebben over het verwachte nut van tijd besteed aan de studie versus dat van tijd besteed aan het sociale netwerk etc.
De 70% maatregel heeft zeker geleid tot betere kwaliteit en dus betere doorzichtigheid van toetsen. In het ATM is doorzichtigheid geoperationaliseerd als voorspelbaarheid. Deze voorspelbaarheid hangt af van de informatie over de eigen stofbeheersing, en die informatie is geoperationaliseerd als de score die op een proeftoets is verkregen. Hoe langer de proeftoets, hoe beter de informatie. Voorwaarde is natuurlijk dat de proeftoets uit dezelfde toetsvragenverzameling wordt getrokken als de te voorspellen toets. Die proeftoets is slechts een denkmodel, maar zou in de praktijk ook werkelijk gebruikt kunnen worden. Veronderstel nu dat het gaat om een toets waarvoor alleen een voldoende resultaat telt, dat betekent dat voor het examen ieder onderdeel voldoende gemaakt moet zijn. Voor zo'n toets is het verwachte nut eenvoudig gelijk aan de slaagkans (zie parallel-paper). Zonder in de technische details van het ATM te treden, is het nu mogelijk aan de hand van enkele grafische afbeeldingen te analyseren wat het effect is van kwaliteitsverbetering van de toetsen. Figuur 1 is een afbeelding van de voorspelling voor een student die op een proeftoets van 200 vragen de helft van de vragen goed heeft gemaakt, dus voor een student met veel informatie over de eigen beheersing. Omdat in het ATM ook een leermodel is ingebouwd, is het mogelijk voorspellingen op te stellen wanneer er extra studietijd wordt uitgetrokken: Figuur 2 geeft een voorbeeld voor een verdriedubbeling van de studietijd.
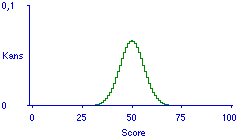
Figuur 1. Voorspelling voor toets met 100 vragen, na proeftoets met 100 goed uit 200 vragen.
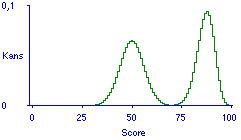
Figuur 2. Dezelfde voorspelling als in Figuur 1, aangevuld met de voorspelling na verdriedubbelde studietijd.
Iedere voorspelling levert een verwachte slaagkans op. Voor de grensscore 75 is de slaagkans in Figuur 1 effectief nul, na verdubbeling van de studietijd is die 0,99. Verwachte slaagkansen zijn ook te berekenen voor andere posities in het leertraject, laten we zeggen dat het leertraject tot maximaal zestig uur gaat; Figuur 3.
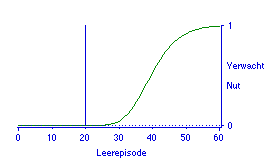
Figuur 3. De verwachte slaagkans (verwacht nut), berekend over een beoogd leertraject van 60 uur [juni 2003: of meer algemeen: 60 episoden; ook bij alle nog volgende in 2003 gereconstrueerde figuren zal in de legenda sprake zijn van episoden in plaats van uren].
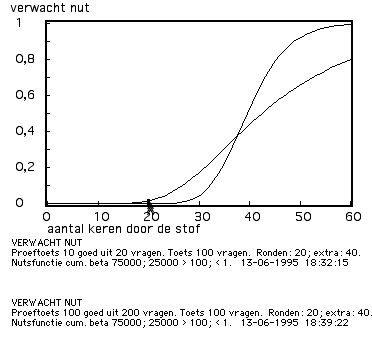
De geplotte ontwikkeling in de verwachte slaagkans krijgt pas betekenis door deze te contrasteren met de verwachte slaagkansen in een andere, minder doorzichtige toetssituatie: Figuur 4 geeft zo'n contrast in voorspellingen, door confrontatie met een toets waarvoor de beschikbare informatie equivalent is met een proeftoetsresultaat van slechts 10 uit 20 vragen, in plaats van 100 uit 200. Figuur 5 breidt de analyse uit tot de functies van de slaagkans over het beoogde leertraject.
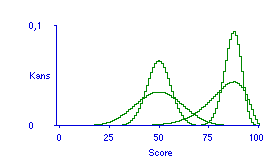
Figuur 4. Contrast tussen doorzichtige en ondoorzichte toetsen; doorzichtig: proeftoets 100 goed uit 200; ondoorzichtig: 10 uit 20.
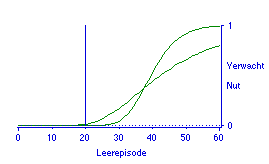
Figuur 5. De verwachte slaagkans (verwacht nut), berekend over het hele beoogde leertraject van 60 uur, voor doorzichtige (steile curve) en ondoorzichtige toets.
Figuur 5 geeft een vergelijking tussen twee toetsen die in alle opzichten gelijk zijn, behalve in doorzichtigheid of kwaliteit. Omdat lage verwachte slaagkansen niet interessant zijn, gaat het om het bereiken van de hogere slaagkansen: dat kan veel sneller en tot een blijvend hoger niveau bij de doorzichtige toets.
Figuur 5 laat ook zien dat een uur extra voor de doorzichtige toets meer extra verwacht nut oplevert dan een uur extra voor de ondoorzichtige toets, tenzij de stofbeheersing heel erg hoog wordt. Het effect is dat de student die beide toetsen tegelijk voorbereidt, allereerst de doorzichtige toets goed zal voorbereiden, en dan pas aan de ondoorzichtige toets begint. Wat geldt voor concurrentie in tijd tussen de ene en de andere toets, geldt ook voor concurrentie met andere aantrekkelijke bezigheden: het effect is dat bij doorzichtige toetsen de student minder snel in de verleiding komt de studie uit te stellen ten gunste van andere activiteiten. Ondoorzichtigheid en uitstelgedrag (Schouwenburg, 1993) hebben direct met elkaar e maken. Een deel van het succes van de propedeuse geneeskunde is dus mogelijk aan de 70% regel voor toetsen toe te schrijven.
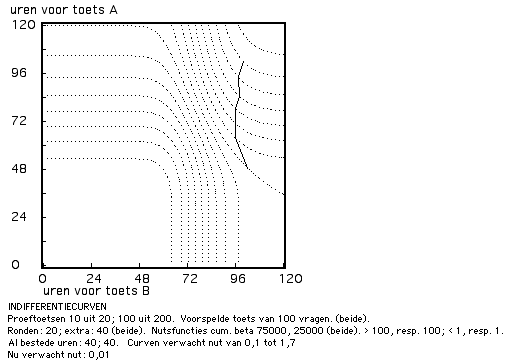
Figuur 5 kan nog op een andere manier worden geanalyseerd: namelijk door voor ieder beschikbaar tijdbudget na te gaan hoe die tijd optimaal over beide toetsen is te verdelen. De gegevens uit Figuur 5 kunnen voor die analyse het best worden omgezet tot wat in de micro-economie indifferentiecurven heet: zie Figuur 6.
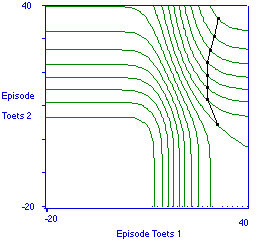
Figuur 6. Indifferentiecurven voor verdeling van tijd over de voorbereiding op een doorzichtige (1) en een ondoorzichtige (2) toets.
De curven in Figuur 6 stellen combinaties van tijdsbesteding voor die een gelijke gesommeerde slaagkans (= verwacht nut) opleveren; de curven zijn, van linksonder tot rechtsboven: 0,1 tot 1,7. Voor iedere curve is het optimale punt het punt waar de rechte van -135 graden de kromme raakt; voor alle andere punten op de curve is de gesommeerde tijdbesteding hoger. De optima liggen zo dat voor toets B altijd ongeveer 100 uur uitgetrokken wordt, voldoende om op die toets een hoge verwachte slaagkans te realiseren. De strategie is dus eenvoudig: bij ieder reëel tijdsbudget, besteed in ieder geval 100 uur aan de voorbereiding op de doorzichtige toets, trek pas daarna tijd uit voor de ondoorzichtige toets. De docent die ondoorzichtige toetsen afneemt, krijgt bij calculerende studenten dus te maken met 'uitstelgedrag.'
Maar ook voor iedere toets afzonderlijk is er over de periode van voorbereiding heen een gradiënt van toenemende doorzichtigheid, dus een verminderde kwetsbaarheid voor uitstelgedrag. Toenemende beheersing van de stof staat immers gelijk aan toenemende informatie over die eigen beheersing.
Er zijn meerdere bronnen van ondoorzichtigheid, die met het ATM zijn te analyseren. Toetslengte is een voor de hand liggende bron van ondoorzichtigheid, waarvan het effect direct met het ATM is te analyseren. Ook onzekerheid over de aftestgrens draagt bij aan ondoorzichtigheid. Die onzekerheid komt neer op een vermindering van de waarde van de informatie die de student heeft: een proeftoetsresultaat van 100 goed uit 200 is bij een niet tevoren bekend gemaakte aftestgrens in werkelijkheid dus minder informatief. Een andere bron van ondoorzichtigheid is het stellen van vragen die buiten de stof gaan. Omdat die vragen ook in de proeftoets voorkomen, krijgt de student de (terechte) indruk met de studie niet zo hard op te schieten als wel zou kunnen. Daardoor levert extra studietijd minder op, en wordt het aantrekkelijker om tijd aan andere zaken te besteden. Het effect is hetzelfde als dat van niet precies weten wat op welke manier over welk deel van de stof gevraagd zal worden, waardoor de studie niet doeltreffend kan zijn. Al deze bronnen van ondoorzichtigheid leiden bij analyse tot hetzelfde type contrast met wel doorzichtige toetsen als in figuur 5 en 6 is afgebeeld.
Is compensatie toestaan doelmatiger?
Voor het studiejaar 1987-88 is de examenregeling voor de propedeuse Geneeskunde in Groningen gewijzigd, waarna het numeriek rendement na 12 maanden sterk is gestegen. De vraag is of het ATM in staat is een verklaring te geven voor deze stijging. Het gaat niet om een toets op de juistheid van het ATM, daarvoor is dat model veel te complex. Waar het wel om gaat is om theoretisch inzicht te krijgen in de redenen waarom de in 1987 doorgevoerde wijzigingen in de examenregeling een gunstige uitwerking zouden kunnen hebben op het studietempo. De wijzigingen hebben te maken met compensatie-mogelijkheden. Lord (1962, 1963) heeft al eens overtuigend aangetoond dat enige vorm van compensatie tussen selectie-instrumenten altijd doelmatiger is dan geen compensatie. Wat voor personeelsselectie of psychodiagnostiek geldt, is voor toetsen in het onderwijs niet vanzelfsprekend ook geldig, omdat studenten zich actief en vaak strategisch voorbereiden op toetsen.
De kern van de doorgevoerde wijzigingen is als volgt: gehandhaafd is de regel dat voor het examen in beginsel alle toetsen voldoende moeten zijn (conjunctieve regeling), het aantal toetsen is verminderd van 9 tot 6; sinds 1992 is een lichte vorm van compensatie toegestaan; iedere toets bestaat uit twee of drie deeltoetsen die vrijstellend zijn, en wel volledig compensatoir en zonder herkansingen.
De vraag is hoe een dergelijke complexe examensituatie is te analyseren. De adviseur van de faculteit, Hofstee, (1987) beveelt aan om het examen in beginsel conjunctief te houden (een verrassend standpunt) maar het aantal toetsen in dat examen dan klein te houden. Ook beveelt hij aan om vaak te toetsen, in de vorm van vrijstellende deeltentamens die volledig te compenseren zijn, en die niet zijn te herkansen. De faculteit heeft het advies overgenomen, en deze maatregelen hebben het numeriek rendement van de propedeuse na één jaar overtuigend verbeterd. Voordat andere faculteiten ook tot dergelijke maatregelen overgaan, zal er toch een theoretische onderbouwing voor gevonden moeten worden. Nu is het bepaald niet handig om meteen te proberen zoiets ingewikkelds als de combinatie van toetsen in deze of gene examenregeling te modelleren. Het risico is bovendien dat iedere examenregeling zijn eigen theoretische model vraagt. De beste benadering is om toetsen te modelleren, en de combinatie van toetsen op te vatten als een analytisch probleem dat met hulp van een dergelijk toetsmodel is aan te pakken. Met 'modelleren van toetsen' is dan bedoeld het 'modelleren van het gedrag van studenten en docenten rond toetsen.' Het ATM is een geschikt instrument om met de ingrepen in de propedeuse geneeskunde te analyseren.
Twee vrijstellende deeltoetsen: conjunctief
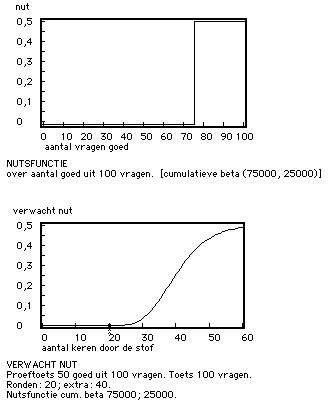
De nutsfunctie voor een conjunctieve deeltoets die voor de helft meetelt is een drempelfunctie met maximum nut gelijk aan de helft van het nut van de hele toets. Stel het nut voor de toets op 1, dan is het nut voor de conjunctieve deeltoets 0,5. Zakken voor een deeltoets levert nut nul op: er is dan aan de verplichting nog niet voldaan. Figuur 7a toont de nutsfunctie, de aftestgrens is 75 goed uit 100 vragen. Toepassing van het ATM geeft dan voor een gegeven proeftoetsresultaat de curve voor het verwachte nut over het leertraject (Figuur 7b).
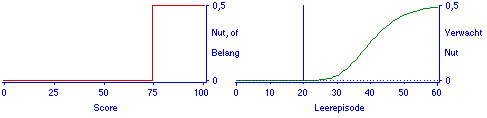
Figuur 7a/b. Nutsfunctie voor conjunctieve vrijstellende deeltoets, en de functie van het verwachte nut over het leertraject.
Twee vrijstellende deeltoetsen: compensatoir
Veronderstel twee deeltoetsen van 100 vragen, en de eis voor de hele toets dat tenminste 150 vragen goed zijn. Een neutrale nutsfunctie is een exacte afbeelding van de formele beslisregel, en is als volgt te construeren (Figuur 8). De nutsfunctie voor de eerste vrijstellende compensatoire deeltoets heeft een maximum van 67, omdat tweederde van de benodigde punten al met deze deeltoets behaald kunnen worden. Het minimum is nul, omdat bij scores lager dan 50 het halen van de toets door vrijstellingen is uitgesloten. Tussen score 50 en 100 verloopt de neutrale (want niet subjectieve) nutsfunctie dan rechtlijnig (Figuur 8). Een realistische persoonlijke nutsfunctie is risico-zoekend voor de lagere, en risico-mijdend voor de hogere scores, en is dus een of andere ogief tussen de scores 50 en 100. Figuur 9 geeft een ogief die de nutsfunctie van ene Joke P. Arts zou kunnen zijn.
Een analogie met nutsfuncties over geld kan helpen om een en ander uit te leggen. De neutrale nutsfunctie over geld is lineair: een tweemaal hoger geldbedrag heeft een tweemaal groter nut. Personen zijn zelden neutraal in het nut dat zij aan geldbedragen toekennen: voor kleine bedragen willen ze wel risico's nemen bij weddenschappen of in de handel; bij grotere bedragen worden risico's gemeden en zekerheden gezocht. Welnu, bij mogelijk te behalen toetsscores is dat niet anders, vandaar de algemene vorm van de ogief voor persoonlijke nutsfuncties.
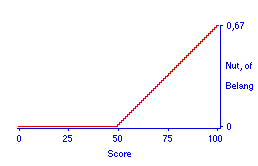
Figuur 8. Neutrale nutsfunctie voor compensatoire vrijstellende deeltoets van 100 vragen: 2/3e van de punten voor de toets zijn hier te behalen, scores lager dan 50 zijn niet meer te compenseren.
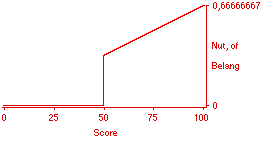
[juni 2003: Figuur 8 erratum. NB: deze analyse van nut bij een compenserende deeltoets berust op een misvatting. De in latere jaren verder uitgewerkte theorie voor objectieve nutsfuncties laat zien dat bij de score 75 het nut natuurlijk gelijk is aan dat voor een voldoend resultaat op een conjunctief gewaardeerde deeltoets (in dit voorbeel de helft), namelijk 0,5, en dat bij de score 50 het nut gelijk is aan 0,5 - 0,1666... = 0,333333... . Zie bovenstaande plot. Voor de verdere analyse betekent het dat de conclusies mbt de voordelen van compenserende deeltoetsen scherper zijn te stellen.
Uit de verbeterde theorie voor objectieve nutsfuncties in compensatoire situaties volgt dat ook bij compensatie verwacht nut mag worden geïnterpreteerd als slaagkans.]
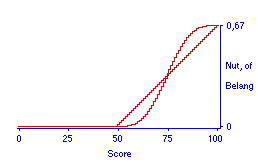
Figuur 9. Neutrale en persoonlijke nutsfunctie compensatoire vrijstellende deeltoets. Deze persoonlijke nutsfunctie is risico-mijdend boven score 75, en risico-zoekend daarbeneden.
Noot: De ogief is de cumulatieve betafunctie met parameters 3, 3 over het bereik van 49 tot 100.
[juni 2003: NB: zie de aantekening bij Figuur 8. Voor een persoonlijke variant op de objectieve functie geldt een nogal ingrijpend andere vorm van de functie dan hier afgebeeld. Het hier gegeven voorbeeld van aanpassen bij houding tegenover risico is ook in een ander opzicht minder gelukkig. Mijn huidige positie is dat het best zo zal zijn dat leerlingen verschillen in de mate van risicogeneigdheid, of dezelfde leerling in verschillende situaties, maar dat de objectieve situatie zo dominant is dat rekening houden met risicogeneigdheden vooralsnog een te luxueuze verfijning van het model op zou leveren.]
De student die risico's wil vermijden kan een steilere ogief kiezen. De maximaal risico-mijdende nutsfunctie is de drempelfunctie met de score 75 als drempel, het verschil met de conjunctieve vrijstellende deeltoets is dan gereduceerd tot alleen het hogere bereik van de nutsfunctie: 0,67 in plaats van 0,5.
Dan is ook voor de eerste compensatoire deeltoets de functie van het verwachte nut over het leertraject te berekenen (Figuur 10).
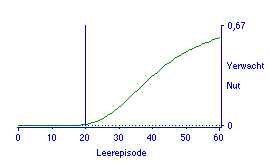
Figuur 10. Verwacht nut voor de eerste vrijstellende compensatoire deeltoets.
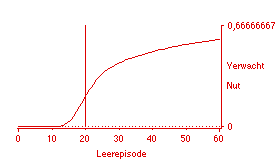
[juni 2003: NB: De functie van verwacht nut uitgaande van de gecorrigeerde nutsfunctie voor de compenserende deeltoets in bovenstaande plot weergegeven.]
Voor de tweede en laatste compensatoire deeltoets ontstaat de opmerkelijke situatie dat deze in werkelijkheid conjunctief is. Dat mag nog eens als waarschuwing gelden dat conjunctief en compensatoir geen absolute kenmerken van examenregelingen zijn, maar vaak in combinatie voorkomen. Immers, de score op deze deeltoets moet samen met de al bekende score op de eerste deeltoets tenminste 150 zijn, anders moet de hele toets (de combinatie van de beide deeltoetsen) worden overgedaan. Voor de nutsfunctie houdt dit in dat deze loopt van nul tot één. De punten die al behaald waren op de eerste deeltoets spelen hier hun rol in de bepaling van de grensscore die juist voldoende is om aan de eis van 150 goed voor de hele toets te voldoen. Figuur 11 geeft de nutsfunctie, waarin de score op de eerste deeltoets is verwerkt in de vorm van de plaats van de grensscore of drempel. De afmetingen van deze figuur weerspiegelen het in verhouding tot de eerdere deeltoets en ook tot de conjunctieve deeltoets veel hogere nut dat met deze deeltoets is te behalen. Figuur 12 geeft de bijbehorende functie van het verwachte nut, gegeven een resultaat van 50 goed uit 100 op een proeftoets.
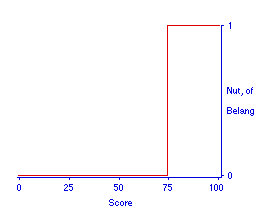
Figuur 11. Nutsfunctie voor de tweede en laatste vrijstellende compensatoire deeltoets van 100 vragen, waarvoor in dit geval tenminste 75 vragen goed moeten worden gemaakt.
In dit casus kunnen deeltoetsen niet worden overgedaan. In het algemene geval is het open of deeltoetsen of toetsen wel of niet kunnen worden overgedaan. Voor de laatste toets in het programma is de nutsfunctie een drempelfunctie omdat immers tenminste een aan de drempel gelijk aantal vragen goed moet zijn. Hoe ziet nu de nutsfunctie eruit wanneer er nog een negatief compensatiepunt staat? Stel voor een eerdere toets is een compenseerbare 'vijf' gehaald, die moet op de laatste toets worden gecompenseerd, de daarvoor benodigde score is de drempel voor de nutsfunctie. Het lijkt nu alsof met een score groter of gelijk aan de drempel er TWEE toetsen voldoende worden gemaakt. Dat is een drogredenering. In het algemeen moet er een voorziening in de examenregeling zijn voor gevallen waarin op de laatste toets niet aan de gestelde eisen wordt voldaan. Doorgaans zal dat in de vorm van een extra taak of een 'herkansing' op een nieuwe toets zijn. Het treurige fenomeen van overdoen van oude stof is niet onontkoombaar: bij een onvoldoende kan een extra vak worden opgelegd, inclusief afsluitende toets. Voor die toets geldt dan nog steeds de verhoogde drempel in verband met het nog openstaande negatieve compensatiepunt. In het speciale geval dat op zich de laatste toets wel 'voldoende' is gemaakt, maar het compensatiepunt niet is gehaald, kan het zijn toegestaan het nog te compenseren onderdelen 'alternatief' af te leggen (taak, herkansing, of nieuwe stof). Het hoogste nut op de laatste toets kan dus wel boven 1 worden gesteld (met het nut van de hoeveelheid negatieve compensatiepunten die op de laatste toets nog zijn in te halen), maar het is zeker niet twee maal het nut van een enkele (deel)toets.
Een verrassende ontwikkeling eind 2005 is dat het mogelijk is om de formele objectieve nutsfuncties te vervangen door realistische nutsfuncties, waarvoor de modeluitkomsten nodig zijn. Zie het spa-project modulen 7, 8 en 9.
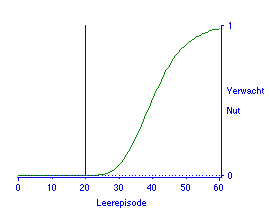
Figuur 12. Verwacht nut voor de tweede vrijstellende compensatoire deeltoets.
Noot. Proeftoets: 50 goed uit 100, na 20 uur studeren / keer door de stof.
Vergelijk Figuur 12 met Figuur 7b, dan valt op dat bij concurrentie tussen deze conjunctieve en compensatoire deeltoets de laatste een tweemaal hoger verwacht nut oplevert bij een gelijke investering in uren. Het is de structuur van het nut van deeltoetsscores die bepalend is voor de analyse. Dat is een verrassend resultaat, maar het betekent niet dat verschillen in ondoorzichtigheid geen rol meer zouden spelen: een ondoorzichtige compensatoire toets zou het nog kunnen verliezen van een doorzichtige conjunctieve. De examenregeling op zich is echter bepalend voor de beloningsstructuur, de prikkels, die rechtsstreeks hun vertaling krijgen in nutsfuncties. De analyse zal nog worden afgerond met het opstellen van indifferentiecurven.
Figuur 12 laat ook nog eens zien dat zekerheden buiten het bereik van de student liggen: het is niet realistisch om het maximale verwachte nut na te jagen, zodat er altijd een niet te verwaarlozen kans blijft om te zakken. Hierin ligt zeker een reden om lichte compensatie tussen examenonderdelen toe te staan, zoals bij geneeskunde ook ingevoerd. Bij een beperkt aantal beslissende toetsen, is een verwacht nut van ca. 0,9 aanvaardbaar, en bij pech in het begin van de reeks toetsen kan er met een extra inspanning voor latere tentamens worden gecompenseerd.
Indifferentiecurven
Het is mogelijk om de functies voor verwacht nut met elkaar te vergelijken, en zo te proberen de voor- en nadelen van conjucntie en compensatie te wegen. Economen gebruiken een handige techniek om in één figuur een overzicht te krijgen van de optimale strategieën die voorhanden zijn. De curven voor verwacht nut worden dan vertaald in indifferentiecurven van telkens gelijk verwacht nut zoals gesommeerd over beide toetsen, zie Figuur 13. Op zo'n curve is het totale verwachte nut overal gelijk, maar verkregen met wisselende investeringen van tijd voor de twee toetsen die op deze wijze worden vergeleken. Op iedere curve is een punt te vinden dat met de kleinst mogelijk investering van tijd is te bereiken: dat is het optimale punt. Die optimale zijn met elkaar te verbinden zodat het pad van optimale strategieën wordt verkregen: de Engel-curve. Voor twee in alle opzichten gelijke toetsen is de Engelcurve de diagonaal vanuit de oorsprong naar de hoek rechtsboven, met uitsluiting van de gedegenereerde curven in de hoek links onder.
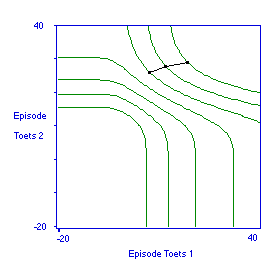
Figuur 13. Indifferentiecurven voor verdeling van tijd over de voorbereiding op een conjunctieve deeltoets (2) en een compensatoire deeltoets (1).
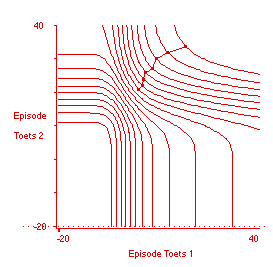
Figuur 13. Indifferentiecurven op basis van de correcte nutsfunctie (zie toelichting erratum bij Figuur 8).
Figuur 13 geeft aan dat de conjunctieve en de compensatoire deeltoets aan elkaar gewaagd zijn. Wanneer het tijdsbudget niet toereikend is om op een hoog gezamenlijk resultaat te mikken, dan wijst de optimale strategie net iets meer tijd toe aan de voorbereiding op de conjunctieve deeltoets. Is het tijdsbudget ruimer, dan 'wint' de compensatoire deeltoets het: de Engel-curve snijdt de diagonale lijn.
Voor de tweede en laatste compensatoire deeltoets is ook zo'n vergelijking tegen de conjunctieve deeltoets te maken, zie Figuur 14. Voor ieder beschikbaar tijdsbudget deelt de optimale strategie meer voorbereidingstijd toe aan deze compensatoire deeltoets dan aan de conjunctieve. Voor een beter perspectief op deze plot: vergelijk Figuur 15, waarin de tweede compensatoire deeltoets met zichzelf is vergeleken.
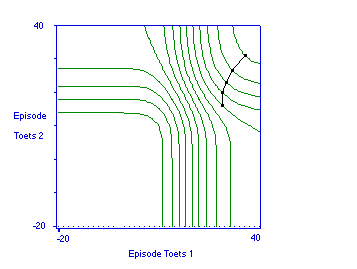
Figuur 14. Indifferentiecurven voor verdeling van tijd over de voorbereiding op een conjunctieve deeltoets (2) en de tweede en laatste compensatoire deeltoets (1) .
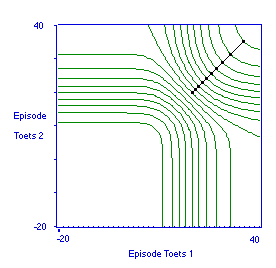
Figuur 15. Indifferentiecurven voor verdeling van tijd over de voorbereiding op twee situationeel identieke compensatoire deeltoetsen (de deeltoets 1 uit Figuur 14).
De conclusie uit de indifferentie-curven is dat in dit voorbeeld compensatie het wint van conjunctie, en dus doelmatiger is: in dezelfde studietijd is bij compensatie een hoger verwacht nut te realiseren. De duidelijke winst van compensatie komt mogelijk alleen van de laatste deeltoets. Te onderzoeken is nog of in minder doorzichtige situaties dan waarvan hier is uitgegaan, compensatie verder in het voordeel komt.
Voor de compenserende deeltoetsen is door die compensatie de inzet voor beide deeltoetsen verhoogd, zonder dat de nodige voorbereidingstijd verhoogd wordt. Omdat beide compensatoire deeltoetsen het winnen van de conjunctieve in doelmatigheid, zal er bij compensatie minder herkanst worden dan onder conjunctie, ook ermee rekening houdend dat voor conjunctie de deeltoetsen, en bij compensatie de toets in zijn geheel wordt overgedaan.
De winst van de compensatoire regeling voor de deeltoetsen ligt in de verhoogde doelmatigheid, waardoor er minder herkanst zal worden, en in een grotere weerstand tegen verlies van het tijdsbudget aan activiteiten buiten de studie.
Compensatie voor deeltentamens, dan ook voor tentamens?
Wat voor deeltoetsen geldt, dat compensatie doelmatiger is, zou ipso facto ook moeten gelden voor toetsen, die immers zijn op te vatten als vrijstellend voor het examen. Toepassen van deze compensatoire regel op de toetsen zou betekenen dat ook voor deze toetsen geen herkansing meer wordt geboden. Niet voldoen aan de compensatoire eis betekent dan dat het hele examen, dus alle toetsen, moeten worden overgedaan. Janke Cohen-Schotanus rapporteert overigens dat het numerieke rendement voor de propedeuse geneeskunde een theoretisch maximum heeft bereikt, nu het boven de 80% is uitgekomen. Als dat juist is, zou er voor geneeskunde met verdere compensatie tussen toetsen geen extra winst meer te behalen zijn.
Conclusie en discussie
Het is mogelijk gebleken om met het ATM als analytisch instrument een verklaring te genereren voor de stijging van het Groningse numerieke rendement na 12 maanden onder een examenregeling die ingrijpend was gewijzigd op advies van Hofstee (1987). Het hanteren van volledige compensatie in combinatie met afschaffen van herkansingen is de sleutel tot het succes, met als opmerkelijk gegeven dat dit alleen is doorgevoerd voor vrijstellende deeltoetsen, ook om zo het aantal conjunctieve toetsen dat telt voor het examen in aantal te kunnen reduceren. De verklaring van het succes is te vinden in de belonings-structuur die daarmee is geschapen voor de inspanningen die studenten zich getroosten. In de analyse komt dat tot uiting in de vorm van de nutsfuncties zoals die voor studenten gelden. Voor compensatoire deeltentamens staat gemiddeld meer 'nut' op het spel, waardoor er een betere koppeling tot stand is gebracht tussen inspanning en resultaat voor de student.
Het effect van de examenregeling is echter niet te onderscheiden van mogelijke effecten die voortvloeien uit de '70%-regeling,' voorzover deze heeft geleid tot kwaliteitsverbetering en dus grotere doorzichtigheid van toetsen. In dit deel van de analyse is gebleken dat het ATM een bruikbaar instrument is om de doorzichtigheid van toetsen en toetssituaties te monitoren .
In beide analyses is aangetoond dat de effecten van doorzichtigheid en compensatie liggen in de sfeer van de optimale verdeling van beschikbare tijd: grotere doorzichtigheid en meer compensatie maken de studiestrategieën beter bestand tegen uitstelgedrag (Schouwenburg, 1993), en bevorderen op die manier het numeriek rendement na 12 maanden.
Omdat de gepresenteerde analyse een casuïstisch karakter heeft, zijn deze resultaten niet noodzakelijk overtuigend. Het probleem met discussies over conjunctie en compensatie (Rekveld & Starren, 1994) is altijd geweest dat er geen analytisch insrument voorhanden was om kwantitatieve analyses uit te kunnen voeren. Met het ATM is er nu wel zo'n instrument voorhanden, zodat in de toekomst ook meer systematische studies over deze en andere varianten van examenregelingen zijn te verwachten.
gerefereerde literatuur
Cohen-Schotanus, J. (1994). Effecten van curriculumveranderingen. Studiewaardering, studeergedrag, kennis, studiedoorstroom in een veranderend medisch curriculum. Proefschrift Rijksuniversiteit Groningen.
Coleman, J. S. (1990). Foundations of social theory. London: Belknap.
Hofstee, W. K. B. (1987). Kort extern advies. Groningen. (niet gepubliceerd)
Lord, F. M. (1962). Cutting scores and errors of measurement. Psychometrika, 27, 19-30.
Lord, F. M. (1963). Cutting scores and errors of measurement - a second case. Educational and Psychological Measurement, 23, 63-69.
Naerssen, R. F. van (1970). Over optimaal studeren en tentamens combineren. Openbare les. Amsterdam: Swets & Zeitlinger. html
Rekveld, I. J., & Starren, J. (1994). Een examenregeling zonder compensatie in het Nederlandse Hoger Onderwijs? Een vergelijking tussen compensatie en conjunctie. [Heymans Bulletins, HB-94-1150-SW, met bijlagen, o.a. opmerkingen van expert-panelleden Hofstee, de Gruijter, Cohen-Schotnus en Wilbrink] Tijdschrift voor Hoger Onderwijs, 12, 210-219.
Schouwenburg, H. (1993): Uitstelgedrag bij studenten. Proefschrift Rijksuniversiteit Groningen.
Wilbrink, B. (1995). Van Naerssen's tentamenmodel in algemene vorm. In B. Creemers e.a. (1995). Onderwijsonderzoek in Nederland en Vlaanderen 1995. Proceedings van de Onderwijs Research Dagen 1995 te Groningen. Groningen: GION. 114-115. Paper: auteur. html
19 juni 2003 bestand in html gezet, figuren opnieuw geconstrueerd. 4 april 2005 de nieuwe inzichten uit het SPA-model, dat betreft wederom de constructie van nutsfuncties, ingewerkt, verwijzingen naar de applets ingewerkt.
Geruime tijd na deze ORD is niet alleen de al bij Figuur 8 gemelde verbeterde constructie van objectieve nutsfuncties ontdekt, maar heb ik mij ook dit gevolg gerealiseerd:
Compensatie voor deeltoetsen, dan ook voor terugkoppeling tijdens het onderwijs (formatieve toetsing)?
Het algemene toetsmodel zoals onder andere op de ORD 1995 gepresenteerd wekt de indruk dat het alleen betrekking heeft op afsluitende toetsen, en daarom geen betekenis heeft voor terugkoppeling die de docent de student geeft tijdens het onderwijs of tijdens het leren. Omdat een afsluitende toets vervangen kan worden door vrijstellende deeltoetsen waarop het algemene toetsmodel evenzeer van toepassing is, volgt bij inductie dat ook opsplitsen van een vrijstellende deeltoets mogelijk is met behoud van de toepasbaarheid van het algemene toetsmodel op de daaruit resulterende beoordelingen, enzoverder. Het algemene toetsmodel is dus ook algemeen in de zin dat het zowel op formatieve als op summatieve toetsing toepasbaar is, om de termen uit de zeventiger jaren maar even te lenen.
Gelijktijdige en latere publicaties op dit onderwerp van Janke Cohen-Schotanus:
Cohen-Schotanus, Janke (1995). Studieduur en de kwaliteit van tentamens. Onderzoek van Onderwijs, 24, 26-28.
"Het zijn niet alleen studenten die de stof niet beheersen die zakken voor tentamens, ook studenten die de stof wel beheersen blijken nogal eens te zakken. Dit laatste heeft te maken met de kwaliteit van tentamens (onduidelijke stofomschrijving, te gedetailleerde vraagstelling, onnauwkeurige formuleringen, etcetera). Het is opmerkelijk dat veel studenten deze praktijken over zich heen laten komen. Ze zouden zich veel actiever op kunnen stellen wat betreft de kwaliteit van tentamens en vaker in beroep kunnen gaan."
Cohen-Schotanus, Janke (1995). De praktijk van de compensatie. Onderzoek van Onderwijs, 24, 60-62.
"Bij de discussies over de studierendementen in het Hoger Onderwijs wordt vaak een pleidooi gehouden voor de mogelijkheid van compensatie tussen tentamens. Compensatie in een examenregel zou moeten leiden tot minder studievertraging. Toch wordt in het Nederlandse Hoger Onderwijs weinig gebruik gemaakt van compensatorische examenregels. Tot nu toe zijn de beschouwingen over compensatie vooral theoretisch [Rekveld & Starren TvHO 1994; De Gruijter OvO 1989; Wilbrink, ORD 1995]. In deze studie komt de praktijk van de compensatie aan de orde. Beschreven wordt hoe vaak en op welke wijze doctoraalstudenten geneeskunde gebruik zijn gaan maken van de compensatieregel die in augustus 1991 is ingevoerd. Het blijkt dat het aantal studenten dat voor het doctoraalexamen slaagt met één of meer gecompenseerde vijven steeds verder toeneemt. Geschat wordt dat na invoering van de compensatieregel de gemiddelde verblijfsduur tot het doctoraalexamen met twee tot drie maanden bekort is. Er zijn weinig aanwijzingen dat dit ten koste is gegaan van de kwaliteit van de opleiding."
NB: De grafische uitvoer van het programma voor het Algemene Toetsmodel is dynamisch van karakter, en is voor gebruik in de html-versie omgezet naar gif-afbeeldingen. Zie hieronder de voor de oorspronkelijke figuren gebruikte grafische output, met bijbehorende beschrijvingen van opgegeven parameters etcetera.
Nieuwe punten in dit paper zijn:
-
Toepassing van het ATM op een casus.
- Verklaren van het succes van een majeure herinrichting van een examenregeling.
- In casu gaat het om modelleren en kwantificeren van verschillen tussen compensatie en conjunctie.
- Deze poging is maar deels geslaagd omdat de constructie van de nutsfunctie bij compensatie berustte op een misvatting.
- Compensatie en vrijstellende deeltentamens gaan makkelijk en goed samen, en een dergelijke regeling laat zich helder contrasteren met die van conjunctieve vrijstellende deeltoetsen, die noodzakelijkerwijs bij het halen van een onvoldoende resultaat over moeten. (Vgl. standaardsitatie in stelsels van leren voor beheersing, een vergelijking die in dit paper niet is gemaakt).
- In casu Groningana ook: te verwachten affect van doorzichtigheid als resultaat van beleid om tentamens met lage slaagpercentages onderwijskundig te analyseren. Een inleidend casus als het ware.
- Bij verdelen van tijd over concurrerende bezigheden (toetsen) gaat tijd allereerst naar de meest doorzichtige actititeit (toets); het belang voor voorkomen van uitstelgedrag ligt hier voor de hand.
- Maar ook voor iedere toets afzonderlijk is er over de periode van voorbereiding heen een gradiënt van toenemende doorzichtigheid, dus een verminderde kwetsbaarheid voor uitstelgedrag.
- Probeer niet hele examenregelingen te modelleren, maar modelleer op toetsniveau. Dat voorkomt dat iedere nieuwe regeling de ontwikkeling van een eigen model vergt.
- Voor de laatste compensatoire deeltoets ontstaat als regel de opmerkelijke situatie dat deze in werkelijkheid conjunctief is.
- De techniek van indifferentiecurven en de Engel-curve voor het eerst op deze ORD gepresenteerd.
- "De duidelijke winst van compensatie komt mogelijk alleen van de laatste deeltoets." Dit is dus een onjuiste conclusie, na correctie van de constructie van compensatoir nut.
Over het hoofd geziene conclusies:
Als de toepasbaarheid van het ATM op vrijstellende deeltoetsen is aangetoond, heeft het ook relevantie voor verdergaande vormen van opselen, zoals formatieve beoordeling, en is het ATM niet inherent aan formele situaties gebonden.
SPA-model
Het model is in zijn meest recente (2006) vorm hier te vinden. Het model is nog in ontwikkeling, maar veel onderdelen zijn al voor algemeen gebruik beschikbaar in de vorm van kleine programma's die in uw browser draaien. Bijvoorbeeld applet 1.
BIJLAGE
De oorspronkelijke plotjes in het ORD-paper 1995.
De afbeeldingen zijn nu weergegeven met de bijbehorende legenda, zoals uitgevoerd door het Pascal-programma.
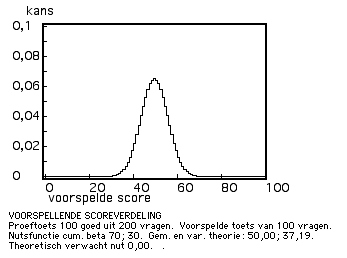
oorspronkelijke Figuur 1.
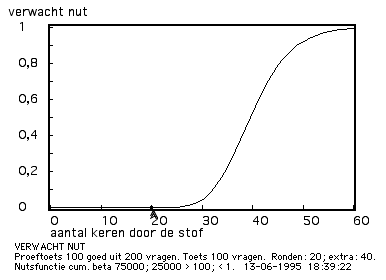
oorspronkelijke Figuur 2.
oorspronkelijke Figuur 3.
oorspronkelijke Figuur 4.
oorspronkelijke Figuur 5.
oorspronkelijke Figuur 6 en 7.
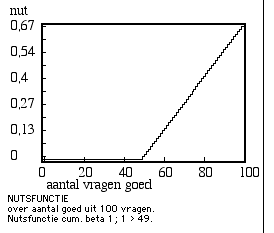
oorspronkelijke Figuur 8.
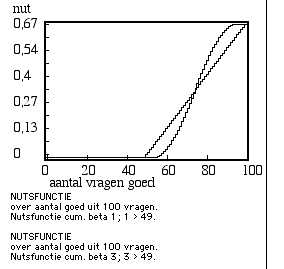
oorspronkelijke Figuur 9.
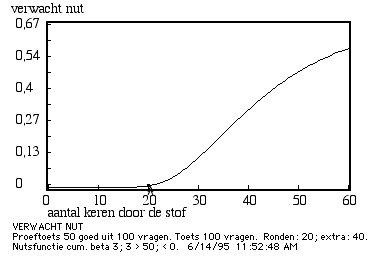
oorspronkelijke Figuur 10.
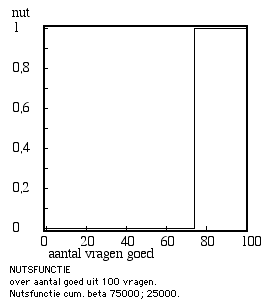
oorspronkelijke Figuur 11.
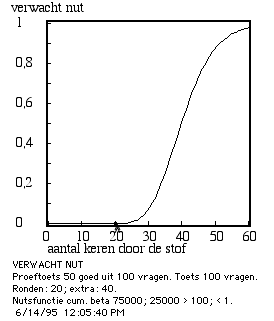
oorspronkelijke Figuur 12.
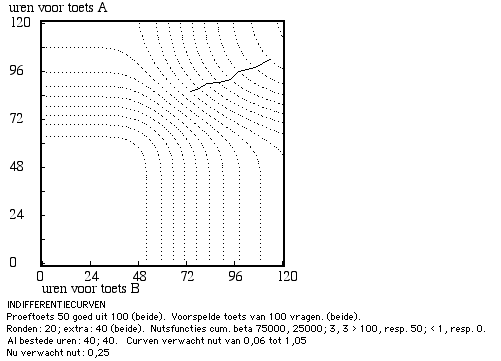
oorspronkelijke Figuur 13.
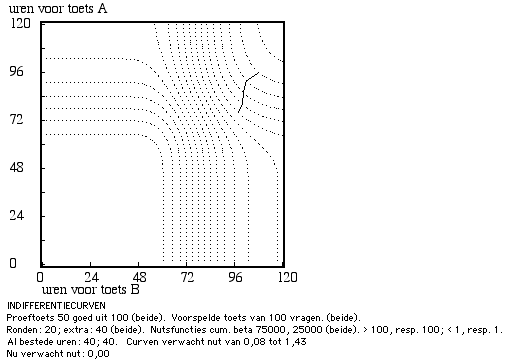
oorspronkelijke Figuur 14.
 http://www.benwilbrink.nl/publicaties/95StudiestrategieORD.htm
http://www.benwilbrink.nl/publicaties/95StudiestrategieORD.htm





























