juli 2016
Het gaat evenwel om een oude discussie, en om ingrepen die in de testpsychologie juist vanzelfsprekend zijn. Kort gezegd: voor ieder vak een zogenaamd voldoende cijfer eisen komt neer op verspilling, mogelijk enorme verspilling.
Wat voor testpsychologen vanzelfsprekend is, blijkt dat voor bestuurders en andere direct betrokkenen niet te zijn. Vandaar een probleem om de informatie over te brengen. Ik heb daar in een ver verleden meermalen publicaties aan gewijd, nieuw is het allemaal dus niet.
Testpsychologen zijn dan weer een ander volkje dan methodologen in psychologisch onderzoek. Recent hebben een aantal methodologen zich in de problematiek verdiept: Smits, Kelderman en Hoekman zie hier. Methodologen aan een universiteit zijn ook docenten, en dat kan best wringen. Er moet dus een antwoord komen op een artikel dat mijns inziens meer verwarring schept over compenseren dan het er duidelijkheid over verschaft. Nu is het ook verdraaid lastige thematiek, reden waarom we onze rendementsproblemen in het onderwijsveld voortdurend maar niet doeltreffend weten aan te pakken. Een korte reactie schrijven op een artikel dat heel veel overhoop haalt is eigenlijk onbegonnen werk. En het is me dan ook niet gelukt, althans niet op de gewenste korte termijn. Eind 2017 is er een nieuwe kans, ik begin weer met een blanco bladzijde voor me.
7, 8, 9 december
Hier vast een eerste reeks afbeeldingen voor mijn powerpoint, met tekst. Op zich is dit al bijna een half uur, ben ik bang. Er komen nog enkele onderwerpen bij, maar die hoeven niet noodzakelijk ook gepresenteerd te worden. Het onderwerp is zo enorm, het meeste moet toch onbesproken blijven ;-)

Figuur 1. De feiten
Bovenstaande rampzalige slaagcijfers voor tentamens in de 70er jaren waren een belangrijke aansporing om de mogelijkheden van meer compensatoir examineren te onderzoeken. Zou de situatie nu echt anders zijn? Een eigen overzicht over propedeuserendementen, in opdracht van OCW, dateert van 1987
Recent publiceerden Smits, Kelderman en Hoeksma (2015) een overzicht van voor- en nadelen. Helaas kan ik het met deze analyse niet eens zijn. Gelukkig zijn hun laatste zinnen, in een paragraaf over wenselijkheid van meer onderzoek naar beslisregels: “Ten tweede kan het simu- latieonderzoek sterk verbeterd worden door niet aan te nemen dat studenten zich onder alle toetssystemen hetzelfde gedragen, maar juist per systeem verschillen in hun gedrag en dit expliciet te modelleren. Het werk van Wilbrink (1995) lijkt daarvoor een goed beginpunt.” En dat is inderdaad het springende punt: het strategische gedrag van studenten. We zullen zien. Ik presenteer nu een aantal grondgedachten die nodig zijn om orde in het denken over compenseren te scheppen. Ik zal de verschillen met Smits c.s. laten voor wat ze zijn, op een enkele uitzondering na. Zo’n uitzondering is dat het startpunt de strategische positie van de studenten moet zijn; kies je, zoals Smits c.s., een testpsychologisch uitgangspunt dan redeneren we ons helemaal vast met platonische beschouwingen over terechte en onterechte beslisisngen.
Niels Smits, Henk Kelderman & Jan Hoeksma (2015). Een vergelijking van compensatoir en conjunctief toetsen in het hoger onderwijs. Pedagogische Studiën, 92, 275-285. open access
Marjon Voorthuis & Ben Wilbrink (1987). Studielast, rendement en functies propedeuse. Relaties tussen wetgeving, theorie en empirie. Deelrapport 2: Evaluatie-onderzoek Wet Twee-fasenstructuur. Amsterdam: SCO-rapport 112. ISBN 90-6813-135-4. pagina
Ben Wilbrink (1995). Studiestrategieën die voor studenten en docenten optimaal zijn: het sturen van investeringen in de studie. ORD. pagina
Ieder examen is sterk contingent, dat wil zeggen: bepaald door locale omstandigheden. Ook voor het meer compensatoir maken van een examen is in die zin sterk contingent: er is geen recept voor, al zijn er wel inspirerende voorbeelden. Dat neemt niet weg dat er algemene inzichten zijn die in vrijwel alle situaties van belang zijn. Er zijn fundamentele inzichten, en er zijn praktische toepassingen. Zonder inzicht aan examens gaan sleutelen kan ik niemand aanraden. Dat inzicht is een noodzakelijke voorwaarde, zij het geen voldoende voorwaarde, voor constructieve verbetering van examens. Aan de slag dus.
Stel u voor, een student heeft op haar toets 17 van de 20 opgaven goed gemaakt. Het mag ook een proeftoets zijn. Laten we het op een proeftoets houden. De toets heeft maar 20 vragen, maar het zijn wel complexe vragen (complexe vragen: Wilbrink, 1998). Als dit het enige is dat u van die student weet, en u zou moeten voorspellen wat haar score zal zijn op de echte toets, hoe pakt u dat aan?
Oké, ik zal een hint geven. Verplaats u in die student, en realiseer u dat voor die student de afgelegde en de komende toets zich in alle opzichten gedragen als random steekproeven uit alle mogelijke vragen over de stof. Sterker nog, iedere volgende opgave is een random trekking. Hebben we daar een handig modelletje voor?
Ja, een binomiaalmodel [info]. Voor iedere opgave is de kans dat de studente de opgave goed maakt gelijk p, haar ware beheersing van de stof, waarvan we helaas de waarde niet kennen. Maar daarom niet getreurd, gegeven die score van 17 goed uit 20, kunnen we voor alle mogelijke waarden van p de waarschijnlijkheid bepalen dat deze de score 17 uit 20 oplevert. Dat levert de volgende aannemelijkheid op. Het meest aannemelijk is dat p = 0,85, en dat verbaast ons niets. Toch? [zie hier over aannemelijkheid]
binomiaalverdeling als model: The Generator. Module one of the SPA model: Scores. pagina
Aannemelijkheid (betaverdeling): The mastery envelope: The likelihood of it all. Module two of the SPA model: Mastery. pagina
Ben Wilbrink (1998). Inzicht doorzichtig toetsen. In Theo H. Joostens en Gerard W. H. Heijnen (Red.). Beoordelen, toetsen en studeergedrag. Groningen: Rijksuniversiteit, GION - Afdeling COWOG Centrum voor Onderzoek en Ontwikkeling van Hoger Onderwijs, 13-29. webpagina
Figuur 2. Aannemelijkheid voor de beheersing, gegeven 17 goed uit 20
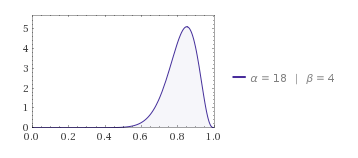
Gegeven die 17 opgaven goed uit 20, kan de ware beheersing van deze student zich overal onder de bovenstaande curve bevinden. Is dat even schrikken? Of kijkt u er helemaal niet van op? Laten we dan de volgende stap nemen, en op basis van deze informatie over de ware beheersing een voorspelling opstellen voor de toetsscore, toets van 20 opgaven getrokken uit hetzelfde domein van vragen over de stof:
Figuur 3. Voorspellende toetsscoreverdeling, gegeven 17 goed uit 20.
Hoe komen we aan deze voorspelling: 1000 keer trekken uit aannemelijkheid die we hierboven zagen, en telkens op basis van de getrokken p-waarde 20 keer een opgave trekken, de groene verdeling. Theoretisch levert dat een betabinomiaalverdeling op, de zwarte lijn.
Je doet als student dan zo’n proeftoets, scoort 17 goed uit 20, en mag dan beslissen om onmiddellijk ook voor de echte toets te gaan, die eveneens 20 vragen heeft. Als de score 16 of hoger een ‘voldoende’ oplevert, dan geeft ons eenvoudige model aan dat de kans daarop 0,68 is. Zou u het doen? En zo ja, waarom dan?
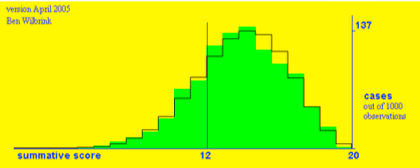
Figuur 3a. Idem, nu gegeven 14 goed uit proeftoets van 20 opgaven, referentie 12.
Vat het allemaal maar op als een gedachte-experiment. De logica ervan is onontkoombaar, bijt er uw tanden maar op stuk. Toetsen zijn voor studenten niet echt goed voorspelbaar. De tragiek daarvan is dat studenten zich niet echt doeltreffend kunnen voorbereiden, en als je er niet van overtuigd bent dat extra investeren van tijd iets gaat opleveren, investeer je dan nog? Ik kom er straks op terug, want alles draait om de tijd die studenten willen investeren.
In een heel ander model functioneert de toets als het wisselkantoor waar studenten hun beloning voor hun inspanningen halen, en docenten die beloning geven. Het is een raar wisselkantoor, want je krijgt er soms veel meer dan je verwacht, soms veel minder. Dat geeft aan dat examens vaak een beroerde economie kennen, waarin partijen (studenten versus docenten) elkaar niet echt vertrouwen. Het is een bijzonder model, voor kostelijke info en empirische data zie Wilbrink 1992.
Ben Wilbrink (1992a). Modeling the connection between individual behaviour and macro-level outputs. In Tj. Plomp, J. M. Pieters & A. Feteris (Eds.), European Conference on Educational Research (pp. pp. 701-704.). Enschede: University of Twente. pagina
Maakt het verschil wanneer we die toets heel, heel veel betrouwbaarder maken door hem 10 keer zo lang te maken? Onze student weet nog steeds niet meer dan zij 17 goed uit 20 heeft gescoord.
Het maakt verdraaid weinig verschil! Hier gaat een niet onbelangrijk geloofsartikel van de psychometrie het raam uit! Laten we het eens omdraaien: heel, heel veel informatie vooraf hebben, door 170 goed uit 200 te hebben, maar de toets die je moet afleggen is gewoon 20 vragen:
Ik geef toe, de voorspelling is wel scherper, maar veel vertrouwen in een goede afloop kan ik het niet noemen: verwacte slaagkans is 0,81.
Wnneer de informatie vooraf in balans is met de lengte van de toets, dan breekt het zonnetje door de wolken. Kunnen we hiermee aan de slag in een discussie over examens? Want 200 opgaven is ongeveer de omvang van een heel examen over het eerste studiejaar.
Stel dat ons examen bestaat uit 10 onderdelen van ieder 20 vragen. Telkens komt onze willekeurig gekozen student op in de wetenschap kort tevoren 17 goed uit 20 proeftoetsopgaven goed te hebben. Dan kunnen we een Mandelbrotje doen: het hiervoor summier gepresenteerde toetsmodel is ook toepasbaar op een examen dat uit 10 onderdelen bestaat, onderdelen die ieder ofwel voldoende (kans 0,68), ofwel onvoloende worden gemaakt: binomiaalmodel met parameters 0,68 en 10. In een gedachte-experiment kunnen we onze student een proefexamen laten afleggen, stel dat ze 6 onderdelen voldoende maakt:
Voor het echte af teleggen examen is dan de aannemelijkheid voor het aantal voldoendes:
En de voorspellende verdeling:
Dat is toch om wanhopig van te worden? Ook al weten we dat we verondersteld hebben dat onze student voor iedere toets dezelfde strategie blijft volgen; in de werkelijke wereld zetten studenten die aanvankelijk onverwacht laag scoren waarschijnlijk toch wel een paar tandjes bij.
Groter contrast is moeilijk denkbaar, toch? We hebben hier een student die voor iedere toets behoorlijk is voorbereid, die ongetwijfeld meteen zou slagen voor alle 10 toetsen gezamenlijk (rechts), maar die bij de middeleeuwse gewoonte van ‘onvoldoendes moeten over’ op verliestijden voor herkansen, en dus op studievertraging wordt gezet (links). (Geschiedenis van beoordelen in onderwijs: Wilbrink, 1997). Onnodige studievertraging: want wie twijfelt eraan dat deze student vlot het tweede jaar zal kunnen doen? En dat moet toch echt het criterium zijn voor een tussentijds examen.
Een tussentijdse conclusie kan eenvoudig zijn dat enige compensatie toestaan een win-winsituatie oplevert: waarschijnlijk veel minder herkansingen, minder verstoring van de studievoortgang (Wilbrink, 1980c), mogelijk betere prestaties.
Over herkansingen gesproken: wie zegt dat die positieve resultaten opleveren? (Wilbrink 1980a) Als een herkansing zinvol is voor wie een ‘onvoldoende’ haalde, waarom niet even zinvol voor wie een ‘voldoende’ haalde? Herhaald toetsen van dezelfde stof is best een goed idee, het is zelfs een uitstekende studiemethode! (Kirschner & Neelen, 2017) Maak er gebruik van bij het ontwerpen van betere examenregelingen.
Ik heb in 2001 al eens een overzicht gemaakt van bekende mogelijkheden (en resultaten) om verliestijden te vermijden voorzover deze voortvloeien uit de examenregeling en de kwaliteit van de toetsen. Ik verwijs u daarnaar, maar zal hierbeneden wel enkele punten aanstippen.
Paul A. Kirschner & Mirjam Neelen (October 31, 2017). Tips and Tricks for Spaced Learning blog
(1980). Ben Wilbrink (1980). Enkele radicale oplossingen voor kriterium gerefereerde grensskores. Tijdschrift voor Onderwijsresearch, 5, 112-125. html
Ben Wilbrink (1980c). Toetsen, herkansen, studievertraging: achterliggende mechanismen. Onderzoek van Onderwijs, 9 nr. 2, 7-11. html
Ben Wilbrink (1997). Assessment in historical perspective. Studies in Educational Evaluation, 23, 31-48. html
Ben Wilbrink (2001). Examens doeltreffend regelen. Ongepubliceerd. pagina
Wat is ons houvast om ons hieraan te ontworstelen? In het onderwijs kennen we geen absolute normen: alle normen zijn relatief. Alleen sleutelen aan de normen is een favoriet spel voor politici, maar dat gaat niet zomaar resultaat opleveren. Daarom is het nodig om door studenten te investeren tijd erbij te betrekken.
Het is een volledig recursief structural equations model, met een geschikte dataset is je het model uit te rekenen (Tromp & Wilbrink 1977). Maar dat terzijde, want het gaat nu vooral om houvast bij de discussie over het examen. De resultaten hangen af van tal van factoren, waarvan de tijdbesteding van studenten de meest interessante is: als we betere resultaten willen, zullen we studenten moeten verleiden of nudgen om meer tijd te investeren. Eens? Kan dat door te spelen met compensatie? Laten we even in de wacht zetten dat we studenten ook kunnen helpen hun tijdinvestering op orde te krijgen door de kwaliteit van de toets te verhogen (Schotanus, 2015), door verliestijden te minimaliseren (Vos & van dr Drift 1987) en/of door de kwaliteit van de tijdbesteding te verhogen (Wieman, 2014).
Let ook even op dat streefniveau: als studenten in het duister tasten over wat er precies van ze gevraagd gaat worden, is het toch raar om ze te vragen om de lat voor zichzelf hoog te leggen. Als niet duidelijk is wat ‘hoog’ is, is dat op voorhand al een verloren zaak. Adriaan de Groot waarschuwde er al voor in 1970.
Janke Cohen-Schotanus (19 juni 2015). Maatregelen ter verbetering van het rendement in het Hoger Onderwijs: waar is de evidentie? Keynote OnderwijsResearchDagen 2015 Leiden. keynote en powerpoint
Koen D. J. M. van der Drift en Peter Vos (1987). Anatomie van een leeromgeving. Een onderwijseconomische analyse van universitair onderwijs. Lisse: Swets en Zeitlinger. Proefschrift Rijksuniversiteit Leiden.
Adriaan D. de Groot (1970). Some badly needed non-statistical concepts in applied psychometrics. Nederlands Tijdschrift voor de Psychologie pagina
Dick Tromp & Ben Wilbrink (1977). Het meten van studietijd. Paper ORD. html Carl Wieman (2014). Large-scale comparison of science teaching methods sends clear message. open access
9 december.
Richtinggevend voor het examen van het eerste studiejaar moet zijn dat het enige garantie geeft voor een goede voortzetting voor deze student in de direct volgende studie. Dat is een andere opvatting dan van dit examen als een afsluiting van het eerste jaar, een tussentijds diploma zeg maar. Er moet ruimte zijn om af te wijken van formules die specificeren welke resultaten tenminste behaald moeten zijn om geslaagd te kunnen zijn. Dit is niet wezenlijk verschillend van overgangen in het voortgezet onderwijs, al gaat men in het voortgezet onderwijs hier niet altijd even zorgvuldig mee om. Ik druk me voorzichtig uit.
[morgen, 9 december, verder]
7 december
Ik heb een half uur de tijd om een paar fundamentele zaken over het voetlicht te brengen. Dat moet gereedschap zijn waarmee men aan de slag kan, in de discussie zowel als bij het vormgeven van betere examenregelingen. Ik heb een eerste mindmap gemaakt waarmee ik al heel ver kom (steekproef, voorspelbaarheid), en waar ik een aantal andere zaken aan op kan hangen: het gaat allereerst om strategische keuzes van de student (wybertjesmodel Wilbrink 1977), er zijn geen absolute normen, dus houd de tijdbesteding scherp in de gaten; herkansingen bieden is geen goed idee.
Waar ik nog mee aan de slag moet: op welke manier kan een compensatoire toets de studenten nudgen tot investeren van meer tijd (dan bij een conjunctieve toets). [basis: er is dan geen optimale strategie meer die verwacht benodigde tijd minimaliseert, er staat dus geen boete op extra investeren. Klopt dat? Modale studenten kunnen al punten verdienen die bij latere toetsen inzetbaar zijn. Studenten die moeite hebben met de studie kunnen wel proberen vijfjes te scoren, maar gaan het daarmee dus niet halen.] Koppel dit aan de vraag van splitsen en/of combineren van toetsen. Hoe pakt een en ander uit in termen van belasting van docenten?
Marginale punten, althans, niet direct gekoppeld aan enig model: kwaliteit van de toets en de toetsvragen (Schotanus, ORD), loslaten van het idee dat een toets moet differentiëren tussen studenten, verstandige logistiek (Vos & vd Drift, 1987).
Marginale theoretische punten. Achteraf analyseren van examengegevens, en hoe die er onder een ander regime zouden hebben uitgezien, is tricky omdat dat geen rekening houdt met waarschijnlijk andere studiestrategieën: studenten zullen altijd reageren op wijzigingen in examenreglingen etcetera. Wybertjesmodel. Analyses in termen van terechte en onterechte beslissingen slaan eigenlijk nergens op, want dat kunnen we helemaal niet weten (want platonisch), maar het is wel het hoofdpunt van Smits ea (2014?).
Empirische data. Cohen-Schotanus 1994 (geneeskunde Groningen). Wilbrink 1992 (rechten, tachtiger jaren, compensatoire examenregeling)
Meer literatuur (lijstje maken).
Ik maak voor het genereren van grafieken gebruik van mijn applets in het SPA-model. Probleempje hiermee: deze applets draaien alleen nog op heel oude JAVA. Maar als ik het goed heb, dan maak ik eigenlijk alleen gebruik van binomiaal, beta en betabinomiaal. Deze verdelingen zijn in Wolfram beschikbaar. Ik ga dus ook bekijken of ik Wolfram-plotjes kan toevoegen, of uitsluitend Wolfram-plotjes kan gebruiken.
K. D. J. M. van der Drift en P. Vos (1987). Anatomie van een leeromgeving. Een onderwijseconomische analyse van universitair onderwijs. Lisse: Swets en Zeitlinger. Proefschrift Rijksuniversiteit Leiden.
6 december
In 1980 heb ik een paper over het onderwerp gepresenteerd, aan de hand van stellingen. Ik zou het misschien zo weer kunnen gebruiken ;-) [Nou nee, ik heb het nu gelezen, stelt me zeer teleur. Er zitten slaagpercentages in, uit de literatuur 70er jaren]
Waar ik naar op zoek ben: hoe ik kernbegrippen in het compensatie-verhaal zo economisch mogelijk en zo strak mogelijk aan elkaar verbonden kan presenteren. De mentale belasting van de toehoorder moet binnen de perken van het modale werkgeheugen blijven, zeg maar.
Het idee is om de enkele toets als uitgangssituatie te nemen: die is namelijk volledig compensatorisch. Voor de student ziet haar toets er bovendien uit als random getrokken uit alle mogelijke vragen. Briljant, dan hebben we hier dus een binomiaalmodel voor de ware beheersing van de stof. Die ware beheersing zullen we nooit weten, maar we kunnen er wel mee rekenen. Gegeven een behaalde score op deze toets, dan kunnen we een aannemelijkheid voor die ware beheersing simuleren of theoretisch afleiden, en op basis daarvan een voorspelling doen voor de score op een onmiddellijk volgende tweede toets, eveneens voor de student er uitziend als random getrokken. Daar geef ik een paar afbeeldingen van. Dit alles zonder de complicatie van een cesuur en van herkansingen in de beschouwingen mee te nemen.
Afijn, mooi modelletje, wat zegt dit ons voor een examen dat bestaat uit een aaneenschakeling van dergelijke toetsen? Zoals Van Naerssen al opperde: een examen is ook een toets, maar dan een veel langere. En iedereen kent de relatie tussen korte en lange toetsen: de lange toetsen zijn veel betrouwbaarder, zeg maar: veel beter voorspelbaar. Wat hebben we aan die constatering, want dat examen is toch opgeknipt in afzonderlijke toetsen? Oké, voor de student ziet het er nu uit als herhaald random getrokken uit deelverzamelingen van mogelijke toetsvragen. Zou het echt veel verschil maken om hier af te zien van het onderscheid tussen deelverzamelingen? Ik denk het niet, maar kan ik dat laten zien? En dat geldt alleen zonder de complicatie van cesuren, natuurlijk. Oké: neem voor het examen in zijn geheel een proeftoets die even lang is als een enkele toets. Hoe ziet nu de voorspellende toetsscoreverdeling eruit? Als een toets 60 vragen heeft, dan een examen van 10 toetsen dus 600. Hm, indrukwekkend aantal, daar moet iets mee te doen zijn, toch? Kwestie van samenwerken. Ik kan laten zien hoe zo’n heel lange toets toch slecht voorspelbaar is wanneer er weinig informatie vooraf is. En omgekeerd geldt ook: bij heel veel informatie vooraf, terwijl de toets maar kort is, is de voorspelbaarheid ook maar weinig beter dan bij veel minder informatie. Bij veel info vooraf, en een heel lange toets, hebben we een mooie balans.
Maar die 600 vragen zijn in werkelijkheid 10 toetsen. Hoe is dat in model te gieten? Begin eenvoudig, doe een Mandelbrotje, een fractalletje: slagen of zakken is 1 of 0 scoren, en dat 10 keer voor 10 onderdelen: wederom binomiaalmodel etcetera. Plot van de binomiaal laat zien hoe vaak er gezakt wordt. Dan zou je toch onmiddellijk zeggen: je mag twee keer een vijf hebben, en dan ben je nog steeds geslaagd. Maar let op: dit is een achteraf-constatering (of een a priori verwachting), het hele examen is achter de rug. Werkendeweg zien sommige studenten een of twee vijven verschijnen, wat betekent dat ze echt moeten opplussen voor de nog resterende toetsen. De werkelijkheid zal er dus iets anders uitzien dan de binomiaal, maar niet echt heel anders. Afijn, er kan ook een echte voorspellende verdeling worden opgesteld, en dat moet ik dan ook maar doen.
Een toets van 60 vragen is niet representatief voor alle examens. Ik doe een herberekening voor toetsen van 20 vragen. Deze vragen zijn complexer dan de vragen in toetsen van 60 items, ik leg dat uit in 1998; implicatie: de leercurve voor deze toetsstof zal een ogief zijn, een interessant gegeven om bij de overwegingen te betrekken.
Het is waarschijnlijk nodig om een terzijde in te lassen: over cesuren en herkansingen. Wilbrink 1980b dus. Als herkansingen zinvol zijn, waarom dan niet iedereen laten herkansen? Wat is uw antwoord?
[Het beeld dat ik voortdurend in mijn hoofd heb is dat van de studenten die uiteindelijk slagen voor het examen, vrijwel alle herkansingen ten onrechte zijn opgelegd, want het gevolg van steekproeffluctuaties, niet van tekortschietende beheersing. Hier kan ik mijn analyses van data rechten bij te hulp roepen]
5 december
Meten is weten; maar zo gaat het dus niet. Modelleren is weten, dat is andere koek. En waarom is dat: het dwingt om precies te zijn. Een toets is een steekproef. Voor studenten gaat het om het resultaat, kunnen zij zich doeltreffend op de toets voorbereiden? Voor de docent gaat het waarschijnlijk toch vooral om de inhoud, maar die inhoud staat in het examen vooral buiten haakjes. Voor de studenten is de inhoud het middel tot het doel, terwijl docenten juist wensen dat de toets het middel is tot het inhoudelijke doel. Hoe krijgen we dit helder? Omdat er in het onderwijs geen absolute normen zijn, is de tijd die studenten besteden de cruciale, maar makkelijk vergeten factor. Welk model ook, die tijdbesteding heeft er een belangrijke plaats in. En let op: denk voortdurend mee met de student, de student moet het doen, en wat zij doet hangt af van hoe u als docent de zaken hebt voorgekookt en ingericht. Doen de studenten het niet goed? Dan hebt u ergens een foutje gemaakt. Schrik niet, u bent vast niet de enige, en u staat in een heel, heel lange traditie van examineren die als veel te vanzelfsprekend wordt gezien. [Voorbeeld: Posthumus die liet zien hoe de HBS extreem selectief was van 1870 tot 1940, in een samenleving die wel behoefte had aan ingenieurs en wetenschappers, maar slechts mondjesmaat]
De nadruk ligt op de afzonderlijke toets, niet op het complexe geheel van het examen. Er zijn wel mogelijkheden om hele examens te modelleren, maar voor de student is de situatie toch vooral vergelijkbaar met die van de travelling salesman: wat het optimale pad langs alle te bezoeken toetsen is, is vrijwel onmogelijk te bepalen. Al was het maar omdat iedere toets een ingrijpend stochastische gebeurtenis is waardoor het hele spel kan veranderen.
26 november 2017
Kent u dat boekje van A. D. de Groot, Vijven en zessen (1966)? Het beschrijft de strijd tussen vo-leraren en leerlingen, en tussen leraren onderling, met als inzet de tijd van de leerlingen, en de cijfers die ze als beloning krijgen. Ook examens in het HO zijn zo’n arena van armpje drukken tussen docenten en studenten. En docenten verliezen dat, zonder dat studenten winnaars zijn. Het is een verlies-verlies-situatie (Wilbrink, 1992). Kan dat ook anders? Ja, er zijn mogelijkheden om examens beter in te richten.
Om welke examens gaat het: het eerste jaar van de studie in het HO, voor studenten vaak onder druk van een minimum aantal studiepunten dat gehaald moet worden (BSA), voor de instelling onder druk van rendementen die beter moeten (convenanten OCW).
De neiging is sterk om de discussie over compenseren meteen maar te voeren over de voor- en nadelen. Maar zo komen we er niet uit. Het is handiger om eerst te begrijpen waar me met ons examineren eigenlijk mee bezig zijn, en dan het examen zo te ontwerpen dat het optimaal functioneert voor ieder van de betrokken partijen. Dat zou mooi zijn. Dan is immers ook de vraag naar voor- en nadelen beantwoord.
Neem aan dat het iedereen te doen is om de resultaten, de cijfers, het rendement. Dat is legitiem, daar is nauwelijks strijd over mogelijk. Hoe bereik je die resultaten? Laat ik dat anders formuleren: hoe verklaar je de resultaten die zijn bereikt? Want die vraag kunnen we beantwoorden. Ik heb er een handig modelletje voor, ooit in 1977 gepresenteerd op de Onderwijs Researchdagen html
Het is een volledig recursief structural equations model, met een geschikte dataset kun je het model uitrekenen (Wilbrink & Tromp html1977). Maar dat terzijde, want het ons vooral om houvast bij de discussie over het examen. De resultaten hangen af van tal van factoren, waarvan de tijdbesteding van studenten de meest interessante is: als we betere resultaten willen, zullen we studenten moeten verleiden of nudgen om meer tijd te investeren. Eens? Laten we even in de wacht zetten dat zoiets ook kan door de kwaliteit van de toets te verhogen (Schotanus), door verliestijden te minimaliseren (Vos & van dr Drift 1989) en door de kwaliteit van de tijdbesteding te verhogen (Wieman). Of door selectie-aan-de-poort. En studenten gretiger maken om te investeren.
Een heel examen analyseren lijkt ingewikkeld, maar laten we dan beginnen met een enkele toets.
Laat me raden naar het soort toets dat u afneemt. De scores op die toets hebben een grote spreiding, en dat is geen wonder, want u hebt de opgaven nogal moeilijk gemaakt. Stel je voor, makkelijke vragen leveren immers geen informatie, althans, zo is u ooit wijsgemaakt. U vertaalt die scores naar cijfers, en wel zodanig dat sommige studenten een ‘onvoldoende’ cijfer krijgen. Die ‘onvoldoende’ moet echt een ‘voldoende’ worden, en daar is een herkansing voor nodig. Ziedaar een traditioneel en cultureel bepaalde toetspraktijk die op allerlei manieren resulteert in verliezen. [Wilbrink, 1997: geschiedenis]
Dat kan ook anders. Vraag uitsluitend de kern van de stof, die moet in beginsel 100% worden beheerst, maar toetsen zijn feilbaar dus u eist 90% goed, en u zorgt er in uw vraagstelling ook voor dat dat haalbaar is. Studenten weten precies wat er van ze zal worden gevraagd, bereiden zich doeltreffend voor, en scoren vrijwel allen 90% of hoger. A. D. de Groot 1970 prijst u ervoor. De spreiding van de scores is gering, verschillen tussen studenten zijn er eigenlijk niet, cijfergeven is overbodig, iedereen beheerst de stof.
Een prachtige manier om een goed examen af te nemen is dus alle toetsen zo in te richten. Even terug naar het wybertjes-model: deze inrichting van het examen stelt 100% als norm voor het resultaat; grijpt in op het streefniveau: iedereen streeft naar 100%; en vooral op de tijdbesteding: iedereen zal minstens zoveel tijd besteden als nodig is om die 100% te halen. Deze manier van toetsen vergt een enorme cultuuromslag, dat wil ik u niet aandoen. Ik heb deze optie voor de volledigheid genoemd, maar ook wel om even te laten zien dat toetsen op verschillen tussen studenten een traditioneel bepaalde keuze is. Het kan echt anders met onze examens, vasthouden aan tradities vanwege de tradities is verliesgevend.
Andersom dan. Stel dat we alle afzonderlijke toetsen in het examen samenvegen, en éé:n toets afnemen, aan het eind van het eerste jaar. Klinkt dat bekend? Dat was ooit de situatie bij bijvoorbeeld geneeskundige studies. Hoe doelmatig kan dat zijn? Studenten beginnen dan pas laat met voorbereiden, misschien ook vaak te laat, en velen halen dan dat examen niet. Ook met volledige beheersing als model zal dat zo blijken te zijn: uitstelgedrag is menselijk, en juist omdat de student door dat uitstel niet goed weet hoe weinig zij nog weet, kan dat uitstel fataal blijken door uiteindelijk te weinig tijd te hebben voor goede voorbereiding.
Zo’n examen knip je dus op in een groot aantal onderdelen die verstandig gespreid over het jaar worden afgenomen. De studietijd voor al die toetsen gezamenlijk schiet omhoog, evenals de resultaten. Tenzij ...
Maar het gaat mij hier even om iets anders. Merk op dat het cruciaal is wat de studenten doen of laten. Zij zijn de beslissers waar alles om draait. Docenten kunnen hun toetsen en regelingen veranderen, dan zullen studenten hun gedrag ongetwijfeld aanpassen. Maar welke veranderingen zijn verbeteringen? Dan zul je als docent een idee moeten hebben van hoe strategisch studenten zich gedragen. En weer komen studenten hier eerst. Studenten zijn de primaire beslissers. Docenten kunnen de condities veranderen, daarmee zijn zij secundaire beslissers. Dat is makkelijker in te zien aan de hand van een concreet voorbeeld
De klassieke toets levert allereerst het oordeel voldoende of onvoldoende op, in tweede instantie is voor sommige studenten (met een hoog streefniveau) het behaalde cijfer van belang. Voor de meeste studenten telt eigenlijk alleen die voldoende. Dat kunnen we kwantitatief vangen in een drempelnutsfunctie: het nut van een voldoende resultaat is 1, van een onvoldoende resultaat is 0. Hoe inspirerend is dat? Dan kweken we toch zesjesklanten? En wel des te sterker naarmate de leercurve om beter te presteren dan nipt voldoende minder steil is. Erger is dat we ook iets met die onvoldoende scorende studenten moeten doen; dwingen we ze om via herkansingen alsnog een voldoende te halen?
Wat is hier aan de hand? We zijn geneigd om toetsen en examens op dezelfde manier te zien als psychologische tests: ze meten een of ander kenmerk. Voor de psychologische test is dat vaak nog wel vol te houden: de te testen personen zijn naïef, in deze zin dat ze zich niet specifiek op de test hebben kunnen voorbereiden. Bij toetsen veronderstellen we juist het omgekeerde: dat studenten zich er gericht op hebben voorbereid. Voelt u hem al aankomen? Als u, als docent, denkt dat u alleen maar een meting doet, dan wordt u in het pak genaaid door uw studenten. Zoals overal in het leven: zodra er afgerekend gaat worden op specifieke resultaten, in dit geval zijn dat toetsen, verliezen diezelfde resultaten een deel van hun informatieve waarde. Immers, de andere partij laat zich dit niet lijdelijk gebeuren, en zal antwoorden met eigen strategieën.
Een gewaarschuwd mens telt voor twee. De crux zit hem niet in het toetsen zelf, maar in de strategieën die studenten kiezen. Wat voor studenten optimale strategieën zijn, hangt af van de condities die u, als docenten, creëert. Robert van Naerssen begon in 1970 met een en ander uit te werken tot zijn tentamenmodel, een onderneming waarmee ik, als enige, sindsdien ben verder gegaan.
U moet dan weten dat een toets geen meting is, maar een steekproef uit de kennis waarvan we verwachten dat de student die zich eigen heeft gemaakt. Als u een toets van 30 vragen als proeftoets geeft, en een week later een vergelijkbare toets van 30 vragen voor het echt, dan zou iedere student op basis van haar score op de proeftoets een voorspelling kunnen doen van het resultaat op de toets die telt, en zo ook haar verwacht nut kunnen berekenen. Vindt ze het de moeite waard om nog een extra studie-inspanning te doen, dan kan dat verwacht nut verbeteren. Zo gaat dat.
Technisch: de score op de proeftoets is binomiaal verdeeld, gegeven de ware beheersing. Die ware beheersing kent niemand, maar wel de score op de proeftoets. Wat we dan kunnen weten over de ware beheersing is zijn likelihood, theoretisch is dat hier een betaverdeling. Die likelihood maakt het mogelijk te voorspellen wat de score zal zijn op de toets die telt, althans welke statistische verdeling deze zal hebben; theoretisch is dat een betabinomiaalverdeling. Met deze verdeling wegen we de nutsfunctie: dat levert het verwachte nut. Het verwachte nut verbetert met extra investeren van studietijd. [Voor een pass/fail toets is het verwachte nut eenvoudig gelijk aan de slaagkans (zie parallel-paper).]
Een steekproef van 30 vragen is een kleine steekproef, wat betekent dat iemand die (zonder dat exact te weten) een beheersing van 0,7 heeft maar wel tenminste 18 vragen goed moet hebben om een voldoende te halen, een stevig risico heeft op een onvoldoende uit te komen. Op zeker spelen is er voor studenten niet bij, enkele uitzonderingen daargelaten. U moet daar iets mee, u kunt deze stand van zaken niet zomaar laten uitmonden in verlies voor alle betrokkenen. Daar gaat het om.
Dit model is een rationeel model, het beschrijft niet hoe studenten in feite hun strategie kiezen. Maar zij kijken de onzekerheid wel recht in de grote muil. Meer investeren om de kans op zakken te verkleinen is een tamelijk armzalige en niet echt motiverende strategie, veel studenten zullen het te vroeg al wel welletjes vinden. En dat kan echt anders.
Maar eerst toch even stilstaan bij de strategische situatie voor studenten die voor een toets-met-herkansingen staan waar ze een voldoende voor moeten scoren. Wat deknt u, wat is hier de kern van een optimale strategie voor studenten? Aan het precieze cijfer hebben ze niet veel, het moet een voldoende zijn. Het enige dat studenten hier kunnen optimaliseren is de hoeveelheid tijd die het halen van dit onderdeel gaat kosten, inclusief eventueel nodige herkansingen. Robert van Naerssen heeft dat uitgewerkt in zijn eerste tentamenmodel. Een kenmerk van deze situatie is allereerst: er is inderdaad een optimale tijdbesteding, maar die is toch enigszins vaag, zodat studenten voor de keuze staan: de investering voor de eerste gelegenheid laag houden, of juist aan de wat hogere kant gaan zitten. Doorrekenen laat zien dat de gevolgen bepaald niet mals zijn: wie liever wat minder dan wat meer tijd investeert, haalt uiteindelijk wel een voldoende reultaat maar dat is dan op een lager niveau van beheersing. Doe je dat voor meerdere vakken, dan kom je met deze strategie jezelf uiteindelijk tegen: met minder kennis in de ransel dan je medestudenten, ga je het afleggen tenzij je de investering drastisch opschaalt (Wilbrink, 1978). Oké, dan heb ik het nog niet over de storende invloed van de benodigde herkansingen op een vlotte studievoortgang (Wilbrink, 1980 OvO a). Ik doe er nog een waarschuwing bij: wanneer het studenten niet echt duidelijk is wat er op de toets van ze gevraagd zal worden, dan dwingt u ze als het ware tot die onvruchtbare studiestrategie (maar een deel van hun inspanningen is doeltreffend).
Compensatie van cijfers toestaan levert een geheel andere situatie op: het risico van zakken verdwijnt naar de achtergrond, geen angst meer als motivator; omdat hogere cijfers waarde hebben als wisselgeld voor tegenvallende resultaten elders, is het de moeite waard om te investeren voor een hoger beoogd resultaat. Streefniveau en tijdbesteding gaan omhoog, dus ook de resultaten. Onvoldoendes bestaan even niet meer. De mogelijkheid om te herkansen kan nog een spelbederver zijn, en tot uitstelgedrag leiden: schaf herkansen af.
Ben Wilbrink & Dick Tromp (1977). Het meten van studietijd. Congresboek OnderwijsResearchDagen. html
22 maart 2017
25 maart 2017 eerste beginselen 2e versie
Als verschrikkelijk oude rot op deze thematiek ben ik gelukkig in staat een of twee lagen dieper te kijken dan al diegenen die voor het eerst in hun bestaan op dit ondermaanse zich tot compensatie in examenregelingen moeten gaan verhouden. Het idee is om niet met de simpele vraag wel of niet compenseren te beginnen, maar met beginselen op basis waarvan een examenregeling gebouwd zou moeten worden. Een forse omtrekkende beweging dus, maar zie hoe boeiend deze beweging kan zijn!
Ik denk dat ik een insteek zoals deze hier voor het eerst gebruik, maar mijn geheugen kan mij verschrikkelijk bedriegen. Zo bleek dat ik in 2001 al eens een goed overzicht over compensatie op papier heb gezet, kennelijk met de bedoeling deze te publiceren maar dat blijkt er toch niet van gekomen.
Ben Wilbrink (2001). Examens doeltreffend regelen. html
Voor velen is dit misschien een verrassende stelling. Bedenk dat tot eind 19e eeuw het beoordelen in het onderwijs ging in de vorm van rangordenen van leerlingen/studenten naar het totaal van de fouten die ze hadden gemaakt. In die 19e eeuw, de eeuw van nauwkeurig meten en bijhouden van statistieken, is dat rangordenen vervangen door de in zekere zin gestandaardiseerde vorm van cijfergeven (Wilbrink, 1997). De oppervlakkige indruk van objectiviteit die onze cijfers geven, berust dus nergens op: het is pseudo-objectiviteit. Eigenlijk wist iedereen dat al wel, maar we doen ons best in het dagelijks leven te blijven geloven in het sprookje van cijfergeven als iets objectiefs, als iets eerlijks.
Oké, we hebben in feite dus geen absolute normen voor de prestaties van studenten. Maar dat is wel een probleem, want die prestaties zullen wel beslissend zijn voor de vraag of examenregeling A beter is dan regeling B. Een tussenvraag is dan: hoe komen studieprestaties tot stand, hebben we daar een eenvoudig model voor? Ja, een eenvoudig model dat zich goed leent om het denken over studieprestaties scherp te houden is te vinden in Tromp & Wilbrink (1977). Niet dat die auteurs de geniale uitvinders zijn, het gaat om een model dat goed weergeeft dat studieprestaties het gevolg zijn van persoonlijke capaciteiten, motivatie, en bestede tijd. Althans, voorzover het gaat om wat studenten er zelf aan doen.
Het gaat nu even om die tijdbesteding, dat is onze reddende engel. Het moet immers zo zijn dat studenten die de nominale tijd investeren, dan ook horen te slagen. Time on task. Absoluut een cruciaal gegeven in de vormgeving en dus ook de evaluatie van onderwijs.
Twee dingen pro memorie: de task doet er enorm toe, evenals de kwaliteit van inspanning. Multitasken tijdens de studie is dodelijk. Studiemethoden verschillen sterk in doeltreffendheid: herlezen en onderstrepen van de leerstof is tijdverlies, actieve methoden werken beter en kunnen misschien onderdeel zijn van de examenregeling. Tijd besteden aan flauwekulopdrachten is verspilling.
Gek genoeg zien we maar zelden dat beleidsmakers, onderzoekers, maar ook leraren, zich ervan bewust zijn dat niet zij zelf, maar leerlingen en studenten de hoofdactoren in het onderwijs zijn. Al die maatregelen waarbij er geen seconde is nagedacht over gedragsconsequenties voor diezelfde studenten dreigen dus alleen daarom al plat te vallen. Het is de enorme verdienste geweest van Robert van Naerssen (1970) om niet alleen de besliskundige benadering van examens te promoten, maar dus ook de plaats van de student als primaire beslisser daarin. Op het tweede plan komt dan de docent, of de commissie die het OER opstelt. In het volgende kom ik daar nog meermalen op terug; die relatie tussen primaire en secundaire beslissers is razend interessant. Van Naerssen nam deel in de Afdeling Examentechnieken van A. D. de Groot, en ook De Groot (1970) legde het primaat bij de student: toetsen moeten door studenten doeltreffend zijn voor te bereiden. In die voorbereiding moet de time on task dus optimaal zijn. Daar kom ik ook nog op terug. Langs verschillende wegen komen Van Naerssen en De Groot op hetzelfde punt uit: het gaat erom hoe de student in het spel zit, en dat is voorafgaand aan de toets of het examen zelf. Ik benadruk dat maar, omdat toetsdeskundigen er in veel discussies stilzwijgend van uitgaan dat het er niet toe doet hoe studenten zich op de toets hebben kunnen voorbereiden. Maar een toets is geen psychologische test; de core business van de toets zit hem juist daarin dat studenten zich er gericht op voorbereiden. Bij de psychologische test is dat precies andersom (Wilbrink 1986). Wist u dat er Nederlandse richtlijnen zijn voor toetsgebruik? In de editie 1988 (de laatste) van de N.I.P. Richtlijnen is dat cruciale onderscheid tussen toetsen en testen nadrukkelijk aan de orde in het hoofdstuk over toetsen.
Ook langs juridische weg is het evident dat de positie van de student het uitgangspunt moet zijn, en niet bijvoorbeeld het comfort van de organisatie of de docent. Job Cohen (1981) heeft dat in zijn proefschrift Studierechten uitgewerkt, dat nog steeds het enige handboek voor dit onderwerp is. Het boek is zeldzaam, maar Job was er blij mee dat ik het hele boek gescand beschikbaar heb gemaakt zie beneden. Dat studenten zich doeltreffend moeten kunnen voorbereiden op toetsen heet bij Cohen het kenbaarheidsbeginsel. Het is geen algemeen beginsel van behoorlijk bestuur, maar is af te leiden van het fair play en het vertrouwensbeginsel. Het vertrouwensbeginsel: de student moet erop kunnen vertrouwen dat hij tot een voldoende resultaat kan komen wanneer hij afgaat op de informatie van de docent.
Ik noem de rekentoets ook hierom als voorbeeld: eerste beginselen zijn niet een academisch abstract speeltje. Dat half miljard is opgetekend uit de mond van de staatssecretaris, ongeveer twee keer de omvang van het Fyra-drama. En het is niet zo dat actoren niet waren gewaarschuwd: op alle keuzemomenten lagen er contra-expertises voor (jazeker, had ik ook een hand in). Die actoren moeten dan wel in staat zijn die boodschappen te begrijpen, en het lef hebben ernaar te handelen. Zal het ook zo gaan bij discussies over voorstellen voor meer compensatoire examenregelingen? U bent er zelf bij.
Doeltreffend kunnen voorbereiden is dus wezenlijk voor iedere toets en ieder examen. Het kan dus niet zo zijn, en dat is echt het laatste wat ik er nu over opschrijf, dat de vragen van afgenomen toetsen geheim worden gehouden.
M. Job Cohen (1981). Studierechten in het wetenschappelijk onderwijs Proefschrift Rijksuniversiteit Leiden. Zwolle: Tjeenk Willink. deel 1 (t/m blz 100), deel 2 blz 102-149, deel 3 blz 150-197 en deel 4 bijlage, samenvatting, literatuur, index
NIP (1988). Richtlijnen voor ontwikkeling en gebruik van psychologische tests en studietoetsen. Amsterdam: Nederlands Instituut van Psychologen. Tweede editie. [Hoofdstuk] 8. Toetsgebruik in het onderwijs. http://www.ben-wilbrink.nl/Richtlijnen_Toetsgebruik_in_het_onderwijs.pdf
Studenten die onzeker zijn over de studiekeuze die ze hebben gemaakt, zijn niet geneigd om volle bak te gaan in de voorbereiding op de eerste toetsen of tentamens. Als ze dan toch de studie staken, is dat niet een gevolg van slechte toetsresultaten, maar zijn beide het gevolg van een onzekere studiekeuze.
Op dezelfde manier zullen studenten die niet goed weten wat er in het examen van ze wordt verwacht eerder minder dan meer tijd steken in de voorbereiding erop. Daar vliegt de time on task het raam uit. De vraag is nu op welke manieren die doeltreffende voorbereiding valt te verbeteren, en hoe diverse examenvarianten hier presteren.
[dit is een tamelijk uitgebreide thematiek, die ik toch maar kort wil behandelen. Ik zit er nog op te broeden. Punten bv: grote toetsen opsplitsen in een aantal kleinere; langere toetsen zijn beter voorspelbaar dan kortere [steekproef!], dat is interessant want een volledig compensatoir examen is een heel lange toets, terwijl een streng conjunctief examen bestaat uit reeks relatief veel kortere toetsen; enzovoort]
[De Groot 1970] [stel hoge eisen aan toetskwaliteit]
. Gooi geen informatie weg (die ‘onvoldoende’ gemaakte toets). Stapel geen verlies op verlies (ga uit van zero herkansingen).
. Beoordeel practica eenvoudig als ‘voldaan’ [De Groot: Handelingsonderdelen], plak er niet een ‘afsluitende toets’ aan vast.
. Voeg kleine vakken samen tot 1 groot vak. Toets grote vakken eerst in de vorm van vrijstellende deeltoetsen (compensatorisch)
. Hoe combineer je dan cijfers voor die grote vakken: compensatorisch. En wees daar niet kinderachtig in (kernvakken vo, brrr).
. Zoek in de literatuur voorbeelden van een dergelijke aanpak voor de examenregeling. O.a. proefschrift Janke Schotanus.
Janke Cohen-Schotanus (19 juni 2015). Maatregelen ter verbetering van het rendement in het Hoger Onderwijs: waar is de evidentie? Keynote OnderwijsResearchDagen 2015 Leiden.
keynote en powerpoint
. Meerdere instellingen hebben nu ervaring opgedaan met meer compensatoire examenregelingen; leg ze langs de beginselenlat ;-)
. Wees op je hoede met adviezen van methodologen die vooral over terecht en onterecht goede of foute beslissingen oreren.
. Streng maar rechtvaardig: zoek de balans tussen waardering van prestaties en de time on task die daarin is geïnvesteerd.
. Het is mogelijk om de werking van een examenregeling te simuleren. Dus ook om verschillende varianten te vergelijken.
. Los daarvan of iemand zo’n programma schrijft: het is van belang te beseffen dat de werking van een examenregeling exact is te maken.
. Iedere examenregeling is compensatorisch (bv vragen binnen toetsen), weet wat je doet bij stellen van absolute aftestgrenzen.
. Toetsen zijn geen meetinstrumenten maar steekproeven. Neem toetsscores nooit absoluut (wiskundig model bv binomiaalverdeling)
. Als toetsen steekproeven zijn, hoe kun je studenten daar dan op afrekenen? Het is een spel, hè? Zorg voor eerlijke spelregels
. Het is overigens al heel lang bekend dat compensatorische examenregelingen zo’n honderdmiljoen aan besparingen opleveren ;-)
. Maar zoals wel vaker in het onderwijsveld valt te constateren: beleidsmakers blijven domme dingen doen.
. Oké, dit was allemaal telegramstijl, met slechts hier en daar een bron. Ik zou een goed stuk moeten schrijven ;-)
(Smits c.s. PedSt 2015 p. 276). Is this model fitting to the situation?
(Smits cs PedSt 2015 p. 276). Is it really the case that a summative test is a measurement?
(Smits cs PedSt 2015 p. 276). This is the received view on pass-fail decisions. Adequate?
One formulation of the issue of multiple cutting scores (combination of scores) is: Frederic Lord Psychometrika 1962 preview. Educational Testing Service has placed the underlying research bulletin by Lord online: pdf. Figure 1 tells the story: under multiple cutoff, always allow (some) compensation, otherwise you loose money/information/candidates.
Well, Lord 1962 effectively refutes the Smits c.s. claim: the multiple cutting scores problem reduces to false pos/neg evaluation on individual tests.
(Smits cs again) Sense? Nonsense? Just because it is possible to think up and print statements like the last one does not make them likely or even fit for discussion.
Dat zal best—waar gehakt wordt vallen spaanders—maar in concreto zullen we dat nooit weten. Het model ‘verkeerde beslissingen’ is geen adequaat model voor beslissen op basis van toetsscores.
Vooral piekeren en palaveren over beoordeling van afzonderlijke vakken is een ernstige vorm van kokervisie (maar er is een uitzondering op, zie beneden). Mijn zorg is dus ook: kunnen we het grotere verband zien waarbinnen examens en hun regelingen een eigen plaats hebben? Dan gaat het dus om voorspellen op langere termijn, niet alleen of uiteindelijk een ho-studie succesvol wordt afgesloten, maar ook wat over de verdere levensperiode de bijdrage aan de samenleving en het eigen welbevinden is (theorie van het menselijk kapitaal). Het maakt het er even niet eenvoudiger op. Zoals de lezer van deze webpagina al snel merkt: alles houdt met alles verband, en het kunnen zien van verbanden is nu juist een van de moeilijkste verworvenheden die experts onderscheiden van nieuwelingen op terrein X of Y. Dat ik veel naar eigen onderzoek verwijs heeft een eenvoudige verklaring: mijn belangstelling voor compensatorische examenregelingen vloeit voort uit een bredere belangstelling naar selectie en toetsen, ik heb in eigen onderzoek al vele dwarsverbanden gelegd.
Even snel de belangrijkste punten op een rij
Wat is het grotere verband waarbinnen de propedeutische studie is geplaatst? Helpt het genoemde selectiemodel om ook hier een geschikte modelbenadering te vinden?
Bij personeelsselectie is er meestal een sterke randvoorwaarde (constraint): een x-aantal plaatsen beschikbaar.
Als het aantal plaatsen geen randvoorwaarde is, bij numerus-fixusopleidingen althans geen randvoorwaarde die direct richting kan geven aan het beoordelingsproces, welke randvoorden zouden dan kunnen helpen?
Lex Borghans & Andries De Grip (1997) Numerus fixus en de arbeidsmarkt. Economisch Statistische Berichten, 82, 111-113.
dit uitstapje vraagt veel te veel detail, ik moet het zien kort te sluiten (hoe gaan Smits c.s. hier precies mee de ballenbak in? Gebruik dat dan). Wel nog even die beide proefschriften (vd Gaag, Vos) doornemen.
1. Het gaat om de wijze van combineren van resultaten op examenonderdelen tot de uitslag van het examen. En dus niet allereerst om de afzonderlijke examenonderdelen (toetsen). Van Naerssen gaf dat in de titel van zijn inaugurele rede in 1970 al helder aan.
2. Iedere examenregeling is compensatorisch, laten we daar geen misverstand over laten bestaan. Er zijn verschillen in de mate en aard van compensatie. Een zogenaamd volledig conjunctieve examenregeling — ieder examenonderdeel moet ‘voldoende’ zijn — is een examenregeling waarin het uitsluitend binnen de examenonderdelen is toegestaan volledig te compenseren. Je mag bijvoorbeeld vier keer patiënten laten overlijden in plaats van genezen, als je maar vaak genoeg er wèl in slaagt de juiste actie te kiezen.
3. De verleiding is groot om bij discussie over compensatorische regelingen meteen maar te beginnen met een en ander door te rekenen of misschien zelfs wel te simuleren. Het risico is dan groot dat er aannamen worden gedaan (en/of aannamen verborgen blijven) die de hele oefening tamelijk zinledig kunnen maken. Een veronderstelling die zelden echt serieus wordt genomen: al naar gelang de examenregeling, zullen studenten zich anders voorbereiden op de afzonderlijke toetsen. Lees de inaugurele rede van Van Naerssen om daar een beetje gevoel voor te krijgen. Dat betekent dat het niet echt zinvol is om berekeningen over slaagpercentages te gaan maken voor een examenregeling die geheel anders is, uitgaande van de resultaten die zijn behaald onder de vigerende examenregeling. Dat wordt helemaal te gek wanneer de rekenaars uitgaan van als voldoende, respectievelijk onvoldoende beoordeelde resultaten op de onderscheiden examenonderdelen.
4. Ingewikkelde redeneringen opzetten voor varianten van combinaties van examenonderdelen heeft niet zo gek veel zin, wanneer niet eerst helderheid is verschaft over het meest eenvoudige examen: het examen met een enkele toets. De vraag is: hoe is het mogelijk om voor dit eenvoudige examen te bepalen waar de grens tussen zakken en slagen moet komen? De vraag zo stellen is bijna hetzelfde als stellen dat het antwoord moet berusten op een besliskundige analyse. So far so good. Maar dan. Want wie kennis neemt van de literatuur over cesuurbepaling loopt het risico te verzanden in allerlei hocus-pocus-methoden. Met een klein beetje geluk vind je de klasse van compromismethoden van Hofstee. Maar we gaan natuurlijk niet voor het compromis, maar voor een principieel juiste methode. Laat ik die nu al eens geschetst hebben: Wilbrink (1980b).
Ik moet er meteen bij zeggen dat ik naar dit oude werk verwijs met een bijbedoeling: in mijn 1980b maak ik duidelijk dat zogenaamd besliskundige analyses die werken met aantal terecht/onterecht afgewezen/doorgelaten intern tegenstrijdig zijn. Voorbeeld van een proefschrift dat op deze onjuiste methodologie berust is dat van Van de Gaag [ik zoek de gegevens nog wel op], met Don Mellenbergh als promotor. Het spannende is dat al eind negentiende eeuw door Edgeworth erop is gewezen hoe met de waarschijnlijkheden bij vergelijkende selectie moet worden omgegaan. Het is nooit te laat om de klassieken er nog eens bij te nemen. Ook het Cito analyseert graag in abstracto over wat er kan gebeuren bij wijzingen in examenregelingen, en gebruikt dan de onjuiste methodiek van die terecht/onterecht afgewezen/doorgelaten kandidaten. Het gaat dus ergens over.
Robert V. Lindsey, Jeff D. Shroyer, Harold Pashler & Michael C. Mozer (accepted for publication 2013). Improving students' long-term knowledge retention through personalized review. Psychological Science Hal Pashler website
Goes further than the title suggests: might present a model for adaptive/formative testing too. Might be a nice technique to study effects of changes in rules for combination of grades into end-of-course grades [Dutch: examenreglingen die meer of minder compensatorisch zijn met al dan niet vrijstellende deeltoetsen]
Ivo Arnold (2011). Compensatorische toetsing en kwaliteit. Tijdschrift voor Hoger Onderwijs, 29, 31-40. [niet vrij online] abstract
Aan de hand van empirische data uit de eigen opleiding laat Arnold zien dat het oude adagium uit onderwijsonderzoek nog altijd opgaat: studenten zijn meestal prima in staat om eventuele tekorten in beheersing van de stof zelf weg te werken, zodra dat nodig is. Het is koudwatervrees om vast te houden aan voor ieder vak een ‘voldoende’ als een soort waarborg dat het dan met de verdere studie wel snor zit (en anders niet). Dan heb ik het nog niet eens gehad over de toevalligheden in toetsuitslagen, toevalligheden die veel ernstiger zijn dan docenten doorgaans vermoeden.
Uit de discussie de volgende conclusie:
F. M. Lord (1962). Cutting scores and errors of measurement. Psychometrika, 27, 19-30. preview & Research Bulletin.
Lord doet hier een theoretische oefening om effecten te laten zien van conjunctie versus compensatie. Dat zou je ook met een simulatieprogramma kunnen onderzoeken, zoals van Wilbrink (1990).
Een latere analyse is Huynh Huynh (1982).
Ben Wilbrink (1990). Complexe selectieprocedures simuleren op de computer.Amsterdam: SCO. (rapport 246) pdf bijlagen [bijlagen 304k pdf]
Als dit programma complexe selectieprocedures kan simuleren, dan is het ook bruikbaar om varianten van examenregelingen te simuleren. De broncode is beschikbaar in de bijlagen. Het programma is gecompileerd voor Apple systeem 9 (ook onder Classic), en draait helaas dus niet meer onder de nieuwere systemen waar de Classic-emulatie uit is geschrapt. Ik heb geloof ik zelf geen oefeningen gedaan met verschillende examenregelingen, dus dat is nog een mooi project voor een handige student psychologie met psychometrie als specialisme.
Ben Wilbrink (1980a). Optimale kriterium gerefereerde grensskores zijn eenvoudig te vinden. Tijdschrift voor Onderwijsresearch, 5, 49-62. html
Dit artikel is een aanloop naar het vervolgartikel. Het schetst wat de besliskundige benadering inhoudt. Ik moet het nog eens opnieuw bestuderen. Let op figuur 4a: hier is de oorsprong te zien van het denken in terecht en onterecht afgewezen of toegelaten kandidaten. Die redenering deugt niet vanzelfsprekend in gevallen waarin het niet echt gaat om een categoriaal verschil dat moet worden voorspeld, zoals geslacht man/vrouw, sluit de opleiding af met een diploma ja/nee. Ook veel psychologen die denken dat een formele analyse van een selectiesituatie toch niet zo moeilijk kan zijn, weten deze valkuil niet te ontwijken. In mijn eigen geschriften uit de zeventiger jaren heb ik de fout ook regelmatig gemaakt, als ik het goed heb.
Kim Dirkx (2014). Putting the Testing-effect to the Test. Why and When is Testing Effective for Learning in Secondary School? Proefschrift Open Universiteit persbericht
Het belang van dit onderzoek voor de thematiek van compensatoire examenregelingen is een beetje zijdelings, maar het is er wel: tussentijds toetsen levert op zich al leerwinst op, wat wijst in de richting van mogelijke winst in termen van doelmatigheid. Dat zoeken we nog wel verder uit. Promotie in april. Ik zie op internet geen online-versie van het proefschrift. Via Google Scholar "Kim Dirkx" evenmin. Nog maar even geduld dan.
Francis Y. Edgeworth (1888). The statistics of examinations. Journal of the Royal Statistical Society, 51, 599-635. [JSTOR has the pdf]
An authorized summary of this and a second article is published in the little book by P. J. Hartog (1918). Examinations and their relation to culture and efficiency. London: Constable. pdf scan of book
Een grondlegger (profile) van de statistiek (history of statistics) legt hier uit dat examens in behoorlijke mate toevallige uitkomsten geven, en hoe daar verstandig mee om te gaan.
p. 626:
(wat me onmiddellijk nieuwsgierig maakt naar die oude methode en wanneer en waar die werd gebruikt, maar daar zwijgt Edgeworth over). Zie ook (opvragen UB UvA) 'The element of chance in competitive examinations', Journal of the Royal Statistical Society, 53, (1890), pp. 460-75, 644-63. http://www.jstor.org/stable/2979547?seq=1#page_scan_tab_contents JStor read online free
Ben Wilbrink (1979). Universitaire examenregeling: conjunctief of compensatorisch. Onderwijs Research Dagen 1979, in K. D. Thio & P. Weeda (Red.), Examenproblematiek, p. 29-43. ORD bundel. Den Haag: SVO. webpagina
Inge Rekveld (1994). Een examenregeling zonder compensatie in het Nederlandse hoger onderwijs? Een vergelijking tussen compensatie en conjunctie. [Heymans Bulletins, HB-94-1150-SW, met bijlagen, o.a. opmerkingen van expert-panelleden Hofstee, de Gruijter, Cohen-Schotanus en Wilbrink] Tijdschrift voor het Hoger Onderwijs, 12, 210-219. [niet online beschikbaar]
Ben Wilbrink (1980). Beleid bij tentamens en examens. voordracht Nationaal Congres T.U. Eindhoven in A. I. Vroeijenstijn (Red.): Kwaliteitsverbetering hoger onderwijs. Vierde nationaal congres onderzoek van het wetenschappelijk onderwijs. Voorburg: Stichting Nationaal Congres, 380-409. webpagina
Ben Wilbrink (1992). The first year examination as negotiation; An application of Coleman's (1990) social system theory to law education data. In Tj. Plomp, J. M. Pieters & A. Feteris (Eds.), European Conference on Educational Research (pp. 1149-1152). Enschede: University of Twente. webpagina
Dit is een werkelijk spectaculair paper, dat het wegens druk, druk, druk, niet heeft gehaald tot een publicatie in een internationaal toptijdschrift. Op een interessante dataset verzameld in de propedeuse rechten aan de UvA in een reeks van jaren, is de sociale systeemtheorie van James Coleman toegepast. Dat leverde een MMMT-matrix op met dermate hoge coëfficiënten dat daar het eerder gebruikte ‘spectaculair’ door wordt gerechtvaardigd. Dat betekent in concreto dat dit casus het mogelijk maakt een aantal speculaties over wat er gebeurt in de loop van een typisch propedeusejaar aan een Nederlandse universiteit, de grond in te boren. Nou ja, ze te ontkrachten. Het idee dat er sprake is van een impliciete collectieve onderhandeling tussen studenten enerzijds, en docenten anderzijds, is een levensgrote waarschuwing om bij ingrepen in de examenregeling niet uit te gaan van logisch lijkende redeneringen, maar gebruik te maken van wat uit de gedragswetenschappen bekend is dat er kan gaan gebeuren.
We zouden het bijna vergeten, maar de huidige belangstelling voor compensatorische regelingen komt voort uit de bij convenant afgedwongen noodzaak voor de onderwijsinstellingen om hun numerieke rendementen te ‘verbeteren’. De aanhalingstekens geven aan dat het nog maar de vraag is of verhoging van numeriek rendement altijd wel een verbetering is. Het streven om numerieke rendementen in de greep te krijgen is al oud. Laten we eens zien.
Houd in de gaten dat numeriek rendement nogal verschillende betekenissen kan hebben, bijvoorbeeld al naar gelang de nadruk ligt op het behalen van het betreffende examen (of juist niet), of de tijd die voor dat behalen nodig is.
Numeriek rendement is een statistische grootheid, die niet alleen afhangt van de kwaliteit van het databestand dat aan de berekening ten grondslag ligt, maar die bovendien kan verduisteren dat studenten die voor deze opleiding onderwijskunde lijken te falen, zich ook kunnen hebben ingeschreven (gelijktijdig, of volgtijdelijk) voor een opleiding wiskunde waar ze schitterende resultaten boeken. Een aantal commissies en onderzoekers hebben zich in de loop van de tijd over deze thematieken gebogen, waarvan ik de mij goed bekende hier noem.
Commissie Studieduur van de Academische Raad (1964).
Willem Begeer (1968). Numeriek rendement. Het selectieproces in het wetenschappelijk onderwijs. (handelsuitgave van dissertatie bij J. Tinbergen) Wolters Noordhoff.
Merkwaardige studie, tikje losgezongen van wat in de selectiepsychologie gangbaar is. Tijdsbeeld. Raakt aan onderwerpen die van belang zijn bij de thematiek van compensatorische examenregelingen. Ontkomt niet aan de noodlottige constructie van ‘terecht voldoende’ gegeven enzovoort. Jammer dat Jan Tinbergen kennelijk niet op de hoogte was van de artikelen van Edgeworth over selectie via examens.
Wilbrink, B. Uitval en vertraging in het W.O.: een overschat probleem. Onderzoek van onderwijs, 1980, 9 nr. 4, 14-18. webpagina
Dit was een oefening in analyse van CBS-statistieken over numeriek rendement. Dan blijkt de werkelijkheid toch niet helemaal te sporen met de beeldvorming over enorme aantallen studenten die afhaken en misschien wel in de maatschappelijke goot belanden. Natuurlijk niet.
Willem K. B. Hofstee (1985). Notities over onderwijsrendement en -kwaliteit. Universiteit & Hogeschool, 32/3, 145-153.
Marjon Voorthuis & Ben Wilbrink (1987). Studielast, rendement en functies propedeuse. Relaties tussen wetgeving, theorie en empirie. Deelrapport 2: Evaluatie-onderzoek Wet Twee-fasenstructuur. Amsterdam: SCO-rapport 112. ISBN 90-6813-135-4. html
In opdracht van OCW. Hierin een hoofdstuk waarin de numerieke rendementen zoals afzonderlijke opleidingen die opgaven, kritisch tegen het licht zijn gehouden. Het probleem was niet alleen dat iedere opleiding weer net iets anders omging met wat precies de betekenis van numeriek rendement is, maar ook dat er sprake moest zijn van creatief boekhouden.
Ben Wilbrink, Uulkje de Jong en Marjon Voorthuis (1993). No-show en low-show in het wetenschappelijk onderwijs. Hoe beurs-, tempo- en keuzeproblemen leiden tot schijnbare afwezigheid. Amsterdam: SCO-Kohnstamm Instituut. (rapport 339) html of pdf [de pdf-versie is met uitvoerig notenapparaat]
Zoals een kritische analyse van studierendementen zoals door het CBS opgegeven al in 1980 uitwees, komen er in studentenadministraties allerlei vreemde vogels voor die daar eigenlijk niet (meer) in thuishoren. Een bijzonder fenomeen is dat studenten zich wel hebben opgegeven voor een bepaalde opleiding, bijvoorbeeld psychologie aan de Universiteit van Amsterdam, maar daar in feite aan geen enkel tentamen deelnemen, of misschien wel een enkele keer deelnemen en dan een laag cijfer boeken. Uulkje de Jong noemde dat fenomeen de ‘no-show-studenten’. Het CvB van de UvA wilde toch wel eens weten hoe dat dan precies zat met die no-show. Ook landelijk ontstond er enige ophef over, nadat minister-president Kok het fenomeen — volkomen ten onrechte, hij had daar gewoon de feiten niet voor laten controleren — studenten beschuldigde van massale fraude met studiefinanciering.
No-show is natuurlijk niet een fenomeen van de vroege negentiger jaren. Hoewel de studentenadministraties nu waarschijnlijk wat strakker zijn dan enkele decennia geleden, is het toch heel waarschijnlijk dat er in de administraties van afzonderlijke opleidingen nog steeds studenten voorkomen die in feite niet serieus met de betreffende studie bezig zijn, maar dus wel meegaan in de bepaling van het numeriek rendement van de opleiding.
Wat bleek bij zorgvuldig onderzoek van enkele opleidingsadministraties en achter no-show-studenten aan bellen: vrijwel heel de no-show heeft tamelijk gewone verklaringen, waarvan de meest eenvoudige was dat deze studenten zich voor twee opleidingen hadden ingeschreven en er al gauw achter kwamen dat die ambitie moeilijk was te handhaven.
Riekele J. Bijleveld (1993). Numeriek rendement en studiestaking. Utrecht: Lemma. Proefschrift.
Probleem met die proefschrift is dat het oppervlakkig blijft. Dat wreekt zich in de aanbevelingen die worden gedaan om numerieke rendementen te ‘verbeteren’: dat zijn precies het soort maatregelen dat bestuurders altijd al hebben bedacht en genomen — zonder resultaat. Er is dus meer aan de hand met die rendementen dan op het eerste gezicht blijkt.
Mark Adriaans, Gerard Baars, Henk van der Molen & Guus Smeets (2013). Betere studieresultaten dankzij 'Nominaal is normaal'. Thema, nr 1, 30-34.
Dit artikel geeft de resultaten van de nieuwe examenregeling (per september 2011) voor de opleiding psychologie aan de EUR. De auteurs zijn er buitengewoon tevreden over: "Er blijken nu meer studenten in één jaar alle studiepunten uit het eerste jaar te behalen dan voorheen in twee jaar." De geschetste examenregeling lijkt me prima: cluster van 8 toetsen, en 5 practica. Strikt beperkt aantal herkansingen van twee, voor deze 13 onderdelen samen. De te toetsen vakken/blokken zijn na elkaar geprogrammeerd, niet naast elkaar, zodat er een stevig tempo van toetsen is, van meet af aan. Daar komt bij: een BSA-regeling die voorschrijft dat alle 60 studiepunten van het eerste jaar ook in dat jaar behaald moeten zijn (hier is ondertussen door de rechter een streep door gehaald: een dergelijk BSA is geen advies meer, maar gewoon selectie). De eisen zijn verder: gemiddeld tenminste 6,0 voor ieder cluster. Dus volledige compensatie binnen ieder cluster, zij het dat cijfers < 4,5 moeten worden herkanst. Oké, slaagt er nog wel iemand, dan? Ja, de resultaten blijken heel goed te zijn. Het is geen gecontroleerd experiment, maar aangenomen dat docenten niet anders oordelen dan de jaren ervoor, presteert deze nieuwe examenregeling bijzonder goed.
Een enkele opmerking, niet als kritiek bedoeld.
Frans van Vught (vz.) (2 september 2014). Interventies uitval en rendement. Achtergronddocument. Reviewcommissie Hoger Onderwijs en Onderzoek. pdf
Ik ken deze commissie niet (zijn voorzitter wel), en ben dus wel benieuwd wat hier gebeurt. Frans stelt me niet meteen gerust, want ik lees toch in de eerste zin van zijn inleiding een kokervisie op alleen wat er in de eigen opleiding of instelling gebeurt. Immers, het is niet gezegd dat een strengere selectie aan de poort het rendement op landelijke schaal bezien verbetert: afgewezen kandidaten gaan immers een andere opleiding of dezelfde opleiding elders doen. Of selectie aan de poort gebeurt of in het eerste jaar van de opleiding door zelf-selectie: het is geen plaatsing in de meest belovende opleiding. ‘Meest belovend’ in de zin van toegevoegde waarde voor de kandidaat zelf zowel als voor de samenleving. Kortom, ik ga dit achtergronddocument met stevige achterdocht bestuderen.
de eerste zin uit de inleiding door Frans van Vught
Het is erg vervelend dat er geen auteurs van dit achtergronddocument zijn vermeld. Ik neem aan dat het niet het werk is van een of meer commissieleden. Maar wie heeft dit document dan opgesteld? Wie is intellectueel verantwoordelijk hiervoor? Of moeten we het alleen maar zien als de opbrengst van een zoekactie door een documentalist? Het geheel ziet er zeker uit als theorievrij googel-werk. Afijn, laat de tekst voor zich spreken. Iedere publicatie is gekenmerkt als ofwel experimenteel onderzoek, quasi-experimenteel of beschrijvend. Dat suggereert dat het een werkstuk van een onderzoeker is.
Het blijkt te gaan om door OCW gesubsidieerde proefprojecten of pilots, kennelijk in relatie tot de door Bussemaker genomen maatregelen die tot een circus van gesprekken en gedoe hebben geleid rond de overgang van vo naar ho. Kijk, dan ben ik meteen klaarwakker, want ik ben wel heel benieuwd naar de onderbouwing van dat beleid waarvan op basis van eeuwenoud onderzoek voorspelbaar is dat het vooral lasten en weinig lusten oplevert. De Inleiding beschrijft vier tenders: ik word er bij het lezen al moe van. Ik ga me beperken tot het afsluitende hoofdstuk van dit rapport. Houd in de gaten dat de Kohnstamm-onderzoekers een stuk schrijven aan de hand van toegeleverde administratieve gegevens. Zwakker kan het eigenlijk nauwelijks, maar we moeten het ermee doen.
Tevredenheid. Onderzoek naar tevredenheid van wie dan ook, levert altijd tevreden resultaten op. Natuurlijk denken alle gespreksdeelnemers dat die gesprekken zinvol zijn. Zo blijft het idee ook in de wereld. Het zegt niets over zin of onzin van die gesprekken, behalve of deelnemers vinden dat ze er een mooi moment in beleefden. Skip the crap.
Resultaten. Er staat fris en vrolijk dat de resultaten van de arrangementen zijn gemeten. Geloof er niets van. Er is sprake van experimentele en controlegroepen, blijkt hier ineens. Kunnen we daar greep op krijgen, zijn dat behoorlijk opgezette experimenten, dan? De auteurs wijzen er dan ook terecht op dat 'de resultaten' geen bewijskracht hebben, maar op zijn best aanwijzingen zijn, suggestief dus. Goed, dan kunnen we hier de bespreking van de OCW-SURF-projecten beëndigen. Lees dan toch nog even de paragraaf Onverwachte effecten, en zie hoe hier belangrijke vooroordelen over selectie (zoals ook te vinden in het rapport van de commissie-Veerman) worden bevestigd. En dat is niet zo vreemd, natuurlijk. Daarom is stevig onderzoek zo belangrijk: om deze vormen van zelfbedrog buiten de deur te houden.
Wie de moeite neemt om tussen de regels door te lezen, ziet dat de Kohnstamm-auteurs de boodschap proberen over te brengen dat het sop de kool niet waard is, maar dat niet hardop willen zeggen. Morgen moet er ook weer brood op de plank komen.
Laat ik dan maar helder zijn, en oud nieuws verkondigen: die intakegesprekken voegen niets toe, maar zijn wel enorm kostbaar en belastend. De middelen en tijd kunnen beter aan het onderwijs zelf worden besteed.
Klaas Visser, Han van der Maas, Marijke Engels-Freeke & Harrie Vorst (2012). Het effect op studiesucces van decentrale selectie middels proefstuderen aan de poort. pdf
Het stuk begint spannend. Mooi, ik ga het helemaal lezen. Het quasi-experimentele zit hem in de combinatie van via selectie (proefstuderen) toelaten van kandidaten met via loting toelaten van bij die selectoeprocedure afgevallen kandidaten. Daar zit iets in: immers, als dat proefstuderen niet voorspellend is voor studiesucces in het eerste studiejaar, dan doen beide groepen studenten het even goed of slecht in dat eerste jaar. Ha, tenzij er een magisch/placebo-effect is van het geselecteerd zijn dat ontbreekt bij inloten (de commissie-Veerman gelooft in dat effect). O ja: dat er een positief resultaat is van deze selectie hoeft niet te bevreemden, natuurlijk is dat er. De Leidse universiteit heeft geworsteld met dit fenomeen van positieve resultaten van selectie, terwijl toch de negatieve aspecten belangrijker blijken te zijn: het CvB besloot na commissiewerk en pilots om af te zien van de zo vurig gewenste selectie-aan-de-poort (De Gruyter en anderen; commissie-Van der Linden).
Opmerkelijk is dat het artikel geen melding maakt van direct tot de opleiding toegelaten studenten met een gemiddeld eindexamencijfer groter of gelijk aan acht. Ben ik nu in de war, heb ik ergens overheen gelezen, of trekken deze briljante scholieren allemaal naar prestigieuze opleidingen als geneeskunde, tandheelkunde en diergeneeskunde waar echt heel veel meer kandidaten dan plaatsen zijn?
Oké, ik heb het hele artikel gelezen. Ik zou er veel kanttekeningen bij kunnen maken, maar dat lijkt me niet geweldig vruchtbaar. Let op de allerlaatste alinea; ik had graag gezien dat het artikel in zijn geheel doortrokken was van de kritische geest die in deze laatste alinea in wat onhandige bewoordingen even opflikkert. In het bijzonder mis ik de waarschuwing dat hoge aantallen studiestakers bij psychologie aan de UvA niet betekenen dat deze studenten niet in staat zijn een opleiding in WO of HBO af te ronden. Dat inzicht moet vervolgens doorwerken in de manier van onderzoeken en de conclusies die uit het onderzoek vallen te trekken. Zeker van psychologen had ik dat verwacht. Ik geef een klein voorbeeld: het allereerste tentamen dat studenten afleggen heeft een hoge voorspellende waarde voor verder studiesucces, zeker. Maar hoe komt dat? Waarschijnlijk nemen er behoorlijk wat studenten aan deel die voor zichzelf al hebben besloten dat ze met deze studie niet door willen gaan. Onderzoek dat dan even, zou ik zeggen. Als vanzelf kom ik dan op het volgende thema: het zou zomaar kunnen zijn dat het veel belangrijker is dat studenten binnen een half jaar een snelle overstap kunnen maken naar een andere studie, dan een selectie-aan-de-poort op te tuigen. Een onderzoek naar effectiviteit van selectie zou je dus af moeten zetten tegen alternatieven (al bestaande, of mogelijke). Enzovoort. Een oude rot bedenkt ze achter elkaar. Maar ook enkele van de auteurs zijn oude rotten ;-).
Nu ik toch even bezig ben: het gegeven dat het gaat om het vullen van een numerus fixus is van groot belang. Vanuit opleidingsperspectief is dat immers een luxe positie. Daar valt in ethische zin het een en ander over te filosoferen, en dat zal ik hier niet doen. Het belangrijke punt is dat in situaties zonder numerus fixus, extra selectie-aan-de-poort leidt tot verminderde instroom, en voor de afgewezen kandidaten tot het ontnemen van kansen om succesvol te studeren. Voor het CvB van de Leidse universiteit waren dit uiteindelijk de redenen om af te zien van extra selectie-aan-de-poort, hoezeer ook in eerdere beleidsstukken gewenst en bepleit bij (destijds) staatssecretaris Nijssen.
Eigenlijk het enige interessante punt is dat proefstuderen minder arbeidsintensief is voor de opleiding. Daar staat dan weer tegenover dat het de kandidaten juist meer tijd kost. En natuurlijk dit: voorspellende waarde voor de opleiding zelf is interessant, maar waar het in deze wereld om hoort te gaan is voorspellende waarde voor een goede beroepsuitoefening. Hoewel dat laatste moeilijk onderzoekbaar is, valt wel te vermoeden en te beredeneren dat die voorspellende waarde dicht bij nihil ligt. Maar waar slaat dan dat krampachtige selecteren-aan-de-poort op? Op korte-termijn-voordeeltjes voor de opleiding? Bij zo’n fundamentele zaak als recht op onderwijs?
Moet ik hier in algemene zin nog iets over dat BSA (bindend studieadvies) zeggen? Het is een favoriet onder bestuurders. Een krachtdadige versie van de 'schriftelijke raad' uit begin tachtiger jaren (artikel 24bis van de WHW). Allemaal onzin, dus. Over die schriftelijke raad is het nodige op mijn website te vinden. Over BSA minder, dat is gewoon een idiote bureaucratische vorm van selectie, zou verboden moeten worden. Minachting van studenten, behandelt ze alsof het kleine kinderen zijn. En op een laffe manier, want anoniem.
Het zou overigens best kunnen dat BSA-regelingen in strijd zijn met artikel 1 van de Grondwet: ze scheren immers alle studenten over dezelfde kam, maar studenten zijn niet gelijk.
Comment on David Didau blog
On ‘False positives and negatives’: in the psychometric literature this kind of talk is the usual way of treating the ‘unreliability of decisions’. More often than not, it is not the correct analysis of pass-fail decisions. The curious fact is that Edgeworth already in 1888 gave a fine treatment of the fairness of selection decisions (civil service exams), especially around the cut-off point.
Francis Y. Edgeworth (1888). The statistics of examinations. Journal of the Royal Statistical Society, 51, 599-635. here
An authorized summary of this and a second article is published in the little book by P. J. Hartog (1918). Examinations and their relation to culture and efficiency. London: Constable. pdf
Talk of ‘false positives and negatives’ assumes a threshold utility function on the variable (mastery, IQ, whatever) tested for. That is an extremely crude model of the value mastery has (for the institution?), not fair at all, in my opinion. However, it is not at all clear what a reasonable utility function on mastery could be, in particular situations. It is possible to try out a few functions, and do some robustness analyses. There is a catch: it is important to distinguish between stakeholders. The party that is being served by psychometricians is the institution (teacher, school, boss, firm). In educational assessment, however, the primary stakeholder is the (individual) pupil. The pupil should be in a position to be able to adequately predict the result on the coming assessment, for example by getting an opportunity to sit a try-out or preliminary assessment. The utility structure of the assessment is radically different for ‘school’ and pupil (institutional versus individual decision-making, a distinction made by Cronbach & Gleser, see below). In my feeling talk about reliability and validity of assessment should recognize the difference. The Standards do so in a general way by emphasizing the uses to which test scores are to be put. Ultimately, adequate models have to be developed; an example is the work by Robert van Naerssen (his work on selection was mentioned in the 2nd edition of Cronbach & Gleser 1965 Psychological tests and personnel decisions.), extended by myself here Even a simple model is complex, illustrating how talking in a loose way about reliability and validity of assessment will not bring us very far in specific circumstances—especially so where politicians have to be convinced.
Niels Smits, Henk Kelderman & Jan Hoeksma (2015). Een vergelijking van compensatoir en conjunctief toetsen in het hoger onderwijs. Pedagogische Studien, 92, 275-285. preview
Ik zal een reactie voor Pedagogische Studiën schrijven. Het komt goed uit dat de auteurs in het slot van hun artikel aangeven in mijn lijn van analyse verder te willen. Dat wordt dus een win-win situatie voor de verdere discussie. Ik zal hierbeneden aantekeningen maken direct op de tekst van het artikel. Voor een reactie in Pedagogische Studiën werk ik dat netjes om naar een in algemenere termen gesteld betoog.
20 november 2015. Het is me niet gelukt om snel een stuk in elkaar te zetten: ik moet opnieuw in de literatuur duiken. Een paar maanden later lees ik Smits c.s. paragraaf 4 nog eens door, en dan denk ik mijn reactie op deze paragraaf toe te sptsen. Twee redenen daarvoor:
p. 275
Deze formulering miskent dat bij afzonderlijke toetsen de beoordeling eveneens compensatoir is: voor een ‘voldoende’ cijfer is het immers toegestaan een behoorlijk aantal fouten te maken, het maakt niet uit in welke opgaven dat is. Stel je voor dat je pas een ‘voldoende’ aftekening voor je toetst kunt krijgen bij een foutloos gemaakte herkansing! Het is van belang om met deze kritiek te beginnen, immers: wat is een examen anders dan een wat fors uitgevallen toets met een behoorlijk aantal verschillende onderdelen? Dat we ondertussen in het Nederlandse hoger onderwijs gewend zijn om examenonderdelen gespreid over de opleidingsduur af te nemen, doet daar niets wezenlijks aan af. Een examen is dus een lange toets, met het voordeel dat een lange toets heeft boven korte toetsen: het resultaat is beter voorspelbaar voor de studenten. Dat voorspelbaarheid iets anders is dan het psychometrische concept van betrouwbaarheid van examens, daar kom ik in het volgende nog uitvoerig op terug.
Hetzelfde punt is ook anders te formuleren: het gaat niet om een tegenstelling conjunctief-compensatoir, maar om de mate/kwaliteit van compensatie die de specifieke examenregeling biedt. De term ‘conjunctief’ is overbodig. Ik zal deze term dan ook zo weinig mogelijk gebruiken.
p. 275
Dat klopt (het gaat om de eindexamenregelingen): de kernvakkenregel staat nog maar weinig compensatie toe voor Nederlands, Engels en wiskunde op het centraal schriftelijk examen, en ook is er geen compensatie meer mogelijk tussen schoolonderzoek en centraal schriftelijk. Bij deze ministeriële regelgeving (De basis op orde, de lat omhoog) hebben stukken van de Onderwijsraad, Dronkers, en het Cito een rol gespeeld. De publicaties van het Cito (Van Rijn en anderen) zijn direct van belang voor de discussie over compensatoir toetsen, en ook door Smits c.s. gebruikt. Ik zal nog uitgebreid op die stukken ingaan.
De auteurs gaan uitleggen wat compensatoir toetsen inhoudt.
p. 275
Oké, dat is een mooi doel. Ik doe mee.
De definitie van compensatoir toetsen van Rekveld & Starren, 1994, is niet gelukkig. Ik weet nog niet of het een parafrase is, maar goed, hier is wat Smits c.s. ervan maken:
p. 275
We beschouwen de kwestie wetenschappelijk, dus laten we eerst deze ‘definitie’ bevrijden van taalgebruik met surplus-betekenissen. Wie zegt dat het over voldoendes en slagen gaat? Laten we het neutraal houden, en spreken over een beslissing, die overigens ook best gelijk kan zijn aan een al dan niet gewogen score. En waarom zou het een gemiddelde moeten zijn? Waar het om gaat is dat een combinatie van scores de grondslag vormt voor een beslissing. Maar dat is niet uniek voor compensatoir toetsen! Immers, ook in een concreet casus dat iedere toets afzonderlijk ‘voldoende’ moet zijn gemaakt is er sprake van een combinatie van scores. Ik gaf eerder al aan dat er geen noodzaak is voor gebruik van de term ‘conjunctief’.
De overkoepelende vraag is dus: wat is in een gegeven situatie een optimale combinatie van scores? Ofwel: wat is een optimale beslissing? En voor wie dan, voor welke actor(en) of belanghebbende(n). Herken dit als een besliskundige formulering van het combineerprobleem. Ik heb wel een neutraal voorbeeld: Een instelling hanteert verschillende instrumenten en methoden voor de selectie van nieuw personeel. De actor is de instelling. De vraag is: wat is, gegeven de kenmerken en onderlinge verbanden van de instrumenten, de combinatie van scores die een optimaal resultaat van de selectieprocedure oplevert? Voor een antwoord daarop, zie Wilbrink, 1990. En nee, niemand heeft mij de afgelopen jaren gevraagd om deze eenvoudige techniek eens uit te werken voor meer of minder compensatoir maken van examenregelingen.
Dat denken in termen van voldoendes en onvoldoendes zet ons voortdurend op het verkeerde been. Een voorbeeld is wat er gebeurt in het voortgezet onderwijs: sinds de invoering van de kernvakkenregel vertonen de gemiddelde cijfers voor wiskunde B vwo een stijgende lijn. Alleen cijferfetisjisten denken dat hier sprake moet zijn van een reële stijging van het prestatieniveau. Er zijn in het onderwijs altijd compenserende mechanismen (ja, zo heet dat!) die in werking treden zodra beleidsmakers weer eens iets nieuws hebben bedacht en ingevoerd, en ja, dat is op zijn minst al sinds de negentiende eeuw bekend bij onderwijsonderzoekers. Ik kom op dit fenomeen later nog terug, want het is allemaal leuk en aardig om over examenregelingen te keuvelen, maar uiteindelijk is er een benchmark nodig waar niet zo makkelijk mee valt te sjoemelen: tijdbesteding van de studenten. Als eerste begin dan, nietwaar?
De gebruikelijke manier van toetsen in het hoger onderwijs zou zijn dat examenonderdelen ‘voldoende’ moeten zijn om voor het examen te slagen (Smits c.s. p. 276). Dat is kort door de bocht: er zijn ongetwijfeld veel examenregelingen waarin vormen van compenserende combinaties voorkomen. Een bekend casus is door Janke Cohen-Schotanus in haar proefschrift (1994) beschreven (zie ook Wilbrink 1995; op de ORD 2015 heeft zij in een keynote daar een mooie en bijzonder leerzame update van gegeven; de video-opname is online beschikbaar. Onderzoek van Wilbrink 1992a in de propedeuse rechten aan de UvA is een ander casus dat publiekelijk beschikbaar is. En pro memorie dan: binnen ieder examenonderdeel is meestal volledige compensatie toegestaan: maximaal x gemiste punten, als daar maar tenminste N-x behaalde punten tegenover staan (N is het maximum aantal te behalen punten, zoals bijv gebruikelijk in schriftelijke eindexamens van het CvTE).
Dan lijken Smits c.s. aan te sluiten bij wat zij als een gewoonte zien: dat de grens voor voldoende beheersing van de stof vaak bij 55% zou liggen (p. 276); daar komt zelfs een verwijzing naar publicaties van De Gruijter en Mellenbergh bij, maar die zullen daar niet van wakker liggen. Smits c.s. nuanceren het later (ik kom daar nog op terug), en dat is maar goed ook, want dit is natuurlijk ergerlijke flauwekul. Bedenk zelf een paar redenen waarom dat zo moet zijn.
En daarmee ben ik aan het eind van sectie 2.
3. Is compensatoir toetsen betrouwbaar?
We doen het al sinds mensenheugenis, dus het zal wel. Toch? Afijn, hier komt het veel misbruikte begrip betrouwbaarheid aan de orde. Het wordt een interessante sectie.
Zodra het over toetsen gaat, begint iedereen ook over betrouwbaarheid, en dat is bij verandering van examenregelingen niet anders. Smits c.s. willen er daarom duidelijkheid over verschaffen.
p. 277
Maar hier wordt toch de ene verwarrende term door de andere vervangen—betrouwbaarheid door meetfouten, precisie, en beslisfouten—dat schiet niet op. Er zijn ernstige bezwaren aan te voeren tegen dit taalgebruik, dat overigens vrij algemeen wordt gebezigd in psychometrische kringen (ook in mijn eigen werk in de zeventiger jaren wel). Ik zal proberen die bezwaren glashelder uit te werken, gebaseerd op vooral Wilbrink 1980b (ja, ik ben gemeen: twee artikelen in 1980 bevatten alle informatie om miskleunen in latere jaren te voorkomen; maar iedereen heeft het druk met schrijven, aan lezen komen we niet meer toe ;-).
Laat ik eerst die malle meetfouten uit hun lijden verlossen. De suggestie die ervan uitgaat is dat een toets net zoiets is als een meetlat om lengte te bepalen: het aflezen van de lengte is niet oneindig nauwkeurig, en dat levert (meestal heel kleine) afwijkingen op. Een toets is evenwel niet een soort meetlat, maar iets volstrekt anders: een steekproef uit wat er over de stof kan worden gevraagd. Daarbij kunnen zich ook meetfouten voordoen, bijvoorbeeld omdat beoordelaars dezelfde antwoorden toch verschillend kunnen beoordelen, maar belangrijker is nu dat de ene steekproef een ander resultaat op zal leveren dan de andere (ook al zijn de verschillende steekproeven tau-equivalent, zoals Lord & Novick dat noemen). Een eenvoudig model daarvoor is: gegeven de ware beheersing van de kandidaat (neem dat nu maar even aan, for the sake of argument) is de score op een studietoets van n vragen binomiaal verdeeld. Smits c.s. weten dat ook, verwijzen naar het proefschrift van Wulfert van den Brink over binomiaalmodellen, maar maken er niet meteen mooi gebruik van. Dat binomiaalmodel is natuurlijk veel te eenvoudig, want niemand kent welke ware beheersing dan ook, maar het is een mooi begin. Zie ook Wilbrink SPA-project, dat op zijn beurt weer teruggaat op het tentamenmodel van Van Naerssen 1970. Begint u een beetje te zien hoe alles hier met alles verband houdt, en dat verhelderen van dat kader beslist noodzakelijk is? Wat zeggen Smits c.s. nu:
p. 277
Dit is een halve waarheid. Laten we eens de tentamenmodel-benadering volgen, en uitgaan van de strategische positie waarin de kandidaten zich bevinden voorafgaand aan de toets. Om zich te verzekeren van een voldoende resultaat op de toets, hoe goed voorbereid moeten zij dan zijn? En is het wel mogelijk om 100% zeker te zijn van een voldoende resultaat? Voor het beantwoorden van deze vragen is een complexer model nodig, dat wiskundig reduceert tot het in de literatuur goed bekende betabinomiaalmodel (Wilbrink_SPA-predictor dat ik voor de duidelijkheid meteen maar een voorspellende toetsscoreverdeling noem. Dan blijkt dat ‘in de buurt van de cesuurscore’ met enige korrels zout is te nemen.
Van Rijn c.s. p. 130
Is het bovenstaande citaat alleen maar slordigheid? Maar als het alleen maar slordigheid is, hoe slordig is de analyse van Van Rijn c.s. dan? Voordat er misverstanden rijzen: kandidaten met een score gelijk aan de cesuur kunnen niet fout worden geklassificeerd. Per definitie niet. Hier had voor Van Rijn c.s. en hun meelezers toch een batterij rode stoplichten moeten gaan branden. Heel dat begrip misklassificeren deugt niet in deze context. In de volgende sectie gaan Smits c.s. er op door. Ik sla de onduidelijke tekst over enkele simulatiestudies (p. 277-8) dan maar over.
4. Is een fout-negatief erger dan een fout-positief?
De titel is absoluut de verkeerde vraag, maar om dat helder te krijgen moet ik even stevig mijn best doen. Dit is besliskundig terrein, ook al benoemen Smits c.s. het hier niet zo. Deze sectie staat bol van slap geouwehoer over fout-negatief en fout-positief, daar is nou echt helemaal niets ‘wetenschappelijk’ aan terwijl de auteurs dat wel hebben beloofd. Kunnen we uit dit drijfzand geraken? Zeker wel.
Handig is om te beginnen met kandidaten die net onder danwel net boven de cesuur scoren: daar vallen dan verschillende beslissingen over terwijl niemand kan volhouden dat ze echt verschillende prestaties hebben geleverd. Adriaan de Groot (1972 Selektie voor en in het hoger onderwijs, als ik het goed heb, dat kijk ik nog na) vond dit dus helemaal niet zo fraai, maar slaagde er niet in om een rechtvaardiging te geven. Terwijl die rechtvaardiging echt iedere statisticus en zeker iedere psychometricus bekend hoort te zijn, want hij is op zijn minst al eind negentiende eeuw gegeven door Edgeworth. Ik geef de redenering kort weer. Die begint met de constatering dat iedere toets slechts een steekproef is, en die kan voor de kandidaat meer of minder gunstig uitvallen. Kwestie van toeval, dus. Een loterij eigenlijk (loting die is gewogen met de mate van stofbeheersing van de kandidaat, dat dan weer wel). Iedereen weet dat eigenlijk ook wel, ik vertel niets nieuws. Is het dan oneerlijk wanneer de ene kandidaat net slaagt, en een ander met slechts een enkel puntje minder zakt? Nee, want dit is een achteraf-redenering. De situatie moet in zijn strategische aspecten worden bekeken, zoals Smits c.s. uiteindelijk ook doen onder verwijzing naar het tentamenmodel van Van Naerssen 1970. De situatie vooraf is evident: een betere voorbereiding op de toets geeft een hogere kans om te slagen. Eerlijk genoeg? Nee, want zoals De Groot 1970 uitlegt is een extra voorwaarde dat de toets doeltreffend moet zijn voor te bereiden. Voor een psychologische test kan dat laatste dan weer niet, dan daar is dan de redenering dat wie betere capaciteiten heeft dan ook betere kansen heeft (om te worden aangenomen/toegelaten). Over dat belangrijke verschil tussen toetsen en testen, en welke consequenties dat heeft voor de methodologie van een en ander, zie ook Wilbrink 1986. Terug dan naar die fout-positieven/negatieven: in de buurt van de cesuur heeft het geen zin om in die termen te spreken over de genomen beslissingen. Oké, maar dan moet er dus een alternatieve methodiek of een alternatief model komen, laten we eens zien of dat inderdaad beschikbaar is.
De eerste stap op weg naar een alternatief model is: te laten zien hoe het model van fout-positief/negatief intern tegenstrijdig is. Het bewijs daarvoor is hopelijk tevens een constructief bewijs voor een beter model.
Ik wil hier dan een helder onderscheid maken tussen het perspectief van de studenten en dat van de instelling; Smits c.s. maken het onderscheid ook, maar op een te vluchtige wijze. Ik neem eerst de individuele beslisser: de student die zich gaat voorbereiden op de toets. Het mooie van deze sitatie is dat er voor de student een objectieve nutsfunctie over toetsscores is te construeren, gegeven de precieze regeling die voor de examens geldt (zie ook de figuur verder hierbeneden). Een en ander is zorgvuldig uitgewerkt te vinden in mijn The Ruling: How the result will count (his master's voice). Module four of the SPA model: Utility functions (first generation). webpagina. Lezen die tekst, want ik ga hem hier echt niet nog eens overschrijven. De oplettende lezer zal opmerken dat aan de wens van Smits c.s. (laatste zin van het artikel) al ruimschoots is voldaan ;-)
Wait a minute. Lees The Ruling toch nog maar niet: al die bomen vergroten de kans het bos niet meer te zien. Dat is in de kern ook het probleem met examenregelingen: dat is een zo complex onderwerp dat maar weinigen in staat zijn er echt iets zinnigs over te zeggen. Tot die weinigen behoren Willem Hofstee en de door hem op het goede spoor gezette Janke Cohen-Schotanus (echt even de moeite nemen haar keynote ORD 2015 te zien en horen!). Ik zal dus proberen nu in een paar zinnen/alinea’s duidelijk te maken wat het probleem is met de benaderring van Smits c.s. over de boeg van fout-negatieve/positieve gevallen. Nog even geduld, ik moet de theorie ook weer even boven water halen ;-)
Wat het erg lastig maakt, ook voor een oude rot (mijn eerste publikatie is 1977, en jawel: met enkele misvattingen die ik hier nu juist aan de orde stel): er spelen meerdere fundamentele misverstanden tegelijk. Ik zal dan toch proberen ze stuk voor stuk te behandelen, in hopelijk een handige volgorde:
25 augustus 2015. Ik heb de uitwerking van een en ander een tijdje laten liggen, omdat het toch veel en veel lastiger bleek dan ik in mijn eerste optimisme dacht. Ik schets opnieuw een grote lijn, hopelijk is dat het bos, en niet een opeenstapeling van gekapt hout.
Het probleem (combineren van toetsresulaten tot examenuitslag) laat zich mogelijk het best behandelen in de vorm van een stapelende opbouw van argumenten. Ik wil dan inderdaad beginnen met het eenvoudige model van een enkele toets waarop studenten slagen of zakken, en eindigen met een methodiek voor het vinden van redelijk optimale combinaties van toetsresultaten tot examenuitslagen. Daar zitten een behoorlijk aantal stappen tussen, en ieder van die stappen is bovendien allesbehalve vanzelfsprekend (want in tegenspraak met wat in de testliteratuur als de geaccepteerde visie geldt). Smits c.s. zitten stevig in de hoek van de received view, dan moet het lukken om het contrast goed uit te werken.
Laat ik beginnen met het drempelnutmodel zoals dat typisch in de literatuur, en bij Smits c.s. is te vinden. Dat model kent een aantal problemen die zich prima laten oplossen, ook onder de veronderstelling dat de belanghebbende bij het optimaliseren niet de student, maar de docent is. Niet de studenten, maar de instelling. Dat Smits c.s. werken met een nutsfunctie over ware beheersing van de stof is niet echt handig, maar voor een modelmatige uitwerking geen beletsel. Wat echt wel een probleem is: modelleren in termen van terechte/onterechte beslissingen. Ik zal aan de hand van een alternatief model laten zien dat het zonder deze onhandigheden kan. (Want onhandigheden zijn het: de terechte vraag is immers hoe valt te rechtvaardigen dat de ene student slaagt, de andere zakt, terwijl ze vrijwel dezelfde totaalscore hebben. En zoiets valt niet uit te leggen, zoals A. D. de Groot (1972) zich realiseerde, zonder het probleem op te kunnen lossen.)
De onmacht van het drempelnutmodel bij Smits c.s. zit hem hierin dat het criterium voor optimaliteit gezocht wordt in een kluwen van subjectieve inschattingen rond de betreffende toets zelf (waar ligt de cesuur in de ‘ware beheersing’, hoe ‘erg’ is een onterechte voldoende t.o.v. een onterechte onvoldoende, het moeten herkansen buiten het model zelf laten).
De koninklijke weg is om beheersing van de stof tot doelvariabele te nemen, en over die beheersing een (overal stijgende) nutsfunctie f(u) aan te nemen (en eventueel concreet te bepalen).
Neem ten behoeve van het model aan dat gezakte studenten later voor een nieuwe afname op moeten komen, en dat dat de enige herkansing is. Merk nu al vast op dat de consequenties van zakken voor beide toetsen afhangen van de aard van de examenregeling: die consequenties zijn contingent. Ik kom er later op terug, uiteraard.
Zoals in andere situaties van testgebruik is het ook hier wenselijk om een onderzoek naar validiteit te doen. Dat wordt lastig, want cruciaal is dat de student die bij de eerste gelegenheid zakt, dat ook meegedeeld krijgt. Het liefst zouden we immers voor een validiteitsonderzoek de situatie hebben dat na de eerste afname alle studenten te horen krijgen dat ze deel moeten nemen aan de tweede toetsgelegenheid. Een rare situatie? Het komt wel eens voor dat voor groepen examinandi een onderdeel ongeldig wordt verklaard, en dat iedereen het—jammer maar helaas— over moet doen. Als deze examinandi hun resultaat op de eerste toets kennen, hebben ze dus de gelegenheid zich te verbeteren door een extra studie-inspanning. Afijn, ons denkbeeldige valideringsonderzoek levert dus twee sets van toetsscores op. De vraag is nu: hoe volgt daaruit op welk punt de zak-slaaggrens op de beide toetsen (of op zijn minst op de eerste toets) optimaal is? Wat optimaal is, hangt af van het verwachte nut, en dat krijgen we in handen op basis van de nutsfunctie over ware beheersing en een geschikt statistisch model. Dat statistisch model kan eenvoudig beperkt zijn tot de verzamelde empirische data: een plot van de score op de eerste versus die op de tweede toets, voor alle deelnemers. Ruwe data zijn vaak wel erg ruw, misschien is het inzichtelijker wanneer de ruwe data worden vereffend (verschillende vereffeningstechnieken zijn daarvoor beschikbaar [Kolen], of statistische modellen [betabinomiaalmodel bijvoorbeeld]).
Wat het valideringsonderzoek concreet oplevert is voor iedere score X op de eerste toets een verdeling van scores op de tweede toets. Stel dat de toetsen 50 items hebben, kijk dan voor de studenten die 40 goed scoren op de eerste toets, naar de scores die zij op de tweede toets boeken. Zouden we onze nutsfunctie niet over de ware beheersing, maar over de behaalde scores hebben genomen, dan zou het verwachte nut bij herkansen van deze groep met X1=40 gelijk zijn aan de som over alle scores op de tweede toets van frequentie keer nut van de betreffende score. Idem voor de studenten die op de eerste toets X1=41 scoren; voor deze groep is het verwachte nut waarschijnlijk iets groter. Doe deze oefening voor alle scores op de eerste toets, en plot de resultaten.

Het resultaat is een geleidelijk sterker stijgende en dan afnemend stijgende functie. (Voor de hoogst scorenden op toets 1 geldt waarschijnlijk dat zij gemiddeld slechter scoren op toets 2 [regressie naar het midden], een kniesoor die daar op let ;-) (Strict genomen gaat het bij toetsscores zelf niet om verwacht nut, maar is het gerealiseerd nut; de verwachting zit hem als het ware hierin: dat andere groepen studenten het ongeveer gelijk zullen doen) (Aha, het laatste alleen wanneer overige omstandigheden gelijk blijven, dus de examenregeling niet verandert).
Waar komt nu de optimale cesuur te liggen? Dat is nog steeds knap lastig, maar er is een satisficing (Herbert A. Simon) oplossing mogelijk: leg de zak-slaaggrens bij score X=c waar het verwachte nut minder sterk stijgt dan bij de score X=c-1.
Als dit experiment uitkomt bij een cesuur zoals die toch al werd gehanteerd, dan weten we nu dat dat een redelijk optimale cesuur is. Is het echt een andere cesuur, dan krijgen we een beleidswijziging, gaan studenten zich anders gedragen, en moeten we het valideringsexperiment onder de gewijzigde omstandigheden overdoen. Enzovoort. Maar goed, maak er niet al te veel drukte over, kies een redelijke oplossing.
Wat hebben we nu bereikt? Een oplossing, binnen de gedane aannames, waaraan geen speculaties over een ‘ware’ cesuur ten grondslag liggen, noch over terechte/onterechte beslissingen en hoe erg die in onderlinge verhouding zijn. Het gedachtenexperiment is gedaan met waargenomen scores, maar het is niet echt lastig om het model uit te breiden naar ware beheersing en nut over ware beheersing. Met dat laatste winnen we overigens niets, want ware beheersing is een platonisch concept: het model wordt er vooral onbegrijpelijker mee. Dat wordt des te duidelijker wanneer de student zelf in beeld komt als de primaire beslisser, de strateeg over de eigen investering in de voorbereiding op de toets (tentamenmodel van Van Naerssen, 1970): de beloning voor de student is immers niet allereerst zijn ware beheersing van de stof, maar het cijfer dat hij of zij scoort, slagen of zakken, en de nutsfunctie over die doelvariabele (SPA-model module True utility: What the result is worth (the student's calculation)).
Ik denk dat de eerste bouwsteen hiermee is gelegd. Wie het model te eenvoudig vindt: groot gelijk, we gaan het ingewikkelder maken. Bovenstaand gedachtenexperimentje heeft natuurlijk een aantal problematische aspecten die in de weg staan om het te vertalen naar beleidsopties. Het is ook te formalistisch, in de zin dat de inhoud van het betreffende vak en het domein van de toetsvragen geheel buiten beschouwing is gelaten. Maar het is evident het geval dat vakken onderling (sterk) verschillen in de aard van de stof, de wijze waarop deze geleerd en beheerst moet worden, etcetra. Maar dat zijn voor beslsikundige cesuurbepaling geen onbelangrijke zaken! Voor het rekenonderwijs, bijvoorbeeld, zou het onderwijsdoel tenminste een geautomatiseerde beheersing van de elementaire bewerkingen op gehele, gebroken en decimale getallen moeten zijn. Rekening houdend met onvermijdelijke vergissinkjes zou op een dergelijk onderdeel een beheersing van rond de 90% een redelijk niveau van gevraagde beheersing zijn, de nutsfunctie over beheersing zou op zichzelf dan een ogief zijn die erg veel wegheeft van de afbeelding hierboven. Voor wat ingewikkelder rekenopgaven volstaat een eenvoudig model (zoals Wilbrink 1998) om een redelijk niveau van beheersing te bepalen. Etcetera. Allerlei kwesties rond examineren hebben juist te maken met merkwaardigheden die tot de traditie zijn gaan behoren, en die we beter vandaag dan morgen uit onze examens kunnen slopen. Een belangrijk probleem in die categorie is het speeltje van psychometrici: dat tentamenvragen vooral niet makkelijk moeten zijn; wat is dat voor onzin, hoe kun je zoiets in ernst voorstellen zonder de te toetsen stof te kennen? Afijn, lees eens de klassieker van De Groot en Van Naerssen uit 1969 over studietoetsen, en zie hoe zij op dat moment niet in staat zijn wetenschap en ideologie gescheiden te houden.
Ik ga even door op dat rekentoetsje dat is gericht op toetsen van mate waarin het basale rekenen is geautomatiseerd en dus heel snel gaat. Met als nutsfunctie over de schaal van beheersing zo’n ogief die zijn steilste helling heeft ergens tussen .8 en .9. Laten we zeggen dat er voor dit toetsje één herkansing is. Voor die herkansing is de nutsfunctie? Precies, het gaat om dezelfde rekenvaardigheid, de nutsfunctie is dus dezelfde. Laten we in ons gedachtenexperiment aannemen dat alle leerlingen ook de herkansing doen, bijvoorbeeld onder de conditie dat het hoogste behaalde resultaat zal gelden. Het experiment levert twee sets van rekenscores op. Aha, dan kunnen we dus voor iedere score op de eerste afname voor de betreffende deelnemers het verwachte, sorry: behaalde nut op de herkansing bepalen: de som over alle mogelijke scores op de herkansing van frequentie keer nut. En een plotje maken. Statistisch gezien is voor alle deelnemers de verwachting dat zij zich met die herkansing zullen verbeteren, maar niet alle verbeteringen zijn groot genoeg om die herkansing de moeite waarde te maken. Waar trekken we dan de grens? Moeten we niet tevens weten hoe groot die verbeteringen zijn t.o.v. de eerste afname? Maak dan voor de eerste afname eveneens een plot van frequentie keer nut voor alle scores. Afijn, dit is allemaal behandeld in Wilbrink 1980b, met correctie op de destijds gemaakte fouten wat betreft in rekening te brengen kosten (aantekening 7 augustus 2015 op die webpagina). Geruststellend: ik heb hier zojuist herontdekt wat op 7 augustus al noteerde.
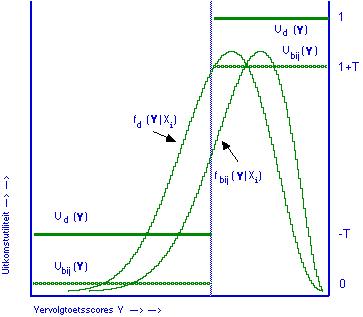
Thea van Lankveld & Silvester Draaijer (2010). Compensatorisch toetsen. (intern document).
Genoemd in Smits, Kelderman & Hoeksma.
Task Force Studiesucces (2009). Studiesucces: Rapport van de task force studiesucces. RU Leiden pdf ophalen
Genoemd in Smits, Kelderman & Hoeksma.
Werkgroep Studiesucces (2009). Studiesucces aan de Universiteit van Amsterdam. Universitaire Commissie Onderwijs. pdf
Genoemd in Smits, Kelderman & Hoeksma.
H. Adriaens (2010). Het ontstaan en de implementatie van het leerkrediet in het Vlaamse hoger onderwijs. Masterthese, U van Antwerpen.
Genoemd in Smits, Kelderman & Hoeksma. Vindbaar in Google, maar alleen via de cache binnen te halen.
Dato N. M. de Gruijter (2008). Al dan geen compensatie in de propedeuse. pdf
Genoemd in Smits, Kelderman & Hoeksma.
Rutger Bregman (12 juli 2013). Plofstudenten. De Volkskrant. webpagina
Genoemd in Smits, Kelderman & Hoeksma. Ik mag Rutger wel, maar dan weer niet hoe hij in dit stukje te keer gaat. Grappig blijft het. Jammer is dat hij compensatie zelf belachelijk maakt, in plaats van zich te concentreren op wat er zoal scheef kan gaan lopen (en dat kan, natuurlijk).
Ivo J. M. Arnold & W. A. van den Brink (). Onrust over diploma halen met onvoldoendes onterecht. De Volkskrant webpagina
Genoemd in Smits, Kelderman & Hoeksma.
Maartje Bakker (30 januari 2012). Vijven, en toch een UvA-diploma. De Volkskrant webpagina
Genoemd in Smits, Kelderman & Hoeksma.
Eline Peters & Joost Verhoeks (7 februari 2012). Met compensatie onvoldoende begint verschraling hoger onderwijs. De Volkskrant
Genoemd in Smits, Kelderman & Hoeksma.
Ben Wilbrink (1977). Cesuurbepaling. Uitgave in de serie docentenkursussen van het Centrum voor Onderzoek van het Wetenschappelijk Onderwijs van de Universiteit van Amsterdam. Kursus 6. webpagina
Ben Wilbrink (1978). Studiestrategieën en examenregeling.. Uitgave in de serie docentenkursussen van het Centrum voor Onderzoek van het Wetenschappelijk Onderwijs van de Universiteit van Amsterdam. Kursus 9. webpagina
Ben Wilbrink (1979). Universitaire examenregeling: conjunctief of compensatorisch. Onderwijs Research Dagen 1979, in K. D. Thio & P. Weeda (Red.), Examenproblematiek, p. 29-43. ORD bundel. Den Haag: SVO.
Genoemd in Smits, Kelderman & Hoeksma, als bron voor de definitie van conjunctief toetsen! In feite is het de presentate van een wiskundig model voor het combineren van examenonderdelen, geïnspireerd op het tentamenmodel van Van Naerssen_1970. Sindsdien is daar overigens nog wel het een en ander aan verscherpt.
Ben Wilbrink (1995). Studiestrategieën die voor studenten en docenten optimaal zijn: het sturen van investeringen in de studie. Korte versie in Bert Creemers e.a. (Red.), Onderwijsonderzoek in Nederland en Vlaanderen 1995. Proceedings van de Onderwijs Research Dagen 1995 te Groningen (218-220). Groningen: GION. html
Genoemd in Smits, Kelderman & Hoeksma. Zij verwijzen naar de in 1995 gepubliceerde samenvatting; op mijn website staat eveneens de tekst van het paper zelf, in de loop van de jaren aangevuld met nieuw verschenen relevante literatuur. Mijn oorspronkelijke analyse in 1995 bevatte de nodige missers, die ondertussen zijn hersteld (ik heb een en ander in de tekst zelf aangegeven, zodat duidelijk is wat de oorspronkelijke misvattingen waren, en hoe die zijn gecorrigeerd). Een uitvoeriger behandeling van de betreffende theorie is in het Engels gegeven in het spa_project.htm, in het bijzonder in de delen 4, 9 en 10 daarvan (het werk aan dat project is in 2005 onderbroken, en moet ooit verder worden voortgezet).
Robert F. van Naerssen (1970). Over optimaal studeren en tentamens combineren. webpagina
Genoemd in Smits, Kelderman & Hoeksma. Mogelijk is dit de eerste publicatie over het combineren van examenonderdelen binnen eenzelfde examenregeling.
P. W. van Rijn, Anton Béguin & Huub H. F. M. Verstralen (2012). Educational measurement issues and implications of high stakes decision making in final examinations in secondary education in the Netherlands. Assessment in Education: Principles, Policy & Practice, 19, 117-136. abstract researchgate.net. [I have requested the test again (foutje)]
Genoemd in Smits, Kelderman & Hoeksma.Dit artikel verwijst niet naar eerdere kritiek op Van Rijn, Béguin & Verstralen, 2009; het Cito luistert slecht of helemaal niet naar kritische geluiden, en prefereert om eerder Nederlands werk (niet door het Cito) niet te kennen (hoewel Huub Verstralen er perfect van op de hoogte is).] [Misschien moet ik dan ook op dit artikel maar eens een reactie schrijven. Maar eerst Smits c.s. annoteren]
W. P. van den Brink & G.J. Mellenbergh (Red.) (2006 3e). Testleer en testconstructie. Boom. hr>
Smits c.s. verwijzen naar de editie van 1998, blz. 401 (zakken/slagen voor een toets betreft een beheersingssituatie) (ik zie zo gauw niet waar in hoofdstuk 12 2006 dat dan precies is, nog steeds blz. 401? Maar daar staat geen uitwerking.). En 19-20 (criterium-gerefererd toetsen).
Als we de hierbeneden geciteerde beschrijving volgen, dan hebben Smits c.s. geen zaak, want iedere vorm van combinatie met andere toetsen is hier buiten haken geplaatst, ook de conjunctieve combinatie is hier niet aan de orde. In splendig isolation wordt hier maar waar wat aangerotzooid, dus. Maar dat kan niet waar zijn. En dat is het natuurlijk ook niet, omdat er consequenties zijn in het vervolg van de opleiding. Dan is het toch wel droevig dat Van den Brink en Mellenbergh hun te smalle beschrijving laten bungelen, door er geen verdere modelmatige uitwerking aan te geven.
Ben Wilbrink (1980b). Enkele radicale oplossingen voor kriterium-gerefereerde grensskores. Tijdschrift voor Onderwijsresearch, 5, 112-125. webpagina
Uit dit artikel is van belang dat er een principieel volledige methode wordt gegeven voor het bepalen van zak-slaaggrenzen bij bijvoorbeeld examenonderdelen, gesteld dat de examenregeling dergelijke grenzen voorschrijft dan. Daarbij is ook van belang dat de hier geschetste besliskundige methode niet opgevat kan worden als een verfijning van de vaak gehanteerde ‘drempelverlies-methode’ (bijvoorbeeld in het proefschrift van Van der Gaag, en publicaties van de groep van Wim van der Linden in Twente): die laatste methode is gewoon fout, en levert misleidende resultaten (zoals twee proefpersonen van Van der Gaag al vermoedden . . . ).
Ben Wilbrink (1992a). Modeling the connection between individual behaviour and macro-level outputs. In Tj. Plomp, J. M. Pieters & A. Feteris (Eds.), European Conference on Educational Research (pp. pp. 701-704.). Enschede: University of Twente. pagina
Het lijkt er sterk op dat ik in dit paper de compensatiemogelijkheden juist buiten beschouwing heb gelaten. Er zijn twee clusters van vakken waarbinnen een bescheiden vorm van compensatie is toegestaan (tegenover een vijf moet dan minstens een zeven staan). Afijn, ik heb dit paper nog wel nodig bij mijn aantekeningen bij Smits c.s.
N. van der Gaag (1990). Empirische utiliteiten voor psychometrische beslissingen. Proefschrift Universiteit van Amsterdam.
Er is geen versie online beschikbaar van dit proefschrift. Het is wel een document van enig belang, omdat een aantal misvattingen die in 1980 al bekend waren, er toch in terugkomen, inclusief de misvatting dat voor optimale cesuurbepaling de cesuur op de onderliggende ware scores gegeven zou moeten zijn. En zo kunnen de misvattingen voortleven, ook in op Van de Gaag volgende publicaties uit Twente (zoals die van Hans Vos). Zie voor annotaties toetsen.htm#Gaag_1990
Janke Cohen-Schotanus (1994). Effecten van curriculumveranderingen. Studiewaardering, studeergedrag, kennis, studiedoorstroom in een veranderend medisch curriculum. Proefschrift, Rijksuniversiteit Groningen. samenvatting
Janke Cohen-Schotanus (19 juni 2015). Maatregelen ter verbetering van het rendement in het Hoger Onderwijs: waar is de evidentie? Keynote OnderwijsResearchDagen 2015 Leiden. keynote en powerpoint
Edward G. Rozycki (2008). Classification Error in Evaluation Practice: the impact of the "false positive" on educational practice and policy. Educational Horizons webpage
Werts, Rock, Linn, & Jöreskog, A general method of estimating the reliability of a composite. EPM 1978, 38, 933-938. abstract
Pieter J. D. Drenth (1975/1980). Inleiding in de testtheorie. Deventer: Van Loghum Slaterus. isbn 9060014685
Hierin Hoofdstuk 7 De bijdrage van de test in het beslissingsproces. Drenth spreekt over treffers en missers in het selectieproces. Dat zullen Taylor & Russell ook wel zo hebben gedaan.
Linden, W. J. van der, & Vos, H. J. (1996). A compensatory approach to optimal selection with mastery scores. Psychometrika, 61, 155-172. pdf
p. 155
Hier zitten twee belangrjke vooronderstellingen in: (1) met onderwijs heeft dit alles niets van doen, dus ook niet met de manier waarop lerlingen zich op beslissingen voorbereiden, en (2) er moet nog steeds een standaard worden aangewezen op een onderliggende schaal van ware scores!
p. 155
Goed, het lijkt me sterk dat 1973 het ontdekkingsjaar was, maar ongetwijfeld binnen een nauw opgevatte onderzoektradditie zal dat wel ongeveer kloppen. ‘Nauw’ is dan: Bayesian decision theory, in plaats van gewoon de besliskunde. Ik maak me sterk dat de besliskunde in zijn algemeenheeid, of laten we zeggen in zijn Von Neumann & Morgenstern gedaante, niets met Bayes heeft te maken.
Huynh Huynh (1982). A Bayesian procedure for mastery decisions based on multivariate normal test data. Psychometrika, 47: 309. abstract
Cronbach & Gleser (1965: 50)
p. 50
165
Dato N.M. de Gruijter & Ronald K. Hambleton (1984). On Problems Encountered Using Decision Theory to Set Cutoff Scores Applied Psychological Measurement, 8, 1-8. [hardcopy] abstract
Exercises in reliability, again? It seems so.
Bastiaan J. Vrijhof, Gideon J. Mellenbergh & Wulfert P. van den Brink (1983). Assessing and Studying Utility Functions in Psychometric Decision Theory. Applied Psychological Measurement, 7, 341-357. abstract
Saskia Wools, Theo J.H.M. Eggen & Anton A. Béguin (2015). Constructing validity arguments for test combinations. Studies in Educational Evaluation, 48, 10-18. paywalled [on research.net]
Henry L. Roediger, III, and Jeffrey D. Karpicke (2006). Test-Enhanced Learning. Taking Memory Tests Improves Long-Term Retention. Psychological Scienve, 17, 249-255. [testing-effect, mock exams proeftoets] pdf
Nicole Goossens (2015). Distributed Practice and Retrieval Practice in Primary School Vocabulary Learning. Dissertation Erasmus University Rotterdam. pdf download
Ad de Jongh Bespreekt Smits, Kelderman & Hoeksma EXAMENS - november 2015 - NR 4 blz. 41
“Het BSA is op zijn hoogst een lapmiddel” Bescheiden positief effect van BSA op studierendement in Nederland. Interview | de redactie 19 december 2017 | “Het positieve effect van het BSA is dat er op de 100 studenten zo’n zes tot zeven studenten meer binnen de norm afstuderen.” Eline Sneyers deed onderzoek naar verschillende maatregelen in het hoger onderwijs die de efficiëntie en het studiesucces moesten verbeteren. bericht
Sicco de Knecht (26 sept 2018). Wat doen studenten die een negatief bsa krijgen? Ze gaan dezelfde studie elders doen . . . tweet
Ik kijk er niet van op ;-) Dat BSA is goed voorbeeld van beleidsdrukte. Per saldo levert beleidsdrukte negatieve resultaten (want: extra kosten voor een of meer partijen). Probleempje bij dit onderzoek: het kijkt alleen naar BSA-grensgevallen, conclusies beperkt tot die groep. Dit onderzoek doet denken aan het eerste onderzoek naar studie-uitval: in de 50er jaren aan de TH Delft. Veel hoogleraren psychologie werkten daaraan mee (kom daar tegenwoordig nog eens om ;-) Belangrijk resultaat: meeste ‘uitvallers’ studeerden in dezelfde richting door aan HTS. Belangrijk verschil deze uitval en BSA: het eerste is een eigen beslissing, BSA is opgelegd. Opvallend verschil met dat onderzoek 60 jaar geleden: BSA-uitvallers houden het bij dezelfde studie op universitair niveau. Maar dit is dan ook een sub-groep van uitvallers: randgevallen. Het onderzoekrapport: http://acla.amsterdam/workingpapers-wp20181/
![]() http://www.benwilbrink.nl/projecten/14compensatie_en_rendement.htm#AMBS
http://www.benwilbrink.nl/projecten/14compensatie_en_rendement.htm#AMBS