Bekend inzicht 40% (L) (inzicht = 5 weten)
De basis voor de nu volgende analyse en modellering van het doorzichtig toetsen van inzicht is gelegd door De Groot en Van Naerssen. De Groot (1970) vroeg aandacht voor de maatschappelijke context waarin toetsen en psychologische tests worden gebruikt. Voor het onderwijs spitste hij dat toe op de eis dat studenten zich gericht moeten kunnen voorbereiden op af te leggen toetsen en noemde dat de eis van 'doorzichtigheid' (transparency). Tegelijkertijd legde Van Naerssen (1970) in een 'tentamenmodel' vast hoe de inrichting van examens van het gedrag van studenten stuurt. Hij modelleerde hoe examens als 'hefboom op het onderwijs' werken, omdat examens definiëren hoe de studiestrategie de slaagkans kan bepalen. Het werk van Van Naerssen is te zien als een poging om de doorzichtigheid van De Groot te operationaliseren, hoewel beide publicaties uit 1970 niet naar elkaar verwijzen. Op dit idee voor een tentamenmodel is een algemeen toetsmodel ontwikkeld (Wilbrink, 1995), waarmee de doorzichtigheid van De Groot praktisch toepasbaar wordt, en waarmee ook vorm is te geven aan wat 'toetsen van inzicht' kan zijn.
De uitersten van doorzichtigheid zijn goed zichtbaar in de Chinese keizerlijke examens, die in 1910 zijn afgeschaft. Deze examens waren doorzichtig in de zin van weten wat de vragen zullen zijn en wat telt als goede antwoorden. De nadruk viel op uit het hoofd leren en op geoefend zijn in het antwoorden volgens strakke formele regels. Maar ze waren tegelijk ondoorzichtig omdat het vergelijkende examens waren, erg selectieve bovendien, en met een extreme maatschappelijke beloning voor degenen die tot de numerus fixus van de besten behoorden.
In het westerse onderwijs is door de humanisten de systematiek ingevoerd van rangordenen van leerlingen op basis van het aantal geregistreerde fouten. Aan het Stedelijk Gymnasium van Groningen is dat pas in 1903 vervangen door de systematiek van cijfergeven. Deze vorm van rangordenen is erg doorzichtig. Zo hield iedere leerling in een puntenboekje niet alleen de eigen punten bij, maar ook die van alle andere leerlingen in de klas. De keerzijde van die doorzichtigheid was dat veel leerlingen al snel konden zien dat zij toch kansloos waren voor de prijzen voor de besten (Wilbrink, 1997).
Zowel De Groot (1970) als Cohen (1981) geven een definitie van doorzichtigheid waarin de context van de toetsing en de belangen van de studenten voorkomen.
Cohen spreekt bij voorkeur niet over doorzichtigheid maar over kenbaarheid. Het kenbaarheids-beginsel houdt in dat
Voor de student ziet een toets eruit alsof de vragen toevallig zijn getrokken uit een grote verzameling of kaartenbak van toetsvragen. 'Toevallig' wil zeggen dat het ook andere vragen hadden kunnen zijn. Een toets afleggen betekent dus onderworpen zijn aan een statistisch gebeuren. Veronderstel eens dat deze student een beheersing van 60% heeft, dat wil zeggen dat zij 60% van de vragen uit de genoemde verzameling goed zou maken. Als de toets uit maar een enkele vraag zou bestaan, is de kans dat op die toets de score 0 of 1 wordt gehaald respectievelijk 40% en 60%. Voor een toets met 2 vragen is de kans op score 0, 1 of 2 respectievelijk 16%, 48% of 36%. Voor een toets met 25 vragen zijn de kansen ook te berekenen. Een alternatief voor de wiskundige benadering is om te simuleren.

Bekend inzicht 40% (L) (inzicht = 5 weten)
Gebruik het (2005) Java-applet om in de browser de simulatie en analyse ook voor andere parameterwaarden te doen. Verzeker u ervan dat de browser is ingetseld op Java; mogelijk moeten ook pop-ups zijn toegestaan.
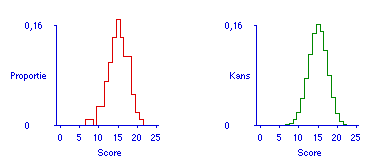
Figuur 1 (links) laat een tienvoudige simulatie zien van een toets van 25 vragen voor een student met beheersing 60%. Telkens worden denkbeeldig 25 nieuwe vragen uit de kaartenbak toevallig getrokken en als toets voorgelegd. Een andere interpretatie van deze figuur is dat het een simulatie is van een groep van 10 studenten, allen met beheersing 60%, die ieder een andere toevallig getrokken toets maken. Dat 'toevallig trekken' kan met de computer heel goed worden gedaan, en net zo vaak herhaald als men wil. Figuur 1 laat zien dat bij een beheersing van 60% de resultaten op een toets van 25 vragen nog kunnen variëren tussen 10 en 20. Die brede spreiding van (mogelijke) scores is een enorm probleem voor de eis van doorzichtigheid, want bij een zo groot verschil in uitkomst bij gelijke beheersing is er evident sprake van een gebrekkige voorspelbaarheid van de toetsuitkomst. Wie hoopt door gebruik te maken van onderlinge correlatie van toetsvragen deze spreiding te kunnen verkleinen, moet bedenken dat in het binomiale model geen correlaties zijn gedefinieerd.
Figuur 1 (rechts) laat de voorspelling zien wanneer de student geen 100, maar een oneindig aantal toetsen zou afleggen, telkens onder dezelfde conditie van gegeven beheersing 60%: dat levert een gelijkmatige verdeling op die bekend staat als de theoretische binomiaalverdeling.
In werkelijkheid is de beheersing van de stof onbekend, al zijn er altijd wel aanwijzingen over de waarschijnlijke grootte ervan. Het resultaat op een proeftoets zou zo'n aanwijzing kunnen zijn. De vragen in de proeftoets komen uit dezelfde kaartenbak met toetsvragen waaruit de toets wordt 'samengesteld,' wat er voor de student uitziet als 'willekeurig getrokken.' Veronderstel dat een student een score van 15 op een proeftoets van 25 vragen heeft gemaakt. Dat betekent niet dat de beheersing 60 procent is, maar dat is wel de meest aannemelijke waarde voor de beheersing. Een lager of hoger percentage heeft een geringere aannemelijkheid, en des te geringer naarmate de beheersing verder van 60 procent af ligt.
Noot 2003: Simulatie noch theorie kunnen in deze praktijk als continu worden opgevat; beide zijn gebaseerd op een raster van, in dit geval, 25 punten op de dimensie van beheersing.
Gebruik het (2005) Java-applet om in de browser de simulatie en analyse ook voor andere parameterwaarden te doen.
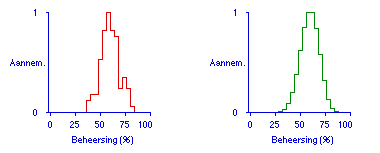
In Figuur 2 is te zien dat een proeftoetsscore van 15 uit 25 een beheersing lager dan 30 en hoger dan 85 procent vrijwel uitsluit. Een student met deze proeftoetsscore weet dan alleen nog maar dat haar beheersing ergens tussen 30 en 85 procent ligt. Hier ligt dus een tweede bron van onzekerheden die een bedreiging voor de doorzichtigheid kunnen zijn.
Dezelfde figuur laat zien dat de onzekerheid zelf wel precies is te kwantificeren, bijvoorbeeld naar hoe aannemelijk het is dat de beheersing in werkelijkheid ligt tussen 50 en 60 procent. Van deze techniek is handig gebruik te maken door ook andere informatie over de beheersing van de stof uit te drukken in zo'n proeftoetsscore. Stel dat een student een aantal werkstukken heeft gemaakt en daaruit een bepaald idee heeft gekregen over haar beheersing van de tentamenstof, een idee dat evenveel waard is als een proeftoets met een lengte van 20 vragen, en daarvan 15 goed. In combinatie met de proeftoetsscore van 15 uit 25 uit het voorbeeld is dat 30 goed uit een proeftoets met een totale lengte van 45, en dat levert een betere voorspelling op. Er is hier enige verwantschap met Bayesiaanse statistische methoden, maar het model blijft gebaseerd op objectieve gegevens zoals de uitslag van een proeftoets, en doet geen schattingen over de ware beheersing maar een voorspelling van een toekomstige toetsscore.
Gebruik het (2005) Java-applet om in de browser de simulatie en analyse ook voor andere parameterwaarden te doen.
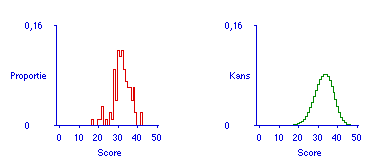
Figuur 3 illustreert wat er valt te voorspellen op basis van een proeftoetsscore. De figuur laat zien dat voorspellen onder tamelijk gangbare condities voor tentamens in het hoger onderwijs een breed scala aan mogelijke resultaten oplevert: in dit geval kan de student een score verwachten ergens tussen 20 en 45 op een toets van 50 vragen. Dat is onaangenaam breed, want stel dat voor een voldoende tenminste 30 vragen goed moeten zijn, dan is voor deze student de toets een loterij met teveel nieten.
Het voorgaande is een rechtlijnige toepassing van eenvoudige statistiek. Er valt niet te ontkomen aan de conclusie dat de situatie afgebeeld in Figuur 3 nogal ondoorzichtig is. Een breed gespreide voorspelling is een kwaliteitsprobleem voor het onderwijs. Deze ondoorzichtigheid betekent immers dat de student met extra studietijd de eigen slaagkans wel kan verbeteren, maar deze alleen met extreme inspanning in de buurt van 90 of 100 procent kan brengen. Deze stand van zaken draagt niet echt bij aan de studiemotivatie.
Gebruik het (2005) Java-applet om in de browser de simulatie en analyse ook voor andere parameterwaarden te doen.
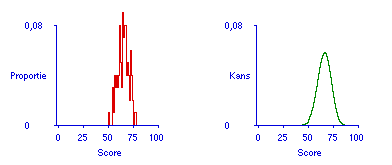
De doorzichtigheid is te verbeteren door meer informatie te geven, bijvoorbeeld door de proeftoets en de toets te verlengen. Figuur 4 laat zien hoe verdubbeling van de lengte van zowel de toets als de proeftoets een minder breed gespreide voorspelling oplevert (vergelijk Figuur 3), zij het dat de winst beperkt is. Het is duidelijk dat het meten van studieprestaties iets totaal anders is dan het meten van lengte en gewicht, waarvoor in de 19e eeuw zulke spectaculaire resultaten in standaardisatie en nauwkeurigheid, en dus in eerlijkheid en doorzichtigheid, zijn bereikt.
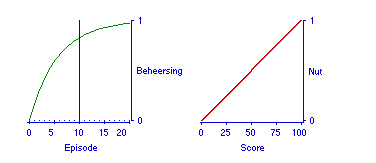
De voorspelling wordt interessanter wanneer er ook iets valt te zeggen over de opbrengst van extra studietijd. Van Naerssen gebruikte daar een eenvoudig leermodel voor, een model dat stipuleert dat halveren van de hoeveelheid nog niet geweten stof telkens evenveel tijd kost. Figuur 5, links, laat een leercurve zien die op zo'n model berust. Het is typisch een model voor het vergaren van kennis, niet van inzicht. Het leren van een rij vreemde woorden gaat eerst snel, terwijl de laatste nog niet gekende woorden relatief meer tijd vragen. Dit model past evident niet op complex leren, op het verwerven van 'inzicht,' waarvoor veelal een lange aanloop nodig is voordat er gepresteerd wordt. De oplossing voor dit probleem volgt straks bij de operationalisatie van 'inzicht,' het toetsmodel wordt hier eerst afgerond op basis van het leermodel voor kennis.
Gebruik het (2005) Java-applet 'Expectation' Java-applet 'The Ruling'om in de browser de analyse en de nutsfunctie ook voor andere parameterwaarden te doen.
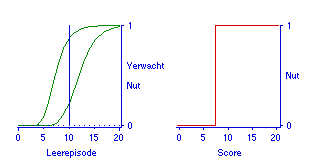
In Figuur 5 (links) is als voorbeeld gegeven hoe het verwachte toetsresultaat verbetert bij extra studietijd. Let op dat in Figuur 5 telkens de verwachte waarde, dat is het gemiddelde, is ingetekend: in individuele gevallen kunnen er behoorlijke afwijkingen naar boven of beneden zijn. Voor de rol van de in Figuur 5 rechts afgebeelde nutsfunctie zie hierbeneden.
Er is in de literatuur over toetsen weinig aandacht voor het probleem dat scores worden omgezet naar cijfers, en dat er ingewikkelde overgangs- en examenregelingen zijn waarin die cijfers een hoofdrol spelen. Daarom moeten cijfers en de betekenis die zij in de examenregeling krijgen ook een plaats krijgen in het model. Cijfers raken immers direct aan doorzichtigheid.
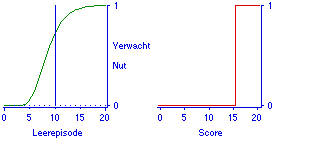
Cijfergeven is op te vatten als een manier om de prestaties, dat zijn de ruwe scores op de toets, te waarderen of te wegen. In de praktijk worden cijfers vaak berekend op manieren die sterk doen denken aan het tellen van fouten zoals dat in het oude stelsel van rangordenen van leerlingen gebeurde. De omzetting van scores naar cijfers is op te vatten als een nutsfunctie. Door met nutsfuncties te werken kunnen veel meer verschillende toetssituaties in het model worden opgenomen dan alleen die van het cijfergeven. Bij iedere score hoort een bepaald nut, en omgekeerd. In Figuur 5 (rechts) is de neutrale nutsfunctie afgebeeld, waar het nut gelijk is aan de score zelf. Wanneer cijfers van proefwerken elkaar volledig compenseren, zoals binnen vakken in het voortgezet onderwijs vaak het geval is, komt dat overeen met het hanteren van zo'n neutrale nutsfunctie. Een tweede voorbeeld is het drempelnut wanneer alleen voldoende resultaten tellen. In dat geval worden scores vervangen door een 0 of een 1, al naar gelang het 'zakken' of 'slagen' wordt (Figuur 6, rechts).
Gebruik het (2005) Java-applet 'Expectation' Java-applet 'The Ruling'om in de browser de analyse en de nutsfunctie ook voor andere parameterwaarden te doen.
In combinatie met de omzetting van resultaten naar cijfers geeft het leermodel aan hoe het verwachte cijfer stijgt met de studietijd. Door cijfers te vervangen door nut geeft het model de toename van het verwachte nut. In het bijzondere geval van drempelnut (Figuur 6, rechts) is het verwachte nut gelijk aan de slaagkans (Figuur 6, links).
Bij de vigerende examenregelingen, waar in beginsel voor ieder vak een voldoende resultaat nodig is, mag strategisch gedrag van studenten worden verwacht: mikken op zesjes. Het regime van de tempobeurs versterkt dat strategische gedrag: hogere prestaties tellen daar immers niet mee, maar vergen wel kostbare tijd. Dat studenten, evenals docenten, te optimistische ideeën over de nauwkeurigheid van dat 'mikken op zesjes' hebben, draagt mede bij aan de overmatige studievertragingen in ons onderwijsstelsel.
In grote lijnen is hiermee het model geschetst waarmee de doorzichtigheid van toetsen hanteerbaar is te maken. In dit model heeft het toetsen van inzicht nog geen plaats gekregen.
Over inzicht is veel geschreven, maar dat betreft vooral 'Archimediaans' inzicht, dat is het plotselinge inzicht in de oplossing van een moeilijk probleem. Het probleem van Archimedes was om uit te zoeken of een kroon van zuiver goud was of niet, waarvoor hij het volume van de kroon moest vinden. Zijn inzicht was dat het water dat door een ondergedompeld voorwerp wordt verplaatst gelijk is aan zijn volume. Dat type inzicht is veelvuldig in de geschiedenis van de wetenschap gesignaleerd en in de psychologie onderzocht (Sternberg & Davidson, 1995). Met het toetsen van inzicht bedoelen docenten evenwel iets anders, zoals het kunnen leggen van verbanden tussen onderdelen van de bestudeerde stof. Bedoeling en werkelijkheid van het toetsen op inzicht kunnen makkelijk uiteenlopen. Crombag, Gaff & Chang (1975) vonden in een onderzoek over studiemethoden en studieresultaten dat "... putting the subject matter into ones own words is a dangerous habit" (p. 3). Studenten die de gewoonte hebben de stof voor zichzelf inzichtelijk verwerken, lopen daarmee het risico slechtere tentamenresultaten te behalen.
Een ervaring die niet zeldzaam is maar toch zelden in de literatuur is beschreven, is dat na een intensieve voorbereiding er kort voor het tentamen zelf een kwalitatief andere beleving van de leerstof ontstaat. De stof wordt transparant, de verschillende onderdelen ervan vallen ieder op hun plaats en het is ineens makkelijk om dwarsverbanden in de stof te leggen. Entwistle (1995) duidt de zo ervaren leerstof aan met de term knowledge object. Dit is zeker een vorm van inzicht, en voor het onderwijs een niet onbelangrijke vorm.
Een bijzonder verschijnsel en een variant op het knowledge object is een mentale toestand van mensen die gedurende korte tijd een volledig overzicht moeten hebben over een complex samenstel van gebeurtenissen. Dat geldt bijvoorbeeld voor vluchtleiders en voor procesoperatoren in kerncentrales. In de Amerikaanse marine gebruiken officieren in de operatiekamer voor deze mentale toestand de term having the bubble. De term stamt uit de tijd dat de meetinstrumenten in de operatiekamers vooral op het waterpas waren gebaseerd en al die luchtbellen tegelijk in de gaten moesten worden gehouden. Rochlin (1997) geeft een gedocumenteerde beschrijving van het verschijnsel. De dienstdoende officier moet een doorlopend overzicht hebben over zeer veel soms snel veranderende gegevens. Het gaat niet zozeer om het hebben van een mentale kaart van al die gegevens, als wel om het vermogen om de gebeurtenissen in die mentale kaart te beheersen en te sturen. Dat lijkt mysterieus, maar het is ongeveer hetzelfde als een voordracht houden over een ingewikkeld onderwerp: dan is het ook een ramp om van je à propos te raken. Het onderzoek van Rochlin strekt zich uit over veel andere situaties waar controle over complexe processen plaatsvindt en van het ene moment op het andere complexe ingrepen gedaan moeten kunnen worden. Dat overzicht kan 'zomaar' weg zijn en dan moet iemand anders die taak onmiddellijk over kunnen nemen. Bovendien gaat het hier om high stakes situaties, waar zeer veel op het spel staat als de zaken uit de hand zouden lopen. Having the bubble is een bijzonder soort inzicht, maar kan door zijn extreme aard wel helpen om inzicht in inzicht te krijgen.
Inzicht is op zijn minst een verband tussen twee afzonderlijke begrippen, wat nog heel dicht tegen kennis of vaardigheid aan kan liggen. Analyseren en gevolgtrekkingen maken zijn vormen van inzicht. Het overzicht hebben over een domein van kennis of van gebeurtenissen is een vorm van inzicht.
Een strengere en eenvoudiger beschrijving is nu dat inzicht gelijk is aan het gelijktijdig weten van de verschillende kenniselementen waaruit dat inzicht bestaat. Dit is zeker een versimpeling van de werkelijkheid. Het is evenwel door zijn eenvoud, door het afzien van iedere mogelijke surplus-betekenis van wat inzicht nog meer zou zijn dan dat gelijktijdig weten, een veelbelovend uitgangspunt. In de cognitieve psychologie zijn aanknopingspunten voor een dergelijke theorie te vinden, bijvoorbeeld in Anderson e.a. (1993), en in Langley & Jones (1988) die inzicht postuleren als een op het geheugen gebaseerd proces. Overigens ligt aan deze cognitieve psychologie ook werk van De Groot (1946) ten grondslag, waaruit de volgende passage over 'actualiseerbare disposities' zo'n aanknopingspunt vormt.
De grondslag van alle 'meesterlijke' prestaties, ook op schaakgebied, is de 'ervaring' van den meester, dat systeem van onmiddellijk actualiseerbare disposities tot typische probleemtransformaties, dat stelsel van algemene en speciale denkgewoonten, waarover hij beschikt. (De Groot, 1946, p. 241; in de Engelse editie van 1965 uitgebreider en preciezer op p. 308).
De operationalisatie van inzichtvragen is nu dat er tegelijkertijd kennis van twee of meer afzonderlijke dingen of gebeurtenissen wordt gevraagd. Deze kennis is niet gegeven, maar moet geproduceerd kunnen worden. Een inzichtvraag is dan opgebouwd te denken uit twee of meer kennisvragen die tegelijk 'geweten' moeten worden. De mate of complexiteit van inzicht is dan het aantal dingen of gebeurtenissen waarvan tegelijk kennis nodig is. De inzichtvraag reduceert tot een kennisvraag wanneer er kennis van slechts een enkel ding of gebeurtenis nodig is. Op basis van deze operationalisatie is het algemene toetsmodel uitgebreid met de mogelijkheid ook toetsen met inzichtvragen te modelleren.
Gebruik het (2005) Java-applet om in de browser de simulatie en analyse ook voor andere parameterwaarden te doen.
Hoe een en ander in zijn werk gaat is allereerst in Figuur 7 geïllustreerd. De afgebeelde situatie is die waar bekend wordt verondersteld dat de student 83% van de kennisvragen beheerst. Als voor inzichtvragen zou gelden dat daarvoor telkens kennis van vijf dingen tegelijk nodig is, dan is de beheersing van inzichtvragen 40 procent. Dat resultaat is verkregen door 0,83 tot de vijfde macht te nemen en naar een percentage om te zetten. Op dit niveau van inzicht gaat een hoge kennisbeheersing samen met een matige beheersing van inzichtvragen, (zie de twee curven in Figuur 7). Dat is misschien verrassend, maar het volgt onmiddellijk uit de operationalisatie van inzicht. Hier blijkt ook het nut van het hebben van een model. Immers, statistisch ingewikkelde situaties zijn onmiddellijk door te rekenen en dan ook grafisch af te beelden. Dan kan blijken dat het idee dat het niet teveel gevraagd is dat studenten dwarsverbanden door de stof kunnen leggen makkelijk kan leiden tot het stellen van vragen die (veel) moeilijker zijn dan bedoeld.
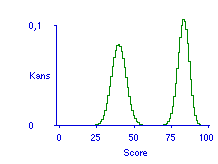
Hoewel bij het toetsen op inzicht het leren plaats blijft vinden in termen van kennis, worden de prestaties nu afgemeten aan het aantal goed beantwoorde inzichtvragen, en dat levert verrassende resultaten op, zoals de in Figuur 8 tegenover elkaar gezette situaties laten zien.
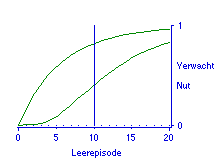

Gebruik het (2005) Java-applet om in de browser de analyse ook voor andere parameterwaarden te doen. Hierboven/naast de replicatie van Figuur 8 (de nutsschaal loopt door tot 2 omdat er volledige compensatie over de scorereeks is verondersteld), met bovendien simulaties (op 100 observaties).
In Figuur 8 is te zien hoe de gekozen operationalisatie van inzicht leidt tot een resultaat dat intuïtief overeenstemt met leerpatronen in het hoger onderwijs. Het verwerven van inzicht verloopt aanvankelijk moeizaam en later sneller. Bij het eenvoudige leermodel voor kennis leidt de eerste keer doornemen van de stof tot de grootste leerwinst. Bij het model met inzicht vindt het leren nog steeds plaats in termen van kennis, en moet die kennisbeheersing al op een behoorlijk niveau zijn voordat de eerste inzichtvraag met enige kans op succes goed kan worden beantwoord. Voor het onderwijskundig ontwerp van een curriculum ligt het dan voor de hand om in het begin met oefenvragen op een laag niveau van inzicht te werken, en aan het eind op een hoger niveau.
In Figuur 8 is als mate van inzicht gekozen het gelijktijdig kennis hebben van vijf dingen of gebeurtenissen. Of vijf veel of weinig is hangt af van de context, zoals de aard van de leerstof, de daarbij gehanteerde doelen, of stof van eerdere vakken bekend wordt verondersteld, etcetera. Het model vraagt bij toepassing in een specifieke situatie dus om invulling vanuit de kenmerken van die situatie. Zonder daar al verder onderzoek naar te hebben gedaan, neig ik ertoe vijf als een laag niveau van inzicht te zien. Bedenk dat voor het beantwoorden van een inzichtvraag ook geldt dat er kennis is die juist niet voor de betreffende vraag gebruikt moet worden. Zoiets geldt zeker bij diagnostische problemen waar bepaalde aangereikte of opvraagbare gegevens irrelevant zijn voor het stellen van de juiste diagnose in een specifiek geval.
Een leermodel als onderdeel van een toetsmodel opnemen, is vragen om moeilijkheden. Wanneer dat toetsmodel zowel een analytische uitwerking als een via simulatie krijgt, wordt het niet doorzichtiger. De verleiding is groot om voor het leermodel een procesmodel te nemen, dat zich ook laat simuleren.
Een verstandige insteek lijkt nu te zijn om het leren alleen als een beschrijvend model binnen het toetsmodel op te nemen, en dit model als deterministisch te behandelen. In het SPA-model 2005 is deze vereenvoudiging gerealiseerd.
Een en ander impliceert dat er over leren en leerprocessen wel iets meer valt te zeggen dan wat nodig is voor een algemeen toetsmodel. In de bijdrage van Pieter Been (1989) aan dit symposium is de weg gewezen. Interessant is dat het ACT-model van Anderson een proces is waar simulatiestudies mee mogelijk zijn, zoals Been laat zien. Het is niet onmogelijk om een dergelijk leermodel toch weer in het toetsmodel op te nemen, al was het maar in een onderzoekvariant van het model.
Duidelijk is in Figuur 8 te zien dat het toetsen op inzicht hoge eisen stelt aan de beschikbare kennis. Met extra studie valt de grootste winst in termen van goed gemaakte inzichtvragen te behalen op een moment in het studiepad waarop de toename van kennis veel minder snel gaat. De inzichtvragen vergroten de kleinere winst in kennisniveau als het ware uit. Het onderwijs en de toetsing zouden zo moeten worden ingericht, dat voor een redelijk toetsresultaat de beste strategie is om door te studeren totdat de vorderingen in inzicht duidelijk moeizamer worden.
De gegeven demonstratie leidt nog tot een volgende observatie. Krediet geven voor goede deelantwoorden op een inzichtvraag ondergraaft het eigen karakter van inzichtvragen ten opzichte van kennisvragen. De toetsing degradeert dan tot kennistoetsing, en de bijzondere prikkel om door te studeren tot een hoog niveau van kennisbeheersing vervalt daarmee. Zie Biggs (1996) voor voorbeelden van docenten die door goede deelantwoorden te belonen handelen in strijd met hun intentie om inzicht te toetsen. Zij sporen studenten daarmee immers aan tot oppervlakkige verwerking van de stof.
Dat de wijze van prestatiebeloning het studiegedrag mede bepaalt was al bekend. Nu is daaraan toegevoegd dat de mate waarin inzicht wordt gevraagd eveneens een sturende werking heeft. Ook dat klinkt niet als een echte ontdekking, maar er is nu een instrument beschikbaar, een model, waarmee kan worden gekwantificeerd wat anders vaag blijft.
Het komt wel eens voor dat een afsluitende toets vragen bevat die meer inzicht eisen dan de vragen die in het onderwijs zijn behandeld en geoefend. Met hulp van het model valt nu te onderzoeken wat dat voor de doorzichtigheid van de toets betekent.
In Figuur 9 is te zien hoe een verdubbeling van het niveau van inzicht, een verdubbeling waar studenten zich niet goed op hebben kunnen voorbereiden, vergaande gevolgen kan hebben voor de slaagkansen. Studenten die in hun voorbereidingsstrategie rekening houden met inzichtvragen van niveau 3, maar in werkelijkheid vragen van niveau 6 krijgen, zien hun slaagkansen drastisch zakken. Een concreet voorbeeld zou een tentamen rechten kunnen zijn waar studenten casusposities met drie partijen krijgen voorgelegd, waar in het onderwijs slechts casusposities met twee partijen zijn behandeld. Twee partijen plus de relatie tussen die partijen zou inzichtniveau 3 kunnen zijn. Drie partijen met de relaties tussen die partijen is dan inzichtniveau 6.
Gebruik het (2005) Java-applet 'Expectation' Java-applet 'The Ruling'om in de browser de analyse en de nutsfunctie ook voor andere parameterwaarden te doen.
Het verschil in slaagkansen is dramatisch. Vergelijk daarvoor in Figuur 9 op een gegeven punt in het studiepad verticaal daarboven de slaagkans voor de eerste en de tweede situatie. Het ligt niet aan de operationalisatie van inzicht dat het verschil zo dramatisch is, die operationalisatie is wat de moeilijkheid van inzichtvragen betreft conservatief. Het spaarzame model, waarin alleen beschikbare kennis een rol speelt, ziet immers af van de mogelijkheid dat inzichtvragen ook nog moeilijker kunnen zijn omdat voor het bereiken van inzicht het niet toereikend is alleen de nodige kennis beschikbaar te hebben .
Het model zou een verklaring kunnen geven voor hardnekkig lage slaagpercentages bij tentamens waarin nadrukkelijk om inzicht wordt gevraagd, maar waar het de docenten ontbreekt aan goed begrip van de gevolgen die dat voor de moeilijkheid van de vragen heeft.
De voorgestelde operationalisatie van inzicht lost op elegante wijze het probleem op van een te weinig flexibel leermodel. Het beschreven model is nu toepasbaar op een breder scala van situaties, ook op die situaties in het hoger onderwijs waarin nadrukkelijk op 'inzicht' wordt getoetst. De gecombineerde analyse van doorzichtigheid en het toetsen van inzicht maakt het beter mogelijk verklaringen te genereren voor hardnekkige problemen met studeerbaarheid: lage slaagpercentages, lage numerieke rendementen, en trage studievoortgang.
Anderson, J. R., et aliis (1993). Rules of mind. Hillsdale, New Jersey: Lawrence Erlbaum.
Biggs, J. (1996). Enhancing teaching through constructive alignment. Higher Education, 32, 347-364. abstract
Cohen, M. J. (1981). Studierechten in het wetenschappelijk onderwijs. Zwolle: Tjeenk Willink.
Crombag, H. F., Gaff, J. G., & Chang, T. M. (1975). Study behavior and academic performance. Tijdschrift voor Onderwijsresearch, 1, 3-14.
Edwards, A. W. F. (1972). Likelihood: an account of the statistical concept of likelihood and its application to scientific inference. Cambridge: Cambridge University Press.
Entwistle, N. (1995). Frameworks for understanding as experienced in essay writing and in preparing for examinations. Educational Psychologist, 30, 47-54. scihub pdf
Groot, A. D. de (1946). Het denken van den schaker. Een experimenteel-psychologische studie. Amsterdam: Noord-Hollandsche Uitgevers Maatschappij. online beschikbaar
Groot, A. D. de (1965). Thought and choice in chess. The Hague: Mouton.
Groot, A. D. de (1970). Some badly needed non-statistical concepts in applied psychometrics. Nederlands Tijdschrift voor de Psychologie, 25, 360-376. html
Langley, P., & Jones, R. (1988). A computational model of scientific insight. In R. S. Sternberg (Ed.), The nature of creativity (p. 177-201). Cambridge: Cambridge University Press.
Naerssen, R. F. van (1970). Over optimaal studeren en tentamens combineren. Openbare les. Amsterdam: Swets & Zeitlinger. html
Rochlin, G. I. (1997). Trapped in the net. The unanticipated consequences of computerization. Princeton, New Jersey: Princeton University Press. integraal online
Sternberg, R. J., & Davidson, J. E. (Eds.) (1995). The nature of insight. Cambridge, Massachusetts: The MIT Press.
Wilbrink, B. (1995). Studiestrategieën die voor studenten én docenten optimaal zijn: het sturen van investeringen in de studie. In B. Creemers en anderen: Onderwijsonderzoek in Nederland en Vlaanderen 1995. Proceedings van de Onderwijs Research Dagen 1995 te Groningen (p. 218-220). Groningen: GION. Paper: auteur. html
Wilbrink, B. (1997). Assessment in historical perspective. Studies in Educational Evaluation, 23, 31-48. html
Omissie in de oorspronkelijke publicatie: Job Cohen's proefschrift niet in de literatuurlijst opgenomen. Hier verbeterd.
In de bijdrage van Pieter Been aan het COWOG-symposium behandelt hij onder andere het modelleren van leren, inclusief simuleren van het leerproces onder het ACT-model van Anderson:
Been, Pieter (1998). Individuele studiesystemen: ondergang, varkenscyclus of feniks. In Theo H. Joostens en Gerard W. H. Heijnen (Red.). Beoordelen, toetsen en studeergedrag. Groningen: Rijksuniversiteit, GION - Afdeling COWOG Centrum voor Onderzoek en Ontwikkeling van Hoger Onderwijs, 33-53.
Figuren in oorspronkelijke COWOG publicatie zijn gereconstrueerd en kunnen er iets anders uitzien dan in de publicatie, in ieder geval nu in kleur.
En eerder, natuurlijk. In de korte termijn die beschikbaar was voor het uitwerken van het onderwerp, heb ik de spreading activation theory niet gezien: Anderson (1984), Anderson & Pirolli (1984), en Collins & Loftus. Stellan Ohlsson (2011) gata er uitvoerig op in (p. 98 en volgende), beginnend met de verwising naar de genoemde publicaties.
John R. Anderson. A spreading activation theory of memory. Journal of Verbal Learning and Verbal Behavior, 22, 261-295. pdf
John R. Anderson (1984). Spreading activation. In J. R. Anderson & S. M. Kosslyn: Tutorials in Learning and Memory. Freeman. [niet gezien]
J. R. Anderson & P. L. Pirolli (1984). Spread of activation. Journal of Experimental Psychology: Learning, Memory, and Cognition, 10, 791-798.
A. M. Collins & E. F. Loftus (1975). A spreading-activation theory of semantic processing. Psychological Review, 82, 407-428.
Trina C. Kershaw & Stellan Ohlsson (2004). Multiple causes of difficulty in insight: The case of the nine-dot problem. Journal of Experimental Psychology: Learning, Memory and Cognition, 30, 3-13.
Zet negen punten in de vorm van een vierkant (drie rijen/kolommen van drie). Trek, zonder het potlood van het papier te halen, drie rechte lijnen, zo dat alle punten zijn verbonden. Dit is een klassiek inzicht-probleem (Maier, 1930). Maar dit inzicht is toch een tikje verschillend van het inzicht zoals ik dat in 1998 heb uitgewerkt: het inzicht waar het bij toetsvragen om hoort te gaan, is de juiste verbinding van kennis uit het domein van het betreffende vak. Het contrast met het inzicht uit psychologisch onderzoek zoals dat van Maier, of hier van Kershaw & Ohlsson, is interessant: het gaat daar niet om het verbinden van kennis, maar om het negeren van kennis of andere disposities die een oplossing belemmeren. Dat is dus echt totaal iets anders. Het volgende artikel, onmiddellijk na dat van Kershaw en Ohlsson geplaatst, demonstreert dat ook in de titel.
Edward P. Chronicle, James N. MacGregor & Thomas C. Ormerod (2004). What makes an insight problem? The roles of heuristics, goal conception, and solution recoding in knowledge-lean problems. Journal of Experimental Psychology: Learning, Memory and Cognition, 30,14-27.
Boeiend. Ik begin te vermoeden dat deze twee totaal verschillende interpretaties van wat inzicht is, te maken kunnen hebben met de misverstanden over het belang van leren probleemoplossen in het onderwijs, ook als dat probleemoplossen domein-specifiek is. Ik ga dit waarschijnlijk uitwerken in het rekenproject: probleemoplossen.htm.
Heathcote, A., & Mewhort, D. J. K. (2000). The evidence for a power law of practice. In R. Heath, B. Hayes, A. Heathcote, & C. Hooker, The Proceedings of the 4th Conference of the Australasian Cognitive Science Society, The University of Newcastle, Australia.
http://www.newcastle.edu.au/school/behav-sci/ncl/lop.pdf
http://www.newcastle.edu.au/school/behav-sci/ncl/publications.html
Heathcote, A., Brown, S. & Mewhort, D.J.K. (2000) Repealing the power law: The case for an exponential law of practice. Psychonomic Bulletin and Review, 7, 185-207.
http://www.newcastle.edu.au/school/behav-sci/ncl/publications.html
Brown, S. & Heathcote, A. (2003). Averaging learning curves across and within participants. Behaviour Research Methods, Instruments & Computers, 35, 11-21
http://www.newcastle.edu.au/school/behav-sci/ncl/publications.html
Simonton, Dean Keith (2003). Scientific creativity as constrained stochastic behavior: The integration of product, person, and process perspectives. Psychological Bulletin, 129, 475-494. abstract
Simonton leent van Csikszentmihalyi the termen domein en veld. Het domein voor een wetenschappelijke discipline 'consists of a large but finite set of facts, techniques, heurstics, themes, questions, goals, and criteria,' of wel tesamen 'the population of ideas that make up a given domain.' 'The field consists of all those individuals who are working with the set of ideas that define the domain.'
Voor beoordelen in het onderwijs is het domein meest strikt ingeperkt, maar dat maakt het in mijn bijdrage gehanteerde domein van kennis-items niet anders dan het bredere domein van Csikszentmihalyi.
Het punt van de bijdrage van Simonton is 'the central features of productivity across and within careers can be explicated by assuming that creativity operates like a stochastic combinatorial procedure.' Dat is vrijwel gelijk aan prestaties tussen en binnen leerlingen verklaren als een waarschijnlijkheidsproces op de elementen in het kennisdomein. Omdat bij beoordelen het domein klein en overzichtelijk is, zien de prestaties van studenten er ordelijker uit dan de uitzonderlijke bijdragen die wetenschappers gedurende hun loopbaan aan het vakgebied schenken, maar het model kan hetzelfde zijn.
Gebruikte sheets beschikbaar [208kb pdf]
Een overzicht van de nieuwe punten in deze bijdrage. html
Krediet geven voor deelantwoorden lijkt zo rechtvaardig, en inderdaad is er een uitspraak van een College van Beroep voor de Examens dat impliceert dat studenten daar recht op zouden hebben. In het onderhavige geval gaat het College zelfs voorbij aan wat de betrokken docent zag als de kern van de vraag waarvan de student het oordeel aanvocht (afgaande op de weergave van Van Berkel). Zie de bespreking van dit casus:
Berkel, Henk J. M. van (1991). In beroep; 2 + 2 = 5 + 7 = 12. Onderzoek van Onderwijs, 20, 9.
In dit verband — grote examenopgaven opsplitsen in deelvragen — is een scherpe observatie van Kruijtbosch (1936) relevant:
Naar aanleiding van deze opgave [een lastige wiskundeopgave, b.w.] is de opmerking niet misplaatst, dat het verkeerd is den leerlingen een bepaalde gedachtengang te willen opdringen. Toch wordt bij examenopgaven dikwijls aan die verkeerde neiging toegegeven, o.a. door splitsing van een opgave in onderdelen, waarvan dan het volgende met behulp van het voorafgaande moet worden bewezen of berekend.
Kruijtbosch p. 30
D. J. Kruijtbosch (1936). Avontuurlijk wiskundeonderwijs. Bijdragen tot een meer boeiende didactiek van de beginselen der wiskunde. W. L. & J. Brusse’s Uitgeversmaatschappij
Simon, Herbert A. (1974). How big is a chunk? Science, 183, 482-488. Reprinted in Simon (1979) Models of thought. Yale University Press.
Alexandre Linhares and Paulo Brum (2007). Understanding our understanding of strategic scenarios: What role do chunks play? Cognitive Science, 31, 989-1007.
Wilbrink, Ben (2005, in ontwikkeling). The SPA Model: Strategic Preparation for Achievement Tests. html In dit onder handen zijnde project wordt het Algemene Toetsmodel opnieuw en uitvoerig gepresenteerd in het Engels, voorzien van volledig werkende instrumenten die in de browser beschikbaar komen (in de vorm van Java-applets). De serie van 7 kern-modulen in evenzovele applets: 1 2 3 4 5 6 7 8.
P. Pauli, L. E. Bourne, Jr., & N. Birbaumer (1998). Extensive practice in mental arithmetic and practice transfer over a ten-month retention interval. Mathematical Cognition, 4, 21-46. pdf
dat ‘unit of knowing’ intrigeert me: ik heb zoiets in abstracte vorm gebruikt voor mijn primitieve tentamenmodel met inzicht-parameter (1998).
John R. Anderson (1978). Arguments concerning representations for mental imagery. Psychological Review, 85, 249-277. pdf dupliek Werk van Campbell kom ik nog wel tegen, o.a. in 1995 in Mathematical Cognition. Ryle staat in de boekenkast, maar ik ken het natuurlijk al lang niet meer. Zou daar die unit of knowing in voorkomen?
Michael Frank (Thursday, February 21, 2019). Nothing in childhood makes sense except in the light of continuous developmental change. blog
Abigail Entwistle & Noel Entwistle (1992). Experiences of understanding in revising for degree examinations. Learning and Instruction, 2, 1-22. abstract
N. J. Entwistle & Abigail Entwistle (1991). Contrasting forms of understanding for degree examinations: the student experience and its implications. Higher Education, 22, 205-228. abstract
John Patrick, Afia Ahmed, Victoria Smy, Helen Seeby, and Katie Sambrooks (2015). A Cognitive Procedure for Representation Change in Verbal Insight Problems. Journal of Experimental Psychology, Association Learning, Memory, and Cognition, 2015, Vol. 41, No. 3, 746–759 http://dx.doi.org/10.1037/xlm0000045 [via academia.edu] abstract
Toetst een theorie van Ohlsson: representational change theory (RCT) (Ohlsson, 1992, 2011).
Ben Wilbrink (1 maart 2023) Toetsvragen ontwerpen. Hoe verhouden kennis en inzicht zich tot elkaar? Is hier een exact model voor geven, zonder concreet te maken om welke kennis en inzicht het gaat? Twitter draadje
Neem aan dat de stof voor een toets bestaat uit een groot aantal elementaire weetjes. Het is denkbaar in de toets uitsluitend vragen naar elementaire kennis op te nemen.
Ik geef toch maar een voorbeeld. De tafels van vermenigvuldiging. 2 x 2 = 4; 7 x 8 = 56; etcetera. Neem aan dat de hele klas die tafels beheerst op 83% niveau. Neem dan een toets af, en constateer dat de scoreverdeling er ongeveer uitziet als de rechter curve in deze figuur [7 hierboven (in het paper van 1998)].

Nu gaan we een toets ontwerpen met vragen waarbij telkens 5 dingen tegelijk geweten moeten worden. Zeg dat dat vermenigvuldigingen zijn waarvoor telkens 5 tafelvermenigvuldigingen goed moeten zijn. Had u dat gedacht, dat de toetsscores dan verdeeld zijn als de linker curve?
In dit eenvoudige model is 'inzicht' opgevat als het weten van 5 stukjes elementaire kennis om een opgave goed te beantwoorden. Dat is een voorzichtige benadering, want er komt wel meer bij kijken dan alleen die 5 dingen weten. De figuur geeft dus zeker een te optimistisch beeld.
Dit eenvoudige model geeft een mogelijke verklaring voor het verschijnsel dat leraren vaak de moeilijkheid van toets- en examenvragen behoorlijk ONDERschatten. [De wiskunde van het modelletje—binomiaal model etc—is in het eerste deel van het 1958-paper behandeld]
Is dit niet een wat al te eenvoudige opvatting van wat 'inzicht' is? Ja, dat is het ongetwijfeld. Maar het aardige van een te simpel model is dat het zonder allerlei moeilijke toeren uit te halen toch inzicht in inzicht kan geven. En kan waarschuwen voor onbedoeld veel te moeilijke proefwerken en examens. Een voorbeeld van dat laatste heeft Nederland mee mogen maken bij het experiment van de #rekentoets toegevoegd aan de examens-vo. Die context-rekenopgaven bevatten zoveel verborgen kennisvereisten dat experts de moeilijkheid sterk onderschatten.
Wat in het onderwijs vaak voorkomt: dat in toetsen en examens vragen worden gesteld die iets complexer zijn dan wat in het onderwijs is behandeld. Hans Crombag noemt als voorbeeld casusposities met 3 partijen, waar in het onderwijs slechts 2 partijen zijn behandeld. Niet doen.
Bij contextopgaven rekenen/wiskunde is het een probleem dat de ontwerpers ervan contexten bedenken die echt nieuw zijn voor de meeste leerlingen. Ik vind dat een kunstfout, dat is zoiets als voor chirurgen dat zij het verkeerde been afzetten. Maar wie ben ik, simpele toetsziel?
Nog even over het idee van 'inzicht'. Een bekende en indrukwekkende vorm van inzicht is de 'Aha Erlebnis'. Het plotseling zien van een verband tussen twee dingen, waardoor een hardnekkig probleem een oplossing vindt.
In het onderwijs moeten we liever niet zo hoogdravend zijn, en genoegen nemen met 'inzicht' als het wendbaar omgaan met de opgedane kennis: die kennis in onderling verband kunnen zien en gebruiken. Onderling verband: relaties leggen tussen kennisonderdelen.
Het blijft natuurlijk zo dat het eenmaal gelegd hebben van een bepaalde relatie—inzicht—vervolgens beschikbaar is als: kennis. Kennis is een gelaagd fenomeen; met toenemende kennis of expertise wordt die kennis zelf ook complexer. De wereld van cognitieve 'chunks'.
![]() http://www.benwilbrink.nl/publicaties/98InzichtToetsenCOWOG.htm
http://goo.gl/ynRfe
http://www.benwilbrink.nl/publicaties/98InzichtToetsenCOWOG.htm
http://goo.gl/ynRfe