CBE 27-3-2013 15-4-2013
Url: http://goo.gl/4fzKX
Wat wil je meenemen van deze middag? toelichting
aandachtspunten van de tweede groep
1. Wat is goed rekenonderwijs? #
2. Zijn er strategieën voor het talige aspect van contextopgaven?
3. Automatiseren en/of
4. Inzicht (begrijpen)
5. Optimale leeftijd voor rekenen #
6. Integratie van rekenen in andere vakken #
7. Rekentoetsen
8. Leerstijlen - leerstrategieën
mijn eigen lijstje aandachtspunten
Wirwar #
Fibonacci had veel woorden nodig, in 1200 #
Met breuken naar de MULO 1924 #
Hoofdrekentest 1968 #
Rekenvaardigheid van de Nederlandse leerling: PPON #
Altijd doorvragen naar bronnen #
Wat is goed rekenonderwijs? #
Niet realistisch: ‘Reken zeker’ (Noordhoff) #
Referentieniveaus rekenen #
Contextopgaven: kun je daar onderwijs in geven? #
Intellectuele capaciteiten in contexten #
Bij deze ‘rekenopgave’ ontspon zich een discussie op het forum van BON; de discussie zelf, maar niet de afbeelding, is hier te vinden. toelichting
Wij zijn ongelooflijk veel beter in abstract redeneren dan onze groot- en overgrootouders dat waren, aan het begin van de vorige eeuw. De samenleving is sterk verwetenschappelijkt, zou je kunnen zeggen. We laten ons vandaag de dag geen knollen voor citroenen meer verkopen, zou je denken. Toch is in veel geschrijf over het rekenonderwijs te zien dat het om knollen gaat, niet om citroenen: veel napraten, veel beweringen zonder bronnen, veel twijfelachtige empirische gegevens zoals op rekentoetsen die door het Cito worden aangeleverd. Kortom: wie begint met vragen naar de evidentie van het beweerde, zal menig pak kleren van de keizer ontdekken.
En omgekeerd: wie zich bekommert om bronnen, zal menig belangrijk gegeven ontdekken, zoals ik laat zien in het puntenlijstje voor de vraag ‘Wat is goed rekenonderwijs?’.
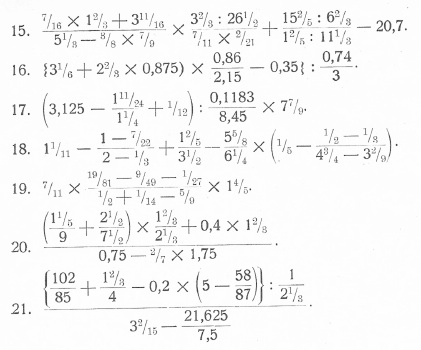
De afbeelding: enkele breukensommen voor de zesde klas, 1924, voor leerlingen die toelating voor mulo, hbs of gymnasium willen gaan doen.
P. Wijdenes (1924). Voorlooper op de rekenboeken voor de H.B.S en voor M.U.L.O., tevens slotstukje voor het rekenonderwijs op de lagere school. P. Noordhoff.
15.B.6. Hoofdrekentest (zesde klas) Tijd: 5 min.
30 x 4 1⁄2 = 25 - 3⁄4 = 9 x 25 = 17 - 2⁄3 = 1⁄3 x 72 = 7 x 12,5 = 27 : 4 = 8 x 13,5 = 27 + 38 = 13 - 1⁄5 is 9 x 4,5 = 92 - 47 = 12 1⁄2 + 1 1⁄4 = 7 x 8,5 = 21 : 4 = 4 x 27,5 = 43 : 5 = 5⁄6 - 1⁄3 = 16 x 125 = 44 st. = .. gld. 28 rijksd. = ƒ . . . 36 kw = ƒ . . . 1/5 x 120 = 40 rijksd. = ƒ . . .
F. Goffree, A. A. Hiddink & J. M. Dijkshoorn (1970 4e). Rekenen en didactiek. Wolters-Noordhoff. Voor een hoofdrekentoets zie bijvoorbeeld ook hier
Vraag ‘6. 48 : 0,12 = . . . . ’
Vraag ‘9. 286 + 1034 = . . . . ’
Vraag ‘10. 25 × 128 = . . . . ’
Vraag ‘29. Mieke heeft met ingang van 1 januari 2010
een loonsverhoging van 4% gekregen.
Op 1 januari 2011 kreeg ze opnieuw een loonsverhoging,
maar nu van 2%.
Met hoeveel procent is haar loon na deze twee verhogingen
in totaal gestegen?
A. Met 6%
B. Met iets meer dan 6%
C. Met iets minder dan 6%
D. Dat kun je niet weten want je weet niet hoeveel Mieke
voor de loonsverhoging verdiende.’
Voorbeeldtoets 3F, havo/vwo, voor veldraadpleging
http://staff.science.uva.nl/~craats/Voorbeeldtoets3F.pdf of
Wilbrink en Hulshof (2011). in Examens concept (het nummer is op dit moment niet beschikbaar op de site van de NVE, gebruik in tussentijd: pdf; zie ook een voorgaand artikel over het toetsen van taalverzorging bij de eindexamens pdf
Zie de Rekentoetswijzer 3S, voorbeeldopgaven blz. 21 e.v. pdf
In internationale studies zoals PISA en TIMSS zouden Nederlandse leerlingen het nog steeds uitstekend doen.
Er is nu een complete rekenmethode (groep 3 - 8) op de markt die berust op een mix van elementen uit zowel conventionele als realistische rekendidactiek: Piet Terpstra & Arjen de Vries (hoofdauteurs). Reken zeker. Noordhoff. http://goo.gl/MOEIQ. Ik heb moeite met die mix, maar omdat in de kerndoelen de realistische rekendidactiek als staatsdidactiek is voorgeschreven, begrijp ik wel dat geen enkele actuele rekenmethode om die kerndoelen heen kan. Enkele belangrijke uitgangspunten die anders zijn dan in de realistische rekendidactiek:
Centraal staan de algemeen geldende algoritmes voor optellen, aftrekken, vermenigvuldigen en delen, die leerlingen via systematisch opgebouwde opdrachten aangeboden krijgen.
Reken zeker kiets voor maximale duidelijkheid: kinderen leren één rekenstrategie voor elk rekenprobleem, die altijd naar de oplossing leidt. Eén strategie per rekenprobleem geeft de kinderen meer zelfvertrouwen.
Door steevast één nieuw onderwerp per les te behandelen, hebben de leerlingen meer mogelijkheden zich te kunnen concentreren op dat onderwerp.
Reken zeker. Handleiding 3 I: Theoretische achtergronden.
Jan van de Craats heeft in zijn voordrachten over Daan en Sanne, die niet meer kunnen rekneen, de kerngedachten van de methode ‘Reken zeker’ goed aangegeven, zie hier. Van de Craats biedt veel belangrijk materiaal aan op zijn website. Terug naar de methode ‘Reken zeker’
De Wet op de referentieniveaus taal en rekenen heeft de werkstukken van de commissie-Meijerink op in ieder geval niet door de commissie-Meijerink voorziene wijze tot wet gebombaardeerd, met alle details en trivialiteiten. Destijds minister van onderwijs Rouvoet heeft in de Tweede Kamer vastgelegd dat deze referentieniveaus opgevat moeten worden als een nadere uitwerking van de kerndoelen basisonderwijs, niet als iets dat naast die kerndoelen een eigenstandige betekenis heeft.
Of testen contextopgaven vooral verschillen in intelligentie? En als dat het geval is, wat is dan ‘plan B’ voor het onderwijs?
Toetsen met contextopgaven testen waarschijnlijk vooral verschillen in intellectuele capaciteiten. Daar helpt geen lieve moederen aan, anders dan ophouden met deze verkapte intelligentietesterij. De data van Turkstra demonstreren dat eigenlijk al overduidelijk. Wie er nog aan twijfelt, hoeft maar naar de uitslagen van de pilots van de rekentoets-3F te kijken (2012 [tabelletje in Wilbrink, Hulshof & Pfaltzgraff in gepubliceerde versie pdf], 2013 [de WiskundE-brief van zondag 21 april heeft waarschijnlijk al enkele eerste gegevens]).
Omdat Nederland voorlopig nog wel opgescheept zal zitten met deze verkapte intelligentietests, is de vraag: is er toch niet een klein beetje een verstandige voorbereiding op die tests mogelijk?
Wanneer kun je het beste met het eigenlijke rekenonderwijs beginnen, is dat in groep drie?
Een goede vraag, waarop geen helder antwoord is. Eigenlijk een hele cluster van vragen, waarop alleen op basis van empirisch onderzoek antwoor is te krijgen. Het probleem is natuurlijk dat er in het onderwijs heel veel tegelijk speelt: er zijn altijd ook wel enkele andere factoren waarop er belangrijke verschillen zijn, dus waar moeten de resultaten dan aan worden toegeschreven? Er zou een systematische vergelijking tussen landen gemaakt kunnen worden, landen met een verschillende aanvangsleeftijd voor het rekenonderwijs.
Nu is er een recent proefschrift van Ron Diris, waarin is uitgezocht aan de hand van internationale literatuur en van in Nederland beschikbare data, hoe het zit met de vraag wat het beste aanvangstijdstip is, voor rekenonderwijs bijvoorbeeld. Het antwoord is, volgens dit onderwijseconomisch onderzoek: zo vroeg mogelijk. Een goede basis leggen. Na groep twee geen leerlingen meer laten doubleren.
Een heel andere beschouwing die ik aan deze vraag heb gekoppeld: we zijn met zijn allen de laatste eeuw heel wat slimmer geworden — het Flynn-effect — en dat zou je in het onderwijs terug moeten kunnen zien. Het gaat om het vermogen om abstract te redeneren, abstracte relaties te zien. Bij uitstek is dat ook rekenen, zou je denken. Het gaat bovendien om een enorm groot verschil: bij ons vergeleken zou je moeten zeggen dat onze groot- en overgrootouders gemiddeld genomen nauwelijks tot abstract redeneren in staat waren. Zij leefden in een vooral heel concrete wereld, waar heel direct mee werd omgegaan. Wat een koe en een haas gemeenschappelijk hebben is niet dat het zoogdieren zijn, maar dat de koe de haas vangt. Tot mijn grote verwondering zie ik dan in het rekenonderwijs over de laatste halve eeuw een omgekeerde trend: met alle macht wordt geprobeerd het abstraheren uit te stellen tot na een fase waarin er met concrete materialen of tenminste met afbeeldingen daarvan wordt gewerkt. Met bussen waar passagiers in- en uitstappen. En daarbovenop een evidente trend in het gemiddeld voor 12-jarigen bereikte eindniveau: steeds lager. Is dat laatste op zich al beroerd genoeg, het Flynn-effect incalculerend moeten we waarschijnlijk van een nationale ramp in ons rekenonderwijs spreken. Gelukkig staat Nederland hierin niet alleen: veel landen lijden onder dezelfde afbraak, zodat we internationaal nog steeds goed mee kunnen doen. Met de klompendans.
Ron Diris (2012). The Economics of the School Curriculum. Proefschrift Universiteit Maastricht. pdf
Bij de eindexamens havo en vwo zien we de merkwaardige figuur dat wiskunde wordt geëxamineerd met contextopgaven, terwijl in andere examenonderdelen er wiskunde bij de zaakvakken moet worden gebruikt. Dat laatste lijkt me precies de bedoeling: wiskunde gebruiken voor probleemstellingen in een vakgebied waar de kandidaat mee vertrouwd moet zijn, zoals natuurkunde. Het eerste, wiskunde examineren met in het wilde weg bij elkaar gesprokkelde contexten, of toch stiekem ontleend aan de zaakvakken, lijkt mij van de gekke. In het basisonderwijs zien we hetzelfde fenomeen: rekenen wordt gegeven en getoetst in contexten, terwijl bij de zaakvakken het rekenen op een natuurlijke wijze zker ook aan de orde komt: alles wat getalsmatig is, verbanden tussen of tenminste reeksen van getallen, benoemde getallen,. en ga zo maar door. Dat laatste hoort, en is een prima gelegenheid om te laten zien waar rekenvaardigheid nuttig voor is behalve voor rekenen zelf. Een zaakvak is een ideale context, zou je kunnen zeggen. Terwijl de typische contextopgave in het rekenonderwijs en de rekentoets van een ongekende armzaligheid is: een context van super korte duur, een snipper wereldkennis waar ook nog eens de eis aan gesteld mag en moet worden dat álle leerlingen voldoende van dat nievau van wereldkennis hebben (als zaakvak zou het dus geen donder voorstellen!). Ongelooflijk. Nog daargelaten de twijfelachtigheid van het vooronderstelde transfer-probleem waarvoor dat hele leren-in-contexten een oplossing zou moeten bieden.
In de LinkedIn-groep PO-Netwerk heb ik naar aanleiding van uitspraken van staatsseceretaris Dekker dat de Cito Eindtoets Basisonderwijs een ‘objectieve’ toets zou zijn, over die uitspraak een discussie geopend. Daarin werd door Geeke Bruin-Muurling de vraag gesteld naar wat goed rekenonderwijs is, althans persoonlijke opvattingen daarover. Dat bracht mij tot het volgende lijstje van acht punten. Zie ook de discussie op LinkedIn.
(1) Goed rekenonderwijs geeft een basis voor gezond en ook overigens goed functioneren in het leven. (gezondheid: Reyna c.s. 2009 http://goo.gl/kgErd) (voor financiële kwesties in het leven geldt ongetwijfeld hetzelfde) (Hier helpen geen rekenmachientjes http://goo.gl/Amjm8) (Zie ook Lynn Steen 1999 http://goo.gl/cgdW6)
Valerie F. Reyna, Wendy L. Nelson, Paul K. Han & Nathan F. Dieckmann (2009). How Numeracy Influences Risk Comprehension and Medical Decision Making. Psychological Bulletin, 135, 943-973. pdf
(2) Goed rekenonderwijs maakt het meer leerlingen mogelijk om in vervolgonderwijs exacte profielen/opleidingen te kiezen, en daar ook beter in te presteren. (Siegler c.s. 2012 http://goo.gl/yLJKl)
R. S. Siegler, G. J. Duncan, P. E. Davis-Kean, K. Duckworth, A. Claessens, M. Engel, M. I. Susperreguy & M. Chen (2012). Early predictors of high school mathematics achievement. Psychological Science. concept
(3) Beter rekenonderwijs is al te bereiken door eens op te houden met het rekenonderwijs te gebruiken om leerlingen te ‘leren denken’. http://goo.gl/qnMuB
(4) Beter rekenonderwijs is al te bereiken door het gekleuter drastisch te schrappen: weg met de kleurdoos en de leuk bedachte rekenpuzzeltjes. http://goo.gl/EHL9Q
(5) Jan van de Craats geeft in zijn ‘Daan en Sanne kunnen niet rekenen’ uitstekende uitgangspunten voor goed rekenonderwijs http://goo.gl/R3Ckn. Zie ook zijn voorstel voor een ‘alternatieve kennisbasis rekenen en wiskunde voor de pabo’ http://goo.gl/Ns4L6. Bij de PPON is ook gevraagd naar voorkeur voor en gebruik van realistisch kolomrekenen en standaard-algoritmen: realistisch kolomrekenen blijkt dan een marginaal verschijnsel te worden http://goo.gl/dWhj2
(6) De Noordhoff-methode ‘Reken zeker’ werkt de uitgangspunten van Van de Craats concreet uit http://goo.gl/MOEIQ maar heeft onvermijdelijk (gezien de heersende staatsdidactiek die realistisch van snit is) nog wel overmatig te worstelen met contexten (‘leren denken')
(7) We moeten ophouden met het afnemen van landelijke rekentoetsen die in feite verschillen in intellectuele capaciteiten toetsen (Wilbrink c.s. 2012 http://goo.gl/9OzGo) en terug naar rekentoetsen zoals nog in Goffree, Hiddink en Dijkshoorn 1970 te vinden ( bv http://goo.gl/a4CwY) of in deel 1 van de rekentoets-3S (commissie-Van de Craats http://staff.science.uva.nl/~craats/#rtw3S)
(8) Voor PISA en TIMSS (Scheerens c.s. http://goo.gl/1DdfG) geldt het laatste waarschijnlijk ook; Nederlandse scores geven waarschijnlijk ook een vertekend beeld door niet-representatieve deelname. Ergo: PPON is het beste dat we nu hebben, en de resultaten voor rekenvaardigheid zijn beroerd (onderzoek Hickendorff http://goo.gl/OHVyB) ( http://goo.gl/uAexu)
De spagaat voor het basisonderwijs is dat goed rekenonderwijs en de rekentoetsen van het Cito (LVS, Eindtoets) in het geheel niet op elkaar aansluiten. Het Cito werkt uitsluitend met contextvragen, waarvan vermoed mag worden dat ze vooral verschillen in intellecuele capaciteiten toetsen. Onderwijs geven met als doel ‘intelligentie’ te verhogen, is een ijdele onderneming. Dus ook: rekenonderwijs in de vorm van contextopgaven verspilt kostbare tijd van leerlingen. De beste voorbereiding op Cito-rekentoetsen bestaat waarschijnlijk uit het geven van goed rekenonderwijs, en de leerlingen vertrouwd maken met contextopgaven. Voor de scholen is het helemaal niet zo’n gek idee om naast de rekentoetsen in het LVS ook ‘gewone’ rekentoetsen af te nemen: die zijn eenvoudig op te stellen, in korte tjd door de leerlingen te maken, en eenvoudig te administreren. NB: in het aanbieden van echte rekentoetsen heeft het Cito geen verdienmodel; dat is ongetwijfeld een reden waarom ze zo ingewikkeld doen met contextopgaven/redactiesommen.
Een en ander sterkt mij in de gedachte dat het de hoogste tijd is om die contextopgaven-misstand aan te pakken. Het ligt nu voor de hand om voor ‘Examens’ een volgende artikel te schrijven, waarin de stelling dat rekenopgaven in de vorm van contextopgaven vooral verschillen in intelligentie testen, een uitwerking krijgen in de thematiek van de uitsplitsing van contexten en zuivere rekenopgaven. Dit is precies het thema dat Joost Hulshof aan de orde stelde in de expert-meeting van Victor Schmidt, april 2011, waar de aanwezige experts mee instemden, en waar de commissie-Schmidt vervolgens niets mee heeft gedaan.
Ik heb al een korte emailwisseling gehad met Annemarie van Eekelen, hoofdredacteur van Examens. In het laatste nummer van dit jaar zou zo’n artikel mee kunnen gaan. Het zal vooral een artikel met psychologische argumenten zijn, waarschijnlijk ga ik opnieuw medewerking zoek van Denny Borsboom, of misschien (ook) van Lieven Verschaffel. Maar eerst moet ik een voorlopige opzet van een dergelijk artikel formuleren, een opzet waaruit duidelijk moet zijn dat zo’n artikel mogelijk is en dat het als een bom zal inslaan in Arnhem. Nou ja, ik overdrijf, en ik mag niet onaardig zijn tegen het Cito. Tenslotte heeft Anton Béguin goed meegewerkt aan het promotieonderzoek van Marian Hickendorff. Wat me doet bedenken dat ik zou kunnen proberen het artikel (‘intellectuele capaciteiten in contexten’) zó te schrijven dat het een uitnodiging is om op het onderwerp een promotieonderzoek te laten doen (niet door mij).
Zie verder de ontwikkelpagina voor het bedoelde artikel: capaciteiten_in_contexten.htm. Dat is voorshands vooral een verzameling van relevante onderzoeksbronnen, met korte annotaties, maar dat is al verrassend genoeg.
Het idee is nu wat verder aangescherpt: voor typische contextsommen zoals in de Cito Eindtoets Basisonderwijs laten zien hoe de onderzoeksliteratuur uitwijst dat dergelijke opgaven vooral testen op verschillen in intellectuele capacitetien, en veel en veel minder op verschillen in rekenvaardigheid. Ik wil de analyse dus echt inperken tot specifiek die contextopgaven. De verborgen agenda is natuurlijk: wat geldt voor deze eenvoudige contexten in rekentoetsen, moet zeker ook gelden voor de uitgebreidere contexten zoals die typisch in de huidige eindexamens voorkomen, in ieder geval die examens welke door het Cito worden verzorgd (onder verantwoordelijkheid van het College voor Examens).
Stephen W. Raudenbush (2008). Advancing Educational Policy by Advancing Research on Instruction. American Educational Research Journal, 45, 206-230. abstract
Ik zal de deelnemers vragen wat zij van deze middag verwachten: welke rekennood geledigd, welk rekenprobleem verhelderd, enz. Een knellende vraag is natuurlijk ‘Wat is goed rekenonderwijs?’ Ik zal de aangedragen onderwerpen aan bod te laten komen: we hebben een vrijelijk in te vullen programma.
Mijn eigen doel is dat de middag een andere houding tegenover de rekenproblematieken in het PO oplevert, of die houding bevestigt: dat het mogelijk is om er greep op te krijgen, om te weten waar je als school mee bezig bent, om resultaten te boeken, en resultaten te monitoren.
Deze webpagina blijft voorlopig bestaan, en zal af en toe een aanvulling krijgen. Mail mij wanneer er vragen/suggesties/kritieken zijn.
Dit is een huiswerkopgave voor een kleinzoon. Voor mij is dit ongeveer het toppunt van gekkigheid: kleuteren, kleuren, irrelevante dingen moeten doen zoals zoeken in het tabelletje, en mogelijk ook: ontdekken dat iedere slang, als het goed is, maar één kleur heeft. Wereldkennis! De wirwar was zo groot, dat ook opa met de handen in het haar zat (er zijn opgaven waarvan het antwoord NIET in het tabelletje staat). Slotconlusie: niet IK ben gek, maar ZIJ zijn het. Ik heb geen idee uit welke methode, if any, deze opgave afkomstig is.
Een belangrijk ethisch beginsel voor onderwijsgevenden lijkt mij — met Deanne Kuhn — dat tijd van leerlingen niet mag worden verknoeid. ‘Wirwar’ is verknoeien van tijd, wat er verder ook over zijn didactische onzin valt te zeggen. ‘Wirwar’ staat model voor rekendidactische opvattingen waarin de leukigheid belangrijker lijkt dan het rekenen zelf. Ik reken het ook de uitgevers van rekenmethoden aan: blader eens door willekeurig welke huidige rekenmethode, ook ‘Reken zeker’, en verbaas u over de visuele overdaad. Dit is wat de kosten van rekenmethoden betreft een verlies-verlies-situatie: door het beeldmatig optuigen van rekenmethoden worden deze kostbaar, terwijl het tegelijk de didactische doeltreffendheid vermindert.
Aantekening bij de laatste opmerking: scholen kunnen natuurlijk een eigen, sobere maar uiterst doeltreffende rekenmethode ontwikkelen. Ik ken daar nog geen actuele voorbeelden van, wèl van een wiskundemethode (Barlaeus, wiskunde voor het eerste leerjaar, zie hier om de cursus te downloaden).
http://www.benwilbrink.nl/projecten/rekenen_27-3-2013.htm
http://goo.gl/4fzKX
Ook via http://www.benwilbrink.nl/projecten/rekenen_15-4-2013.htm