stukken bij Cesuurbepaling 1977

Uitgave in de serie docentenkursussen van het Centrum voor Onderzoek van het Wetenschappelijk Onderwijs


CESUURBEPALING

kursus 6       eerste versie

ben wilbrink

mei 1977

Universiteit van Amsterdam


0       VOORWOORD blz. 3
0.1     tekstwijzer

1       MOTIVERING VOOR DE CURSUS blz. 5
1.1     strekking van de cursus
1.2     het belang van, en de ruimte voor, verbetering van cesuurbepaling.
1.2.1   eerste vraag aan de lezer
1.2.2   toelichting op de beantwoording van de vragen
1.2.3   tweede vraag aan de lezer
1.2.4   toelichting op de beantwoording van de vragen
1.2.5   derde vraag aan de lezer
1.2.6   uitbreiding van de analyse: optimaal kiezen van de aftestgrens
1.3     risico's van cesuurbepaling: onnodige studieduurverlenging
1.3.1   foute beslissingen in soorten
1.3.2   oplossingen ook in onderwijs en beoordelingsstelsel zoeken

2       UITGANGSPUNTEN VOOR VERANTWOORDE CESUURBEPALING
2.1     overzicht van te presenteren uitgangspunten

3       LOSKOPPELING VAN ANDERE ONDERWIJSDOELEN
3.1     examenregeling en cesuurbepaling
3.2     exameneisen: het hordenloop model
3.3     koppeling van selectie en cesuurbepaling bijzonder inefficiënt
3.4     illustratieve vergelijking van conjunctieve en compensatorische examens
3.5     conclusies voor het dagelijks beleid van de docent (vakgroep)

4       TRANSPARANTIE VAN TOETS EN AFTESTGRENS blz. 22
4.1     voorbeeld van een redelijk transparante procedure
4.2     de Hofstee variant van transparantie
4.3     toets-transparantie: hoe te realiseren op korte termijn
4.4     op korte termijn overgaan van meerkeuze- op open-eind-vragen
4.5     aanpak van toetstransparantie op wat langere termijn
4.6     voorbeeld van uiteenleggen van leerstof en vraagconstructie
4.7     transparantie (?) bij meerkeuzevragen
4.8     transparantie van de aftestgrens bij schriftelijke tentamens
4.9     onderscheid tussen objectieve en transparante aftestgrens
4.10   transparantie: minimaal te behalen score vooraf bekend
4.11   de pechfactor waar de student mee moet rekenen
4.12   conclusies voor het dagelijks beleid van de docent (vakgroep)
inhoud

5   BEHOORLIJKE INSPANNING IS VOLDOENDE blz. 50

5.1     wat is behoorlijke studie-inzet?
5.2     behoorlijke inspanning ook voldoende beoordelen: een noodzakelijke (maar niet voldoende) voorwaarde voor transparantie
5.3     betekent dit verlaging van eisen?
5.4     conclusies voor het dagelijks beleid van de docent (vakgroep)

6       BIJ BESLISSINGEN OVER PERSONEN GELDEN REGELS blz. 56

6.1     Algemene Beginselen van Behoorlijk Bestuur
6.1.1   fair play
6.1.2   zorgvuldigheid
6.1.3   zuiverheid van oogmerk
6.1.4   verbod van willekeur
6.1.5   gelijkheid
6.1.6   rechtszekerheid
6.1.7   vertrouwen
6.1.8   motivering
6.2     Standards for Educational and Psychological Tests.
6.3     toevallige invloeden: raden bij meerkeuzetoetsing
6.4     toevallige invloeden: de vragen waaruit de toets is samengesteld
6.5     toevallige invloeden: andere bronnen van ordeverstoring
6.6     stelselmatige invloeden: interpretatie van toetsscores
6.7     conclusies voor het dagelijks beleid van de docent (vakgroep)

7       DE AFTESTGRENS OPTIMAAL KIEZEN blz. 85

7.1     een voorbeeld van de techniek
7.2     hoe is het verlies van foute beslissingen te bepalen?
7.3     discussie

BIJLAGE blz. 95
BIBLIOGRAFIE blz. 101

 

0 VOORWOORD.

In deze cursus wil ik laten zien hoe beslissingen voor afsluitende tentamens op verantwoorde wijze te nemen zijn. Hoe je dat probleem ook aanpakt, de beste oplossingen leiden tot het afschaffen van een merkwaardige gewoonte die wij Nederlanders (en vele andere Europeanen) in ons onderwijs koesteren: nogal wat onvoldoendes uitdelen, en daarbij ook nog eisen dat de studenten de betreffende studieonderdelen overdoen tot ze wel voldoende zijn. Vandaar dat ik naast beschrijving van de aanpak van het cesuurprobleem in deel 2, een reeks argumenten presenteer om in ieder geval het instituut onvoldoendes worden ingehaald af te schaffen. De argumenten voor afschaffing van het overdoen zijn nogal uiteenlopend van aard, en voor de lezer waarschijnlijk in hoge mate verrassend.(tot het verschijnen van deel 2 is een samenvatting verkrijgbaar).

Het is niet onwaarschijnlijk dat de lezer de kwalificatie verrassend als nogal eufemistisch gaat beschouwen. Veel argumenten zullen op het eerste gezicht onwaarschijnlijk, onjuist, of weerzinwekkend lijken. Daarom wil ik hier in het kort ingaan op aard en functie van onderwijskundige producties als deze.

De docent is, niet onbegrijpelijk, geneigd om de boodschap van onderwijskundigen te toetsen aan zijn eigen ervaringen in het onderwijs, zowel waar het om het geven van onderwijs gaat, als om inzichten in capaciteiten van studenten, de beste methode om kennis en inzicht van die studenten te toetsen, en de wijze waarop je selectie voor het onderwijs zou moeten inrichten. De inzichten die de docent zich al doende eigen maakt omtrent onderwijs en alles wat er zoal mee samenhangt, zijn echter noodzakelijk onsystematisch, gekleurd door persoonlijke opvattingen en toevallige ervaringen, beïnvloed door niet noodzakelijk juiste common sense ideeën. De gedachtenwereld van de docent staat bijna per definitie op gespannen voet met die van de onderwijskundige. Daarmee bedoel ik het volgende: het is eenvoudig niet de taak van de onderwijskundige om de docent te bevestigen in zijn ideeën over hoe je onderwijs verzorgt. De samenleving heeft geen behoefte aan onderwijskundigen die bestaande onderwijs praktijken bevestigen (tenzij toevallig het resultaat van alle onderzoek zou zijn dat de manier waarop we het tot nu toe gedaan hebben, inderdaad de beste is), maar aan onderwijskundigen die direct of indirect de nodige informatie verschaffen om dat onderwijs te verbeteren (vernieuwen) Dezelfde gedachtengang is van toepassing op de vraag op welke punten dat onderwijs dan wel in eerste instantie voor verbetering vatbaar zou zijn: ook daar is vaak te constateren dat er een grote afstand bestaat tussen wat de docent, in de praktijk van het onderwijs, als de belangrijkste tekortkomingen van dat onderwijs ziet, en wat de onderwijskundige aanwijst als de belangrijkste te repareren tekorten. De kloof in denkwereld is in dit geval ernstiger dan het verschil van mening dat je met de loodgieter kunt hebben over wat de oorzaak van een bepaalde lekkage kan zijn: we zijn nu eenmaal makkelijker geneigd een vraagteken te plaatsen achter onze amateuristische kennis van het loodgieten dan achter onze kennis van het onderwijs. En ach, dat geeft ook niet, zolang beide partijen zich er maar een beetje bewust van zijn: de onderwijskundige dat hij voor zijn uiteenzettingen niet direct op een al te willig gehoor mag rekenen, en de man of vrouw uit de praktijk dat hij er niet op moet rekenen van die onderwijskundige argumenten te horen die hem of haar direct zullen bevallen.

Zo ook met deze cursus. Hij zou niet geschreven zijn, wanneer de inhoud ervan niet verrassend zou zijn, wanneer de docent zich af en toe niet eens behoorlijk aan de vreemdheid van de hier gepresenteerde ideeën zou stoten. Met mijn waarschuwing hoop ik te bereiken dat deze cursus wat minder in ergernis, en meer in bereidheid om althans de argumenten een kans te geven, gelezen wordt. Dan zullen er toch nog punten van commentaar en kritiek genoeg overblijven.

0.1 Tekstwijzer

Het voornaamste doel van deze cursus is het stimuleren van discussie over methoden van cesuurbepaling, en de aard van gehanteerde examenregelingen. Voor degenen die een bescheiden begin willen maken met het opzetten van verantwoorde beslissingsprocedures langs de in deze cursus te schetsen lijnen, worden voldoende aanwijzingen gegeven. Het was echter niet mogelijk om tot in details de technieken en methoden in deze cursus uit te werken: de omvang van de cursus zou veel te groot worden, en het uitbrengen ervan zou nog geruime tijd op zich laten wachten. Wie met de summiere praktische aanwijzingen in deze cursus, begrijpelijkerwijze, niet goed uit de voeten komt, kan met de auteur contact opnemen voor meer gedetailleerde informatie of op zijn of haar specifieke onderwijssituatie beter toegesneden adviezen.

De hoofdstukken zijn nogal ongelijk van karakter: In hoofdstuk 1 wordt de cursus gemotiveerd door te laten zien dat er inderdaad nog erg veel ruimte is om tot verbetering van beoordelingsprocedures te komen. In de volgende hoofdstukken worden richtlijnen gegeven die ófwel kunnen dienen om voorgestelde procedures voor het nemen van zak-slaagbeslissingen aan te toetsen, ófwel gebruikt kunnen worden om passende procedures te ontwikkelen. Technieken die voor dat laatste nodig zijn, worden in de tekst summier aangegeven. Omdat cesuurbepaling voor afzonderlijke studieonderdelen niet los gezien kan worden van het soort examenregeling dat gehanteerd wordt, was het noodzakelijk ook aan de huidige examenregeling in het w.o. kritisch aandacht te schenken(in deel 2).

Tenslotte nodig ik de lezer uit tot het leveren van kritiek of aanvullingen, vooral ook van hen die dat vanuit hun eigen vak (rechten, economie, besliskunde, onderwijskunde, psychologie) kunnen doen. Bijzonder veel prijs stel ik ook op het vernemen van ervaringen die opgedaan worden bij het ten uitvoer leggen van aanbevelingen uit deze cursus.

Hoofdstuk 1.
MOTIVERING VOOR DE CURSUS.

Waarom opnieuw zoveel aandacht gevraagd voor de problematiek van het bepalen van zak-slaaggrenzen, terwijl er toch al het een en ander aan literatuur op dit gebied ter beschikking is en bij vele docenten ook bekend is? (kernitem methoden, methode Wijnen, e.d.). En waarom de presentatie niet beperkt tot een overzicht van reeds eerder gepresenteerde methoden, in plaats van een aanpak te presenteren die een geheel nieuwe overdenking van het probleem vraagt?

Beantwoording van deze vragen is eigenlijk niet goed mogelijk zonder het hele rapport door te nemen. Voor de lezer, u dus, is dat een behoorlijke dooddoener, omdat de vraag op dit moment is: Wat heb ik hieraan? Waarom zou ik deze cursus door moeten werken? Is de manier waarop ik tot vandaag de zak-slaaggrens voor mijn tentamen vaststelde voor forse verbetering vatbaar?

Dat vrijwel iedere docent het persoonlijk moeilijk heeft met de vraag waar hij de grens tussen onvoldoende en voldoende moet leggen, is op zich nog geen reden om een cursus te organiseren in het verantwoord bepalen van zak-slaaggrenzen. De zin van een dergelijke cursus hangt af van de adviezen en technieken die gegeven kunnen worden en van de belangstelling die de docent heeft voor dergelijke informatie. Of de cursus bruikbare nieuwe informatie en technieken bevat, zal bij het doorwerken er van moeten blijken.

Omdat ik van niemand kan en wil vragen tijd en energie te steken in een onderneming die draait zonder investeringsgaranties, wordt in paragraaf 1.2 een demonstratie gegeven van de ruimte die er nog steeds is om tot verbeteringen in de cesuurbepaling te komen. De bedoeling is hier allereerst om belangstelling voor cesuurbepalingsmethodieken te wekken, of om al belangstellende lezers in hun motivatie te bevestigen.

Dat er bij het uitdelen van onvoldoendes en voldoendes fouten gemaakt worden mag bekend heten. Het beantwoorden van de vraag: Hoeveel fouten ongeveer? is de uitdaging aan de lezer, in paragraaf 1.2 gepresenteerd. Mijn verwachting is dat de docent niet in staat zal zijn een behoorlijke gok te doen, hoewel ik hem alle relevante informatie zal geven. De te geven informatie is dezelfde als waarover de docent, u dus, altijd al kon beschikken. De schatting van het aantal fouten die u geeft is een soort maat voor het geloof dat in de eigen cesuurbepaling gesteld wordt. Dat geloof zal ik vervolgens op de proef stellen door uw schatting te vergelijken met de mijne, afgeleid uit een zeer eenvoudig model. De discrepantie tussen beide schattingen zal groot genoeg zijn om verdere bestudering van deze cursus te kunnen motiveren.

Mocht de demonstratie in paragraaf 1.2 in een enkel geval mislukken, dan doe ik in paragraaf 1.3 nog een geheel andere poging om de praktische relevantie van het in deze cursus gebodene te laten zien. Het gaat dan niet zozeer om de wijze van cesuurbepaling zoals de individuele docent (vakgroep) die toepast, maar om de effecten van het gebruikelijke beoordelingsstelsel op de studie als geheel. In het bijzonder wil ik laten zien dat zonder kwaliteitsverlies van de studie de duur ervan gemiddeld met een half jaar (ruw geschat) teruggebracht kan worden. En dat is te realiseren door enkele administratieve maatregelen die, vergeleken met de herstruktureringsoperatie, van eenvoudige aard kunnen zijn.

1.1 Strekking van de cursus.

Een aantal uitgangspunten worden geformuleerd, waaraan cesuurbepalings-methoden bij voorkeur moeten voldoen. De uitgangspunten zijn van nogal uiteenlopende aard: sommige bevatten aanwijzingen voor de uitvoering van de beslissingsprocedure, andere bevatten normen waaraan beslissingsprocedures (in redelijke mate) moeten voldoen.

Bekende cesuurbepalingsvoorstellen kunnen tegen deze uitgangspunten getoetst worden. Dat gebeurt (in de bijlage) met de kernitem methoden, en met de methode Wijnen. Geen van deze methoden zal aan minimale voorwaarden blijken te voldoen. Voor de methode Wijnen wordt daar echter als belangrijke aantekening bij gegeven dat zij wel, en bij voorkeur, bruikbaar is in al die situaties waarin niet over de nodige gelegenheid en informatie beschikt kan worden om de cesuurbepaling in overeenstemming met de gegeven uitgangspunten op te zetten.

Het gaat er in de hier te presenteren benadering inderdaad om dat de wijze van cesuurbepaling geconstrueerd moet worden in overeenstemming met de gepresenteerde uitgangspunten. Het zou bijzonder toevallig zijn wanneer een bepaalde gegeven methode in een bepaalde onderwijssituatie in overeenstemming zou blijken te zijn met de genoemde uitgangspunten.

De doelstellingen van de cursus zoals hij voor u ligt zijn tamelijk bescheiden: inzicht bij te brengen in de ruimte voor verbetering van de gebruikelijke cesuurbepalings-methoden (paragraaf 1.2), demonstratie van de wijze waarop gebruikelijke cesuurbepalings-methoden tekort schieten, adviezen voor het korte termijn beleid van de docent en het lange termijn beleid van docenten en faculteit, en wat deel 2 betreft: inzicht bij te brengen in de mate waarin huidige beoordelingsgewoonten bijdragen tot onnodige studieduurverlenging. Op basis van het laatst genoemde betoog over mogelijkheden om door veranderde beoordelingsgewoonte de studieduur te verkorten zonder kwaliteitsverlies, zou subfaculteitsbeleid (bijv.) gevoerd kunnen worden.

Kortom: het gaat er om dat de docent na doorwerking van de cursus een goed inzicht in de problematiek rond de cesuurbepaling heeft, en op grond van dat inzicht gemotiveerd is geraakt om metterdaad veranderingen in beoordelingsprocedures door te voeren.

1.2 Demonstratie van het belang van, en de ruimte voor, verbetering van de cesuurbepaling.

Zowel bij docenten als bij onderwijskundigen is onvoldoende bekend in welke mate er foute beslissingen genomen worden bij de beoordelingsprocedures zoals wij die in het wetenschappelijk onderwijs kennen. Uiteenzettingen over cesuurbepalingsmethoden bevatten vrijwel nooit een aanduiding over de mate waarin het aantal foutieve beslissingen door deze methoden teruggebracht wordt, laat staan dat aannemelijk gemaakt wordt dat de aangeprezen methode resulteert in een minimum aan fouten (dat in de gegeven situatie haalbaar is). Het vertrouwen dat de onderwijskundige in de door hem gepresenteerde methoden heeft wordt in dit opzicht geëvenaard door het vertrouwen dat de docent doorgaans heeft in de mate waarin de door hem genomen zak-slaagbeslissingen ook terecht zijn.

Ik hoop dat de lezer de uitdaging aanneemt, en meedoet aan de volgende proef op de som. Ik geef straks een beschrijving van een bepaalde zakslaag beslissing genomen voor een denkbeeldig tentamen. Ik geef daarbij alle relevante informatie om tot een goede schatting van het aantal foute beslissingen te kunnen komen: een omschrijving van wat ik met 'foute beslissing' bedoel, de gekozen aftestgrens (in termen van % onvoldoendes), de betrouwbaarheid van de toets (KR 20), en dat de scores op de toets op de bekende belvormige wijze verdeeld zijn (een meer technische term: normaal verdeeld. Maar trekt u zich niets van die terminologie aan). Wanneer voor uw eigen tentamens geldt dat de scores niet al te eenzijdig aan één kant van de score schaal opgehoopt plegen te liggen, kunt u het best dergelijk soort resultaat in gedachten nemen.

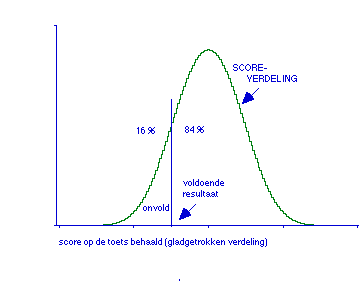
77Cesuur1COWO359281.gif
horizontaal: score op de toets behaald (gladgetrokken verdeling)
verticaal: aantal studenten dat een bepaalde score op de toets haalde

FIGUUR 1.2.1 Cesuur zo getrokken dat 16 % onvoldoende krijgt.

 
In figuur 1.2.1 is een schets gegeven van de situatie. Op de horizontale as zou het aantal goed gescoorde items op de toets kunnen staan; omdat ik hier afzie van het bepaalde aantal items dat de toets had, zijn er geen concrete getallen ingevuld. De getekende curve geeft de aantallen studenten die een bepaalde totaalscore behaalden; omdat we niet geïnteresseerd zijn in allerlei toevalligheden zoals die tot uiting komen in een bepaalde scoreverdeling bij een bepaalde tentamenafname, is de curve te zien als een gladgetrokken freguentieverdeling (een frequentieverdeling van het soort zoals op de meeste computer scoringen in de output gegeven wordt).

1.2.1 Eerste vraag aan de lezer.

In figuur 1.2.1 is de situatie geschetst die als gegeven wordt beschouwd. In dit geval wordt 16 % van de studenten beloond met een onvoldoende beoordeling. Wie (terecht) liever niet denkt in termen van af te wijzen percentages studenten, kan die 16 % beschouwen als bijvoorbeeld het resultaat van toepassing van de kernitem methode, of een andere gebruikelijke aanpak.
Ga ervan uit dat de toets bestaat uit vragen over een stuk leerstof van niet al te uiteenlopend karakter, zodat de KR 20 waarde gebruikt mag worden als schatting voor de betrouwbaarheid van de toets als meetinstrument (gemakshalve ga ik er van uit dat de lezer in het verleden al geconfronteerd is geweest met de noodzaak om zak-slaaggrenzen voor zijn tentamen te bepalen, en dat hij eigenlijk met begrippen als betrouwbaarheid e.d. vertrouwd zou moeten zijn. Is dat niet het geval, lees er dan voorlopig gewoon overheen en probeer gewoon naar beste overtuiging de gestelde vragen te beantwoorden. Tenslotte is dit geen cursus over toets constructie maar over cesuurbepaling.

Gegeven: KR 20 = .60. Dat is een niet al te hoge waarde, maar voor de meeste door docenten zelf in elkaar gezette studietoetsen wel reëel.

Ga ervan uit dat er een tweede toets is samengesteld over dezelfde stof, met dezelfde soort vragen, en met dezelfde relevante toetseigenschappen als de eerste toets. De vraag die gesteld gaat worden heeft betrekking op enkele resultaten die u denkt dat afname van deze tweede toets (bijv. direct na de eerste toets) bij dezelfde groep studenten zou opleveren. Dit experiment-in-gedachten is dus een herhaling, een replicatie, van de cesuurbepaling.

Wat met een foute beslissing bedoeld wordt, is in de stam van de vraag beschreven. De meerkeuze vraagvorm heb ik gebruikt om bij de beantwoording van de vragen enig houvast te geven voor wat betreft de aard van het antwoord dat hier verlangd wordt. Het juiste antwoord zal in de tekst gegeven worden.

Voordat we overgaan tot bespreking van de juiste antwoorden kan de lezer zichzelf misschien nog verbeteren: Merk op dat beide aangestreepte antwoorden samen 16 % moeten zijn! (omdat op de tweede toets 16 % onvoldoendes gegeven worden). Pas zo nodig beide of één van beide antwoorden aan deze randvoorwaarde aan. Wie het nu al leuk begint te vinden, kan uit de door hem zelf gegeven antwoorden nog afleiden welk percentage van de totale groep studenten op beide toetsen voldoende beoordeeld zou worden.

1.2.2 Toelichting op de beantwoording van de vragen.

Wanneer KR 20 gebruikt mag worden als de betrouwbaarheid van de toets als meetinstrument, dan betekent KR 20 = .60 dat deze studietoets een correlatie heeft van .60 met een parallel toets (toets die over dezelfde stof gaat, met dezelfde soort vragen, en dezelfde toetseigenschappen). Wat correlatie is, hoeft hier niet uitgelegd te worden: waar het om gaat is dat voor het afwijzingspercentage van 16 % op de ene zowel als op de andere toets in tabellen voor de normaalverdeling en de bivariate normaalverdeling (zie bijlage) opgezocht kan worden (hoewel berekening natuurlijk ook mogelijk is) welk percentage van de totale groep op beide toetsen een onvoldoende zal behalen, welk percentage op de eerste een voldoende, op de tweede een onvoldoende zal halen, etcetera. Welnu, het juiste antwoord op de beide gestelde vragen is respectievelijk ongeveer zeven en een half procent en acht en een half procent. Vergelijk dat met de door u gegeven antwoorden.

Tabel 1. in de bijlage geeft voor enkele andere cesuren ook de percentages van deze verschillende deelgroepen. De bijlage geeft eveneens een iets uitgebreider en technischer uitleg van het model dan hier in de tekst gegeven werd.

Vanwege de symmetrie is het percentage dat op de eerste toets onvoldoende, en op de parallel toets voldoende beoordeeld zou worden eveneens ongeveer 8.5 %. Het percentage studenten dat op beide toetsen voldoende beoordeeld zou worden is gelijk aan 84 - 8.5 = 75.5 %. Een andere manier is 100 - 7.5 - 8.5 - 8.5 = 75.5%

Voor 8.5 + 8.5 = 17 procent van de studenten geldt dat de beslissing .anders uitvalt al naar gelang ze de ene dan wel de andere toets gekregen zouden hebben, hoewel beide toetsen in alle relevante opzichten als gelijkwaardig beschouwd kunnen worden.

De gegeven vraagstelling en de toelichting er op zijn behoorlijk uitgebreid geweest. De verontschuldigingen daarvoor zijn ten eerste dat het zonder enige toelichting niet erg zinvol zou zijn om de vragen zoals hier geformuleerd, te stellen; ten tweede dat in de uitgebreidheid van de behandeling meteen een stuk exemplarisch denken over cesuurproblematiek gegeven wordt, die de lezer hopelijk de indruk kan geven dat over het nemen van zak-slaagbeslissingen heel goed in heldere termen gesproken kan worden, en dat meningen en opvattingen heel goed ingeruild kunnen worden tegen feitelijke gegevens, of resultaten verkregen op grond van aannemelijke vooronderstellingen (gegoten in de vorm van een model).

De vragen in 1.2.2 waren een aanloopje voor vragen die dieper op de problematiek ingaan. We weten bijvoorbeeld nog niet hoeveel foute beslissingen in het voorbeeld genomen zouden zijn, omdat de toets slechts vergeleken werd met een parallel toets waar óók foute beoordelingen gegeven werden.

De gedachtengang van afnemen van een toets én een parallel vorm van die toets is analoog aan wat er gebeurt wanneer studenten deelnemen aan een herhaling, als de herhaling van tentamen te beschouwen is als een parallel toets voor de eerste toets afname. Wanneer het dan A is dat op de eerste toets 16 % van de deelnemers een onvoldoende kreeg, dan kunnen we uit het antwoord op de beide eerder gestelde vragen concluderen dat van hen die het tentamen over moeten doen de helft een voldoende zou halen ook al weten ze bij de herhaling evenveel van de stof af als de eerste keer. Dit resultaat wordt voor een deel verkregen omdat nogal wat studenten de eerste keer ten onrechte een onvoldoende hadden gekregen (maar daarover straks meer) en voor een deel omdat enkele studenten bij de herhaling ten onrechte een voldoende krijgen. Onder degenen die beide keren een onvoldoende scoren zijn er enkele die ten onrechte beide keren een onvoldoende kregen. In de cursus wordt aan deze samenhangen uitgebreid aandacht besteed.

1.2.3 Tweede vraag aan de lezer.

In i.2.1 werden de beslissingen resulterend uit twee gelijkwaardige toetsen afgenomen over dezelfde groep studenten, met elkaar vergeleken. Daaruit resulteerde bijvoorbeeld het percentage studenten voor wie de uitslag verschillend zou zijn, al naar gelang of de ene dan wel de andere toets gebruikt was. Het is natuurlijk erg belangrijk om een goede indruk te hebben van de mate waarin de tentamenuitslag voor de student door toevallige factoren beïnvloed wordt, en het zou nog beter zijn wanneer we zouden kunnen schatten hoe groot het aantal beslissingen (voldoende, respectievelijk onvoldoende) is waarvoor geldt dat de student ten onrechte zo beoordeeld is. Een ten onrechte gegeven onvoldoende is een onvoldoende die gegeven is aan een student die in wezen de stof voldoende beheerste. Dit soort taalgebruik is een beetje riskant (platonisch zou je ook kunnen zeggen), want wat is een in wezen voldoende beheersing? Er zijn verschillende mogelijkheden om dit begrip te concretiseren, en een voor de hand liggende is de score die de student zou behalen op een perfect betrouwbare toets. Dat perfect betrouwbare toetsen in werkelijkheid ook niet voorkomen mag ons hier niet hinderen, omdat we wél de gedachtenconstructie kunnen maken, en daar relevante conclusies uit kunnen trekken. Iets dat in de buurt komt van een perfect betrouwbare toets is een toets die uit zeer, zeer veel vragen bestaat. Voor de eenvoud: stelt u zich bij de te stellen vragen voor dat de perfect betrouwbare toets een parallel toets is met een bijzonder groot aantal vragen die in principe best gemaakt en aan de studenten voorgelegd zou kunnen worden.

Gegeven: KR 20 = .60. Uit dit gegeven, dat wil ik best verklappen, is af te leiden dat de correlatie van deze toets met zijn perfect betrouwbare parallel toets ongeveer .75 is (om praktische redenen afgerond op .75) (afleiding en toelichting: zie bijlage).

Ga er van uit dat het percentage gegeven onvoldoendes uitkomt op 16 % (laten we ons er niet aan gewennen te denken in termen van hoge afwijzijngspercentages). Ga er ook vanuit dat, mirabele dictu, in wezen ook 16 % van de studenten een onvoldoende verdient, dat is: op de perfect betrouwbare parallel toets een onvoldoende zou krijgen.

Merk op dat het aantal studenten dat een voldoende verdient (84 %) gelijk is aan het aantal studenten dat terecht een voldoende krijgt (het antwoord op de tweede vraag) plus het aantal studenten dat ten onrechte een onvoldoende krijgt (het antwoord op de eerste vraag). De beide gegeven antwoorden moeten dan ook sommeren tot 84 %. Verander zo nodig de aangekruiste antwoorden om aan deze randvoorwaarde te voldoen.

1.2.4 Toelichting op de beantwoording van de vragen.

Op dezelfde wijze als voor de beantwoording van de vragen in 1.2.1 kunnen de gevraagde percentages opgezocht worden in de geschikte statistische tabellen. De resultaten zijn voor beide gestelde vragen respectievelijk zeven procent en zeven en zeventig procent. Vergelijk dat met de schatting die u naar beste weten als antwoorden op de vragen gegeven hebt.

De situatie kan als volgt geresumeerd worden:


Het totale percentage foutieve zak-slaag beslissingen ligt lager dan het percentage beslissingen dat op een parallel toets anders uit zou vallen: voor dat laatste vonden we (in 1.2.2) immers 17 %. Het verschil is begrijpelijk wanneer bedacht wordt dat een even lange parallel toets even feilbaar is als de eerste toets. Op een parallel toets worden natuurlijk evenveel foutieve beslissingen genomen als op de toets waaraan hij parallel is, terwijl op de perfect betrouwbare toets in het geheel geen fouten gemaakt worden (daar is hij perfect betrouwbaar voor). (zie noot 2)


1.2.5 Derde vraag aan de lezer.

Natuurlijk moet je bij het nemen van beslissingen over zakken en slagen enig idee hebben over de mate waarin je dezelfde beslissingen genomen zou hebben wanneer je andere vragen gesteld had die op dezelfde wijze de gestelde onderwijsdoelen zouden dekken. En we hebben gezien dat het niet makkelijk valt om over de relatieve aantallen foute beslissingen optimistisch te zijn.
Maar het gaat bij cesuurbepaling niet om de vraag hoeveel studenten anders beoordeeld zouden zijn wanneer een andere, vergelijkbare toets zou zijn afgenomen. Zak-slaag beslissingen worden met andere woorden niet zomaar genomen, maar op zijn minst met een bepaald (traditioneel impliciet of verzwegen ?) doel. De moeilijkheid met die cesuurbepaling is zelfs dat er zoveel verschillende doelstellingen door elkaar lijken te lopen. Ik noem er een aantal:


Afgezien van mijn woordkeus, die misschien niet helemaal eerlijk is, gaat het hier om voorspellingen: toekomstig studiesucces, beroepsvaardigheid, wat er zou gebeuren wanneer je de eis tot overdoen van onvoldoende tentamens zou laten vallen, de mate waarin de stof in wezen beheerst wordt. Andere doelen of voorspellingen zijn denkbaar.

Het gaat hier om wat in de literatuur validiteitsproblematiek heet. De pretenties zijn behoorlijk hoog, en dat terwijl een halve eeuw onderzoek van precies dit soort pretenties uitgewezen heeft dat er bij gedegen onderzoek niet veel van over blijft. Laten we zeggen dat de validiteit van uw tentamen voor een belangrijk doel dat u daarbij altijd voor ogen heeft gestaan, .35 is. Een beetje technisch misschien, maar dat geeft niet: die technische taal is alleen nodig om een antwoord op de volgende vragen te kunnen berekenen. Om het voorbeeld te concretiseren: stel dat u altijd verondersteld hebt dat er een samenhang bestaat tussen op uw tentamen behaalde cijfers, en studieresultaten in een latere fase van de studie, en dat die samenhang gekwantificeerd kan worden als een correlatie van .35 (correlatie van tentamencijfer met bijvoorbeeld gemiddeld cijfer in het laatste studiejaar). Laten we zeggen dat ook in dat gemiddeld studieresultaat in het laatste jaar van de studie een kritische grens aangegeven kan worden, waarboven de prestaties voldoende zijn, en waar beneden de prestaties onvoldoende zijn, en dan gebleken is dat (toevallig) 16 % van de studenten uiteindelijk niet aan deze norm voldoet. Voor uw tentamen worden ook 16 % van de studenten als onvoldoende beoordeeld, en de kwaliteit van die beslissing wordt afgemeten aan het aantal foute beslissingen wanneer latere studieresultaten in aanmerking worden genomen.


Het was waarschijnlijk een erg lastige vraag, omdat ik niet voldoende heb toegelicht waarom het hier eigenlijk gaat. Ik heb dat niet gedaan, omdat een korte toelichting niet goed mogelijk lijkt zonder meer problemen op te roepen dan op te lossen. Misschien kan ik het nog eens als volgt zeggen: Cesuurbepaling kan natuurlijk geen kunst om de kunst zijn. Het gaat altijd ergens om, en dat kan bijvoorbeeld het veronderstelde verband met later studiesucces zijn. De gedachtengang achter die cesuurbepaling zou dan moeten zijn dat iemand met een onvoldoende gewoon door laten studeren met een grote mate van waarschijnlijkheid tot brokken zal leiden, terwijl het laten overdoen dat kan voorkomen (dat voorkomen is op twee manieren te denken: ofwel de student herstelt zich bijtijds en behaalt alsnog een voldoende, ofwel de student heeft er zoveel moeite mee dat hij besluit niet door te studeren (een beslissing die meestal niet los zal staan van moeilijkheden die hij ook al met andere vakken had)). Welnu, een dergelijk verondersteld verband is niet geheel onschuldig: er worden ondertussen mensen op afgewezen. Dergelijke veronderstelde samenhangen behoren dan ook uitgesproken, onderzocht, en gekwantificeerd te worden. Al was het alleen maar omdat voor afwijzende beslissingen over mensen tenminste enige argumentatie gegeven moet kunnen worden. (zie 6. 1 ).

In het gegeven voorbeeld waarover de vraag gesteld werd, was de veronderstelling dat de veronderstelde samenhang bekend was, nl. .35. Bovendien werd verondersteld dat er een duidelijke grens aangewezen kon worden tussen voldoende en onvoldoende gemiddelde prestatie in de latere studie (16 % van de studenten zou onvoldoende prestaties leveren). Dat is nogal een boude veronderstelling, maar het is hier niet de plaats om daar verder op in te gaan (ik wil wel kwijt dat het niet mijn veronderstelling is, maar veeleer de impliciete veronderstelling van al diegenen die voldoendes en onvoldoendes uitdelen).

In de geschetste situatie beschikken we dan over alle nodige gegevens (aangenomen dat ook studieprestaties in de latere studie normaal verdeeld zijn), om in de geschikte tabellen het gevraagde percentage op te zoeken. Dan blijkt dat 11 % van de studenten op het tentamen een onvoldoende krijgen terwijl hun toekomstige studieprestaties voldoende zijn. Voor slechts 4 % van de studenten geldt in de geschetste situatie dat hun onvoldoende beoordeling ook terecht was, opgevat als voorspelling van later studiesucces.

In de bijlage worden tabellen gegeven voor andere cesuren, en voor meerdere correlaties met de toepasselijke criterium variabele (alweer zo'n technische term, waar voor dit moment rustig overheen gelezen kan worden).

1.2.6 Uitbreiding van de analyse: optimaal kiezen van de aftestgrens.

op twee manieren werd tot nu toe bekeken welke foutieve beslissingen er bij zak-slaag beslissingen vallen. Het beeld dat daaruit te voorschijn kwam over de kwaliteit van zak-slaag beslissingen kan moeilijk rooskleurig genoemd worden. Toch is de situatie nog slechter dan dat. Om dat te demonstreren, niet uit sadisme maar om het belang van overdenking van de cesuurproblematiek zo duidelijk mogelijk te maken, zal deze inleidende analyse van het probleem op twee manieren uitgebreid worden. Allereerst moet er rekening mee worden gehouden dat ten onrechte een onvoldoende geven in veel onderwijssituaties meer betreurd moet worden dan ten onrechte een voldoende geven. Vervolgens moet dan nog de vraag beantwoord worden welke zin het eigenlijk heeft om onvoldoendes uit te delen, ook al zouden die terecht zijn.

Wil je de aftestgrens in bepaalde opzichten optimaal kiezen, dan moet er rekening gehouden worden met het relatieve nut van verschillende mogelijke uitkomsten van zak-slaagbeslissingen op basis van die cesuur genomen. In de bijlage over selectieparameters, evenals in hoofdstuk 7, zijn voorbeelden gegeven hoe een dergelijke analyse in haar werk gaat.

Zonder hier een diepgaande beschouwing over de meest gewenste beslissingen in het onderwijs te houden, kan toch wel gesteld worden dat slechts bij uitzondering aan het ten onrechte geven van een voldoende beoordeling zowel voor de betrokken student, als voor de onderwijs instelling echt vervelende consequenties zitten. Aan de andere kant is het nut van het terecht over laten doen van een studieonderdeel veelal ook klein of geheel verwaarloosbaar wanneer een en ander afgemeten wordt aan de kosten (tijdverlies, extra toetsing, de-motivatie).

Het nut van ten onrechte iemand de zaak over laten doen is daarentegen zeer negatief, en het nut van terecht iemand een voldoende geven is als behoorlijk positief op te vatten. Met gegevens als deze, en dan natuurlijk liever niet in verbale, maar in gekwantificeerde vorm, kan wat gestoeid worden (volgens strenge regels overigens) om tot een goede aftestgrens te komen.

Bij het kiezen van de cesuur gaat het er onder andere om het totale verlies zo klein mogelijk te houden. In deze inleiding zal ik dit niet verder door analyseren, maar volsta ik met op te merken dat in de tot nu toe gevolgde onderwijspraktijk slechts bij uitzondering en dan waarschijnlijk nog op de grofste en meest intuïtieve wijze met deze verschillende verliezen rekening is gehouden bij het bepalen van zak-slaaggrenzen voor tentamens. Het eenvoudiger geval, namelijk het zo klein mogelijk houden van het totaal aantal foutieve beslissingen, is voorzover mij bekend in geen enkele cesuurbepalingsprocedure expliciet verwerkt. Het zwaarder inschatten van onterechte afwijzingen is min of meer expliciet wel bij de methode Wijnen aan de orde gesteld, maar Wijnen gaat daarbij (de correctie op het referentiepunt, zie voor een samenvatting van de methode Wijnen de bijlage) intuïtief te werk.

1.3 Risico's van cesuurbepaling: onnodige studieduurverlenging.

De bespreking in paragraaf 1.2 heeft laten zien dat er bij zak-slaag beslissingen, hoe ook bekeken, grote aantallen fouten worden gemaakt. Er worden nogal wat studenten ten onrechte verplicht om vakken over te doen, wat voor hen resulteert in een studieduurverlenging die eigenlijk niet voor had mogen komen. Wanneer het in een subfaculteit gebruikelijk is om bij tentamens slechts kleine aantallen studenten af te wijzen (zeg minder dan 20 %), dan is het effekt van die genomen foute beslissingen misschien nog wel aanvaardbaar wanneer het tevens zo is dat het overdoen van studieonderdelen niet al te veel tijd hoeft te kosten. Voor de meeste studies geldt echter dat er nogal hoge afwijzingspercentages voor tentamens worden gehanteerd. Dat zal vaak vooral in de propedeuse het geval zijn, maar ook voor tentamens in de laatste fasen van de studie is het allerminst zeldzaam zeer hoge afwijzingspercentages te vinden. In dergelijke gevallen ligt het voor de hand dat de studieduur fors verlengd kan worden door het verschijnsel dat studenten ten onrechte studieonderdelen moeten herhalen.

Wat in specifieke gevallen precies onder ten onrechte begrepen moet worden is vaak bijzonder moeilijk uit te duiden; dat betekent dan allerminst dat je toch niet van ten onrechte zou mogen spreken, omdat juist dan geen behoorlijke argumentatie gegeven kan worden voor afwijzende beslissingen. De mate waarin zak-slaag beslissingen op deze wijze willekeurig blijken te zijn, in die mate mag je ook verwachten dat beslissingen ten onrechte genomen worden.

1.3.1 Foute beslissingen in soorten.

Foutieve zak-slaagbeslissingen zijn op twee manieren mogelijk: studenten krijgen ten onrechte een onvoldoende, of studenten krijgen ten onrechte een voldoende. In zekere mate zijn beide soorten van fouten tegen elkaar in te wisselen: door het verschuiven van de aftestgrens kan het aantal fouten van de ene soort verkleind worden ten koste van het aantal fouten van de andere soort. Zo kan door het hoger stellen van de aftestgrens het aantal ten onrechte gegeven voldoendes terug gebracht worden, maar dat kan alleen door het aantal ten onrechte gegeven onvoldoendes te laten groeien. Bovendien is het nog zo dat het inruilen van fouten van de ene soort tegen fouten van de andere soort geen kwestie is van gelijke afruil. Ik bedoel daar mee dat het bij hoger stellen van de aftestgrens al snel zo kan zijn dat het verminderen van het aantal ten onrechte gegeven voldoendes met één ten koste gaat van het vergroten van het aantal ten onrechte gegeven onvoldoendes met twee.

Daaruit mag blijken dat het nooit zo kan en mag zijn dat de aftestgrens gesteld wordt op een niveau dat men er praktisch zeker van kan zijn dat geen enkele student ten onrechte een voldoende in de wacht sleept: de prijs die daarvoor betaald wordt is dat een relatief bijzonder groot aantal studenten noodzakelijkerwijs (vanwege de feilbaarheid van het tentamen als meetinstrument) ten onrechte een onvoldoende krijgt. Natuurlijk kan in de gegeven omstandigheden wel naar een optimale aftestgrens gezocht worden, maar het vervelende is dat de gegeven omstandigheden bij zorgvuldige analyse nogal ongunstig zijn.

1.3.2 Oplossingen ook in het onderwijs en het beoordelingsstelsel zoeken.

Een en ander betekent natuurlijk ook dat het niet zonder meer mogelijk is om het aantal ten onrechte gegeven onvoldoendes heel klein te houden zonder erg veel studenten ten onrechte voldoendes te geven. En hoewel het ten onrechte geven van een voldoende een klein kwaad is, wordt het toch wel iets anders wanneer dat kleine kwaad in omvangrijke mate voorkomt.

Maar wie zegt dat cesuurbepaling altijd moet gebeuren ongeveer op de manier zoals we het altijd gedaan hebben, maar dan misschien met meer sophisticated technieken? Er zijn mogelijkheden te over om aan de problematiek te sleutelen wanneer we eenmaal onze blik verruimen tot de hele onderwijssituatie waarin tenslotte die cesuurbepaling plaats vindt. Is het niet mogelijk, zo kun je je afvragen, om er voor te zorgen dat studenten alleen deelnemen aan een tentamen wanneer ze zich ook inderdaad voldoende voorbereid hebben? Daar zijn maatregelen voor te bedenken. Een aantal mogelijkheden zijn: het transparanter maken van de toetsingssituatie zodat studenten vrij goed weten welke de minimum eisen zijn; het houden van een proeftentamen o.i.d. waaraan de student kan toetsen of hij met voldoende waarschijnlijkheid aan de minimum eisen kan voldoen; het afschaffen van de mogelijkheid om tentamens over te doen (behoudens uiteraard uitzonderingsgevallen) zodat behaalde onvoldoendes blijven staan; toetsing automatiseren zodat de student zich kan laten toetsen op het moment dat hij denkt de stof voldoende te beheersen; etc.

Een geheel ander beoordelingsstelsel dan wat nu gebruikelijk is, zou onder meer kunnen resulteren in volledige uitschakeling van het verschijnsel dat tentamens nogal eens ten onrechte overgedaan worden. De exameneisen zouden niet meer gesteld moeten worden in het tenminste voldoende gemaakt hebben van alle (vrijwel alle) studieonderdelen, maar in termen van het behaald hebben van een bepaalde gemiddelde studieprestatie. Slechte cijfers op sommige onderdelen behaald zouden dan gecompenseerd kunnen worden door betere resultaten elders behaald. Tentamengelegenheden zijn in de regel éénmalig (geen herkansingen dus), zodat het op goed geluk deelnemen aan tentamens weinig of in het geheel niet meer zal voorkomen (behalve dan bij die studenten die overigens al ruimschoots aan de minimum vereisten hebben voldaan, maar daar kan dan ook weinig bezwaar tegen bestaan). De geringe betrouwbaarheid en validiteit van het afzonderlijke tentamen is dan ook geen probleem meer, omdat ongelukkigerwijs behaalde lage cijfers voor een bepaald vak ergens anders wel weer gecompenseerd worden door toevallig hoog uitvallende cijfers (dit gaat natuurlijk minder op wanneer het totaal aantal tentamens dat meedoet in de bepaling van de vereiste gemiddelde studieprestatie kleiner wordt). Is dit een revolutionair voorstel? Geenszins, het komt neer op het sinds jaar en dag in de Verenigde Staten gebruikelijke Grade Point Average systeem (Zie Bevers in Wiegersma, 1976). Is dat GPA stelsel nu zo'n fantastisch goed beoordelingsstelsel? Nee, zeker niet, er worden telkens weer pogingen gedaan om het door andere methoden te vervangen (pass-fail grading bijvoorbeeld) en er bestaan ongeveer evenveel varianten op als er instellingen van hoger onderwijs zijn. Maar waar het om gaat is dat aan dat Grade Point Average stelsel niet die absurde mate van onnodige studieverlenging inherent is als aan het stelsel dat tot op de dag van vandaag in Nederland gebruikelijk is. Onnodige herhalingen van studieonderdelen komen daar immers niet in voor.

Een voorbeeld van de studievertraging die onder het huidige beoordelingsstelsel mogelijk is valt te geven onder een aantal heel grove aannamen, die vrijwel zeker in geen enkele onderwijssituatie op deze wijze opgaan, maar toch een heel globale indruk kunnen geven van de orde van grootte waarin gedacht kan worden.

Stel het studieprogramma bestaat uit 25 onderdelen (5 studieonderdelen per studiejaar). Het is, blijkens de administratieve gegevens, de gewoonte om bij ieder tentamen 40 % een onvoldoende te geven. Stel ook dat we het voorbeeld alleen doorrekenen voor die studenten die uiteindelijk de studie afmaakten. Stel, heel conservatief, dat bij ieder tentamen 15 % ten onrechte, en 25 % terecht die onvoldoende krijgt.

Veronderstel dat het moeten overdoen van een studieonderdeel twee maanden kost, óók voor degenen die in feite de stof voldoende beheersten maar toch een onvoldoende kregen (toelichting: de student weet niet of hij zelf behoort tot de categorie ten onrechte onvoldoende beoordeeld of niet, en zal dus een poging doen de stof beter onder de knie te krijgen dan de eerste keer. Voor veel vakken geldt dat de herkansing zoveel later is dat ook de eerder al gekende stof nog intensief gerepeteerd zal moeten worden. Overigens betekent het moeten herhalen van een tentamen altijd buiten proportioneel veel tijdverlies omdat het gewone studieprogramma er door in de war geschopt wordt).

Welnu, dan is de gemiddelde studievertraging opgelopen per tentamen gelijk aan (.15)x(2 maanden) is 3/10e maand.

Neem aan dat het ten onrechte onvoldoende beoordeeld worden iets is dat iedere student die de stof in feite voldoende beheerst in gelijke mate kan overkomen. Dan is de gemiddelde studieduurverlenging voor de totale studie bestaande uit 25 van deze studieonderdelen gelijk aan 712 maand. Wie er behoefte aan heeft een groep uitmuntende studenten te onderscheiden kan als volgt te werk gaan (Bijvoorbeeld): stel voor 10 % van degenen die afstuderen geldt dat zij in de regel zeer goede resultaten behalen en gemiddeld maar één studieonderdeel hebben herhaald. Stel dat in de helft van het aantal herhalingen die herhaling ten onrechte gevraagd werd. Dan is de gemiddelde studieduurvertraging als gevolg van onnodig overdoen voor deze groep studenten 1 maand. Voor de overige 90 % van de studenten blijft de gemiddelde studieduurvertraging zoals die zojuist uitgerekend werd: 7,5 % maand. Gaan we beide groepen middelen, dan zou als overall gemiddelde daaruit komen 6.85 maand.
Verdere verfijningen liggen voor de hand, maar het voorbeeld is wel duidelijk. Dat het relatieve aantal foutief gegeven onvoldoendes zo hoog ligt, werd in paragraaf 1.2 uitgelegd.


Hoofdstuk 2. Uitgangspunten voor verantwoorde cesuurbepaling.

Het cesuur probleem als PROBLEEM schijnt eigenlijk alleen in Nederland enige aandacht te hebben gekregen. Enige uitzondering daarop zouden dan enkele publikaties zijn die zich bezig houden met het iets andere probleem van het cijfergeven zoals dat in het Amerikaanse Grade Point Average systeem bestaat (Nedelsky, Downie, Ebel). In Nederland was Posthumus één van de eersten die de eigenaardigheden van onze onderwijs beoordelingsgewoonten bloot legde. Deze vijven en zessen problematiek werd door De Groot uitgebreid beschreven in zijn bekende Vijven en zessen. Vlak voor publikatie van Vijven en zessen presenteerde De Groot in Paedagogische Studiën een methode voor het bepalen van de cesuur: de kernitemmethode.

In vrijwel ongewijzigde vorm werd deze methode overgenomen in Studietoetsen (1969). Van Naerssen werkte een modificatie van de methode uit, die eigenlijk van de uitgangspunten van De Groot weinig meer over liet, maar toch nog als kernitemmethode aangeduid werd, en als vervanging van de oudere methode opgenomen werd in de nieuwe editie van Studietoetsen (1975). De kernitemmethode is helaas vrijwel niet kritisch besproken, noch onderzocht, afgaand op het ontbreken van publikaties. Uitzondering daarop is een korte bespreking in kritische termen door Wijnen, die tevens een alternatief presenteerde, bekend geworden als de 'methode Wijnen' (Swets en Zeitlinger, 1972). Grote verdienste van de bijdrage van Wijnen is dat er een grondige correctie mee gegeven werd op de misstand die uit hantering van de kernitemmethode voortvloeide: de veelal fantastisch hoge afwijzingspercentages werden in de methode Wijnen tot meer aanvaardbare proporties teruggebracht.

Bij al deze pogingen voor het aanreiken van een cesuurbepalingsmethodiek moesten verschillende heren tegelijk gediend worden: beoordeling, cesuur en selectie werden niet van elkaar onderscheiden; cesuurbepaling bleef impliciet een middel waarmee tevens selectieve bedoelingen gerealiseerd moesten worden. Géén van deze methoden, hoewel op grote schaal in de praktijk toegepast (vooral de kernitemmethoden), is dan ook bevredigend gebleken, niet in de laatste plaats door het ontbreken van een behoorlijke argumentatie voor juist dize methode. Dat geldt ook voor de methode Wijnen, die een aantal willekeurige momenten bevat die de docent voortdurend het gevoel geven op glad ijs te staan: de keuze van het gemiddelde als referentiepunt, en 2 x de standaard meetfout als correctie daarop (zie bijlage). Hoewel Wijnen bij zijn zoeken naar een goede methode er expliciet van uitging dat een directe argumentatie voor een bepaalde cesuur vrijwel niet gegeven kan worden omdat daarvoor de nodige gegevens over de onderwijssituatie ontbreken, waarbij hij uitkwam op een methode die volstrekt relatief zou moeten zijn, kon ook hij er niet onder uit om die relatieve methode aan enkele nogal willekeurige ankers (zoals het gemiddelde als referentiepunt) op te hangen. Een bevredigende aanpak van het cesuurprobleem lijkt dan ook slechts te doen door een en ander fundamenteler aan te pakken, door er niet van uit te gaan dat bestaande beoordelingsgewoonten ontzien moeten worden, maar er juist voor te zorgen dat de doelstellingen van het onderwijs er mee gediend zijn, de efficiëntie van het onderwijs niet in de wielen gereden wordt, en de behandeling van de student billijk is. Een en ander leidt dan tot een aantal uitgangspunten die richting moeten geven aan de constructie van de procedure die in een bepaald geval bij de cesuurbepaling gevolgd zal worden.

2.1 Overzicht van de te presenteren uitgangspunten.

De uitgangspunten waaraan cesuurbepalings methoden bij voorkeur moeten voldoen, of in overeenstemming waarmee ze geconstrueerd moeten worden, zijn:

  1. Het cesuurprobleem wordt gescheiden gehouden van andere problemen als selectie, differentiële beoordeling, motivatie.
  2. Toetsing op voldoende beheersing van de stof moet transparant zijn. Ook de te hanteren zak-slaaggrens moet transparant zijn.
  3. In principe krijgt iedere tot dit onderwijs toegelaten student die het onderwijs ook behoorlijk volgt, een voldoende.
  4. De hele procedure, zowel de toets als de wijze waarop zak-slaag beslissingen genomen worden, moet voldoen aan Algemene Beginselen van Behoorlijk Bestuur. Ook de meer technische normen zoals gesteld in de Standards moeten aangehouden worden om kwaliteitsbeheersing van toetsing en zak-slaag beslissingen mogelijk te maken.
  5. Is de procedure eenmaal vastgesteld, dan wordt de grens zakken - slagen op besliskundige wijze geoptimaliseerd.

Een methode voor het bepalen van de cesuur is aanvaardbaar in de mate waarin aan genoemde uitgangspunten voldaan is. Tenminste moet van een 1 cesuurbepalings procedure duidelijk zijn of, en zo ja in hoeverre, zij aan ieder van de uitgangspunten voldoet. Omdat deze informatie op zich nog weinig zinvol is, moet ook bekend zijn waarom een bepaalde procedure slechts in beperkte mate aan een bepaald uitgangspunt kan voldoen, welke pogingen ondernomen zijn om de procedure te verbeteren, op welke punten de procedure eventueel wél verbeterd kan worden, en zo mogelijk ook hoe de gevolgde procedure zich laat vergelijken met andere mogelijke of eerder gevolgde procedures op ieder van deze uitgangspunten.


Hoofdstuk 3. Eerste uitgangspunt: loskoppeling van ándere onderwijsdoelen.

Eerste uitgangspunt is dat het probleem waar de grens zakken-slagen gelegd moet worden, los gekoppeld moet worden van problemen als eventuele selectie-onderweg, functie van het tentamen als stok achter de deur, en het verschillend willen belonen van verschillende studieprestaties. Het laatste is al heel makkelijk los te zien van de zak-slaag problematiek; de stok achter de deur functie kan langzamerhand toch wel vervangen worden door modernere onderwijskundige methoden; alleen wat de verwarring met selectie (of niveaubewaking) betreft is enige toelichting hier op zijn plaats.

De Groot besteedde er in zijn presentatie van de kernitemmethode in 1964 de volgende woorden aan:


De koppeling die traditioneel in ons onderwijs stelsel bestaat tussen cesuurbepaling en selectie is het onderwerp van herhaalde scherpe aanklachten van De Groot, zoals ook in zijn eerste deel van het tweeling artikel over de kernitemmethode (1964). In principe moet de onderwijsinstelling de verantwoordelijkheid voor een goede studievoortgang op zich nemen voor alle toegelaten studenten. Dat op praktisch ieder niveau de mogelijkheid, dat een leerling geacht wordt te zijn afgevallen als gevolg van ongeschiktheid - "zodat de school zich dit afvallen niet als fout aanrekent" bestaat, is een flagrante misstand.

Met name is het ook onjuist dat cesuurbepaling voor afzonderlijke vakken gekoppeld is aan examenregelingen, in de trant van: een onvoldoende voor een bepaald vak betekent dat je gezakt bent voor het gehele examen (en allerlei misschien wat mildere varianten op dit grond thema).

Nooit uitgesproken bedoeling is nogal eens om de zwakkere student door het laten herhalen onder druk te zetten om de studie te beëindigen ( = af te breken). Het is duidelijk dat op deze manier een zeer groot aantal studenten, die uiteindelijk wel af zullen studeren, een stuk studievertraging oplopen omdat andere studenten zo nodig onder druk gezet moesten worden. Maar relevanter is, dat selectie hier via een slinkse omweg gerealiseerd wordt, en niet in een expliciet beleid (waarvoor overigens ook de wettelijke basis waarschijnlijk zou ontbreken). Een expliciet selectiebeleid zou het mogelijk maken de kwaliteit van die selectieprocedure te bewaken, met name ook er voor te zorgen dat een goede balans getroffen wordt tussen onbedoelde selectie van studenten die anders met voldoende resultaat de studie zouden hebben kunnen beëindigen enerzijds, en onbedoeld door laten gaan met de studie van studenten die alsnog in een latere studiefase zullen stranden anderzijds (zie ook hoofdstuk 7).


3.1 Examenregeling en cesuurbepaling.

Expliciete selectie vindt in het wetenschappelijk onderwijs plaats via de academische examens: aan de gestelde exameneisen moet de student voldoen, wil hij door mogen gaan met de vervolgstudie of zijn doctoraalbul in ontvangst nemen. Voorzover de exameneisen nog gesteld zijn in termen van: tenminste alle studieonderdelen voldoende gemaakt hebben (plus verzachtende uitzonderingsregelingen), zitten er aan die exameneisen erg vervelende consequenties vast voor de cesuurbepaling.

Allereerst, en daar wees De Groot al op, zijn de gevolgen van het geven van een onvoldoende beoordeling voor de docent moeilijk te overzien. Het kan zijn dat de door hem gegeven onvoldoende tot gevolg heeft dat de student voor het examen zakt, terwijl hij voor alle overige vakken voldoende of zelfs goede prestaties leverde. Een dergelijke situatie betekent ook dat een behoorlijke afweging van de consequenties van de zak-slaagbeslissing voor de docent bijzonder moeilijk of onmogelijk wordt (omdat aan uitgangspunt 5 niet voldaan kan worden). Dat betekent niet veel minder dan dat onder deze omstandigheden de zak-slaagbeslissing een groot element van irrationaliteit moet en zal omvatten.

In heel andere bewoordingen gegoten zou je kunnen zeggen dat door dergelijke examenregelingen de docent opgescheept wordt met een verantwoordelijkheid die hij niet kan dragen: zijn zak-slaag beslissingen zullen in bepaalde gevallen de examenbeslissing volledig bepalen. De docent is gedwongen beslissingen te nemen die in principe niet aan hem, maar aan de examencommissie toevallen. Heel concreet kan de door hem uitgedeelde onvoldoende betekenen dat een student ook een aantal andere vakken waarvoor hij wel ruim voldoende beoordelingen had gekregen, nog eens moet overdoen.

Het bovenstaande is geen prietpraat: het gaat niet om onvermijdelijke gevolgen van anderszins noodzakelijke regelingen. Examenregelingen kunnen ook in termen gegoten worden die een veel minder extreem gewicht toekennen aan de beoordeling voor een enkel vak. Datzelfde geldt waar het gaat om gevolgen van een dergelijke examenregeling die uit onderwijskundig oogpunt ongewenst of verkwistend zijn. Ik zal er enkele van noemen:

Door onvermijdelijke beoordelingsfouten (zie hoofdstuk 1 en 6) doen nogal wat studenten verschillende studieonderdelen ten onrechte over. Dat kan als gevolg hebben dat enkele studenten ten onrechte menen de studie te moeten staken, maar vooral dat de gemiddelde studieduur onnodig (althans voor deze categorie studenten) verlengd wordt. Over het laatste gevolg handelt deel 2 , waarin gedemonstreerd wordt dat het hier om een geenszins verwaarloosbare verspilling van studietijd en onderwijsmiddelen gaat.

Onderwijskundig moeilijk te verantwoorden is de eis van herhaling in het geval van een onvoldoende beoordeling voor een vak. Dat is eenvoudig in te zien wanneer bedacht wordt dat voor een herhaling een behoorlijk stuk al voldoende gekende stof nog eens herhaald moet worden (wat ongewenst is, en dan ook van andere studenten, die wel een voldoende kregen, niet geëist wordt), en vooral dat er alternatieven voor het examenbeleid zijn die gezien vanuit de doelstellingen van onderwijs geen negatieve, maar juist een positieve rol kunnen spelen:

Wanneer een onvoldoende voor een bepaald vak gecompenseerd moet worden door betere prestaties elders, kan de student zijn tijd besteden aan het bestuderen van nieuwe stof, in plaats van al eens eerder bestudeerde stof; of door het intensiever bestuderen van een ander vak, waartoe hij misschien meer affiniteit heeft.

3.2 Exameneisen: het hordenloop model.

In de vorige paragraaf werd aan de orde gesteld dat exameneisen gesteld in termen van het tenminste voldoende gemaakt hebben van ieder studieonderdeel, het de docent moeilijk, zo niet onmogelijk, kunnen maken om een rationele beslissingsprocedure te volgen bij het toekennen van voldoendes en onvoldoendes. Exameneisen in deze vorm hebben bovendien vervelende gevolgen voor wat betreft de zak-slaagbeslissingen voor alle betrokken studieonderdelen bij elkaar genomen.

Ik kan dit misschien het makkelijkst toelichten met het volgende gedachte experiment. Laten we eens veronderstellen dat de onnauwkeurigheid waarmee beheersing van de stof gemeten wordt, tot gevolg heeft dat een student die in wezen de stof voldoende beheerst, voor een afzonderlijk tentamen een kans heeft van 1/10e ten onrechte een onvoldoende beoordeling te krijgen.

Veronderstel dat het gaat om een propedeuse programma, dat uit vijf studieonderdelen bestaat, en dat onze student voor ieder tentamen opkomt terwijl hij in wezen de stof voldoende beheerst, en voor ieder tentamen een kans van 1/10e heeft een onvoldoende te krijgen.

Wanneer de examenregeling is dat ieder vak tenminste voldoende gemaakt moet zijn (merk op dat een dergelijke exameneis geformuleerd is in behaalde studieprestaties en niet in termen van wezenlijke beheersing van de stof), is het duidelijk dat voor onze student de kans om in één keer voor de propedeuse te slagen, gelijk is aan

(1 - 0,1 )5 = 0,59049

De berekening is als volgt: voor ieder studieonderdeel is zijn slaagkans 1 - 0,1 = 0,9. Verondersteld wordt dat de slaagkansen voor verschillende studieonderdelen onafhankelijk van elkaar zijn, zodat de slaagkans voor alle vijf studieonderdelen tegelijk gelijk is aan het product van de afzonderlijke slaagkansen voor de vijf vakken. Je zou ook omgekeerd de kans om niet in één keer te slagen kunnen berekenen. Die berekening is iets ingewikkelder omdat er nogal wat verschillende mogelijkheden zijn om te zakken: de student kan immers zakken met één, twee, etc. voldoendes, en dat voor verschillende vakken. De berekening ziet er als volgt uit:

5 x 0,1 - 10 (0,1)2 + 101(0,1)3 - 5(0,1)4+ (0,1)5=

0,5 - 0,1 + 0,01 - 0,0005 + 0,00001 = 0,40951.

Zoals het behoort, zijn de kans om te slagen en de kans om te zakken bij elkaar geteld gelijk aan 1.

Dat levert al met al een ontstellend hoge zak-kans voor onze exemplarische student op, en dat is typerend voor alle hordenloopmodellen, of zoals ze in de literatuur vaak genoemd worden: conjunctieve examenmodellen. Het is een ongewenste eigenschap, en bovendien één die men zich moeilijk realiseert. (zie noot l).

De ongewenste consequenties kunnen natuurlijk wat afgezwakt worden door de student de gelegenheid tot herkansing te geven voor de afzonderlijke studieonderdelen waarvoor hij gezakt is. En dat is in feite ook de bestaande situatie in ons onderwijs (al kwamen er tot voor kort, en misschien nog steeds, wel studierichtingen voor waarin het hordenloop model in strikt onverkorte vorm werd gehanteerd).

Veronderstel dat het overdoen van een bepaald studieonderdeel de studieprestaties voor andere studieonderdelen niet ongunstig beïnvloedt, en dat ook bij de herkansing de kans om ten onrechte een onvoldoende te krijgen nog steeds 1/10e is. Wat is dan de kans voor onze student die in wezen ieder vak voldoende beheerst, om voor de propedeuse te slagen? Wel, onder de omstandigheden van dit model is dat het produkt van de kansen om voor ieder vak te slagen in hooguit twee keer:

(0,9 + 00.0,9)5 = 099)5 = 0,951.

Met andere woorden, zelfs onder deze omstandigheden heeft de student nog een kans van één op twintig om ten onrechte voor de propedeuse te worden afgewezen.

De kans om te worden afgewezen ligt onder het hordenloop model voor de student op de grens van voldoende natuurlijk een stuk ongunstiger. Met de student-op-de-grens-van-voldoende bedoelen we de student die in wezen de stof juist voldoende beheerst, en daaruit volgend ook een slaagkans heeft van ongeveer 0,50. (Die slaagkans. kan hoger of lager liggen al naar gelang de uiteindelijke overwegingen voor het vaststellen van de aftestgrens in termen van prestaties op de toets: zie daarvoor de toelichting en uitwerking in hoofdstuk 7).

Laten we voor ons voorbeeld er van uit gaan dat de slaagkans voor deze student, voor ieder van de vijf studieonderdelen, gelijk is aan 0,5, en dat dat ook geldt voor de herkansing (één per vak) voor het geval hij bij de eerste gelegenheid zou zakken. Voor deze grens-student is de kans om voor de propedeuse te slagen onder de condities van het hordenloop of conjunctieve examenmodel:

(0,5 + 0,5 x 0,5)5 = (0,75)5 = 0,240.

De gevolgen van het hordenloop model kunnen voor de grensstudent dus al heel snel desastreus worden: hoewel hij voor ieder afzonderlijk vak de stof in wezen juist op het randje beheerst, leidt het hanteren van het hordenloop model, er toe dat hij al erg makkelijk niet meer dan een kans van één op vier overhoudt om voor de propedeuse te slagen. Wat er gebeurt wanneer afzonderlijke docenten menen streng te moeten zijn in hun beoordeling, en als gevolg daarvan de grensstudent niet meer dan een kans van, zeg, 0,3 geven om bij toetsing ook te slagen, laat zich raden.

Berekenen we die kans:

(0,3 + 0,7 x 0;3 )5 = 0,0345,

d.w.z. de kans om te slagen voor de propedeuse is voor deze student bijna verwaarloosbaar klein, zeker wanneer men bedenkt dat in de praktijk de student ongetwijfeld door het relatief forse aantal herhalingen waaraan hij moet deelnemen, in tijdnood zal geraken.

Het doel van deze uiteenzetting op deze plaats is om te laten zien dat op zich verantwoord lijkende zak-slaag beslissingen voor een bepaald studieonderdeel, in samenhang met een exameneisen pakket van het hordenloop type, kunnen leiden tot resultaten die misschien niemand wenselijk vindt. Voor een korte toelichting op de hier gevolgde modelmatige wijze van illustreren, zie noot 2.


3.3 Koppeling van selectie en cesuurbepaling bijzonder inefficiënt.

Als laatste illustratie van de ongelukkige gevolgen van de verwarring tussen, en gelijkschakeling van, selectie en cesuurbepaling wil ik het informatieverlies noemen.

Ik bedoel daarmee, dat het examen op te vatten is als voorspelling van te verwachten studiesucces in de verdere studie, waarbij als materiaal waar die voorspelling op gebaseerd wordt, de al geleverde studieprestaties gebruikt worden. Iemand slaagt voor het examen, wanneer de voor hem gedane voorspelling van toekomstig studiesucces voldoende is.

Welnu, het is duidelijk dat voor het doen van een dergelijke voorspelling wij alle beschikbare informatie over zijn geleverde studieprestaties zouden willen gebruiken. Daaruit volgt onmiddellijk dat iedere examenregeling die geformuleerd is in termen van te behalen aantal voldoendes, inefficiënt is omdat de informatie die in de behaalde studieresultaten aanwezig is, versmald wordt tot het aantal behaalde voldoendes. Er wordt m.a.w. informatie weggegooid, of verdonkeremaand. Deze beschuldiging zou ik hard kunnen maken door in een voorbeeld te laten zien hoe goed toekomstig studiesucces te voorspellen is op basis van gemiddelde behaalde studieprestatie (of liever nog: de studieprestaties voor ieder afzonderlijk vak gecombineerd in een formule waarin de weging van afzonderlijke vakken 0 gekozen is dat de best bereikbare voorspelling verkregen wordt), en hoe die voorspelbaarheid ineenzakt wanneer alleen maar het al dan niet voldoende gemaakt hebben van afzonderlijke vakken gebruikt mag worden. Een en ander lijkt me echter zo evident, dat een rekenvoorbeeld aan de hand van een bestaande situatie in een of andere faculteit, mij niet nodig lijkt om het punt verder te adstrueren.

Aan het bovenstaande zijn nog een aantal belangrijke opmerkingen toe te voegen. Veronderstel dat het inderdaad het belangrijkste doel is van de examens om degenen door te laten die een goede verwachting van verder studiesucces hebben, en de overigen tegen te houden. Het is dan ook snel in te zien dat de koppeling van exameneisen aan cesuurbepaling voor de afzonderlijke vakken zoals die in het hordenloop model plaats vindt, inclusief het fenomeen dat onvoldoendes overgemaakt worden totdat aan de exameneisen voldaan is, leidt tot voorspellingen die veel slechter zijn dan voorspellingen die verkregen worden door uit te gaan van de cijfers voor afzonderlijke vakken behaald waarbij geen (of slechts in heel beperkte mate) herhalingen van tentamens voorkomen.

Hoewel daarover te discussiëren zou zijn, kunnen we er voorlopig toch wel van uitgaan dat het bij de voorspelling van toekomstig studiesucces er voornamelijk om gaat verschillen in de mate van studiesucces voor verschillende studenten te kunnen voorspellen. Voor het doen van dergelijke voorspellingen zijn uitsluitend gegevens van belang die te maken hebben met verschillen tussen studenten, dat wil zeggen met verschillen in behaalde cijfers voor vak A bijvoorbeeld. Het opmerkelijke is dan, dat voor dat vak A alleen de verschillen tussen gegeven cijfers van belang zijn, en bijvoorbeeld niet de hoogte van het gemiddelde cijfer dat de docent heeft gegeven, en al helemaal niet of cijfers beneden of boven de aftestgrens liggen (voldoende of onvoldoende zijn). Je zou het met andere woorden ook kunnen zeggen dat het voor het doen van voorspellingen van toekomstig studiesucces voldoende is de verschillen van de studie prestaties van de studenten te kennen, en dat de cijfers zelf, alsmede het al dan niet voldoende zijn van die cijfers, geen informatie toevoegen die de voorspelling kan verbeteren.

Ik wil het hierbij laten, omdat uitwerking van deze opmerkingen het kader van deze cursus te buiten zou gaan. Bedoeld is slechts om duidelijk te maken dat het in één adem noemen van exameneisen en cesuurbepaling niet of bijzonder moeilijk te rechtvaardigen zal zijn.

3.4 Illustratieve vergelijking van conjunctieve en compensatorische examens.

Stel, voor het doctoraal bestaat de studie uit 12 onderdelen. Een conjunctieve examenregeling zou in kunnen houden dat ieder studieonderdeel tenminste voldoende gemaakt moet zijn (per vak drie herkansingsgelegenheden). Een compensatorische examenregeling zou in kunnen houden dat gemiddeld de vakken juist voldoende gemaakt zijn (zoals Hofstee het graag zou zien, zie paragraaf 5.4 ), maar in principe is ook iedere andere gemiddelde studieprestatie als minimum eis te formuleren (de vraag is wáár, gezien de doelstellingen en de geldende randvoorwaarden, de optimale grens ligt, d.i. de te vragen minimale gemiddelde studieprestatie; zie daarvoor hoofdstuk 7)

Laten we eerst eens de conjunctieve examenregeling bekijken, en daarvoor een bijzonder gunstig speciaal geval, namelijk waar de student in staat is bij de voorbereiding voor ieder afzonderlijk tentamen er op te mikken de stof A goed te beheersen dat zijn kans op een onvoldoende beperkt blijft tot 1/10. Dat vereist zowel een bijzonder grote transparantie van toetsing en aftestgrens (zie hoofdstuk 4 ), als realisering van uitgangspunt 3 (hoofdstuk 5 ) dat in principe iedere student binnen de daarvoor gestelde tijd bij behoorlijke studie-inspanning een voldoende moet kunnen halen (vandaar dat dit een bijzonder gunstig voorbeeld is).

Neem tevens aan dat voor iedere herkansing hetzelfde geldt als voor de eerste tentamengelegenheid, dus dat de student Voor de herkansing de stof op precies hetzelfde niveau beheerst als bij de eerste tentamen afname. Neem daarbij aan dat het tijdverlies voor de student voor het doen van een herhaling op één maand gesteld moet worden, en dat andere ongunstige effecten van het moeten overdoen ook in tijdverlies omgerekend kunnen worden (zie voor dergelijke technieken Keeney & Raiffa 1976) en uitkomen op een halve maand. De totale kosten voor de student van iedere herhaling zijn dan anderhalve maand.

Aangenomen dat alle studieonderdelen en hun toetsing in alle voor ons relevante opzichten aan elkaar gelijk zijn, kan uitgerekend worden welke studieduurvertraging voor de student resulteert uit een conjunctieve examenregeling. Die vertraging is voor ieder afzonderlijk studieonderdeel (verwachte waarde)

0,1 x 1,5 + (0,1)2 x 1,5 + (0,1)3 x 1,5 = 0,166 maand.

(met een verwaarloosbare kans na 3 herhalingen nog niet geslaagd te zijn) Voor de doctoraal studie is de verwachting van de studieduurverlenging

12 x (0,166) = 2 maanden.

Dat valt dan nogal mee, zou je kunnen zeggen. Maar vergeet dan niet dat bijzonder gunstige aannamen over de toetsingen zijn gedaan. Wat zouden de resultaten zijn wanneer de student zijn zak-risico tot slechts één op vijf kan beperken? De verwachte studieduurverlenging is dan:

12 (0,2 x 1,5 + (0,2)2 x 1,5 + (0,2)3 x 1,5) = 12 (0,3 + 0,06 + 0,012)

= 4,464 maanden.

Bekijk de zak-slaaggegevens voor studieonderdelen in de eigen faculteit maar eens, dan ligt de conclusie voor de hand dat zelfs een studieverlenging van 412 maand een optimistische schatting moet zijn.

Het punt is natuurlijk, en dat is hopelijk niemand ontgaan, dat deze studieduurverlenging geldt voor een student die in wezen voor ieder afzonderlijk studieonderdeel bij opkomst voor het eerste tentamen de stof al ruim voldoende beheerste (zeg, in de ons vertrouwd in de oren klinkende cijferschaal, eigenlijk een 612 a 7 zou verdienen voor al die gevallen waar de standaard meetfout van het tentamen (zie de bijlagen, uitleg van de methode Wijnen) nogal gunstig pleegt uit te vallen). De studieduurverlenging is voor deze studenten louter verlies. Daarnaast zijn er natuurlijk studenten die terecht wel eens onvoldoendes krijgen; maar het bestaan van deze gevallen rechtvaardigt nog geenszins het hanteren van conjunctieve, hordenloop examenregelingen (zie hoofdstuk 3).

Dan nu een illustratieve analyse van de werking van een compensatorische examenregeling. Laten we er dan van uit gaan dat op basis van goede argumenten (van het soort dat in hoofdstuk 7 ter sprake komt) als exameneis gehanteerd wordt dat de gemiddelde studieprestatie ten minste 6,5 moet zijn (in de gebruikelijke cijferschaal, hoewel die ook nodig vervangen moet worden door iets beters). Dit omwille van de vergelijkbaarheid met het juist gegeven voorbeeld van de uitwerking van het hordenloop model voor de student die voor ieder vak afzonderlijk in wezen een 6,5 á 7 verdiende (maar niet altijd kon krijgen door de onnauwkeurigheid van de toetsing).

Omdat er 12 studieonderdelen zijn, die alle even zwaar en belangrijk zijn, moet de student tenminste 12.6,5 = 78 punten halen. De student in ons voorbeeld zal dan vrijwel altijd zonder extra inspanningen slagen. Veronderstel dat zijn stofbeheersing voor ieder studieonderdeel 6,75 punt waard is, en dat voor ieder studieonderdeel de standaardmeetfout 1 punt is. Onder deze omstandigheden is de verwachte totaalscore voor deze student 12.6,75 = 81. Maar er is een risico dat hij door pech niet alleen die 82 punten niet haalt, maar misschien zelfs geen 78 punten. Hoe groot is de kans dat hij (zonder af en toe een extra spurt te maken om een voldoende zekerheidsmarge op te bouwen wanneer hij bijvoorbeeld in het begin een aantal malen nogal pech heeft gehad), niet tenminste 78 punten haalt? Met behulp van de aanname over de standaardmeetfout is die pechkans te berekenen, en die is verwaarloosbaar: de standaardmeetfout van de totaalscore is

12 x 1 x 1/12 = 1 punt.

Niet zo gek dus. Maar bedenk wel dat de hier gestelde minimum eis aan de hoge kant is (zie het voorstel van Hofstee, die een lage minimum eis verdedigt, paragraaf 5.4. Merk ook op, dat bij deze examenregeling geen herhalingen van tentamens voorkomen (hoewel die op zich door het model niet verboden worden), en ook geen studieduurvertraging. (En verknoei de zaak vervolgens niet, door het onderwijs zo in te richten dat relatief nogal wat studenten voor het examen zakken, voor dat examen weer herhalingen doen, etcetera).

Wat betekent een en ander nu voor het scheiden van selectie en cesuurbepaling? In het gegeven voorbeeld van een compensatorische (grade point average) examenregeling hebben het voldoende-onvoldoende oordelen van de prestatie voor een bepaald vak, en de examenbeslissing niet direct meer iets met elkaar te maken. Bij de compensatorische examenregeling zijn de voorwaarden aanwezig om zowel de cesuurproblematiek, als de selectieproblematiek langs beproefde lijnen tot verantwoorde oplossingen te brengen. Dit alles voor zover men bij een dergelijke examenopzet nog behoefte heeft aan een onderscheid voldoende-onvoldoende voor afzonderlijke studieonderdelen.

Onder de hordenloop examenregeling is cesuurbepaling direct gekoppeld aan selectie, en zijn geen van beide verantwoord uit te voeren. Houdt de conjunctieve regeling zelfs in situaties waarin mild beoordeeld wordt, al een behoorlijke studieduurverlenging voor belangrijke groepen studenten in, wanneer afwijzingspercentages op de niet gebruikelijke hoogten van 40, 50 of zelfs 60 % en hoger komen kan eenvoudig uitgerekend worden dat de gevolgen rampzalig zijn voor wat betreft het studierendement. Zie deel 2 voor meer gedetailleerde uitwerking van de bezwaren van conjunctieve examenregelingen.

3.5 Conclusies voor het dagelijks beleid van de docent (vakgroep).


Dit advies staat in schril contrast tot het beleid dat gewoonlijk wordt gevolgd, waarin juist de voldoendes met de uiterste behoedzaamheid gegeven worden. Tenminste verwacht ik van de lezer dat hij uit dit hoofdstuk het besef overhoudt dat er onderscheid gemaakt moet worden tussen het onvoldoende oordelen van een prestatie, en de eis een tentamen over te doen (die onvoldoende prestatie te verbeteren).


Hoofdstuk 4. Tweede uitgangspunt: transparantie van toets en aftestgrens.

Tweede uitgangspunt is dat de student zich met een efficiënte studiestrategie moet kunnen voorbereiden op het behalen van een voldoende Niet alleen moet hij op de hoogte zijn van het soort vragen dat hij op de toets mag verwachten (en op welke wijze die goed beantwoord moeten worden), maar ook zou hij van te voren op de hoogte moeten zijn hoe de aftestgrens bepaald gaat worden, zodat hij daar in zijn voorbereiding van het tentamen rekening mee kan houden. In andere woorden (De Groot 1970):

Zowel toetsing als de beslissingsprocedure zakken-slagen moeten transparant zijn. Geen van beide eisen is triviaal: dat studenten nog op het tentamen zelf geconfronteerd worden met soorten vraagstelling die in het onderwijs niet aan de orde zijn geweest is allerminst zeldzaam (maar in strijd met het transparantie principe); dat zak-slaag beslissingen langs ondoorzichtige weg tot stand komen is een regel vrijwel zonder uitzonderingen (ondoorzichtig, niet alleen voor de student maar vaak ook voor de docent).

Transparantie is geen eis die in absolute vorm te stellen is: waar het om gaat is dat een mate van transparantie gerealiseerd wordt die voor alle betrokkenen aanvaardbaar is. Wat je aanvaardbaar zou willen noemen hangt af van de mogelijkheden die je nog ziet om de transparantie van de toetsing of van de beslissingsprocedure over zakken of slagen te vergroten, en een aantal van die mogelijkheden wil ik hier behandelen.

4.1 Voorbeeld van een redelijk transparante procedure.

Een werkwijze die soms gevolgd wordt, zij het dan ook meestal in latere fasen van de studie, is dat de toetsing en beoordeling van bestudeerde literatuur plaats vindt door een gesprek met de student aan de hand van een door hem of haar gemaakte korte scriptie over die stof.

Transparantie van de toetsing kan in dit geval bereikt worden door het geven van enkele regels voor het schrijven van een dergelijke literatuurscriptie, het beschikbaar stellen van een aantal (niet noodzakelijk uitstekende) voorbeelden van eerder gemaakte scripties, en begeleiding bij het concipiëren en uitwerken van de scriptie.

Transparantie van de beslissingsprocedure over zakken-slagen wordt gerealiseerd door de af spraak dat accepteren van de gemaakte scriptie betekent dat de student tenminste een voldoende voor dit studieonderdeel zal krijgen. Het gesprek tussen student en docent over de scriptie en de daarvoor gebruikte literatuur zal niet dienen om na te gaan of deze student wel een voldoende verdient, maar kan misschien leiden tot enige cijferdifferentiatie in het voldoende gebied. De implicatie is natuurlijk dat de docent een zijns inziens onvoldoende voorbereide scriptie niet accepteert, en in dat geval de student ook begeleidt in het verbeteren van een en ander.

Bijkomend voordeel van een dergelijke procedure is dat de docent de handen vrij krijgt om tijdens het gesprek met de student dieper in te gaan op het onderwerp van de scriptie zonder zich daarbij zorgen te hoeven maken of bespreking van misschien slechts een enkel aspect niet leidt tot een mogelijk onbillijke beoordeling van de student. De student hoeft niet in spanning te zitten of het tentamen hem niet alsnog een paar maanden extra werk oplevert door een eventuele onvoldoende beoordeling.

Uit de gegeven beschrijving zal duidelijk zijn dat een en ander ook een geschikte procedure zou zijn voor practica, of voor al die studieonderdelen die De Groot (1972) Handelings-onderdelen noemt.

4.2 De Hofstee-variant van transparantie.

Een interessante mogelijkheid voor het transparant maken van zowel de toetsing als van de aftestgrens, wordt geopperd door Hofstee (1973). Omdat zijn voordeel expliciet uitgaat van het principe zoals onder 5 als derde uitgangspunt geformuleerd, zal zijn voorstel in 5.3 en 5.4 aan de orde komen. Vooruitlopend daarop vast het volgende:

Er zijn nogal wat onderwijssituaties in w.o. waar, wat toetsing betreft, er mee volstaan kan worden na te gaan of de student de literatuur inderdaad bestudeerd heeft; of, in de formulering van paragraaf 2.4, of hij een behoorlijke studie-inspanning geleverd heeft. De scheiding tussen selectie en cesuurbepaling wordt hier strikt aangehouden: aangenomen wordt dat selectie voorafgaand aan het onderwijs heeft plaats gevonden. Toetsing heeft als functie: controleren of de student het onderwijs gevolgd heeft (participatiecontrole).

Dat betekent dat de toets vragen moet bevatten die beantwoord kunnen worden door de student die het onderwijs gevolgd, de literatuur bestudeerd of doorgewerkt heeft, en dat deze vragen niet beantwoord moeten kunnen worden door de student die het onderwijs niet gevolgd heeft. Daar zitten twee kanten aan waarop ik verder zal ingaan: wat betekent dit voor de transparantie van de toetsing en de aftestgrens, en wat zijn dat voor vragen die aan de juist genoemde eis voldoen?

Transparantie: de student moet de zekerheid hebben dat hij bij een behoorlijke studie-inspanning een voldoende beoordeling zal krijgen. De vragen die hem gesteld worden moet hij voor het grootste deel kunnen beantwoorden als hij de stof inderdaad doorgenomen heeft. Voldoende prestatie is dan ook het grotendeels (met een behoorlijke veiligheidsmarge, zie hoofdstuk 7 ) kunnen beantwoorden van de vragen. Natuurlijk wordt de student van te voren ingelicht over het soort vragen dat hij mag verwachten. Omdat het soort vragen dat hier bedoeld wordt nogal eenvoudig is (geen diepe inzichtvragen, geen detailvragen, geen meerkeuzevragen met meer dan twee alternatieven), zijn ze bijzonder snel en in grote hoeveelheid te maken. Hofstee suggereert dat het vaak mogelijk zal zijn alle vragen die over de hoofdzaken van de stof te stellen zijn, op deze wijze ook metterdaad te formuleren. In dat geval kan de transparantie van de toetsing nog verder opgevoerd worden door de volledige lijst van vragen van te voren de studenten bekend te maken.

Niet iedere vraag over hoofdzaken van de stof is zonder meer voor gebruik geschikt: onderzocht moet worden of de vragen inderdaad deelname aan het onderwijs meten. Wanneer toch alle vragen bekend gemaakt worden, is de volgende onderzoekopzet heel eenvoudig te realiseren:


Voor sommige stukken onderwijs en soorten leerstof zal een en ander beter te realiseren zijn dan voor andere. Wanneer veel literatuur bestudeerd moet worden, ligt deze vorm van toetsing al erg voor de hand. Maar ook voor vakken waarvan je het op het eerste gezicht niet zou denken, is de Hofstee variant te overwegen. Een voorbeeld van het laatste zou toetsing in wiskunde vakken kunnen zijn: het is daar al heel eenvoudig om vraagstukken te maken die door vrijwel alle studenten die het onderwijs gevolgd hebben, gemaakt kunnen worden, maar niet door studenten die het onderwijs niet gevolgd hebben. In dit voorbeeld heeft de Hofstee variant bovendien het voordeel dat de docent niet in de verleiding komt opgaven te bedenken die veeleer wiskundige genialiteit dan behoorlijke studie-inzet meten.

In de woorden van Hofstee:


4.3 Toets-transparantie: hoe te realiseren op de korte termijn.

In deze paragraaf een aantal mogelijkheden die op korte termijn te realiseren zijn. In 4.2 werd een suggestie van Hofstee besproken, die het mogelijk maakt een op zich volledig de stof dekkende verzameling vragen in korte tijd te construeren, en de studenten bekend te maken. Iets dergelijks kan natuurlijk ook in gevallen waar de docent (in ieder geval voorlopig) aan zijn eigen vragen vast wil houden: het beschikbare bestand aan vragen is meestal groot genoeg om de stof ook goed te dekken, in welk geval er weinig bezwaar tegen kan bestaan de verzameling vragen aan de studenten te geven. Voor het tentamen is er dan de mogelijkheid om geheel nieuwe vragen (maar van dezelfde aard als in de vorm van een vragenboek eerder bekend gemaakt) te maken; wanneer het laatste moeilijkheden op zou leveren, en ook in het geval waarin het gepubliceerde vragenbestand groot genoeg is, kan ook best volstaan worden met het tentamen samen te stellen uit het gepubliceerde vragenbestand (bijvoorbeeld door een steekproef te nemen).

Een andere mogelijkheid die voor bepaalde soorten leerstof heel geschikt kan zijn, is het geven van een lijst waarin alle soorten vragen beschreven zijn die op het tentamen gegeven worden, met daarbij enkele concrete voorbeelden. In meer uitgebreide vorm komt hetzelfde aan de orde onder 4.4 en 4.5. De student moet dan voldoende informatie hebben om zelf te kunnen bedenken welke vragen zoal over welke delen van de leerstof op het tentamen te verwachten zijn.

Een mogelijkheid die niet als alleenzaligmakend maar als goede aanvulling op de al gedane suggesties gezien moet worden, is het geven van proef tentamens en dergelijke kort voor het eigenlijke tentamen (maar niet zo kort dat de student zich niet meer kan herstellen van dan ontdekte tekorten in zijn voorbereiding.

Het geven van proeftentamen gelegenheid is ook één van de mogelijkheden om het aantal studenten dat zonder voldoende voorbereiding aan het tentamen deelneemt, te verminderen. Het laatste is, zoals in deel 2 aan de orde zal komen, belangrijk voor het verminderen van het aantal foute beslissingen bij het uitdelen van voldoendes en onvoldoendes.

Tentamens die over zeer omvangrijke stukken stof gaan (of over kleinere stukken stof die echter zeer gedetailleerd gekend moeten worden) zijn zelfs op bovengenoemde manieren moeilijk transparant te krijgen. De oplossing is natuurlijk om traditioneel gegroeide weerstanden tegen opsplitsing van een dergelijk tentamen te overwinnen, en de leerstof in kleinere eenheden tegelijk te toetsen.

De inventieve docent zal voor zijn eigen vak meerdere maatregelen kunnen bedenken om op korte termijn de toetsing transparanter te maken voor de student. Het verbeteren van toetstransparantie hoeft natuurlijk niet tot het uiterste doorgevoerd te worden; stelregel is dat transparantie belangrijker is, naarmate van de zak-slaag beslissingen voor de student méér afhangt. In een compensatorisch beoordelingsstelsel zoals in 3.5 geschetst is transparantie van de afzonderlijke tentamens heel wat minder kritisch dan onder de huidige conjunctieve examenregelingen!

4.4 Op korte termijn overgaan van meerkeuze- op open-eind-vragen.

Veel docenten gebruiken voor hun tentamens vragen van het meerkeuze type. De argumenten die ten gunste van deze vraagsoort aangevoerd worden, zijn o.a. de automatische scoring die mogelijk is, de objectiviteit, en, naar men meent, het onderwijskundig verantwoord zijn van deze vraagvorm. Ondanks het feit dat vele onderwijskundigen deze opvattingen delen, kan er ernstige twijfel over uitgesproken worden, een soort twijfel bovendien die voor de docent de zelf zijn toetsen construeert gerede aanleiding mag zijn voortaan geen meerkeuzevragen te hanteren. Een aantal van de overwegingen bespreek ik hier, maar zie ook 6.3.

Objectiviteit. De meerkeuzevragen leveren bij het nakijken geen problemen op, omdat van te voren afgesproken is welke alternatieven de goede zijn. Daar kun je bij opmerken dat weliswaar de afspraken op zich wel duidelijk zijn, maar dat de argumenten waarom dit alternatief als antwoord op deze vraag het enig juiste, of het beste is dan nog willekeurig zijn (in de zin dat collega's daarover van mening kunnen verschillen bijvoorbeeld). Belangrijker is, dat er nogal wat leerstof is die in open-eind vorm terug gevraagd, objectief scoorbaar is: rekenopgaven, contructieproblemen, bewijsvoeringen, vragen naar namen, data, e.d. Iets minder objectief, maar met een beetje zorg goed objectief scoorbaar te houden, zijn vragen naar definities, beschrijvingen, voorbeelden van begrippen en regels. In open-eind vorm niet objectief scoorbaar, maar met enige zorg wel betrouwbaar, zijn vragen waarin nieuwe oplossingen voor nieuwe problemen worden gevraagd, samenvattingen gemaakt worden, of van de student beschouwingen in essay vorm worden gevraagd; maar voor juist dit soort vraagstellingen is het bijzonder moeilijk en levert het gekunstelde resultaten, wanneer geprobeerd wordt om ze te vangen in objectief scoorbare, meerkeuze vorm.

Nakijken. De meerkeuze toets kan met behulp van de computer gescoord worden. Het is echter nog maar de vraag of open-eind vragen wel zo veel nakijktijd van de docent vragen dat dit tot een wezenlijk nadeel van de open-eind vorm ten opzichte van de meerkeuze vraagvorm wordt. Iedere docent die een toets maakt die aan minder dan, zeg, 500 studenten voorgelegd wordt, moet zich afvragen of voor hem of haar de mogelijkheid van automatische scoring wel van belang is.

Open-eind vragen zijn makkelijker te bedenken dan meerkeuze vragen; dat is een voordeel dat ook uitgebuit kan worden door met minder moeite een vragen collectie te maken die de stof tamelijk volledig dekt, en bekend gemaakt kan worden.

Tegenover de tijdbesparing bij het maken van de vragen, staat extra tijd nodig voor het nakijken (te bekorten door efficiënte lay-out, e.d.). Wat de scoring betreft: ervan uitgaand dat gemiddeld ongeveer 1:5e van de vragen fout is, kan de score bepaald worden door het aantal foutstreepjes op het antwoordformulier, en dat zijn er zo weinig dat een enkele oogopslag daarvoor voldoende is.

Stel dat de docent zijn 300 studenten vroeger een toets met 60 4-keuze vragen afnam, dan zou hij nu kunnen volstaan met een toets van zeg 50 open-eind vragen, waarbij de antwoorden van de student in ongeveer 2 minuten te scoren zijn. De totale correctietijd is dan 10 uur (vergeleken met bijv. 2 uur administratieve rompslomp bij computerscoring). Omdat de scoring volledig in eigen hand gehouden wordt, kan de student zeer snel uitslag krijgen: wordt de toets 's morgens afgenomen, en kijken 4 mensen na, dan kunnen deze 300 studenten in de loop van de middag hun uitslag krijgen. Het minieme nadeel van extra nakijktijd, voorzover niet weggevallen tegen al genoemde voordelen, betekent altijd nog dat op een koopje de onderwijssituatie voor de student een stuk doorzichtiger wordt, vanwege de grotere transparantie van de open-eind-vraag (zie volgende alinea) Wanneer de aard van de stof of de doelstellingen leidt tot open vraagvormen waarop uitgebreide antwoorden geformuleerd worden, neemt de correctietijd wél aanzienlijk toe, vooral wanneer het gewenst is de werkstukken door meer dan één beoordelaar na te laten kijken. Het is een nadeel dat in de meeste gevallen aanvaard zal moeten worden, omdat juist voor deze stof of doelstellingen ook de meerkeuze vorm geen geschikt alternatief biedt.

Berekeningen. Computerscoring levert ook gegevens over de toets en de afzonderlijke vragen op, zoals gemiddelde, homogeniteit, p-waarden, etc. De docent die open-eind vragen gebruikt, kan deze bij het nakijken scoren op IBM formulieren, waarna ook hij de toets op dezelfde wijze m.b.v. beschikbare computer programma's kan laten analyseren. Of dit soort routine berekeningen voor de docent wel zulke relevante gegevens opleveren, is een vraag die elders (cursus toets constructie) aan de orde zal komen.

Wie zijn eigen berekeningen wil maken voor open-eind toetsen: Diverse berekeningen zijn ook met de hand snel te maken: als foute antwoorden 1 en goede 0 gescoord worden, kan snel een score matrix personen bij vragen gemaakt worden door daar alleen de 1-tjes in te vullen, waarna variantie analyse en variantiecomponenten snel te berekenen zijn (zie de bijlage voor een uitwerking).

Relatie met doelstellingen. Het maken van meerkeuze vragen is meer een kunst, dan een kunde. Er zijn wel aanwijzingen te geven over welke fouten je moet vermijden, maar constructieregels zijn nergens te vinden (behalve heuristieken die de fantasie van de vragenmaker moeten prikkelen).
Het ontbreken van een theorie waarop de constructie van meerkeuze vragen kan stoelen, is een ernstige zaak. Er is niet zo veel leerstof die zich van nature leent tot de meerkeuze vorm. Voor alle leerstof die met enig kunst en vliegwerk in deze vorm geperst moet worden, geldt niet alleen dat het maken van de vragen erg moeilijk is, naar ook dat onduidelijk blijft wat deze vragen meten. Immers, wil je weten wat er met dergelijke vragen gemeten wordt, dan moeten de resultaten van de toets interpreteerbaar zijn, en daarvoor heb je een stuk theorie als vaste grond onder de voeten hard nodig.

De ontbrekende theorie zou met name aanwijzingen moeten geven hoe onderwijsdoelstellingen in toetsvragen te vertalen zijn. Omdat die theorie niet voorhanden is, zijn er nogal wat pogingen ondernomen het probleem te omzeilen door allereerst de doelstellingen ook te formuleren in termen van het soort vragen dat de student moet kunnen maken. Dit soort operationalisatie, waar verhitte discussie over gevoerd is, getuigt van nostalgie naar het tijdperk waarin de grootspraak van de Münchhausens nog geloofwaardig kon zijn.

Ik zou dit alles niet geschreven hebben, wanneer het niet zo zou zijn dat de meerkeuze vorm veel kwetsbaarder is wat dit punt betreft, dan de open-eindvorm. Natuurlijk heeft de laatste ook zo haar moeilijkheden (de docent zal ook deze vragen heel zorgvuldig moeten maken en controleren), naar die verdwijnen in het niet bij de complicaties die geïntroduceerd worden door de afleiderkeuze bij de meerkeuze vraag.

Voor de keuze van afleiders heeft de docent een oneindig aantal mogelijkheden, met als gevolg dat de student op het tentamen geconfronteerd wordt met discriminatieproblemen (kiezen tussen de geboden alternatieven) waarop hij zich bij de bestudering van de stof niet heeft kunnen voorbereiden. In deze zin hebben open-eindvragen het grote voordeel dat transparantie van de toetsing veel makkelijker te realiseren is.

Conclusie. De docent die zijn of haar toets construeert, kan daarbij beter gebruik maken van open-eind, kort antwoord of aanvul vragen. Wanneer het aantal studenten zo groot is dat het nakijken bij voorkeur automatisch moet kunnen gebeuren, kan de docent de vraag- en toetsconstructie beter uit handen geven aan daarin gespecialiseerde collega's, bijgestaan door deskundigen die van te voren de kwaliteit van de vragen aan onderzoek kunnen onderwerpen.

4.5 Aanpak voor toetstransparantie op wat langere termijn.

In de vorige paragraaf werd opgemerkt dat een theorie op grond waarvan meerkeuze vragen geformuleerd kunnen worden, niet bestaat. Hetzelfde geldt ook enigszins voor de hier aanbevolen open-eind vragen, wat niet hoeft te betekenen dat er geen goede voorschriften te geven zijn voor het formuleren van open-eind vragen, voorschriften die niet alleen een zekere onderwijskundige plausibiliteit hebben, maar die bovendien uitgebuit kunnen worden bij het transparanter maken van de toetsing. In deze paragraaf een korte uiteenzetting over de aanpak (die tezijnertijd in de cursus toets constructie uitvoeriger aan de orde zal zijn) in abstracte termen, en in de volgende paragraaf een concreet voorbeeld. Nog een opmerking vooraf: voor practica, werkstukken, en diverse vakken in de laatste studiefase doet de problematiek van zak-slaag beslissingen zich vrijwel niet voor. Waar die problemen er wel zijn, is er meestal ook sprake van leerstof die in schriftelijke vorm getoetst wordt; zolang dergelijke toetsing in niet al te opstel-achtige vorm plaatsvindt, is de hier te schetsen aanpak toepasbaar.

Leerstofanalyse. De meeste leerstof valt uiteen te leggen in begrippen en regels. Begrippen zijn dingen en verschijnselen als: stoel, electriciteit, neurose, zwart gat, kapitaal, etcetera. Regels zijn relaties tussen begrippen of wetmatigheden als: e = mc2, de economische achtergronden van de Pacific War, het kort geding, etcetera. Overigens is het onderscheid tussen begrippen en regels niet scherp te trekken, en voor analyse van de leerstof is zuiverheid in deze leer niet van belang. (Zie Gagné 1970, Klausmeyer c.s. 1974, voor wie daar belang in stelt). Voor een bepaald tentamen kan een volledige lijst van begrippen en regels gemaakt worden, voorzover deze onder de doelstellingen vallen. (Een dergelijke lijst is in een paar uur te maken).

Soorten vragen die te stellen zijn over begrippen en regels. Alleen een lijst van alle relevante begrippen en regels waarover de student op het tentamen vragen mag verwachten, is wel een bijdrage tot de transparantie van de toetsing, maar maakt daar nog slechts een begin mee.

Belangrijker is immers dat de student weet welk soort vragen over welke onderwerpen hij wél of juist niet kan verwachten. Voor de docent zou het prettig zijn aanwijzingen te hebben hoe hij over zijn begrippen en regels goede vragen kan formuleren, waarbij het meestal zo zal zijn dat niet alle mogelijke vraagsoorten over ieder begrip uit de lijst van belang zijn. Wat zijn nu die vraagsoorten?

Iedere vraag is op te splitsen in de vraagstelling, en het antwoord; in de vraagstelling, de stam van de vraag, worden ook de gegevens verstrekt die voor de beantwoording nodig zijn. Tussen stam en antwoord bestaat een zekere symmetrie, voorzover bijvoorbeeld de naam van een begrip zowel in de stam, als in het gevraagde antwoord voor kan komen (maar niet in beide tegelijk). Ook een voorbeeld van het begrip zou in de stam gegeven kunnen worden (met de vraag naar de naam van het begrip waar het een voorbeeld van is), of juist gevraagd worden (geef een voorbeeld van (het begrip ... In de vorm van het gegeven, of in de vorm van het gevraagde, kunnen voorkomen:

  1. de naam van het begrip (de regel)
  2. (definitie of) beschrijving van het begrip
  3. een (nieuw) voorbeeld van het begrip
  4. naam van een kenmerkende eigenschap van het begrip
  5. voorbeeld van een kenmerkende eigenschap van het begrip
  6. toepassing of gebruik van het begrip
  7. hoger geordend begrip ( waardoor dit begrip omvat wordt
  8. naast geordend begrip (omvat door hetzelfde hoger geordend begrip)
  9. lager geordend begrip (door dit begrip omvat).


De lijst is kort, en dekt vrijwel alle relevante vragen die over tentamenliteratuur te stellen zijn. Een bepaalde vraag kan geconstrueerd worden door uit de lijst te kiezen wat als gegeven in de stam van de vraag opgenomen wordt, en wat gevraagd zal worden. Het aantal zinvolle combinaties is niet erg groot, en afhankelijk van het belang van een bepaald begrip binnen de leerstof kan behoorlijk gesnoeid worden in alle eventueel wel mogelijke vraagsoorten.

Het zou prachtig zijn wanneer voor de leerstof die getoetst wordt, het mogelijk is om de student de lijst met begrippen en regels waarover vragen gesteld kunnen worden, te geven, met bij ieder begrip op de lijst vermeld welke soorten vragen daarover gesteld kunnen worden (wat er in veel gevallen niet meer dan drie of vier hoeven te zijn, die niet noodzakelijk voor alle begrippen in de lijst gelijk hoeven te zijn). Hoe ziet een en ander er in de praktijk uit?

4.6 Voorbeeld van uiteenleggen van leerstof en vraagconstructie.

Laat ik als voorbeeld nemen het volgende stuk tekst, dat onderdeel van een tentamen onderwijskunde zou kunnen zijn.


Het bovenstaande zou een stuk tekst kunnen zijn, dat als uitgangspunt bij het onderwijs gefunctioneerd heeft (onderwijs heeft bestaan uit het geven van voorbeelden, de studenten berekeningen laten maken, toepassingen bedenken, etcetera voorzover, gezien de doelstellingen, van belang).

Bekijk dan eerst welke begrippen er in de tekst voorkomen, die het onderwerp van onderwijs kunnen zijn. Dat zijn: - spreidingsmaat - verschilscore - variantie - standaarddeviatie - gemiddelde

Het begrip spreidingsmaat

wordt in de tekst wel gebruikt, maar is verder niet belangrijk genoeg om er eventueel vragen over te stellen. Dat zou anders zijn, wanneer verschillende spreidingsmaten behandeld zouden worden, zoals bij onderwijs in de mathematische statistiek het geval zou zijn. Dan zou 'spreidingsmaat' een hoger geordend begrip zijn t.o.v. variantie, standaard deviatie, gemiddeld verschil zoals gepresenteerd door Gini, etcetera. Voor dit stukje onderwijs zien we er van af om vragen te stellen over spreidingsmaten.

Het begrip verschilscore wordt als zodanig in de tekst eigenlijk niet genoemd, en dat zou een tekortkoming in de tekst kunnen zijn wanneer later veelvuldig van dat begrip gebruik wordt gemaakt. De tekst zou verbeterd kunnen worden door het begrip verschil score (verschil tussen score en gemiddelde) expliciet te presenteren, zodat variantie in andere woorden omschreven kan worden als het gemiddelde van de gekwadrateerde verschilscores. In het onderwijs kan aan deze tekortkoming van de tekst voldoende aandacht worden besteed.

Het begrip variantie, samen met het begrip standaarddeviatie, is uiteraard de kern van de tekst, en de vragen die de student op de toetsing kan verwachten zullen dan ook op deze begrippen betrekking hebben. De presentatie naar de student toe van te verwachten vragen kan vereenvoudigd worden door je te beperken tot één van beide begrippen, wanneer aangenomen mag worden dat de relatie tussen beide begrippen zo eenvoudig is dat de student daar geen moeite mee zal hebben.

Het begrip gemiddelde is kennelijk al eerder behandeld, maar komt in dit stukje tekst in een bijzondere vorm voor: niet als gemiddelde van de behaalde scores, maar gemiddelde van de absolute waarde van de verschilscores (waarover geen vragen gesteld zullen worden) en gemiddelde van de kwadraten van de verschilscores. De student moet daar in het onderwijs attent op gemaakt worden. Er ligt vervolgens ook nog een analogie wat dit betreft tussen de begrippen variantie en gemiddelde: ook voor variantie geldt dat je die kunt berekenen over behaalde scores, zowel als over varianties of gemiddelden; ook daar moet in het onderwijs op gewezen worden.

Dit ziet er nogal uit als een woordenbrij, maar denk er aan dat de docent voor zijn eigen leerstof dit soort analyses in enkele seconden kan maken, en zeker niet hoeft uit te schrijven. Waar het om gaat is het isoleren van de hoofdzaken uit de tekst, waarbij het goed is tevens te signaleren op welke punten de tekst door onderwijs (opgaven, uitleg, toelichting, voorbeelden) ondersteund moet worden.

Besloten wordt om alleen over het begrip variantie vragen in de toets op te nemen. Sommige andere vragen zouden wel interessant zijn, maar moeten we buiten beschouwing laten om zodoende de lijst van mogelijke vragen beperkt genoeg te houden dat de student aan de hand van die lijst zich efficiënt op het tentamen kan voorbereiden.

Welke vragen over variantie komen in aanmerking? Laten we allereerst concluderen dat het vragen van de definitie van onderwijskundige betekenis ontbloot is. Het vragen van een beschrijving van het begrip variantie in eigen woorden is wel relevant, maar niet voor de eindtoetsing gezien de lange antwoorden die dit op zal leveren (wel vragen tijdens het onderwijs, in diagnostische tussen-toetsjes, e.d.).

Relaties tot hoger geordende begrippen, naastgeordende, lager geordende zijn (althans op dit moment, later in de cursus zal het begrip variantie nodig zijn om met complexere technieken te kunnen werken) niet van belang. Toepassing van het begrip betekent in dit verband ongeveer hetzelfde als het geven van een voorbeeld: nl. berekeningen maken.

Kenmerkende eigenschappen van het begrip variantie zijn er wel, maar worden in de tekst niet genoemd, kennelijk omdat ze in verband met het doel van dit stuk onderwijs niet belangrijke genoeg worden gevonden.

Zodat alleen berekeningen overblijven, waarbij het dan ook nog zo is dat het in dit geval niet erg zinvol is om van de student bij een gegeven berekening te vragen wat er berekend is; alleen vragen in de vorm: bereken de variantie van ... zijn van belang.

Voor dit stuk tekst krijgt de student dan ook de eenvoudige boodschap mee dat hij op de toets één of meer vragen kan verwachten waarin hij gegeven een aantal scores (die ook best gemiddelden, varianties, kunnen zijn) de variantie van die scores of delen van die scores moet berekenen.

De abstracte formulering van het soort vragen dat de student mag verwachten moet dan nog aangevuld worden met enkele concrete voorbeelden van de bedoelde soort vragen:

Voorbeelden. Gegeven is een tabel met scores, bijvoorbeeld de scores van 6 studenten op 5 vragen in een studietoets:

 __________________________________________________________________
 vragen  studenten
             JAN      ELS      JOS      BEN      DIK      ANS
 -------------------------------------------------------------------
 1             0        1        1        0        0        0
 2             1        0        1        1        1        1
 3             1        0        1        1        0        0
 4             0        1        0        1        0        0
 5             0        1        1        0        0        1
 __________________________________________________________________


Het soort vragen dat je over dit soort scores mag verwachten in verband met de paragraaf over variantie, zijn:

  1. bereken de variantie van de 30 scores in de tabel.
  2. bereken de variantie van de totaalscores van de studenten.
  3. als de proportie studenten die een bepaalde vraag goed maken de moeilijkheid van die vraag is, bereken dan de variantie van de moeilijkheid van de vragen 1 t/m 5.
  4. bereken de variantie van de scores op vraag 1.
  5. bereken de variantie van de scores van Ben.
  6. welke student heeft de kleinste score variantie? (ev. meer studenten).
  7. welke vraag (of vragen) hebben de grootste score variantie?

    (antwoorden: a): 14. b): 11/12. c): 1/30. d): 2/9. e): 6/25. f): Jos en Dik. g): vraag 3 en 5.)


Hoogstwaarschijnlijk zal voor andere onderwerpen binnen dit vak nodig zijn dat de student weet wat variantie is, of die kan berekenen. In die zin zou je kunnen zeggen dat het soms voldoende is om vragen op te nemen in de toets waarvan het berekenen van varianties een onderdeel is, en geen afzonderlijke vragen over het begrip variantie. Dat komt de duidelijkheid, en dus de transparantie, ten goede. Maar het is ook mogelijk, en misschien wel zo transparant, over variantie wél vragen in de toets op te nemen, en vragen over onderwerpen waar varianties bij te pas komen, deze in gegeven vorm, dus in de stam van de vraag, op te nemen. Dat komt overigens ook de interpreteerbaarheid van de toetsresultaten ten goede: de student die het begrip variantie niet goed beheerst zal alleen vragen rechtstreeks over variantie fout maken, en vragen over complexere problemen die hij op zich wél beheerst, goed kunnen maken omdat het berekenen van varianties daarbij niet gevraagd is.

4.7 Transparantie (?) bij meerkeuze vragen.

In paragraaf 4.4 heb ik de docent aangeraden om, voorzover hij meerkeuze vragen gebruikte, over te gaan op open-eind, kort antwoord of aanvul vragen. De argumenten daarvoor hoef ik hier niet te herhalen. Ik kan er wel aan toe voegen dat een belangrijk argument tégen meerkeuzevragen de geringe transparantie van dit soort vragen is. De student wordt vaak op het tentamen geconfronteerd met vragen waar hij een keus moet maken tussen het goede alternatief (dat in het onderwijs aan de orde geweest is) en foute alternatieven, waarbij die laatste als zodanig meestal niet in het onderwijs aan de orde zijn geweest. Met andere woorden: de student krijgt bij meerkeuzetoetsen een groot aantal problemen voorgelegd die nieuw voor hem zijn, waarop hij in het onderwijs niet goed is voorbereid. Aansluitend bij het voorbeeld in paragraaf is het hier gesignaleerde probleem als volgt te schetsen.

Stel dat de vraag is om de variantie van de totaalscores van de studenten te berekenen (de gegevens daarvoor staan in de tabel in 4.6). Er zijn dan een oneindig aantal mogelijkheden voor de docent voor het formuleren van de foute alternatieven. Hij kan daarvoor nemen de uitkomsten van vragen a), d), en e). Het risico is dan dat ook de student die zijn zaakjes goed kent, in de war gebracht wordt, omdat hij er snel achter komt dat de alternatieve uitkomsten ook varianties zijn, en dan moet hij wel erg zeker in zijn schoenen staan om zich te houden aan zijn eerste (en goede) alternatief keuze.

De docent kan als alternatieven ook willekeurige getallen nemen. Het probleem daarmee is dat dan vrijwel iedere student tot het goede antwoord komt, omdat net zo lang proberen tot je antwoord klopt met één van de alternatieven ook het goede antwoord oplevert (en omdat voor tentamens altijd ruime tijd beschikbaar moet zijn, kan de student deze strategie ook volgen).

Een derde mogelijkheid is dat de docent als foute alternatieven kiest de resultaten die je zou verkrijgen bij het maken van bepaalde vergissingen. Misschien is dat nog wel aanvaardbaar wanneer in het onderwijs deze vergissingen ook als zodanig behandeld zijn, maar ook dan blijft er het risico in zitten dat de student in verwarring gebracht wordt.

Een vierde mogelijkheid is dat als foute alternatieven genomen worden de waarden van ándere spreidingsmaten (standaard deviatie, gemiddelde verschil, e.d. voorzover behandeld in het onderwijs). Ook dan weer het risico dat de student die zijn zaakjes niet feilloos kent, aan het twijfelen gebracht wordt.

Voor meerkeuze vragen over begrippen die veel minder scherp omschreven zijn dan het begrip variantie in ons voorbeeld, geldt in nog veel sterkere mate dat bijzonder veel soorten foute alternatieven gebruikt kunnen worden, zodat het voor de student vrijwel onmogelijk wordt zich daar effectief op voor te bereiden.

Een mogelijkheid voor de docent die om hem moverende redenen toch aan meerkeuze vragen wil vasthouden, is dat hij zich in de te gebruiken foute alternatieven voor zijn vragen strikt beperkt, tot één of twee soorten alternatieven bijvoorbeeld, zodat hij de student van te voren hopelijk voldoende kan inlichten over het soort problemen dat hij op de toets mag verwachten dat de student zich daarop ook kan voorbereiden. Voor ons variantie voorbeeld zou een mogelijkheid zijn dat de docent afspreekt als afleiders (foute alternatieven) uitsluitend getallen te nemen die het resultaat zijn van fouten in de berekeningsprocedure (vergeten de verschilscores eerst te kwadrateren, vergeten te delen door het aantal scores, e.d.). De student kan bij de voorbereiding op dit tentamen zijn inzicht dan ook speciaal op dit punt toetsen, en voor het geval hij in dit opzicht niet zeker van zichzelf is, nog wat extra oefenen.

4.8 Transparantie van de cesuur bij schriftelijke tentamens.

Zoals we gezien hebben, is transparantie van de toetsing goed haalbaar, zij het in mindere mate voor meerkeuze vragen dan voor de open vraagvormen. De eis van transparantie voor de beslissingsprocedure zakken-slagen, verder gewoon transparantie van de cesuur te noemen, is heel wat complexer. Het gaat er immers niet alleen maar om dat de student een bevredigende verklaring-achteraf krijgt waarom hij gezakt of geslaagd is, maar het gaat er juist om dat hij tijdig van de eisen op de hoogte is, zodat hij zijn studiestrategie af kan stemmen op het met redelijke zekerheid behalen van een voldoende. In de formulering van De Groot, die het begrip transparantie introduceerde (1970, 1972):


4.9 Het onderscheid tussen een objectieve en een transparante cesuur.

Omdat er enige verwarring mogelijk lijkt met een andere eis die aan de wijze van vaststellen van de grens zakken-slagen gesteld kan worden, de eis van objectiviteit van de beslissingsregel, zal ik hier op het onderscheid tussen objectiviteit en transparantie kort ingaan.

Een objectieve beslissingsregel, of objectieve cesuurbepaling, houdt in dat de wijze waarop de cesuur vastgesteld, aangewezen, of berekend zal worden, vastgesteld is voordat de toetsingsresultaten bekend zijn, en houdt ook in dat wie de cesuurbepaling vervolgens ook uitvoert er altijd dezelfde aftestgrens uitkomt.

Een voorbeeld van objectieve cesuurbepaling is de regel dat tenminste 30 van de 60 vragen goed beantwoord moeten worden voor een voldoende beoordeling, mits deze regel vastgesteld werd voordat de tentamenresultaten bekend waren. Nadeel van de beslissingsregel in dit voorbeeld is dat eventueel noodzakelijke correcties erop omdat het tentamen buiten verwachting erg moeilijk bleek te zijn, de objectiviteit van de regel aantasten. Maar ook dan kan van te voren afgesproken worden in welke gevallen de cesuur naar beneden bijgesteld zal worden (en hoe ver)

Een ander voorbeeld van objectieve cesuurbepaling is de afspraak vooraf dat de cesuur volgens Wijnen gehanteerd zal worden. Dat betekent dat de cesuur berekend zal worden volgens de formule: gemiddelde minus tweemaal de standaardmeetfout. De bepaling is objectief, omdat over de procedure geen misverstanden kunnen ontstaan, en wie de cesuur ook uitrekent, het resultaat moet (behoudens rekenfouten, of afrondingsproblemen die ook van tevoren beslist moeten worden) hetzelfde zijn.

In deze objectieve regel is al ingebouwd dat eventueel bijzonder moeilijk blijken van het tentamen niet leidt tot meer afwijzingen dan misschien de bedoeling van de docent was (het probleem bij het eerstgegeven voorbeeld). Nadeel: weliswaar objectief, maar niet transparant.

Ook de kernitemmethode De Groot kan een objectieve procedure genoemd worden. De gewijzigde kernitemmethode volgens Van Naerssen is op dit punt erg onduidelijk.

De mogelijke verwarring met het begrip transparantie zit hem dan hier in, dat objectieve cesuurbepaling aan de student voorafgaand aan het tentamen bekend gemaakt kan worden. De student kan dan (in principe) zelf de cesuurbepaling controleren (uitvoeren), hij weet hoe een en ander in zijn werk zal gaan. Maar dat geeft niet vanzelfsprekend ook aan de student de mogelijkheden om de wijze waarop de beslissing voor hem zal uitvallen, te beïnvloeden door zijn studiestrategie op bepaalde wijze in te richten. Maar het laatste is nu juist de eis waarom het gaat bij transparante cesuurbepaling.

4.10 Transparantie: minimaal te behalen score vooraf bekend.

Het aantal mogelijkheden om transparantie van de cesuur te bereiken is erg klein. Er zijn er eigenlijk maar twee die in aanmerking komen: de eerste is formulering van de minimum eis in termen van aantal goed te maken vragen; de tweede is een variant daarop: formulering van de minimum eis in termen van aantal goed te maken vragen over onderscheiden onderdelen van de stof. In het laatste geval wordt de stof verdeeld in een aantal parten die nogal uiteenlopend van aard, moeilijkheid of belangrijkheid zijn, zodat verschillende minimum eisen gesteld zouden kunnen worden. (Een waarschuwing voor degenen die een dergelijk voorstel in praktijk willen brengen: de minimum eisen voor afzonderlijke onderdelen moeten een stuk lager gesteld worden dan men in eerste instantie wenselijk zou vinden omdat anders erg veel studenten een onvoldoende zullen scoren omdat het erg snel kan gebeuren dat op een van de onderdelen de minimum eis niet gehaald wordt. Alternatieve procedures kunnen dan ook gebruikt worden: snelle herkansing (de volgende dag bijv.) op onvoldoende gemaakte onderdelen, of compensatie van onvoldoende prestaties op een bepaald onderdeel door hogere prestaties op andere onderdelen. Maar zoals te zien: dit soort procedures verhoogt op zich de transparantie van de cesuur allerminst).

Ingewikkelder regels zijn wel mogelijk, maar zouden oefening vooraf vereisen.

Een afspraak over het minimum aantal goed te maken vragen is op zich natuurlijk niet voldoende voor een transparante cesuur. Essentieel is dat de student zijn studiestrategie efficiënt hierop af kan stemmen, en dat betekent op zijn minst al in een vroegtijdig stadium de gelegenheid tot het afleggen van proeftentamens (eventueel gecomputeriseerd, of gewoon door de student thuis te maken tentamens).

Transparantie (en daarmee efficiëntie van de tijdbesteding van de student) kan vervolgens verhoogd worden door aan te geven uit welke delen van de stof geen vragen gesteld zullen worden, uit welke delen van de stof in ieder geval vragen gesteld zullen worden, etc. Ofwel: voor transparantie van de cesuur is transparantie van de toetsing een voorwaarde.


4.11 De pechfactor waar de student mee moet rekenen.

Jammer genoeg is het bekend maken van de minimaal te behalen score voor een voldoende beoordeling niet zo'n spijkerhard gegeven dat de student in alle gemoedsrust precies op een mate van stofbeheersing kan mikken die hem waarschijnlijk die score op de toets op zal leveren. Zoals we in het inleidende hoofdstuk, en ook in 6.4 zullen zien, is toetsing van studieprestatie een kwestie van nogal grote onnauwkeurigheden. Een noodzakelijk onderdeel van de docenten strategie bij het transparant maken van toetsing en zak-slaag beleid, is dat die mate van onnauwkeurigheid van de toetsing naar de student toe vertaald kan worden in termen van voor de student efficiënte studiestrategieën.

Tenminste zal de mate van onnauwkeurigheid bekend moeten zijn, in ieder geval in al die onderwijssituaties waar nog vast gehouden wordt aan het traditionele hordenloop model voor de examenregeling. Wanneer zakken automatisch ook overdoen betekent (tijdverlies, stress, en verwarring), moet de student een eerlijke kans krijgen om zich met een voor hem of haar aanvaardbaar zak risico op het tentamen voor te bereiden. In paragraaf werd een illustratie gegeven van zo'n studentstrategie, en het daaruit resulterende verlies in studietijd. Dat was echter een voorbeeld waarin van een bepaalde strategie uitgegaan werd, terwijl hier juist de vraag aan de orde is welke strategie de student zou moeten kiezen, en hoe de docent de voor die keuze noodzakelijke informatie kan geven.

De problematiek die hier over het voetlicht gesleurd wordt is verre van simpel. Een bevredigende oplossing zal ik hier dan ook niet schetsen, zij het dat noodoplossingen wél voorhanden zijn. Zo'n noodoplossing is het geven van een proeftentamen kort voor het eigenlijke tentamen. Dat proeftentamen moet in alle opzichten gelijkwaardig zijn aan het tentamen zelf (de vragen zullen natuurlijk niet identiek kunnen zijn), zodat de student op grond van zijn prestaties op het proeftentamen een schatting kan maken van de prestaties op het tentamen! Komt die schatting te laag uit, dat wil zeggen dat er een voor hem of haar te groot risico om te zakken in zit, of eventueel ook dat de student vindt dat zijn cijfer weliswaar voldoende zal zijn, maar niet hoog genoeg, dan kan de student leemten in zijn kennis (zoals die ook in het proeftentamen bleken) aanvullen. Twee opmerkingen hier bij: de docent zal de student ook moeten informeren wat de kans op een voldoende op het tentamen zal zijn, welke kans eenvoudig berekend kan worden wanneer over de betrouwbaarheid van toets, beoordeling, en cesuur goede schattingen gemaakt kunnen worden. Hopelijk kan ik in de bijlage de techniek demonstreren.

Tweede opmerking: voor het proeftentamen hoeven geen nakijk problemen te bestaan, omdat de studenten hun eigen werk kunnen beoordelen aan de hand van de beoordelingsrichtlijnen zoals de docent die opgesteld heeft.

Van Naerssen (1976) heeft een oplossing voor het hier gesignaleerde probleem gepresenteerd. Helaas kleven aan zijn model teveel bezwaren (wat de daarin gehanteerde aannamen betreft) om voor ons doel bruikbaar te zijn. Zie de bijlage voor een korte beschrijving van Van Naerssen's tentamenmodel, en de kritiek daarop.

4.12 Conclusies voor het dagelijks beleid van de docent (vakgroep).

  1. Geen meerkeuzevragen gebruiken, wanneer deze maar enigszins vermeden kunnen worden (zie ook 6.3).
  2. In veel gevallen zal het mogelijk zijn om zowel onderwerpen waarover op het tentamen gevraagd kan worden, als de soort vragen die over afzonderlijke onderwerpen verwacht mogen worden, in een relatief kort overzicht aan de studenten bekend te maken. Tevens wordt op deze wijze voorkomen dat in het tentamen vragen over details en triviale zaken gesteld worden.
  3. Het verdient aanbeveling om voor toetsing van het eigen vak de suggestie van Hofstee, zoals in de tekst (en in 5.4) beschreven, te overwegen (d.w.z. ofwel over te nemen, ofwel op grond van argumenten niet over te nemen).
  4. Welke ingewikkelde procedures ook gevolgd worden bij de bepaling van de cesuur, altijd kan van te voren aan de studenten meegedeeld worden welke score minimaal voor een voldoende behaald moet worden. Bouw daar ook afspraken in m.b.t. de gevallen waarbij een lagere esuur dan de tevoren bekend gemaakte, gehanteerd zal worden.
  5. Geef de studenten proeftentamen gelegenheid; verstrek hen daarbij de informatie die ze nodig hebben om op basis van de daarbij behaalde score een schatting te maken van hun kans op voldoende bij het tentamen zoals dat niet lang daarna afgenomen zal worden.



Hoofdstuk 5. Derde uitgangspunt: behoorlijke inspanning is voldoende.

Derde uitgangspunt: in principe krijgt iedere student die zich behoorlijk heeft ingespannen, het onderwijs gevolgd heeft, een voldoende beoordeling.

Eigenlijk een vanzelfsprekende zaak, dit uitgangspunt. De veronderstelling is dat de student gekwalificeerd is om aan het studieonderdeel deel te nemen. Is aan het laatste voldaan, dan moet het toch zo zijn dat iemand die zich gedurende de voorgeschreven tijd op behoorlijke wijze voor zijn studie inspant, een voldoende beoordeling verdient. Je kunt het, met Wijnen (1972) als volgt formuleren:


Wijnen veronderstelt dat de student een behoorlijke studie-inspanning levert, waarbij hij er overigens op wijst dat twijfel alleen aan die behoorlijke inspanning niet voldoende kan zijn om de student hard te beoordelen: ten minste zal aannemelijk gemaakt moeten worden dat er inderdaad iets ontbrak aan de juiste taakopvatting van de student(en).

Ook Hofstee (1973) onderschrijft ons uitgangspunt, zij het dat hij het tot het participatie-beginsel heeft omgedoopt :


5.1 Wat is behoorlijke studie-inzet?

Er zijn onderwijssituaties waarin behoorlijke studie-inzet zich ondubbelzinnig laat vaststellen, zoals bij praktische oefeningen, stages, en werkgroepdeelname. Dat zijn studieonderdelen waar zich geen cesuurproblemen voordoen. Zodra het gaat om zelfstudie, als voorbereiding op tentamens waar kennis van de stof wordt getoetst, is het minder duidelijk of de studenten zich behoorlijk hebben voorbereid. De truc die wel wordt toegepast is om behoorlijke voorbereiding te definiëren aan de behaalde toetsresultaten: wie goede cijfers behaalde, moet zich wel behoorlijk hebben voorbereid; wie slechts prestaties boekte heeft zich kennelijk niet behoorlijk voorbereid. Deze simpele wijze van redeneren is niet vol te houden. Sommige studenten zijn in staat redelijke prestaties te behalen met een minimale hoeveelheid bestede tijd; anderen besteden alle tijd die ze redelijkerwijs maar hebben aan tentamenvoorbereidingen en komen dan net (niet) met de hakken over de sloot. De grondgedachte is dat tijd en prestatie sámen iets zeggen over de studie-inzet van de student. Het vervelende is dat noch die tijdbesteding van de student, noch de mate waarin hij in wezen de stof beheerst, nauwkeurig te bepalen zijn. Van de student uit gezien is de situatie dat hij bijvoorbeeld mikt op juist voldoende voor dit bepaalde vak, maar als hij redelijk verzekerd is van een voldoende dan moet hij in zijn voorbereiding mikken op zeg een zeven en zal hij zoveel tijd besteden als hem daarvoor nodig lijkt. Dan nog loopt hij het risico een onvoldoende te behalen, omdat hij het tentamen onderschatte, zijn planning onhandig maakte, of gewoon pech had met de gestelde vragen (zie 6.4).

Omdat in onderwijs waarin slechts telt of je prestatie voldoende is of niet, omdat in dat onderwijs het aanvaardbaar of zelfs gewenst is dat de student een strategie volgt zoals juist beschreven, kan de student niet verweten worden ondanks zijn juiste studieaanpak toch een onvoldoende te scoren. Het is onjuist dan te zeggen dat deze student onvoldoende tijd in de voorbereiding heeft gestoken, ook al was die tijd minder dan voorgeschreven. Door dezelfde onnauwkeurigheid van de beoordelingsprocedure is het omgekeerde ook vaak het geval: dat studenten die een gok-strategie volgen door zich matig voor te bereiden, daarvoor vaak beloond worden met een voldoende beoordeling; in deze gevallen is het onjuist om uit het behalen van een voldoende prestatie te concluderen dat de student zich wel behoorlijk op het tentamen voorbereid zal hebben. Tentamenresultaten zeggen op zich nog niets over het zich behoorlijk voorbereid hebben van de studenten. Zijn de resultaten gemiddeld als goed beoordeeld, dan wil dat niet zeggen dat de studenten er niet de kantjes afgesloft hebben, en zijn de resultaten gemiddeld als slecht beoordeeld dan is het best mogelijk dat de studenten zich toch bijzonder uitgesloofd hebben. Zonder empirische gegevens moet aangenomen worden dat de studenten zich naar omstandigheden redelijk ingespannen zullen hebben in de voorbereiding op hun tentamen.

In het bijzonder is het laatste het geval wanneer het gaat om een men waar traditioneel erg veel studenten voor afgaan. Komt het keer op keer voor dat grote aantallen studenten geen voldoende scoren bij hun eerste tentamengelegenheid, dan is kennelijk de inrichting van het onderwijs of van de beoordeling dusdanig dat het de studenten niet mogelijk is om meer te presteren dan ze doen. Betekent dat dat in een dergelijk geval een hoog afwijzingspercentage gerechtvaardigd is? Natuurlijk niet; omdat studenten het keer op keer (jaar op jaar) niet beter blijken te doen, is er het nodige mis in het onderwijs, en ligt de verantwoordelijkheid voor het zogenaamde falen van de studenten niet bij hen, maar bij degenen die verantwoordelijk zijn voor de inrichting van dat onderwijs en de beoordeling. Een aantal mogelijke gebreken in de onderwijs- en beoordelingssituatie die aanleiding kunnen geven tot dit soort niet te rechtvaardigen hoge afwijzingspercentages zijn:


Hoge afwijzingspercentages die bij herhaling voorkomen, wijzen er op dat de inrichting van onderwijs en beoordeling het de studenten onmogelijk maken om behoorlijk te studeren. Wat hoog is hangt af van de consequenties die zakken voor de student teweegbrengt; hoe ernstiger gevolgen, bij des te lager afwijzingspercentage men argwanend moet worden. Wanneer onvoldoende overdoen betekent, zijn percentages afwijzingen van 15 of 20 al verdacht.

5.2 Behoorlijke inspanning ook voldoende beoordelen: een noodzakelijke (maar niet voldoende) voorwaarde voor transparantie.

Het tweede uitgangspunt is dat de student in staat moet worden gesteld om zich effectief op het behalen van een voldoende voor te bereiden, wat hem mogelijk gemaakt wordt door voldoende transparantie omtrent de wijze waarop de zak-slaag beslissingen genomen zullen worden. Welnu, daar volgt redelijkerwijs ook uit dat de student binnen het afgesproken tijdsbestek dat minimumniveau kan bereiken. Het heeft met andere woorden niet zo veel zin om een beslissingssituatie fijn transparant te maken, en tegelijkertijd de eisen zo hoog te stellen dat een deel van de studenten daaraan binnen de beschikbare tijd niet zal kunnen voldoen.

Hofstee (1973) noemt dan ook als belangrijkste eigenschap van zijn voorstel om toetsing als participatiecontrole te gebruiken:


Natuurlijk eist het ten uitvoer leggen van uitgangspunt 3 niet noodzakelijk ook de vorm van toetsing zoals Hofstee die propageert; ook de aard van de leerstof kan voor Hofstee toetsing minder geschikt zijn. Het principe is slechts dat de behoorlijk studerende student ook bij moeilijke toetsen kan rekenen op een voldoende beoordeling.

Voor de docent zal het niet direct eenvoudig zijn om het uitgangspunt in praktijk te brengen. Dat vereist immers niet alleen een andere opstelling van de docent bij de cesuurbepaling, maar het zal in de meeste gevallen ook om onderwijsmaatregelen vragen. Wat ik hiermee bedoel is aan een voorbeeld duidelijk te maken.

In de praktijk zal de docent van een bepaalde student niet weten of hij zich behoorlijk voor de studie ingezet heeft of niet. (Trouwens, als hij dat wel zou weten, zou toetsing kennelijk overbodig zijn). Maar in bepaalde gevallen kan hij van groepen studenten wél weten of zij zich behoorlijk hebben voorbereid of niet. Voorbeeld: de docent geeft intensief werkgroeponderwijs voor studenten die daarop ingetekend hebben. Uit de presentie op de groepsbijeenkomsten, en de inbreng van de studenten daarbij, kan de docent conclusies trekken m.b.t. de mate waarin deze studenten zich inderdaad behoorlijk hebben voorbereid op het afsluitende tentamen.

Welnu, de prestaties van deze groep studenten op het tentamen kunnen voorzichtig gebruikt worden om de cesuur in overeenstemming met dit uitgangspunt 3 te kiezen: met een bepaalde marge van onzekerheid zouden tenminste alle werkgroepdeelnemers voldoende beoordeeld worden, evenals alle studenten die dezelfde scores halen als door werkgroepdeelnemers behaald. De voorzichtigheid bij het beoordelen van de prestaties van anderen, die scores behalen lager dan die behaald door werkgroepdeelnemers, zit hem hierin dat niet zonder meer aangenomen mag worden dat werkgroepdeelnemers in alle opzichten lijken op niet-werkgroepdeelnemers: het is niet onwaarschijnlijk dat juist studenten die door bijzondere omstandigheden wat meer moeite met de studie hebben, door diezelfde bijzondere omstandigheden ook niet aan de werkgroepen konden deelnemen, naar overigens wel een behoorlijke studie- inspanning geleverd hebben. Met andere woorden: blind afgaan op de resultaten van de groep studenten waarvan vrij zeker bekend is dat ze goed aan het onderwijs hebben deelgenomen, kan tot onrechtvaardigheden voor de overige studenten leiden. Maar goed, voorzichtig moeten we altijd zijn bij het beoordelen van personen. dus dat is niets bijzonders.

Een andere mogelijkheid is dat proeftentamens over onderdelen van de leerstof afgenomen worden, zodat op basis van de resultaten inzicht verkregen wordt in de mate waarin bepaalde studenten zich behoorlijk op het eindtentamen voorbereiden. Ook hierbij eenzelfde waarschuwing tegen het al te snel generaliseren naar andere (deelgroepen) studenten.

5.3 Betekent dit verlaging van eisen?

Of het gevolg van hanteren van dit uitgangspunt verlaging van eisen betekent, hangt er van af of het niveau daalt. Immers, verlaging van eisen is volkomen onschuldig wanneer desondanks het niveau gelijk blijft. Om moeilijkheden te vermijden, definieer ik het begrip niveau niet. Een aantal opmerkingen:

Wanneer er onderscheid gemaakt wordt tussen het examen als afsluiting van een studiefase, en het examen als toelatingsdrempel tot een volgende studie(fase), dan kunnen we het er snel over eens worden dat m.b.t. de afsluiting van het onderwijs het niet veel zin heeft om over niveau daling of stijging te spreken: waar het om gaat is of van degenen die voor het afsluitend examen slagen aangenomen mag worden dat ze de onderwijsactiviteiten behoorlijk gevolgd hebben (en andersom dat we mogen aannemen dat allen die het onderwijs behoorlijk gevolgd hebben ook voor het afsluitend examen geslaagd zijn).

Voor het examen als toelatingsdrempel tot de verdere studie heeft het wel zin om de vraag naar het niveau te stellen. Dat zelfs het vergaande voorstel van Hofstee niet tot niveaudaling hoeft te leiden, is eenvoudig in te zien wanneer je je realiseert dat bijv. na het propedeutisch examen niet alle studenten de vervolgstudie gaan doen: ook wanneer selectie niet dwingend is zullen studenten op grond van inzicht in de eigen capaciteiten en wat van hen op dit punt in de verdere studie gegist wordt eventueel besluiten een andere studie of beroep te kiezen. De koppeling tussen tentameneisen en niveau bij de groep studenten die uiteindelijk ook afstudeert, is evenmin evident of noodzakelijk.

Een andere argumentatie richt zich op analyse van de huidige situatie, waar geen expliciet selectiebeleid gevoerd wordt met als gevolg dat velen de studie ten onrechte staken, en vele anderen de studie evenzeer ten onrechte op hun botte zitvlees afmaken. Met andere woorden, de vergelijking van niveau onder de hier voorgestelde alternatieve regeling (inclusief de Hofstee variant) met het niveau onder de huidige beoordelingsgewoonten, zou voor de laatste weleens slecht uit kunnen vallen.

De verdediging die Hofstee voert gaat over het verschil tussen de niveau- garantie zoals die onder conjunctieve examenregelingen gestalte krijgt, en zijn participatiebeginsel:


Overigens wil ik nog wel kwijt dat de strekking van deel 2 juist is de fundamentele ondergraving van het idee dat onder de huidige beoordelingsgewoonten van niveaubewaking sprake zou zijn.

Nu kan het gebeuren dat de docent ontdekt dat in deze alternatieve praktijk de studenten die net voldoende scoren eigenlijk te weinig van de stof af weten. Het is dan zaak om de problematiek aan te kaarten in het faculteitsoverleg, omdat er kennelijk sprake is van te weinig tijd voor dit studieonderdeel in het studieprogramma. Met andere woorden: de docent moet niet willen proberen door middel van strengere eisen, waardoor grotere aantallen studenten zijn tentamen moeten overdoen, een groter aantal uren voor zijn vak te claimen dan in het studieprogramma tot uitdrukking werd gebracht.

5.4 Conclusies voor het dagelijks beleid van de docent (vakgroep).

Dit hoofdstuk is misschien meer een discussie hoofdstuk dan de overige, ook al omdat allerlei praktische maatregelen wel bedacht kunnen worden (waarvan een aantal voorbeelden werden gegeven), maar die zijn sterk afhankelijk van de specifieke aard van een bepaalde onderwijssituatie. Het werken naar het realiseren van dit uitgangspunt zal zijn tijd wel vragen. Toch kan dit uitgangspunt nu al een leidraad zijn bij het te voeren beleid, bij de eerstvolgende keer dat het bepalen van de grens zakken-slagen weer aan de orde is.


Hoofdstuk 6. Vierde uitgangspunt: Bij beslissen over personen geldende regels.

In het onderwijs is het helaas nog steeds zo dat beslissingen over personen, leerlingen of studenten, aan weinig of geen normen onderworpen zijn. Beslissingen over zakken of slagen, bevorderen of niet, toelaten afwijzen, worden genomen in het rotsvaste geloof dat de cijfers waarop men zich baseert de beslissingen ook volledig kunnen dragen. Dat geloof is jammer genoeg op weinig anders gebaseerd dan de onbetwijfelde traditie, kritiekloos nagevolgde folkloristische beoordelingsgewoonten.

Op vrijwel geen enkel gebied is het in onze complexe samenleving nog mogelijk een stap te zetten, zonder daarbij normen, voorschriften en gedragsregels, plichten van jezelf en rechten van anderen in acht te nemen. Bij het oordelen over studenten ontbreken normen en rechtsregels waar het om de inhoudelijke rechtvaardiging van de beslissingen gaat. Voorzover normen en rechtsregels wél beschikbaar zijn, zijn ze in onderwijsgevend en onderwijsontvangend Nederland vrijwel onbekend.

In deze paragraaf geef ik een beknopt overzicht van rechtsregels die van toepassing zijn op oordelen over personen (zak-slaag beslissingen e.d.), en een beschrijving van normen die technisch-inhoudelijk aan toetsen en aan het gebruik van de daarbij verkregen gegevens gesteld moeten worden.

6.1 Algemene Beginselen van Behoorlijk Bestuur.

Het beoordelen van studieprestaties is een ingewikkelde bezigheid, zowel wat de inhoudelijke juistheid van de antwoorden van de student betreft, als voor de procedure die gevolgd wordt bij het vaststellen of de student gezakt of geslaagd is voor een tentamen of examen. Is het voor de docent al een moeilijke opgave om op verantwoorde wijze te werk te gaan, voor de student is het dubbel zo moeilijk de hele gang van zaken te overzien. Door de ingewikkeldheid van de beoordelingsprocedures, al dan niet door de docent onderkend, ontstaat voor de student het gevaar onrechtvaardig behandeld te worden, waarbij het voor de laatste bovendien erg moeilijk is om begane onrechtvaardigheden ook concreet te benoemen. Het laatste is van belang wanneer de student tegen genomen beslissingen in beroep wil gaan, waartoe hij op grond van artikel 40 WUB de mogelijkheid heeft: de individuele student kan verzoeken om het bijeenroepen van een geschillencommissie die zijn beargumenteerde klacht behandelt, waarbij de betrokken partijen gehoord worden.

De door Nicolai genoemde ongeschreven rechtsbeginselen, of Algemene Beginselen van Behoorlijk Bestuur, kunnen de docent dienen als richtlijnen bij het vaststellen van het cesuurbeleid. Ook de faculteitsraad, verantwoordelijk voor de examenregeling, moet zich deze Beginselen aantrekken bij haar beleidsbepaling. Wanneer docenten zich bij het beoordelen moeten richten naar geldende rechtsregels, geldt voor studenten dat zij bezwaar kunnen aantekenen tegen een beoordeling wanneer rechtsregels geschonden zijn. Er is een rechtsregel dat personen over wie besluiten worden genomen, door motivering van die besluiten in staat gesteld moeten worden beroep aan te tekenen.

De bedoeling van deze paragraaf is niet om een administratief-rechtelijke beschouwing over cesuurbepaling te geven; ik laat zien hoe deze Beginselen zich laten vertalen in onderwijsbeleid, en dat slechts illustratief omdat het karakter van deze Beginselen, als richtlijnen bij het administratieve handelen, een naar volledigheid strevende opsomming onmogelijk maakt. De docent laat zich hopelijk hierdoor aansporen zijn beoordelingsprocedure te verbeteren; de student vindt hier aanwijzingen waarvan hij gebruik kan maken om in voorkomende gevallen gemotiveerd beroep aan te tekenen (ex art. 40 WUB); geschillencommissies kunnen hopelijk goed gebruik maken van de hier gegeven informatie. De te geven voorbeelden zijn een eerste concretisering van deze Beginselen tot onderwijsbeleid, en berusten niet op enige jurisprudentie; wel word ik graag op de hoogte gehouden van de resultaten van beroepsprocedures, om deze in volgende edities te kunnen vermelden.

6. 1.1 Fair play.

Dit is een beginsel dat volgens Van Wijk en Konijnenbelt in de jurisprudentie weinig voorkomt. Dat maakt het wat moeilijker om toepassingen van dit beginsel in verband met cesuurbepaling te noemen.

Het fair play beginsel betekent dat de student in staat gesteld wordt om de besluitvorming in ieder geval op inhoudelijke punten, te controleren. Dat wil zeggen dat hij het gemaakte werk terugkrijgt (in copie), met de beoordeling van dat werk, en de door de docent gehanteerde beoordelingssleutel. Bij meerkeuzetoetsen is een mogelijkheid de student een copie van zijn antwoordformulier mee te geven, met de scoringssleutel, zodat hij zelf na kan gaan of de scoring van zijn werk correct is.

Wanneer vragen in de toets geheim gehouden worden is het voor de student niet mogelijk om de juistheid van de scoringssleutel te controleren, of om met de docent van mening te verschillen over wat het juiste of beste alternatief bij bepaalde vragen is (daarbij eventueel ondersteund door andere vakdeskundigen dan de docent in kwestie). Geheim houden van toetsvragen, een beetje kinderachtige en ook onnodige handelwijze, komt niet alleen met dit, maar ook met andere Beginselen in botsing.

Bij open-eindvraagvormen, of meer essay-achtige werkstukken, moet de student zelf kunnen nagaan of de beoordeling van zijn werk conform de beoordelingssleutel is. Een dergelijk beoordelingsvoorschrift moet dan ook door de docent opgesteld worden, en aan de studenten verstrekt.

Waarom hebben de genoemde maatregelen met het fair play beginsel te maken? Omdat in het geval van beoordelingsfouten en vergissingen de student in de gelegenheid moet zijn deze op te sporen, wanneer de verantwoordelijke docent deze niet opmerkt. Dat dit geen academisch puntje is, zal vrijwel iedere docent uit eigen ervaringen bekend zijn. Rond de aftestgrens is een enkel puntje meer of minder beslissend voor zakken of slagen.

Mijns inziens is ook het principe van transparantie van toetsing en besluitvorming (zie 4 ) een uitwerking van het fair play beginsel voor beoordelingssituaties.

6.1.2 Zorgvuldigheidsbeginsel.


Zorgvuldige voorbereiding van zak-slaag beslissingen houdt in dat:>

Je kunt zeggen dat deze cursus cesuurbepaling tot doel heeft de docent in staat te stellen op genoemde punten zijn zak-slaag beslissingen met de vereiste zorgvuldigheid te nemen. Omgekeerd kan de student, ook op grond van deze cursus, de docent aan concrete uitwerkingen van het zorgvuldigheidsbeginsel houden.

Bij conjunctieve (hordenloop) examenregelingen zou het wel eens moeilijk of onmogelijk kunnen blijken de vereiste zorgvuldigheid te bereiken (zie ook deel 2 ) waaruit mijns inziens best de conclusie getrokken mag worden dat conjunctieve examenregelingen in strijd zijn met dit beginsel van behoorlijk bestuur. Voorzover de wet niet uitdrukkelijk een conjunctieve regeling voorschrijft, staan afwijzende beslissingen vanuit het zorgvuldigheidsbeginsel bezien erg zwak wanneer conjunctieve examenregelingen gebruikt worden.

6.1 .3 Zuiverheid van oogmerk

Het bestuur mag een bevoegdheid alleen gebruiken voor het doel waarvoor die bevoegdheid is gegeven.


Dit beginsel sluit bepaalde motiveringen voor het kiezen van toetsingsprocedure en aftestgrens uit, zoals:


Je kunt verdedigen dat het de taak van de docent is om onderwijs te geven, en voorzover daar toetsing bij hoort, dat het de taak van de docent is om de te stellen vragen te kiezen in overeenstemming met hetgeen in dat onderwijs behandeld werd, en de beantwoording te beoordelen naar inhoudelijke juistheid, en niet meer dan dat.

Neem als voorbeeld de studietoets, dan moet de docent ervoor zorgen dat de vragen de behandelde stof behoorlijk dekken, en dat de scoringssleutel juist is (het laatste hoeft niet direct eenvoudig te zijn, zie bijv. 6.5. De docent heeft niet als taak aan de toetsscores ook cijfers toe te kennen, of er het oordeel voldoende of onvoldoende aan te verbinden, behalve volgens de richtlijnen daartoe uitgevaardigd door de faculteitsraad. Heeft de raad die richtlijnen niet gegeven dan valt er over te discussiëren of de docent die voldoendes en onvoldoendes uitdeelt misschien handelt in strijd met dit beginsel zuiverheid van oogmerk. De hier gegeven gedachtengang doet enigszins vreemd aan, omdat we niet gewend zijn in deze termen over het beoordelen van studieprestaties te denken; maar het volstaan met het rapporteren van ruwe scores, zonder deze om te zetten in cijfers en zak-slaagbeslissingen, is gelijk aan het geven van een dossier diploma voor dit studieonderdeel. De regels voor het behalen van het afsluitend examen kunnen dan gesteld worden in termen van ruwe scores voor afzonderlijke studieonderdelen behaald.

In gevallen waarin de faculteitsraad wél regels heeft gegeven voor cijferbeoordeling en zak-slaagbeleid, spreekt het vanzelf dat ook die voorschriften te toetsen zijn aan de beginselen.

6.1.4 Verbod van willekeur.

Van willekeur is sprake wanneer de aftestgrens zonder expliciete argumentatie op een bepaalde score vastgesteld wordt, omdat dan geen enkele belangenafweging plaats vindt. Van willekeur is ook sprake wanneer de kernitemmethode wordt toegepast, omdat daarin geen belangenafwegingen plaats hebben (anders gezegd: degenen die kernitem methoden gebruiken bij de cesuurbepaling, zijn daarmee nog niet af van de plicht van een behoorlijke belangenafweging (zie ook 6.1.2). De methode Wijnen heeft wel een bepaalde vorm van belangenafweging in zich, en is wat moeilijker als willekeurig in de hier bedoelde betekenis te kenmerken. Zie voor kritische bespreking van kernitemmethoden en methode Wijnen de bijlagen.

Alle gevallen waarin eenzijdige belangenafweging heeft plaats gevonden, leveren ook willekeur op. Van eenzijdige belangenafweging is sprake wanneer de aftestgrens bepaald wordt uitsluitend om het aantal ten onrechte gegeven voldoendes te beperken: daardoor worden de belangen van hen die ten onrechte onvoldoendes krijgen niet meegewogen.

Van eenzijdige belangenafweging kan ook sprake zijn wanneer de aftestgrens uitsluitend door afwegen van aantallen ten onrechte gegeven voldoendes en ten onrechte gegeven onvoldoendes bepaald wordt, omdat daaruit een ándere aftestgrens resulteert dan wanneer ook met aantallen terecht gegeven voldoendes en terecht gegeven onvoldoendes rekening zou zijn gehouden (zie hoofdstuk 7 en deel 2).

In individuele gevallen kunnen beslissingen kennelijk onredelijk zijn, afhangend van bijzondere persoonlijke omstandigheden van deze student. Mijns inziens moet het zo kunnen zijn, dat in bijzondere gevallen een bepaalde prestatie die niet aan de gestelde norm voldoet, toch als voldoende beoordeeld wordt Onder herkansing, mondelinge herhaling of andere altijd vanzelfsprekend gevonden procedures.

6.1.5 Gelijkheid.


De huidige beoordelingspraktijk is dat studenten met dezelfde score op de toets, hetzelfde beoordeeld worden: wanneer de cesuur bepaald is op een score van 28, dan zakt iedere student die 27 punten heeft behaald ongeacht wie hij is. Deze beoordelingsgewoonte heeft niets te maken met het rechtsbeginsel waar het in deze paragraaf om gaat. Het gaat om mensen en niet om scores.

Gelijke gevallen worden in beginsel gelijk behandeld, en niet gelijke scores op dezelfde wijze als gelijke monniken in beginsel gelijk behandeld worden, en niet gelijke kappen; of zoals Van Wijk en Konijnenbelt het zeggen: 'wanneer twee monniken inderdaad gelijk zijn komt dat in belangrijke mate door de gelijkheid van hun kappen.' Kort en goed komt het bovenstaande er op neer dat het behalen van eenzelfde score op een toets niet betekent en niet mag betekenen dat de betreffende studenten dan ook vanzelfsprekend gelijk zijn in de betekenis van het onderhavige beginsel.

Omdat er in de onderwijspraktijk van alledag wel degelijk zeer grote ongelijkheden tussen studenten en leerlingen voorkomen, is het geen academische strijdvraag of toepassing van het gelijkheidsbeginsel tot ándere zak-slaagbeslissingen voor bepaalde studenten of voor bepaalde deelgroepen studenten zou kunnen en moeten leiden.

Er zijn nogal wat studierichtingen waar de wet studenten met zeer uiteenlopende vooropleidingen toelaat. Moeten dan ook deze studenten zonder onderscheid naar hun vooropleiding beoordeeld worden, of juist wel rekening houdend met verschillen in vooropleiding? Het gelijkheidsbeginsel (liever ongelijkheidsbeginsel in dit geval) wijst op het laatste, hoewel nog niet direct duidelijk is hoe aan dit rechtsbeginsel in voldoende mate tegemoet gekomen kan worden. Voor het laatste moeten middelen en methoden gezocht worden die het mogelijk maken om bij de te nemen beslissingen rekening te houden met de mate van ongelijkheid die er tussen verschillende studenten of groepen studenten kan bestaan. Hoewel er in de testliteratuur wel pogingen ondernomen zijn om methoden en technieken te ontwikkelen, zijn daar nog geen eenduidige resultaten uitgekomen. Zie voor een overzicht het themanummer 'On bias in selection' Journal of Educational Measurement, 1976, volume 13, blz. 1-99.

Bij het propedeutisch examen, waar een voorspelling van toekomstig studiesucces of van geschiktheid voor de verdere studie (impliciet) aan de orde is, is het wel zeker dat deelgroepen in verschillende mate voorspelbaar zijn en niet over die éne zelfde selectiekam geschoren mogen worden. Deze groepen studenten zijn ongelijk, en moeten in de mate van hun ongelijkheid ook ongelijk behandeld worden.

In de praktijk is te verwachten dat de eisen voor studenten met geringere vooropleiding milder gesteld moeten worden dan voor anderen. Wanneer blijkt dat voor bepaalde tentamens HBS-A studenten in grote getale zakken, en studenten met Gymnasium B vooropleiding niet, dan is er zeker reden om aan de besluitvorming te gaan twijfelen op grond van het gelijkheidsbeginsel.

Er zijn nog een aantal, meer subtiele, manieren waarop het gelijkheidsbeginsel geschonden kan zijn. De gelijke behandeling van gelijke gevallen vereist dat de eisen bij de ene tentamenafname niet verschillen van die bij een vorige tentamenafname (tenzij als gevolg van een expliciete beleidswijziging op dit punt). Er zijn technieken beschikbaar op grond waarvan de zwaarte van het tentamen bij verschillende afname vergeleken kan worden; worden dergelijke technieken niet gebruikt dan is het erg lastig om opeenvolgende tentamens (voor hetzelfde vak) in moeilijkheid te vergelijken, en is er in zekere zin sprake van schending van het fair play beginsel omdat ook de studenten niet in staat gesteld worden om te controleren of dit tentamen nu moeilijker was dan de vorige keer. Worden die technieken wel toegepast, dan kan blijken dat de tevoren afgesproken aftestgrens te hoog gesteld was, in welk geval hij alsnog verlaagd kan worden. Voor dit soort technieken zie De Gruijter (proefschrift, in druk).

De geringe nauwkeurigheid die met tentamens bereikbaar is, doet de vraag rijzen of een bepaalde mate van toevalligheid die op deze wijze in de beoordeling binnensluipt, niet onaanvaardbaar kan zijn gezien vanuit het gelijkheidsbeginsel. Het is moeilijk te verkopen aan studenten dat grote aantallen van hen ten onrechte een onvoldoende beoordeling kregen, waar tegenover een relatief belangrijk aantal studenten staat die de kantjes er af gelopen hebben en dat beloond zagen met een voldoende beoordeling. Zijn betere examenregelingen mogelijk (deel 2) dan zouden die bij voorkeur ook gebruikt moeten worden.

Al met al is het gelijkheidsbeginsel een belangrijk beginsel bij zakslaag beleid, maar levert het realiseren ervan moeilijkheden op. Dat neemt niet weg dat het veronachtzamen van het beginsel leidt tot gelijke behandeling van ongelijke gevallen, of ongelijke behandeling van gelijke gevallen, zodat er geen andere weg is dan werken aan procedures waarin aan dit beginsel zoveel mogelijk recht gedaan wordt.

6.1.6 Rechtszekerheid.


Dit is een erg duidelijk beginsel, waaraan niettemin in de praktijk nogal eens niet voldaan wordt. Wanneer voor het slagen voor een practicum of groepsonderwijs de afspraak gemaakt wordt dat de student in het algemeen aan de activiteiten deel moet hebben genomen, dan is een dergelijke afspraak te vaag, en brengt ze voor de studenten rechtsonzekerheid mee.

Een voorbeeld uit mijn eigen studietijd: een practicum werd gegeven waarin zes onderzoekjes gedaan en gerapporteerd moesten worden. Ieder rapportje werd beoordeeld en van een cijfer voorzien, maar dat cijfer werd de student niet meegedeeld. Op deze manier bleef je in het onzekere over het peil van de eigen prestaties, en was de student niet in staat om een eventueel slechte start tijdig te onderkennen en latere werkstukken dienovereenkomstig te verbeteren. Hoewel ik dacht een redelijk voldoende gemiddelde prestatie geleverd te hebben, mocht ik tot mijn stomme verbazing na afsluiting van het practicum horen dat mijn verslagen de allerlaagste beoordeling hadden gekregen, en ik het practicum over mocht doen.

Strijd met het rechtszekerheidsbeginsel kan misschien ook ontstaan wanneer de docent een keurige lijst met onderwerpen heeft gemaakt die de kernpunten van zijn onderwijs behelzen en waarover hij vragen zou kunnen stellen, maar hij maakt de lijst niet aan studenten bekend.

Het beginsel kan ook in het geding komen bij het beoordelen van gegeven antwoorden. Het komt wel eens voor dat de docent een vraag onzorgvuldig formuleert, en antwoorden gaat beoordelen niet op wat hij in feite gevraagd heeft, maar op wat hij bedoelde te vragen.

6.1.7 Vertrouwen

Wanneer voor een bepaald tentamen altijd een afwijzingspercentage dat fluctueerde rond de 15 % werd gehanteerd, en plotseling wordt voor het tentamen zeg 30 % afgewezen zonder dat daarvoor argumenten gehanteerd kunnen worden die laten zien dat studenten zich deze keer inderdaad veel slechter op de toets voorbereid hadden dan gebruikelijk, kan er sprake zijn van schending van het vertrouwensbeginsel. Dit soort schending komt waarschijnlijk in het w.o. vaak voor.

Het vertrouwensbeginsel is overal dáár aan de orde waar afspraken gemaakt worden over wat de student op het tentamen mag verwachten: afspraken over welke delen van de stof, welk soort vragen, de wijze van beoordeling van de antwoorden, de wijze van scorebepaling en cesuurbepaling. Is een bepaald tentamen jarenlang als meerkeuzetoets afgenomen, en wordt zonder kennisgeving overgegaan op een ander soort vraagstelling, dan is dit beginsel geschonden.

6.1.8 Motivering.


Het gaat er hier mijns inziens om dat de docent (vakgroep) gehouden is expliciet te motiveren waarom zij de cesuur gelegd heeft op déze plaats. De argumenten die daarvoor van belang zijn, zijn in deze cursus cesuurbepaling wel ongeveer te vinden, en daaruit zou je kunnen afleiden dat een motivering onvoldoende is wanneer aan belangrijke argumenten zoals in deze cursus aan de orde, geen aandacht werd besteed.

In ieder geval is een motivering van een zak-slaagbeslissing in de trant van: 'je bent gezakt omdat je score beneden de aftestgrens bleef,' onvoldoende. (deze motivering is niet meer dan het in andere woorden formuleren van de genomen beslissing).

De allerbelangrijkste soort motivering die uiteindelijk wél door de docent of vakgroep gegeven moet kunnen worden, is de mate van nauwkeurigheid en geldigheid van de toetsresultaten (zie 6.2 en volgende paragrafen). De kwaliteit van de toetsresultaten en van het valideringsonderzoek zal de zak- slaag beslissingen moeten kunnen dragen. Je zou kunnen zeggen dat de kwaliteit van de toetsresultaten, en de resultaten van het valideringsonderzoek (zie 6.7 ) de mate van feitelijke juistheid van de gegevens op grond waarvan de beslissingen genomen worden, aangeven.

6.2 Standards for Educational and Psychological Tests.

De toenemende invloed van het overheidshandelen op het dagelijks leven leidde tot de ontwikkeling van Beginselen van Behoorlijk Bestuur, zoals in de voorgaande paragraaf beschreven. Iets dergelijks deed zich voor bij het op steeds groter schaal gebruiken van tests en toetsen: ook hier groeide de behoefte aan waarborgen voor toetskwaliteit, en omschrijving van de zorgvuldigheid waarmee beslissingen over personen omgeven moeten zijn. Commissies uit beroepsorganisaties van psychologen en onderwijskundigen in de Verenigde Staten brachten de belangrijkste normen voor toetsconstructie, toetsafname, en gebruik van toetsresultaten bij beslissingen over personen, bijeen in de brochure Standards for Educational and Psychological Tests, laatst herziene editie 1974. Aan deze Standards zijn niet alleen psychologen en onderwijskundigen gebonden, maar vooral ook docenten die beoordelingen van studenten, in welke vorm ook, uitvoeren.

Deze Standards, voor circa 20 gulden te bestellen, behelzen stringente, in afschuwelijk jargon gestelde voorschriften. Voor deze cursus vertaal ik de strekking van de Standards in concrete informatie die de docent helpt zich een indruk te vormen van de mate waarin zijn zak-slaag beslissingen beïnvloed zijn door irrelevante en onbedoelde factoren. Een essentiële stelregel is namelijk dat de docent op de hoogte is de wijze waarop, en de mate waarin, zijn beslissingen in hun gevolgen kunnen afwijken van de bedoelde gevolgen.

De juistheid van beslissingen wordt op twee manieren aangetast: door toevallige invloeden, en door systematische invloeden.

Toevallige fouten zijn beslissingsfouten die ontstaan door toevallige invloeden, door ongecontroleerde omstandigheden. In de literatuur wordt de technische term betrouwbaarheid (reliability) gebruikt voor de mate waarin de rangorde van toetsscores voor verschillende studenten vrij is van toevallige fouten, en de term 'standaardmeetfout' (standard error of measurement) voor de mate waarin, ruw gezegd, de score van de individuele student door toevalligheden beïnvloed is.

Systematische fouten ontstaan door invloeden of samenhangen die een systematische vertekening in scores, of in resultaten van beslissingen, geven. Het gaat hier om de mate waarin aan de bedoelingen van de toetsing of de zak-slaag procedure door de gehanteerde toets of procedure niet voldaan kan worden. Omdat de omvang van de toevallige fouten in principe altijd gekwantificeerd kan worden, zijn toevallige fouten een bijzonder geval van systematische fouten, en dan ook in de laatste categorie inbegrepen. ook in empirisch onderzoek is het zo, dat het wel mogelijk is de omvang van de toevallige fouten te onderzoeken, maar niet de omvang van de systematische fouten vs. van toevallige fouten. In jargon heet het dat betrouwbaarheid een (niet voldoende) voorwaarde voor validiteit is; vergeet het jargon, ik zal er verder geen gebruik van maken.


6.3 Toevallige invloeden: raden bij meerkeuzetoetsing.

Bij meerkeuzetoetsing hebben we te doen met een wel heel zuivere vorm van toevallige beïnvloeding van de score, omdat de student de vragen die hij niet weet moet raden. De docent die van de meerkeuzevraagvorm gebruik maakt, moet inzicht hebben in de mate waarin toetsscores gevoelig zijn voor toevalsfluctuaties die uit dat raden ontstaan, moet weten of deze invloed van het raden te vermijden is door op andere toetsvormen over te gaan, en moet beseffen dat hetzelfde geldt voor de invloed van raadkansen op de mate waarin zijn zak-slaag beslissingen juist zijn.

Het doel van deze cursus is om de docent dit soort inzichten bij te brengen, en daarom zal ik een aantal cijfermatige illustraties geven. De aanpak die ik daarbij volg is onorthodox: omdat het uiteindelijk gaat om slaagkansen voor de individuele student, ga ik na wat een student in bepaalde situaties te wachten staat. Daarbij veronderstel ik telkens dat bekend is wat in werkelijkheid nooit bekend zal zijn: wat de mate van ware stofbeheersing van de student is, hoeveel van de toetsvragen hij wist en hoeveel hij er moest raden, e.d. De klassieke analyse aanpak, die voor leken weinig doorzichtig is, is om uitgaande van waargenomen scores iets te weten zien te komen over de ware scores zoals die zonder toevallige en systematische vertekeningen zouden zijn. Niet alleen is de laatste aanpak weinig inzichtelijk en mathematisch complexer, maar voor cesuurproblematiek is ze niet relevant omdat het er dan om gaat of studenten die de stof behoorlijk beheersen een aanvaardbare kans hebben om ook voldoende te scoren, en niet zozeer of studenten die voldoende scoren ook met een voldoende mate van waarschijnlijkheid de stof in wezen voldoende beheersen. Dit mag overigens ook best gelezen worden als een soort belangentegenstelling tussen studenten en docenten respectievelijk, waarbij het expliciete uitgangspunt van mij is dat, mede gezien de algemene beginselen van behoorlijk bestuur, de belangen van de studenten horen te prevaleren.

Stel je dan voor dat de student een meerkeuzevraag ofwel weet en goed beantwoordt, ofwel niet weet en raadt tussen twee of meer alternatieven. Dit is een vereenvoudiging die op gespannen voet met de werkelijkheid staat, d.w.z. dat we er zeker van kunnen zijn dat in werkelijkheid dit onderscheid niet zo valt te maken. Dat neemt niet weg dat het een benadering is die op de resultaten van de analyse waarschijnlijk geen grote vertekenende invloed zal hebben, en dat de vereenvoudiging noodzakelijk is om tenminste een begin met die analyse te kunnen maken.

Maak dan de vereenvoudiging dat bij vierkeuzevragen de student die de vraag niet weet tenminste in staat is één van de afleiders af te strepen, zodat zijn raadkans 1/3 is. Een enkele keer zal hij méér afleiders uit kunnen schakelen, maar daar staat misschien tegenover dat hij een enkele keer zich ook letterlijk door een afleider laat afleiden; om ingewikkeldheden te vermijden zou je het daarom maar het beste op die raadkans van 1:3 kunnen houden. Ook wordt er dan van afgezien dat de raadkans voor hoogscorende studenten anders zal zijn dan voor laagscorende (zie bijv. Wood 1976 JEM).

Doe net alsof je van een bepaalde student weet hoeveel van de meerkeuzevragen hij weet, en hoeveel hij er zal raden, zodat zijn toetsscore zal bestaan uit het aantal geweten vragen plus het resultaat van het raden van de overige vragen. De vraag is, welke invloed dat raden op zijn toetsscore kan hebben. Omdat het hier gaat om een eenvoudig soort raadkans, is op relatief makkelijke wijze te berekenen wat de kans van onze student op een bepaald aantal goed is. De raadkans van 1/3 kun je simuleren door voor iedere vraag een dobbelsteen te werpen en het boven komen van 1 of 2 ogen als succes, dus als goed te beschouwen. De kans op een bepaald aantal goed kun je ook van te voren berekenen op een wijze die hier niet uiteengezet kan worden (maar zie de toelichting bij tabel 6.3.1). De resultaten van dergelijke berekeningen zijn uitgezet in de tabel op de volgende bladzijde.

Tabel 6.3.1 laat zien dat pech of geluk een bijzonder groot effect op de toetsscore van de student kunnen hebben, en wel des te meer naarmate de student meer vragen moet raden. Wat onze cesuurproblematiek betreft zitten we dan met de ongelukkige complicatie dat juist voor studenten rond de grens van voldoende - onvoldoende mate van stofbeheersing geldt dat zij nogal wat meerkeuzevragen moeten raden. Het is beslist niet zo dat raden bij meerkeuzetoetsen relatief weinig voorkomt, en de lezer kan dat aan de hand van eventueel zijn eigen meerkeuze tentamen makkelijk nagaan: wanneer gemiddeld 70 % van de antwoorden op iedere vraag goed zijn, zou je vereenvoudigenderwijs kunnen stellen dat in 30 % van de gevallen studenten fout geraden hebben, en wanneer de kans op fout raden 2/3 is, is in te zien dat in totaal in 45 % van de gevallen naar het antwoord geraden moet zijn (ongeveer)!

__________________________________________________________________
aantal    aantal vragen waarbij  geraden wordt; raadkans 1:3 aantal
 goed  12  18  24  30  36  42  48  54  60
 0      1
 1      5   1
 2     13   3
 3     21   7   2
 4     24  13   4   1
 5     19  18   8   2   1
 6     11  20  12   5   1
 7      5  17  16   8   3   1
 8      1  12  17  12   5   2   1
 9          6  15  15   8   4   1
10          3  11  15  11   6   2   1
11          1   7  14  13   8   4   1
12              4  11  14  11   6   3   1   
13              2   8  13  13   8   4   2
14              1   5  11  13  10   6   3
15                  2   8  12  12   8   4
16                  1   5  10  12  10   6
17                  1   3   8  11  11   8
18                      2   5  10  11  10
19                      1   3   8  11  11
20                          2   6   9  11
21                          1   4   8  10
22                              2   6   9
23                              1   4   8
24                              1   3   6
25                                  2   4
26                                      3
27                                      2
28                                      1
29                                      1
30


TABEL 6.3.1 Kansen (in honderdsten) op bepaald aantal vragen goed.
[noot: samengesteld m.b.v. The Staff of the Computation Laboratory's Tables of the cumulative binomial probability distribution. Cambridge, Massachusetts: Harvard University Press, 1955.]

De tabel kan ook (voor andere raadkansen bijvoorbeeld) berekend worden met behulp van de formule voor de binomiaalverdeling

formule 6.3.1 >     ( n! / (r! (n-r)!)) x pr x (1-p)n-r

n = aantal vragen
r = aantal goed
p = kans op goed

n! (lees: n faculteit) kan voor grote waarden van n benaderd worden door:

(Stirling) n! = √(2πn) x nn e-n

e = 2,71828 .....

voor kleine n is n! = n.(n-1)(n-2)(n-3) .... (3)(2)(1) exact te berekenen.

 ___________________________________________________________________
 aantal  getrokken  kans ten onrechte  kans ten onrechte
 toets-  cesuur     voldoende          onvoldoende
 vragen             geweten:           geweten
                    17  18  19         20  21  22  23
 -------------------------------------------------------
   41      27       25  35  46         42  30  19  10
   44      28       27  36  46         42  31  22  12
   47      29       28  36  46         43  32  22  14
   50      30       29  37  47         43  33  23  15
   53      31       29  38  47         43  34  25  17
   56      32       30  38  47         44  34  26  19
   59      33       31  38  47         44  35  27  19
   62      34       31  39  47         44  36  27  20
   65      35       32  39  47         44  36  28  21
 ___________________________________________________________________


TABEL 6.3.2 Kansen op ten onrechte voldoende, resp. onvoldoende als de raadkans voor niet-geweten vragen 1/3 is. De cesuur zonder raden is tenminste 20 vragen weten voor alle getabelleerde toetslengten.

 
Het belang van deze toevallige beïnvloeding door raden hangt af van het gebruik dat van de toetsscores gemaakt gaat worden. Voor ons is het dan ook zaak na te gaan wat de invloed van het raden is op zak-slaag beslissingen. Ook dit zal ik hier doen voor wat betreft de individuele student, omdat voor hem in de allereerste plaats van belang is hoe groot het risico om te zakken blijft, ook wanneer hij in wezen de stof voldoende beheerst. Dit geval is natuurlijk voor de docent ook van belang, maar de laatste zal bovendien geïnteresseerd zijn in de resultaten van zijn cesuurprocedure voor de groep studenten in haar geheel (zie daarvoor par. 7, en deel 2), waarover in de inleiding al het een en ander gezegd is (1.2).

Stel dat in een concreet geval een toets is samengesteld uit 41 meerkeuzevragen, en dat na een behoorlijk afwegingsproces de docent heeft besloten dat een minimaal voldoende beheersing van de stof betekent dat tenminste 20 van deze 41 vragen geweten moeten worden. Je zou dit de zuivere cesuur kunnen noemen, waarbij nog geen rekening is gehouden met de invloed van het raden. Stel dat de docent als volgt redeneert: de student die 20 vragen weet, zal er 21 moeten raden, en de meest waarschijnlijke score voor de geraden vragen is 7 goed. Dus leg ik de cesuur voor deze toets op 20 + 7 = 27 vragen minimaal goed (Dat dit waarschijnlijk een onjuiste redenering is, laat par. 7 zien). Dan kunnen we in de bovenstaande tabel 6.3.2 op de eerste regel zien wat de slaagkans is voor de student die 17 van de 41 vragen weet, 18 van de 41 vragen weet, etcetera. De docent kan in de tabel zien dat hoewel hij de studenten die maar 17 van de 41 vragen weten een onvoldoende zou willen geven, 25 % van deze studenten (gemiddeld) ten onrechte een voldoende zullen krijgen omdat hun totaalscore boven de gestelde minimumscore uitkomt. De volgende regels in de tabel geven zak- en slaagkansen bij dezelfde zuivere cesuur maar een langere toets, waarbij het groter aantal vragen dat geraden mag worden leidt tot ophoging van de gehanteerde cesuur. Voor eigen behoefte kan een tabel opgesteld worden voor een andere zuivere cesuur m.b.v. de bronnen in noot 1 genoemd, of kan de auteur om een dergelijke tabel gevraagd worden.

Uit tabel 6.3.2 is als conclusie te trekken dat de kans op onjuiste zak-slaag beslissingen door de invloed van het raden te groot is om nog aanvaardbaar te zijn, te groot is om de meerkeuze vraagvorm nog te blijven gebruiken. Het gaat hier immers om een toevallige beïnvloeding van zak-slaag beslissingen die te vermijden is door over te gaan op open-eind of kort-antwoord vragen waarbij raadkansen vrijwel geen rol meer spelen. De student die is afgewezen omdat zijn score net beneden de aftestgrens lag, doet er goed aan tegen die beslissing in beroep te gaan wanneer de toets samengesteld was uit meerkeuzevragen en de docent geen overtuigende argumenten heeft waarom hij aan die vraagvorm vasthoudt in plaats van op minder raadgevoelige vraagvormen over te gaan.

Er wordt nogal eens gesuggereerd dat meerkeuzevragen als groot voordeel hebben dat het scoren van de vragen geen fouten meer op kan leveren, en dat hier een tegenwicht gevonden zou zijn tegen de hier geanalyseerde raadgevoeligheid. Niets is minder waar, zoals ik in 6.5 hoop te laten zien.

Een stukje verwarring voor de lezer die hier denkt dan formules voor correctie voor raden wil ik tenslotte vlug wegnemen: correctie voor raden heeft alleen zin wanneer we niet geïnteresseerd zijn in de scores van individuele studenten, maar meer in het algemene prestatie niveau (bijvoorbeeld bij het evalueren van het gegeven onderwijs). Zak-slaag beslissingen gaan altijd over individuele studenten, en het is ten enen male uitgesloten om individuele scores te corrigeren voor de mate waarin raden er invloed op heeft gehad.

Er zijn veel pogingen ondernomen om raadkansen te reduceren door verschillende vormen van zekerheidsscoring, zonder succes overigens. Een simpele mogelijkheid om raadkansen te reduceren doe ik de lezer hier aan de hand, hoewel geen onderzoek naar het functioneren van deze regeling ooit gedaan is (om de reden dat voorzover mij bekend dit nooit eerder gesuggereerd, werd): geef de student een bonus van een 2 punt voor iedere onbeantwoorde vierkeuzevraag. Het idee is: als je niet kruideniert met die bonus voor niet-raden, zullen studenten er ook graag gebruik van maken. Het resultaat is dat toetsscores in veel geringer mate door raadeffecten bepaald zijn.

6.4 Toevallige invloeden: de vragen die gesteld worden.

Een forse mate van toevalligheid beheerst de samenstelling van de toets uit juist deze vragen (en niet een stel andere vragen die evengoed gesteld hadden kunnen worden). Wanneer de docent beschikt over een grote verzameling vragen waaruit hij kan kiezen voor het samenstellen van zijn toets, is het zelfs wenselijk dat hij zijn vragen random (d.i.: strikt willekeurig) - uit die verzameling kiest. (Vragen kunnen gegroepeerd zijn naar onderwerpen of moeilijkheid, en dan wordt binnen zo'n groep op random wijze een bepaald aan vragen voor de toets uitgekozen).

Veronderstel dat je een grote verzameling toetsvragen hebt (geen meerkeuzevragen), die de stof goed dekken. Een student die 60% van de stof beheerst, zou dan ook 60% van alle vragen goed kunnen maken; maar een toets bestaat niet uit de hele verzameling vragen, maar uit een steekproef van vragen uit die verzameling. Welnu, de vraag is hoe ver de score van onze student af kan wijken van 60% goed. Bij de beantwoording van die vraag kunnen we gebruik maken van de analyse zoals die in paragraaf 6.3 al gedaan werd.

Voor een student die verondersteld wordt 60% van de vragen in een grote verzameling van vragen goed te kunnen maken, kunnen we zeggen dat de kans dat hij een willekeurig getrokken vraag uit die verzameling goed kan beantwoorden 0,6 is (of 60% zo je wilt). In paragraaf 6.3 hadden we te maken met vragen waarbij de kans op goed (door raden) 1/3 was. Formeel is de te analyseren situatie dan ook gelijk aan die in de vorige paragraaf, het verschil is dat de kans-op-goed in het ene geval 1/3, in het andere geval 0,6 is.

Wanneer voor ieder van de toetsvragen geldt dat hij willekeurig gekozen is uit de verzameling van vragen, is voor iedere vraag opnieuw de kans dat de student er een goed antwoord op weet 0,6. Dan kunnen we eenzelfde tabel als in de vorige paragraaf berekenen voor de respectievelijke kansen op een bepaalde toetsscore bij bepaalde toetslengten. Het resultaat is tabel 6.4.1 op de volgende bladzijde.

Voor toetsen bestaande uit verschillende aantallen vragen geeft tabel 6.4.1 de spreiding in scores die de student kan verwachten afhankelijk van de vragen die in de toets opgenomen worden (of niet opgenomen worden) wanneer hij 60 % van alle denkbare vragen over de stof kan beantwoorden. Uit de tabel valt onmiddellijk te zien dat de kans dat de student op een bepaalde toets aanzienlijk minder of juist meer dan 60 % van de vragen kan beantwoorden, heel behoorlijk is. Dat heeft uiteraard zijn weerslag op de kans ten onrechte of terecht een voldoende beoordeling te krijgen (of een onvoldoende beoordeling, wanneer de minimale stofbeheersing op minder dan 60 % gesteld werd). In tabel 6.4.2 zijn deze kansen getabelleerd. Bestudering van deze tabel loont dubbel en dwars de moeite, omdat het bijzonder moeilijk is zonder het hulpmiddel van een dergelijke tabel een concrete voorstelling te maken hoe groot het effect van de min of mier toevallige keuze van vragen voor de toets kan zijn op de zak-slaag beslissing voor de individuele student.

 ___________________________________________________________________
 aantal:
 goed vragen  goed vragen  goed vragen  goed vragen
 _____________________________________________________________
      10  20       30  40       50  60       70  80
      ------       ------      ------       ------ 
    0          10           20           30
    1          11   1       21           31
    2  1       12   7       22           32
    3  4       13   3       23   2       33   1
    4 11       14   5       24   3       34   1
    5 20       15   8       25   4       35   2
    6 25       16  11       26   6       36   3
    7 21   1   17  14    1  27   8   1   37   5
    8 12   4   18  15    2  28  10   1   38   6   1
    9  4   7   19  14    4  29  11   2   39   7   1
   10  1  12   20  11    6  30  11   3   40   9   2
   11     16   21   9    8  31  11   4   41  10   3
   12     18   22   5   10  32  10   6   42  10   4
   13     17   23   3   12  33   8   8   43   9   5
   14     12   24   1   13  34   6   9   44   9   6
   15      8   25       12  35   4  10   45   8   7
   16      3   26       11  36   3  10   46   6   8
   17      1   27        8  37   1  10   47   5   9
   18          28        6  38   1   9   48   3   9
   19          29        4  39       8   49   2   9
   20          30        2  40       6   50   1   8
               31        1  41       5   51   1   7
               32           42       3   52       6
               33           43       2   53       5
               34           44       1   54       4
               35           45       1   55       3
                                         56       2
                                         57       1
                                         58       1
                                         59
 ___________________________________________________________________


Tabel 6.4.1   Kansen (in honderdsten) op bepaald aantal vragen goed bij stofbeheersing van 60% en geen raadkansen. (voor toetsen met 10, 20, ... , 80 vragen resp.).

 
Ook de kansen in tabellen als de bovenstaande kunnen berekend worden met de binomiaalformule die onder tabel 6.3.1 . gegeven werd, waarbij   p de proportie van de leerstof die beheerst wordt, voorstelt,
  n het aantal vragen waaruit de toets (geen meerkeuze, maar kort antwoord toets!) bestaat,
  r het aantal goed beantwoorde vragen.

 ___________________________________________________________
 aantal   kans ten onrechte     kans ten onrechte 
 toets-   onvoldoende           voldoende
 vragen
          cesuur: 50% 55% 60%   cesuur: 65% 70% 75%
 --------------------------------------------------
   10             17  37  37            38  38  17
   20             13  24  40            42  25  13
   30             10  29  42            29  18   4
   40              7  21  43            32  13   4
   50              6  23  44            24  10   1
   60              4  18  44            26   7   1
   70              3  20  45            20   5   0
   80              3  15  45            21   4   0
 ______________________________________________________________


TABEL 6.4.2 Kansen op ten onrechte voldoende, resp. onvoldoende als de stofbeheersing 60% is, bij cesuren van 50, 55, ... 75% en verschillende toetslengten. Géén raadkansen (geen meerkeuze dus).

 
Voor zijn eigen onderwijssituatie kan de lezer zelf tabellen opstellen, eventueel laten opstellen. Daaruit blijkt dan hoe groot de effecten van de gekozen samenstelling van de toets zijn op score variabiliteit en kansen ten onrechte afgewezen of toegelaten te worden.

Bij de behandeling van de effecten van raden bij meerkeuzevragen (in 6.3) kon als conclusie getrokken worden dat alle mogelijke moeite gedaan moet worden om de meerkeuzevraagvorm te vermijden, zodat het raad effect zich niet kan manifesteren. Hier, bij het probleem van de toevalligheid van samenstelling van de toets uit een grote verzameling (of denkbare verzameling) vragen, is het niet mogelijk om te zeggen dat een toets bij voorkeur niet door het kiezen van vragen uit de verzameling van mogelijke vragen zou moeten gebeuren: er is geen andere mogelijkheid voor het samenstellen van je toets. Daarom is hier de vraag van belang, hoe de invloed van toevallige vraagkeuze op zowel toetsscores als zak- slaagbeslissingen klein gehouden kan worden, of binnen aanvaardbare grenzen gebracht. Uit de gegeven tabellen kunnen aanwijzingen daarvoor gevonden worden.

In tabel 6.4.1 zien we dat de kansverdelingen omvangrijker worden naarmate de toets langer is; bijv. bij een toets van 20 vragen is de kans groot dat onze student die 60% van de stof beheerst een score maakt tussen, zeg, 10 en 14, terwijl bij een toets van 80 vragen hij ongeveer dezelfde kans heeft om een score te krijgen tussen 43 en 53. Nu zou je kunnen zeggen dat het laatste interval, gezien naar de lengte van de toets, korter is dan het eerste (11/80 tegen 5/20), dus dat het meten met de langere toets nauwkeuriger is. Maar daarbij wordt over het hoofd gezien dat het hier niet er om gaat om nauwkeurig te meten, maar nauwkeurige zak-slaag beslissingen te nemen. En bij zak-slaag beslissingen is het nog steeds zo dat een puntje meer of minder het verschil tussen zakken en slagen kan betekenen. Wel, dan is het duidelijk dat juist bij de langere toets er meer ruimte is voor het toevallig aan de verkeerde kant van een dergelijke zak-slaaggrens terecht komen.

Het ongunstige effect van toetsverlenging zoals juist besproken, wordt enigszins goed gemaakt door het gunstige effect van toetsverlenging zoals dat blijkt uit tabel 6.4.2: hoe langer de toets wordt, des te kleiner worden de kansen op onjuiste beslissingen wanneer de student iets meer, of iets minder van de stof beheerst dan minimaal gevraagd wordt. Dit is een erg belangrijke eigenschap van toetsverlenging. Voor het concrete beleid betekent het dat er naar gestreefd wordt een zo groot mogelijk aantal vragen in de toets op te nemen (maar wel met de beperking dat de toets binnen de gestelde tijd door de studenten gemaakt kan worden zonder in tijdnood te komen), en dat de cesuur een stukje beneden de eigenlijk gewenste cesuur gelegd wordt, en dat de studenten er op gewezen wordt dat ze in hun voorbereiding moeten streven naar een mate van stofbeheersing die een veilig stuk boven de gestelde cesuur ligt. O.a. in hoofdstuk 7 worden voor een en ander nog wat technieken aangereikt.

Niet direct uit de gegeven tabellen te halen is een andere belangrijke samenhang: de kansverdelingen zoals in tabel 6.4.1 gegeven worden minder gespreid wanneer de stofbeheersing van de student hoger is (dan de 60 % zoals bij de berekening van de tabel aangehouden), en ook wanneer de stofbeheersing van de student minder wordt dan 40 %. Minder moeilijk uitgedrukt: de spreiding in scores is het grootst voor het geval van een stofbeheersing van 50 %, en wordt minder hoe verder de mate van stofbeheersing van die 50 % af komt te liggen.

Genoemd verband kan en moet uitgebuit worden bij het opzetten van de toetsen beslissingsprocedure. De keuze van 50 % stofbeheersing is in dit opzicht de slechtste keuze voor de cesuur die je kunt maken, omdat juist voor studenten met deze mate van stofbeheersing de kansen op foutieve zak-slaag beslissingen het grootst zijn. Meestal zal een veel geringere mate van stofbeheersing dan 50% als minimum niveau weinig reëel zijn, dus moet optimalisering gezocht worden in de richting van het zo hoog mogelijk stellen van de minimaal vereiste mate van stofbeheersing. Wat ik hier vraag is natuurlijk heel iets anders dan het maar zo hoog mogelijk stellen van de aftestgrens; gedoeld wordt op onderwijsmaatregelen die het mogelijk maken om de minimumeisen in termen van percentage van de leerstof dat gekend moet worden, hoger te stellen. Dergelijke maatregelen zijn bijv.: het transparanter maken van de toetsing (hoofdstuk 4), het uitsplitsen van het eindtentamen naar een aantal deeltentamens, het vereenvoudigen van de aan te bieden leerstof in die zin dat allerlei materiaal dat niet voor de strikte minimale stofbeheersing noodzakelijk wordt geacht, buiten de tentamenstof wordt gehouden. Hoe ver je met dit soort maatregelen kunt gaan, zal weer afhangen van de specifieke onderwijssituatie, en de grootte van de winst die met deze maatregelen te bereiken is.

Een slotopmerking: het laat zich raden dat voor meerkeuzetoetsen de rol van raadkansen mede in het scenario moet worden opgenomen. Ik geef voor dit geval geen afzonderlijke tabellen, en volsta met er op te wijzen dat de lezer zelf een en ander kan berekenen door voor niet geweten vragen in tabellen 6.4.1 en 6.4.2 de invloed van raadkansen in te vullen op de wijze als in paragraaf 6.3 behandeld. Overigens herhaal ik nog maar eens dat het gebruik van de meerkeuze vraagvorm ten sterkste afgeraden moet worden.

6.5 Toevallige invloeden: andere bronnen van ordeverstoring.

Een groot aantal andere bronnen van toevallige beïnvloeding kunnen genoemd worden, maar zie daarvoor Stanley 1971. De belangrijkste wil ik hier noemen, zonder getalsmatige uitwerkingen te geven. Ook voor maatregelen om dergelijke invloeden minimaal te houden althans te beheersen, verwijs ik naar Stanley 1971.

toevalligheden die de score van de individuele student beïnvloeden:


Van de genoemde bronnen van toevalligheden wil ik er toch nog één bespreken, omdat daarover ook onder onderwijskundigen een groot misverstand bestaat. Het gaat om de mate waarin de beoordeling van gegeven antwoorden beïnvloed wordt door de toevallige beoordelaar, en dat vooral in verband met de scoring van meerkeuzevragen.

Het is maar voor weinig soorten leerstof het geval dat er vragen over geformuleerd kunnen worden waarvoor geldt dat de deskundigen het met elkaar volstrekt eens zijn over wat het juiste antwoord is: denk aan eenvoudige rekenopgaven. Meestal moet er rekening mee gehouden worden dat deskundigen met elkaar van mening kunnen verschillen over het juiste antwoord, of in de beoordeling van door studenten gegeven antwoorden. De ene deskundige of docent zal een bepaald antwoord goed rekenen, terwijl zijn collega daar heel anders over kan denken, en terwijl beiden menen voor hun beoordeling goede argumenten te hebben. Het is dan ook niet verbazingwekkend dat aan het gesignaleerde probleem door onderwijskundigen (psychometrici e.d.) nogal wat aandacht is besteed, in zekere zin culminerend in de studie van Cronbach, Gleser, Rajaratnam, & Nanda (1972).

Als een klein onderzoekje gedaan wordt, door tentamens door enkele docenten onafhankelijk van elkaar, dus ook zonder elkaars beoordelingen te kennen, na te laten kijken, kan nagegaan worden in hoeveel van de gevallen gemiddeld twee docenten met elkaar van mening verschillen over het goed of fout beoordelen van een door de student gegeven antwoord.

Daaruit zou kunnen blijken dat in 10 % van de gevallen twee docenten die van te voren geen overleg met elkaar hebben gepleegd over wat het juiste antwoord op de vragen zou moeten zijn, het met elkaar oneens zijn over de beoordeling van een gegeven antwoord. Voor de student betekent het dat hij in één van de tien geweten vragen een kans van 1 op 2 heeft dat zijn antwoord desondanks niet goed gerekend zal worden. Daardoor ontstaat een toevallige invloed op zijn totaalscore, die van belang kan zijn voor de zak-slaag beslissing omdat die beslissing er door beïnvloed kan worden. Allerlei variaties zijn mogelijk, bijvoorbeeld dat voor bepaalde soorten leerstof zelfs in de helft van de gevallen er onenigheid tussen docenten kan bestaan over het goed of fout beoordelen van gegeven antwoorden. De lezer zou ondertussen zelf in staat moeten zijn om het effect daarvan in te schatten, door te werk te gaan op dezelfde wijze als in 6.3 en 6.0 wanneer voor X % van de vragen geldt dat het antwoord goed of fout gerekend wordt al naar gelang de docent die het werk moet beoordelen,en de kans op goed is P, kan m.b.v. de formule voor de binomiaalverdeling (toelichting bij tabel 6.3.1) het mogelijke effect op de toetsscore uitgezet worden. De kans P ontstaat (of zou empirisch verkregen kunnen worden) door te schatten dat P % van alle in principe in aanmerking komende beoordelaars het antwoord goed zouden rekenen, en (1 - P) % het antwoord fout zouden rekenen.

Wat betreft meerkeuzevragen wordt vaak als voordeel van deze vraagvorm aangevoerd dat bovenstaande beoordelingsproblematiek zich niet zou voordoen, omdat in de gegeven scoringssleutel de beoordeling volledig bepaald is (altijd hetzelfde resultaat geeft, wie het ook nakijkt). Deze redenering is volstrekt onjuist. En het is nu eenvoudig uit te leggen waarom: de crux ligt natuurlijk in het vaststellen van de scoringssleutel. Er kan tussen docenten nogal wat verschil van mening bestaan over wat het juiste of beste alternatief is in een gegeven meerkeuzevraag. Als dat het geval is, maakt het nogal wat uit of de ene, dan wel de andere docent de scoringssleutel vaststelt, omdat in beide gevallen die sleutel anders zal zijn. De toetsscore van de student is afhankelijk van de persoon die de scoringssleutel opstelt. Aan die omstandigheid wordt niets veranderd wanneer de docenten in onderling overleg eventuele verschillen van inzicht bijleggen, omdat desondanks de situatie blijft dat sommige antwoorden van de student gelijk zijn aan antwoorden die een vakdeskundige ook gegeven zou kunnen hebben, maar fout gerekend worden omdat ándere vakdeskundigen hún opvatting er in het onderling overleg wisten door te halen.

Hoewel het effect van deze meningsverschillen tussen vakdeskundigen over wat goede en wat foute antwoorden zijn niet erg groot is (maar dat in bepaalde gevallen natuurlijk wel kan worden, zoals bij de beoordeling van opstellen en grote werkstukken), moet er wel naar gestreefd worden om een en ander onder controle te houden. Daar is een simpele methode voor: probeer alle voor het tentamen in aanmerking komende vragen eerst uit op een groepje vakdeskundigen die niet zelf de vragen gemaakt hebben en met elkaar niet kunnen overleggen wat de juiste antwoorden zouden moeten zijn. Besluit op grond van de uitkomsten van dat onderzoek om alleen de vragen die door deskundigen, onafhankelijk van elkaar, op dezelfde wijze beantwoord worden, voor opname in het tentamen ter overweging te nemen. Dit geldt natuurlijk zowel voor kort antwoord en open-eindvragen, als voor meerkeuzevragen.

6.6 Stelselmatige invloeden: interpretatie van toetsscores.

Hoe ingrijpend de eerder besproken toevallige invloeden ook lijken te zijn, van veel groter belang zijn bronnen van stelselmatige fouten bij interpretatie van toetsscores, en bij het beslissen op grond van toetsscores (het laatste is ook als interpretatie van de toetsscores te beschouwen). Het interpreteren van toetsscores of studieresultaten is een vreselijk ingewikkelde bezigheid. Essentiële voorwaarde, zoals in 6.2 gezegd, is dat de doelstellingen (van toetsing of van cesuurbeleid) goed omschreven zijn, omdat iedere vorm van interpretatie alleen maar mogelijk is tegen de doelen zoals die gesteld zijn. Een essentiële voorwaarde: wanneer doelstellingen niet gegeven zijn, is iedere vorm van interpretatie een slag in de lucht, zijn beslissingen over personen niet te verantwoorden en dus volstrekt willekeurig. Hoewel doelstellingen essentieel zijn, zal ik hier niet aangeven hoe ze te formuleren zijn, welke doelen de docent in overweging kan nemen, etc.

Jammer genoeg kan ik in deze paragraaf niet meer doen dan een enkel probleem aanstippen, de lezer een klein beetje een idee geven welke kant het allemaal opgaat. Daar staat tegenover dat het onderzoek naar de wijze waarop zak-slaag beslissingen stelselmatig fout kunnen zijn, bij uitstek het onderwerp van deel 2 zal zijn. Een voorschotje op die behandeling wordt in het tweede deel van deze paragraaf gegeven, daaraan voorafgaand presenteer ik een denkmodel om de beperkte interpreteerbaarheid van toetsscores te demonstreren.

Wat betekent een bepaalde toetsscore, of cijfer? Geeft het de mate waarin de student de stof beheerst? Geeft het een aanwijzing over de tijd die hij aan de voorbereiding besteed heeft? Is het niet meer dan een aanduiding op welk cijfer de student gemikt heeft in zijn voorbereiding? Is het cijfer gecorreleerd met de intellectuele begaafdheden van de student? Zegt het studieresultaat iets over de motivatie van de student? Zeggen de gemiddelde studieresultaten van de studenten iets over de kwaliteit van het onderwijs of van de gehanteerde examenregeling?

Stuk voor stuk belangrijke vragen, die schril contrasteren met de gewoonte om cijfers alleen te zien als aanwijzingen omtrent het meer of minder beheersen van de leerstof. Antwoorden op de gestelde vragen zijn dáárom belangrijk, omdat hier toch de mogelijkheden gezocht moeten worden voor evaluatie van het onderwijs, en de mogelijkheden voor verbeteringen in de inrichting van het onderwijs (inclusief de beoordelingsgewoonten).

Om te beginnen is het vanzelfsprekend dat intellectuele capaciteiten samenhangen met studieprestaties. Dat wil zeggen, studenten die verschillen in intellectuele capaciteiten zullen, ceteris paribus, verschillende studieprestaties behalen. Het ceteris paribus is een belangrijk voorbehoud: het betekent dat we een positief verband veronderstellen tussen verschillen in intellectuele capaciteiten en studieprestaties voor studenten die overigens in gelijke omstandigheden verkeren, evenveel tijd aan de studie besteden, gelijk gemotiveerd zijn, dezelfde vooropleiding hebben, etcetera. De moeilijkheid voor de onderzoeker is natuurlijk dat in werkelijkheid het ceteris paribus nooit opgaat, zodat het willen aantonen van het veronderstelde verband vraagt om methodologische hoogstandjes en uiterste voorzichtigheid bij het interpreteren van onderzoeksresultaten.

Als eenheid voor onze analyse heb ik het studieonderdeel gekozen, en die eenheid is klein genoeg om te mogen veronderstellen dat intellectuele capaciteit een gegeven is, waarop het onderwijs in dit kleine tijdsbestek weinig of geen invloed uit kan oefenen. Voor onze analyse zal ik dergelijke variabelen exogene variabelen noemen. Andere exogene variabelen zullen op dezelfde wijze als voor intellectuele capaciteiten geschetst, ook verband (kunnen) houden met verschillen tussen studenten in studieprestaties, altijd onder de veronderstelling van ceteris paribus. Welke andere exogene variabelen kunnen van belang zijn? Ik noem er enkele:


Studenten die op één of meer van deze exogene variabelen van elkaar verschillen zullen, ceteris paribus, verschillende studieprestaties boeken. Omgekeerd: verschillen in studieprestaties zullen, ceteris paribus, terug te voeren zijn op verschillen tussen studenten op één of meer van deze exogene variabelen.
Als de voor de hand liggende veronderstelling gemaakt mag worden dat voor één enkel studieonderdeel verschillen in studieprestaties niet van invloed zijn op verschillen op exogene variabelen zoals die voorafgaand aan het tentamen bestaan, zou je kunnen zeggen dat er een oorzakelijk verband bestaat van exogene variabelen naar studieprestatie, maar niet omgekeerd. Symbolisch is dat als volgt aan te geven

 
77gif/77Cesuur2COWO344040.gif

 
Verschillen in studieprestaties hangen niet alleen samen met genoemde exogene variabelen, maar bijvoorbeeld ook met verschillen in tijdbesteding. De student die meer tijd in zijn tentamenvoorbereiding steekt zal, ceteris paribus, hogere toetsscores halen. Ceteris paribus betekent hier: wanneer studenten op exogene variabelen aan elkaar gelijk zijn, zullen verschillen in tijdbesteding verband houden met verschillen in studieresultaat. Daar mag je onmiddellijk aan verbinden dat verschillen in studieresultaten terug te voeren zijn op Wwel verschillen in exogene variabelen (intellectuele capaciteiten bijv.), Ofwel verschillen in tijdbesteding, ofwel een combinatie van beide.

Om het plaatje volledig te maken: veronderstel dat het studieonderdeel klein genoeg is, zodat studieprestaties geen invloed kunnen hebben op verschillen in tijdbesteding bij de voorbereiding op het tentamen; dat verschillen in tijdbesteding geen invloed hebben op exogene variabelen; en dat exogene variabelen, ceteris paribus, samen kunnen hangen met verschillen in tijdbesteding (die veroorzaken). Een voorbeeld van laatstbedoeld verband: wanneer al het andere gelijk is, zullen verschillen in studiemotivatie leiden tot verschillen in tijdbesteding, zullen verschillen in intellectuele capaciteiten leiden tot verschillen in tijdbesteding, etc. Symbolisch samenvattend:

77gif/77Cesuur3COWO413169.gif

Tenslotte is voor de interpretatie van verschillen in toetsscores erg belangrijk te weten op welk cijfer de student eigenlijk mikte, omdat ceteris paribus verschillen in streefniveau zullen leiden tot verschillen in tijdbesteding, misschien zelfs directe invloed hebben op verschillen in toetsscores. Via de verschillen in tijdbesteding zal er een grote invloed zijn van verschillen in streefniveau op verschillen in toetsscores. Met streefniveau bedoel ik niet meer dan dat de ene student mikt op net voldoende, de ander op een 8, een derde bereidt zich bewust maar matig voor en hoopt op voldoende geluk om een voldoende te scoren, e.d. Het is duidelijk dat verschillen in streefniveau voor een deel terug te voeren zijn op exogene variabelen (vooropleiding, persoonlijkheidsverschillen etc.), en dat er geen omgekeerd oorzakelijk verband bestaat van streefniveau naar exogene variabelen. Neem aan dat er ook geen oorzakelijk verband bestaat van verschillen in tijdbesteding naar verschillen in streefniveau, dan gaat het denkmodel er als volgt uitzien:

 
77gif/77Cesuur4COWO413169.gif

FIGUUR 6.6.1 Denkmodel voor het interpreteren van verschillen tussen studenten in toetsscores. (voor details van dit soort modellen, zie de literatuur over causale of structural equation modellen).

 
Het zal duidelijk zijn dat beslissingen gebaseerd op toetsscores stelselmatig fout kunnen zijn, wanneer de veronderstelling bij die beslissingen is dat verschillen in toetsscores het gevolg zijn van verschillen in tijdbesteding (studenten met lage scores hebben er niet voldoende tijd aan besteed, moeten het vak dus nog maar eens over doen), terwijl bij onderzoek zou kunnen blijken dat er geen noemenswaardige verschillen in tijdbesteding zijn, maar wel in, zeg, vooropleiding. Talloze alternatieve interpretaties van verschillen in studieprestaties kunnen op basis van het gegeven denkmodel opgesteld worden; verschillende interpretaties zullen leiden tot verschillende conclusies, ofwel ten aanzien van maatregelen m.b.t. individuele studenten te nemen, ofwel ten aanzien van maatregelen m.b.t. de inrichting van het onderwijs te nemen. Zodat we terecht komen bij het onderzoek naar de juistheid van zak-slaagbeslissingen, het onderwerp van deel 2, waarop hieronder een summiere voorgift.

Waar het om gaat: voor de eis dat onvoldoende prestaties op een volgende gelegenheid alsnog voldoende gemaakt worden, moet een rechtvaardiging gegeven worden. Die rechtvaardiging bestaat uit de formulering van de bedoelingen die men heeft bij het volgen van dit beleid, en argumenten (zo mogelijk op grond van gedegen onderzoek) dat het gevoerde beleid ook leidt tot de bedoelde resultaten. Geen eenvoudige zaak, daarom wil ik in deze paragraaf volstaan met een aantal opmerkingen die ook zonder uitgebreide toelichting de lezer een indruk kunnen geven waarin bij het zak-slaag beleid de stelselmatige fouten kunnen schuilen.

Studenten die aan een tentamen deelnemen vormen geen homogene groep: je kunt daarin dagstudenten van werkstudenten, degenen die de eerste keer opkomen van de herhalers, zij die uiteindelijk de studie afmaken van degenen die dat niet doen, onderscheiden. Een goede tentamenadministratie moet voor dergelijke deelgroepen studenten afzonderlijk de tentamenresultaten kunnen geven, als allereerste stap op de weg van empirisch onderzoek en de vinger op pols houden. Uit cijfers voor dergelijke deelgroepen kunnen soms heel aardige veronderstellingen geput worden over de kwaliteit van de genomen zak-slaag beslissingen, veronderstellingen die vervolgens onderwerp van een klein (experimenteel) onderzoek zouden kunnen worden.

Boven genoemde deelgroepen van studenten zijn makkelijk te vinden, maar ook heel andere indelingen zijn mogelijk, waarbij meer theoretische onderscheidingen gemaakt moeten worden. Te denken valt daarbij aan schattingen van relatieve aantallen studenten die zich behoorlijk op het tentamen hebben voorbereid (of juist niet), die terecht een voldoende of onvoldoende kregen (of juist niet), en dergelijke. Dergelijke onderscheidingen kunnen gemaakt worden om het beoordelingsbeleid onderzoekbaar te maken, en kunnen gebruikt worden om ook Ander empirisch onderzoek het cesuurprobleem te verhelderen, significante problemen te signaleren, etcetera. Neem bijvoorbeeld de groep studenten die terecht een voldoende kregen. Het doet er niet toe dat we nooit zullen weten welke studenten terecht een voldoende kregen, het belangrijke punt is dat we weten dat er studenten zijn die terecht een voldoende kregen (en dat we in sommige gevallen ook kunnen schatten hoe groot het aantal van die studenten zou kunnen zijn). Met betrekking tot de student die terecht een voldoende kreeg, zal de voorstander van de conjunctieve examenregeling zeggen dat het niet zinvol zou zijn om hem het tentamen te laten overdoen.

Als je het daar mee eens bent, en er prijs op stelt in je opvattingen coherent te zijn, zul je-ook van oordeel zijn dat het ten onrechte geven van een onvoldoende te betreuren is, omdat het voor de student die ten onrechte een onvoldoende krijgt ook niet zinvol is om het tentamen over te doen. Als dit geconcludeerd is, liggen de volgende conclusies onder handbereik:

De student die ten onrechte een onvoldoende kreeg, weet dat evenmin als de docent, met als gevolg dat deze student zich voor de herhaling beter zal prepareren dan de eerste keer hoewel hij zich voor die eerste keer al voldoende voorbereid had.

Je mag nu niet zeggen dat het toch maar mooi meegenomen is dat deze student zich voor die herhaling beter in het vak verdiept. Je zou immers deze student het tentamen helemaal niet willen laten overdoen, omdat hij de eerste keer in wezen de stof al voldoende beheerste (maar door toevallige en stelselmatige fouten in de beoordelingsprocedure geen voldoende kreeg).

Je kunt je voorstellen dat juist de studenten die ten onrechte een onvoldoende kregen, voor de herhaling in grote spanning zitten, omdat het voor hen moeilijker moet zijn om de stof nog beter te bestuderen dan ze de eerste keer al deden, dan het is voor de studenten die terecht een onvoldoende kregen.

Effect van een en ander zal zijn dat de gemiddelde prestatie binnen de groep herhalers omhoog gestuwd wordt door juist de studenten die ten onrechte een onvoldoende gekregen hadden, zodat hier de voorstanders van overdoen (van conjunctieve examenregelingen) zich ten onrechte van schijnbaar sterke empirische gegevens kunnen voorzien.

Laat ik eens kijken naar het onderscheid tussen studenten die uiteindelijk de studie afmaken, en zij die dat niet doen. Voor al degenen die de studie niet afronden, en tentamens hebben overgedaan, kun je stellen dat zij hun tijd beter hadden kunnen besteden aan het bestuderen van nieuwe stof dan aan het herhalen van oude (of dat herhalen terecht was of niet doet er zelfs niet zoveel toe). Achteraf gezien was het voor deze studenten niet zinvol om hen het tentamen te laten overdoen (wat niet betekent dat ze dan maar voldoende beoordeeld zouden moeten worden, omdat er geen logisch verband bestaat tussen het onvoldoende beoordelen van prestaties, en de eis tentamens over te doen) De meeste argumenten die ten gunste van het laten overdoen worden aangevoerd hebben uitsluitend betrekking op studenten die tenslotte ook af zullen studeren. Dan ligt het ook voor de hand om bij de procedure voor het bepalen van de cesuur alleen gebruik te maken van gegevens over (en de scores van) studenten die uiteindelijk zullen afstuderen. Het punt is van belang omdat bij het kiezen van optimale procedures (hoofdstuk 7) de aftestgrens vrijwel zeker ánders zal komen te liggen wanneer de groep studiestakers buiten de overwegingen wordt gehouden, of wanneer dat onderscheid niet gemaakt wordt. Zodat het voor de student verschil uitmaakt of die uitsplitsing gemaakt is of niet (eventueel een reden om in beroep te gaan tegen een genomen zak-slaag beslissing).

Een afgesleten argument ten gunste van conjunctieve examenregelingen is dat voldoende kennis van ieder studieonderdeel een voorwaarde is voor behoorlijk verder kunnen studeren. Ik wil daar de volgende stelling tegenover stellen:

Voor de groep studenten die voor een bepaald vak bij eerste deelname een onvoldoende halen, het tentamen overdoen, én afstuderen, geldt dat er geen relatie aantoonbaar is tussen het al dan niet ingehaald hebben van die onvoldoende, en later studiesucces (eventueel een negatieve relatie). Om de stelling te toetsen zou een onderzoek nodig zijn waarin een deel van deze studenten het tentamen overdoet, en een deel het tentamen niet overdoet, en waarbij latere studieresultaten van beide groepen met elkaar vergeleken kunnen worden.

Een dergelijk experiment hoef je niet werkelijk uit te voeren om je een voorstelling te kunnen maken van de waarschijnlijke uitkomst: Degenen die het tentamen overdoen verliezen daarmee studietijd, waarvoor ze een beetje betere beheersing van dit studieonderdeel terugkrijgen. Van die betere beheersing hebben ze niet veel plezier, omdat voor de meeste studierichtingen in het w.o. geen sterk hiërarchische relatie tussen verschillende studieonderdelen aanwezig is (en dan nog zou een verband onwaarschijnlijk zijn, zie Hills 1971). Degenen die het niet overdoen verliezen geen studietijd, en hebben van een eventuele mindere stofbeheersing van dit vak in hun verdere studie om dezelfde al genoemde reden weinig hinder.

Ja maar, het effect van één afzonderlijk vak kan natuurlijk ook niet groot zijn. Wie deze tegenwerping maakt, mag bedenken dat voor studenten die inderdaad afstuderen zal gelden dat ze maar een heel klein aantal vakken terecht zouden hebben overgedaan, zodat er geen ruimte is voor enige cumulatie van effecten. (Ze zullen wat meer vakken ten onrechte hebben overgedaan, en dat dat volstrekt ongewenst is werd al eerder vastgesteld).

Dan is er een groep studenten die aan het tentamen deelneemt zonder zich daar voldoende op voorbereid te hebben. Erg belangrijk is in dit verband dat het aantal foutieve beslissingen samenhangt met de grootte van deze groep malafide tentamendeelnemers: hoe kleiner deze groep gehouden kan worden, des te kleiner kan ook het aantal foutieve beslissingen zijn. Zie voor cijfermatige illustratie van dit verschijnsel de tabellen in de bijlage. Het klein houden van het aantal studenten met onvoldoende voorbereiding moet gebeuren door geschikte onderwijsmaatregelen, en zo mogelijk andere beoordelingsmethoden en vooral examenregelingen. Bij een compensatorische examenregeling is het voor de student niet voordelig om met onvoldoende voorbereiding aan tentamens deel te nemen ( geluk en pech), waarop deze studenten speculeren, middelen zich bij compensatorische regelingen uit, zodat er voor de student geen voordeel van te verwachten is: de student zal zich gemiddeld voldoende op de tentamens moeten voorbereiden). Lukt het om dit de studenten voldoende duidelijk te maken, dan zal het aantal studenten dat met onvoldoende voorbereiding aan het tentamen deelneemt, drastisch teruglopen, met een zeer grote reductie in het aantal onjuiste zak-slaag beslissingen (mits aan ons derde uitgangspunt, hoofdstuk 5, voldaan is).

Ik wil er in dit verband nog op wijzen dat onder de huidige examenregeling de student die gokt op een voldoende, dat doet ten koste van zijn medestudenten die zich wél behoorlijk op het tentamen hebben voorbereid. Door de aanwezigheid van een groep studenten met onvoldoende voorbereiding, wordt het risico voor de student die in wezen de stof voldoende beheerst om desondanks onvoldoende beoordeeld te worden groter dan wanneer er weinig of geen gokkende tentamendeelnemers zouden zijn.

Over die groep studenten met onvoldoende voorbereiding op het tentamen wil ik nog wel iets meer zeggen. Dat studenten, die zich niet behoorlijk op het tentamen voorbereid hebben in het traditionele beoordelingsstelsel een groot risico lopen het tentamen te moeten overdoen, is geen verdienste van dit beoordelingsstelsel, maar één van zijn ernstigste gebreken. Omdat geen enkele cesuurbepalingsmethode opgewassen is tegen de opgave malafide van bonafide deelnemers te onderscheiden (omdat hun scores elkaar o.a. door toevallige fouten zoals in 6.2, 6.3, en 6.4 besproken, zullen overlappen), is er altijd ofwel een belangrijke kans van slagen voor de student die zich niet behoorlijk heeft voorbereid, ofwel een behoorlijke kans op zakken voor de student die zich wél behoorlijk heeft voorbereid, al naar gelang de aftestgrens laag of hoog wordt gesteld. Wáár de cesuur ook getrokken wordt, laag of hoog, altijd zal het voor de student aantrekkelijk zijn om met onvoldoende voorbereiding deel te nemen: in het ene geval door de hoge slaagkans, in het andere geval door de hoge zak-kans die je toch nog ebt wanneer je je wel voldoende zou voorbereiden.

Dat een groot aantal studenten met in wezen onvoldoende voorbereiding aan het tentamen pleegt deel te nemen, is een gevolg van de conjunctieve (hordenloop) examenregeling, en geen reden om het over laten doen van onvoldoende studieonderdelen te handhaven.

Het is niet onwaarschijnlijk dat het instituut van overdoen in stand gehouden wordt door de observatie dat de student bij herhalen van het tentamen betere resultaten boekt, of dat gemiddeld de hele groep herhalers betere resultaten boekt dan de eerste keer. Dat zegt niets over het nut van het laten overdoen van onvoldoende gemaakte studieonderdelen.

Deze student, of deze groep herhalers, had misschien nog betere resultaten kunnen bereiken wanneer ze gewoon met de studie doorgegaan waren, of wanneer ze een nieuw stuk leerstof hadden bestudeerd in plaats van oude stof te herkauwen.

De situatie is zelfs nog verrassender dan al aangegeven werd: stel dat bij onderzoek blijkt dat alternatieven voor laten overdoen niet tot betere resultaten leiden dan door het laten overdoen bereikt worden. Daaruit volgt logisch niet dat laten overdoen in die situatie het beste beleid is. Het is namelijk perfect mogelijk dat ook voor de groep studenten die géén onvoldoende kreeg, bij onderzoek zou blijken dat het laten overdoen van dat studieonderdeel beter is dan doorgaan met de studie. Ondanks de gevonden betere resultaten van het laten overdoen zou je immers concluderen dat overdoen in alle gevallen een onzinnige zaak is. Ik heb ook geen bezwaar tegen de alternatieve conclusie dat kennelijk een onjuiste of onzinnige definitie van betere of slechtere uitkomsten van beleid gehanteerd werd.

Tenslotte het belangrijkste argument: Het laten overdoen verandert niets aan de redenen waarom de student in de eerste plaats geen voldoende prestatie kon leveren. Voorzover die redenen niet in gebrekkige toetskwaliteiten of onderwijsopzet, maar bij de student gezocht moeten worden, is het laten overdoen een vergaand simpel beleid waarop dezelfde kritiek te leveren is als door Jackson (1975) gegeven voor het analoge geval van het laten doubleren van leerlingen!


6.7 Conclusies voor het dagelijks beleid van de docent (vakgroep).

De conclusies zijn te talrijk om hier nog eens weer te geven: de tekst loopt als het ware over van de conclusies. Het zijn niet het soort conclusies die zich makkelijk laten vertalen in een vernieuwd beleid, maar de conclusies zijn wel dermate zwaarwegend dat de docent aan die vernieuwing van zijn beleid voortdurend zou moeten werken in de hier aangegeven richting. Dit geldt vooral voor de paragraaf over Algemene Beginselen van Behoorlijk Bestuur, de vervanging van meerkeuzetoetsen door toetsen met andere vraagvormen, en de beheersing van toevallige invloeden op de toetsresultaten (6.4 en 6.5). De bespreking in 6.6 van mogelijke stelselmatige fouten in de beslissingsprocedure droeg een meer inleidend, zo je wil bewustmakend of sensitiverend karakter, en wat de daar behandelde onderwerpen betreft is misschien eerst het wachten op het verschijnen van deel 2.

Hoofdstuk 7 is vervallen.

Voor de reden daarvan verwijs ik naar

B. Wilbrink: Enkele radikale voorstellen voor grensskore bepaling bij kriterium gerefereerde toetsen. Te verschijnen in het Tijdschrift voor Onderwijs Research html

en naar de nieuwe versie van Cesuurbepaling, die eind 1979 gereed kan zijn. [nog geen digitale versie beschikbaar]

 
[noot 2002: de methodiek zoals in de genoemde latere publicaties geschetst, is een verbetering op die welke in hoofdstuk 7 is gebruikt. Evenwel, ook op de in 1980 gepubliceerde methodiek zijn ernstige bedenkingen te geven. Belnagrijker nog: het is mogelijk een veel beter model op te stellen, zie bijvoorbeeld

Wilbrink, B. (1998). Inzicht doorzichtig toetsen. In Joostens, Th. H., & Heijnen, G. W. H. (Red.). Beoordelen, toetsen en studeergedrag. Groningen: Rijksuniversiteit, GION - Afdeling COWOG Centrum voor Onderzoek en Ontwikkeling van Hoger Onderwijs, 13-29. html

Al met al geen reden om het ooit verguisde hoofdstuk 7 hier niet alsnog integraal weer te geven.]

7 De aftestgrens optimaal kiezen.

Uiteindelijk gaat het er om de aftestgrens zo goed mogelijk te kiezen. Dat 'zo goed mogelijk' is op verschillende manieren te bereiken. Zo is het zich houden aan principes zoals geformuleerd in de al behandelde vier uitgangspunten één van de mogelijkheden om tot verantwoorde beslissingen in het onderwijs te geraken. Andere procedures kunnen daarnaast gehanteerd worden, denk alleen maar aan het voeren van goed overleg met alle betrokkenen.

Wanneer volgens voorgaande uitgangspunten een procedure is geconstrueerd voor het bepalen van de cesuur, blijft een wezenlijk probleem: gegeven deze procedure, bij welke score moet dan precies de cesuur gelegd worden?
Voor dit probleem is een rationele of zo men wil een technische aanpak mogelijk. De techniek is een besliskundige, en het aardige er van is dat ze niet specifiek is voor het cesuurprobleem, maar van toepassing is op een scala van beslissingsproblemen waarmee iedereen in het dagelijks leven te maken heeft: het stellen van diagnoses, het nemen van beslissingen op grond van diagnostische toetsen, examenbeslissingen, beslissingen om al dan niet geld of energie in een bepaald project te investeren, studiekeuze problemen, het klassificeren of determineren van personen (objecten), selectieproblemen, of dat nu is voor het onderwijs, of in de maatschappelijke sfeer.
Begonnen wordt met een voorbeeld waarin de methode sec geïllustreerd wordt, daarna wordt aandacht besteed aan voorbereidend werk om de technische truc toe te kunnen passen.

7.1 Een voorbeeld van de techniek.

Ga ervan uit dat:

  1. de cesuur in termen van ware mate van beheersing van de stof, is vastgesteld.
    toelichting: het vaststellen van de minimaal vereiste stofbeheersing lost het cesuurprobleem nog niet op, omdat zak-slaag beslissingen genomen moeten worden op grond van feilbare toetsscores. De score die de student voor zijn tentamen maakt, is een onzekere aanwijzing voor de mate waarin hij in wezen de stof beheerst.
    Optimale cesuurbepaling houdt rekening met de onnauwkeurigheid van de
    gegevens waarop de beslissing moet stoelen.
  2. de relatie van de tentamenscores tot de gestelde cesuur is bekend.
    toelichting: voor iedere mogelijke tentamenscore is voor de groep studenten met die score de proportie bekend, die in wezen de stof voldoende beheersen (zie figuur 7.1).
  3. het verlies van het ten onrechte onvoldoende beoordelen van een student is afgewogen tegen het verlies van het ten onrechte voldoende beoordelen van een student.
    toelichting: heel onnauwkeurig geformuleerd: vastgesteld is hoeveel erger we het vinden om een student ten onrechte een onvoldoende te geven, dan wel ten onrechte een voldoende. Aan deze veronderstelling zit heel wat meer vast dan op dit moment besproken kan worden, ik kom daar in 7.2 op terug.


Veronderstel dat een tentamen bestaat uit 100 vragen, en dat het gemiddelde tentamenresultaat (zoals de laatste jaren waargenomen bij vergelijkbare groepen studenten) 60 vragen goed was, met een standaardafwijking van 10.

Veronderstel dat we voor iedere tentamenscore tussen 40 en 60 een goede schatting kunnen maken van de proportie studenten die in wezen de stof voldoende beheersen. Veronderstel dat minimaal voldoende mate van beheersing van de stof overeenkomt met een ware score van 52 (d.i., tenminste 52 % van de vragen die gesteld zouden kunnen worden, weten). We hebben dus voor iedere tentamenscore een schatting van de proportie studenten met die score, die in wezen tenminste 52 % van de vragen die gesteld kunnen worden, weten. Veronderstel dat die schattingen neerkomen op wat in figuur 7.1 geschetst is:

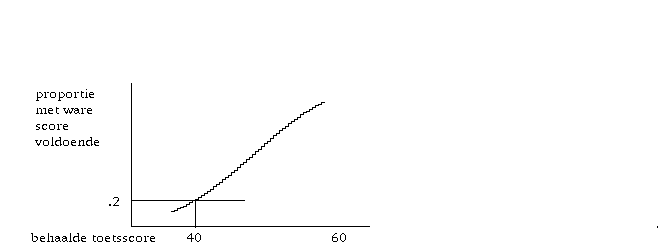
77gif/77Cesuur5COWO413169.gif
FIGUUR 7.1.1 Proportie in wezen voldoende studenten bij gegeven toets score.
[verticaal: proportie met ware score voldoende; horizontaal: behaalde toetsscore]

Het is niet uit deze figuur af te lezen, maar deze gegevens zijn in overeenstemming met een percentage in wezen onvoldoende voor de hele groep studenten van circa 16 % (zie tabel in de bijlage).

Geef veronderstelling e) concrete inhoud door de verliesverhouding op 4 te stellen: het is vier keer zo erg ten onrechte een student het tentamen te laten overdoen, dan het is om ten onrechte een student een voldoende te geven.

Dan zijn we nu klaar om de optimale cesuur te bepalen. Die cesuur is de toetsscore waarvoor geldt dat we (de docent) het even slecht zouden vinden alle studenten met deze score een onvoldoende te geven, als het zou zijn ze alle een voldoende te geven. Immers, voor een iets hogere toetsscore zou dan gelden dat het verlies dat optreedt wanneer alle studenten met die score een voldoende krijgen, kleiner is dan het verlies dat we zouden hebben wanneer al deze studenten een onvoldoende zouden krijgen.

Hetzelfde voor een iets lagere toetsscore: daar zou de minst verliesgevende beslissing zijn alle studenten met deze score een onvoldoende te geven.
Welnu, het juist gestelde is niet meer dan een ingeklede vergelijking, die eenvoudig op te lossen valt. Noem p de proportie studenten die in wezen de stof minstens voldoende beheersen (in figuur 2.6.1 verticaal afgezet).
Het verlies dat optreedt wanneer alle studenten met een bepaalde toets score een onvoldoende krijgen, is
4 x p, (verlies van ten onrechte onvoldoende, maal p).

Het verlies dat optreedt wanneer al deze studenten een voldoende zouden krijgen, is


De cesuur is die toetsscore waarbij de proportie p hoort die maakt dat beide verliezen aan elkaar gelijk zijn. De vraag is: los p op uit:
4 x p = 1 x (1-p).
zodat
p = 0, 2.

zoals eenvoudig te controleren is. Ons probleem is op een haar na gevild: zoek in figuur 7.1.1 verticaal de proportie 0,2, en trek vandaar een horizontale lijn totdat de kromme gesneden wordt; trek vanuit dat snijpunt een verticale lijn naar beneden en de toetsscore waar die lijn uitkomt, is de cesuur. Natuurlijk krijgen studenten met precies deze score het voordeel van de twijfel (het kan ons immers niet schelen of studenten met deze score een voldoende, dan wel een onvoldoende krijgen, dus we geven niets weg).

De cesuur valt nogal laag uit, omdat de veronderstellingen regelrecht naar een lage aftestgrens leiden. Ga maar na: wanneer bekend is dat het percentage studenten in de hele groep dat in wezen de stof minstens voldoende beheerst in de buurt van 84 % ligt, en aan het ten onrechte een onvoldoende geven een veel groter gewicht wordt toegekend dan aan het ten onrechte een voldoende geven (wat voor onderwijs juist is), worden weinig studenten afgewezen.

Bedenk dat de veronderstelling ook is dat dit het normale zak-slaagbeleid is, zodat er geen plaats is voor de vrees dat studenten de situatie kunnen uitbuiten door minder te gaan studeren (dan zouden ze dat al eerder gedaan hebben en zou dat in de gebruikte gegevens verdisconteerd zijn!) Op basis van deze analyse kan bekend gemaakt worden dat een toetsscore van 41 voldoende is. Is dat een lage aftestgrens vergeleken met het uitgangspunt dat een voldoende beheersing een ware score van tenminste 52 is? Ik dacht het niet, het verschil is een direct gevolg van het beleid om liever een student ten onrechte een voldoende te geven, dan ten onrechte een onvoldoende. Wie het verschil wil verkleinen, kan de kwaliteit van de toets verhogen; of de consequenties van het krijgen van een onvoldoende verzachten (door snelle herkansingen o.i.d.) waardoor het relatieve verlies van ten onrechte onvoldoende beoordelingen kleiner gekozen kan worden.

7.2 Hoe is het verlies van foute beslissingen te bepalen?

Een rationele aanpak vraagt dat verliezen van foute beslissingen op rationele wijze gekozen worden. In het in 7.1 gegeven voorbeeld werd er van uit gegaan dat de verliezen bekend waren. Verlies tussen aanhalingstekens, want het is een technisch begrip dat niet helemaal gelijk is aan wat we in het dagelijks leven met verlies bedoelen.

Beslissingsproblemen zijn er wanneer we in onzekerheid verkeren over het weer (jas meenemen of niet?), over de juiste diagnose voor deze patiënt, etcetera. Het risico bestaat dat verkeerde beslissingen genomen worden: de beslissing past niet bij de situatie die in wezen bestaat. De beste beslissing is altijd de beslissing die past bij de situatie zoals die in wezen is (later blijkt-te zijn); verlies is het verschil tussen de beste beslissing en de genomen beslissing, gemeten in utiliteiten. Utiliteit, is een technische term voor het nut of de opbrengst, en ondanks de wanstaltigheid van het woord wil ik het verder blijven gebruiken omdat het om een technisch begrip gaat. Om met verliezen om te kunnen gaan, blijken we eerst kennis te moeten maken met utiliteiten, laat ik daar dan mee starten:

De ingrediënten van ons cesuurprobleem zijn 2 beslissingsalternatieven, en 2 mogelijkheden voor de mate waarin de student de stof in wezen beheerst, die tezamen 4 mogelijke uitkomsten leveren, in de tabel aangeduid met de letters A, B, C en D.

_______________________________________________________________
wezenlijke stofbeheersing
voldoende         onvoldoende
_______________________________________________________________
onvoldoende beoordelen         A         C
voldoende beoordelen           B         D
_______________________________________________________________
TABEL 7.2.1 Uitkomstentabel voor cesuurbepaling.

 
Het komt goed uit om de letters A, B, C en D tevens te gebruiken om de utiliteit van de bijbehorende uitkomsten aan te geven. Dus: de utiliteit van het ten onrechte onvoldoende beoordeeld hebben van een student is A, de utiliteit van het terecht voldoende beoordeeld hebben van een student is B, etc.

Het verlies van ten onrechte voldoende beoordelen is in deze terminologie gelijk aan C - D (omdat voor een student die in wezen de stof onvoldoende beheerst, de beste beslissing is hem ook onvoldoende te beoordelen; de uitkomsten van de beste beslissing en van de genomen beslissing zijn C en D respectievelijk, en omdat C en D tevens de utiliteit van die uitkomsten aangeeft (hoewel we die nog niet kennen) is het verlies van de genomen beslissing gelijk aan het verschil C - D ).

Het verlies van terecht voldoende beoordelen is op dezelfde manier gelijk aan C - C, dat is gelijk aan nul.
Houd goed vast wat de betekenis van A, B, C en D is:


In paragraaf 7.1 heb ik een voorbeeld gegeven waarvoor alleen het relatieve verlies van de ene foute beslissing ten opzichte van de andere foute beslissing nodig was (de verhouding 4 : 1 van het verlies van ten onrechte een onvoldoende geven ten opzichte van het ten onrechte voldoende geven). Algemeen geldt dat voor rationeel beslissen geen absolute utiliteiten of verliezen, maar slechts relatieve nodig zijn. Ofwel: voor ons cesuurprobleem is het niet nodig om A, B, C en D te kennen; ook de verschillen B - A en C - D hoeven we niet te kennen, maar slechts de verhouding

    ( A - B ) / ( C - D )

moeten we kennen (bepaald hebben). De consequentie van een en ander is dat we over een aantal vrijheden beschikken bij het kiezen van waarden voor A, B, C en D. Met name zijn we vrij om voor de utiliteit van de slechtste uitkomst nul te kiezen, voor de utiliteit van de beste uitkomst één, en de utiliteiten van de beide andere moeten dan nog bepaald worden.

De beste uitkomst moeten we kiezen uit B en C, de student terecht voldoende beoordeeld hebben, of de student terecht onvoldoende beoordeeld hebben. Ik moet waarschuwen dat de veronderstelling daarbij is dat

  1. gegeven dat de student de stof voldoende beheerst, het beste besluit is om hem een voldoende te geven; en
  2. gegeven dat de student de stof in wezen onvoldoende beheerst, het beste besluit is hem een onvoldoende te geven.

Met de eerste veronderstelling zullen weinigen moeite hebben, maar de tweede is discussiabel; zoals op verschillende plaatsen in deze cursus al opgemerkt werd, en in deel 2 uitgebreid besproken wordt, is het onder conjunctieve (hordenloop) examenregelingen geenszins vanzelfsprekend dat het laten overdoen beter is dan het niet laten overdoen. De vraag is, of uitkomst C wel hoger te waarderen is dan uitkomst D (een hogere utiliteit heeft). Laten we eens zien.

Om de keuze verantwoord te kunnen maken, moeten we ons goed realiseren wat beide mogelijke uitkomsten voor de student, voor het onderwijs, en voor de samenleving betekenen. Een goede beschrijving van iedere uitkomst is daar tenminste voor nodig, en in veel gevallen zullen speciale technieken aangewend moeten worden om het probleem overzichtelijk te houden (zie voor het laatste Keeney & Raiffa 1976). Zulke omschrijvingen zouden er in beknopte en verbale vorm voor C en D als volgt uit kunnen zien:

C: de student zal het tentamen overdoen;


D: de student zal het tentamen niet overdoen, gaat dus gewoon door met het normale studieprogramma;


De docent die zelf dergelijke lijstjes maakt, kan ze nog laten aanvullen door collega's, studenten en andere betrokkenen, die hem er in dit geval op zouden kunnen wijzen dat in de beschrijving van uitkomst C niet vermeld is dat de student na het tentamen overgedaan te hebben de stof misschien beter (voldoende) beheerst.

Het is niet eenvoudig om tussen C en D te kiezen, die uitkomst aan te wijzen die het best is (naar jouw persoonlijke mening). De beschrijving van C is een stuk minder aantrekkelijk dan de beschrijving voor D, zodat je al snel geneigd zou zijn om uitkomst D het hoogst te waarderen. Maar dat zou betekenen dat het altijd beter zou zijn de student een voldoende te geven, dan een onvoldoende; ik heb in deel 2 (zie ook 6.6) een forse reeks argumenten gegeven dat deze conclusie juist is wanneer conjunctieve (hordenloop) examenregelingen gehanteerd worden waarin de gevolgen van uitkomst C inderdaad zijn zoals juist omschreven. In andere woorden: de docent die onvoldoendes uitdeelt en van deze studenten verlangt dat ze het tentamen overdoen, waardeert uitkomst C hoger dan uitkomst D; kennelijk is het kleine stukje betere stofbeheersing na het overgedaan hebben van het tentamen belangrijk genoeg om alle nadelen van C en voordelen van D te overtroeven.

Omdat er geen cesuurprobleem meer zou zijn wanneer het altijd beter is de student een voldoende te geven, ga ik er omwille van het voorbeeld van uit dat het onvoldoende beoordelen van een student die in wezen de stof onvoldoende beheerst, beter is dan deze student voldoende beoordelen.

Dan nu terug naar de keuze van de beste uitkomst uit B en C. Het is niet nodig om voor die keuze ook van B een uitgebreide beschrijving te maken, omdat meestal de utiliteit van B duidelijk hoger is dan die van C (als de docent zou mogen kiezen, zou hij liever een terecht voldoende beoordeelde student hebben, dan een terecht onvoldoende beoordeelde student).

Dus: B = 1.

Voor de uitkomst met de laagste utiliteit moet de keuze dan gemaakt worden tussen A en D, en omdat het minder vervelend voor student (en docent) is om ten onrechte voldoende beoordeeld te zijn dan ten onrechte onvoldoende, is het makkelijk om A als minst gewenste uitkomst aan te wijzen:

A = 0.

De utiliteiten van C en D liggen ergens tussen 0 en 1. Bij de procedure voor het bepalen van die utiliteiten kunnen we er gebruik van maken dat onze tussen 0 en 1 (inclusief) variërende utiliteiten dezelfde eigenschappen hebben als ook tussen 0 en 1 variërende waarschijnlijkheden.

Ik zal proberen dit in het voorbeeld goed uit te laten komen, en verwijs voor details naar Lindley 1971.

We zullen een beschrijving van uitkomsten A en B nog nodig hebben:

A: dezelfde beschrijving als voor C, met dit verschil, dat nu niet zo
makkelijk aangenomen mag worden dat de student na de herhaling de
stof beter beheerst, en ook al zou dat wél het geval zijn, dat toch
geen pluspuntje is omdat deze student om te beginnen de stof in wezen
al voldoende beheerste en het tentamen niet had horen over te doen.
B: normale studievoortgang, behoeft nauwelijks uitgebreide beschrijving.

Voor het bepalen van de nu nog onbekende utiliteiten C en D wordt van de docent een hem ongetwijfeld onwezenlijk voorkomend gedachtenexperiment gevraagd. Hoewel het moeilijk zal zijn om de gevraagde voorstellingen in gedachten te maken, kan de docent zich troosten met de idee dat wat hier van hem gevraagd wordt zeker niet moeilijker kan zijn dan het bepalen van de zak-slaaggrens zonder de hulp van technieken als hier gepresenteerd. Tegen de beslissingnemer die zich niet in staat voelt gedachtenexperimenten van het nu te bespreken soort te maken, wordt wel eens gezegd dat hij altijd al in staat is geweest om de beslissingen waar het om gaat ongewapend" te nemen, zodat hij het zeker ook moet kunnen wanneer hem keuzen aangeboden worden die heel wat minder complex zijn.

Bij beslissingen in het onderwijs, of waar dan ook, moet de docent accepteren dat er altijd onjuiste beslissingen genomen worden. Gewoonlijk is het niet mogelijk om de individuele studenten aan te wijzen over wie een verkeerde beslissing genomen is, maar weet je bij benadering wel om welke aantallen het gaat. Stel je nu eens voor dat je door bijzondere externe informatie wél van bepaalde studenten zou weten of de over hen genomen beslissingen juist is of niet; een gedachtenspelletje dus, zij het dat je je wel moet realiseren dat het gedachtenspelletje gegevens oplevert op grond waarvan de cesuur bepaald wordt, op grond waarvan belangrijke beslissingen over individuele personen worden genomen.

Stel dat ik een bepaalde student kan aanwijzen die ten onrechte een voldoende beoordeling heeft gekregen. Stel dat ik een andere student kan aanwijzen die in wezen de stof voldoende beheerst, maar het tentamen nog moet afleggen zodat hij nog het risico loopt een onvoldoende beoordeling te krijgen. Veronderstel tenslotte eens dat ik je het voorstel kan doen de eerste student (student 1) in te ruilen tegen de tweede student (student 2). Om over die ruil te kunnen beslissen, moet je weten wat de slaagkans van student 2 is; anders geformuleerd: wat we zoeken is de slaagkans voor student 2 die maakt dat jij, de docent, onverschillig staat tegenover deze ruil, geen voorkeur voor de ene, noch voor de andere student hebt. Deze gezochte slaagkans, de waarschijnlijkheid dat student 2 voldoende beoordeeld wordt, is de gezochte utiliteit van uitkomst D.

Deze techniek voor het bepalen van utiliteiten is uitgebreid beschreven door Raiffa 1968, en kamt er op neer dat je moet bepalen voor welke onzekere uitkomsten je een bepaalde zekere uitkomst wilt ruilen. Het voorbeeld van een loterij om geld is het duidelijkst: de vraag is dan of je een bepaald bedrag contant in de hand wilt ruilen voor een lot met een bepaalde kans op een groter bedrag (en het omgekeerde van die kans op een niet).

Door bedragen en/of waarschijnlijkheden te variëren, kan bepaald worden welk 'zeker' bedrag iemand nog net zou willen ruilen tegen een bepaalde kans op een groter bedrag (of niets).

In ons voorbeeld hebben we iets dergelijks. Je kunt zeggen dat we een loterij voor student 2 hebben: hij beheerst de stof in wezen voldoende, maar loopt bij het afleggen van het tentamen een risico desondanks onvoldoende beoordeeld te worden. Noem de waarschijnlijkheid dat student 2 een voldoende beoordeling krijgt (u), zodat de waarschijnlijkheid dat hij ten onrechte onvoldoende beoordeeld wordt gelijk is aan (1 - u).

Bestudeer zorgvuldig de uitkomstbeschrijvingen A, B en D, omdat je voor de (denkbeeldige) keuze gesteld wordt de zekere uitkomst D voor student 1 in te ruilen tegen de onzekere uitkomst A of B voor student 2. Bedenk, om het experiment wat realistischer te maken, dat niet gezegd is dat student 2 de stof maar net voldoende beheerst, of zeer goed beheerst, of iets dergelijks; het is redelijk om te veronderstellen dat de waarschijnlijkheid dat student 2 een voldoende beoordeling krijgt, afhankelijk is van de mate waarin hij de stof net voldoende, redelijk, goed, of uitmuntend beheerst. De slaagkans van student 2 is dus niet bekend. De vraag is dan: hoe hoog zou die slaagkans minimaal moeten zijn, dus hoe groot moet (u) tenminste zijn zodat je student 2 liever hebt dan student 1? Bedenk dat na je beslissing, de werkelijke (geschatte) slaagkans voor student 2 bekend gemaakt zal worden, en je aan je genomen beslissing gehouden zult worden.

Het is moeilijk om dit te beslissen, maar het is nog moeilijker om zonder dit uiteenrafelingsproces de zak-slaaggrens te bepalen, en dat laatste is een beslissing die je in het verleden altijd hebt kunnen nemen. Dus moet je deze beslissing ook kunnen nemen. Probeer eens om verschillende waarden voor (u) in te-vullen, bijvoorbeeld 0,9, 0,8, 0,7 en dergelijke. Knip desnoods je eigen beschrijvingen van de uitkomsten A, B en D uit, en schrijf bij uitkomst A de kans daarop van zeg 0,9, en bij uitkomst B de daarbij behorende kans (1 - 0,9) = 0,1, zodat je een goed overzicht krijgt van de keuze waarom het gaat.

Laten we zeggen dat na een paar keer proberen, overleg met collega's en enige bedenktijd tussendoor, je besluit dat de zekere uitkomst D voor student 1 equivalent is aan de onzekere voor student 2 als de laatste een kans 0,75 om te slagen heeft. Zodat D = 0,75.

Hetzelfde gedachtenexperiment wordt vervolgens gedaan om de utiliteit C te bepalen. Zouden we daarbij vinden dat C kleiner is dan D, dan hebben we ergens een vergissing gemaakt, of hebben we ontdekt dat het onder een regeling dat onvoldoendes overgedaan moeten worden, altijd beter is om studenten voldoende te beoordelen.

O.K., veronderstel dat in de gedachtengang van een voorstander van de conjunctieve examenregeling de utiliteit C volgens dezelfde procedure als hierboven voor het bepalen van D geschetst bepaald wordt op C = 0,90. Dan wordt de beslissingstabel: wezenlijke stofbeheersing voldoende onvoldoende

 _______________________________________________________________
                            wezenlijke stofbeheersing 
                          voldoende         onvoldoende
 _______________________________________________________________
 onvoldoende beoordelen         A             C
 voldoende beoordelen           B             D
 _______________________________________________________________


TABEL 7.2.1 Uitkomstentabel voor cesuurbepaling.

Na al deze omwegen beschikken we dan over het relatieve verlies van ten onrechte onvoldoende en ten onrechte voldoende:

( B - A )/( C - D ) = 1/( 0,15 ) = 6,67.

Deze verliesverhouding is een stuk groter dan het voorbeeld in 7.1. De lezer kan voor zichzelf nagaan dat de aftestgrens in dat voorbeeld bij deze nieuwe verliesverhouding nog lager zal komen te liggen. Vindt de docent dat hij ondanks zorgvuldige overwegingen bij het vaststellen van de utiliteiten voor C en D, uiteindelijk tot een te laag aantal onvoldoendes komt, dan kan hij controleren of zijn uitkomsten beschrijvingen wel volledig waren, of hij toch niet een iets hogere waarschijnlijkheid (u) had moeten kiezen etcetera; maar het kan natuurlijk ook zijn dat de tot nu toe gevolgde zak-slaag procedures altijd al veel te hoge afwijzingspercentages hebben opgeleverd, zodat de fout niet in de bier gevolgde aanpak zit, maar in de klassieke aanpak met de natte vinger.

Natuurlijk is ook de hier geschetste aanpak nog steeds enigszins intuïtief, zij het een stuk minder dan het Onder deze gedetailleerde aanpak proberen te bepalen van de aftestgrens. De gegeven aanpak is niet de beste voor het cesuurprobleem, een betere procedure zal tijd en onderzoek vragen om te ontwikkelen. Daarbij is de vraag of die moeite uiteindelijk wel juist besteed zal zijn, omdat niet verwacht mag worden dat het cesuurprobleem zoals we dat vandaag de dag nog kennen, bij verbeterde examenregelingen nog zal bestaan. Daarom ook lijkt een grove aanpak zoals hier gedemonstreerd wel voldoende, omdat daar al duidelijk uit wordt welke de moeilijk houdbare impliciete veronderstellingen van de oude cesuuraanpak zijn. Wie desondanks verfijndere technieken wil zoeken of ontwikkelen, kan zijn gang gaan met de uitgebreide aanwijzingen daartoe gegeven door Keeney & Raiffa 1976.


7.3 Discussie.

De geïllustreerde toepassing veronderstelde dat de cesuur in termen van wezenlijke beheersing van de stof al vastgesteld was, en dat het probleem was om de cesuur in termen van toetsscores te bepalen. Het is duidelijk dat het kiezen van de cesuur in termen van wezenlijke stofbeheersing met de nodige zorgvuldigheid moet gebeuren, onder andere met inachtnemen van de uitgangspunten zoals in deze cursus besproken. Wanneer dat gebeurd is, is het aan te raden een beetje te experimenteren met andere waarden voor deze cesuur, door na te gaan hoe de optimale cesuur in termen van toetsscores verandert. Mogelijk leveren uitkomsten van die onderzoekjes informatie op, op grond waarvan de aanvankelijk gekozen cesuur in termen van wezenlijke beheersing van de stof bijgesteld kan worden.

De technieken in 7 gedemonstreerd, lenen zich ook voor averechtse toepassingen: het is vaak mogelijk om terug te redeneren naar de impliciet gehanteerde uitgangspunten bij een bepaald zak-slaagbeleid.

Directe aanbevelingen voor het dagelijks beleid van de docent of vakgroep zijn moeilijk te geven, behalve het advies om tenminste eens te proberen de techniek in de grove vorm zoals hier gepresenteerd, een keer toe te passen. Aanwijzingen daarbij zijn:

  1. zorgvuldig beraad over de doelstellingen van onderwijs.
  2. op grond van het resultaat van 1 kiezen voor een voorlopige cesuur, geformuleerd in ideale termen, dat is in termen van wezenlijke beheersing van de stof.
  3. verzamelen van informatie over de mate waarin de ruwe toetsscores die wezenlijke stofbeheersing meten (daarvoor kan misschien gebruik gemaakt worden van een model zoals in de bijlagen besproken wordt, en ook in het inleidende hoofdstuk kort gememoreerd werd).
  4. constructie van een curve van het soort als in figuur 2.6.1 getekend (zowel t.a.v. 3 als van 4 zou de docent zich moeten laten bijstaan door deskundigen).
  5. zorgvuldig beschrijven van de mogelijke uitkomsten A, B, C en D. Leidraad bij die beschrijving zijn de uitgangspunten zoals in deze cursus besproken.
  6. niet alleen hoe een ander naar het inzicht van de docent het best zou zijn is van belang, maar ook moet bij de analyse gelet worden op hoe de student de diverse afwegingen voor zichzelf of voor zijn groep medestudenten zou maken, terwijl ook maatschappelijke belangen tot ándere cesuren kunnen leiden. Wanneer het niet goed mogelijk is om conflicterende belangen in deze ene analyse onder te brengen, kunnen verschillende analyses worden gemaakt voor ieder van de betrokkenen (belangengroepen).

Tenslotte: al die moeite hoeft niet noodzakelijk tot werkbare procedures te leiden, maar zal in ieder geval een dieper inzicht in de aard van het cesuurprobleem opleveren. Uit dat gerijpte inzicht volgt een grotere zorgvuldigheid bij het in de toekomst nemen van zak-slaag beslissingen. Een zorgvuldigheid die ongetwijfeld beter aan zal sluiten bij de ongeschreven regels van behoorlijk bestuur, waarop de student zich uiteindelijk altijd kan beroepen.

 
De hier gegeven bijlage is een onderdeel van het afzonderlijke deel Bijlagen dat in de loop van 1978 zal verschijnen.


BIJLAGE
Tabellen van percentages foute beslissingen bij cesuurbepaling.

Voor het maken van schattingen van het aantal foute beslissingen, is het noodzakelijk modellen voor de werkelijkheid te bouwen, gestoeld op aannamen die de werkelijkheid voldoende vereenvoudigen om er iets hanteerbaars van te maken. Onder andere is het aantal foute beslissingen afhankelijk van de bedoelingen die men met de cesuurbepaling heeft, zodat al naar gelang die bedoelingen een aantal verschillende situaties bekeken moeten worden.

Allereerst is er het relatief eenvoudige probleem van foutieve beslissingen door toevallige invloeden (zie ook 6.2 t/m 6.5). Eerste stap op weg naar kwantificering is het analyseren van beslissingsresultaten wanneer de studenten niet één, maar twee keer hetzelfde tentamen doen. Met dien verstande dat beide tentamens over dezelfde stof gaan, ongeveer even moeilijk zijn, evenveel vragen bevatten, niet dezelfde vragen maar wel vragen die in alle relevante opzichten met elkaar vergelijkbaar zijn. Twee van dergelijke toetsen worden paralleltoetsen genoemd.

Je zou best het experiment ook kunnen uitvoeren, maar nodig is het niet. Het is ook mogelijk om een theoretisch plausibel model te construeren, en daaruit de verlangde oplossingen voor ons probleem te berekenen. Ik gebruik daarvoor een model dat zich in de testtheorie als handig, en niet te ver van de realiteit af staand, heeft bewezen.

Voor het eerste model neem ik aan dat scores van studenten op ieder van de parallel toetsen normaal verdeeld zijn (zie voor eigenschappen van de normaalverdeling de statistische literatuur, of Alf & Dorfman 1967 voor een beschrijving die direct op onze situatie past). Voor een aantal verschillende cesuren (in termen van afwijzingspercentages) kunnen we dan berekenen, of uit tabellen voor de bivariate normaalverdeling aflezen, hoe groot het aantal beslissingen is dat op beide paralleltoetsen gelijk is, en hoe groot het aantal beslissingen is dat verschillend uitvalt al naar gelang welke van beide paralleltoetsen als basis voor de zak-slaag beslissing genomen werd. Het enige gegeven dat daarvoor nog nodig is, is de correlatie tussen scores op de ene, en scores op de andere parallel toets. Die correlatie is in de klassieke testtheorie gelijk aan de betrouwbaarheid van de toets (een van beide paralleltoetsen), en je zou daar met heel erg veel goede wil de KR 20 waarde van de toets (als de docent over die berekening beschikt) kunnen gebruiken.

In figuur 1 is het model in tekening gebracht. In tabel 1 en 2 zijn voor verschillende cesuren (de percentages zijn niet in ronde getallen omdat de te gebruiken tabellen anders niet op het probleem zouden passen) de percentages gegeven voor de groep die in beide gevallen voldoende (groep b) en onvoldoende (groep c), in beide gevallen verschillend (groep a en groep d samen) beoordeeld zouden worden. Voor de precieze wijze van berekening zie o.a. Tables of the bivariate normal distribution function. Washington: National Bureau of Standards, 1959.

77gif/77Cesuur6COWO432378.gif

FIGUUR 1 Cesuur op twee paralleltoetsen (beide normaal verdeeld).

 

 _______________________________________________________________
 (toetsbetrouw-)     % studenten dat onvoldoende krijgt
 (baarheid .60 )           24.2 21.2 15.9 11.5  6.7  2.3
 _______________________________________________________________
 groep 
 a (toets 1 onvoldoende) 11.3 10.5  8.6  6.8  4.4  1.7
 b (beide voldoende)     64.5 68.3 75.5 81.7 88.9 96.0
 e (beide onvoldoende)   12.9 10.7  7.3  4.7  2.3   .6
 d (toets 2 onvoldoende) 11.3 10.5  8.6  6.8  4.4  1.7
 a+d (1 onvoldoende)     22.6 21.0 17.2 13.6  8.8  3.4
 _______________________________________________________________
 TABEL 1 Percentages in de diverse groepen, bij verschillende
 cesuren en bij toetsbetrouwbaarheid .60.
[noot: niet-proportioneel lettertype voor de tabel gebruikt ]

  
_______________________________________________________________
 (toetsbetrouw-)        % studenten dat onvoldoende krijgt
 (baarheid .70 )           24.2 21.2 15.9 11.5  6.7  2.3
 _______________________________________________________________
 groep
 a (toets 1 onvoldoende)    9.8  9.0  7.5  5.9  3.9  1.6
 b (beide voldoende)       66.0 69.8 76.6 82.6 89.4 96.1
 c (beide onvoldoende)     14.4 12.2  8.4  5.6  2.8   .7
 d (toets 2 onvoldoende)    9.8  9.0  7.5  5.9  3.9  1.6
 a+d (1 onvoldoende)       19.6 18.0 15.0 11.8  7.8  3.2
 _______________________________________________________________


TABEL 2 Percentages in diverse groepen, bij verschillende cesuren en bij toetsbetrouwbaarheid .70.
[noot: niet-proportioneel lettertype voor de tabel gebruikt ]

De tabellen geven inzicht in de percentages verschillende beslissingen die zouden vallen bij parallel toetsen, maar dat is nog niet hetzelfde als percentages foute beslissingen die op basis van één toets genomen zouden worden. Een eerste suggestie voor het zoeken van laatstgenoemde percentages is om uit te gaan van de correlatie van de toets met een perfect betrouwbare (foutloze) paralleltoets. (Een perfect betrouwbare paralleltoets zou je je kunnen voorstellen als een oneindig lange parallel toets). Omdat volgens de klassieke testtheorie de correlatie van een toets met een perfect betrouwbare paralleltoets gelijk is aan de wortel uit de correlatie van de toets met zijn (gewone) parallel toets, kan op dezelfde wijze als voor tabellen 1 en 2 gedaan werd, het percentage foute beslissingen (opgesplitst naar beide mogelijke soorten van foute beslissing) berekend worden. Omdat de cesuur die op de toets gehanteerd wordt af kan wijken (en in de praktijk zeker af zal wijken) van de cesuur die gehanteerd zou worden wanneer de docent over perfecte informatie zou beschikken m.b.t. de mate waarin de studenten de stof in wezen beheersen, heb ik percentages fouten ook getabelleerd voor gevallen waarin gekozen cesuur afwijkt van 'in wezen juiste' cesuur. Zie Tabel 4.

Tenslotte zou je de genomen zak-slaagbeslissingen kunnen refereren aan uiteindelijk studiesucces, of andere criteriumvariabelen. Wanneer ook dan de veronderstelling gemaakt kan worden dat toetsscores en criterium scores bivariaatnormaal verdeeld zijn, kan voor een groot aantal situaties in de tabellen opgezocht worden welke percentages foutieve beslissingen gemaakt worden (foutief betekent hier dus onjuist, afgemeten aan de criterium variabele). Omdat het hier niet om onderzoek naar het verband tussen tentamenresultaat en later studiesucces, maar om de juistheid van zak-slaagbeslissingen gaat, werk ik met de verkregen scores (op toets, zowel als criterium variabele) ongecorrigeerd voor onbetrouwbaarheid. De resultaten zijn getabelleerd in Tabel 5.

(Omdat hoge afwijzingspercentages in het onderwijs niet voor mogen komen, zijn ze ook niet in de tabellen 1 t/m 4 verwerkt).

_________________________________________________________
 afwz.     % studenten dat de stof in wezen 
             onvoldoende beheerst
 perc.  24.2      21.2      15.9      11.5      6.7
 -------------------------------------------------------
 24.2    8.9 66.9 10.2 68.6 12.7 71.4 15.2 73.3 18.5 74.8
        15.3  8.9 14.0  7.2 11.5  4.4  9.0  2.5  5.7  1.0
 21.2    7.2 68.6  8.2 70.6 10.5 73.6 12.7 75.8 15.7 77.6
        14.0 10.2 13.0  8.2 10.7  5.2  8.5  3.0  5.5  1.2
 15.9    4.4 71.4  5.2 7316  0.9 77.2  8.6 79.9 11.0 82.3
        11.5 12.7 10.7 10.5  9.0  6.9  7.3  4.2  4.9  1.8
 11.5    2.5 73.3  3.0 75.8  4.2 79.9  5.4 83.1  7.3 86.0
         9.0 15.2  8.5 12.7  7.3  9.6  6.1  5.4  4.2  2.5
  6.7    1.0 74.8  1.2 17.6  1.8 82.3  2.5 86.0  3.6 99.7
         5.7 18.5  5.5 15.7  4.9 11.0  4.2  7.3  3.1  3.6
 _________________________________________________________
 (correlatie met perfect betrouwbare paralleltoets .75)

_________________________________________________________
 afwz.     % studenten dat de stof in wezen 
             onvoldoende beheerst
 perc.  24.2      21.2      15.9      11.5      6.7
 -------------------------------------------------------
 24.2    6.9 68.9  8.2 70.6 11.1 73.0 14.1 74.4 17.9 75.4
        17.3  6.9 16.0  5.2 13.1  2.8 10.1  1.4  6.3   .4
 21.2    5.2 70.6  6.4 72.4  8.9 75.2 11.5 77.0 15.1 78.2
        16.0  8.2 14.8  6.4 12.3  3.6  9.7  1.8  6.1   .6
 15.9    2.8 73.0  3.6 75.2  5.3 78.8  7.3 81.2 10.2 83.1
        13.1 11.1 12.3  8.9 10.6  5.3  8.6  2.9  5.7  1.0
 11.5    1.4 74.4  1.8 77.0  2.9 81.2  4.2 84.3  6.4 85.9
        10.1 14.1  9.7 11.5  8.6  7.3  7.3  4.2  5.1  1.6
 6.7     .4 75.4   .6 78.2  1.0 83.1  1.6 85.9  2.8 90.5
         6.3 17.9  6.1 15.1  5.7 10.2  5.1  6.4  3.9  2.8
_________________________________________________________


(correlatie met perfect betrouwbare paralleltoets .85)
(correlatie met perfect betrouwbare paralleltoets .85)

TABEL 3 Percentages foute en goede beslissingen bij verschillende cesuren en verschillende percentages studenten die in wezen de stof voldoende beheersen. Voor ieder viertal getallen is: linksboven (groep a) ten onrechte onvoldoende beoordeeld rechtsboven (groep b) terecht voldoende beoordeeld linksonder (groep c) terecht onvoldoende beoordeeld rechtsonder (groep d) ten onrechte voldoende beoordeeld.
[noot: niet-proportioneel lettertype voor de tabel gebruikt ]


_________________________________________________________
 afwz.     % studenten onder kritische grens op 
             criteriumvariabele
 perc.   24.2      21.2      15.9      11.5      6.7
 -------------------------------------------------------
 24.2    10.6 65.2 11.8 67.0 14.1 70.0 16.3 72.2 19.1 74.2
         13.6 10.6 12.4  8.8 10.1  5.8  7.9  3.6  5.1  1.6
 21.2     8.8 67.0  9.8 69.0 11.8 72.3 13.8 74.7 16.4 76.9
         12.4 11.8 11.4  9.8  9.4  6.5  7.4  4.1  4.8  1.9
 15.9     5.8 70.0  6.5 72.3  8.1 76.0  9.6 78.9 11.7 81.6
         10.1 14.1  9.4 11.8  7.8  8.1  6.3  5.2  4.2  2.5
 11.5     3.6 72.2  4.1 74.7  5.2 78.9  6.4 82.1  8.0 85.3
          7.9 16.3  7.4 13.8  6.3  9.6  5.1  6.4  3.5  3.2
 6.7      1.6 74.2  1.9 76.9  2.5 91.6  3.2 85.3  4.1 89.2
          5.1 19.1  4.8 16.4  4.2 11.7  3.5  8.0  2.6  4.1
_________________________________________________________
(correlatie van toets met criterium variabele .65).

_________________________________________________________
 afwz.     % studenten onder kritische grens op 
             criteriumvariabele
 perc.   24.2      21.2      15.9      11.5      6.7
 -------------------------------------------------------
 24.2    12.0 63.8 13.1 65.7 15.3 68.8 17.3 71.2 19.8 73.5
         12.2 12.0 11.1 10.1  8.9  7.0  6.9  4.6  4.4  2.3
 21.2    10.1 65.7 11.1 67.7 13.0 71.1 14.8 73.7 17.1 76.2
         11.1 13.1 10.1 11.1  8.2  7.7  6.4  5.1  4.1  2.6
 15.9     7.0 68.8  7.7 71.1  9.2 74.9 10.5 78.0 12.4 80.9
          8.9 15.3  8.2 13.0  6.7  9.2  5.4  6.1  3.5  3.2
 11.5     4.6 71.2  5.1 73.7  6.1 78.0  7.2 81.3  9.6 94.7
          6.9 17.3  6.4 14.8  5.4 10.5  4.3  7.2  2.9  3.8
 6.7      2.3 73.5  2.6 76.2  3.2 80.9  3.8 84.7  4.7 88.6
          4.4 19.8  4.1 17.1  3.5 12.4  2.9  9.6  2.0  4.7
_________________________________________________________
 (correlatie van toets met criterium variabele .55).


TABEL 4 (a) Percentages foute en goede beslissingen t.o.v. een criterium variabele waarmee de toets respectievelijk .65 en .55 correleert. Voor ieder viertal getallen is:

linksboven (groep a) ten onrechte onvoldoende beoordeeld rechtsboven (groep b) terecht voldoende beoordeeld linksonder (groep c) terecht onvoldoende beoordeeld rechtsonder (groep d) ten onrechte voldoende beoordeeld.
[noot: niet-proportioneel lettertype voor de tabel gebruikt ]


 

_________________________________________________________
 afwz.     % studenten onder kritische grens op 
             criteriumvariabele
 perc.   24.2      21.2      15.9      11.5      6.7
 -------------------------------------------------------
 24.2 13.4 62.4 14.2 64.6 16.4 67.7 18.2 70.3 20.4 72.9
      10.8 13.4 10.0 11.2  7.8  8.1  6.0  5.5  3.8  2.9
 21.2 11.2 64.6 12.3 66.5 14.1 70.0 15.7 72.8 17.7 75.6
      10.0 14.2  8.9 12.3  7.1  8.8  5.5  6.0  3.5  3.2
 15.9  8.1 67.7  8.8 70.0 10.1 74.0 11.4 77.1 12.9 80.4
       7.8 16.4  7.1 14.1  5.8 10.1  4.5  7.0  3.0  3.7
 11.5  5.5 70.3  6.0 72.8  7.0 77.1  7.9 80.6  9.1 84.2
       6.0 18.2  5.5 15.7  4.5 11.4  3.6  7.9  2.4  4.3
  6.7  2.9 72.9  3.2 75.6  3.7 80.4  4.3 84.2  5.1 88.2
       3.8 20.4  3.5 17.7  3.0 12.9  2.4  9.1  1.6  5.1
_________________________________________________________
 (correlatie van toets met criterium variabele .45)

_________________________________________________________
 afwz.     % studenten onder kritische grens op 
             criteriumvariabele
 perc.   24.2      21.2      15.9      11.5      6.7
 -------------------------------------------------------
 24.2 14.6 61.2 15.6 63.2 17.4 66.7 19.0 69.5 20.9 72.4
       9.6 14.6  8.6 12.6  6.8  9.1  5.2  6.3  3.3  3.4
 21.2 12.6 63.2 13.4 65.4 15.0 69.1 16.5 72.0 18.2 75.1
       8.6 15.6  7.8 13.4  6.2  9.7  4.7  6.8  3.0  3.7
 15.9  9.1 66.7  9.7 69.1 11.0 73.1 12.1 76.4 13.4 79.9
       6.8 17.4  6.2 15.0  4.9 11.0  3.8  7.7  2.5  4.2
 11.5  6.3 69.5  6.8 72.0  7.7  7.3  8.5 80.0  9.6 83.7
       5.2 19.0  4.7 16.5  3.8 12.1  3.0  8.5  1.9  4.8
 6.7   3.4 72.4  3.7 75.1  4.2 79.9  4.8 83.7  5.4 87.9
       3.3 20.9  3.0 18.2  2.5 13.4  1.9  9.6  1.3  5.4
_________________________________________________________
 (correlatie van toets met criterium variabele .35)



TABEL 4 (b) Percentages foute en goede beslissingen t.o.v. een criterium variabele waarmee de toets respectievelijk .45 en .35 correleert. Voor ieder viertal getallen is:

linksboven (groep a) ten onrechte onvoldoende beoordeeld rechtsboven (groep b) terecht voldoende beoordeeld linksonder (groep c) terecht onvoldoende beoordeeld rechtsonder (groep d) ten onrechte voldoende beoordeeld.

BIBLIOGRAFIE.

Ahmann, J. S., & Glock, M. D. An evaluation of the effectiveness of a freshman mathematics course. Journal of Educational Psychology, 1959, 509 41-45. Ook besproken in Hills, 1971. <

Alf, E. F., & Dorfman, D. D. The classification of individuals into two criterion groups on the basis of a discontinuous payoff function. Psychometrika, 1967, 329 115-123.

Atkinson, J. W., Lens, W., & O'Malley, P. M. Motivation and ability: interactive psychological determinants of intellective performance, educational achievement, and each other. In Sewell, W. H., Hauser, R. M., & Featherman, D. L. (Editors) Schooling and achievement in american society. London: Academic Press, 1976.

Berliner, D. C., & Cahen, L. S. Trait-treatment interaction and learning. In Kerlinger, N. (Editor) Review of Educational Research, volume 1. Itasca, Illinois: Peacock, 1973.

Bevers, J. A. A. M. Het amerikaanse studiepuntenstelsel. Een literatuurstudie. In Commissie Ontwikkeling Hoger Onderwijs De invoering van een studiepuntenstelsel in het hoger onderwijs. Den Haag: Staatsuitgeverij, 1975.

Bishop, Y. M. M., Fienberg, S. E., & Holland, P. W. Discrete multivariate analysis, theory and practice. London: M.I.T. Press, 1975.

Cronbach, L. J. Evaluation for course improvement. In Gronlund, N. E. (Editor) Readings in measurement and evaluation. New York: MacMillan, 1968.

Cronbach, L. J. Test validation. In Thorndike, R. L. (Editor) Educational measurement. Washington, D.C.: American Council on Education, 1971.

Cronbach, L. J., Gleser, G. C., Nanda, H., & Rajaratnam, N. The dependability of behavioral measurements: theory of generalizability for scores and profiles. London: Wiley, 1972.

Dawes, R.M. Graduate admission variables and future success. Science, 1975, 187, 721-723.

Gagné, R. F. The conditions of learning. New York: Holt, 1970.

Groot, A. D. de - Waaraan voldoet een 'onvoldoende' prestatie niet? Paedagogische Studiën., 1964, 41, 1-16.

Groot, A. D. de - De kernitemmethode voor de bepaling van de caesuur voldoende/onvoldoende. Paedagogische Studiën, 1964, 41, 425-440.

Groot, A. D. de - Vijven en zessen. Cijfers en beslissingen: het selectieproces in ons onderwijs. Groningen: Wolters, 1966.

Groot, A. D. de - Some badly needed non-statistical concepts in applied psychometrics. Nederlands Tijdschrift voor de Psychologie, 1970, 25, 360-376.

Groot, A. D. de - Selectie voor en in het hoger onderwijs. Een probleemanalyse. Den Haag: Staatsuitgeverij, 1972.

Groot, A. D. de -, van Naerssen, R. F., en anderen Studietoetsen: construeren, afnemen. analyseren. Den Haag: Mouton, 1973.

Hannan, M. T. Problems of aggregation. In Blalock, H. M. (Editor) Causal models in the social sciences. Chicago: Aldine Atherton, 1971.

Hills, J. R. Use of measurement in selection and placement. In Thorndike, R. L. (Editor) Educational Measurement. Washington, D.C.: National Council on Education, 1971.

Hofstee, W. K. B. De betrouwbaarheid van zak-slaag beslissingen. Nederlands Tijdschrift voor de Psychologie, 1970, 25, 380-383.

Hofstee, W. K. B. Participatiekontrole door 'onbenullige' toetsitems. Nederlands Tijdschrift Voor de Psychologie, 1973, 28, 189-198.

Hofstee, W. K. B. Selectie van personen. Inaugurele rede. Assen: Van Gorcum, 1970.

Jackson, G. B. The research evidence on the effects of grade retention. Review of Educational Research, 1975, 45, 613-636.

Keeney, R. L., & Raiffa, H. Decisions with multiple objectives preferences and value tradeoffs. London: Wiley, 1976.

Klausmeier, H. J., Ghatala, E. S., & Frayer, D. A. Conceptual learning and development. A cognitive view. London: Academic Press, 1974.

Klausmeier, H. J., Rossmiller, R. A., & Saily, M. Individually guided elementary education. Concepts and practices. London: Academic Press, 1977.

Lindley, D. Making decisions. London: Wiley, 1971.

Lord, F. M., & Novick, M. R. Statistical theories of mental test scores. London: Addison-Wesley, 1968.

Naerssen, R. F. van - Over optimaal studeren en tentamens combineren. Openbare les. Amsterdam: Swets & Zeitlinger, 1970. html

Naerssen, R. F. van - Psychometrische aspecten van de kernitemmethode. Nederlands Tijdschrift voor de Psychologie, 1974, 29,421-430.

Naerssen, R. F. van - Rapport aan de examencommissie candidaats-I betreffende de invloed van herkansingen op het niveau van voor de propedeuse geslaagde studenten. Amsterdam: Subfaculteit psychologie Universiteit van Amsterdam, ongedateerd (ca 1975).

Naerssen, R. F. van - Het derde tentamenmodel met een toepassing. Tijdschrift voor Onderwijsresearch, 1976, 1, 161-171.

Novick, M. R., & Jackson, P. H. Statistical methods for educational and psychological research. London: McGraw-Hill, 1974.

Page, E. B., Jarjoura, D., & Konopka, C. D. Curriculum design through operations research. American Educational Research Journal, 1976, 13, 31-50.

Pitz, G. F. A structural theory of uncertain knowledge. In Wendt, D., & Vlek, Ch. (Editors) Utility, probability and human decision making. Dordrecht: Reidel, 1975.

Pryor, N. M., & Gordon, M. E. A statistical model for the examination of the validity of prerequisites. Educational and Psychological Measurement) 1974, 34, 349-356.

Raiffa, H. Decision analysis. Introductory lectures on choices under uncertainty. London: Addison-Wesley, 1968.

Rorer, L. G., Hoffman, G. E., LaForge, R., & Hsieh, K-Ch. Optimum cutting scores to discriminate groups of unequal size and variance. Journal of Applied Psychology, 1966, 50, 153-164.

Rorer, L. C., Hoffman, P. J., & Hsieh, K-Ch. Utilities as base-rate multipliers in the determination of optimum cutting scores for the discrimination of groups of unequal size and variance. Journal of Applied Psychology, 1966, 50, 364-368.

Salomon, G. Heuristic models for the generation of aptitude-treatment interaction hypotheses. Review of Educational Research, 1972, 42, 327 - 344.

Standards for educational and psychological tests. Washington, D.C. 1200 Seventeenth Street, N.W.: American Psychological Association, 1974.

Stanley, J. C. Reliability. In Thorndike, R. L. (Editor) Educational measurement. Washington, D.C.: American Council on Education, 1971.

Thorndike, R. L. (Editor) Educational measurement. Washington, D.C.: American Council on Education, 1971.

Tromp, Th. J. M., & Wilbrink, B. Het meten van studietijd. In O.R.D. Congresboek 1977. html

Vastenhouw, J. Optimale rationele selectie: een waardenprobleem. Onderzoek van onderwijs, 1973, 2, 12-13.

Wijk, H. D. van -, & Konijnenbelt, W. Hoofdstukken van administratief recht. Den Haag: Vuga boekerij, 1976.

Wijnen, W. H. F. W. Onder of boven de maat. Een methode voor het bepalen van de grens voldoende-onvoldoende bij studietoetsen. Amsterdam: Swets & Zeitlinger, 1972.

Wood, R. Inhibited blind guessing: the effect of instructions. Journal of Educational Measurement, 1976, 13, 297-307.


inlegvel


Aantekeningen bij cursus 6 Cesuurbepaling Ben Wilbrink.


De voor u liggende cursus is een eerste versie, terwijl de delen 2 en 3 nog in voorbereiding zijn. Wie op de hoogte wil blijven van verbeteringen en ontwikkelingen, wordt verzocht mij te schrijven. Een aantal punten kan ik nu al noemen:


In hoofdstuk 1 worden geen illustraties aan de hand van regëlee toetsresultaten gegeven. Voor het behandelde in 1.2.1 en 1.2.2 heb ik wel enig materiaal. De docent kan aan zijn eigen toets het model nagaan, door zijn toets in twee gematchte (of ev. random) delen te splitsen en de consistentie van zak-slaagbeslissingen op iedere helft afzonderlijk genomen, te bepalen (door turven).


De aanpak in par. 6.2 t/m 6.5 gaat niet uit van het klassieke test model, althans zoals dat meestal uitgewerkt wordt, maar van de standaardmeetfout voor de gegeven student (Lord & Novick)( = de standaarddeviatie van de waarschijnlijkheidsverdeling voor de totaal score voor de gegeven student zoals die in het binomiale model is).


De laatste alinea van par. 6.4 op blz. 74 is enigszins misleidend: voor overigens vergelijkbare kort-antwoord en meerkeuze toetsen geldt dat de standaardmeetfout voor de gegeven student kleiner is bij de meerkeuzetoets. Omdat het verschil tussen beide toetsvormen slechts is dat bij de meerkeuze toets een stuk random variatie extra ingevoerd wordt, is het duidelijk dat de kleinere standaardmeetfout voorzichtig geïnterpreteerd moet worden: ze is louter een artefakt van het gebruikte binomiale model. Aantoonbaar is dat ondanks die kleinere standaardmeetfout de kans op onjuiste beslissingen bij de meerkeuze toets groter is: de student die de stof in wezen voldoende beheerst heeft bij meerkeuze toetsing een grotere kans te zakken, de student die de stof in wezen onvoldoende beheerst heeft een grotere kans te slagen.


Hoofdstuk 7 geeft een uiterst globale besliskundige aanpak van het cesuurprobleem; hoewel de mate van detaillering veel groter is dan tot nog toe gebruikelijk bij publicaties over meer besliskundige benaderingen van selectie problemen, criterium gerefereerde_ toetsing e.d., is een degelijker aanpak dan in dit hoofdstuk beschreven erg hard nodig. Bij een solide besliskundige aanpak met gebruikmaking van de besliskundige know-how zoals die door Keeney & Raiffa recentelijk is bijeengebracht, is ondertussen een begin gemaakt. Het is te verwachten dat zich daarbij zeer grote problemen zullen voordoen, maar ook dat betere inzichten in de problematiek van de cesuurbepaling verkregen zullen worden. De uitwerking van deze punten zal gegeven worden in de nog verschij-nende delen, of in de tweede versie van deel 1.


Ik was in 2021 verbaasd dat ik volgende delen van Cesuurbepaling had beloofd. Ik heb er niet meteen enig idee van wat de inhoud daarvan dan zou moeten zijn. Een eerste poging tot herzien van de cursus is in 1980 gedaan, die wil ik ook online zetten maar daar moet ik nog wat lastige transcripties voor maken. Voor de cursus Toetsen is het wel gelukt een definitieve versie te maken die als Aula 809 is gepubliceerd. Voor de overige cursussen heeft de gelegenheid ontbroken om er voldoende tijd in te steken: Allereerst omdat ik gewoon veel te veel hooi op mijn vork had genomen met al die cursussen (de tweede heltft van de 70er jaren ben ik ongekend productief geweest); ten tweede omdat ik begin 80er jaren in opheffingsperikelen verzeild raakte, en de overplaatsing naar opdrachtonderzoek geen ruimte meer liet voor afronden van al dit cursusmateriaal. Ook mijn voorgenomen promotie is daardoor tot sint juttemis uitgesteld geworden. Dat laatste was overigens niet onvermijdelijk: collega's Van Berkel en Mirande hebben wel de gelegenheid te baat genomen om te promoveren en naar elders te vertrekken. De makke is een beetje geweest dat de serieuze arbeid voor 'Toetsvragen schrijven' mij vrijwel volledig in beslag nam, terwijl dat inoudelijk geen directe relatie had tot wat het onderwerp van mijn proefschrift zou moeten worden: examenregelingen. Zeg maar dat beloofde deel B van de kursus Examenregelingen. Het is wat. Toch heb ik geen idee, bijna een halve eeuw later, of ik die ontwikkelingen wel moet betreuren.

NB augustus 2006

Recenter literatuur

In Examens: Tijdschrift voor de Toetspraktijk, 2006 nummer 4, is een interview afgedrukt, waarin ik onder andere iets over cesuurbepaling zeg: er zijn geen absolute standaarden anders dan bij afspraak vastgestelde, dat betekent dat uiteindelijk de werkelijke tijdbesteding van de leerlingen/studenten voor wie de cursus is bedoeld, de doorslag moet geven bij het vaststellen van een zak-slaaggrens (als zo'n grens al moet worden vastgesteld).

Gregory J. Cizek and Michael B. Bunch (2007). Standard setting. A guide to establishing and evaluating performance standerds on tests. Sage.

R. K. Hambleton and M. J. Pitoniak (2006). Setting performance standards. In R. L. Brennan: Educational measurement 4th edition pp. 433-470.

C. J. Cizek (Ed.) (2001). Setting performance standards: Concepts, methods, and perspectives. Erlbaum. questia

Willem K. B. Hofstee (1983). The Case for Compromise in Educational Selection and Grading. In Scarvia B. Anderson and John S. Helmick (Eds) (1983). On educational testing. San Francisco: Jossey-Bass Publishers. p. 109-127. html

Ben Wilbrink (1980). Cesuurbepaling. Niet gepubliceerd.

File:Edgeworth.jpeg Francis Y. Edgeworth (1888). The statistics of examinations. Journal of the Royal Statistical Society, 51, 599-635.

Stukken bij Cesuurbepaling 1977

laatst aangevuld april 2021 \ contact ben apenstaartje benwilbrink.nl

Valid HTML 4.01!   http://www.benwilbrink.nl/publicaties/77CesuurbepalingCOWO.htm