Literatuur over partijdigheid: bias

Annotated by Ben Wilbrink (work in progress)

Ik heb hier even alles uit mijn literatuurbestand opgenomen dat waarschijnlijk interessant is. Heel veel gaat dubbelop: niet alleen worden dezelfde wielen telkens uitgevonden, ieder artikel begint al gauw met een overzicht van verschillende in omloop zijnde modellen. Veel artikelen zijn ook overzichtsartikelen, in die categorie zijn eigenlijk alleen de allerlaatste misschien interessant. Ik zal een en ander tzt uitwieden.

Arvey, R.D., & Faley, R.H. (1988). Fairness in selecting employees. (2nd edition) Amsterdam: Addison-Wesley.

• Een sleutelpublicatie. Niet beperkt tot technisch-statistische zaken, maar behandelt ook het sollicitatiegesprek, het gebruik van lichamelijke kenmerken bij slectie, etcterea. Gaat uitvoerig in op jurisprudentie (Amerikaanse).

Berk, Ronald A. (Ed.) (1982). Handbook of methods for detecting test bias. Baltimore: The Johns Hopkins University Press.

• Zeker, een handboek op het onderwerp.
• o.a. Lorrie A. Shepard: Definitions of bias (9-30) — Carol Kehr Tittle: Use of judgmental methods in item bias studies (31-63) — Janice Dowd Scheuneman: A posteriori analysis of biased items (180-198) — Cecil R. Reynolds: Methods for detecting construct and predictive bias (199-228) — chapter 9: Methods used by test publishers to ‘debias’ standardized tests (228-314)

Bichel et al. (1975). Sex bias in graduate admissions: data from Berkeley. Science, 187, 398-404. Reprint in Fairley & Mosteller (1977): Statistics and public policy.

Boehm, V.R. (1978), Populations, preselection, and practicalities: a reply to Hunter and Schmidt. Journal of Applied Psychology, 63, 15-18. (Arguments are presented indicating that Hunter and Schmidt's (1978) conclusions are both statistically questionable and irrelevant to practical issues involved in differential prediction.)

K. Bügel en P. F. Sanders (1998). Richtlijnen voor de ontwikkeling van onpartijdige toetsen. Arnhem: Cito. pdf

• Biedt wat de titel belooft, met voorbeelden van toetsvragen die partijdig kunnen zijn, en waarom dat zo is.

Denny Borsboom, Jan-Willem Romeijn and Jelte M. Wicherts (2008). Measurement invariance versus selection invariance: Is fair selection possible? Psychological Methods, 13, 75-98 pdf

• For annotation, see the special page borsboom.romeijn.wicherts.2008.htm.

Sorel Cahan 1 Eyal Gamliel (2006). Definition and Measurement of Selection Bias: From Constant Ratio to Constant Difference. Journal of Educational Measurement, 43, 131 - 144. [nog niet gezien]

Gregory Camilli and Lorrie Shepard (1987). The inadequacy of ANOVA for detecting test bias. Journal of Educational Statistics, 12, 87-99. pdf

• In ouder onderzoek naar bias is vaak variantieanalyse gebruikt, op basis waarvan nogal wat conclusies zijn getrokken over afwezigheid van bias. Ook door Jensen in zijn 1980 boek. Dit artikel laat zien dat variantieanalyse niet in staat is zelfs heel ernstige bias aan te tonen. En om bias aan te tonen waar die in feite afwezig is. Tamelijk verontrustend, dus. Het punt is: er is nijna eindeloos veel achterdocht nodig bij het studeren van de literatuur, zeker wanneer beweerd wordt dat het met partijdigheid allemaal wel mee valt.

Cleary, T. Anne (1968). Test bias: prediction of grades of negro and white students in integrated colleges. Journal of Educational Measurement, 5, 115-124.first page JSTOR (toegang via KB lidmaatschap: hele artikel)

• Een methodologisch bezien gezond idee, dat daarom ook in vrijwel ieder later atuk over terugkomt, onder verwijzing naar dit artikel.
• Het idee is dat een toets partijdig is wanneer een subgroup systematisch te hoog of te laag wordt ingeschat op een criterium dat de toets bedoeld is te voorspellen.
• Craig J. Russell heeft een handige samenvatting van dit regressiemodel beschikbaar hier

Cleary, & Hilton (1968). An investigation of test bias. Educational and Psychological Measurement, 28, 61-75.

Cleary, et al. (1975). Educational uses of tests with disadvantaged students. American Psychologist, 30, 15-41.

Cohen, A. S., & Kim, S-H (1993). A comparison of Lord's chi-square and Raju's area measures on detection of DIF. APM, 17, 39-52.

Cole, Nancy S. (1972). Bias in selection. ACT Research Reports, no. 51. Ook gepubliceerd onder dezelfde titel in Journal of Educational Measurement, 10, 237-255.

• Petersen en Novick (1976) noemen dit Cole-model het Conditional Probability Model. Het idee is dat kandidaten die succes zouden hebben op het criterium, de toelatingskansen gelijk moeten zijn ongeacht tot welke subgroep ze behoren.
• Dit lijkt niet onredelijk, maar het model blijkt innerlijk tegenstrijdig, en is door Petersen en Novick (1976) afgeserveerd. Een verdediging is ook verworpen:Sawyer, Cole & Cole (1976).

Cole, N.S., and Moss, P.A. (1989). Bias in test use. In Linn, R.L. (Editor) (1989). Educational Measurement. London: Collier Macmillan Publishers, 201-220.

Cole, Nancy S., and Michael J. Zieky (2001). The new faces of fairness. Journal of Educational Measurement, 38, 369-382.

• Een beschouwing over een lange periode, advies om het niet in statistische methoden te zoeken maar in andere maatregelen.

Cronbach, Lee J. (1976). Equity in selection - Where psychometrics and political philosophy meet. Journal of Educational Measurement, 13, 31-42.

Crooks (1972). An investigation of sources of bias in the prediction of job performance. A six-year study. Proceedings of the inivitational conference, E.T.S.

Darlington, R.B. (1971). Another look at 'cultural fairness'. Journal of Educational Measurement, 8, 71.

• "Four definitions of 'cultural fairness' are examined and found to be not only mutually contradictory, but all based on the false view that optimum treatment of cultural factors in test construction or test selection can be reduced to completely mechanical procedures."
• Besproken in Peterson & Novick, 1976, p. 22. In dat themanummer ook een nieuwe bijdrage van Darlington.
• Ik begrijp dit niet echt goed. Het lijkt een soort compromismethode, waarbij de criteriumvariabele een weging krijgt die over subgroepen verschillen kan worden gekozen.

Drasgow (1982). Biased test items and differential validity. Psychological Bulletin, 95, 526-531.

Edith van Eck, Ard Vermeulen en Ben Wilbrink (1994). Doelmatigheid en partijdigheid van psychologisch onderzoek bij de selectie van schoolleiders in het primair onderwijs. Amsterdam: SCO-Kohnstamm Instituut. (rapport 359) [Hoofdstuk 3. Het psychologisch onderzoek html; Hoofdstuk 5. Seksepartijdigheid en rendement html]

Einhorn, H. J., and A. R. Bass (1971). Methodological considerations relevant to discrimination in employment testing. Psychological Bulletin, 75, 261-269.

• In deze visie, het Equal Risk Model, is een selectieprocedure onpartijdig wanneer toegelaten kandidaten dezelfde kans op succes (of falen) hebben, ongeacht de subgroep waaruit zij afkomstig zijn. Het model is verwant aan het regressiemodel van Cleary (1968), met dit verschil dat het Cleary-model van de gemiddelde gekwadrateerde voorspellingsfout minimalisseert, en het Equal Risk Model het verwachte drempelverlies. Peterson en Novick (1976) klassificeren die twee modellen als toepassingen van statistische beslissingstheorie (p. 19), en daarmee als methodologisch gezonde methoden.

Feingold, A. (1994). Gender differences in personality: a meta-analysis. Psychological Bulletin, 116, 429-456.

Flaugher, The many definitions of test bias. American Psychologist, 1978, 33, 671- .

Henk Van Der Flier, Gideon J. Mellenbergh, Herman J. Adèr, Marina Wijn (1984). An Iterative Item Bias Detection Method. Journal of Educational Measurement, 21, 131-145.

Frazer, Miller and Epstein (1975), Bias in prediction: a test of three models with elementary school children. Journal of Educational Psychology, 67, 490-494.

Mark J. Gierl, Jeffrey Bisanz, Gay L. Bisanz, Keith A. Boughton (2003). Identifying Content and Cognitive Skills That Produce Gender Differences in Mathematics: A Demonstration of the Multidimensionality-Based DIF Analysis Paradigm. Journal of Educational Measurement, 40, 281-306. jstor

• Een intellectuele worsteling om statistische analyse en interpretatie dichter bij elkaar te brengen. Maar of dat dan ook is gelukt?

Gifford, B.R. (Editor, 1989). Test policy and test performance: education, language and culture. National Commission on Testing and Public Policy. Dordrecht: Kluwer Academic Publishers.

Goldman and Hewitt (1976). Predicting the success of black, chicano, oriental and white college students. Journal of Educational Measurement, 13, 107-118.

Gross, and Su (1975). Defining a 'fair' or 'unbiased' selection model: a quesion of utilities. Journal of Applied Psychology, 60, 345-351.

Hedges, L. V., & Friedman, L. (1993). Gender differences in variability in intellectual abilities: a reanalysis of Feingold's results. Review of Educational Research 63, 94-105.

Helms, J.E. (1992). Why is there no study of cultural equivalence in standardized cognitive ability testing? American Psychologist, 47, 1083-1101.

Paul W. Holland (1985?). On the study of differential item performance without IRT. pdf

Hook and Cook (1979). Equity theory and the cognitive ability of children. Psychological Bulletin, 86, p. 429.

Hunter, J. E., & Hunter, R. F. (1984). Validity and utility of alternative predictors of job performance. Psychological Bulletin, 96, 72-98.

Hunter, J.E., Schmidt, F.L., and Rauschenberger, J.M. (1977). Fairness of psychological tests: imlications of four definitions for selection utility and minority hiring. Journal of Applied Psychology, 62, 245-260.

Hunter, Schmidt & Hunter (1979). Differential validity of employment tests by race: a comprehensive review and analysis. Psychological Bulletin, 86, 721-735.

Ironson, Gail H., and Michael J. Subkoviak (1979).A comparison of several methods of assessing item bias. Journal of Educational Measurement 1979, 16, 209-226.

Ironson, G.H., Guion, R.M., and Ostrander, M. (1982). Adverse impact from a psychometric perspective. Journal of Applied Psychology, 67, 419-432. (Applying latent trait theory to an analysis of a 64-item multiple choice skill test administered to 1,035 police recruits, we illustrate how two shorter tests measuring the same attribute, but having different test characteristic curves, have different degrees of adverse impact. ... We propose that the concept of adverse impact be redefined in terms of the degree to which test scores distort any underlying true subgroup differences in the attribute measured.)

Jensen, A. R. (1980). Bias in mental testing. London: Methuen.

Kaye, D. (1982). Statistical evidence of discrimination. Journal of the American Statistical Association, 77, 773-783.

• (It is suggested that the classical method of hypothesis testing used by the Supreme Court is not appropriate to testing whether a given defendant discriminated. Presentation of p values, prediction of confidence intervals, and likelihood functions are shown to be preferable. Bayesian methods are also considered. Comments by S.E. Fieberg, D.H. Jones, L. Brilmayer, and rejoinder by D. Kaye 783-792.

Frank Kok (1988). Vraagpartijdigheid. Methodologische verkenningen. Proefschrift UvA. SCO-publicatie 88.

Frank G. Kok, Gideon J. Mellenbergh, Henk Van Der Flier (1985). Detecting Experimentally Induced Item Bias Using the Iterative Logit Method. Journal of Educational Measurement, 22, 295-303.Jstor

Ledvinka, J., Markos, V.H., & Ladd, R.T. (1982). Long-range impact of 'fair selection' standards on minority employment. Journal of Applied Psychology, 67, 18-36.

Lewy (1973). Discrimination among individuals versus discrimination among groups. Journal of Educational Measurement, 10, 19-24.

Linn, Robert L (1973). Fair test use in selection. Review of Educational Research, 43, 139-163.

• Presenteert op p. 153 een model voor onpartijdige selectie dat Petersen en Novick (1976) het Equal Probablity Model noemen, en vernietigend verwerpen omdat het innerlijk tegenstrijdig is.
• Het idee achter dit model is dat , gegeven dat kandidaten zijn toegelaten, zij als afkomstig uit verschillende subgroepen dezelfde kans op succes moeten hebben.

Linn, Robert L. (1976). In search of fair selection procedures. Journal of Educational Measurement, 13, 53-58.

Linn, Robert L. (1978). Single-group validity, differential validity, and differential prediction. Journal of Applied Psychology, 63, 507-512.

Linn, Robert L. (1984). Selection bias: multiple meanings. Journal of Educational Measurement, 21, 33-47.

Linn, Robert L, & Harnisch, D.L. (1981). Interactions between item content and group membership on achievement test items. Journal of Educational Measurement, 18, p. 109-..

Linn, R. L., and C. N. Hastings (1984). Group Differentiated Prediction. Applied Psychological Measurement Vol. 8, No. 2, Spring 1984, pp. 165-172. abstr Studies of predictive bias have frequently shown that a prediction equation based on majority group members tends to overpredict the criterion performance of minority group members. Two statistical artifacts that may cause the overprediction finding are reviewed and evaluated using data for black and white students at 30 law schools. It is shown that (1) the degree of overprediction decreases as the predictive accuracy for white students increases, and (2) that overprediction can be caused by the effects of selection on variables not included in the regression model. Use of Heckman's (1979) procedure to adjust the estimates of the regression parameters was found to essentially eliminate overprediction. p. 165: Predictive bias has been the focus of a substantial number of studies in a wide variety of selection situations, including military, employment, and educational settings. The basic paradigm of these studies is quite familiar by now. Within-group regression equations are computed and the standard errors of prediction, the slopes, and the intercepts are compared. If different prediction systems are obtained for two groups, e.g., a minority group and a majority group, or men and women, then the use of an equation based upon one group will result in systematic errors of prediction when applied to the other group. The natural question is then: What is the magnitude and direction of those systematic errors? A common approach to answering this question is to use the majority group prediction equation to obtain predictions for values of the predictors equal to the minority group means and to compare these predictions to the actual minority group mean on the criterion. Alternatively, predictions based on the two equations may be made for various combinations of the two predictors to define regions where one equation yields higher predictions than the other. The naive expectation, in keeping with a belief that tests are biased against minority group members, was that the predicted criterion performance from the majority group equation would be lower than the actual performance of minority group members. That is, that there would be a bias against minority group members in the sense that their criterion performance would be underpredicted. However, the results of most studies run counter to this expectation. The bulk of the evidence shows either no difference in the predictions from minority and majority group equations or that the majority group equation tends to overpredict the minority group performance (Linn, 1982; Schmidt & Hunter, 1981). These results led Schmidt and Hunter (198 1, p. 1128) to conclude that "cognitive ability tests . . . are fair to minority group applicants in the sense that they do not underestimate expected job performance of minority groups."

Gitta H. Lubke, Conor V. Dolan, Henk Kelderman, Gideon J. Mellenbergh (2003). On the relationship between sources of within- and between-group differences and measurement invariance in the common factor model. Intelligence 31, 543–566

Gideon J. Mellenbergh (1982). Contingency table models for assessing item bias. Journal of Educational Statistics, 7, 105-118. Jstor

• Mellenbergh's method uses correct response probabilities conditional on latent ability. Scheuneman (1979) uses probabilities conditional on the observed test score. Mellenbergh contrasts both methods, using, a.o., Scheuneman's empirical data.

Mellenbergh, G. J. (1989). Item bias and item response theory. International Journal of Educational Research, 13, 127–143.

Meredith, William (1965). A method for studying differences between groups. Psychometrika, 30, 15-30.

• Gebruikt multiple discriminant analyse om die verschillen te bestuderen. Hoe zoiets gaat: zie ook Wilbrink (1968 html).

Meredith, William (1993). Measurement invariance, factor analysis and factorial invariance. Psychometrika, 58, 525-543.

• abstract Dit is een onleesbaar artikel, ook al is het gebaseerd op een presidential address van Meredith. Iets dat onleesbaar is, in dit geval ook voor specialisten, kan niet bijdragen aan goed begrip, ook al doet de auteur nog zo zijn best. Vergeet dit, lees dan liever Millsap 2007.

Meredith, William, and Roger E. Millsap (1992). On the misuse of manifest variables in the detection of measurement bias. Psychometrika, 57, 289-311.

• abstract Measurement invariance (lack of bias) of a manifest variable Y with respect to a latent variable W is defined as invariance of the conditional distribution of Y given W over selected subpopulations. Invariance is commonly assessed by studying subpopulation differences in the conditional distribution of Y given a manifest variable Z, chosen to substitute for W. A unified treatment of conditions that may allow the detection of measurement bias using statistical procedures involving only observed or manifest variables is presented. Theorems are provided that give conditions for measurement invariance, and for invariance of the conditional distri- bution of Y given Z. Additional theorems and examples explore the Bayes sufficiency of Z, stochastic ordering in W, local independence of Y and Z, exponential families, and the reli- ability of Z. It is shown that when Bayes sufficiency of Z fails, the two forms of invariance will often not be equivalent in practice. Bayes sufficiency holds under Rasch model assumptions, and in long tests under certain conditions. It is concluded that bias detection procedures that rely strictly on observed variables are not in general diagnostic of measurement bias, or the lack of bias.

Millsap, Roger E. (2007). Invariance in measurement and prediction revisited. Psychometrika, 72, 461-473. fc

• Dit op zijn Presidential address gebaseeerde artikel probeert verdedigers van traditionele methodologie voor het onderzoeken van testbias, zoals Jensen 1980, Sackett, nog eens te overtuigen van de ernstige tekortkomingen daarin. Doet dat helaas door de recente ontwikkeling rond measurement invariance nog eens opieuw uit te leggen, in algebraïsche taal, met weliswaar een helder getallenvoorbeeld, maar geen grafische uitwerking van het verpletterende verschil met traditionele methodologie. De lezer moet vooral zelf de nodige conclusies trekken, wat voor een nieuwkomer in deze thematiek buitengewoon lastig is. Zie ook Wicherts en Millsap (in press).

Millsap, Roger E., and Howart T. Everson (1993). Methodology review: Statistical approaches for assessing measurement bias. Applied Psychological Measurement, 17, 297-334. [nog niet gezien, moet nog een pdf zien te bemachtigen, of gewoon een fotokopie]

• abstract Statistical methods developed over the last decade for detecting measurement bias in psychological and educational tests are reviewed. Earlier methods for assessing measurement bias generally have been replaced by more sophisticated statistical techniques, such as the Mantel-Haenszel procedure, the standardization approach, logistic regression models, and item response theory approaches. The review employs a conceptual framework that distinguishes methods of detecting measurement bias based on either observed or unobserved conditional invariance models. Although progress has been made in the development of statistical methods for detecting measurement bias, issues related to the choice of matching variable, the nonuniform nature of measurement bias, the suitability of current approaches for new and emerging performance assessment methods, and insights into the causes of measurement bias remain elusive

Millsap, Roger E., and Oi-Man Kwok (2004). Evaluating the Impact of Partial Factorial Invariance on Selection in Two Populations. Psychological Methods, 9, 93-115.

• "We say that a test fulfills measurement invariance across populations when individuals who are identical on the construct being measured, but who are from different populations, have the same probability of achieving any given score on the test (Meredith & Millsap, 1992)."
• De start is wonderlijk, de auteurs introduceren hier een begrip ‘selectie’ dat tenminste op het eerste gezicht niet anders is dan de test (meting) zelf: "In this article, we consider the use of a measure as a basis for selecting individuals. This selection seeks to use the measure to identify individuals who are in a desired range on the construct being measured. Selection in relation to an external criterion measure is not considered." [my emphasis, b.w.] selecteren = meten? Ik ben benieuwd. In hun verdere uitleg in deze alinea beschrijven zij een aanpak die mij heel bekend voorkomt uit een onderzoekje dat ik in 1968 heb gedaan: Wilbrink (1968 html)
• De vet gedrukte passage hierboven doet ook denken aan opvattingen over cesuurbepaling als een in de toets of test zelf besloten probleem. Criterium-gerefereerd toetsen zoals in publicaties van Mellenbergh en Van der Linden in Psychometrika en Applied Psychological Measurement in 1980 en eerder hebben datzelfde kenmerk. Het zou interessant kunnen zijn de theorie van Millsap en Kwok eens te contrasteren met die van Van der Linden in zijn overzichtsartikel in APM 1980. Maar handiger is om te bedenken dat Mellenbergh nu juist degene is die het begrip meetinvariantie heeft geïntroduceerd in zijn 1989, als ik het goed heb. Mijn vergelijking met criterium-gerefeerd meten is niet zomaar een ideetje: in mijn beide artikelen in 1980 in het Tijdschrift voor Onderwijsresearch neem ik juist de vooronderstellingen van onderzoekers zoals Mellenbergh en Van der Linden onder vuur. De argumenten in die beide artikelen zijn waarschijnlijk ook de argumenten die tegen de benadering van Millsap en Kwok zijn in te brengen, En dan bedoel ik niet het begrip meetinvariantie op zich, maar hun uitwerking naar accuratesse van ‘selectieve’ beslissingen. In essentie is simpelweg: als je al een simpel schema van terechte en onterechte beslissingen wilt hanteren, dan moet dat op zijn minst in termen van drempelnut. Dat nalaten, betekent dat drempelnutwaarden impliciet zijn bepaald door de vooronderstellingen in het versimpelde model. Dat is niet handig, en je ziet in dit artikel dat Millsap en Kwok op verschillende momenten wel met wegingen willen werken, dus met expliciteren van iets in de sfeer van nut (maar is dat dan nut zelf, of verwacht nut? Om maar eens een verwarring uit de literatuur van de zeventiger jaren te noemen).
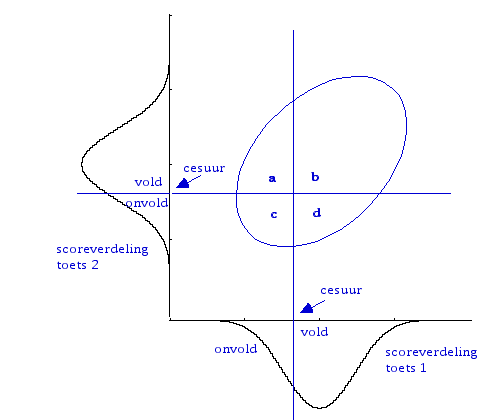• Een eenvoudig voorbeeld van het schema is te verkrijgen door een toets te splitsen in twee helften, en dan te tellen welke leerlingen op beide helften een onvoldoende scoren, alleen op de eerste helft, alleen op de tweede, of twee keer een voldoende. Dit levert in ieder geval geen metafysische problemen op met latente trekken. De figuur is Figuur 1 uit mijn Cesuurbepaling 1977 html.
• "We assume that two distinct populations are of concern in discussing invariance. The two populations are denoted the reference and focal populations (Holland & Thayer, 1988), a terminology found in the literature on differential item functioning. Ordinarily, the reference group refers to the majority group, or the higher scoring group. The focal group is the group that is presumably penalized by any lack of invariance." Dit is een riskante beschrijving omdat de referentiegroep best de lager scorende subgroep kan zijn. Denk voor hoger scorende focale groepen in de sfeer van onderwijs aan subgroepen met Aziatische of Joodse achtergrond.
• Figuur 1 is dan weer het afgezaagde plotje met false positives etcetera. (Vgl. figuur 3 in Petersen en Novick). Kijk, wat moeten we daar nu mee? Cronbach (1976, het themanummer dat opent met Petersen en Novick, 1976) kraakt er een kritische noot over maar is wel bereid om in dit versimpelde model mee te denekn, en hij doet dat goed, moet ik zeggen. Het gaat Millsap en Kwok om sophisticated statistische methoden (net als Millsap, 1997), en dan wordt een kunstmatige situatie bestudeerd die uit een grijze oudheid stamt en een versimpeling is van selectieproblematiek. Dat dichotomiseren komt neer op het impliciet hanteren van drempelnut in situaties waarin het evident is dat geleidelijk verlopende nutsfuncties gebruikt moeten worden. Maar goed, misschien komen Millsap en Kwok daar nog aan toe [nee, dus].
• Figuur 2 laat dan een focale groep zien die t.o.v. de referentiegroep lagere scores op de test krijgt dan in overeenstemming is met de ware status op het onderliggende construct (vgl. figuur 1a in Petersen en Novick, 1976, voor de vergelijkbare situatie van voorspellen van een criterium). Dit is een situatie die door Cleary (1968) voor voorspellen van een criterium is beschreven: zo partijdig als wat. Maar wat doen Millsap en Kwok hier precies, de score voorspellen op basis van de onderliggende trek? Waarom zou je zoiets willen? Het is een gedachte die ook is te vinden bij de ontwikkeling van tentamenmodellen (Van Naerssen, 1970; mijn SPA-model), omdat daar het binomiaalmodel voor de score van de individuele student het vertrekpunt is. Hebben Millsap en Kwok misschien ook zoiets in gedachten?
• Hoe zit dat eigenlijk, die vergelijking met voorspellen van een criterium op basis van een te st (Petersen en Novick, 1976) met een testscore zien als criterium voor de onderliggende ('ware') trek? Precies dat. Jammer dat we die onderliggende scores dus niet hebben, want die zijn 'latent.' Maar goed, stap daar even overheen, en dan hebben we gewoon de Petersen en Novick situatie, met dit verschil dat Millsap en Kwok werken met somscores die wat ingewikkeld zijn verkregen. Kijk even over de ingewikkeldheid heen: er is gewoon een reeks somscores beschikbaar, ga daar lekker mee aan de slag.
• Begrippen die de auteurs hanteren: succesverhouding of positive predicted value: proportie terecht geselecteerd onder de geselecteerden
• gevoeligheid de proportie geselecteerd onder degenen die bij perfecte selectie geselecteerd zouden worden (mijn herformulering)
• specificity laat ik maar even onvertaald, het is een raar begrip voor selectiepsychologen: de proportie niet geselecteerd van degenen die bij perfecte selectie niet geselecteerd zouden worden.
• accuracy: "Our primary interest lies in the accuracy of selection in two populations of individuals (e.g., males and females). Accuracy is defined with respect to the single common factor that underlies the measures that form the composite. For example, if we seek to use the composite measure to select the top 25% of individuals on the composite, accuracy can be evaluated by whether selection on the composite leads to selection of the top 25% on the common factor." Ik heb geen idee hoe nuttig dit begrip 'nauwkeurigheid is.' Ik zie wel. Impliciet is dit een kwestie van drempelnut, wat bij diagnosticeren in twee natuurlijke categorieën 'mannen' 'vrouwen' toepasselijk kan zijn, maar in het algemeen bij selectie niet ('geschikt' of 'on geschikt', hoe ook operationeel gedefinieerd, zijn geen natuurlijke categorieën).
• p. 94. "What is the intended use of the measure in practice? Once this is described, we can then ask whether particular violations interfere with this use." Dit gaan Millsap en Kwok dus niet uitwerken, en Borsboom Romeijn en Wicherts juist wèl. Dat is de relatie tussen beide artikelen: Millsap en Kwok beperken zich tot meetinvariantie op zich, Borsboom c.s. hanteren dezelfe accuratess-benadering om gevolgen voor echt selectieve beslissingen (gericht op optimaliseren van een criterim) te bestuderen. Dat betekent dat kritiek op de accuratesse-benadering van Millsap en Kwok dus ook de studie van Borsboom c.s. direct raakt.

Moran, M. P. (1990). The problem of cultural bias in personality assessment. In Reynolds, C. R., & Kamphaus, R. W. (Eds.) (1990). Handbook of psychological and educational assessment of children. Personality, behavior, & context. London: The Guildford Press 491-523.

Novick, Melvin R., & D. D. Ellis (1977). Equal opportunity in educational and employment selection. American Psychologist, 32, 306-320.

Novick, Melvin R., & Nancy S. Petersen (1976). Towards equalizing educational and employment opportunity. Journal of Educational Measurement, 13, 77-88.

• Dit is een dupliek op vier reacties op Petersen & Novick (1976) in hetzelfde themanummer.
• Een belangrijke nieuwe ontwikkeling presenteren zij onder het kopje ‘A new model for culture-fair selection.’. Het is een onbegrijpelijk stuk zoals het er staat, en de auteurs flirten daar ook mee: gebruik het computerprogramma CADA, en zelfs als je geen staartdeling kunt maken, kun je dan toch utiliteitsfuncties specificeren. CADA was in die jaren een bekend programma, ook in Nederland. Iets anders is dat ze een formule voor een functie van verwacht nut presenteren, een cumulatieve normaalverdeling, zonder de bijbehorende afleiding (die is te vinden in een niet gepubliceerd stuk, maar mogelijk ook in andere publicaties, zoals genoemd in mijn ../projecten/spa_ruling.htm, bv. Novick and Lindley 1978 in het Journal of Educational Measurement. Ze maken het nodeloos ingewikkeld. In een paar zinnen uitgelegd, gaat het immers om het volgende: Over het criterium moet een nutsfunctie worden gekozen. Dat is niet noodzakelijk een wiskundige formule, maar een desnoods uit de losse hand geschetste functie. Bijvoorbeeld hoeveel meer of minder iemand voor de organisatie waard is dan haar salaris bedraagt. Dat zal Borsboom aanspreken: er moet iets reëels corresponderen aan die functie, het moet niet een fictief geval zijn dat de opsteller een goed gevoel geeft. Dan is er een voorspellende verdeling nodig over die criteriumvariabelen, gegeven een op de selecterende test behaalde score. Ook daar zijn Novick en Petersen niet helder over: ze laten de conditie ten onrechte achterwege (ik kan hem niet vinden). Voor de gegeven score op de selecterende test willen we immers weten wat het verwachte nut is. Welnu, dat verwachte nut is gelijk aan de nutsfunctie over de criteriumvariabele, gewogen door de voorspellende criteriumscoreverdeling. Exact: de som over alle onderscheiden scores van de producten van de betreffende scorefrequentie met de betreffende score-utiliteit. Doe dat voor alle mogelijke scores op de selecterende test, en dan kan de functie van verwacht nut worden geplot. Ik geef toe, het is wat ingewikkelder dan ik heb voorgespiegeld, maar er hoeven in principe geen wiskundige functies aan te pas te komen. Het is natuurlijk niet verboden om handige functies te kiezen, en dat is wat Novick en Petersen doen. Het bemoeilijkt nodeloos hun presentatie van het ‘Nieuwe Model’. Dat een en ander, ook in eenvoudige casus, best wel complex wordt, is op de voet te volgen in de ontwikkeling van mijn spa-model (een verdere ontwikkeling van het tentamenmodel van Bob van Naerssen) http://www.benwilbrink.nl/projecten/spa_project.htm.
• Wie goed heeft opgelet, mist in de juist gegeven uiteenzetting het element ‘culture-fair’. Dat is het punt van het ‘goede gevoel’ dat onder CADA toch op een wat vreemde manier in de nutsfunctie over de criteriumvariabele kan worden gestopt. Niet doen, zou ik zeggen. Het is toch onherroepelijk zo dat een bepaald bedrijfsresultaat zoals gerealiseerd door een individuele medewerker, niet op zich iets heeft te maken met een subgroep waartoe die medewerker behoort. Het model van Novick en Petersen suggereert hier ten onrechte een eenvoudige oplossing. Die eenvoudige oplossing is er gewoon niet. Om met mogelijke partijdigheid in de selectieprocedure rekening te houden, of met beleid om uit bepaalde subgroepen meer personeelsleden of studenten te werven, moet er nog een doelvariabele worden gespecificeerd, en wordt het beslissingprobleem er eentje met tenminste twee doelvariabelen. Ik ga hier verder niet op in, maar vermeld wal dat er een uitbebreide literatuur is over multiple objective decisionmaking, wat ook zo'n beetje de meest gebruikelijke manier is van beslissen (kopen van een huis, een relatie aangaan, locatie van een vliegveld kiezen). Zie bijv. Keeney en Raiffa (1976). Decisions with multiple objectives: preferences and value tradeoffs. Wiley

Oppler, S.H., Campbell, J.P., Pulakos, E.D., & Borman, W.C. (1992). Three approaches to the investigation of subgroup bias in performance measurement: review, results, and conclusions. Journal of Applied Psychology, 77, 201-217.

Steven Osterlind (1987). Psychometric validity for test bias in the work of Arthur Jensen. In Sohan Modgil and Celia Modgil (Eds) (1987). Arthur Jensen. Consensus and controversy (191-198). The Falmer Press. (Shepard replies to Osterlind, Osterlind replied to Shepard, Gordon replies to Shepard Gordon replies to Osterlind, Scheuneman replies to Osterlind, Osterlind replies to Gordon, Osterlind replies to Scheuneman; 199-211) Petersen, Nancy S., & Melvin R. Novick (1976). An evaluation of some models for culture-fair selection. Journal of Educational Measurement, 13, 3-30.

• Absoluut een sleutelpublicatie. Analyseert in een samenhangend kader de belangrijkste dan beschikbare modellen, construeert drie tegenmodellen, en werkt uit dat alleen besliskundige modellen voor de problematiek van partijdigheid coherente oplossingen kunnen bieden. Probleem is alleen dat de keuze van nutsfuncties subjectief is, maar dat hoeft bij een democratisch proces van gedachten- en besluitvorming allerminst een beletsel te zijn (daar gaat het maatschappelijk debat juist over).
• from the abstract: "It is then suggested that the necessary level of compensatory treatment for disadvantaged persons can be guaranteed only through the formal use of an appropriate model based on the Von Neumann-Morgenstern theory of maximizing expected utility. Three of the models studied (Cleary, Einhorn and Bass, Gross and Su) are based on what we judge to be the correct conditional probability and are special cases of the Expected Utility Model, but each has limited applicability."

Rudner, Lawrence M., Pamela R. Getson & David L. Knight (1980). Biased item detection techniques. Journal of Educational Statistics, 5, 213-233.

• Limitations and advantages of the approaches in terms of their underlying assumptions and psychometric soundness are discussed.

Rudner, Lawrence M., Pamela R. Getson & David L. Knight (1980). A Monte Carlo Comparison of Seven Biased Item Detection Techniques. Journal of Educational Measurement, 17, 1-10.

Sawyer, R.L., Cole, N.S., & Cole, J.W.L. (1976). Utilities and the issue of fairness in a decision theoretic model for selection. Journal of Educational Measurement, 13, 59-76.

• Verdedigt het Cole (1973) model tegen de vernietigende analyse ervan door Petersen en Novick (1976), die ook geen goed woord over hebben voor deze verdediging (Novick & Petersen, 1976).

Janice Scheuneman (1979). A Method of Assessing Bias in Test Items A Method of Assessing Bias in Test Items. Journal of Educational Measurement, 16, 143-152

Janice Dowd Scheuneman (1982). A posteriori analysis of biased items. In Ronald A. Berk: Handbook of methods for detecting test bias (pp. 180-198). The Johns Hopkins University Press.

• "This chapter is organized into three main sections. The first will focus on sources of high bias indices. I will argue that the major sources of the differences reflected by these indices are, first, flaws in the item or test to which members of different subgroups are differentially sensitive abd, second, genuine differences between groups that nay or may not be the result of the cultural characteristics of the groups and that may or may not reflect valid differences in the ability being measured. Next, strategies for dealing with the bias results will be discussed. These will include blind screening of items, distractor analyses, and item review. Examples will be provided to show how the interpretation of certain results can also suggest appropriate action. In the last section of the chapter a practical step-by-step procedure will be suggested for conducting a review of those items identified as biased by a statistical procedure."
• I like this chapter very much. It shows how helpless the researcher is as soon as her statistical analysis results are in.
• A point of special interest is that bias may not be detectable at all at the level of the individual item. Scheueneman, p. 193: "More often, detecting the reasons for high bias indices will require reviewing groups of items, noting contrasts and similarities, in order to detect patterns that might account for unexpected performance differences. The cumulated weight that comes from selecting large numbers of a specific type of item will suggest problems that might not be evident from the review of any one of these items."

Janice Dowd Scheuneman (1979). An Experimental, Exploratory Study of Causes of Bias in Test Items. Journal of Educational Measurement, 24, pp. 97-118

• ".... argues that the causes of bias that are likely to be important, in the sense of a greater distortion of score differences between groups, are those that lie in characteristics common to several items in a test. Further, several such characteristics may be operating in a single test. Each such characteristic may, by itself, have relatively little impact, but the cumula- tive effect of several such characteristics may be significant. Such effects would be unlikely to be readily discernible by an investigator, particularly if items were examined in isolation. This may explain why item bias results have so frequently been found to be uninterpretable. "

Janice Dowd Scheuneman (1987). An argument opposing Jansen on test bias: The psychological aspects. In Sohan Modgil and Celia Modgil (Eds) (1987). Arthur Jensen. Consensus and controversy (155-170). The Falmer Press. (Reply by Gordon, Reply to Gordon; 171-175) Janice Dowd Scheuneman and Kalle Gerritz (1990). Using Differential Item Functioning Procedures to Explore Sources of Item Difficulty and Group Performance Characteristics. Journal of Educational Measurement, 27, 109-131.

• abstract Statistics used to detect differential item functioning can also reflect differen- tial strengths and weaknesses in the performance characteristics of population subgroups. In turn, item features associated with the differential performance patterns are likely to reflect somefacet of the item task and hence its difficulty, that might previously have been overlooked. In this study, several itemfeatures were identified and coded for a large number of reading comprehension items from the two admissions testing programs. Item features included subject matter content, various properties of item structure, cognitive demand indica- tors, and semantic content (propositional analysis). Differential item function- ing was evaluated for males and females and for White and Black examinees. Results showed a number of significant relationships between item features and indicators of differential item functioning-many of which were consistent across testing programs. Implications of the results for related areas of research are discussed.

• samenvatting
• reactie Cito

Schmitt, A.P., and Dorans, N.J. (1990), Differential item functioning for minority examinees on the SAT. Journal of Educational Measurement 27, 67-80.

Shepard et al. (1981). Comparison of procedures for detecting test-item bias with both internal and external ability criteria. Journal of Educational Statistics, 6, 317-375.

Lorrie Shepard (1982). Definitions of bias. In Ronald A. Berk: Handbook of methods for detecting test bias (pp. 9-30). The Johns Hopkins University Press.

• "The purpose of this chapter is to provide a conceptual definition of item bias. To do this, I review two closely related topics: the larger issue of culture-fair testing and bias in selection. Together, these provide a context for understanding what is meant by bias in individual test items."

Lorrie Shepard, Gregory Camilli and David M. Williams (1984). Accounting for statistical artifacts in item bias research. Journal of Educational Statistics, 9, 93-128. pdf

Lorrie A. Shepard (1987). The case for bias in tests of achievement and scholastic aptitude. In Sohan Modgil and Celia Modgil (Eds) (1987). Arthur Jensen. Consensus and controversy (177-190). The Falmer Press. Lorrie Shepard, Gregory Camilli and David M. Williams (1985). Validity of Approximation Techniques for Detecting Item Bias Validity of Approximation Techniques for Detecting Item Bias. Journal of Educational Measurement, 22, 77-105.

Gary Skaggs, Robert W. Lissitz (1992). The Consistency of Detecting Item Bias across Different Test Administrations: Implications of Another Failure. Journal of Educational Measurement, 29, 227-242.

Stanley (1971). Predicting college success of the educationally disadvantaged. Science, 171, 640-647. Reprinted in Aiken (1973: 130).

Martha L. Stocking, Ida Lawrence, Miriam Feigenbaum, Thomas Jirele, Charles Lewis, Thomas Van Essen (2002). An Empirical Investigation of Impact Moderation in Test Construction. Journal of Educational Measurement, 39, 235-252.

• Sommige verschillen tussen subgroepen zijn irrelevant voor het gemeten construct, en zouden dus verwijders moeten worden. Het verwijderen van partijdigheid dus. Technieken, beschouwingen.

Thomas, G.E. (1980). Race and sex group equity in higher education: institutional and major field enrollment statuses. American Educational Research Journal, 17, 171-181.

Thorndike, Robert L. (1971). Concepts of culture-fairness. Journal of Educational Measurement, 8, 63-70.

• Thorndike presenteert hier een model gebaseerd op de gedachte dat het eerlijk is wanneer uit een subgroep proportioneel zoveel kandidaten worden toegelaten als in overeenstemming is met de kans op succes voor ongeselecteerde kandidaten uit die subgroep. Ik formuleer het wat onhandig, maar het idee is ook een beetje onhandig. En dat blijkt, want het model van Thordndike wordt door Petersen en Novick (1976) afgeserveerd als innerlijk tegenstrijdig.
• Het idee dat kansen op toelating in goede verhouding moeten staan tot kansen op succes, over de diverse subgroepen, blijkt namelijk niet te verenigen met de omgekeerde eis, dat kansen op terecht te worden afgewezen over subgroepen heen in dezelfde relatie moeten staan tot de kans voor ongeselecteerde kandidaten om te falen op het criterium.
• Ook dat klink allemaal heel ingewikkeld. Er is een interessante parallel met lotingskansen bij een numerus fixus. Voor de gewogen loting is een formule opgesteld die de inlotingskansen voor subgroepen met bepaalde cijfergemiddelden op het eindexamen in gewenste verhouding tot elkaar stelt. Ik meen me te herinneren dat het mogelijk is aan te tonen dat er dan rare dingen gebeuren met de verhoudingen tussen uitlotingskansen. Trouwens, ook met de inlotingskansen gebeuren vreemde dingen, afhankelijk van de verhouding van het aantal beschikare plaatsen tot het aantal kandidaten. Zie mijn 1975 html . Nu ik er even over nadenk: zou de gwogen loting coherenter zijn vorm te geven door de weging op besliskundige wijze, dus via nutsfuncties, te doen? Voorzover mij bekend, is dit in de literatuur een witte vlek.

Toepasbaarheid van psychologische tests bij allochtonen. Rapport van de testscreeningscommissie ingesteld door het LBR in overleg met het NIP. Utrecht: Landelijke Bureau Racismebestrijding, 1990.

Henny Uiterwijk heeft bij het Cito interessante studies gedaan, die zijn helaas (behalve de samenvatting van zijn proefschrif) niet op de site avn het Cito beschikbaar, en ik heb ze nog niet in hard copy verzameld.

• Uiterwijk, H., en Vallen, T. (1992). Een toets mag moeilijk zijn, maar niet onbedoeld moeilijk. De toetsesultaten van allochtone leerlingen en de 'itembias'. Tijdschrift voor Onderwijs en Opvoeding, 51, 7, 15-21.

• Uiterwijk,J.H. Item- en testbias in de Eindtoets Basisonderwijs 1987. Arnhem: Cito; 1990. 111 blz. (Onderzoeksrapport basis- en speciaal onderwijs Nr.1); 90/176.

• H. Uiterwijk (1994). De bruikbaarheid van de Eindtoets Basisonderwijs voor allochtone leerlingen. Proefschrift. Arnhem: Cito.
  • samenvatting pdf. Er bestaat geen voor download beschikbare digitale versie van dit proefschrift.
  • Wat mij trof, bij snel doornemen, is hoe ontzettend moeilijk het is om zinvolle empirische data te krijgen. Eigenlijk is dat onbegonnen werk, maar dat zal ook wel de ervaring van Uiterwijk zijn geweest. Er gebeurt zo ontzettend veel, de leerlingen zwermen uit, met twee adviezen op zak, waar ouders nog weer eens overheen gaan, en dan komen die koters in heel andere onderwijssituaties terecht dan ze gewend waren. Dat levert geen keurig nette gecontroleerde gegevens op waarmee je wat zou kunnen gaan rekenen aan bias-modellen.

• H. Uiterwijk en T. Vallen (1997). Onderzoek naar bias voor allochtone leerlingen in de Cito-Eindtoets Basisonderwijs. Pedagogische Studiën, 74, 21-32.

• H. Uiterwijk and T. Vallen (2005). Linguistic sources of item bias for second generation immigrants in Dutch tests. Language Testing, 22, 211-234.
  • hier bestaat een pdf van, wie deze graag toegestuurd wil hebben, stuur mij een mailtje
  • Dit artikel adresseert het ontwerpen van toetsvragen. Wat is het dat een toetsvraag partijdig kan maken? Bestaat daar inzicht in, dan is het mogelijk er bij het ontwerpen rekening mee te houden.

• H. Uiterwijk and T. Vallen (2003). Test bias and differential item functioning: A study on the suitability of the cito primary education final test for second generation immigrant students in The Netherlands. Studies in Educational Evaluation, 29, 129-143. [niet gezien, moet ik nog zien te veroveren.]

Wicherts, J. M., Dolan, C. V., & Hessen, D. J.(2005). Stereotype threat and group differences in test performance: A question of measurement invariance. Journal of Personality and Social Psychology, 89, 696-716.

Jelte M. Wicherts, Conor V. Dolan, David J. Hessen, Paul Oosterveld, G. Caroline M. van Baal, Dorret I. Boomsma, Mark M. Span (2004). Are intelligence tests measurement invariant over time?Investigating the nature of the Flynn effect. Intelligence 32) 509–537.

Jelte M. Wicherts & Roger E. Millsap (2009). The absence of underprediction does not imply the absence of measurement bias. American Psychologist, 64, 281-283.

• Reacts to Sackett, P. R., Borneman, M. J., & Connelly, B. S. (2008). High-stakes testing in higher education and employment: Appraising the evidence for validity and fairness. American Psychologist, 63, 215–227.
• Een hoeksteen in dit betoog is gewoon weggelaten onder verwijzing naar Millsap 2007, dat helaas een erg technisch artikel is. Ik trok uit Wicherts en Millsap de verkeerde conclusie: dat twee bronnen van partijdigheid elkaar neutraliseren. De auteurs maken onvoldoende duidelijk dat overprediction geen vorm van partijdigheid is, maar een gevolg van gebruik van een eerlijke test waarop subgroepen gemiddeld verschillen.
• Sackett, P. R., Borneman, M. J., & Connelly, B. S. (2009). Responses to issues raised about validity, bias, and fairness in high-stakes testing. American Psychologist, 64(, 285-287

Wilbrink (1968). Multiple discriminant analyse van de Cattell 16 P.F.Q. voor studenten in zeven studierichtingen aan de T. H. E. Eindhoven: Groep Onderwijsresearch. (verslag stage-onderzoek, niet gepubliceerd) html

• Laat zien hoe op basis van een persoonlijkheidsprofiel een goede voorspelling is te doen van de studierichting die aankomende studenten hadden gedaan, binnen de TH Eindhoven. Niet onderzocht is of studenten die qua persoonlijkheid niet goed 'passen' bij de gekozen studie, in hun studieloopbaan daar dan ook moeilijkheden van ondervinden (ik geloof niet dat ik ooit dergelijk odnerzoek heb gezien, hoewel er in Amerika werkelijk heel grootschalige studies zijn gedaan). De reden om geen publicatie te zoeken voor dit onderzoekje was dat in 1968 er veel beroering was in de samenleving, waarbij ik het niet voor onmogelijkhield dat misbruik kon worden gemaakt van een onderzoek dat aantoonde hoe eenvoudig het eigenlijk is om scholieren te 'sorteren' naar bepaalde vervolgopleidingen. Partijdigheid in extreme vorm, zou je kunnen zeggen. Achteraf is het makkelijk om te constateren dat ik spoken zag, maar in die jaren hadden de spoken namen: Posthumus, Maris en Van Os, regeringscommissarissen die opdrachten voor herstructurering van het universitaire bestel hadden.

Meer literatuur ouder, technischer, meer van hetzelfde)

P. W. Holland and D. T. Thayer (1988). Differential item performance and the Mantel-Haenszel procedure. In H. Wainer and H. Braun: Test validity. Erlbaum. (pp. 129-146). questia

Paul W. Holland and Howard Wainer (1993). Differential Item Functioning. Erlbaum. questia

• DIF-analysis is a technique for the specialist, and for the adequate development of standardized tests/examinations. It is not a kind of technique (there are many differents methods!) that one might apply on automatic pilot, because DIF-analyses identify many 'biased' items falsely, and in all other cases it is, more often than not, unclear what might be the reason the item is biased. On researching the reasons why items might be biased, see for example Scheunemann, 1982.

Xiaohui Wang, Eric T. Bradlow, Howard Wainer and Eric S. Muller (2008). A Bayesian method for studying DIF: A cautionary tale filled with surprises and delights. Journal of Educational and Behavioral Statistics, 33, 363-384.

• If you are not already an expert in this field, do not try to become one by studying this article.

      http://www.benwilbrink.nl/literature/bias.htm