In 1970 presenteerde Van Naerssen zijn tentamenmodel, dat de belofte in zich droeg een instrument te worden om studeergedrag te kunnen verklaren als afhankelijk van de toets(situatie), en om toetsen en examens zo te kunnen inrichten dat deze met een minimum aan verliestijden zijn te behalen. Dit tentamenmodel is een van de eerste pogingen om beoordelen in het onderwijs te modelleren als een proces van keuzen van zowel studenten als docenten, met technieken uit de economische besliskunde. De uitdaging is nu om dit tentamenmodel verder te ontwikkelen tot een algemeen toetsmodel (ATM) zodat het ook in andere situaties is te gebruiken, en om het te verbinden met de micro-economische theorie en Coleman's (1990) theorie van sociale systemen.
In het tentamenmodel is de optimale strategie voor de student om met een minimum aan studietijd, inclusief eventuele herkansingen, voor het tentamen te slagen. Een generalisatie van dit criterium is: minimaliseren van de tijd nodig om een bepaald verwacht totaal nut te realiseren over twee of meer toetsen (of over een toets en vrije tijd). Dit criterium vraagt om een model waarmee het mogelijk is indifferentiecurven op te stellen. Werken met indifferentiecurven is een grondtechniek in de micro-economie (Odink & Schoorl, 1984); ook Coleman gebruikt deze techniek, voor deze curven neemt hij de wiskundige vorm van Cobb-Douglas functies aan. Het paper geeft de details hoe het ATM uitmondt in indifferentiecurven, en dat onafhankelijk van elkaar doet langs wiskundige weg, en door simulatie.
De studiestrategie van de leerling berust op enige vorm van voorspelling van de te behalen toetsresultaten gegeven de stofbeheersing nu, of na extra studietijd. Van Naerssen introduceerde de proeftoets en een daarop behaalde score als informatie over de eigen stofbeheersing. Die informatie is algemeen te operationaliseren als de waarschijnlijkheid (likelihood) voor de stofbeheersing, gegeven het proeftoetsresultaat. De voorspelling van de toetsscore is dan een betabinomiaalverdeling (Wilbrink, 1978; Van den Brink, 1982).
Voor Van Naerssen is een complex leermodel met een aantal persoonlijke parameters essentieel; in zijn tentamenmodel zit het probleem immers in de herkansingen met tussentijds vergeten en weer opnieuw leren. Een algemeen model doet het met een eenvoudig leermodel zonder vergeten; een herkansing is eenvoudig een 'andere' toets.
Voor het ATM is een nutsfunctie van de leerling over toetsscores nodig. In het ATM is iedere functie toegestaan, maar de vorm van de nutsfunctie is bij uitstek de weerspiegeling van de condities die een overgangsregeling of examenregeling oplegt. Zie Van der Gaag, 1990, voor mogelijkheden leerlingen nutsfuncties te laten opstellen. Met de nutsfunctie en de voorspelling van toetsscores is het verwachte nut over te investeren studietijd te berekenen. De nutsfunctie en de functie van het verwachte nut zijn verschillende functies over resp. scores en tijdbesteding (Wilbrink, 1980), een onderscheid dat in besliskundig onderzoek over toetsen niet altijd is gemaakt.
Omdat het verwachte nut toeneemt met extra te investeren studietijd, heeft deze functie geen bruikbaar optimum om die investering van af te laten hangen. Wat nog mist is dat tijd kostbaar is, en alternatief besteed kan worden. Het gaat er in essentie om het maximale verwachte nut te vinden dat met het beschikbare tijdsbudget, 24 uur per dag, is te behalen. Dat probleem is te reduceren tot deelproblemen: hoe een beschikbaar tijdsbudget optimaal te verdelen over de voorbereiding op twee toetsen. Met voor beide toetsen de functie van verwacht nut over studietijd als gegeven, zijn indifferentiecurven te construeren, waaruit voor een gegeven verwacht somnut is af te lezen hoe de tijd over twee toetsen zo te verdelen dat deze minimaal is. Is dat minimum gelijk aan het beschikbare budget, dan correspondeert daarmee het maximale verwachte nut.
Met dit ATM is een verbinding gemaakt tussen toetstheorie en micro-economische theorie. Dit ATM is een potentieel belangrijk instrument bij het ontwerpen (en evalueren) van toetsen en examens, en het beheersen van studievertraging en uitstelgedrag. Een parallel-paper in de sectie Hoger Onderwijs geeft gebruiksmogelijkheden, en analyses met empirische data .
Het model is geïmplementeerd in een computerprogramma waarmee de verwachte effecten van soms complexe varianten van toetssituaties kunnen worden afgebeeld. Omdat het model bijna uitsluitend op basis van simulatie is te ontwikkelen (het paper gaat daar dieper op in), is het mogelijk het in korte tijd aan docenten uit te leggen, die het dan kunnen toepassen. De wiskundige vorm van het model is onafhankelijk van de simulatie: de wiskunde voegt aan het model geen betekenis toe, maar maakt het mogelijk (omvangrijke) problemen te berekenen ipv. te simuleren.
Het programma is beschikbaar voor Macintosh- (menugestuurd en met grafische output), en DOS- systemen (voorshands zonder de genoemde opties) .
Brink, W. P. van den (1982). Binomiale modellen in de testleer. Proefschrift Universiteit van Amsterdam.
Coleman, J. S. (1990). Foundations of social theory. London: Belknap.
Gaag, N. van der (1990). Empirische utiliteiten voor psychometrische beslissingen. Proefschrift Universiteit van Amsterdam.
Naerssen, R. F. van (1970). Over optimaal studeren en tentamens combineren. Openbare les. Amsterdam: Swets & Zeitlinger. html
Naerssen, R. F. van (1976). Het derde tentamenmodel met een toepassing. Tijdschrift voor Onderwijsresearch, 1, 161-171.
Odink, J. G., & Schoorl, J. S. (1984). Inleiding tot de micro-economie. Groningen: Wolters-Noordhoff.<
Wilbrink, B. (1978). Studiestrategieën. Amsterdam: SCO-Kohnstamm Instituut. html
Wilbrink, B. (1980). Enkele radicale oplossingen voor kriterium gerefereerde grensscores. Tijdschrift voor Onderwijsresearch, 5, 112-125. html
Paper Onderwijsresearchdagen 1995 Groningen
Ben Wilbrink
SCO-Kohnstamm Instituut van de Universiteit van Amsterdam
Omdat toetsen in het onderwijs iets anders is dan testen voor diagnostische doeleinden of voor personeelsselectie, is er voor dat toetsen een andere methodologie nodig dan die uit de testleer. Dat was voor Van Naerssen (1970) de overweging om een tentamenmodel te ontwikkelen als basis voor een docimologie of examenkunde. Zo'n model zou psychometrische technieken kunnen gebruiken, maar zelf niet tot de psychometrie behoren. Het model komt op het volgende neer. De student die voor iedere toets moet slagen, eventueel na herkansingen, zal proberen de daarvoor nodige tijd te minimaliseren. Het minimum hangt af van enkele parameters die specifieke waarden hebben voor de examenregeling, de toets, het leren en vergeten, en de student. Latere publicaties, tot en met het derde tentamenmodel (Van Naerssen, 1976), zijn geen pogingen geweest om het model een algemener vorm te geven, maar om dit model voor conjunctieve examenregelingen te verfijnen. Conjunctief betekent dat ieder examenonderdeel voldoende moet zijn.
Van Naerssen was geïnspireerd door de besliskundige benadering in de testleer, waarvan vooral zijn proefschrift over de selectie van chauffeurs getuigt. De klassieke vindplaats voor de besliskundige testleer is de studie uit 1957 van Cronbach en Gleser. Typerend voor het werk van Cronbach en Gleser is dat de beslisser dezelfde is als de testafnemer; in het onderwijs is dat de docent. Dat is een theoretische vooringenomenheid, zoals blijkt in het contrast met de benadering die Van Naerssen kiest. Hij gaat juist uit van de student als beslisser. De student volgt een strategie om zo weinig mogelijk in te teren op het schaarse eigen kapitaal: tijd. Zeker, ook de docent kan optimaliseren, maar doet er verstandig aan dat te doen door de parameters van het onderwijs en de toets zo te veranderen dat de studenten hun studiestrategieën in de gewenste richting aanpassen.
Na Van Naerssen's pleidooi voor een tentamenmodel zijn de ontwikkelingen in de testleer doorgegaan in de lijn van Cronbach & Gleser. Een studie van Davis, Hickman & Novick (1973) zette vele pennen in beweging over het probleem hoe optimale grensscores besliskundig te bepalen. Vrijwel zonder uitzondering gaan al deze studies, ook de taltrijke Nederlandse, uit van de testafnemer als beslisser: het gedrag van studenten doet er in het geheel niet toe. Voor toetsen waar leerlingen verondersteld worden zich op voor te bereiden, is dat geen adequate benadering. Deze benadering is behept met methodologische misvattingen, o.a. over het karakter van nutsfuncties (waarover straks meer), waardoor ten onrechte de conclusie is getrokken dat de besliskundige benadering een veredelde vorm van betrouwbaarheidsanalyse zou zijn, (Van der Linden, 1980) wat een abrupt het einde aan dit type onderzoek markeerde.
Een generalisatie van Van Naerssen's tentamenmodel zou kunnen leiden tot een ware examenkunde waar op de onderwijsvloer profijt mee is te behalen, en tot een herstel van de besliskundige benadering voor het beoordelen in het onderwijs.
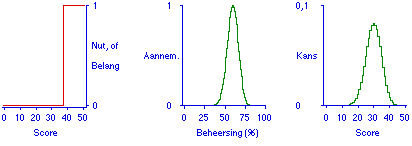
Van Naerssen veronderstelt dat de student de eigen beheersing kent, en met die kennis de optimale strategie zal kiezen. Gegeven de stofbeheersing is de voorspelling voor de toetscore de binomiaalverdeling. In werkelijkheid heeft de student maar een vaag idee over hoe hoog die eigen stofbeheersing is. Dat vage idee is te operationaliseren als een score behaald op een proeftoets die op dezelfde manier is samengesteld als de toets, maar niet per se dezelfde lengte hoeft te hebben. Gegeven die proeftoetsscore, kan de aannemelijkheid (likelihood) voor de stofbeheersing worden opgesteld: bij een binomiaalmodel voor de toetsscore is dat de betaverdeling met als parameters het aantal goed, resp. fout op de proeftoets. De voorspelling voor de toetsscore is de betabinomiaalverdeling met dezelfde parameters. De wiskunde is standaard (Wilbrink, 1978; van den Brink, 1982), het idee van proeftoetsscores als operationalisatie van de informatie van de student is een verdere uitwerking van Van Naerssen suggestie (1974, appendix). In een voorbeeld ziet een en ander er als volgt uit (Figuur 1).

Figuur 1. Voorspelling op basis van proeftoetsresultaat.
De verwachte slaagkans voor de student in het voorbeeld van Figuur 1 is 0,05. Voor conjunctieve toetsen is dat gelijk aan het verwachte nut, omdat de nutsfunctie voor de student in dit geval de afgebeelde drempelfunctie is. Dat introduceert het volgende onderwerp: nutsfuncties.
De voorspellende scoreverdeling is geen ideale basis voor beslissingen. Van Naerssen vertaalt die verdeling naar de slaagkans, omdat voor conjunctieve toetsen alleen de slaagkans telt. Om hier te kunnen generaliseren is de nutsfunctie van de student nodig: de waarde die de student toekent aan mogelijke scores. Onder het conjunctieve model is dat de drempelfunctie (figuur 1 links). Vanzelfsprekend is dat niet, omdat de literatuur voorbeelden van analyses met drempelnut geeft waarbij de docent de eigenaar van die functie is, of analyses waar het helemaal niet gaat om wat in de economische besliskunde een nutsfunctie heet, maar om een functie van het verwachte nut.
(noot: Nog weer een ander gebruik: Coleman (1990) gebruikt de term nutsfunctie voor wat in de literatuur en in dit paper een indifferentiecurve wordt genoemd.)
Een ander belangrijk verschil is dat in de literatuur drempelnut meestal over ware scores gaat, terwijl het in het tentamenmodel gaat om te behalen scores.
In de literatuur zijn nutsfuncties vaak subjectieve functies. Maar bij conjunctieve tentamens is er geen vrijheid om de nutsfunctie naar eigen voorkeur te kiezen: de aftestgrens is volledig bepalend, de nutsfunctie is voor alle studenten gelijk aan de drempelfunctie. In het algemeen is het zo dat uit de geldende examenregeling een 'neutrale' nutsfunctie valt af te leiden. Een voorbeeld is gegeven in Figuur 2. Persoonlijke nutsfuncties wijken op een karakteristieke manier af van de neutrale functie: voor de hoge scores zullen studenten, evenals voor hoge geldsommen, risico-mijdend zijn, voor de lagere scores risico-zoekend. De ogief in Figuur 2 geeft zo'n persoonlijke nutsfunctie weer.
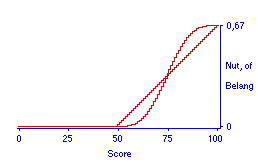
Figuur 2. Neutrale (lineaire) en persoonlijke (ogief) nutsfunctie over toetsscores (scores beneden 45 hebben geen waarde, andere scores zijn volledig compenseerbaar).
[Noot: deze figuur is gelijk aan Figuur 9 in het andere ORD-paper over Studiestrategieën.]
juni 2003: De objectieve lineaire functie krijgt in dit paper geen interpretatie, in het parallel-paper is dat wel het geval, zie de aantekening daar bij Figuur 8. De afgebeelde nutsfunctie is correct wanneer het gaat om een toets waarbij de score 75 het referentiepunt is (gemiddeld over dit soort toetsen moet de student 75 punten halen), en plus of min 25 punten compenseerbaar zijn. Het is niet handig om dit volledige compensatie te noemen: tenslotte is het zo dat de student met een score 49 voor dit onderdeel een onvoldoende resultaat behaalt, daar is de regeling dus conjunctief van karakter.
Figuur 3 geeft een voorspelling waarbij de persoonlijke nutsfunctie uit Figuur 2 is gebruikt. Het gaat niet om de kansverdeling voor de score zelf, maar om de weging van die verdeling met de nutsfunctie, in dit geval resulteert dat in het verwachte nut 0,15.
De weging impliceert dat bij een nutsfunctie die lineair is over het hele scorebereik, het verwachte nut gelijk is aan de verwachte (proportionele) score.
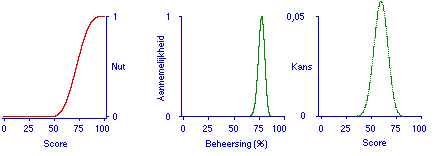
Figuur 3. Voorspelling met persoonlijke nutsfunctie: het verwachte nut is 0,15.
De student die een optimale studiestrategie zoekt moet ook kunnen voorspellen wat extra studietijd oplevert. Er is dus een leermodel nodig. Dat kan een eenvoudig model zijn, zoals Van Naerssen in zijn eerste tentamenmodel hanteerde: iedere keer doornemen van de stof kost evenveel tijd, en daarin wordt telkens hetzelfde deel van de dan nog niet gekende stof geleerd; 'hetzelfde deel' noem ik de (leer-)capaciteit van de leerling. Voor toepassingen van het model is de precieze aard van het leermodel van ondergeschikt belang: zolang leerprocessen voor verschillende toetsen ongeveer gelijk zijn, kan het ATM zinvolle vergelijkingen tussen die toetsen maken. (noot: In het model moet niet alleen de leerfunctie zelf, maar ook zijn inverse worden gebruikt. Het is dus niet eenvoudig mogelijk in het computerprogramma deze leerfunctie te vervangen door een andere.)
Wanneer naast de proefoetsscore ook bekend is hoe vaak de stof al is doorgenomen, is de aannemelijkheid voor de capaciteit te bepalen, en kan deze worden gebruikt om de voorspellende toetsscoreverdeling na extra studietijd te berekenen. Figuur 4 laat dit zien aan de hand van een voorbeeld.
juni 2003. Het algemene toetsmodel blijkt veel later, in 2002, ook zonder deze 'capaciteit' als parameter te kunnen, en zonder poging ook het leerproces te simuleren. Vervolgens is het dan mogelijk om het leermodel een zelfstandige plaats te geven, zodat er een grote vrijheid ontstaat om bijvoorbeeld leercurven als lijst op te geven, zonder wiskundige formalisering. Een kwestie van evolutie van het model, niet van een foute conceptie in 1995.
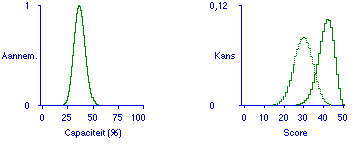
Figuur 4. Aannemelijkheid voor de capaciteit, en voorspellingen voor het toetsresultaat: nu en na verdubbelde tijdsinvestering. Gegeven zijn: proeftoetsscore van 30 uit 50; en nutsfunctie cumulatieve beta 70, 30. Het voor de laatste voorspelling verwachte nut is 0,90.
Het verwachte nut voor de voorspelling (strategie) in Figuur 4 is 0,90. Dat verwachte nut krijgt pas betekenis in vergelijking met andere toetsen of bezigheden die mogelijk in korter tijd meer nut opleveren, of in langer tijd minder nut. De voorspelbaarheid van toetsresultaten hangt zowel af van de beschikbare informatie, zeg de proeftoetslengte, als van de lengte van de toets. Tabel 1 laat zien hoe de kwaliteit van de informatie vooraf, dus de doorzichtigheid van de toetssituatie, meer bepalend is voor het verwachte nut dan de toetslengte. Toetslengte speelt wel een rol, maar is niet belangrijker dan de informatie vooraf. Van Naerssen vond bij analyses met het tentamenmodel dat toetslengte weinig verschil maakte.
(noot: In 1974, in een analyse met zijn tweede tentamenmodel, komt van Naerssen tot een andere conclusie (p. 445): It turns out that the length of the preliminary test, with which the student estimates his true score, is just as important as the length of the examination itself.)
Tabel 1. Verwacht nut bij variërende proeftoets- en tentamenlengte
_________________________________________________
tentamenlengte
25 50 100
__________________________________________
proeftoets- 25 0,80 0,83 0,85
lengte 50 0,86 0,90 0,93
100 0,90 0,94 0,96
_________________________________________________
Het ATM is vrijwel geheel te ontwikkelen via simulatie. Het enige wiskundig gespecificeerde onderdeel is dan het leermodel, maar ook het leren zelf wordt gesimuleerd. In de ontwikkelde computerprogrammatuur zijn beide analyses, de wiskundige en de simulatie, tegelijk mogelijk. Het voordeel van de ontwikkeling van het model via simulatie is dat het op deze manier makkelijk is uit te leggen aan bijvoorbeeld docenten. Het voordeel van de wiskundige vorm is zijn snelheid. Het voordeel van beide beschikbaar te hebben is dat zij een controle op elkaars juistheid vormen. Figuur 5 laat zien hoe een simulatieresultaat is te plotten, met op de achtergrond de theoretisch berekende verdelingen.
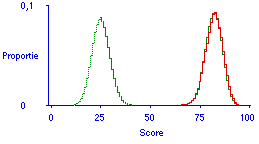
Figuur 5. Voorbeeld van resultaten van simulatie, vergeleken met de theorie (uitvoer van computerprogrammatuur). (20000 gesimuleerde scores, voorspelling voor verzesdubbelde tijdbesteding, proeftoets 250 goed uit 1000).
Omdat nu voor iedere hoeveelheid extra studietijd een voorspelling en het bijbehorende verwachte nut is te berekenen (of te simuleren), kan over het hele leertraject het bijbehorende verwachte nut worden bepaald en geplot. Figuur 6 geeft de het verwachte nut als functie van de studietijd voor de situatie waarin de nutsfunctie lineair is, in dit geval is de functie voor het verwachte nut gelijk aan de leercurve. Figuur 7 geeft de situatie bij conjunctief toetsen, dus bij drempelnut; hier is het verwachte nut gelijk aan de slaagkans. Een snelle evaluatie van het bieden van compensatie is gegeven in de Figuren 8 en 9, waaruit blijkt dat het bieden van een beetje compensatie op zich, al het andere gelijkblijvend, de koppeling tussen inspanning en resultaat verzwakt. Al het andere blijft echter niet gelijk, omdat compensatie betekent dat er een bonus is te behalen, dus dat het te verkrijgen nut groter wordt (zie het parallel-paper). Deze set van 4 functies voor het verwachte nut laat zien dat dit model in beginsel houvast biedt aan docenten die hun toets of examen zó willen regelen dat studenten een bepaald niveau nastreven bij het voorbereiden op toetsen.
Psychometrici zijn verstrikt geraakt in het onderscheid tussen nutsfuncties en functies voor het verwachte nut, omdat zij het onderscheid tussen beide niet voldoende expliciet hebben gemaakt. Bij optimale grensscorebepaling veronderstellen psychometrici dat nutsfuncties elkaar moeten snijden wil er een optimale grensscore zijn. Dat zou inderdaad gelden voor functies van verwachte nut, maar voor nutsfuncties is dat geen zinnig idee (zie Wilbrink, 1980, voor een uitwerking).
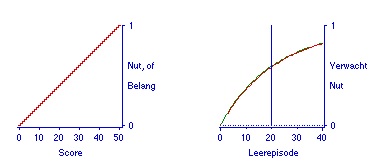
Figuur 6. Verwacht nut over het hele leertraject, ook het al afgelegde deel (t/m 20). Bij deze lineaire nutsfunctie is het tevens de leercurve.
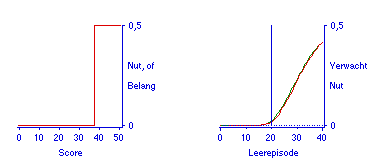
Figuur 7. Bij dit drempelnut is de functie van het verwachte nut tevens de functie van de slaagkans.
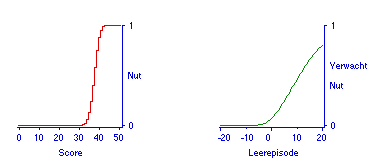
Figuur 8. Lichte compensatie. Vergelijk de conjunctie in Figuur 7.
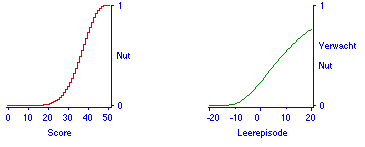
Figuur 9. Nog meer compensatie. Door het afwaarderen van scores vlak boven de conjunctieve aftestgrens vlakt de functie voor het verwachte nut af.
Het verwachte nut over een leertraject heen laat zien wat extra tijdsbesteding oplevert. De curve zelf geeft weinig aanwijzingen over wat een optimale strategie kan zijn. Meer investeren levert altijd een hoger verwacht nut op. Het optimum ligt daar waar de extra investering en het extra verwachte nut de student evenveel waard zijn. Dat punt zou bij ogief-vormige curven bereikt kunnen worden aan het eind van het traject met de grootste stijging, maar zeker is dat niet. Wat wèl zeker is: tijd is schaars. Het zou al een belangrijke verdienste voor een ATM zijn deze kosten van de voorbereiding op tentamens zichtbaar te kunnen maken. Dat kan door het verwachte nut van alternatieve tijdsbesteding in beeld te brengen. Het ligt dan voor de hand om te beginnen met alternatieve tijdsbesteding binnen de studie zelf, zoals voor een gelijktijdig af te leggen andere toets. Maar ook het nut van andere tijdsbesteding is af te zetten tegen dat van studietijd. Welnu, de klassieke manier om zo'n vergelijking te maken is in de vorm van indifferentiecurven, bijvoorbeeld voor twee toetsen die verschillen in doorzichtigheid, zoals blijkt uit de functies voor het verwachte nut in Figuur 10.
Figuur 11 helpt in de interpretatie van indifferentiecurven: hier is een toets tegen zichzelf geplot, zodat de optimale verdeling van tijd tussen de voorbereiding op deze identieke tweelingtoets op de diagonaal vanuit de oorsprong komt te liggen. Figuur 12 plot de indifferentiecurven voor de doorzichtige versus de ondoorzichtige toets. De Engel-curve rechts in de figuur verbindt de punten waar het gegeven verwachte nut het kleinst mogelijke tijdsbeslag vergt. De Engel-curve geeft het pad voor de optimale strategie voor de voorbereiding op deze twee toetsen. De figuur laat zien dat voor ieder reëel beschikbaar tijdsbudget de optimale strategie is om allereerst ongeveer 70 uur te reserveren voor de voorbereiding op de doorzichtige toets, en de rest voor de ondoorzichtige toets.
Met deze techniek van indifferentiecurven is het criterium van Van Naerssen in essentie gelijk gebleven: optimale besteding van schaars beschikbare tijd. Met de techniek van indifferentiecurven is het gelukt om los te komen van de specifieke tentamenmodel-situatie van onbeperkt te herkansen toetsen. Deze algemeen bruikbare techniek is een basistechniek in de micro-economie (zie bijv. Odink & Schoorl, 1984), waarmee een interessante mogelijkheid is verkregen om examenkunde en micro-economische theorie met elkaar te verbinden.
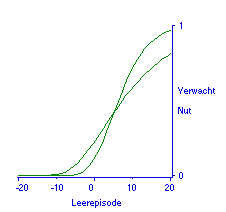
Figuur 10. Verwacht nut voor relatief doorzichtige toets (steile curve) en ondoorzichtige toets.
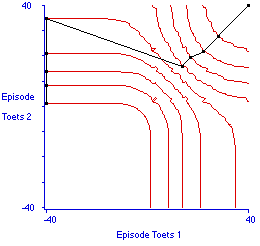
Figuur 11. Indifferentiecurven voor toets A tegenover een identieke toets B. Optimale strategieën liggen op de diagonaal vanuit de oorsprong.
Noot 2003: in afwijking van de oorspronkelijke plot is hier de analyse op gesimuleerde gegevens afgebeeld, en is de Engelcurve doorgetrokken over de 'kinky' indifferentiecurven. De Engelcurve is dus niet hetzelfde als een strategisch pad dat is te volgen, immers, de sprong van het laatste 'kinky' Engelpunt (linksboven) naar het eerste realistische (midden)betekent inleveren van al aan toets 2 bestede tijd, iets dat met tijd niet mogelijk is.
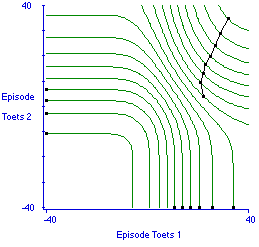
Figuur 12. Indifferentiecurven voor ondoorzichtige toets (A) tegenover doorzichtige toets (B). Optimale strategieën liggen op de geplotte Engelcurve rechts in de figuur.
De schijnbare eenvoud van het gepresenteerde ATM is bedrieglijk: daarachter gaan een aantal belangrijke keuzen schuil waarmee afstand is genomen van de testleer als methodologische inspiratie voor toetsen in het onderwijs. Van Naerssen heeft deze keuzen voor zijn tentamenmodel gemaakt, en deze keuzen zijn in het daaruit ontwikkelde ATM overeind gebleven. Het gaat in het model zelf om de strategische keuze van de student in een situatie van onzekerheid; op dit punt is een statistische benadering gevolgd omdat de onzekerheden stochastisch van aard zijn. De docent kan het ATM hanteren om zelf ook een optimale koers uit te zetten, maar de docent heeft daarbij niet te maken met onzekerheden van stochastische aard, maar met onzekerheden over het strategische gedrag van studenten. De besliskundige statistiek veronderstelt dat onzekerheden beslist worden door de gegeven maar onbekende toestand in de wereld (state of nature). Dat uitgangspunt gaat op voor het model voor de optimale strategie voor de student. De docent daarentegen heeft niet een onbekende toestand in de wereld als 'tegenspeler', maar zich strategisch gedragende studenten, die in hun strategie juist zullen reageren of anticiperen op de docent. Voor een beschouwing over het onderscheid tussen beide vormen van onzekerheid bij beslissingen verwijs ik naar de eerste bladzijden van Ferguson (1967). Voor optimale grensscorebepaling bij toetsen is de implicatie van een en ander dat het daarbij niet gaat om nutsfuncties van docenten over de dimensie stofbeheersing, zoals in de geaccepteerde theorie op dit gebied wordt gedaan, maar om nutsfuncties van studenten over mogelijk te behalen scores. Voor docenten is dan de optimale strategie de parameters van de toetssituatie zo af te regelen dat studenten ongeveer de programmatisch voorgeschreven studietijd nodig hebben om de toetsen voor te bereiden en naar genoegen af te leggen.
In dit ATM ligt een simpele opvatting over menselijk gedrag besloten: de mens maximaliseert nut. Dit is een economisch gedragsmodel, geen psychologisch model. Er woedt een strijd tussen economen en psychologen over de nutsmaximaliserende medemens: psychologen hebben ondertussen voldoende aangetoond dat er situaties in het dagelijks leven zijn waarin er geen sprake is van nutsmaximalisatie, of preciezer: waarin niet voldaan is aan de vooronderstelling dat voorkeuren consistent zijn. Voor het meest recente overzicht van de stand van zaken in dit debat verwijs ik naar Slovic (1995). Het strijdpunt is niet of besliskundige modellen rationeel zijn, dat wordt niet bestreden. Nee, het strijdpunt is of menselijk gedrag in deze zin rationeel is, en dat is geen logische maar een empirisch te onderzoeken kwestie. De pragmatische benadering is nu om het besliskundige model als een eenvoudig basismodel te beschouwen, waar vervolgens psychologen de nodige amendementen op kunnen leveren. Dat komt neer op het aloude inzicht dat besliskundige modellen normatieve modellen zijn die aangeven wat het maximaal haalbare is voor een rationele beslisser; in de praktijk moeten beslissers zich doorgaans tevreden stellen met eenvoudiger overwegingen dan een besliskundige analyse. Voor het ATM betekent dit dat het een ideaalbeeld geeft van de keuzesituaties waar studenten zich in bevinden, en dat studenten in de praktijk er niet in zullen slagen hun keuzen zo optimaal te doen zijn als het model aangeeft dat ze zouden kunnen zijn. Het ATM is dan te gebruiken om richting te zoeken (voor het instellen van de parameters van examenregelingen), of voor het genereren van hypotheses over sub-optimaal gedrag van studenten zodat daar maatregelen voor zijn te treffen. Op dat laatste punt is dan weer aansluiting te vinden bij de theorie in de school van Slovic, die ook hypothesen kan genereren over de wijze waarop studenten in gegeven situaties hun strategieën mogelijk stelselmatig sub-optimaal kiezen.
Voor een toepassing van het ATM als een analytisch instrument zie Wilbrink (1995) (parallel-paper sectie Hoger Onderwijs)
Brink, W. P. van den (1982). Binomiale modellen in de testleer. Proefschrift Universiteit van Amsterdam.
Coleman, J. S. (1990). Foundations of social theory. London: Belknap.
Cronbach, L. J., & Gleser, G. C. (1965). Psychological tests and personnel decisions. Urbana: University of Illionois Press.
Davis, Ch. E., Hickman, J., & Novick, M. R. (1973). A primer on decision analysis for Individually Prescribed Instruction. Iowa City: American College Testing Program (ACT Technical Bulletin 17).
Linden, W. J. van der (1980). Decision models for use with criterion-referrenced tests. Applied Psychological Measurement, 4, 469-492.
Naerssen, R. F. van (1970). Over optimaal studeren en tentamens combineren. Openbare les. Amsterdam: Swets & Zeitlinger. html
Naerssen, R. F. van (1974). A mathematical model for the optimal use of criterion referenced tests. Nederlands Tijdschrift voor de psychologie, 29, 431-446.
Naerssen, R.F. van (1976). Het derde tentamenmodel met een toepassing. Tijdschrift voor Onderwijsresearch, 1, 161-171.
Odink, J. G., & Schoorl, J. S. (1984). Inleiding tot de micro-economie. Groningen: Wolters-Noordhoff.
Slovic, P. (1995). The construction of preference. American Psychologist, 50, 364-371.
Wilbrink, B. (1978). Studiestrategieën. Amsterdam: COWO. pdf
Wilbrink, B. (1980). Enkele radicale oplossingen voor kriterium gerefereerde grensscores. Tijdschrift voor Onderwijsresearch, 5, 112-125. html
Wilbrink, B. (1995). Studiestrategieën die voor studenten én docenten optimaal zijn: het sturen van investeringen in de studie. In B. Creemers e.a. (1995). Onderwijsonderzoek in Nederland en Vlaanderen 1995. Proceedings van de Onderwijs Research Dagen 1995 te Groningen. Groningen: GION. 218-220. Paper: auteur. html
Bestand aangemaakt in html: juni 2003.
De opnieuw geconstrueerde figuren zijn gemaakt met een ondertussen verbeterd model, waardoor kleine verschillen met de oorspronkelijke plots bij overigens dezelfde parameterwaarden kunnen zijn ontstaan. Het belangrijkste verschil is de geheel andere positie die het leren in het model heeft gekregen.
In 1995 is een tweede techniek voor optimaliseren, investeringstheorie, nog niet beschikbaar, zij het dat er in het tentamenmodel (minimaliseren van tijd) en in eerdere vormen van het algemene toetsmodel (plotten van marginale analyses) wel rudimentaire vormen van aanwezig zijn.
In 1995 is het algemene toetsmodel nog niet losgekomen van die persoonlijke leerparameters, de individuele capaciteit, waardoor het model nog lang erg complex en onhandelbaar zou blijven (niet alleen door traagheid van de toenmalige computers, maar ook door de ingewikkelde en tijdrovende tussenstappen van simuleren van leren en van de aannemelijkheid van capaciteit).
![]() http://www.benwilbrink.nl/publicaties/95ModelVanNaerssenORD.htm
http://www.benwilbrink.nl/publicaties/95ModelVanNaerssenORD.htm