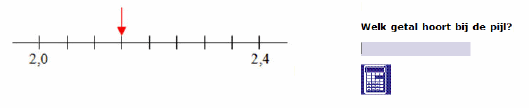

Zie ook de annotaties bij de toets 3F cito_voorbeeldtoets_3F.htm
Cito webpagina voorbeeldtoetsen
Voorbeeldtoets 3F 2013
Voorbeeldtoets_2F 2013
Voorbeeldtoets_2F 2013 Foutenanalyse
Voorbeeldtoets_3F 2013
Voorbeeldtoets_3F 2013 Foutenanalyse
antwoorden voorbeeldrekentoetsen
omzettingstabellen voorbeeldrekentoetsen
Deze voorbeeldtoetsen vragen erom kritisch te worden besproken.
Er zijn meerdere reden om deze oefening te doen. Een daarvan heeft te maken met de mededeling dat de pilototetsen zelf geheim blijven. Dat is een omineus teken: ik verwacht dat het beleid van het Cito zal zijn, ongetwijfeld met toestemming van het CvE, om straks ook de ‘echte’ rekentoetsen geheim te houden. Dat geheimhouden is een ernsitige inbreuk op de rechten van examendeelnemers om hun examenwerk te mogen inzien.
Wanneer nu deze pilottoetsen duidelijk maken dat er ernstige kwaliteitsproblemen aan tenminste enkele rekentoetsopgaven (het woord rekenopgaven durf ik niet te gebruiken) zijn, is dat een aanwijzing dat een politiek van geheimhouding inderdaad op ernstige bezwaren stuit.
De reden van het Cito om voor geheimhoudingte kiezen is uiteraard dat zij deze rekentoetsen digitaal willen afnemen, en op meerdere momenten per jaar daar de gelegenheid voor willen bieden. Dan gaat het om afweging van practische belangen tegen rechtszekerheid voor leerlingen. Een en ander klemt des te meer omdat leerlingen op alleen de rekentoets kunnen zakken voor HEEL het examen (nog niet bij de eerste keer dat rekentoetsen deel uit gaan maken van de eindexamens, maar ik ken deze ingewikkelde regeling niet uit mijn hoofd).
Ik zal zelf naar de rekentoetsopgaven kijken vanuit ontwerptechnische hoek. Gezien ervaringen met de voorbeeldtoetsen van de commissie-Schmidt, evenals met de rekenopgaven in de Cito Eindtoets Basisonderwijs, moeten we aannemen dat er ook wiskundig gezien wel eens vreemde zaken in deze voorbeeldtoetsen voor kunnen komen. Graag vanuit wiskundige hoek ook serieuze aandacht voor deze opgavensets.
raden
Er wordt wel meegedeeld dat sommige vragen meerkeuzevragen zijn, maar niet of je meerkeuzevragen onbeantwoord mag laten als je het antwoord niet weet. Waarschijnlijk dwingt Examentester de leerling om te raden. Dit gedwongen raden is een omstreden kwestie, die ook in de reguliere centraalschriftelijke eindexamens niet goed is opgepakt.
meerkeuzevragen
De opdracht is om bij meerkeuzevragen het juiste antwoord aan te klikken. De leerling mag er dus op rekenen dat er maar één juist antwoord is, en dat de andere alternatieven onjuiste antwoorden zijn. Dus geen gradaties in de zin van een ‘beste’ alternatief tegenover ‘minder goede’ alternatieven. Dit maakt bijvoorbeeld uit voor de antwoordstrategie: zodra een antwoord is gevonden dat juist is, is het niet meer nodig om de andere alternatieven nog te bestuderen. Voor mij is het dan telkens de vraag of de concrete rekentoetsopgave voldoet aan dit model: naast het als juist bedoelde alternatief mogen er dus geen alternatieven zijn die volgens een heldere gedachtengang ook juist zijn.
intypen van getallen
Bij een toets met een zo hoge inzet als deze rekentoets, mag het niet zo zijn dat het gebruiken van een punt in een groot getal, leidt tot verwerpen van het antwoord. Ik hoop dan ook dat Examentester zo is geprogrammeerd dat de leerling in een dergelijk geval erop wordt gewezen dat het gebruik van een punt niet is toegestaan. Ook dan is dit een hoogst verwarrende kwestie: deze flauwekul mag in deze rekentoets gewoon niet voorkomen. Hetzelfde geldt voor het minteken bij negatieve getallen: wanneer er een spatie na het minteken wordt getikt, moet dan gewoon goed zijn. antwoord verbeteren
Het is een hele sterke beperking van de bewegingsruimte van de leerling door deze de mogelijkheid te ontnemen om achteraf nog eens terug te keren naar een gemaakte som. Nu is het mogelijk het geval dat onderzoek uitwijst dat achteraf nog veranderen van antwoorden vaker wel dan niet leidt tot verslechtering; het Cito zou dat aan kunnen grijpen als toelichting.
Ik mag toch hopen dat Examentester het toestaat om een vraag in eerste aanleg onbeantwoord te laten, om er later naar terug te kunnen keren. Als deze mogelijkheid er niet is, dan diskwalificeer ik Examentester. Ik ben benieuwd. Uit de toelichting bij de voorbeeldrekentoets begrijp ik evenwel dat terugkeren naar een vorige opgave niet mogelijk is, dus ook niet in het geval deze nog niet is beantwoord. Is het dan dus ook mogelijk om per abuis door te gaan naar een volgende vraag nog zonder dat een antwoord is gegeven?
1) 8 - 1,25 = . . . .
Ik heb hier vragen bij. Is dit niveau 2F, en zo ja, waarom dan?
Hoe vergelijkt deze opgave zich met opgaven in de PPON rekentoets, en als dat inderdaad vergelijkbaar is, wat weten we dan over de problemen met dit type opgave? Ik doel natuurlijk op leerlingen die dit te makkelijk uit het hoofd doen, en zich daarbij vergissen. Als dat het geval is, zijn we hier dan bezig om ‘rekenen’ te toetsen, of wat?
Dit is een mooie rekenopgave om een aantal kritische vragen bij te stellen, juist omdat er geen kerstboom van een afbeelding omheen hangt, en er geen rekenmachne beschikbaar is.
2) Welk getal hoort bij de pijl? . . . .
De stam van de vraag is: Welk getal hoort bij de pijl?
Op basis van de stam van de vraag, is er geen zinnig antwoord te geven. De leerling moet dus de afbeelding gaan bestuderen die bij de vraag is gegeven.
Ik zal de bijbehorende afbeelding hier reproduceren, omdat de voorbeeldtoetsen in het publieke domein zijn geplaatst lijkt me daar geen auteursrechtelijk bezwaar tegen; de bron is genoemd. Dat voorkomt dat de lezer voortdurend moet wisselen tussen twee teksten: deze webpagina, en de voorbeeldtoets.
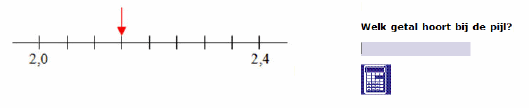
Dit is in het algemeen geen goed ontwerp voor toetsvragen, omdat de leerling nu de aandacht moet verdelen over de vraagstelling en een afbeelding. Dit probleem doet zich bij bijna alle rekenopgaven voor. Er is ongetwijfeld in de internationale literatuur enig relevant onderzoek voorhanden, denk ook aan Sweller’s theorie van mentale belasting, maar ik heb die nog niet op een rijtje. Ik ken incidentele empirische gegevens waar vergelijkingen zijn gemaakt tussen opgaven met een plaatje, en dezelfde opgave zonder een plaatje, waarbij de uitkomst kan zijn dat opgaven met een plaatje juist makkelijker zijn. Het is dus geen eenvoudige kwestie.
Als deze vraag ‘realistisch’ moet zijn, wat me heel geforceerd voorkomt, dan kan ik me voorstellen dat een vakman het probleem wel eens tegenkomt; waarschijnlijk is dan een wezenlijk verschil met deze toetsopgave dat in een praktijksituatie de vraag op natuurlijke wijze ontstaat, terwijl in deze toets de vraag van buiten is opgelegd. Denkpsychologisch is dat waarschijnlijk een geheel verschillende situatie, empirisch te toetsen met hulp van een fMRI-scanner, of eenvoudig in een experimentje waarin oogbewegingen van leerlingen gevolgd kunnen worden.
Taal: in de rekenkunde horen geen getallen bij pijlen. In dit geval kan men zeggen dat de pijl een schaalwaarde aanwijst, welk waarde is dat? Naar welke schaalwaarde wijst de pijl? Naar welke waarde wijst de pijl? Het gaat hier niet om getallen, maar om schaalwaarden. De schaal hoort niet bij de getallen, de getallen horen bij de schaal. Ben ik hier aan het raaskallen? Nee, dat denk ik niet. Maar ik ben niet scherp genoeg. Het probleem met deze vraag en deze figuur is dat het hier gaat om een onvolledige vraagstelling: de leerling die 2,15 invult, zou daar eigenlijk als toelichting bij moeten geven: ‘Ik neem aan dat de schaalverdeling in centimeters is, en dus dat de streepjes gelijke afstanden aangeven.’
Is dit half-realisme, of wat? Wel een schaalverdeling geven, maar niet aanduiden waarvan? Kan dat verwarrend werken? Dit is toch geen vraag naar getalbegrip? (getallenlijn, groep 2 en 3) (onderzoek zoals door Siegler).
Dit is een type vraag waar ik graag een onderbouwing zie dat dit GEEN intelligentietestvraag is. Hij past namelijk prima in de categorie opgaven zoals we die in Nederland kennen in de behangseltest (Raven Matrices): een aantal figuurtjes zijn gegeven, daarin zit een reeks, en de vraag is wat het volgende figuurtje in de reeks zal zijn. Dat is geen wiskunde, maar een typische vraag om abstract te redeneren. Zou in de figuur zijn aangegeven dat het om afstanden gaat, of om temperatuur, of een andere lineaire variabele, dan zou dit probleem er niet zijn. Zonder die aanduiding, kunnen de tussen 2.0 en 2.4 liggende markeringen van alles en nog wat voorstellen, en is het aan de leerling om daar een verhaal en getallen bij te verzinnen. Zie over dit type probleem in rekentoetsen ook Milgram, 2007, p. 39:
R. James Milgram (2007). What Is Mathematical Proficiency? In Alan H. Schoenfeld:. Assessing mathematical proficiency (pp. 31-58). Cambridge University Press. pdf
Hoe ernstig is het dat een vraag zoals deze een intelligentietestvraag is? Dat is voor een rekentoets die onderdeel is van een afsluitend examen een zeer ernstige zaak. We moeten daar niet luchtig over doen. Het onderwijsprogramma is nu eenmaal niet gericht op groei van intellectuele capaciteiten — al is dat wel een neveneffect — maar op toename van kennis. Leraren kunnen hun leerlingen niet voorbereiden op toetsen die in feite verschillen in intellectuele capaciteiten meten. Het is niet voorspelbaar met welke intelligentietestvragen de teams van het Cito de volgende keer op de proppen komen.
Waarom krijgt de leerling hier de mogelijkheid om een rekenmachine te gebruiken? Dat werkt toch alleen maar verwarrend?
Nog weer iets heel anders: de rekentoetsen gaan dus uit 60 vragen bestaan, met de zak-slaaggrens ergens bij 39, en een stevige raadkans (een deel van de opgaven is meerkeuze, bij de overige opgaven is er waarschijnlijk ook wel gelegenheid om een beetje te gokken).
Ik heb in ‘Examens. Tijdschrift voor de Toetspraktijk’ december 2011 samen met Joost Hulshof de suggestie gedaan om voor de rekentoetsen op enigerlei wijze onbeperkt herkansen toe te staan. Het Cito verzet zich daar fel tegen, om waarschijnlijk redenen van Cito-belang. Het zal dus wel blijven bij één herkansingsgelegenheid (als ik me goed herinner heeft het ministerie expliciet uitgesproken dat er na het CSE voor de rekentoets-gezakten GEEN extra herkansingsmogelijkheid zal zijn).
Een en ander vraagt om wat modelberekeningen. Ik zal eens kijken of ik daar mijn SPA-model voor kan gebruiken. De WolframAlpha calculateor is natuurlijkj ook gecshikt voor een eerste oefening, onder de veronderstelling dat een leerling een stofbeheersing van 70% heeft, inclusief raden, gaat het om de kans op een score van 39 of hoger op een test van 60 items: gewoon de binomiaalverdeling gebruiken.
http://staff.science.uva.nl/~craats/WolframAlphaVoorbeelden.pdf(blz. 8: binomiaalverdeling)
binomial distribution, n = 60, p = 0.7
spa_generator.htm (applet 1, binomiaalverdeling)
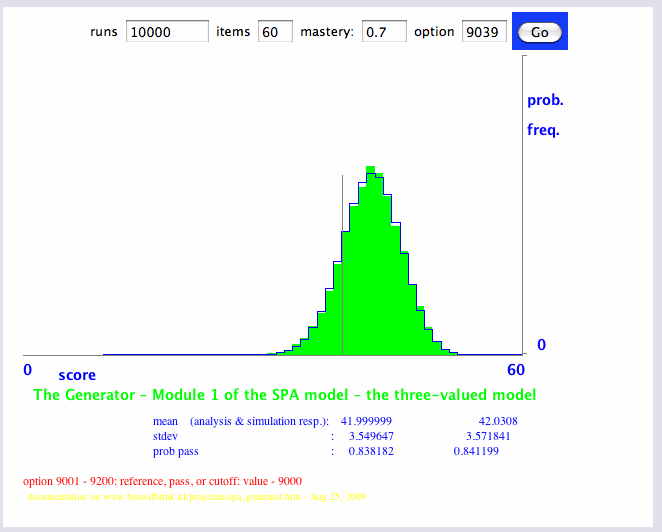
0,84 gegeven beheersing 0,7 is een schandelijk lage slaagkans voor een toets met een zo hoge inzet. Bedenk dat geen enkele leerling de eigen beheersing precies kent, dan wordt het nog weer wat vervelender:
Stel nu dat de leerling een proefrekentoets heeft afgelegd, en daar de score 42 uit 60 op heeft behaald. De aannemelijkheid voor zijn beheersing van de stof is dan te berekenen (het is een beta-dichtheid), respectievelijk te simuleren.
spa_likelihood.htm (applet 2, betadichtheid)
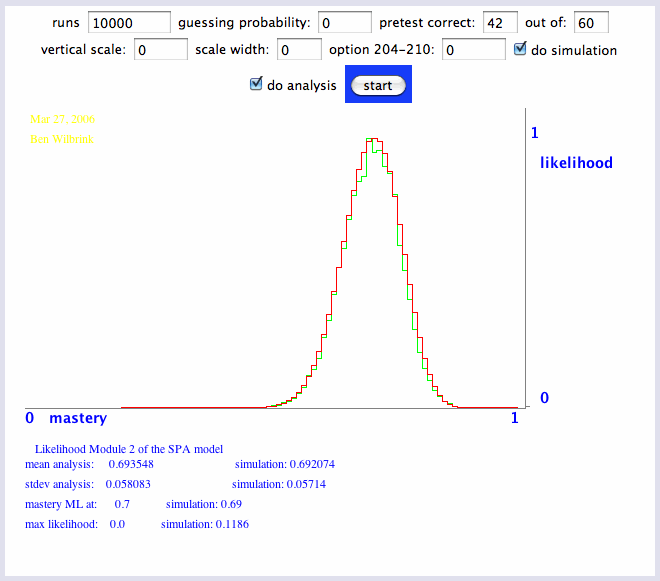
Deze aannemelijkheid laat zien dat een proeftoets van 60 rekentoetsopgaven de leerling best nog op een heel verkeerd been kan zetten.
Wat is de voorspelling voor de kansen die deze leerling heeft op de nog af te leggen rekentoets? Die voorspellende toetsscoreverdeling is een betabinomiaalverdeling.
spa_predictor.htm (applet 3, betabinomiaalverdeling)
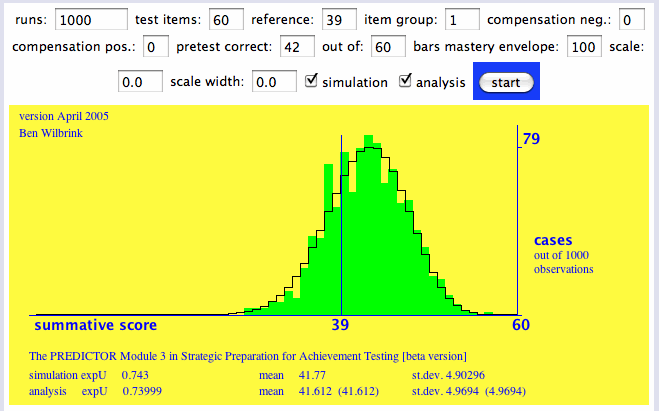
De slaagkans voor de leerling die zojuist op een proefrekntoets een score van 42 uit 60 heeft gehaald, is 0,74 op de af te leggen rekentoets met eveneens 60 vragen. Een heel stuk minder kansrijk dus dan wanneer het zeker zou zijn dat de eigen stofbeheersing 0,7 is.
Ho ho, waar komt die slaagkans van 0,74 vandaan? In de bovenstaande applet is de slaagkans gelijk aan het verwachte nut (parameter expU), waarbij slagen het nut = 1 heeft, zakken het nut = 0. Die nutsberekening loopt vooruit op module 4 van het SPA-model.
![]() http://www.benwilbrink.nl/projecten/cito_voorbeeldtoets_2F.htm
http://www.benwilbrink.nl/projecten/cito_voorbeeldtoets_2F.htm