Teveel om allemaal langs te lopen. Waarom dan niet één stelling, maar 14: op de een of andere manier hangt het allemaal samen, en zijn die struikelvakken alleen goed aan te pakken door een integrale benadering. Suggesties van aanwezigen bepalen waar we mee beginnen, en anders doen we eerst de tabel bij stelling 1.
In het thema ‘leren bewijzen’ hebben een aantal stellingen, en zeker stelling 14, wel raakvlakken met het wiskundige van ‘leren bewijzen’. Mijn benadering is echter niet wiskundig, maar zeg maar psychologisch: bewijsvakken als struikelvakken, wat kunnen we daarmee?
Stelling 1. Het cijfer op een struikelvak voorspelt niet de wiskundige toekomst van de student (tenzij er een self-fulfilling prophecy van wordt gemaakt)
Stelling 2. Vraag studenten hoeveel tijd zij hebben geïnvesteerd. Dat is eigenlijk het enige anker voor de beoordeling.
Stelling 3. Beoordelen en beoordeeld worden is een spel tussen partijen, een impliciete onderhandeling.
Stelling 4. Als studenten hun tentamenresultaat niet goed kunnen voorspellen, zullen ze zich terughoudend voorbereiden. Het resultaat wordt dan vanzelf: veel vijven en zessen, weinig uitschieters. Een struikelvak.
Stelling 5. Een eerlijk tentamen is een doorzichtig tentamen, dus doeltreffend voor te bereiden. (De Groot, 1970)
Stelling 6. Bij doorzichtige tentamens is het mogelijk om de lat op de gewenste hoogte te leggen. (Van Naerssen, 1970)
Stelling 7. ‘Ieder vak voldoende’ verkwanselt informatie en verspilt dus tijd van studenten en docenten. Overtreed de wet (tot het absurde is niemand gehouden), en sta compensatie toe.
Stelling 8. Studenten zijn geneigd tot procrastinatie (uitstellen). Verklein het probleem: knip grote tentamens op in vrijstellende en compenserende delen. (Groningse examenregeling op advies van Hofstee)
Stelling 9. Haal de herkansings-bonus weg, bv.: limiteer herkansingen, maak ze moeilijker dan de eerste gelegenheid, reken het resultaat van de eerste gelegenheid mee. Inzicht: leg de lat op andere tentamens een stukje hoger, i.p.v. te laten herkansen.
Stelling 10. Voorkom dat studenten moeten herkansen, zet deze studenten niet op extra achterstand waardoor ze extra risico lopen op andere vakken ook te moeten herkansen, enzovoort (bifurcatie?). (Wilbrink, 1980)
Stelling 11. Een bewijs leveren is vergelijkbaar met een opstel schrijven, een wetenschappelijke verklaring geven, een tandheelkundige preparatie maken. De boordelingsproblemen bij dit type werkstukken zijn berucht.
Stelling 12. Onderzoek regelmatig de overeenstemming tussen onafhankelijk verkregen oordelen over dezelfde werkstukken.
Stelling 13. Zoek de confrontatie met opvattingen van collega’s over tentamineren en beoordelen (intervisie?)
Stelling 14. Bewijzen is ook een vorm van probleemoplossen, en dat lukt alleen wanneer de nodige stukjes informatie tegelijk mentaal beschikbaar zijn. Kortom: of dat bewijs wordt gevonden is een kwestie van kansrekening . . . (pfff, conjunctieve kansen; lijkt wel een examenregeling!) en psychologie (inzicht toetsen)
Stelling 15. Ga niet winkelen in deze stellingen: om struikelvakken aan te pakken is integraal beleid op al deze fronten nodig.
paper: http://www.benwilbrink.nl/projecten/12struikelvakkenICAB.htm

Ik ben weer eens een buitenbeentje, in dit gezelschap: ik zal niet over wiskunde spreken. Ik ga u onderdompelen in een reeks mogelijke oorzaken van, en oplossingen voor, struikelvakken in het algemeen, en vakken waarin bewijzen het struikelpunt is in het bijzonder. Deze website is er om een en ander nog eens na te slaan, en bronnen op te volgen. De grote lijn: het gaat om psychologisch onderwijsonderzoek dat relevant is voor deze struikelproblematiek. Er zijn modellen beschikbaar die met empirische data zijn te voeden, maar voor beleidsingrepen hoeft onderzoek niet noodzakelijk herhaald te worden. Ik volg verschillende benaderingen naast elkaar: van buiten (de examenregeling, tijdbesteding), van binnen (doorzichtigheid van tentamens, het beoordelen van geleverde bewijzen), van boven (opvattingen van docenten), van papier (stuk UvA; stuk TU Delft).
Ik heb aan deze universiteit mijn stage en tentamen onderwijsreseach gedaan. Ik mocht uitzoeken of er iets zinvols viel te doen met een nieuw programma voor de PDP-11: multiple discriminant analyse (MDA) (verslag). In die tijd werden aankomende studenten een hele middag beziggehouden met tests en vragenlijsten, waaronder een persoonlijkheidstest. Het idee was: zegt die persoonlijkheidstest iets over het vak dat studenten kiezen? Dat deed het. (technisch: MDA vergroot tussen-groepen variantie t.o.v. binnen-groepen variantie, op basis van subtestscores) Onderwerp van gesprek bij mijn tentamen: is een persoonlijkheidstest bruikbaar bij selectie, advisering of begeleiding? Mijn stelling was een onverwachte: Ja, het is immers te verwachten dat een student die sterk afwijkt van het ‘profiel’ van bijvoorbeeld de groep wiskundestudenten, meer problemen in de studie zal ondervinden. Maar pas op: het zijn juist deze buitenbeentjes die een opleiding moet koesteren, zij zijn het zout in de pap, zorgen voor onrust en tegenspraak. Ook in het vak. Eindhoven heeft met zijn Edsgar Dijkstra geen goed track record in het vasthouden van buitenbenen: weggetreiterd naar de VS (pm: in de vijftiger jaren lag Nederland aan kop op het terrein van informatica, twintig jaar later in de achterhoede).
Verwacht van mij een eigenwijze inbreng, psychologie, van modelmatige handvatten voorzien, plus een omgevallen boekenkast aan relevant onderzoek. En aan het eind van de dag het idee dat struikelproblemen goed zijn aan te pakken.
O ja. Ik ben geen wiskundige, maar ik was als dertigjarige nog eens begonnen aan econometrie (UvA), haalde een mooi resultaat op het eerste tentamen Analyse, maar brak daarna mijn studie af (ik heb decaan Neudecker uitgelegd dat ik heel veel verliestijden had bij deze studie (irrelevante activiteiten, onhandige roosters), en dat zou ik geen jaren volhouden). Vandaag heb ik belangstelling voor rekenen en wiskunde vanuit de problematiek wat goede toets- en examenvragen zijn; mede dankzij Joost Hulshof is dat nu uitgegroeid tot een diepgravende studie van de ontwikkelingen in het huidige reken- en wiskundeonderwijs (zie hier).
Stelling 1. Het cijfer op een struikelvak voorspelt niet de wiskundige toekomst van de student (tenzij er een self-fulfilling prophecy van wordt gemaakt)
Kort: er zijn tal van redenen voor de juistheid van de stelling. O.a. dat beoordelen relatief is, en dat ook binnen een groep studenten die briljante wiskundecijfers in het vwo hadden, er studenten zjn die even een stuk lager scoren dan anderen. De valkuil van permanente selectie. De stelling is vooral bedoeld als waarschuwing: ga voorzichtig om met het beoordelen van studenten, raak niet onnodig talent kwijt. De volgende tabel, in Van Gool (2008), laat zie dat de opleidingen waarschijnlijk niet zorgvuldig omgaan met het talent dat binnenkomt. Ik vind dit ongelooflijk, vooral gezien het toch al heel geringe aantal kandidaten dat vandaag nog kiest voor een opleiding wiskunde.

Ik lees deze tabel als volgt: Dit is een teken van een sterke wervingscampagne omder middelbare scholieren: ga vooral geen wiskunde studeren. Voor de studenten die desondanks zijn begonnen aan deze studie, zijn deze slaagcijfers een aanmoediging om juist niet voluit te gaan in de voorbereiding op deze tentamens; dat is immers een investering waarvan onzeker is of die zich terugbetaalt. Het kan dus zijn dat het grote aantal gezakten terecht is omdat er te weinig tijd is geïnvesteerd. Wat doet u zichzelf aan?
In het verleden waren de numerieke rendementen voor wiskunde en natuurkunde altijd al beroerd, bijvoorbeeld vergeleken met die van geneeskunde. En dat had altijd al alarmerend moeten zijn, omdat wis- en natuurkunde de jongste studenten met de beste eindexamencijfers binnenhaalt, en geneeskunde de oudere studenten met lage eindexamencijfers (Voorthuis & Wilbrink, 1987). (Voor geneeskunde is onder andere door de invloed van de gewogen loting, over de decennia sinds 1975 heen de instroom radicaal veranderd: waar vroeger de brekebeentjes van de gymnasia geneeskunde gingen studeren, zijn het nu de briljante meiden die dat gaan doen. Wiskundigen van Nederland: laat u dat niet gebeuren: geneeskunde snoept het wiskundetalent weg, met staatssteun).
Stelling 2. Vraag studenten hoeveel tijd zij hebben geïnvesteerd. Dat is het enige anker voor de beoordeling.
Het is maar een stelling, dus een beetje te stellig. Maar het punt is dit: docenten weten niet goed hoe moeilijk de tentamenopgaven zijn, en gebruiken dus de antwoorden van studenten om tot een waardering op een cijferschaal te komen. Dat is relatief beoordelen. Het risico: dat studenten het in de smiezen krijgen, en zich steeds minder degelijk gaan voorbereiden. Hoe kom je daar achter: vraag standaard naar de hoeveel bestede tijd (contacttijd, studietijd), op een afzonderlijke blad papier, desgewenst anoniem in te vullen; doe het nog korter dan in deze vragenlijst (gebruikt voor de dataverzameling van de onderzoeken die bij stelling 3 zijn vermeld):

Er zullen best grappenmakers zijn die wonderlijke tijden invullen, maar heb er vertrouwen in dat studenten dergelijke vragen gewoon naar beste weten zullen beantwoorden. Er is veel tijdbestedingsonderzoek gedaan, en daarbij is het vertrouwen nooit geschaad. Iets anders is dat studenten hun tijdbesteding moeilijk kunnen schatten; als iedereen onderschat, blijkt dat nergens uit, wees dus attent. Gebruik deze informatie nooit om een oordeel over individuele studenten bij te stellen. Het gaat natuurlijk om de globale informatie die het oplevert: gemiddelde tijdbesteding, standaarddeviatie van tijdbesteding, eventueel relatie tijdbesteding - resultaten - streefniveau. Hierbeneden komen nog voorbeelden van gebruik van tijdbestedingsgegevens. Misschien is het toch aardig om een heuristisch modelletje bij de hand te hebben, voor relaties tussen individuele capaciteiten (‘exogene variabelen’), streefniveaus, tijdbesteding, en studieresultaten (Tromp & Wilbrink, 1977).
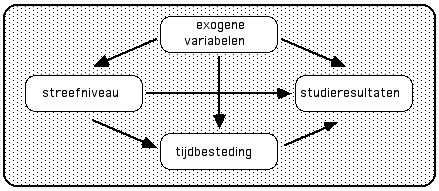
Stelling 3. Beoordelen en beoordeeld worden is een spel tussen partijen, een impliciete onderhandeling.
Zowel studenten als docenten hebben in het beoordelingsspel een zekere machtspositie, een machtspositie waar ook weer grenzen aan zijn gesteld. ‘De lat hoger leggen’ werkt, maar slechts tot op zekere hoogte. ‘Lijntrekken’ werkt, maar slechts tot zekere hoogte. In de situatie waarin er zowel dramatisch lage slaagcijfers zijn, als een veel te lage tijdbesteding van studenten, lijkt het op het eerste gezicht mogelijk om de situatie aan te pakken door veel hogere eisen te stellen. Maar dat is buitengewoon riskant, omdat het best eens zo zou kunnen zijn dat studenten heel goede redenen hebben om zich minimaal voor te bereiden: ondoorzichtige eisen en toetsing bijvoorbeeld, zie volgende stellingen.
Stelling 4. Als studenten hun tentamenresultaat niet goed kunnen voorspellen, zullen ze zich terughoudend voorbereiden. Het resultaat wordt dan vanzelf: veel vijven en zessen, weinig uitschieters. Een struikelvak.
Een voorbeeld van enkele decennia terug: een postdoctorale opleiding accountancy liep tegen het probleem aan dat de examenresultaten eigenlijk uitsluitend vijven en zessen waren. Dat examen bestond uit vier grote casus, ieder in een dagdeel te beschrijven. Dat was waarschijnlijk een zo onvoorspelbaar examen, dat de deelnemers bewust met een matige voorbereiding de gok namen om het een volgend jaar nog eens te moeten afleggen; een rationele strategie vanuit het gezichtspunt van de examenkandidaten. Maar wat een enorm maatschappelijk en persoonlijk verlies! [Ik zal mijn advies destijds, 1979, nog opzoeken]
Stelling 5. Een eerlijk tentamen is een doorzichtig tentamen, dus doeltreffend voor te bereiden. (De Groot, 1970)
Een naïeve kijk op proefwerken, tentamens en examens is dat het hier alleen maar gaat om het ‘peilen’ van de kennis van de studenten, dus iedere goede peilstok voldoet. Minder naïef, maar nog steeds in de categorie misvattingen: het gaat erom de lammeren van de schapen te scheiden, de beste studenten de kans te geven om uit te blinken, of ook: de competitie tussen studenten onderling aan te jagen. Maar hier wordt buiten de waard gerekend: wat en hoe er wordt getoetst, is natuurlijk mede bepalend voor de manier waarop de studenten zich op de proef gaan voorbereiden. En niet alleen studenten: ook scholen die hun leerlingen op de Cito Eindtoets Basisonderwijs prepareren (Aleid Truijens, De Volkskrant 25 januari, p. 29). Ik noem het fenomeen meestal feedforward. In de literatuur is het beter bekend als backwash (zie bv, Bishop, 2002).
De verdienste van A. D. de Groot is dat hij uit die backwash een helder beginsel haalt: onderwijs wat je toetst, toets wat je onderwijst. Studenten moeten zich doeltreffend op toetsen voor kunnen bereiden. Dat is niet om aardig te zijn voor studenten, maar om verspilling, demotivatie en herkansen tegen te gaan.
Stelling 6. Bij doorzichtige tentamens is het mogelijk om de lat op de gewenste hoogte te leggen. (Van Naerssen, 1970)
Bob van Naerssen kwam bij zijn inaugurele rede in 1970 met een opmerkelijk ‘tentamenmodel’ dat bedoelde de strategische situatie te modelleren voor de student die zich op een tentamen voorbereidt. Voor wie een klein beetje bekend is met het redeneren van psychometrici en testpsychologen, maakt Van Naerssen hier een uitzonderlijke wending door niet te redeneren vanuit het perspectief van de docent die tentamineert, maar dat van de student die zich aan dat tentamineren gaat onderwerpen. En nog steeds, meer dan 40 jaar na dato, is er nog nauwelijks een toetsdeskundige te vinden die vertrouwd is met dit perspectief vanuit de student. Het gaat hier om een dramatisch tekort bij toets- en andere onderwijsspecialisten, want het is toch evident dat het leeuwendeel van de resultaten in het onderwijs is toe te schrijven aan strategisch gedrag van studenten. Chapeau dus voor Bob Van Naerssen.
Het inzicht van Van Naerssen kwam niet uit de blauwe lucht vallen, maar kwam voort uit besliskundig denken over psychologische selectieproblemen (de selectie van chauffeurs voor de landmacht), steunend op het voorbereidende werk van Cronbach & Gleser (1957/1965), die overigens ook het onderscheid onderstreepten tussen institutionele selectie en individuele advisering, met methodologische consequenties.
Het was Bob van Naerssen niet gegeven om zijn tentamenmodel verder te ontwikkelen: zijn model werd wel steeds ingewikkelder, maar raakte daarmee ook weg van het doel van praktische inzetbaarheid. In mijn eigen werk ben ik met zijn tentamenmodel verder gegaan, en kon ik een aantal problemen oplossen die voor Van Naerssen struikelblokken waren. De actuele stand van zaken in wat ik het SPA-model noem, is op mijn website te vinden. De basis ervan is gepresenteerd in 1998, zie de toelichting bij de laatste stelling (14). Een eerdere presentatie voor de staf van het Cito (1994) viel op dorre aarde.
Terug naar de stelling. Tentamenmodellen bevatten een aantal parameters voor de toets, de toetssituatie en/of de student(en). De grap is dat een bepaald model is door te rekenen voor verschillende mogelijke waarden van deze parameters, zeg maar voor verschillende beleidsopties. Dat zijn natuurlijk maar papieren oefeningen, maar ze geven een richting aan, en empirische beproeving kan uitwijzen of het de juiste richting en orde van grootte van verwacht effect is. That’s all there is to it. Maar dat is onzettend veel meer dan koffietafelgesprekken opleveren (zie ook Stelling 13).
Stelling 7. ‘Ieder vak voldoende’ verkwanselt informatie en verspilt dus tijd van studenten en docenten. Overtreed de wet (tot het absurde is niemand gehouden), en sta compensatie toe.
Discussie over het toestaan van compensatie van (te) lage cijfers met de cijfers van andere vakken, kan snel alle kanten op schieten en onvruchtbaar blijven. Ik stel om te beginnen voor om ervan uit te gaan dat compensatiemogelijkheden een gradueel kenmerk zijn van alle examenregelingen, ook wanneer er een strikte eis is dat ieder onderdeel op zich ‘voldoende’ moet worden gemaakt. In het laatste geval zit er nog compensatie verborgen binnen de afzonderlijke vakken, en een ieder die beweert dat het een doodzonde is om compenseren toe te staan, zal voor die compensatie binnen onderdelen met een goede verklaring moeten komen.
Als we het er over eens zijn dat het ook een doodzonde is om informatie over de prestaties van kandidaten onbenut te laten, dan hebben we een goed vertrekpunt. Een strikte grens zakken/slagen op afzonderlijke onderdelen, laat expliciet bepaalde informatie over de stofbeheersing buiten beschouwing.
Koppel hieraan het feit dat iedere toets een steekproef is uit het betreffende kennisdomein. Dan kunnen we tevens concluderen dat het ondoelmatig is om door het handhaven van een strikte grens zakken/slagen op iedere onderdeel in feite steekproeffluctuaties een dikke vinger in de succes-pap te geven. Een variant op dit argument is: gebruik het hele examen als een enkele lange toets die zowel veel betrouwbaarder is dan de som van de betrouwbaarheden van de afzonderlijke examenonderdelen, als meer valide voor de belangrijke globale doelen van de opleiding.
Toestaan van een bepaalde mate van compensatie is een actueel thema in het beleid van onder andere de Erasmus Universiteit (Arnold, 2011) en de TU Delft. Compensatie was een belangrijk kenmerk in de succesvolle herziening van de propedeutische examenregeling voor geneeskunde aan de RU Groningen, begin negentiger jaren (Cohen-Schotanus, 1995; zie ook mijn 1995, voor een analyse in termen van een tentamenmodel). Nieuw is het allemaal niet. Al in 1968 liet Bob Van Naerssen zien dat de optimale strategie voor studenten onder een compensatorische examenregeling is om de tijd gelijk te verdelen over de vakken, dus niet minder tijd te besteden aan dat vak dat je niet ziet zitten of te moeilijk vindt (op het congres waar voor het eerst studenten zich krachtig lieten horen).
Stelling 8. Studenten zijn geneigd tot procrastinatie (uitstellen). Verklein het probleem: knip grote tentamens op in vrijstellende en compenserende delen. (Groningse examenregeling op advies van Hofstee)
Mijn idee was om hier het advies van Willem Hofstee voor een herziening van de examenregeling geneeskunde te behandelen. Dit onderwerp was bij de voorgaande stelling ook al aan de orde. Maar ja, hoe gaat dat: dit complex stellingen blijkt nauw samen te hangen: het is vooral psychologie, het gaat om mogelijk maatregelen die als maatregel op zich waarschijnlijk gaan mislukken, maar als maatregelen in samenhang een groot succes kunnen zijn (Cohen-Schotanus, 1995).
Ik vermoed dat alle docenten zullen beamen dat uitstelgedrag van studenten een groot probleem is. Gelukkig is daar een promotieonderzoek over gedaan (Schouwenburg, promotor: Hofstee). Ik kom daar nog op terug. Maar let op: uitstelgedrag is natuurlijk ook rationeel, zeker wanneer het erom gaat een piekprestatie te kunnen leveren op intellectueel uitdagende tentamens. Geconcentreerd een aantal dagen volop in de slag gaan met de stof, levert waarschijnlijk een betere prestatie op dan over een langere periode iedere dag er beperkt aandacht aan besteden. Ik ben zelf het voorbeeld: de basisideeën voor mijn presentatie heb ik begin deze maand in een paar minuten op email gesteld; met de uitwerking ben ik een paar dagen terug begonnen. Dat is de enige manier waarop het mogelijk is om een berg informatie op zo’n manier paraat te hebben, dat ik er in de discussie vlot mee uit de voeten kan, en er ook zo ver boven sta dat ik ingewikkelde dingen op een begrijpelijke manier onder woorden kan brengen. Hier zit ook wat psychologie in, die bij stelling 14 terugkomt: bewijzen is een vorm van complex probleemoplossen, wat zijn daar eigenlijk de psychologische condities voor?
En dan is het ineens onduidelijk op welke manier een examenregeling, of de instructievolgorde binnen een vak als Analyse, het best in kan spelen op ongewenst uitstelgedrag. Dan grijp ik naar een ander proefschrift, de dubbelpromotie Van der Drift & Vos (1987): plan het onderwijs op zo’n manier dat er geen gaten vallen in de tijdbesteding van studenten (zoals tentamens onmiddellijk ná een vacantie in plaats van ervoor, maar dat is een gemene). Programmeer dan zo dat studenten gedurende het grootste deel van het semester gelijkmatig maar intensief met de stof bezig zijn, eventueel met vrijstellende deeltoetsen, en geef ze gelegenheid tot intensieve herhaling van de hele stof in de dagen voorafgaand aan het tentamen. Dat het tentamen dan vooral bestaat uit complexe opgaven, die inderdaad vereisen dat de studenten overzicht over de hele behandelde stof hebben en daarin vlot dwarsverbindingen kunnen leggen, kan alleen maar de bedoeling zijn. (Geef het spel dan niet uit handen, door bij het afsluitende tentamen deelkennis te honoreren, wanneer de opgaven zèlf niet tot een goed einde zijn gebracht (zie mijn 1998 op dit punt)).
Stelling 9. Haal de herkansings-bonus weg, bv.: limiteer herkansingen, maak ze moeilijker dan de eerste gelegenheid, reken het resultaat van de eerste gelegenheid mee. Inzicht: leg de lat op andere tentamens een stukje hoger, i.p.v. te laten herkansen.
[Nog uit te werken. De moeilijkheid bij een ontmoedigingsbeleid om het op herkansingen te laten aankomen is dat het mogelijk niet werkt, zodat studenten van de regen in de drup raken.] [Het zou dus best eens kunnen dat het laten bestaan van herkansingsgelegenheden in de huidige vorm, bij het tegelijk bieden van echt royale compensatiemogelijkheden, studenten wèl prikkelt tot extra inspanningen: die leveren immers extra punten op die bijzonder wardevol kunnen blijken.]
Stelling 10. Voorkom dat studenten moeten herkansen, omdat dat deze studenten op extra achterstand kan zetten waardoor ze extra risico lopen op andere vakken ook te moeten herkansen, enzovoort (bifurcatie?). (Wilbrink, 1980)
Heel simpel, en waarschijnlijk waar:
Een algemeen punt, in zekere zin direct volgend uit tentamenmodelberekeningen, is het volgende. Voor tentamens waar een voldoende voor moet worden behaald, eventueel na herkansing(en), is de optimale voorbereiding voor de studenten de voorbereiding die de verwachte benodigde tijd om te slagen minimaliseert (het laagste punt van de strategiecurven in onderstaande figuur uit mijn (1978)). De perfecte ‘zesjesstudent’ zou je kunnen zeggen, ware het niet dat die term de schuld bij de student legt, in plaats van bij de opleiding die een premie zet op zesjesstrategie. Deze optimale strategie is natuurlijk niet scherp af te grenzen: er is een wat breder gebied dat als ongeveer optimaal valt te kenmerken. Maar dat is merkwaardig: iets minder tijd investeren dan strikt genomen optimaal is levert hetzelfde resultaat op als juist iets meer tijd investeren. Althans: resultaat in termen van slagen. Maar de student die aan de lage kant is gaan zitten, gaat uiteindelijk door met een lagere stofbeheersing en na meer kansingen, de student die aan de hoge kant is gaan zitten gaat door met minder herkansingen en met hogere beheersing. Als dat voor meer vakken gebeurt, wordt het verschil tussen deze studenten steeds groter . . . . terwijl hun tijdbesteding maar weinig verschilt. Ziehier opnieuw een probleem dat direct volgt uit het verbod op compensatie van tentamencijfers en het toestaan van praktisch onbeperkt herkansen.
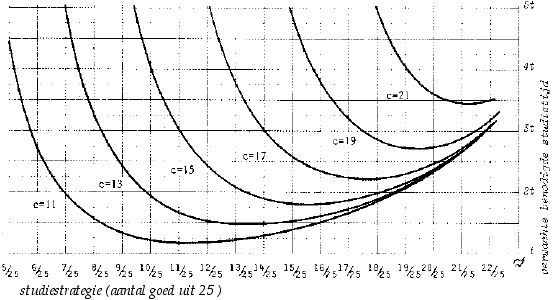
FIGUUR 6.2. Verwachte benodigde studietijd voor verschillende studiestrategieën, en verschillende zak-slaaggrenzen c bij toetsen van 25 vragen. Het laagste punt van iedere kromme correspondeert met de studiestrategie waarbij de studietijd om te slagen het kleinst is.
Stelling 11. Een bewijs leveren is vergelijkbaar met een opstel schrijven, een wetenschappelijke verklaring geven, een tandheelkundige preparatie maken. De boordelingsproblemen bij dit type werkstukken zijn berucht.
Neem bijvoorbeeld eens de waaier van verschillende bewijzevan de Stelling van Pythagoras. Daar is leuke literatuur over (zie beneden) (blog BON). Er zou zomaar een experimentje mee gedaan kunnen worden: laat 96 verschillende bewijzen beoordelen op een aantal expliciete criteria (welke zouden geschikt zijn?) door een aantal wiskundeleraren, wiskundedocenten wo, en studenten wiskunde, onafhankelijk van elkaar natuurlijk.
Deze bewijzen vallen niet in de moeilijkheidsklasse van Analayse I, maar waar het hier om gaat is dat gegeven bewijzen zich niet zomaar intersubjectief perfect laten beoordelen.
Bruno Emst (2002). De interessantste bewijzen voor de stelling van Pythagoras. Epsilon Uitgaven. (2e druk 2006) (bespreking door Christiaan Jongeneel)
Nederlandse website over Pythagoras: .
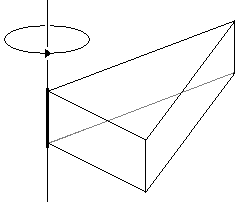
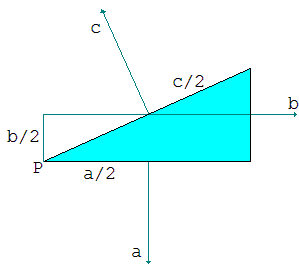
Ik heb het ‘natuurkundig bewijs’ van Levi toegevoegd om er een punt mee te maken: zou u een echt creatief bewijs accepteren als adequaat bewijs? Sterker nog: zou u een dergelijk bewijs meteen als en goed bewijs herkennen? Uit onderwijsonderzoek (bv. Crombag, Gaff & Cahng, 1975) blijkt nogal eens dat studenten die méér doen dan alleen de opgegeven stof bestuderen, of die meer dan anderen gebruik maken van hun wereldkennis, op tentamens juist lagere cijfers krijgen dan hun minder voorlijke medestudenten. U kunt wel vermoeden waarom. Het fenomeen zal zich sterker voordoen in de propedeuse, dan in de masterfase. Het is dus riskant om eigenzinnig te zijn, om meer te doen dan er wordt gevraagd, om anders begaafd te zijn dan alleen maar analytisch.
Stelling 12. Onderzoek regelmatig de overeenstemming tussen onafhankelijk verkregen oordelen over dezelfde werkstukken (bewijzen).
Onze hersenen functioneren op een wonderbaarlijke manier juist zé dat we altijd een bevredigend volledig beeld van de wereld hebben. Probeer eens stereo-foto’ uit begin vorige eeuw te bekijken: eerst alleen maar verwarring, en ineens is daar het dieptebeeld. Wow. Professionals die beoordelen en diagnosticeren, zullen meestal ervaren (‘denken’) dat ze dat heel goed doen, en met tal van factoren rekening hebben gehouden. Maar dat is een bedrieglijk beeld dat onze grijze hercencellen, met elkaar samenspannend, ons voortoveren. Hoe bedrieglijk blijkt pas bij empirische toetsing. De docent die in een dagboekje bijhoudt wat hij denkt dat er van student Piet of Marie terecht kan komen, is tien of twintig jaar later misschien in de positie om die ideeën te toetsen. Nee, ik ken geen docenten die zoiets wel eens hebben gedaan. Maar er is bijvoorbeeld wel veel onderzoek naar oordeelsvorming, bijvoorbeeld bij sollicitatiegesprekken, waar blijkt dat de allereerste indruk bepalend is en niet meer door latere tegensprekende informatie opzij wordt gezet.
Waar wil ik naartoe? Mijn stelling is dat er grote verschillen zijn in de oordelen over gegeven bewijzen, als deze oordelen op onafhankelijke wijze worden gegeven. Denk dan niet alleen aan de collega verderop op dezelfde gang, maar ook aan docenten aan andere instellingen die hetzelfde vak geven. Of juist aan wiskundigen die jouw vak nooit hebben gedoceerd. Studenten die een hoog cijfer haalden en ondertussen een jaar verder zijn in de studie. Doe het experiment. Denk na over wat de resultaten betekenen voor de kwaliteit van het tentamineren. Stel een gewetensvraag: als een bewijs onafhankelijk is beoordeeld en gewaardeerd door drie docenten, krijgt de student van u dan
Hint: iedere beoordelaar is expert, de student is aankomend expert.
werkstuk: 1 2 3 4 5 6 7 8 9 10 ----------------------------------------------------- instructeur a 8 11 14 7 10 11 7 14 9 10 instructeur b 8 14 9 9 11 14 12 9 9 12 instructeur c 6 9 6 13 10 14 13 8 11 9 ----------------------------------------------------- hoogste oordeel 8 14 14 13 11 14 13 14 11 12 laagste oordeel 6 9 6 7 10 11 7 8 9 9
Dick Tromp (1979). Het oordeel van studenten in een individueel-studie-systeem. Onderwijs Research Dagen, 1979. De gegevens van Tromp zijn uitgebreider dan de tabel kan laten zien.
Stelling 13. Zoek de confrontatie met opvattingen van collega’s over tentamineren en beoordelen
Intervisie is in onderwijsland geen gangbaar begrip. Toch hebben docenten niet alleen sterke opvattingen over onderwijs en toetsen, maar verschillen deze opvattingen ook nog eens sterk, ook tussen directe collega’s. Hier is voor zover ik weet verdraaid weinig onderzoek naar gedaan, behalve mogelijk met veilige vragenlijstjes en oppervlakkige vragen. Hier heb ik zelf wel een klein interviewonderzoek gedaan, onder docenten binnen dezelfde faculteit aan de UvA (nee, geen wiskunde). Dat onderzoekje was toegespitst op opvattingen over tentamens, komt dat even mooi uit. Zelfs in deze kleine groep komen sterk wisselende opvattingen voor. Maar nog opvallender is dat deze docenten, evenals hun collega’s elders, hun opvattingen niet echt sterk kunnen articuleren en onderbouwen. Er is dus een enorme ruimte om inzichten in het fenomeen tentamineren te vormen en aan te scherpen, bijvoorbeeld door systematisch overleg met collega-docenten te organiseren — intervisie dus.
Enig systeem van intervisie lijkt een voorwaarde te zijn om tot een cultuuromslag in het tentamineren te komen. Zouden ze dat in Delft ook hebben begrepen?
Stelling 14. Bewijzen is ook een vorm van probleemoplossen, en dat lukt alleen wanneer de nodige stukjes informatie tegelijk mentaal beschikbaar zijn. Kortom: of dat bewijs wordt gevonden is een kwestie van kansrekening . . . (pfff, conjunctieve kansen; lijkt wel een examenregeling!) en psychologie (inzicht toetsen)
Ik schreef op 8 januari “Als bewijsvaardigheid de drempel is waarover velen struikelen, verandert dat de situatie? Mogelijk, maar dat ligt denk ik meer op de weg van Rainer, is die bewijsvaardigheid los te peuteren uit de stof voor analyse etc. Als dat zo zou kunnen zijn, is het misschien denkbaar een aanloop te organiseren met gedeeltelijk vrijstellende toetsen die specifiek gericht zijn op bewijsvaardigheid, bijvoorbeeld door niet zozeer ingewikkelde bewijzen te vragen, maar in hoog tempo eenvoudige bewijzen kunnen produceren. Het idee daarachter zou kunnen zijn dat verschillende bewijstechnieken behoorlijk geautomatiseerd beschikbaar moeten zijn om in staat te zijn complexe bewijsopgaven aan te pakken.”
De psychologie van probleemoplossen is allesbehalve eenvoudig. De beste tekst/theorie op dit moment is die Stellan Ohlsson (2011) Deep Learning, Cambridge University Press. Typisch voor probleemoplossen is dat er vaak een verkeerde start is: de beschikbare gegevens suggereren een bepaalde aanpak, maar die blijkt niet te werken. Dan is het heel moeilijk om die verkeerde aanpak los te laten, en je hersenmassa de gelegenheid te geven een andere mogelijkheid te opperen. Het springende punt is: dit probleemoplossen is niet echt geschikt voor tentamens waar in korte tijd en onder hoge druk wordt gewerkt. Althans, dan toets je niet of iemand de gestelde problemen goed kan aanpakken, maar of hij/zij dat met een superieur gemak kan, beter dan anderen. En dat is niet exact wat een tentamen bedoeld is te toetsen.
Dan de kansrekening. Als er twee stukjes informatie nodig zijn om een oplossing te geven, dan hebben we te maken met de waarschijnlijkheid a dat de student het eerste stukje informatie beschikbaar krijgt, idem b voor het tweede stukje informatie, dus a × b dat de student de oplossing ziet. Het stukje psychologie in de voorgaande alinea laat zien dat dit modelletje wel heel erg simpel is, maar laten we ons daar even niets van aantrekken. Het laat zich raden wat er gebeurt bij complexe problemen ...... . Zie ook het paper dat ik in 1998 hierover schreef, en dat een verdere ontwikkeling inhield van het tentamenmodel van Van Naerssen (1970).
Van Gool (2008)
Deze uitspraak van Chris Zaal is een prachtige illustratie van de stelling. Die extra twist maakt een probleem veel en veel moeilijker dan de docent in kwestie vermoedt. De kans om op die twist te komen is al knap gering, en moet vermenigvuldigd worden met de kans dat de student de andere benodigde elementen eveneens beschikbaar heeft en in combinatie met de twist kan zien. Hans Crombag heeft deze twist-opvatting van docenten scherp veroordeeld. Hij kwam deze namelijk in Leiden nogal eens tegen bij juristen die in hun onderwijs uitvoerig casusposities met twee procespartijen behandelden, en op het tentamen ineens casus presenteerden met drie procespartijen. Dan gaat de docent buiten de orde van het onderwijs, op het pad van de vergelijkende selectie (en waarvoor dan eigenlijk?).
Ik citeer hierbeneden uit mijn (1998 html) een modelvoorspelling met inzichtvragen, gecontrasteerd met dezelfde voorspelling maar dan voor enkelvoudige kennisvragen. De toets bestaat telkens uit 100 vragen.
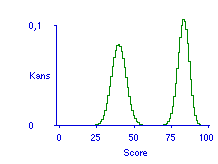
Gebruik het (2005) Java-applet om in de browser de simulatie en analyse ook voor andere parameterwaarden te doen.
En uit dezelfde publicatie de slotparagraaf, die prcies de door Chris Zaal aangekaarte opgaven met een ‘extra twist’ behandelt. Zie hoe dramatisch de slaagkansen kunnen terugvallen onder toevoeging van zo’n ‘extra twist’.
Het komt wel eens voor dat een afsluitende toets vragen bevat die meer inzicht eisen dan de vragen die in het onderwijs zijn behandeld en geoefend. Met hulp van het model valt nu te onderzoeken wat dat voor de doorzichtigheid van de toets betekent.
In Figuur 9 is te zien hoe een verdubbeling van het niveau van inzicht, een verdubbeling waar studenten zich niet goed op hebben kunnen voorbereiden, vergaande gevolgen kan hebben voor de slaagkansen. Studenten die in hun voorbereidingsstrategie rekening houden met inzichtvragen van niveau 3, maar in werkelijkheid vragen van niveau 6 krijgen, zien hun slaagkansen drastisch zakken. Een concreet voorbeeld zou een tentamen rechten kunnen zijn waar studenten casusposities met drie partijen krijgen voorgelegd, waar in het onderwijs slechts casusposities met twee partijen zijn behandeld. Twee partijen plus de relatie tussen die partijen zou inzichtniveau 3 kunnen zijn. Drie partijen met de relaties tussen die partijen is dan inzichtniveau 6.
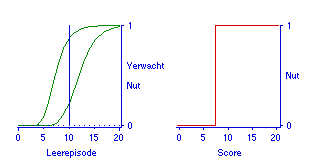
Gebruik het (2005) Java-applet 'Expectation' Java-applet 'The Ruling'om in de browser de analyse en de nutsfunctie ook voor andere parameterwaarden te doen.
Het verschil in slaagkansen is dramatisch. Vergelijk daarvoor in Figuur 9 op een gegeven punt in het studiepad verticaal daarboven de slaagkans voor de eerste en de tweede situatie. Het ligt niet aan de operationalisatie van inzicht dat het verschil zo dramatisch is, die operationalisatie is wat de moeilijkheid van inzichtvragen betreft conservatief. Het spaarzame model, waarin alleen beschikbare kennis een rol speelt, ziet immers af van de mogelijkheid dat inzichtvragen ook nog moeilijker kunnen zijn omdat voor het bereiken van inzicht het niet toereikend is alleen de nodige kennis beschikbaar te hebben .
Het model zou een verklaring kunnen geven voor hardnekkig lage slaagpercentages bij tentamens waarin nadrukkelijk om inzicht wordt gevraagd, maar waar het de docenten ontbreekt aan goed begrip van de gevolgen die dat voor de moeilijkheid van de vragen heeft.
De hierboven geciteerde publicatie is de weergave van een voordracht in Groningen 1998, waar een belangrijk deel van de onderzoekers en adviseurs van universitaire onderwijsonderzoek- of adviescentra aanwezig waren, zeg maar van Wynand Wijnen tot jongste collega’s. Waarom anno 2012 er dan nog steeds uit de hand gelopen tentamensituaties voorkomen, is een goede vraag. De analyse is immers glashelder, de beschikbare reparatiemogelijkheden zijn evident. Tom Poes heeft de list al enige tijd geleden verzonnen, Heer Bommel mist het ‘inzicht’ in de list.
Opleidingen die volharden in gewoonten van vergelijkende beoordeling die resulteren in hoge studieuitval, zijn bezig zichzelf daarmee op te heffen: de (financiële) risico’s voor hun potentiële studenten zijn torenhoog geworden.
Stelling 15. Ga niet winkelen in deze stellingen: om struikelvakken aan te pakken is integraal beleid op al deze fronten nodig.
Ik hoop dat na het lezen van de toelichting op de voorgaande 14 stellingen, de waarheid van stelling 15 in graniet staat gegrift. Of zoiets, toch?
Sam van Gool (2008). Analyse 1: onvermijdelijk struikelvak? Rapport in opdracht van de opleidingscommissie Wiskunde. (pdf is gemaild aan de deelnemers)
Universiteit Leiden (2009). Task Force Studiesucces. Eerste advies. pdf
Werkgroep Studiesucces (2009). Studiesucces aan de Universiteit van Amsterdam. pdf [Dymph van den Boom (2009). Plan van aanpak pdf
Koersen op studiesucces. TU Delft. pdf [reactie van Lijst βèta hier]
Mijn presentatie liep een beetje in het honderd, ik hoop maar dat dat niet al te opvallend was. Op een laat moment bleek dat mijn eigen laptop niet was aan te sluiten op de beamer (ik was te gast bij wiskunde en informatica, TU Eindhoven), en dat ik zelf niet overweg kon met de laptop van Joost Hulshof waarop ik wel de beschikking had over deze webpagina. Een tikje op het verkeerde been gezet, merkte ik na korte tijd dat ik een verhaal aan het houden was, in plaats van meteen de discussie te starten, zoals het voornemen was. De aftrap van de discussie ging meteen in de richting van selectie (vragen uit Utrecht), een kant die ik niet uit wilde omdat het een ander onderwerp is, maar waar ik toch met enige tegenzin op in ging. Ik zal er inhoudelijk straks iets meer over noteren. Daarna liep het wel, vooral dank zij de interventie van Erik Koelink, die wel met dat laptopje om kon gaan, en enkele stellingen prikte voor discussie. (Mijn plan B was om aan de hand van de stellingen te discussiëren; ik had een plan C moeten hebben: een briefje met een vijftal onderwerpen, voor het geval plan B zou haperen. Mijn volstrekte onervarenheid als docent wreekte zich hier ..... ) Ik hoop ondanks het zijpad van de selectie toch duidelijk gemaakt te hebben dat ‘struikelvakken’ niet noodzakelijk zijn, dat er maatregelen genomen kunnen worden, en dat het waarschijnlijk nodig is om een gebalanceerd pakket van maatregelen te nemen. Dat is nodig omdat anders is te voorspellen dat positieve effecten van een enkele maatregel (denk aan: ofwel compensatie, ofwel rationeler omgaan met de moeilijkheid van bewijsopgaven) dan uit zullen blijven. (Overigens begrijp ik uit een bericht in De Volkskrant van 30 januari, dat er door de affaires rond ten onrehcte uitgereikte diploma’s, zoals bij InHolland 2011, nu een klimaat is ontstaan waar discussie over compensatie in examenprogramma’ in de sfeer wordt getrokken van verlichting van exameneisen en dus diploma-inflatie. Wat baarlijke nonsens is, mar leg dat maar eens uit (zie de stellingen daarvoor).
Selectie. Op zich is het natuurlijk terecht dat in de discussie de selectie van studenten aan de orde kwam, want hoe docenten denken over de ongeschiktheid van studenten is mede een oorzaak van het fenomeen van struikelvakken. Zie ook stelling 13, over opvattingen van docenten, hoe die niet alleen van elkaar kunnen verschillen, maar ook uit de pas kunnen lopen met wat op goede wetenschappelijke gronden bekend is over selectie enzovoort. Ik wil er op deze plaats in heel kort bestek iets over zeggen, want op deze website van mij is juist over dit onderwerp ongelooflijk veel materiaal beschikbaar, om te beginnen de voordracht voor de HS Zuyd (voor het HBO is de selectieproblamtiek complexer dan voor het WO, maar overigens natuurlijk gewoon hetzelfde).
De opvatting dat struikelvakken terecht struikelvakken zijn, omdat sommige studenten nu eenmaal niet in staat zullen zijn de opleiding wiskunde met succes af te ronden, is voor falsificatie vatbaar. Ik geef een paar argumenten. Als docent weet je niet zomaar of een onvoldoende resultaat voor een struikelvak te wijten is aan onvoldoende doorzittingsvermogen en intellectuele capaciteiten van de betreffende student(en). De situatie is dezelfde als bij het testen van intelligentie: een hoge score bewijst intelligentie, een lage bewijst niet het omgekeerde. Er is bij dit soort testen en toetsen sprake van asymmetrie: het is niet mogelijk te doen alsof je intelligent bent, of je Analyse tot in de puntjes beheerst; het is wèl mogelijk om zo’n test of toets beroerd te maken om allerlei redenen die niet hebben te maken met intellectuele capaciteiten. Om ieder misverstand uit te sluiten: een belangrijke reden voor lage scores op struikelvakken kan zijn dat studenten zich er niet goed op willen voorbereiden, er dus geen grote investering in willen doen. Iedere opleiding met een verstandige opleidingscommissie zal willen weten waarom veel studenten, of misschien maar een kleine groep, zich niet zo goed op het betreffende tentamen wil voorbereiden dat ze een behoorlijke slaagkans hebben. Zie stelling 1, en diverse andere stellingen.
Maar laat ik eens meedenken met de stelling dat vooral het eerste studiejaar selectief moet zijn, in de zin van de wet: dat studenten in staat zijn om op inhoudelijke gronden hun studiekeuze te bevestigen of te herzien. Ik zie hier maar even af van de problematiek van bindende studieadviezen: universiteiten die gebruik maken van de bevoegdheid om BSA’s af te geven, bewijzen zichzelf daarmee geen dienst (het is hetzelfde probleem als selectie-aan-de-poort, maar dan een jaar of twee jaar later; de Universiteit Leiden heeft met het schaamrood op de kaken moeten erkennen dat die zo graag gewilde selectie-aan-de-poort meer nadelen dan voordelen brengt). Oké; wanneer dan het idee is om de relatief minder intelligente studenten middels struikelvakken aan het verstand te peuteren dat ze beter iets anders kunnen gaan studeren dan wiskunde, wees dan zo moedig om geruime tijd voor de aanvang van de studie alle vwo-ers die zich hebben opgegeven, aan een stevige intelligentietest te onderwerpen. Hoe zo iets gaat: zie de evaluatie (1990) van de selectie voor de Nederlandse Politie Academie html. Ik zeg er meteen maar bij dat het grootste probleem dan is: meer kandidaten krijgen ten onrechte het advies om geen wiskunde te gaan studeren, dan er terecht dat advies krijgen. Ik zie nog maar even af van het kleine probleempje dat eigenlijk niet valt te bewijzen dat welke afwijzing dan ook met grote waarschijnlijkheid ‘terecht’ is, afgezet tegen criteria die ver in de toekomst liggen (bekwaam wiskundige zijn). Het is hetzelfde probleem als bij het inzetten van de leugendetector om leugenaars te identificeren: er zijn maar weinig leugenaars, dus het is voorspelbaar dat met een leugendetector er meer mensen ten onrechte als leugenaar worden aangemerkt, dan er terecht als leugenaar worden aangemerkt. Zo’n instrument mag dus never ever ooit worden gebruikt.
Interessante thematiek, niet?
![]() http://www.benwilbrink.nl/publicaties/12struikelvakkenICAB.htm
http://www.benwilbrink.nl/publicaties/12struikelvakkenICAB.htm