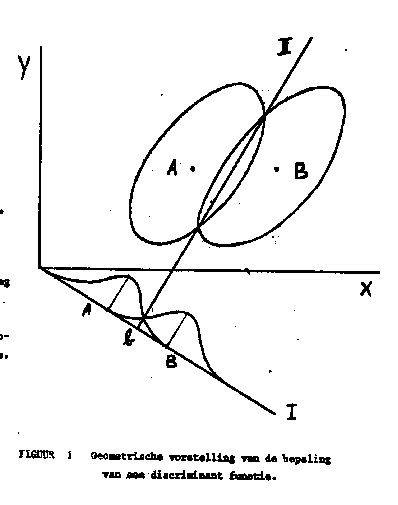
FIGUUR 1 Geometrische voorstelling van de bepaling van een discriminant functie.
Gegeven zijn Cattell 16 PF [16 Personality Factor Questionnaire] scores voor eerstejaars van 1967 en van 1968, de studie-keuzen die zij gemaakt hebben, en een Algol programma voor multiple discriminant analyse en klassificatie van individuen (van de Wijgaart en Schell, 1968 ).
Dit materiaal vormde een uitnodiging om te onderzoeken of de 16 PF in staat is te discrimineren tussen de zeven studierichtingen die de T.H.E. als mogelijkheden biedt, nl. : Bouwkunde, Bedrijfskunde, Wiskunde, Natuurkunde, Werktuigbouwkunde, Technologie en Electrotechniek. Het discriminant analyse programma geeft de mogelijkheid om te toetsen of het onderscheidend vermogen van de gebruikte predictor-variabelen (de 16 PF ) significant is.
Wanneer de 16 PF blijkt te discrimineren tussen de verschillende studierichtingen, bestaat er dan een bepaalde samenhang tussen het 16 PF profiel en de studiekeuze? Zo ja, is het mogelijk deze samenhang te beschrijven, uitgaande van de door Cattell gegeven omschrijvingen van de persoonlijkheids-factoren ?
Een geheel andere doelstelling van dit onderzoek is exploratie van de mogelijkheden die de discriminant analyse en klassificatie techniek bieden voor differentieel onderzoek. Aandacht zal daarom besteed worden aan de werking van de discriminant analyse en interpretatie van de resultaten in termen van bruikbaarheid van deze techniek, zowel als in termen van betekenis in verband met de eerder genoemde doelstelling.
Een onderzoek op zich, dat gebaseerd kan worden op de resultaten van dit onderzoek, is dat naar de construct-validiteit van de 16 PF. Vragen als : tot hoeveel dimensies kan de 16-dimensionale testruimte teruggebracht worden zonder belangrijk verlies aan discriminerend vermogen?, en: is er overeenstemming tussen eventueel gevonden significante discriminant functies en de in andere onderzoekingen gevonden onderliggende dimensies ( secondary factors ) zoals bijvoorbeeld introversie - extraversie, en anxiety ( neuroticism) ? , deze vragen zijn belangrijk in verband met de construct validiteit van de 16 PF.
Cooley and Lohnes (1962) geven een uitstekende uiteenzetting over multiple discriminant analyse en klassificatie procedures, waarvan bij de volgende bespreking een dankbaar gebruik is gemaakt.
Doel van de multiple discriminant analyse is de groepen die verschillende studiekeuzen hebben gedaan, zo duidelijk mogelijk te onderscheiden door optimale weging van de oorspronkelijke testvariabelen, wat gebeurt door het bepalen van één of meer significante discriminant functies. Wanneer het predictieve vermogen van de test niet door één discriminant functie uitgeput wordt, kunnen meerdere functies, orthogonaal op elkaar, berekend worden.
Aan de hand van een geometrische interpretatie van de discriminant analyse zal de werking geschetst worden. ( fig. 1, overgenomen uit Cooley and Lohnes)
FIGUUR 1 Geometrische voorstelling van de bepaling van een discriminant functie.
Toelichting fig. 1: voorgesteld is een bivariate plot voor 2 groepen, A en B. 2 Tests, X en Y, zijn positief gecorreleerd. De ellipsen zijn zgn. centile contouren, kortweg centouren genoemd (zie tekst). Lijn 1 is de ééndimensionale discriminant ruimte.
Figuur 1 toont een bivariate plot voor twee groepen, A en B. Twee tests, X en Y, zijn positief gecorreleerd. ledere ellips in het diagram stelt voor de plaats van punten van gelijke dichtheid (of frequentie) voor een bepaalde groep. De getekende ellipsen bepalen bijv. het gebied waarbinnen 90 % van de punten behorende bij de resp. groep ligt. De grootte van de ellips, of de afstand van de ellips tot het groepsgemiddelde (de groeps-centroide), is uit te drukken in chi-kwadraat. Dus voor ieder punt xij zijn aan te geven de afstanden tot iedere groeps-centroide in termen van de proportie steekproefpunten waarvan verwacht wordt dat zij buiten de ellips liggen waar xij op ligt. Deze ellipsen noemen we centouren (centile contouren) . De twee punten waar corresponderende centouren elkaar snijden definiëren een rechte lijn II. Wanneer de tweede rechte lijn I loodrecht op II gezet wordt en wanneer dan de punten in dit vlak geprojecteerd worden op I, zal de overlapping tussen de twee groepen kleiner zijn dan voor iedere andere mogelijke lijn. De discriminant functie nu transformeert de individuele testscores tot een enkele discriminant score, die de plaats van ieder individu op lijn I bepaalt. Het punt waar lijn I lijn II snijdt verdeelt de eendimensionale discriminant-ruimte in twee gebieden : waarschijnlijk lidmaatschap van A, resp. B.
Eén van de belangrijke voordelen van de multiple discriminant analyse blijkt eveneens uit fig. 1: de discriminant functie I heeft een hoge lading op variabele X, een kleinere lading op variabele Y. We zien dus dat var. Y een bijdrage levert aan de klassificatie (predictie van groepslidmaatschap) en dit gebeurt ondanks het feit dat de gemiddelden van A en B op variabele Y gelijk zijn! Voor individuen met gemiddelde X scores is de Y score dus bruikbaar voor de juiste klassificatie.
De getoonde procedure blijft in principe dezelfde wanneer we werken met meerdere variabelen, groepen en eventueel discriminant functies.
Multiple discriminant analyses werden uitgevoerd voor een groep van eerstejaars in 1968 ( allen die op de introductiedagen aanwezig waren,), en voor een groep van 504 eerstejaars in 1967 (ook allen die op de introductiedagen aanwezig waren). Van deze individuen zijn 16 PF scores bekend (Form B).
Met behulp van de 1968 discriminant functies (d.w.z. de functies die op deze groep ontwikkeld werden), werden twee klassificaties verricht: op de 645 eerstejaars van 1968, en op de 504 eerstejaars van 1967 (bij wijze van kruis-validatie).
Met behulp van discriminant functies ontwikkeld op de groep van 1967 werd op dezelfde groep een klassificatie programma uitgevoerd.
Het onderscheidende vermogen van de 16 PF wordt aangegeven door Wilks' lambda, welke een functie is van de wortel van W-1 A (W-1 is de inverse van de binnen-groepen spreidingsmatrix, en A is de tussen groepen spreidingsmatrix). De grootte van Wilks' lambda bedraagt .713, p .00001. De 16 PF blijkt dus significant te discrimineren tussen de zeven studierichtingen.
Wanneer we dit weten, is het zinvol te kijken naar de gevonden discriminant functies en hun respectievelijke bijdragen aan het onderscheidende vermogen (ofwel 'spoor') van de test. (Wanneer de test niet onderscheidt, hebben de gevonden discriminant-functies geen enkele betekenis). Het criterium voor significantie van de discriminant functies is, dat zij 80 - 90 % van het spoor verklaren. Volgens dit criterium zijn er 4 significante functies, de eerste 4 functies verklaren n1. respectievelijk 47,3 %, 24,3 %, 13,8 % en 6,8 % van het spoor. We zien dus grote verschillen in importantie van de 4 functies.
Deze 4 functies bepalen een vier-dimensionale ruimte, waarin iedere studie, en iedere individu, door een punt gelocaliseerd kan worden. Ter illustratie worden in figuur 2 en 3 de discriminantvlakken met groeps-centroiden weergegeven, zoals die bepaald worden door de discriminant-functies I en II, resp. III en IV. Hieruit zijn ook de overige 4 discriminant-vlakken eenvoudig af te leiden. In tabel I worden voor iedere studierichting de groeps-centroiden gegeven, met in tabel II de bijbehorende standaarddeviaties.
Tabel I. Centroiden van de studierichtingen in de discriminant-ruimte
-------------------------------------- Functie: I II III IV -------------------------------------- B 1768 758 1198 220 Bdk 1790 457 1181 281 N 1562 684 1161 225 E 1468 642 1162 166 T 1564 636 1232 299 W 1553 622 1210 279 Wsk 1479 679 1346 117 --------------------------------------
[De juistheid van de scan is gecontroleerd]
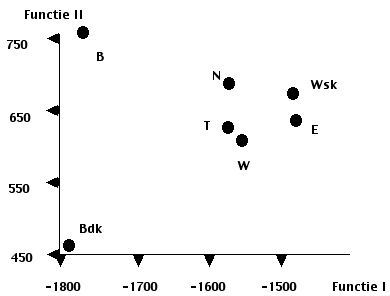
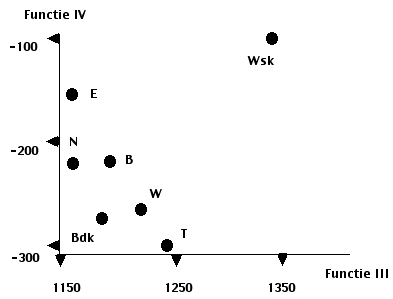
Figuur 2 en 3. Centroiden van de 7 studierichtingen in twee discriminantvlakken
Tabel II. De standaarddeviaties van de discriminant-scores per studierichting
-------------------------------------- Functie: 1 2 3 4 -------------------------------------- B 264 267 223 330 Bdk 258 258 233 367 N 284 267 195 341 E 298 265 222 324 T 280 268 200 343 W 280 296 209 274 Wsk 297 252 211 389 --------------------------------------
[De juistheid van de scan is gecontroleerd]
Kijken we eerst naar de belangrijkste discriminant-functie, functie I (47,32 % van het spoor), dan zien we uit figuur 2 dat op deze dimensie 2 groepen van elkaar onderscheiden worden: B - Bdk vs E - N - T - W- Wsk, van de laatste groep worden Wsk en E dan nog weer iets beter onderscheiden dan T, N en W. Op discriminant-functie 11 (24,3 % van het spoor) worden van elkaar onderscheiden B en Bdk, met de overige vijf studierichtingen daar ergens tussenin. Op de derde, aanzienlijk minder belangrijke functie (13,8 % van het spoor) wordt Wsk onderscheiden van de overige. Interpretatie van discriminant-functie IV wordt een hachelijke zaak, deze functie verklaart nog slechts 6,8% van het onderscheidende vermogen van de test, bovendien is de variantie op deze dimensie aanzienlijk groter dan op de overige dimensies; met enige goede wil kunnen we zeggen dat hier Wsk en T onderscheiden worden (hierop zal bij de bespreking van de klassificatie nog verder ingegaan worden.).
Om de aard van de discriminant-functies te interpreteren is het nodig om te kijken naar de factoren waardoor deze functies bepaald worden. Wanneer we kijken naar de tabel met groepsgemiddelden en discriminantfunctie gewichten voor iedere factor (tabel III), dan zien we dat iedere functie wel een klein aantal gewichten telt die bijzonder groot zijn, en dat op deze factoren er vaak grote verschillen in gemiddelden zijn tussen B en/of Bdk en de overige studierichtingen.
TABEL III Discriminant analyse 16 P.F. 1968
-----------------------------------------------------------------
B Bdk N E T W Wsk I II III IV
-----------------------------------------------------------------
A 9,1 10,9 7,7 7,5 8,2 8,1 8,5 -45,1 -40,3 15,0 41,6
B 8,8 9,0 9,0 8,8 8,7 8,7 8,5 5,7 8,2 19,0 6,6
C 15,5 16,5 15,5 15,5 15,5 15,8 15,2 8,2 3,7 6,4 11,6
E 12,9 14,1 12,8 13,2 13,3 13,7 12,4 5,5 -25,6 5,7 8,0
F 12,9 12,2 11,8 11,0 12,5 12,0 12,7 3,7 29,6 36,9 8,9
G 11,8 11,8 11,9 12,0 11,8 11,7 11,7 12,1 8,5 7,3 1,8
H 11,9 14,2 11,2 10,0 12,1 11,5 9,7 -23,3 -9,4 7,7 55,7
I 9,9 8,6 8,5 8,2 8,5 8,6 8,4 28,8 29,9 13,3 16,3
L 11,6 11,3 11,1 10,9 11,2 11,4 11,4 -21,0 -0,0 5,7 2,5
M 14,7 12,5 12,9 12,3 12,1 11,9 11,8 -44,3 34,1 -30,4 21,7
N 12,2 12,5 11,7 11,9 12,1 11,9 11,2 0,8 4,9 8,8 4,4
O 11,5 9,9 11,8 11,6 11,1 11,0 12,8 15,9 10,6 20,3 22,6
Q1 12,8 13,3 12,6 12,6 12,9 12,6 13,3 3,3 18,9 27,6 15,0
Q2 11,0 10,3 10,7 10,6 10,7 10,9 10,5 7,5 5,1 2,3 30,2
Q3 11,8 12,3 11,5 12,4 12,5 12,2 12,1 7,8 10,5 28,6 0,6
Q4 13,0 11,6 12,8 12,3 12,7 12,9 13,9 6,1 14,0 23,9 12,9
-----------------------------------------------------------------
[De juistheid van de scan is gecontroleerd]
Analyseren we discriminant-functie I, dan kunnen we allereerst constateren dat A en M bijzonder sterk bijdragen aan de discriminant-score, en dat H, I en L dat in mindere mate doen. We hebben uit figuur 2 gezien dat op deze functie B en Bdk enerzijds en E, N, T W en Wsk anderzijds onderscheiden worden. Het overzicht van de groepsgemiddelden (tabel III) laat zien dat op factor:
Deze functie wordt gekarakteriseerd doordat zij onderscheidt tussen enerzijds; koelheid (A-), conventionaliteit (M-), verlegenheid (H-), realisme (I-), en openheid (L-)voor E, N, T, W, en Wsk, en anderzijds: warmte (A+) excentriciteit (M+), aktiviteit (H+), gevoeligheid (I+), en achterdochtigheid (L+) voor B en Bdk. (Factor L past niet in dit patroon. Waarschijnlijk hebben we hier te doen ,met een factor die, ondanks het ontbreken van belangrijke verschillen tussen de groepsgemiddelden aan de discriminant-functie bijdraagt. Een bespreking op welke wijze dit gebeurt wordt gegeven in Bijlage A.)
Uitgaande van de omschrijvingen door Cattell c.s. (1957) gegeven, kunnen we zeggen dat deze discriminant-functie definieert een dimensie:
We concluderen dat de eerste discriminant-functie, die 47,3 procent van het onderscheidend vermogen van de 16 PF test, voor het onderscheiden van deze zeven studierichtingen, verklaart, dat doet doordat zij een factor OPENHEID VOOR DE OMGEVING representeert.
Discriminant-functie II ontvangt grote bijdragen van factoren A, M, I, F en E, in volgorde van grote tot kleinere gewichten. Figuur 2 laat zien dat op deze functie van elkaar onderscheiden worden bouwkunde en bedrijfskunde, met de overige studierichtingen ergens in het midden. Wanneer we nu weer teruggaan naar tabel III, dan is het belangrijk daarbij te letten op de gemiddelden van B en Bdk t.o.v. elkaar en t.o.v. de overige 5 studierichtingen, en dat te doen voor de bovengenoemde 5 factoren.
We zien dat op factor:
Deze functie wordt gekarakteriseerd doordat zij onderscheidt tussen enerzijds: warmte (A+), en dominantie (E+) voor Bdk, en anderzijds: excentriciteit (M+), minder warmte (A0), en gevoeligheid (I+) voor B.
Uitgaande van Cattell's omschrijvingen kunnen we zeggen dat deze discriminant-functie definieert een dimensie:
Hieruit trekken we de conclusie dat de tweede discriminant- functie, die 24,3 procent van het onderscheidend vermogen van de test verklaart, dat doet doordat zij een factor FUNCTIONEREN IN GROEPSVERBAND representeert.
Discriminant-functie III. Uit figuur 3 zien we dat op deze functie Wsk onderscheiden wordt van de vorige studierichtingen. Uit tabel III blijkt dat om deze functie de factoren F, M, Q3, Q1, Q4 en O bijdragen. Kijken we naar de groepsgemiddelden op deze factoren, dan zien we dat op factor:
Uit het bovenstaande komt inderdaad het beeld naar voren dat we in figuur 3 zien, nl. een onderscheid tussen de groep N, E, Bdk en B enerzijds en Wsk anderzijds, met T en W ergens in het midden. Wanneer we een lijstje maken waardoor deze discriminant-functie gekarakteriseerd wordt, dan merken we dat we het lage eind van de discriminant-functie alleen kunnen karakteriseren door dit te definiëren in termen van: niet sober (F0), niet excentriek (M0) etc. Vermelden we bij iedere factor eveneens welke studierichting hier van de overige onderscheiden wordt, dan zien we dat ieder van de groep N, E, B en Bdk op andere factoren van de overige onderscheiden wordt. Hieruit ontstaat een complex beeld, waaruit het zeer moeilijk is een algemeen kenmerk van daze discriminant-functie te destilleren. We zien hier, evenals voor discriminant-functie IV, dan ook af van het naamgeven. Waarschijnlijk doet zich hier gevoelen, dat we gebruik maken van een multivariate techniek, waarbij intercorrelaties tussen factoren, en studierichtingen, een grote, maar niet meer overzienbare, bijdrage aan het onderscheidende vermogen van de test leveren.
Het overzicht:
| (E) | sober | (F-) | vs. niet sober | (F0) (overige studierichtingen) |
| (B) | excentriek | (M+) | vs. niet excentriek | (M0) (overige) |
| (N) | ongecontroleerd | Q3-) | vs. niet ongecontroleerd | (Q30) (overige) |
| (E) | conservatief | (Q1-) | vs. niet conservatief | (Q10) (overige) |
| (Bdk) | gelijkmatig | (Q4-) | vs. niet gelijkmatig | (Q40) (overige) |
| (Bdk) | zelfvertrouwen | (O-) | vs. geen zelfvertrouwen | (O0) (overige) |
Discriminant-functie IV verklaart nog slechts 6,9% van het spoor, en omdat we hier dezelfde interpretatie-moeilijkheden voorzien als bij functie III, zien we van een analyse van de werking van deze functie af.
De resultaten van de discriminant analyse 1968 overziend, kunnen we zeggen dat 71,6% van het vermogen van de 16 PF om te onderscheiden tussen de zeven studierichtingen verklaard worden door een factor die we voorlopig openheid voor de omgeving genoemd hebben (47,3%), en door een factor die we functioneren in groepen genoemd hebben (24,3%).
De benoeming van deze eerste twee discriminant-functies is slechts tentatief, verder onderzoek zal moeten uitwijzen of deze juist zijn. Wat betreft de factor "openheid voor de omgeving" zou onderzocht kunnen worden of er overeenkomst is met de "open and closed mindedness" zoals die uit de onderzoekingen van Rokeach gebleken zijn, of met het divergent versus convergent denken zoals dat door Guilford onderzocht is.
Het principe op grond waarvan geklassificeerd wordt is onder Methode reeds behandeld. Voor ieder individu wordt, voor ieder van de groepscentroiden, de waarde χ2 = xiD-1xi (Cooley and Lohnes 1962) berekend, waarbij chi een maat is voor de dichtheid op een bepaald punt van de puntenwolk. De chi2 tabel geeft (voor df = m, waarbij m = aantal dimensies van de discriminant ruimte, in ons geval m = 4 ) de proportie van degenen die nog verder van de groepscentroide af liggen. leder individu wordt dan geklassificeerd in die groep, waarvoor zijn chi2 het laagst is.
Deze procedure is bruikbaar wanneer van de klassificatie-groepen a-priori verwacht mag worden dat zij even groot zijn, wanneer wij kunnen verwachten dat er bijvoorbeeld evenveel mensen wiskunde kiezen als dat het geval is voor technologie. Het blijkt echter dat er nogal grote verschillen zijn in de aantallen per studierichting, wiskunde kreeg 37, technologie 140 studenten. Wanneer in een dergelijk geval de boven geschetste klassificatieprocedure gebruikt wordt, zullen er te veel mensen bij Wsk, en te weinig bij E geklassificeerd worden.
Cooley and Lohnes (1962) geven een waarschijnlijkheids functie, afgeleid uit het theorema van Bayes, die zowel rekening houdt met verschillen in frequentie van lidmaatschap voor de diverse groepen, als met verschillen in groeps-spreidingen. Het algol programma 0206-1778 maakt van deze formule gebruik. Wanneer bij klassificatie gebruik gemaakt wordt van de output van het discriminant analyse programma, A o206-1777, dan levert deze output tevens de gegevens over de te verwachten grootte van de groepen, waarop de klassificatie afgestemd wordt. Deze grootte van de groepen is afhankelijk van de input van het discriminant analyse programma, wat in ons geval betekent dat de a-priori verwachte grootte van de groepen dezelfde zal zijn als de waargenomen grootte ( eerste kolom tabel IV ). Wanneer we het klassificatie programma uitvoeren op een nieuwe groep, dan kunnen we de verwachting uitdrukken in percentages ( tweede kolom )
De output van het klassificatie programma geeft voor ieder individu de kansen (in proporties uitgedrukt) om in ieder van de 7 studierichtingen geklassificeerd te worden. De klassificatie gebeurt dan bij die groep waarvoor de proportie het grootst is (eventueel, bij gelijke proporties, in meerdere groepen).
TABEL IV. De a-priori verwachting van de grootte van de groepen. (analyse 1968)
| studierichting | verwachting verdeling | verwachting in % |
| voor groep 1968 | ||
| B | 105 | 16,3 |
| Bdk | 65 | 10,0 |
| N | 88 | 13,6 |
| E | 144 | 22,3 |
| T | 130 | 20,2 |
| W | 73 | 11,3 |
| Wsk | 39 | 6,0 |
We kunnen nu tellen hoeveel individuen, die steeds één studierichting werkelijk gekozen hebben, in deze groep geklassificeerd worden (juiste klassificaties), of in welke van de overige groepen (onjuiste klassificaties). Een overzicht hiervan (tabel V) kan dan dienen om te toetsen of het verkregen resultaat significant beter is dan op grond van kans te verwachten is. Hiervoor kunnen we de chi2 toets gebruiken, waarbij we de verwachte cel-frequenties berekenen door uit te gaan van de rij- totalen (aantal individuen die een bepaalde studierichting werkelijk gekozen hebben) en de verwachting van de kolom-totalen, die bij klassificatie van andere dan de groep waarop de analyse verricht is, zullen verschillen van de rijtotalen. De chi2 is dan 424,68 ( p < .001 ), de klassificatie is dus significant beter dan kans. Zij is beter, want 222 van de 666 klassificaties zijn juist (33,3 %). (Het totaal van 666, terwijl er maar 645 personen zijn, ontstaat door gelijke klassificatie kansen waardoor sommige individuen in meer dan één groep geklassificeerd worden )
We kunnen de verwachte celfrequenties ook berekenen door uit te gaan van de werkelijke i.p.v. de verwachte kolom-totalen. Bij gebruikmaking van een klassificatie formule met a-priori verwachting over de relatieve frequenties binnen de groepen , blijkt namelijk het risico te bestaan dat groepen met relatief kleine verwachte frequenties te weinig klassificaties zullen krijgen (zie Cooley and Lohnes 1962). In bijlage B wordt aangegeven hoe, bij gelijke verwachte frequenties, bij een bepaalde groep toch te weinig klassificaties voor kunnen komen; op de daar geschetste wijze kunnen ook bij ongelijke verwachte frequenties bepaalde groepen te weinig klassificaties krijgen.
We mogen dan verwachten dat de zeer kleine aantallen klassificaties die we vinden bij Natuurkunde en Werktuigbouw, ook bij nieuwe te klassificeren groepen verkregen zullen worden, m.a.w. dat deze kleine aantallen geen toevallig resultaat zijn. Maar dan is het ook redelijker bij de berekening van chi2 uit te gaan van de werkelijk verkregen kolom-totalen, en niet van de verwachte totalen. We vinden dan als waarde voor chi2 : 191,29 (p < .001). We vinden nu een kleinere chi2, maar ook bij deze berekeningswijze vinden we dat de klassificatie significant beter dan kans is.
In tabel V zien we uit de chi2 waarden voor iedere rij, dat de klassificaties voor B, Bdk en Wsk (!) grote chi2 waarden geven, voor N en W zien we beduidend kleinere. We kunnen dit zo interpreteren dat voor B, Bdk en Wsk geldt dat van de totale aantallen individuen die hierin geklassificeerd worden (de kolom-totalen), een groot aantal juist geklassificeerd wordt, en dat van hen die werkelijk tot deze groepen behoren (de rij-totalen), een groot aantal ook binnen hun eigen groep geklassificeerd wordt. Voor N en W geldt dat een groot deel van hen die hier ingedeeld zijn (kolomtotalen) onjuist geklassificeerd zijn.
TABEL V. Klassificatie van de criterium groep (discr. analyse 1968)
| werkelijke | voorspelde keuze | rij- | chi 2 | overschr. | ||||||
| keuze | B | Bdk | N | E | T | W | Wsk | tot. | kans | |
| B | 56 | 10 | 2 | 19 | 22 | 1 | 1 | 111 | 44,10 | .001 |
| Bdk | 16 | 23 | 1 | 13 | 13 | 0 | 0 | 66 | 44,24 | .001 |
| N | 24 | 6 | 2 | 36 | 25 | 0 | 2 | 95 | 3,41 | .800 |
| E | 22 | 13 | 3 | 71 | 35 | 0 | 4 | 148 | 18,95 | .010 |
| T | 21 | 8 | 1 | 39 | 62 | 1 | 1 | 133 | 24,34 | .001 |
| W | 16 | 8 | 1 | 26 | 22 | 1 | 0 | 74 | 8,02 | .300 |
| Wsk | 6 | 2 | 0 | 13 | 10 | 1 | 7 | 39 | 48,23 | .001 |
| kolom- | ||||||||||
| totalen | 121 | 70 | 10 | 217 | 189 | 4 | 15 | 666 | 191,29 | .001 |
Op grond van de test-scores van de eerstejaarsgroep 1968 werd de 16-dimensionale test-ruimte, door multiple discriminant analyse, gereduceerd tot een 4-dimensionale discriminant-ruimte, die een optimale klassificatie voor de groep 1968 bewerkstelligt. De aantallen juiste klassificaties vormen een indicatie voor de mate van minimum overlapping tussen de zeven studierichtingen. Wanneer we een nieuwe groep eerstejaars gaan klassificeren, m.a.w. in reële zin de studiekeuze gaan voorspellen, dan zullen we vinden dat de percentages juiste klassificaties minder zijn dan bij classificatie van de criterium groep (shrinkage). Tabel VI geeft een overzicht van de klassificaties, met als resultaat een chi2 van 102,11, i.t.t. 191,29 voor de klassificatie van de criterium groep. Het aantal personen bedraagt 504, het aantal klassificaties is, door enkele gelijke klassificatiekansen, iets groter: 523.
TABEL V. Klassificatie van de criterium groep (discr. analyse 1968)
| werkelijke | voorspelde keuze | rij- | chi 2 | overschr. | ||||||
| keuze | B | Bdk | N | E | T | W | Wsk | tot. | kans | |
| B | 27 | 2 | 0 | 10 | 18 | 0 | 2 | 59 | 28,16 | <.001 |
| Bdk | 7 | 18 | 0 | 11 | 13 | 2 | 3 | 54 | 35,91 | .001 |
| N | 18 | 6 | 1 | 22 | 18 | 2 | 1 | 68 | 4,96 | .70 |
| E | 12 | 5 | 0 | 44 | 30 | 3 | 0 | 94 | 15,86 | .02 |
| T | 19 | 14 | 2 | 44 | 19 | 0 | 4 | 122 | 6,94 | .50 |
| W | 14 | 4 | 0 | 21 | 25 | 0 | 4 | 68 | 4,79 | .70 |
| Wsk | 8 | 5 | 0 | 24 | 17 | 0 | 4 | 58 | 5,49 | .50 |
| kolom- | ||||||||||
| totalen | 105 | 54 | 3 | 176 | 160 | 7 | 18 | 523 | 102,11 | .001 |
Bij de berekening van chi2 is weer uitgegaan van de gegeven rijen kolomtotalen. Merk op dat de kolom-totalen in' relatieve grootte hetzelfde-beeld te zien geven als de kolom-totalen uit tabel V, ondanks minder uiteenlopende rij-totalen dan we in tabel V zagen. We zien ons gebruik van de verkregen kolom-totalen, i.p.v. de verwachte kolom-totalen, voor de berekening van chi2 gerechtvaardigd. We zien eveneens dat de aantallen van iedere groep die in dezelfde groep geklassificeerd worden (de diagonaal-aantallen) in verhouding tot de groepstotalen, niet ver uiteenlopen, (Zie tabel VII, waar de percentages weergegeven worden). Het percentage van het totaal aantal juist geklassificeerden is wel aanzienlijk gedaald.
De predictieve kracht van de discriminant functies zakt dus niet in belangrijke mate in vergelijking tot klassificatie van de criteriumgroep. Wanneer andere groepen geklassificeerd worden, is wel voorwaarde dat aangenomen mag worden dat de samenstelling van de te klassificeren groep gelijk is aan die van de criterium groep; in ons geval : dat de relatieve frequenties van de verschillende studiekeuzen gelijk zijn, of niet in ernstige mate van die van de criterium-groep afwijken.
Tabel VII. Percentages van de juist geklassificeerden per studierichting.
| studie- richting | klass. groep 1968 | klass. gr. 1967 | klass. gr. 1967 | |||||||
| discr. funct. 1968 | discr. f. 1968 | discr. f. 1967 | ||||||||
| B | 50,4 | 45,8 | 40,3 | |||||||
| Bdk | 34,8 | 33,3 | 33,9 | |||||||
| N | 2,1 | 1,5 | 19,1 | |||||||
| E | 48,0 | 46,8 | 44,8 | |||||||
| T | 46,6 | 15,6 | 60,0 | |||||||
| w | 1,4 | 0,0 | 3,0 | |||||||
| Wsk | 17,9 | 6,9 | 23,6 | |||||||
| TOTAAL | 33,3 | 21,6 | 35,9 | |||||||
Een andere manier tot kruis-valideren dan klassificatie van een nieuwe groep, is het uitvoeren van een discriminant analyse op een nieuwe groep.
Dit is gedaan op de groep eerstejaars van 1967. Hier zal volstaan worden met een korte bespreking van de resultaten die deze analyse opleverde, in verband met hun betekenis voor de validiteit van de 1968 analyse.
Vier significante discriminant functies werden gevonden. Bij analyse van de factoren die aan deze functies bijdragen blijkt dat de dubieuze factor L uit de 1968 analyse (1e discr. functie) niet teruggevonden wordt bij de 1967 analyse. Factor A heeft een kleinere lading op de 1e discr. functie gekregen. Factor M, die op de 1e discr. functie van de 1968 analyse een hoge lading heeft, heeft daar bij de 1967 analyse nog maar een onbetekenende lading. Ook factor H blijkt geen rol meer te spelen. Factor I blijft in gelijke mate vertegenwoordigd, nieuw zijn factoren F, N en C. Wanneer we nagaan op welke wijze deze factoren bijdragen aan de eerste discriminant functie van de 1967 analyse, dan kunnen we, uitgaande van de omschrijvingen gegeven door Cattell, deze functie kenmerken als representerend de dimensie: EXPRESSIVITEIT.
De tweede discriminant functie is vrijwel dezelfde gebleven, de factoren A, I en M hebben dezelfde belangrijkheid behouden, factor F telt niet meer mee, evenals factor E, terwijl de factoren O, G en Q4 er bijgekomen zijn. Voor de tweede discriminant functie blijft gelden dat zij representeert
FUNCTIONEREN IN GROEPSVERBAND.
De derde discr. functie toont eveneens een redelijk constant beeld m.b.t. de factoren die hieraan bijdragen. Evenals bij de analyse 1968 zullen we hier echter afzien van een bespreking van de beide laatste functies.
In dit beknopte overzicht zien we dat de "openheid voor de omgeving", waarmee we de eerste discriminant functie van de 1968 analyse gekenmerkt hebben, in de 1967 analyse vervangen moet worden door "expressiviteit". Het verschil is niet bijzonder ingrijpend, maar het blijft een belangrijk verschil. Bij de 1968 analyse vonden we dat op de 1e discr. functie Bouwkunde en Bedrijfskunde van de overige studierichtingen onderscheiden werden, en op de 2e discr. functie van elkaar. Hetzelfde vinden we bij de analyse van 1967. Hoewel we de eerste discriminant functie anders moeten kenmerken, blijkt zijn werking dezelfde te zijn gebleven. Op de 3e discr. functie vinden we, evenals bij de analyse 1968, dat Wiskunde van de overige onderscheiden wordt.
Als informatie kan nog meegedeeld worden dat t-toetsen voor de gemiddelde factor-scores tussen 1967 en 1968, per studierichting, laten zien dat deze gemiddelden., op een uitzondering na, zeer constant zijn. Die uitzondering is factor B, waarvoor significante verschillen tussen 1967 en 1968 gevonden worden. Factor B heeft op de vierde discriminant functie van de analyse 1967 een zeer grote lading, maar komt in de analyse 1968 nergens met een grote lading op een van de factoren te voorschijn.
De klassificatie tabel leverde een chi2 waarde van 220,66 op, hoger dan voor de 1068 klassificatie. Tabel VII geeft per studierichting de percentages juist geklassificeerden ( laatste kolom ).
Deze kruis-validatie laat zien dat de resultaten vrijwel. gelijk blijven voorzover het gaat om de plaats van de groeps-centroiden in de discriminantruimte, en de klassificatie van de criterium groep. De factorladingen op de discriminant functies blijken veranderd te zijn, wat her-benoeming van de eerste discriminant functie noodzakelijk maakt. Misschien zijn de opgetreden verschillen te wijten aan de kleinere relatieve grootte van de groepen Bouwkunde en Electrotechniek, en de grotere relatieve grootte van Wiskunde, in vergelijking tot die van 1968.
Een onderzoek werd verricht naar het vermogen van de 16 PF om te discrimineren tussen 7 studierichtingen. Tevens werd ruime aandacht besteed aan de werking van de hierbij gebruikte techniek: multiple discriminant analyse en de daarop gebaseerde klassificatie.
De 16 PF onderscheidt de 7 studierichtingen voor een belangrijk deel op 2 "dimensies" : openheid voor de omgeving, en functioneren in groepen. De eerste discriminant functie, of dimensie, onderscheidt bouwkunde en bedrijfskunde van de overige studierichtingen, de tweede onderscheidt bouwkunde en bedrijfskunde van elkaar. Klassificatie op grond van de gevonden functies was significant, maar niet frappant goed te noemen. Wat dit betreft is meer van deze techniek te verwachten wanneer, i.p.v. eerstejaars, een duidelijker criterium-groep gekozen wordt, zoals bijvoorbeeld afgestudeerden uit de diverse afdelingen. Wordt dit gedaan, en kiest men naast, of in plaats van, de 16 PF andere geschikte predictoren voor studiesucces, dan zal de techniek van klassificatie m.b.v. discriminantfuncties een bruikbaarder hulpmiddel voor de predictie van studie-succes vormen dan bijv. multiple correlatie ( zie Cooley & Lohnes, 1962, 140-141). Voor enkele merkwaardigheden bij de verkregen resultaten, die bij toepassing van deze techniek verwacht kunnen worden, word in de bijlagen een uiteenzetting gegeven over het hoe en waarom hiervan.
Kruis-validering van de klassificatie liet zien dat de percentages juist geklassificeerden tamelijk constant blijven wanneer een andere dan de criterium groep geklassificeerd wordt. Ook de discriminant-analyse werd op een andere groep nogmaals uitgevoerd, waarbij bleek dat de 1e discr. functie hier gekenmerkt werd door "expressiviteit", een verandering die wel eens samen kan hangen met een andere verdeling van de aantallen studenten over de studierichtingen. Verder onderzoek zal nog verricht moeten worden om tot een juiste omschrijving van de eerste discriminantfunctie te kunnen komen. De resultaten met betrekking tot de relatieve plaats van de groeps-centroiden in de discriminant ruimte, en de klassificatie van de criterium groep, toonden hetzelfde als bij de eerder uitgevoerde analyse.
Het resultaat dat bouwkunde en bedrijfskunde studenten te onderscheiden zijn op grond van hun functioneren in groepen, is een resultaat dat bij analyse van de gemiddelde verschillen in factor scores voor deze beide studie-richtingen waarschijnlijk niet gevonden zou kunnen worden. Ook dit is een belangrijk aspect van discriminant analyse.
R. B. Cattell, D. R. Saunders, & G. Stice : Handbook for the Sixteen Personality Factor Questionnaire "The 16 PF Test" Forms A, B, and C. lnstitute for Personality and ability Testing, Champaign, Illinois, 1957.
Martin K. Chen: Analysis of the discriminant function in Educational and Psychological Research. J. of Exper. Education, vol. 35, 1967, blz 52 - 58.
W. W. Cooley & P. R. Lohnes : Multivariate Procedures for the Behavioral Sciences, 1962, John Wiley & Sons, Inc.
G. H. Dunteman. : Discriminant analyses of the SVIB for female students in five college curricula. J. of Applied Psychology, 1966, vol 50, b1z. 509 - 515.
Vacchiano & Adrian : Multiple discriminant prediction of college career choice. Educ. and Psychol. Measurement 1966, vol 26, blz 985.
C. van de Wijgaart en H. Schell: Algol-programma A 0206 - 1777 Multiple discriminant-analyse, en A 0206 - 1778 Classificatie van proefpersonen. Rekenbureau Wijsbegeerte en Maatschappijwetenschappen, mei '68, bulletin no. 48.
We hebben bij de bespreking van discriminant functie I (analyse 1968), geen aandacht besteed aan factor L, die toch kennelijk inconsistent is met het door ons geschetste beeld van deze functie. Hier moet een reden voor zijn, immers, wij vinden op L wel een klein overwicht van Bouwkunde ( B alleen(5%)groter dan E), maar de inconsistente bijdrage van L aan de discriminant functie laat vermoeden dat we hier te maken hebben met een factor die, ondanks het ontbreken van verschillen tussen gemiddelden, toch een bijdrage aan het onderscheidend vermogen levert (zie Methode).
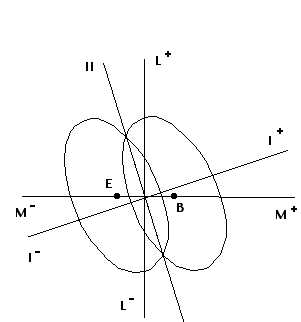
Figuur a. (zie tekst)
In figuur a is de situatie geschetst, uitgaande van een negatieve correlatie tussen factoren L en M (openheid vs. achterdochtigheid negatief gecorreleerd met conventionaliteit vs excentriciteit, wat te verwachten is op grond van de 'openheid voor de omgeving' waar functie I door gekenmerkt is ). We zien dan dat mensen met een gemiddelde M-score toch goed geklassificeerd worden, nl. achterdochtige lieden op het hoge deel van de functie (ruime belangstelling), en omgekeerd. Dit kan een verklaring vormen van de inconsistente bijdrage die L aan de eerste functie levert.
Wat betreft onze aanname van negatieve correlatie tussen factoren L en M, tabel A laat ons zien dat het merendeel van de correlaties tussen L en de factoren die voor deze functie van belang zijn, voor iedere groep afzonderlijk beschouwd, zeer klein zijn. Er zijn vijf correlaties die er uit springen, die niet significant, maar wel alle negatief zijn : L-A (B) -.19; L-M (Bdk) -.19; L-I (Bdk) -.18; L-I (T) -.22; en L-H (W) -.20.
Hiermee is een algemeen bruikbare verklaringswijze voor optredende inconsistenties van de hier besproken soort gegeven, een verklaring die in dit bijzondere geval, door het ontbreken van belangrijke negatieve correlaties, niet geheel kan bevredigen (te wijten aan de gecompliceerdheid van multivariate technieken ?).
TABEL A. Correlaties van factor L met A, H, I en X per groep.
| correlatie | B | Bdk | N | E | T | W | WSK |
| L - A | -.19 | .09 | -.05 | .05 | .08 | -.02 | -.10 |
| L - H | -.08 | .10 | -.09 | -.01 | .04 | -.20 | .03 |
| L - I | .03 | -.18 | .03 | .06 | -.22 | .02 | .02 |
| L - M | .04 | -.19 | -.02 | -.08 | -.04 | .15 | .04 |
Dat alle gewichten van factoren A, E, I, M en F hier negatief zijn verandert niets aan het principe van de argumentering. Ook wanneer alleen voor groep E of B er een negatieve correlatie tussen L en M is, blijft factor L een lading op de discriminant functie behouden (met hetzelfde teken).
Bij de tweede discriminant functie zien we dat factor F bijdraagt, hier is de bijdrage wel consistent met het beeld " functioneren in groepen", dat betekent dat we hier eenzelfde redenering kunnen volgen als boven voor factor L, meet dit verschil, dat we nu een positieve correlaties verwachten tussen F en de andere factoren die voor deze functie van belang zijn. Deze positieve correlaties blijken er inderdaad te zijn ( tabel B ).
T A B E L B Correlaties van factor F met A, E, I en M per studierichting.
| correlatie | B | Bdk | N | E | T | W | WSK |
| F - A | .10 | .30 | .43 | .32 | .27 | .11 | -.03 |
| F - E | .34 | .24 | .44 | .17 | .25 | .14 | .17 |
| F - I | -.09 | -.09 | -.02 | -.11 | -.06 | -.17 | -.04 |
| F - M | .00 | .12 | .26 | .09 | .20 | .33 | .10 |
Uitgaande van de verwachting van gelijke grootte van groepen, zijn er enkele condities waaronder een bepaalde groep te weinig klassificaties kan krijgen. Deze kunnen ook een rol gespeeld hebben bij de door ons uitgevoerde klassificaties. Wanneer we als voorbeeld gebruiken een eendimensionale discriminant-ruimte, en 2 of 3 klassificatie-groepen, dan zijn er diverse mogelijkheden waarop 66n van die klassificatie-groepen minder klassificaties kan krijgen dan de andere.
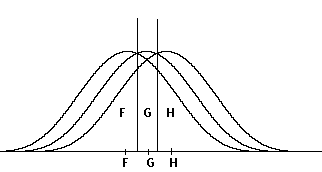
Figuur b.
In figuur b is geïllustreerd een geval waarbij de a-priori verwachting is dat de groepen even groot zullen zijn. De groeps-centroiden liggen vlak bij elkaar. Wanneer we (evenals in figuur 1, zie Methode) de k-klassificatie-grenzen trekken door die punten, gelijke dichtheid hebben voor slechts twee van de groepen (onze definitie van "afstand" tot de groeps-centroiden is immers gesteld in termen van "dichtheid van de puntenwolk", of percentages individuen die verder van de groeps-centroiden af liggen), dan zien we dat slechts een klein aantal van ieder van de drie groepen bij G geklassificeerd zal worden.
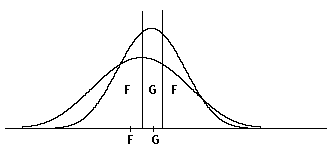Figuur c.
Figuur c geeft het geval weer waar 2 groeps-centroiden vlak bij elkaar liggen, en de verwachte grootte van de groepen eveneens gelijk is, maar de spreidingen verschillen. Dit betekent dat voor de meeste punten het percentage punten dat verder van de beide groeps-centroiden af ligt, groter zal zijn voor de F-groep dan voor de G-groep, zodat het aantal klassificaties bij G gering zal zijn. Wanneer de groeps-centroiden samenvallen zullen er zelfs helemaal geen klassificaties voor G zijn.
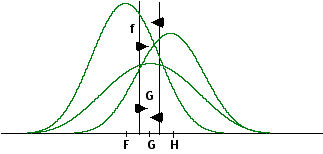Figuur d.
Wanneer bij de klassificatie uitgegaan wordt van verschillende verwachte grootten van groepen, en de groepsspreidingen zijn ongeveer gelijk, wat in de discr. analyse 1968 benaderd wordt, dan kunnen we de groeps-curven tekenen als in figuur D.
De getekende klassificatie-grenzen zijn die, welke bij verwachting van gelijke grootte van de groepen verkregen zou den worden (dus dezelfde als in Figuur B). De vraag is nu, op welke wijze verschuiven deze klassificatie-grenzen wanneer gebruik gemaakt wordt van de formule voor de klassificatie-kansen die gebaseerd is op Bayes' theorema?
Deze formule is een ratio van de dichtheid van groep j en de gecombineerde dichtheid van alle groepen op en bepaald punt in de discriminant-ruimte. Deze ratio wordt, bij aanname van gelijke waarden voor de spreidings-matrix van de diverse groepen, kleiner wanneer de grootte van groep j kleiner wordt. Wanneer in ons voorbeeld de verwachte grootte van groep F groter is dan die voor groep G, zal de klassificatie-kans van het punt, waardoor de oude klassificatie grens getrokken is (lijn f), groter zijn voor groep F dan voor groep G.
M.a.w., bij verwachting van ongelijke grootte van de groepen zullen de klassificatie-grenzen verschuiven in de richting van de centroide van de kleinere groep. (met pijltjes in figuur d aangegeven), wat resulteert in een geringer aantal klassificaties bij deze kleinere groep.
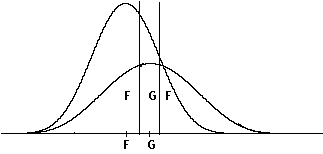Figuur e.
Wanneer een verdeling voorkomt zoals die in figuur e weergegeven is, kan zich op deze wijze het geval voordoen dat voor groep G een heel klein klassificatie-gebied overblijft ( wanneer de twee groeps-centroiden heel dicht naast elkaar liggen zelfs helemaal geen klassificatiegebied meer ) omdat ook rechts van de centroide van G een gebied is waarin niet bij G, maar bij F geklassificeerd zal worden.
De hier geschetste voorbeelden geven weer wat in de door ons uitgevoerde analyse en klassificatie resulteert in een zeer klein aantal klassificaties bij de studierichtingen Natuurkunde en Werktuigbouw. Op deze wijze is het omgekeerd ook mogelijk dat Electrotechniek en Technologie, die in de discriminant ruimte niet die bijzondere plaatsen innemen die we voor B, Bdk en Wsk zien, toch een zeer groot aantal klassificaties krijgen i.v.m. de relatief grote verwachte frequenties voor deze groepen.
Bij dit grote aantal klassificaties zijn dan echter wel een groot aantal onjuiste klassificaties, wat we in tabel VI en tabel VI tot uitdrukking gebracht zien in kleine chi2 waarden voor Electrotechhniek en Natuurkunde afzonderlijk.
Niet gepubliceerd. De politieke context destijds: aankomende hervormingen van het universitaire stelsel op basis van rapporten van Posthumus, Commissie Maris, Commissie van Os, maakten mij huiverig om deze technologie publiek te maken waarmee studiesucces beter is te voorspellen dan alleen op grond van eindexamencijfers. Veel ondergeschikte foutjes zijn dan ook in het concept blijven staan. Een decennium later bleken de ruwe data niet meer beschikbaar voor een heranalyse.
Dit onderzoekt maakte deel uit van het bijvak onderwijsresearch dat ik bij Willem Meuwese heb gedaan. De technische punten uit dit onderzoek zijn later nog terug te zien in stukken over selectie voor numerus-fixus-studierichtingen (met name NRC 1974 html) en de vraag of slecht presterende studenten al vroeg zijn te onderscheiden van de overigen. In dergelijke gevallen wordt de 'kritische groep' overweldigd door de 'normale groep', en is geen demarcatie te maken die behoorlijk uitwerkt, dus zonder studenten in de 'normale' groep onrecht te doen. Vergelijk op dit punt ook de brief van de American Psychological Association over gebruik van de leugendetector, waarin wordt uitgelegd hoe een redelijke success rate voor ontmaskeren van leugenaars samen gaat met een onaanvaardbaar hoge mate waarin niet-leugenaars als leugenaar worden aangemerkt. Tenslotte speelt deze technologie ook weer een rol in besliskundige cesuurbepaling. Ik heb er in ieder geval zelf enorm veel aan gehad al vroeg in mijn loopbaan met deze technologie intensief kennis te hebben gemaakt: het heeft de plunje voor mijn wetenschappelijke bagage (Giere, Explaining science, 1988) al vroeg inhoud gegeven.
R. M. W. Travers (1939). The use of a discriminant function in the treatment of psychological group differences. Psychometrika, 4, 25-32.
A. W. Bendig and Peter T. Hountras (1958). College student stereotypes of the personality traits of research scientists. Journal of Educational Psychology, 49, 309-314. Reprinted in Bernice T. Eiduson and Linda Beckman (Eds) (1973). Science as a career choice. Theoretical and empirical studies. (p. 328-333) New York: Russell Sage Foundation.
Marcel L. Goldschmid (1967). Prediction of college majors by personality tests. Journal of Counseling Psychology, 14, 302-308. abstract Reprinted in Bernice T. Eiduson and Linda Beckman (Eds) (1973). Science as a career choice. Theoretical and empirical studies. (p. 359-365) New York: Russell Sage Foundation.
Lindsey R. Harmon (1964): A multiple discriminant analysis of high school background data, in Scientific Manpower Report no. 4, National Academy of Sciences. Reprinted in Bernice T. Eiduson and Linda Beckman (Eds) (1973). Science as a career choice. Theoretical and empirical studies. (p. 111-123) New York: Russell Sage Foundation. [deels op books.google
Clifford Abe & John L. Holland (1965). A description of college freshmen. I. Students with different choices of major field. ACT Research Reports no. 3
Olgierd R. Porebski (1966). Discriminatory and canonical analysis of technical college data. The British of Mathematical and Statistical Psychology, 19 Part 2, 215-236.
Charles F. Elton & Harriett A. Rose (1966). Within-university transfer: Its relation to personality characteristics. Journal of Applied Psychology, 50, 539-543.
Phillip J. Rulon, David V. Tiedeman, Maurice M. Tatsuoka and Charles R. Langmuir (1967). Multivariate statistics for personnel classification. New York: Wiley. [chapter 8. Discriminant analysis.
Roy D. Goldman & Rebecca Warren (1973). Discriminant analysis of study strategies connected with college grade success in different major fields. Journal of Educational Measurement, 10, 39-47. abstract
George A. Molnar & Robert J. Delauretis (1973). Predicting the curriculum mobility of engineering students: A comparison of discriminant procedures. Journal of Counseling Psychology, 20, 50-59.
harmon Phillip J. Rulon, David V. Tiedeman, Maurice M. Tatsuoka and Charles R. Langmuir (1967). Multivariate statistics for personnel classification. New York: Wiley. [chapter 8. Discriminant analysis.
Rounds, J., & Tracey, T. J. (1993). Prediger's dimensional representation of Holland's RIASEC circumplex. Journal of Applied Psychology, 78, 875-890. Zie ook Tracey & Rounds (1993) Psychological Bulletin, 229-246.
John C. Smart (1982). Faculty teaching goals: A test of Holland’s theory. Journal of Educational Psychology, 74, 180-188.
Terence J. Tracey and James Rounds (1993). Evaluating Holland's and Gati's Vocational-Interest Models: A Structural Meta-Analysis. Psychological Bulletin, 113, 229-246.
Rebecca Zwick & Lubella Lenaburg (2009). Using discrete loss functions and weighted kappa for classification: An illustration based on Bayesian network analysis. Journal of Educational and Behavioral Statistics, 34, 190-200.
Anna Parpala, Sari Lindblom-Ylänne, Erkki Komulainen, Topi Litmanen & Laura Hirsto (2010). Students’ approaches to learning and their experiences of the teaching-learning environment in different disciplines. British Journal of Educational Psychology, 80, 269-282.
Jelte M. Wicherts & Harrie C. M. Vorst (2010). The relation between specialty choice of psychology students and their interests, personality, and cognitive abilities. Learning and Individual Differences, 20, 494-500. pdf
Cyrille A. C. Van Bragt, Anouke W. E. A. Bakx, Theo C. M. Bergen and Marcel A. Croon (2011). Looking for students’ personal characteristics predicting study outcome. Highr Education, 61, 59-75. abstract
Bakker, H. Th. (Red.) (1959). Mislukking en vertraging van de studie. Verslag van een onderzoek verricht aan de Technische Hogeschool te Delft 1953-1957. Delft: Technische Hogeschool.
Alan Feingold (1995). The additive effects of differences in central tendency and variability are important in comparisons between groups. American Psychologist, 50, 5-12. 10.1037/0003-066X.50.1.5 abstract
Anna Vedel (2016). Big Five personality group differences across academic majors: A systematic review. Personality and Individual Differences, 92, 1-10 abstract
Rorer, L. G., Hoffman, P. J., LaForge, G. E., & Hsieh, K-C. (1966). Optimum cutting scores to discriminate groups of unequal size and variance. Journal of Applied Psychology, 50, 153-164. 10.1037/h0022944 abstract
Lloyd G. Humphreys, David Lubinski, and Grace Yao (1993). Utility of Predicting Group Membership and the Role of Spatial Visualization in Becoming an Engineer, Physical Scientist, or Artist. Journal of Applied Psychology, 78, 250-261. researchgate.net
Regressions of criterion performance on predictors may be considered the "classic" approach. Although this approach has much to offer, it also has numerous problems associated with it, as illustrated in the discussion in Standards (AERA, 1985) concerning the evaluation of criteria documents. Research in both civilian occupations and military assignments, extending over many years, points clearly to two concerns: First, any one criterion measure contains a substantial quantity of unique variance, and a composite of several measures of performance having widely varying methods variance components is likely to be the most valid (Carroll, 1985; Humphreys, 1985; Lubinski & Dawis, 1992). A second problem with the classic approach to predictive validation arises from the instability of individual differences in performance over successive occasions of measurement during training, from training to performance on the job, and over occasions on the job. Hulin, Henry, and Noon (1990) have recently reviewed this literature, which led to the following question: How many different time periods between testing on predictors and obtaining criterion measures are required in studies of predictive validity? We really do not know.
Abe, C., & Holland, J. L. (1965). A description of college freshment. I. Students with different choices of major field. ACT Research Reports no. 3. report
Abe, C., & Holland, J. L. (1965). A description of college freshment. II. Students with different vocational choices. ACT Research Reports no. 4. report
John L. Stromberg (). Distinguishing among multinomial populations: a decision theoretic approach. Journal of the Royal Statistical Society. Series B (Methodological) Vol. 31, No. 2 (1969), pp. 376-387 JSTOR read online
Ben Wilbrink (2 februari 2012). Twitterdraadje, aansluitend op deze tweet van Marcel Schmeier Twitter
Een beschrijving van die Big Five: https://ffpi.nl/betekenis.html Het leest als een inventaris van sociale wenselijkheid. In 2e aanleg als vaardigheden van de 21e eeuw, inclusief de soft skills van Heckman, ter Weel en Borghans. Onzin, natuurlijk, het zijn helemaal geen vaardigheden.
Wie het aardig vindt om zich door anderen te laten kenmerken op die Big Five, ga naar: https://ffpi.nl In de levensloop zin er wel enige veranderingen, maar over het geheel genomen verschillen mensen karakteristiek op deze tests.
Het idee van Heckman c.s. dat onderwijs moet trainen op deze 'soft skills', overgenomen door PISA/OECD, slaat nergens op. Heb ik dat niet uitgewerkt in deze blog ? Of lees Hofstee ‘De kennismythe’ In: S. Goorhuis-Brouwer ea. Mythes in het onderwijs. SWP
Op tal van andere manieren speelt persoonlijkheid wel een rol in onderwijs en de wereld. Ik mocht er al in 1968 mee stoeien: zie hier De destijds gebruikte test was Cattell's 16-factor test, zeg maar de voorloper van de daaruit voortgekomen Big Five tests.
Anna Vedel (2016). Big Five personality group differences across academic majors: A systematic review. Personality and Individual Differences, 92, 1-10 abstract and/or the accepted manuscript (post-print version) of the article
http://www.benwilbrink.nl/publicaties/68StudentprofielenTHE.htm
http://goo.gl/GiRUJ