Rekenproject: Historisch — rekenopgaven

Ben Wilbrink

rekendidactiek
    ontwikkelingen in het rekenonderwijs
        pabo
        historisch: rekendidactiek historisch: rekenopgaven
        van Hiele — Freudenthal — Treffers

Collectie Nederlandsch Schoolmuseum, veel titels volledig gescand! website

Universiteit van Amsterdam, Tekstbank: Collectie Nederlansch Schoolmuseum. site

Wat vinden we zoal in deze fraaie collectie, vooral negentiende eeuw?

NN (1895). Beginselen van de theorie der rekenkunde voor d laagste klas van kweekscholen. scan Titel:   Inleiding tot de mathematische weetenschappen. Of gemeenzaame leerwyze der arithmetica en algebra  Bewaard   Auteur:   Strabbe, Arnoldus Bastiaan     Uitgave:   Amsterdam: J.B. Elwe, 1804 2e dr. doorgaans veel verm. en verb     Taal:   Nederlands     Onderwerp:   Wiskunde: wiskunde: algemeen     Trefwoord:   Rekenen | Leermiddelen (vorm)     Opmerking:   Dl. 1

Arnoldus Bastiaam Strabbe (mathematicus en stads wynroeijer te Amsterdam) (1804, 2e). Inleiding tot de mathematische weetenschappen of gemeenzame leerwyze der arithmetica en algebra. Eerste deel behelzende een beknopt samenstel van de eerste beginselen der algemeene rekenkunde. Ten dienste der geenen, welke zich in de eenvoudigste grondbeginselen deezer weetenschap willen oeffenen.. J. B. Elwe. scan

Jan van Olm (in leven onderwijzer in de rekenkunst, te Groningen) (1808 13e). Rekenboek van Jan van Olm. N. Veenkamp en J. Groenewolt. scan

P. J. Prinsen (onderwijzer der schole van het departement Haarlem der Maatschappij tot Nut van ’t Algemeen) (1813). Rekenboek, ingerigt naar de tegenwoordige behoefte der scholen (tweede deeltje) A. Loosjes, Pz. scan

Arnoldus Bastiaan Strabbe (lid en sevretaris van het gezegde genootschap; lid van de sociëteit der kunst-rekenaren te Hamburg, en leermeester der wiskunst te Amsterdam) (1814 2e). Eerste beginselen van de arithmetica of rekenkunst, ten gebruike der scholen vierde deel: opgedragen aan het Genootschap der Mathematische Wetenschappen, onder de spreuk: Een onvermoeide arbeid komt alles te boven . J.B. Elbe. (eerste uitgave 1790) scan

NN (1814). Voorbeelden tot oefening in de hoofdregelen der rekenkunde, met geheele en onbepaalde getallen: benevens eene korte verklaring van dezelve, ten dienste der scholen 's Gravenhage: Gebroeders Giunta D'Albani en wordt uitgegeven, bij de erve Thierry en Mensing en zoon, 1814 scan

NN (bewerker van Willem Bartjens) (1816). De vernieuwde rekenkunst van Mr. Willem Bartjens, uit welke men de voornaamste regelen dier wetenschap leeren kan: op nieuw ieder voorstel nagezien, en elke regel met eene definitie van dezelven vermeerderd door een schoolonderwijzer binnen Rotterdam J. Hendriksen. scan

Willem van den Hoonaard (onderwijzer te Hilligersberg) (1817). Rekenboek voor de scholen in het Koningrijk der Nederlanden: ingerigt overeenkomstig het nieuwe stelsel van maten, gewigten en muntspecien.eerste stukje Amsterdam: Schalekamp en Van de Grampel. scan

Danny Beckers en Marjolein Kool (2004). Willem Bartjens (1604/2004). De Cijfferinghe (1604). Het rekenboek van de beroemde schoolmeester. Hilversum: Verloren.

Het eeuwfeest was aanleiding nog eens te gaan zoeken naar een exemplaar van die eerste editie, en dat is gevonden in Antwerpen. Een facsimile hiervan is in dit boek opgenomen. Dan is nu dus te zien dat de editie van 1779 nauwelijks verschilt van die van 1604, in ieder geval zijn de oorspronkelijke gedichtjes eruit verdwenen.
Verschenen in de serie Rekenmeesters
Zie annotatie in trucjes.htm#Beckers Kool.

Danny Beckers over leven en werk van Bartjens, in NWA 5/5 2004 pdf

P. Wijdenes (1924). Voorlooper op de rekenboeken voor de H.B.S en voor M.U.L.O., tevens slotstukje voor het rekenonderwijs op de lagere school. P. Noordhoff.

Dit boekje geeft een tijdsbeeld. Ik ben wel benieuwd hoe dit past in de historische ontwikkeling van het rekenonderwijs, en het denken over het rekenonderwijs. Als ik het goed heb, spreekt dezelfde Wijdenes zich na de oorlog uit tegen de idioot ingewikkelde breukensommen zoals hierbeneden afgebeeld: kindermishandeling. Ik kijk dat nog na.

Voorbericht




Deze voorlooper heeft tot doel een schakel te vormen tusschen de rekenboeken voor de Lagere School aan de eene zijde en aan de andere zijde mijn veelgebruikte Rekenboeken voor de H. B. S. en voor het M. U. L. O. Het blijkt, gezien de vele vragen, die men omtrent een en ander tot mij richtte, dat de onderwijzers, die opleiden voor de H. B. S. gaarne een slotstukje hebben met geschikte oefenstof en dat men bij het M. U. L. O. liever niet direct het Rekenboek voor M. U. L. O. neemt, maar eerst eens terdege alles wil herhalen.

Dit boekje bevat naar mijn meening precies, hetgeen men wenscht. Een groot deel van de opgaven is er overgenomen van de toelatingsxamens van verschillende H. B. S. en Gymnasia in 1921—1923, zoodat dit boekje als krahtmeter voor deze examens kan dienen.

De stof heb ik gerangschikt naar de meest voorkomende soorten van vraagstukken; de onderwijzer kan nu een bepaald onderwerp terdege behandelen en hij heeft voldoende oefenstof ter beschikking.

Gaarne zal alle mogelijke op- en aanmerkingen van gebruikers vernemen.                     P. WIJDENES.

Wijdenes deelt de stof in 20 paragrafen in. Ik geef uit elke paragraaf een opgave. Dit waren wel de gekke jaren twintig voor de rekentoetsen, zo te zien. Veel verschil met realistische rekentoetsen zie ik niet, behalve dat die van 1924 waanzinnig moeilijk zijn in vergelijking tot de huidige. Het zou me verbazen wanneer ik tussen deze meuk ergens nog opgaven vind die naar redelijke maatstaven vandaag nog door de rekenbeugel kunnen. Zo te zien werd het rekenen in de twintiger vooral gebruikt om de selectie voor de mulo, de hbs, het gymnasium, en de mms te regelen. En natuurlijk schemert overal in door dat er veel functies in de samenleving waren waar wel degelijk stevig en nauwkeurig moest worden gerekend.

Merk op dat Wijdenes de opgaven rubriceert naar opgavetype. Dat is veelzeggend: het rekenonderwijs is in deze zin ook een aanfluiting, omdat de leerlingen wordt geleerd hoe je een beperkt aantal echt schoolse rekenproblemen altijd op dezelfde manier moet aanpakken. Bijvoorbeeld: A doet een werk in 5 dagen, B doet datzelde werk in 7 dagen . . . . Enzovoort.

Hoofdbewerkingen

• 1. Hoeveel cijfers zijn er noodig om alle getallen van 1 tot en met 457 op te schrijven?


Deelbaarheid

• 2. Hoeveel is 54a24 + 7225b, als a zoowel als b één cijfer voorstelt en het eerste getal door 9 en het tweede door 8 deelbaar is?


Percentrekening

• 3. Iemand verkoopt een partij waren met 25% winst. Bij verzending bederft 25% van de partij. Voor wat bedorven is krijgt hij geen betaling. Hoeveel % wint of verliest hij nu aan de partij?


Koop en verkoop

• 4. Iemand koopt appels voor 2 gulden de honderd. Hij verkoopt ze tegen 3 cent het stuk, maar geeft op elke tien appels één appel toe. Hoeveel percent van zijn ontvangst wint hij? (Stel de partij 1100 appels)


Voorloopge onderstelling

• 5. Iemand heeft twee kapitalen samen groot ƒ 16000. Het eerste levert hem 7% winst op en op het tweede verliest hij 3 ²⁄₅ %. Hij wint in het geheel ƒ600. Hoeveel bedragen de kapitalen?


Terugwerken

• 6. Het verschil tusschen teller en noemer van een breuk is 5. Deelt men den noemer door 2 en telt men daarna bij den teller 34 op, dan krijgt men 6 maal de oorspronkelijke breuk. Welke breuk is dit?


Samen werken

• 7. A arbeidde eerst 7 dagen, toen B 12 dagen aan een werk, en daarna maakten zij samen de rest of ¹⁄₄ deel van het werk in 3 dagen af. Welk deel van het werk deed ieder per dag?


Mengen

• 8. Een winkelier mengt onder elkaar 60 KG à 59 cent, 72 KG à 61 cent, en 72 KG à 89 cent; als hij het mengsel met minstens 10% winst wil verkoopen, voor hoeveel cent moet het KG dan minstens verkocht worden?


Inhalen en ontmoeten

• 9. Een sneltrein uit Amstedam en een goederentrein uit Den Haag ontmoeten elkaar steeds iederen dag voor het station Hillegom; de eerste doet 48 KM per uur en de laatste 30 KM. Op een keer was de eerste 4 min. te laat en de tweede 9 min.; op hoeveel M afstand van Hillegom en aan welke zijde ontmoetten ze elkaar toen?


Verhoudingen

• 10. Twee wielrijders gaan elkaar tegemoet. Om 7 uur zijn ze nog 10 KM van elkaar verwijderd en om kwart voor acht zijn ze elkaar reeds 8 KM voorbij. Hoe laat hadden zij elkaar ontmoet?


Som of verschil constant

• 11. Welk zelfde getal moet men bij teller en noemer van ¹¹⁄₂₆ optellen, opdat de breuk gelijk wordt aan ⁴⁄₇?


Oppervlakken

• 1. Een vloer is 7 M lang en 5 M breed. Een kleed ligt overal 5 dM van den wand. Beeken de oppervlakte van het onbedekte deel van den vloer.


Slooten

• 3. Van een stuk land verhoudt zich de lengte tot de breedte als 9 : 4; een weg, evenwijdig aan de kleinste zijde is 18 M breed en een andere weg, evenwijdig aan de lengte is 8 M breed. De omtrek van elk der vier gelijke overblijvende stukken land is 156 M. Hoe lang en hoe breed was dat land?


Inhouden

• 14. Een balk, waarvan het soortelijk gewicht 0,657 is, weegt 906,66 KG. Hoe groot is de oppervlakte van dien balk, als hij 6 M lang en 46 cM breed is?


Tijdrekening

• 5. Het ochtendblad van het ‘Handelsblad’ droeg op Vrijdag 22 Febr. 1924 het nummer 31235; welk nummer had het avondblad van 15 april 1924? ’s Zondags komt er enkel een ochtendblad en Maandags is er geen. Tusschen deze data was er geen feestdag.


Metriek stelsel

• 16.   7,12 Stère  = . . . . . . dM³

    64,38 DL     = . . . . . . dM³

     3373 cM³    = . . . . . . dM³

      0,84 DM³   = . . . . . . dM³

                  ————

          Samen . . . . . . dM³


Tiendeelige breuken

• 2.     16,015625 × 0,025625 × 34,304 : 268

                2,5 × 0,01681


Gewone breuken

• 


Cijferoefeningen

• 3. Als per dollar gerekend wordt ƒ2,69³⁄₄, hoeveel ontvangt men dan voor 4429,50 dollar?
• 98. Uit tien waarnemingen heeft men gevonden:

  766,433; 765,919; 765,892; 766,031; 765,992; 766,005; 766,012; 766,320; 765,980; 766,225; wat moet men als het gemiddelde van één waarneming aannemen? Hoeveel afwijking vertoonen de grootste en kleinste waarde uit de tien gegeven?


Herhaling

• 1. A legt zekeren weg af in ²⁄₃ en B in ³⁄₄ uur. Als A per uur 650 M meer aflegt dan B, hoeveel KM legt B dan per uur af?
• 14. De som van teller en noemer van een breuk is 38. Telt men bij den teller 68 op en vermenigvuldigt men den noemer met 5, dan verandert de waarde van de breuk niet. Welke is die breuk?

H. Scholte (1919 8e). Hoeveel en waarom? Supplement voor hen, die zich voorbereiden voor de toelating op hoogere burgerschool of gymnasium. J. B. Wolters.

De rekenboekjes zelf zijn ws. 1893 uitgegeven als ‘Hoeveel en waarom’; ws heeft de KB de hele serie van de eerste druk?

De opgaven in dit boekje zijn methodisch gerangschikt en ontleend aan of bewerkt naar de vraagstukken, die in de laatste jaren in verschillende deelen van ons land bij de toelatings-examens voor Hooegre Burgerscholen en Gymnasia zijn opgegeven. (..)

Dit supplement is een afgesloten geheel en kan als repetitie-boek voor het zelfstandig rekenen bij elke methode worden gebruikt. Het is evenwel niet nodig met de repetitie te wachten, tot de leerstof in zijn geheel is afgehandeld. Aan de leerlingen, die werken in Hoeveel en Waarom, kan men het b.v. reeds in handen geven, als een paar paragrafen van het Zesde deeltje zijn behandeld. (..)

Daar de eischen, die men bij de toelating op verschillende scholen stelt, zeer uiteenloopen, zullen sommige onderwijzers het onnoodig achten, het geheele boekje te laten doorwerken, terwijl anderen uit een of ander stel examenwerk allicht een vraagstuk kunnen opdiepen, moeilijker dan de door mij opgenomene. (..)

Op grond van een jarenlange ervaring meen ik te mogen verzekeren, dat een leerling, die dit boekje flink heeft doorgewerkt, voldoende voorbereid is voor het onderwijs in de wiskunde, en dat hij op een toelatings-examen voor het schriftelijk rekenen geen slecht figuur zal maken.

De genoemde rekenmethode geeft redelijk uitsluitsel over het rekenonderwijs dat de leerlingen hebben gehad. Onbekend blijft wat Scholte vindt dat de score op een willekeurig uit deze bundel samengetselde toets zou moeten zijn, om gerust te kunnen zijn op het op de toelatingstoets te behalen resultaat. Zouden we het hem kunnen vragen, dan zou hij waarschijnlijk herhalen dat de selectiviteit van die toelatingen per school verschilt, maar mogelijk ook voor dezelfde school van jaar tot jaar kan verschillen. Uit arren moede zouden we dan een heel globale vuistregel aan kunnen houden: voor een redelijke kans om toegelaten te worden, zal toch rond 70% van deze opgaven goed beantwoord moeten kunnen worden. Wat zijn dan de vragen?

1. Als men een getal achtereenvolgens door 12, 15 en
   20 deelt, is de som der quotienten 24 meer dan ¹⁄₇
   van dat getal. Welk getal wordt bedoeld?
2. Bij een getal voegt men het vierde deel van dat
   getal ; van deze som neemt men het vierde deel, en
   krijgt nu 5 ¹⁄₄ minder dan de helft van het oorspron-
   kelijke getal. Welk getal is dat?
3. Van twee getallen, die tot elkaar staan als 2 tot 5,
   is het achtste deel van het grootste 7¹⁄₂ meer dan het
   vierde deel van het kleinste. Welke zijn die getallen?
4. Twee getallen verhouden zich als 2¹⁄₂ en 11. Het vijf-
   voud van het kleinste is 556¹⁄₄ meer dan het achtste
   deel van grootste.
   Wat is het product van die getallen?
5. Van een getal neemt men het vierde deel en 15 af ;
   van de rest neemt men 10 minder af dan het derde
   deel van die rest. Men houdt 64 over.
   Bereken het oorspronkelijke getal.
6. De som van twee getallen is 236. Deelt men het
   kleinste door ³⁄₄ en vermenigvuldigt men het grootste
   met 1 ¹⁄₈, dan krijgt men gelijke uitkomsten.
   Bereken die twee getallen.
7. De inhoud van een schip is:
   
   ²⁄₃ × (⁵⁄₁₂ + 1,75)
   ————————————— DM³
   10 ¹⁄₉ : ¹⁹⁄₁₉ - ⁵⁄₆ × 1 ¹¹⁄₁₅
   
   Hoeveel hektoliter is dat?
8. Iemand koopt 600 M laken tegen f 4,50 den meter.
   Hij verkoopt een gedeelte à f 6 en de rest à f 5,20
   den meter, waardoor hij f 540 wint.
   Hoeveel meter heeft hij à f 5,20 verkocht?
9. A, B en C bezitten elk een zekere som geld. Als A
   25 % van zijn geld aan C geeft en B 20% van zijn
   geld aan C, hebben ze alle drie evenveel. Welk deel
   bedroeg de som, die B oorspronkelijk had, van die
   van A?
10. Het getal 143a7a2, waarin de letters a en a gelijke
    cijfers voorstellen, is deelbaar door 4 en door 9.
    Welke cijfers zijn door die letters voorgesteld?

    par. 22 NB: in het origineel zijn de breuken alle genoteerd met een horizontaal streepje

H. J. Lugtmeijer & J. Boers (1953). Naar aanleg en tempo. Gedifferentieerde rekenmethode voor de lagere school. dertiende deeltje B. 26e druk. W. J. Thieme & Cie.

Op de achterzijde staat de hele rekenmethode beschreven: 14 deeltjes, deel 1 in twee delen; eveneens 14 onderwijzersboekjes met aanwijzingen, rekendictees en antwoorden; drie deeltjes cijferen voor klas 4 tot 6, met 3 onderwijzersboekjes. Ca. 100 gram per deeltje: 3¹⁄₂ kg. :-)

De deeltjes 13 en 14 zijn z.g. opleidingsdeeltjes. De keuze van de behandelde vraagstukken is beïnvloed door de toelatingsexamens voor de middelbare scholen uit het gehele land. Helaas moesten daardoor vraagstukken behandeld worden, die onze sympathie niet hebben, zoals o.a. ingewikkelde breukensommen in redactievorm, werksommen, e.d. We hebben getracht excessen te vermijden. ( .. )

Er is naar gestreefd de opbouw van de vraagstukken zo geleidelijk mogelijk te doen plaatsvinden, het is geen verzameling van examenopgaven. Door de geleidelijke opbouw zal het inzicht versterkt worden.

Er is afwisseling gebracht door het invoegen van vele rekentests, die de vaardigheid moeten verhogen en waardoor zelfvertrouwen wordt gekweekt.

uit het voorbericht

H. J. Lugtmeijer & J. Boers (1963). Redactievraagstukken voor het toelatingsexamen v.h.m.o. Naar onderwerp gerangschikt. Per onderwerp behandeld in opklimmende moeilijkheid. Zutphen: W. J. Thieme & Cie.

Aangezien in 't algemeen nog te weinig en soms geen overleg plaatsvindt tussen het Lager Onderwijs en het v.h.m.o. over de stof, die de toelatingsexamen omvatten, treden er nogal eens moeilijkheden op, met name bij het onderdeel ‘Redactievraagstukken’.

Hierbij geeft de grote keuze van onderwerpen, bij een niet afgebakend terrein, vele opleiders en leerlingen moeilijkheden. Om aan het verlangen van verschillende collega’s, de meest voorkomende onderwerpen, geordend en naar opklimming in moeilijkheid in één boek te zien, tegemoet te komen, is deze uitgave verschenen.

Naar we hopen zullen de a.s. leerligen voor het v.h.m.o. hierdoor de stof als een meer afgerond geheel zien, waardoor meer zelfvertrouwen kan ontstaan en de opgaven tijdens het examen wat zelfstandiger kunnen worden opgelost.

uit het voorwoord

Dertig examenopgaven


1. Iemand betaalde per maand ƒ 56.— voor huur en waterleiding. Het bedrag voor waterleiding was ƒ 6.--.
   1. Op 1 jan. ging de huur met 25% omhoog. Hoeveel moet hij nu betalen?
   2. Hij kreeg ook op 1 jan. 5% loonsverhoging. Voor die tijd verdiende hij ƒ 18750,-- per jaar. Hoeveel % van die salarisverhoging gaat weg aan de huurverhoging?
2. Iemand heeft guldens en rijksdaalders. Totaal zijn er 39 geldstukken. De waarde is ƒ 54,--. Hoeveel guldens en rijksdaalders heeft hij?
3. Jan is 2¹⁄₂ maal zo oud als Piet. Over 3 jaar zijn ze samen 27 jaar. Hoe oud zijn Jan en Piet nu?
4. Van een hoeveelheid knikkers krijgt A ¹⁄₄ deel, B ¹⁄₃ deel van de rest en nog 10 en C de overige. C krijgt 38 knikkers. Hoeveel krijgt A? en B?
5. De omtrek van een stuk land is 600 m. Lengte en breedte verhouden zich als 5 : 1. Men spuit water op het land, 10 cm hoog. Hoeveel hl moet men er op spuiten?
6. Drie getallen verhouden zich als ²⁄₃ : ⁵⁄₃ : 3. De twee grootste getallen verschillen 152. Bereken de drie getallen.
7. ƒ 13000,-- brengt in 1¹⁄₂ jaar ƒ 780,-- rente op. Hoeveel brengt een tweemaal zo groot kapitaal in twee jaar op?
8. Van een breuk is de teller 15 minder dan de noemer. De waarde ervan is ⁵⁄₈. Wat is de breuk?
9. Gekocht: 60 mud aardappels à ƒ 8,50 per mud.
   Verkocht:
         de helft à ƒ 10,90 p. mud
         ¹⁄₄ deel   à ƒ 10      p. mud
         de rest   à ƒ   9      p. mud
   Hoeveel % van de inkoop bedraagt de winst?
10. Jan is 2 jaar ouder dan Gerrit, [sic] Over 3 jaar zijn ze samen 30 jaar. Hoe oud is ieder nu?
11. Iemand verkoopt iets voor ƒ 420,-- en wint dan 12%. Hoeveel had de verkoop moeten zijn om 18% te winnen?
12. Om een rechthoekig grasveld, dat 21 m lang en 15 m breed is, ligt een pad, dat 60 cm breed is. Dit pad wordt betegeld met tegels van 30 bij 30 cm. Hoeveel tegels zijn er nodig?
13. A en B bezitten samen ƒ 12750,--. Als A ƒ 450 ontvangt en B ƒ 150 uitgeeft, heeft A 1¹⁄₄ × zoveel als B. Hoeveel bezit ieder?
14. In een aquarium dat 95 cm lang, 32 cm breed en 48 cm diep is, staat het water tot 6 cm onder de bovenrand. Voor hoeveel % is de bak gevuld?
15. Van een stuk touw wordt ¹⁄₅ deel afgesneden en daarna van de rest nog ²⁄₃ deel. Het touw is nog 8 m lang. Hoe lang was het touw?
16. A kan een werk doen in 10 dagen, B in 15 dagen. Ze werken er samen 4 dagen aan. Daarna maakt C het werk af in 5 dagen. In hoeveel dagen kan C het werk alleen doen?
17. De lengte, breedte en hoogte van een houten blok verhouden zich als 5 : 4 : 3. De lengte is 45 cm. Bereken de totale oppervlakte.
18. Als men achter een zeker getal een 0 plaatst, krijgt men een getal, dat 5634 groter is. Hoe groot is het oorspronkelijke getal?
19. Jan en Henk hadden samen 90 knikkers. Jan wint er 20 van Henk en koopt er bovendien 15 knikkers bij. Nu verhouden hun aantallen zich als 5 : 2. Hoeveel knikkers had ieder eerst?
20. A verkoopt een partij goederen met 10% verlies aan B. B verkoopt de partij en wint 15%. Hij ontvangt ƒ 6210,--. Voor hoeveel heeft A de partij gekocht?
21. Een vloer wordt belegd met tegels van 30 cm bij 30 cm. Gebruikte men tegels van 20 bij 20 dan zou men 240 tegels meer nodig hebben. Hoeveel tegels van de eerste soort heeft men nodig?
22. Van een breuk is de noemer 16 groter dan de teller. Als men teller en noemer met 12 vermeerdert, krijgt men een breuk, die vereenvoudigd de waarde ²⁄₃heeft. Bereken die breuk!
23. Als men een getal door 12 deelt, krijgt men hetzelfde getal, als wanneer men er 396 aftrekt. Welk getal wordt bedoeld?
24. Iemand zet ƒ 8000,-- uit à 3,5% ’s jaars en een tweede kapitaal à 4,5% ’s jaars. De totale rente is ƒ 820,-- per jaar.
    1. Hoe groot is het tweede kapitaal?
    2. Hoeveel % rente krijgt hij gemiddeld?
25. Een gesloten houten holle kubus heeft van buiten gemeten een ribbe van 1,02 m. De dikte van het hout is 1 cm. Hoeveel dm³ hout is er verwerkt?
26. A en B handelen samen. A legt ƒ 3600 in en B ƒ 6000. Ze winnen ƒ 576,-- en verdelen nu de winst. Hoeveel krijgt elk?
27. De plaatsen A en B liggen 105 km van elkaar. Uit A vertrekt een fietser. Twee uur later vertrekt uit B een auto, met een snelheid van 45 km p. uur. Een uur na het vertrek van de auto ontmoeten ze elkaar.
    1. Hoeveel km heeft de fietser afgelegd?
    2. Hoe groot is z’n snelheid geweest?
    3. Hoe lang doet de fietser over de hele weg?
28. Een handelaar koopt 100 liter wijn voor ƒ 480,-- en 60 liter voor ƒ 240,--. Hij mengt deze soorten en verkoopt het mengsel voor ƒ 5,85 per liter. Hoeveel % wint hij?
29. A kan een werk doen in 60 dagen, B in 90 dagen en C in 45 dagen. A en B werken eerst samen 16 dagen. In hoeveel tijd kan C alleen het afmaken?
30. A, B en C verdelen een som geld van ƒ 3250,--. A en B krijgen samen anderhalf maal zoveel als C. A krijgt ƒ 60,-- meer dan B. Hoeveel krijgt ieder?

J. Mooijaart (1963). Parate kennis op de nieuwe kweekschool. Paedagogische Studiën, 40, 483-500. [wel online beschikbaar, ik zoek dat nog op, zie ook PedagStud.htm]

d. hoofdrekenen

Achter de volgende opgaven moesten de antwoorden zonder berekeningen op papier ingevuld worden:

               7 × 99 =
              6 × 375 =
            4848 : 12 =
            4256 : 14 =
            6006 : 12 =
           8 × 12,125 =
14 2⁄7% van Fl.212,10 = 
          9432 – 7432 =
           3007 + 870 =
  20 % van Fl. 120,25 =
          143,39 : 13 =
       8 × 3 × 12 1⁄2 =
          448 : 0,112 =
         25 × 18 × 12 =
           63 : 7 × 3 =
         97 + 61 + 39 =
            8008 – 88 =
           1,818 + 18 =
        2 2⁄7 × 5 × 7 =
      75,375 : 37 1⁄2 =


We menen hier een beroep te doen op parate kennis, die langs de weg van het inzicht is verkregen. Dat hij of zij, die op de lagere school het vak rekenen moet gaan onderwijzen, deze stof voldoende moet beheersen is duidelijk.
In de toelichting bij het betreffende programma voor het kweekschoolexamen wordt “vaardigheid in het hoofdrekenen” met name genoemd.

[Voor het onderdeel hoofdrekenen mochten 10 minuten worden gebruikt, de resterende 40 minuten konden door de deelnemers over de andere vakken verdeeld worden.]

[ . . . met toestemming overgenomen uit het lagere-schooleindexamen, dat in 1955 in Eindhoven werd gehouden onder leiding van de heer H. J. Carpay, nu inspecteur van het Kweekschoolonderwijs. Aan dit examen namen alle zesde-klassers van de Rooms-Katholieke lagere jongensscholen in Eindhoven deel. Aantal kandidaten 1055. Wij maakten van deze opgaven gebruik, omdat de in Eindhoven behaalde resultaten aantoonden, dat deze proeven op het niveau van de zesde klas van de lagere school lagen.]

Zie ook mijn blog Parate rekenkennis op de nieuwe kweekschool 1960 op het BON-forum.

Gerard Alberts & Bert Zwaneveld (2001). Interview Henk Schuring, vertrekkend wiskundeman bij het Cito. Alle dagen eindexamen. NAW 5/2 nr. 3 september 2001. 262-265. pdf

Fred Goffree, Willem Faes & Wil Oonk (1988). Reken vaardig. Wiskunde & didactiek 0. Wolters-Noordhoff.

Basisschoolleraren in opleiding blijken in nood te komen als ze niet in staat zijn de ‘eenvoudige’ rekenopgaven van de basisschool te maken. Voor PABO-studenten van deze tijd ligt de problematiek moeilijker dan voor vele van hun voorgangers. Zij hebben namelijk voor een groot deel mechanistisch ingericht rekenonderwijs ontvangen terwijl ze met grote waarschijnlijkheid worden geplaatst voor opgaven uit reken-wiskundeboekjes van realistische signatuur.

Dit boek is ontworpen om PABO-studenten te helpen door zelfstudie zich het nieuwe rekenen eigen te maken. Wat dat preceis is, kan men weerspiegeld zien in de Reflektieve oplossingen, die aan de opgaven zijn toegevoegd.

De kerngedachte achter dit boek is dat functionele rekenvaardigheid verworven wordt in een ‘natuurlijke omgeving’ en dat dit hoofdzakelijk geschiedt op basis van ‘gezond verstand’. Zorgvuldig geselecteerde opgaven uit de nieuwe reken-wiskundeboekjes, aangevuld met probleemsituaties uit onze dagelijkse omgeving, vormen een inspirerende leeromgeving voor eerstejaarsstudenten.

Dit boek moet beschouwd worden als een ‘voorloper’ in de serie Wiskunde & Didactiek. Ook bij het doorwerken van de drie volgende delen wordt rekenvaardigheid, maar nu in een didactisch perspectief, ge- en beoefend.

flaptekst van de drie auteurs.

Fred Goffree (1993). Kleuterwiskunde Wolters-Noordhoff. Fred Goffree (1982/1994). Wiskunde & didactiek 1. Wolters-Noordhoff.

Fred Goffree (1992). Wiskunde & didactiek 2. Wolters-Noordhoff.

Fred Goffree (1985). Wiskunde & didactiek. Derde deel. Wolters-Noordhoff.

L. N. H. Bunt (1958). The teaching of arithmetic and mathematics to students between 6 and 15 years of age in the Netherlands. Subcommittee for the Netherlands of the International Commission on Mathematics Instruction. J. B. Wolters (77 blz. brochure)

• Chapter IX The promotion from the primary to the grammar school in connection with the teaching of arithmetic. 67-77

Bunt heeft enkele voorbeelden vertaald, zoals Rekenen I en Rekenen II in de toelatingsexamens voor h.b.s. en gymnasium in Hilversum, 1955 (blz 69-70), en een voorbeeld van een rekentoets opgesteld door het Nutsseminarium (p. 70-71). Bunt (blz. 72) noemt nog de volgende publicaties:

• S. Klein (1949). Examineerbare stof voor het toelatingsexamen der middelbare school.
• H. Turkstra (1952). Toelating tot en selectie op de middelbare school.
• Een publicatie van de drie onderwijsonderzoekbureaus: Richtlijnen voor de toelating tot de middelbare school.

Het idee bij al deze drukte is tamelijk simpel: het gaat om de voorspelling van de schoolloopbaan in het vo, en dat doen we dus door de kandidaten een intellectuele uitdaging te geven, zodanig dat de verschillen tussen leerlingen goed worden uitvergroot. Ik vind het maar eng; het gaat hier om 12-jarigen. Ik ben er zelf destijds (1956) ook aan onderworpen (een proefklas zelfs). Die proefklas is beschreven door Stellwag, een boek dat Bunt niet lijkt te kennen.

H. W. F. Stellwag (1955). Selectie en selectiemethoden. Een inleidende studie in het aansluitingsvraagstuk L.O. en V.H.M.O. Groningen: J. B. Wolters.

Bevat voorbeeldmateriaal uit toelatingstoetsen en proefklassen.

D. J. Kruijtbosch (1916). Schriftelijke opgaven van het eindexamen der Hoogere Burgerscholen vanaf 1885. J. B. Wolters.

Kruijtbosch, D. J. Kruijtbosch (1936). Schriftelijke opgaven van het eindexamen der Hogere Burgerscholen-B met vijfjarige cursus. Wolters.

D. J. Kruijtbosch en S. J. Richter (1956). Schriftelijke opgaven van het eindexamen der hogereburgerscholen-B met vijfjarige cursus. Wolters-Noordhoff.

S. J. Richter (1969). Schriftelijke opgaven van het eindexamen der gymnasia. Wolters-Noordhoff.

J. Versluys (1893). De akten-examens voor wiskunde lager onderwijs in 1892. Verslag der examen-commissie en oplossing der vraagstukken. Amsterdam: W. Versluys. schoolmuseum online

W. H. Wisselink (1894). Rekenschool. Oefeningen voor het aanschouwelijk, uit het hoofd en schriftelijk rekenen. Vijfde stukje. Getallen van 1—1000000. Eenvoudigste breuken ¹⁄₂—¹⁄₁₀. P. Noordhoff. dertiende druk schoolmuseum online

• VOORBERICHT. Blijkens de inhoudsopgave bevat dit stukje oefeningen over de getallen van 1—1000000 en over de eenvoudigste breuken (van ¹⁄₂—¹⁄₁₀). Daarmee is ook bij de breuken de ‘concentrische’ leergang gevolgd. Men meene evenwel niet, dat dit wat nieuws is; al voor jaren zijn in Duitschland rekenboekjes verschenen, waarin ook bij de breuken die leergang gevolgd is, b.v. de werkjes van Lorey en Dorschel , van Kieffer , enz. In zooverre hen ik van hunne methode afgeweken, dat ik meer die breuken op den voorgrond geplaatst heb, welke 't meest in ‘'t leven’ voorkomen. Met opzet zijn de oefeningen over de breuken zóó gekozen, dat men ze (desverkiezende) vóór of te gelijk met de behandeling van de getallen van 1—1000000 nemen kan.

W. H. Wisselink (1893). Rekenschool. Oefeningen voor het aanschouwelijk, uit het hoofd en schriftelijk rekenen. Achtste stukje. Vraagstukken ter Herhaling, enz.. P. Noordhoff. derde druk schoolmuseum online

Walda, R. H. Walda (1890). Vraagstukjes ter toepassing van de hoofdregels met geheele benoemde getallen. Rekenboekje voor eerstbeginnenden. Sneek: J. Campen.

• uitsluitend redactiesommetjes, met antwoordenblad; Walda was van 1890 tot 1922 hoofd van de Chr. school in Scharnegoutum
  Ofschoon onderscheiden seriën rekenboeken, in de laatste jaren voor de school geschreven, in vele opzichten aanbeveling verdienen, toch zullen vele onderwijzers met mij de ervaring opgedaan hebben, dat eensdeels de voorstellen niet eenvoudig genoeg, maar doorgaans te ingewikkeld voor eerstbeginnenden zijn — men overschat zoo licht de denkkracht der kleinen — anderdeels de vraagstukjes te dikwijls “zonder cijferen” kunnen uitgerekend worden, zoodat ze meer in werkjes, uitsluitend voor “uit het hoofd rekenen” bestemd, op hun plaats zouden zijn. Ik gevoelde steeds behoefte aan een eerste rekenboekje, waarlijk geschikt kinderen in handen te geven, die in staat zijn tot 100 uit het hoofd te rekenen; geschikt ook als men, na behandeling van elken hoofdregel, dadelijk de behandelde bewerking door het oplossen van vraagstukjes wil laten toepassen. — Het schrifteijk rekenen met benoemde getallen is, mijns bedunkens, voor eerstbeginnenden reeds zóó moeilijk, dat men vooreerst wel tevreden mag zijn, wanneer ze alleen de “routine” ervan verkrijgen. Later kunnen de opgaven zo ingericht worden, dat ze ook de strekking hebben eenigermate de denkkracht op te wekken en te versterken. — Dit een en ander trachtte ik steeds te bereiken, door zelven vraagstukje op ’t bord te geven. Als verzameling van die opgaven beschouwe men dan ook dit rekenboekje, hetwelk ik mijnen mede-onderwijzers thans aanbied. —

  In de Eerste Afdeling van het Eerste Stukje komen alleen getallen beneden 100 voor; in de Tweede Afdeeling van het Eerste en de Eerste Afdeeling van het Tweede Stukje zijn ze tot 1000 genomen, terwijl in de Tweede Afdeeling van het Tweede Stukje geen getallen boven de 10.000 voorkomen. De getallen in de 350 opgaven zijn zoodanig gekozen, dat de leerlingen niet zonder cijferen de “uiitkomsten” vinden. Inzonderheid de “Herhaling en Uitbreiding” geeft m. i. vooreerst genoeg ter opwekking en versterking der denkkracht ! Om het juist begrijpen der vraagstukjes te bevorderen, is bij de inkleeding ervan gestreefd naar de grootst mogelijke eenvoudigheid. —

  
  Tweede Afdeeling

  
  Herhaling en uitbreiding van het voorgaande

  
  

  1. Vader is 36 jaar oud, Moeder 32 jaar, Jan 12 jaar, Pieter 10 jaar en Klaas 8 jaar. Hoeveel jaar tellen Vader, Moeder en deze drie jongens samen?
  2. Eene koopvrouw verkoopt op Maandag 16 koolen, op Dinsdag 14 koolen, op Woensdag 15 koolen, op Donderdan 18 koolen en op Vrijdag 17 koolen. Hoeveel koolen verkoopt zij in die vijf dagen?
  3. Een gulden is 100 centen waard, een halve guulden 50 centen, een kwartje 25 centen, een dubbeltjje 10 centen en een stuivertje 5 centen. Hoeveel centen zijn die geldstukken samen waard?
  4. Oom heeft 30 koeien en Vader 36 koeien. Onze ééne buurman heeft 36 koeien en de andere 32 koeien. Hoeveel koeien hebben die samen?
  5. Verminder 100 gulden met 48 gulden.
  6. Trek van 100 eens 36 af. Hoeveel is nu de rest?
  7. Ik heb 50 centen in mijn spaarpot. Oom geeft mij 25 centen en Tante 20 centen. Als Vader mij 15 centen geeft en Moeder 10 centen, hoeveel centen heb ik dan wel?
  8. Ik zie vijf ramen. In het eerste raam tel ik 32 ruiten, in het tweede 30 ruiten, in het derde 28 ruiten, in het vierde 24 ruiten en in het vijfde 20 ruiten. Hoeveel ruiten heb ik nu wel geteld?
  9. Meester had 144 pennen in een doosje. De kinderen hebben er reeds 96 pennen van gebruikt. Hoeveel pennen zijn er nog in het doosje?
  10. In een bosch staan 200 boomen. Als een houthakker 72 boomen omhakt, hoeveel boomen staan er dan nog?
  11. Een kuiper maakt in één week 125 vaten. Als hij 96 vaten verkoopt, hoeveel vaten heeft hij dan nog?
  12. In de schoolkast liggen 225 schriften. De kinderen hebben 175 schriften ervan gebruikt. Hoeveel schriiften liggen er ni nog?
  13. Tel eens samen: 25 noten, 40 noten, 36 noten, 64 noten en 65 noten.
  14. Een turfschipper verkoopt op Maandag 75 turven, op Dinsdag 90 turven, op Woensdag 100 turven, op Donderdag 125 turven en op Vrijdag 150 turven. Hoeveel turven had die man in die vijf dagen verkocht?
  15. Er staat een stapel van 100 leien in school. Als er 65 leien van aan de kinderen gegeven worden, hoeveel leien staan er dan nu?
  16. Een schipper heeft nog 900 turven in zijn schip. Nu lost hij hiervan 550 turven. Hoeveel turven zijn er nog in het schip?
  17. Maart is 31 dagen en April 30 dagen; Mei is weer 31 dagen en Juni 30 dagen; Juli is ook 31 dagen. Hoeveel dagen zijn deze vijf maanden samen?
  18. Aan de schoolkinderen moeten 90 pennenhouders uitgedeeld worden. De onderwijzer heeft maar 65 pennenhouders. Hoeveel pennenhouders zijn er te weinig?
  19. Schrijf nu eens in woorden: 101, 110, 103, 130, 200, 250, 300, 306, 360 en 450.
  20. Er gaan 175 kinderen op school. In ’t voorjaar komen er 25 kinderen bij en in ’t najaar nog 30 kinderen. Hoeveel kinderen zijn er nu op school?
  21. Als Vader van 500 gulden eens 275 gulden uitleent, hoeveel gulden heeft Vader dan overgehouden?
  22. Een rijksdaalder = 250 centen; een gulden - 100 centen; een halve gulden = 50 centen; een kwartje = 25 centen en een dubbeltje = 10 centen. Hoeveel centen zijn die vijf geldstukken samen?
  23. Een koopman heeft 825 gulden in een zak. Als hij er 350 gulden uit neemt, hoeveel gulden zijn er dan nog in den zak?
  24. Schrijf nu in cijfers: vierhonderd, tweehonderd, driehonderd vijf, driehonderd vijftig, vierhonderd tien, vijfhonderd twaalf, achthonderd een, honderd vijftig, zeshonderd, tweehonderd zeventig.
  25. Ik ken vijf kleine dorpen. In het ééne dorp wonen 135 menschen, in het andere 200 menschen. Als er in het derde dorp 225 menschen, in het vierde 150 menschen en in het vijfde 175 menschen wonen, hoeveel menschen wonen er dan in deze dorpen?
  26. In ons dorp wonen nu 625 menschen. Vroeger woonder er 468 menschen. Hoeveel menschen wonen er nu meer dan vroeger?
  27. Een stuk linnen is 245 meter lang. Als er nu 136 meter van verkocht is, hoeveel meter is dat stuk nu nog lang?
  28. Piet haalde voor 36 cent suiker, voor 45 cent tabak, voor 28 cent stroop, voor 24 cent rijst en voor 16 cent gort. Hoeveel cent moest hij betalen?
  29. Vader en oom hebben samen 900 gulden. Als Vader hiervan 475 gulden toekomt, hoeveel gulden krijgt oom dan wel?
  30. Hoeveel is 100, 200, 150, 250 en 300 samen?
  31. Hendrik heeft 60 knikkers. Geert heeft 12 knikkers meer. Hoeveel knikkers heeft Geert dan?
  32. Reken nu ook eens uit, hoeveel knikkers Hendrik en Geert samen wel hebben.
  33. Moeder is 32 jaar. Grootmoeder is 28 jaar ouder dan Moeder. Hoeveel jaar telt Grootmoeder? En hoeveel jaar zijn zij samen oud?
  34. Zoek de som van: tweehonderd, honderd zes, tweehonderd vier, negentig een driehonderd vijftig.
  35. 64 appels + 36 appels + 75 appels + 125 appels + 250 appels + 325 appels = . . . .
  36. Mijn broeder heeft 110 meter touw voor een vlieger. Vader neemt er 25 meter af. Hoeveel meter heeft mijn broer nu nog over?
  37. 250 pruimen — 135 pruimen = . . . ; 350 gulden — 275 gulden = . . . ; 625 centen &mdahs; 448 centen = . . .
  38. Op eene plank in de boekenkast staat een stapel van 24 boeken en een stapel van 12 boeken. Daar naast staat een stapel van 18 boeken en nog een stapel van 36 boeken. Hoeveel boeken staan er op die plank?
  39. Verminder 732 met 456. Hoe groot is de rest?
  40. Een koopman heeft 2 zakken met geld. In den éénen zak is 295 gulden. In den tweeden zak is 145 gulden meer. Hoeveel gulden is er nu n den tweeden zak?
  41. Reken ook nog uit, hoeveel gulden er in die twee zakken samen is.
  42. Een toren is 119 meter hoog; maar een andere is 216 meter hoog. Hoeveel meter is de laatste toren hooger dan de eerste?
  43. Iemand heeft 3 manden met flesschen. In de ééne mand zijn 80 flesschen, in de andere 66 flesschen en in de derde 74 flesschen. Hoeveel flesschen zijn er in de drie manden?

G. M. Wilson and Kremer J. Hoke (1920). How to measure. New York: The Macmillan Company. two fold-out grading scales (spelling, drawing) Internet Archive

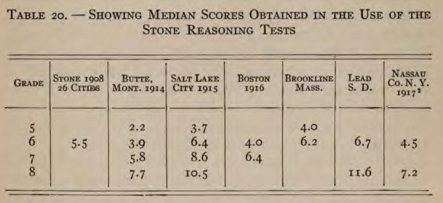
Hoofdstuk 4 The measurement of arithmetic 58-109 geeft enkele toetsen met normtabellen! Tijdcapsule 1920. Blader het boek eens door, op de site van archive.org. Een interessante test is de Stone Reasoning Test, laten we daar eens naar kijken. Ik doe geen poging om de opgaven te vertalen, maar ook zonder vertaling is waarschijnlijk wel in te zien dat dit inderdaad geen rekentoets is, maar een intelligentietest. De tabelletjes met resultaten laten dat ook zien: de basale rekenvaardigheid zal van klas 6 naar 8 niet zo gek veel verbeteren, maar de scores op deze test verdubbelen bijna. Achter iedere opgave het aantal punten voor een goed antwoord.

THE STONE REASONING TEST

Solve as many of the following problems as you have time for; work them in order as numbered:

1. If you buy 2 tablets at 7 cents each and a book for 65 cents, how much change should you receive from a two-dollar-bill ? [1.0]

2. John sold 4 Saturday Evening Posts at 5 cents each. He kept ¹⁄₂ the money and with the other ¹⁄₂; bought Sunday papers at 2 cents each. How many did he buy? [1.0]

3. If James had 4 times as much money as George, he would , have $16. How much money has George? [1.0]

4. How many pencils can you buy for 50 cents at the rate of 2 for 5 cents? [1.0]

5. The uniforms for a baseball nine cost $2.50 each. The shoes cost $2 per pair. What was the total cost of uniforms and shoes for the nine ? [1.0]

6. In the schools of a certain city there are 2200 pupils ; ¹⁄₂ are in the primary grades, ¹⁄₄ in the grammar grades, ¹⁄₈ in the high school and the rest in the night school. How many pupils are there in the night school? [1.4]

7. If 3¹⁄₂ tons of coal cost $21, what will 5¹⁄₄ tons cost? [1.2]

8. A news dealer bought some magazines for $1. He sold them for $1.20, gaining 5 cents on each magazine. How many magazines were there ? [1.6]

9. A girl spent 1⁄₈>1⁄₈ of her money for car fare and three times as much for clothes. Half of what she had left was 80 cents. How much money did she have at first? [2.0]

10. Two girls receive $2.10 for making buttonholes. One makes 42, the other 28. How shall they divide the money? [2.0]

11. Mr. Brown paid one third of the cost of a building; Mr. Johnson received $500 more annual rent than Mr. Brown. How much did each receive? [2.0]

12. 12. A freight train left Albany for New York at 6 o'clock. An express train left on the same track at 8 o'clock. It went at the rate of 40 miles an hour. At what time of day will it overtake the freight train if the freight train stops after it has gone 56 miles? [2.0] >

Toetsnaald

Ik ben op zoek naar deze boekjes. schoolmuseum.uba.uva.nl heeft 16 hits voor ‘toetsnaald’, maar wat stelt het voor? Meest gaat het om uitgeversadvertenties, dat schiet dus niet op. Tenminste één boek is in gescande vorm beschikbaar, zie hierbeneden.

• We wenschen onze lezers opmerkzaam te maken op de uitgave van twee werkjes, die hun bij de examens uitstekende diensten kunnen bewijzen nl.: 1. 2.

  
  Toetsnaald voor Adspirant-Onderwijzers en Onderwijzeressen. Verzameling der schriftelijke werkzaamheden van 51 examens voor 0 n d e r w ij z e r (1894-1897).

  
  Toetsnaald voor Candidaat-Hoofdonderwijzers en Hoofdonderwijzeressen. Verzameling der schriftelijke werkzaamheden van Zes examens voor de Hoofd-acte (1894--1897).

  
  Beide zijn uitgegeven te 's-Gravenhage, bij de Haagsche Boekhandel- en Uitgevers-Maatschappij. Het eerste werkje kost f 0,90, het tweede f 0,75

  dbnl.org

  • Toetsnaald voor Adspirant-Onderwijzers en Onderwijzeressen, Verzameling der Schriftelijke werkzaamheden van LI Akte Examens voor Onderwijzer van 1894-1897.....■ - 0.90 _Ie vervolg 1898..............- 0.25
  • Toetsnaald voor Candidaat-Hoofdonderwijzers en Hoofdonder- wijzeressen. Verzameling der Schriftelijke werkzaamheden van XXV Examens voor de Hoofdakte van 1894-1897 . - 0.75 _lo vervolg 1898 ..............- 0.25
  • Toetsnaald voor Onderwijzers, die voor vergelijkende examens studeeren. Opgaven van XXXVI Examens 1894-1898 . . - 0.75
  • Toetsnaald voor Leerlingen der Vijfde Klasse H. B. S., Scholen voor U. L. 0. en voor zelfoefening; alsmede voor hen, die voor den Handel worden opgeleid. Schriftelijke examen-opgaven. Eind-Examen H. 8. S., Toelating Universiteit, Veerartsenij- school, Kon. Mil. Academie, Leerling-Consul, Instituut Accoun- tants, 1895-1898 ...............- 0.75 [gescand beschikbaar]

  http://goo.gl/hdofU

• Toetsnaald I voor adspirant-onderwijzers en onderwijzeressen. Verzameling der schriftelijke werkzaamheden van LXXIII acte-examens voor onderwijzer van 1894-1899. Tweede vermeerderde uitgave. Haagsche Boekhandel- en Uitgevers-maatschappij 1899. abstract
• Toetsnaald II voor candidaat- hoofdonderwijzers en hoofdonderwijzeressen. Verzameling van schriftelijke werkzaamheden van de examens voor de hoofd-acte van 1894-1899. Antwoorden, oplossingen van reken-vraagstukken en mondelinge examens. Tweede vermeerderde uitgave. Haagsche Boekhandel- en Uitgeversmaatschappij 1899. integraal gescand Toetsnaald III voor onderwijzers die voor vergelijkende examens studeeren. Opgaven van LVII vergelijkende examens voor hoofden van scholen 1894-1899. integraal gescand
• Toetsnaald IV voor leerlinger der vijfde klasse H. B. S., scholen voor U. L. O. en voor zelfoefening; alsmede voor hen, die voor den handel worden opegleid. Schriftelijke examen-opgaven: Eind-examen H. B. S., toelating universiteit, Veeartsenijschool, Kon. Mil. Academie, Leerling-Consul, Instituut-Accountants 1895-1898. 's-Gravenhage: Haagsche Boekhandel- en Uitgevers-maatschappij, 1899. integrale tekst

  ---

• Toetsnaald VI voor de leerlingen van voorbereidingsklassen voor Hoogere Burgerscholen en Gymnasia. Schriftelijke werkzaamheden van XXXIII toelatings-examesn 1895-1898. Haagsche Boekhandel- en Uitgeversmaatschappij 1899. abstract
• Toetsnaald VII voor hen, die zich voorbereiden voor de toelatings-examens tot de kweekscholen en rijks-normaallessen voor onderwijzers en onderwijzeressen. Schriftelijke examen-opgaven 1895-1899. Haagsche Boekhandel- en Uitevers-Maatschappij 1899.
• Toetsnaald VIII acte-examens L. O. en M. O. voor Fransch, Duitsch, Engelsch. 200 vertalingen, oefeningen, dictées van de examens 1897-1899 en vorige jaren. Haagsche Boekhandel- en Uitgeversmaatschappij, 1900. abstract

Het Schoolblad

• In dit 19e-eeuwse tijdschrift staan onderwijzersexamens. Een voorbeeld daarvan is gereproduceerd in Evert Janssen (z.j.):

  Evert Janssen (z.j.). Nederland in 1884: Vreemd vaderland, vertrouwd volk. Terra. isbn 9062551947 blz. 168

H. F. M. de Smet & Victor Julius D’Espallier (1957). Schoolvorderingentest voor rekenen: ten behoeve van hen die het zesde studiejaar L.O. verlaten. Leuvense Universitaire Uitgaven: Standaard-Boekhandel. [aanwezig uitleenbaar KB Den Haag]

• 145 bladzijden. Ik heb juli 2013 geen verwijzingen naar dit boekje gevonden op internet. Wel een exemplaar te koop aangeboden op boekwinkeltjes.nl

J. W. van der Hulst & A. Reens (zd [zestiger jaren]). Cijfers en normen. Leergang voor het grafisch bedrijf. Vereniging tot Bevordering van de Vakopleiding in het Boekdrukkers-, Rasterdiepdruk- en Chemigrafisch bedrijf.

Prachtig materiaal voor wie gek is op contextopgaven. Maar dit zijn wel vakspecifieke contexten! Een aantal opgavenreeksen doorbladerend is het wel duidelijk dat het hier niet gaat om de rekenvaardigheid, maar om het om kunnen gaan met het vakjargon. Dat er daarbij ook gerekend moet worden, zal ongetwijfeld mede de bedoeling hebben om de rekenvaardigheid op peil te houden, niet om deze te toetsen. Interessante visie op redactiesommen/contextopgaven. Toch?

• 1. Een drukker heeft een stalen perforeerlijn nodig ter lengte van 28 cm. Hoe lang is die lijn in typografische punten?
  2. Een binder moet voor de zetter een aantal stroken karton snijden ter lengte van 20 augustijn. Hoe lang, in cm uitgedrukt, moeten de stroken worden?
  3. Hoeveel augustijn is 1 m?
  4. Hoeveel augustijn is een vel papier van 22×28 cm breed en lang?
  5. Een typograaf is 1,80 m lang. De dikte van zijn schoenzolen bedraagt 12 punten. Hoe lang is die typograaf, gemeten in augustijnen? En hoe dik zijn zijn schoenzolen in mm?
  6. Een binder krijgt opgegeven kaarten te snijden uit karton ter grootte van 50×65 cm. De kaarten worden 55¹⁄₃ augustijn breed en 33¹⁄₄ augustijn hoog. Hoe groot worden deze kaarten in mm? En hoeveel kaartjes van 122 mm breed en 50 mm hoog kunnen uit een der overblijvende stroken gesneden worden?

  Attentie! De opgaven met vetgedrukte cijfers [in dit geval: 5, 6 en 7] zijn bestemd voor de hogere leerjaren.

  de eerste reeks opgaven, blz. 8

• Vraag: Een pagina mag 40 augustijn hoog worden. Hoeveel regeles corps 8 kan deze pagina bevatten?
  Antwoord: Deze pagina kan 60 regels bevatten
  Berekening: 40 augustijn = 40×12 punten = 480 punten; 480 punten : 8 = 60; er kunnen dus 60 regels op de pagina.

  blz. 9

C. A. Reeser & H. Turkstra (rapporteurs) (1940). Rapport uitgebracht aan het Nutsseminarium voor Paedagogiek aan de Universiteit van Amsterdam omtrent door de Wiskunde-Werkgroep samengestelde opgaven voor het toelatingsexamen 1939 (Rekenen II) [aanwezig: KB] pdf scans 20 Mb

C. A. Reeser & H. Turkstra (rapporteurs) (1940). Rapport uitgebracht aan het Nutsseminarium voor Paedagogiek aan de Universiteit van Amsterdam omtrent door de wiskunde-werkgroep samengestelde opgaven voor het toelatingsexamen 1940 : (rekenen II)/ [rapporteurs: C.A. Reeser, H. Turkstra] [aanwezig: KB] pdf scans 20 Mb

Tot de in de titel genoemde werkgroep behoorden o.a. Philip Kohnstamm (vz), E. W. Beth, E. J. Dijksterhuis, Tatjana Ehrenfest-Afanassjewa.

Cornelis Adriaan Reeser (1941). Vergelijking van toelatingsexamen rekenen II 1939 (opgaven Nutsseminarium) met de rapportcijfers voor wiskunde in de 1e klasse 1940. Mededelingen van het Nutsseminarium voor Paedagogiek aan de Universiteit van Amsterdam ; no. 35. Wolters. Overdruk uit Paedagogische Studiën, april 1941, 56-66. lees artikel hier

Hessel Turkstra (1952). Toelating tot en selectie op de M.S. Christelijk Paedagogisch Studiecentrum. [aanwezig: KB] pdf scans 20 Mb

Hessel Turkstra (1957). Een onderzoek over de correlatie tussen de vorderingen voor algebra en meetkunde in de eerste klas van de middelbare school en het cijfer voor rekenen op de l.s. en op het toelatingsexamen voor de middelbare school. Euclides, 32, 161-172. annotaties

Karin den Heijer ‏‪@KdenHeijer‬ Apr 14 Karin den Heijer (14 april 2014): Dit is ook een leuk alternatief voor de 3F 'reken'toets klas 6 VWO. Geen rekenmachine, geen kladpapier, voor klas 1! ‪pic.twitter.com/rLSRNBA4yq ‬tweet

Binnen 24 uur meer dan 60 retweets. Heeft landelijke belangstelling getrokken. Is Nederland er dan toch eindelijk klaar voor?

Brouwer, W. H. Brouwer, I. C. Van Houte, P. Post en M. C. J. Scheffer (1955). Schoolkinderen uit sociaal zwakke gezinnen. Groningen: Wolters. Mededelingen van het Nutsseminarium voor Paedagogiek aan de Universiteit van Amsterdam.

• Een intelligentieonderzoek op enige Leidse scholen - Aanleg en vorming van de intelligentie - Is de intelligentie der betreffende bevolkingsgroep in aanleg onvoldoende? - Conclusies uit het onderzoek der zeven volksscholen en keuze van een proefschool - Voorbereiding en aanvang van de proef - Opmerkingen over de leerstof - Resultaat van het experiment
• Het boek geeft een rekentoets die in 1953 is afgenmen op de onderzochte school, en op een andere school met een vergelijkbare leerlingenpopulatie, zij het gemiddeld een behoorlijk stuk ouder. De samenvattende resultaten zijn eveneens gerapporteerd, zodat die een rekentoets is die op een bepaalde manier een vergelijking over zestig jaar heen mogelijk maakt, met leerlingen die dezelfde opgaven anno 2014 maken. Ik ben benieuwd wie dit experimentje willen uitvoeren. Het gaat om de bladzijden 172-175 in het boek, waarvan ik scans op Twitter heb geplaatst: 172-3 en 174-5

Henry van Engen, Maurice L. Hartung, Harold C. Trimble, Emil J. Berger, Ray W. Cleveland, E. Glenadine Gibb, James E. Stochl & Ray Walch (1969). Mathematics: concepts, applications. First course; Second course (2 vols). Teacher's edition. Glennview, Illinois: Scott, Foresman and Company. [The Basic Mathematics Program (6 preceding volumes)] [seems to be extremely rare; no information on the www located?]

A. van de Glind (1986). Elementair rekenen en tekenen algemene economie. Wolters-Noordhoff. isbn 9001338488 Met Meneer van Dalen wacht op antwoord. Er is een afzonderlijke Handleiding bij uitgegeven. Voor klassikaal gebruik bedoeld boekje om rekenvaardigheid op te peppen.

H. J. Ots (z.j., ws ca 1980). Getal en economie. Voor het HAVO. Van Walraven. isbn 9060493230 40 blz octavo ".. voor leerlingen bij het havo, die moeite hebben met de toepassing van elementaire wiskunde bij economie. Met Meneer van Dalen wacht op antwoord ;-)

K. Suzenaar (1942 3e). Algebra voor Lagere Nijverheidsscholen I. Nieuwe N.O. Serie. AE. E. Kluwer

tweet

  http://www.benwilbrink.nl/projecten/hist_rekenopgaven.htm http://goo.gl/r0YDo
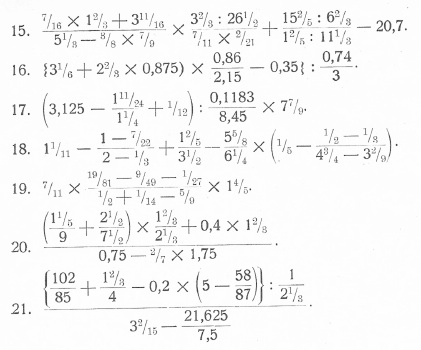