Inleiding
2 Heuristieken voor het construeren van vragen over een enkel begrip.
2.1 Relatie tussen leerstof en vraagvorm.
2.2 Gebruik van de rijkdom aan voorbeelden bij een 'begrip'.
2.3 Heuristieken voor vragen over een enkel begrip.
3 Heuristieken voor het construeren van vragen over discrimineren of combineren van begrippen.
3.1 Onderscheiden, discrimineren, classificeren, diagnosticeren.
3.2 Combineren van begrippen, inzichten etcetera bij probleemoplossen.
4 controle op de kwaliteit van de toetsvragen.
4.1 controle vooraf op de kwaliteit van de gemaakte vragen.
4.2 controle achteraf op de kwaliteit van de gemaakte vragen.
5 Het componeren van de toets.
5.1 Dekking van de stof - dekking van de doelen.
5.2 De 'moeilijkheid' van in de toets op te nemen vragen.
5.3 'Toevallig trekken' van vragen voor de toets.
6 Validiteit, betrouwbaarheid, recht, en vakbekwaamheid.
6.1 Validiteit: functioneert de toets zoals bedoeld?
6.2 De rol van het toeval; betrouwbaarheid, KR 20, objectiviteit.
6.3 Meerkeuzevragen en het begrip 'objectiviteit'.
6.4 Algemene beginselen van behoorlijk bestuur.
6.5 Richtlijnen voor vakbekwaam toetsen.
7 Essay toetsen, het opstel, werkstukken, mondeling.
7.1 Als je kùnt objectiveren, doe dat dan ook.
7.2 Doorzichtigheid ook hier een belangrijke zaak.
7.3 Modelantwoorden en waarderingsvoorschriften.
7.4 Verschillen tussen beoordelaars: wat er mee te doen?
7.5 Mondeling: eigenlijk geen speciaal geval.
8 Interpretatie van toetsresultaten.
8.1 beheersing van de leerstof.
8.2 Wat valt er over de toetsscore te zeggen als de ware beheersing gegeven is?
8.3 Wat kan de student over zijn eigen ware beheersing zeggen voorafgaand aan de toets?
8.4 Hoe kan de student zijn toetsscore voorspellen?
8.5 Wat kan de docent zeggen over de ware beheersing van de student, gezien zijn toetsscore?
8.6 Gemiddelde, standaarddeviatie, en nog enkele begrippen.
8.7 Wegstrijken van toevalligheden in de scoreverdeling.
8.8 Wat kan de docent zeggen over de ware beheersing van de groep studenten, gezien de toetsscores?
8.9 Wat kan de docent zeggen over de ware beheersing van een enkele student, nu ook een groepsresultaat bekend is?
8.10 Denk aan de veronderstellingen bij het gegeven model!
8.11 Antwoorden bij de opgaven.
Bijlage A Bij toetsgebruik in het onderwijs is klassieke betrouwbaarheid minder van belang.
Bijlage B Betrouwbaarheidsgordels.
Gerefereerde literatuur.
Toegevoegde literatuurlijst op onderwerp.
Index.
De bewerking van de oorspronkelijke tekst naar deze web-versie is beperkt gebleven tot het strakker spellen, verbeteren van fouten en al te grote onhandigheden in taal en stijl, reconstrueren van figuren met nu beschikbare computerprogrammatuur, en hier en daar iets andere notatie van symbolen in verband met de beperkte karakterset van HTML. Het irritante gebruik van de 'je'-vorm en van de lijdende vorm heb ik ongemoeid gelaten.
In deze voorlopige versie is een eenvoudige systematiek gevolgd voor het genereren van heuristische regels voor het ontwerpen van toetsvragen, waardoor de tekst abstracter en taaier is geworden dan de bedoeling was. Dat effect is nog versterkt door het op veel plaatsen nog ontbreken van overtuigende voorbeelden van hoe het wel en hoe het niet goed gaat. Ook 'Toetsvragen schrijven' uit 1983 lijdt daar nog onder. Het is de prijs die ik betaalde voor het waagstuk het ontwerpen van toetsvragen op een nieuw fundament te plaatsen.
Het toetsen van de kennis en het inzicht dat de student in onderwijs en zelfstudie heeft opgedaan, lijkt een in plaats en tijd strikt begrensd gebeuren. De docent kan het construeren, afnemen en nakijken van toetsen ervaren als nogal losstaand van zijn andere onderwijsactiviteiten. Ondanks deze schijn van het tegendeel valt het niet lang vol te houden het toetsgebeuren te beschrijven als iets dat buiten het onderwijs zelf staat, er een beetje bijhangt, een bittere noodzakelijkheid, een wezensvreemd element. Studenten zullen trouwens ook niet verrast zijn wanneer ze een toets voorgeschoteld krijgen: daar zijn ze juist voor gekomen, daar hebben ze zich speciaal op voorbereid. Een evidentie waar toetsspecialisten weleens wat minder rekening mee houden dan wenselijk is.
Wàt je toetst, en hòe je toetst, en welke rol toetsresultaten spelen bij beslissingen die over studenten genomen worden, zijn zaken die van invloed zijn op de wijze waarop de student zich op de toetsing voorbereidt. Dat geldt voor de strengheid van de beoordeling: verhogen of verlagen van de zak-slaaggrens zal van invloed zijn op de studie-inspanning die de student bereid is zich te getroosten. Daarbij zal overigens niet vanzelfsprekend een hogere zak-slaaggrens tot een verhoogde studie-inspanning hoeven te leiden, misschien laten studenten het dan juist wat meer op een eventuele herkansing aankomen (zie de cursus Studiestrategieën html of Cesuurbepaling html). Dat geldt ook voor de openheid of juist de geheimzinnigheid rond toetsing en beoordeling. De student zal gebruik maken van alle informatie die hij kan krijgen: over de onderwerpen waarop wel of juist niet getoetst wordt, het soort vragen dat gesteld zal worden, stokpaardjes van de docent, maar bijvoorbeeld ook hoe goed zijn medestudenten zich op de toets voorbereiden. Wanneer het belangrijk genoeg is zal er zelfs handel in toetsvragen ontstaan, en zullen er georganiseerde pogingen worden' ondernomen om geheimhouding van toetsvragen te doorbreken.
Kortom: wanneer de echt belangrijke beslissingen voor de student vallen op grond van zijn behaalde toetsresultaten, dan mag je verwachten dat de student zich bij uitstek, en soms uitsluitend, in zijn studie zal richten op die kennis, inzichten en vaardigheden die metterdaad getoetst worden. Je mag er als docent nog zulke fraaie doelstellingen en goede bedoelingen op na houden, uiteindelijk is hetgeen hij daarvan in de toetsing ook mee kan nemen in hoge mate bepalend voor wat hij met zijn onderwijs bereikt. Althans wanneer het gaat om zogenaamde cognitieve vaardigheden. Met een cyclus van motiverende colleges kun je veel bereiken zelfs zonder toetsing. En hetzelfde geldt voor al die andere onderwijsactiviteiten die niet vragen om (afsluitende) toetsing.
Nu is het niet mijn bedoeling hier een cynische visie op het onderwijs te presenteren. Integendeel, ik wil er op wijzen dat wij ten onrechte geneigd zijn om het soort samenhang tussen toetsing en onderwijs dat ik zojuist schetste als ongewenst te beschouwen. Toetsing is geen Post Scriptum bij het onderwijs, maar maakt er juist integraal deel van uit. De bijzondere plaats van de toetsing daarbij is dat zij richtingbepalend is voor dat onderwijs, voor de studieactiviteiten van de student, voor de resultaten die geboekt worden, de doelstellingen die gehaald zullen worden. Toetsing, hoewel vaak geplaatst aan het eind van het onderwijs, functioneert in feite als sturingsmechanisme voor veel dat in dat voorafgaande onderwijs gebeurt. Dat neemt niet weg dat toetsing nog andere functies kan vervullen, zoals directe terugkoppeling naar de student over zijn vorderingen, zoals in geprogrammeerde instructie, toetsing als instrument voor het evalueren van je onderwijs, e.d.
Uit deze visie volgt op natuurlijke wijze dat aan de wijze van vraagstellen, het soort vragen dat je in je toets opneemt, het afbeelden van je al dan niet expliciet geformuleerde onderwijsdoelen in toetsvragen, veel aandacht te besteden is. Wat je wilt onderwijzen aan kennis en inzichten zul je ook moeten weten te toetsen, anders is het gevaar te groot dat je met je onderwijs blijft steken in de goede bedoelingen. Deze cursus probeert door het geven van een aantal heuristische regels voor het construeren van toetsvragen in te spelen op de noodzaak onderwijs en toetsing op één lijn te brengen.
Dat deze cursus regels aanbiedt voor het genereren van toetsvragen is iets dat hem onderscheidt van andere, ook van amerikaanse, cursussen. Dergelijke constructieregels zijn nog nauwelijks eerder ontwikkeld, hoewel hier en daar wel aanzetten in de literatuur te vinden zijn. Er zijn meer onderwerpen die in deze cursus op een ongebruikelijke wijze behandeld worden. Bijvoorbeeld wordt de keuze tussen meerkeuzevragen en andere, meer open vraagvormen, niet gemaakt op basis van voordelen en nadelen die dergelijke vraagvormen in het algemeen zouden hebben (hoewel gebruik van meerkeuzevragen zeker niet aangemoedigd wordt). Die keus wordt gemaakt op basis van een analyse van de aard van het inzicht waarnaar je wilt vragen.
Er wordt in deze cursus sterk de nadruk gelegd op procedures die inhoudelijke kwaliteiten van de toets en haar afzonderlijke vragen bevorderen, of meer technisch uitgedrukt: op validiteit van de toetsing, op het functioneren van de toets in overeenstemming met wat je bedoelt te bereiken met die toetsing. Daarbij wordt de meer traditionele problematiek van de betrouwbaarheid de coulissen van het onderwijstoneel ingeschoven, zij het dan ook niet zonder plaatsvervangende technieken aan te bieden die de docent bij het interpreteren van zijn toetsresultaten kan hanteren.
Door een en ander heeft deze cursus een wat alternatief karakter gekregen. Er is geen aansluiting gezocht bij bestaande en de lezer mogelijk ook al bekende teksten, hoewel ik mij er zeker niet tegen heb willen afzetten. Ik ben mij ervan bewust dat ik de lezer daarmee voor een keuze stel waar hij of zij het wel eens erg moeilijk mee zou kunnen hebben. Niets staat je echter in de weg om, mochten mijn argumenten niet de overtuiging brengen dat het Andere ook het betere is, nog eens even de kat uit de boom te kijken, kennis te nemen van het hier te presenteren materiaal, en zelf uit te maken welke toetswereld voorlopig nog het prettigst toeven lijkt.
Doelstelling van deze cursus is het aanreiken van procedures, technieken, inzichten, en informatie die de docent kan aanwenden tot het verzorgen van zijn toets en de daarmee samenhangende procedures op een wijze die verantwoord genoemd kan worden vanuit toetstechnisch en onderwijskundig gezichtspunt. Dat klinkt wat dor, maar de gegeven procedures zullen er voor de studenten toe kunnen leiden dat de toetsing een beter verteerbare zaak wordt, minder getypeerd als zwaard-van-Damocles-situatie dan wel als ploeg waar zè de hand aan te slaan is.
Iedereen kan de hier gegeven technieken hanteren wanneer zijn of haar onderwijs situatie daarom vraagt. Het zal niet direct altjd even makkelijk hoeven gaan, maar de smaak van de hier opgediende pudding bewijst zich in de eenvoudige handeling waarvoor een beweging naar de mond altijd nog wel voorwaarde is. Over het aan te bieden materiaal zul je dan ook geen vragen en opgaven aantreffen (met één uitzondering) omdat de gewenste oefening bestaat uit het direct toepassing op de eigen leerstof, de eigen toets (en de eigen collega's). Alleen het hoofdstuk over interpretatie van de toetsresultaten leent zich voor vragen en opgaven (voor wie daar plezier aan kan beleven), maar deze mogen ook best als illustratie van de toepassing van de gegeven 'theorie' beschouwd en bestudeerd worden.
Bij eerste lezing zul je er hopelijk een paar krenten voor directe komsumptie uit kunnen peuren, om deze cursus later pas weer tevoorschijn te halen wanneer er concrete problemen over de (nog af te nemen) toets of daarbij te volgen procedures op te lossen zijn.
Behandeld wordt zoveel mogelijk al datgene wat van belang is voor de docent die zelf toetsen moet construeren, die zelf de resultaten moet interpreteren. Er wordt niet ingegaan op de mogelijk wat speciale problematiek die samenhangt met het gebruik van 'gestandaardiseerde' tests, althans van toetsen die voor meerdere gebruikers gemaakt zijn. Dat wil beslist niet zeggen dat de kwalitatieve eisen waaraan de toets van een individuele docent moet voldoen niet op dezelfde wijze van belang zijn voor toetsen zoals die bijvoorbeeld door het Cito geconstrueerd worden. Bij grootschalig gebruik van een toets worden kleine verbeteringen in zo'n toets belangrijk genoeg om ze ook aan te brengen. Gebruik je een niet zelfgemaakte toets dan doet zich ook de vraag voor hoe je de kwaliteiten van die toets kunt (en moet) beoordelen; zie daarvoor in ieder geval Richtlijnen 1978.
De toets wordt niet in de eerste plaats beschouwd als meetinstrument, er zal dan ook maar weinig aandacht aan meetkwaliteiten van de toets besteed worden. In plaats daarvan ligt het accent op de overeenstemming tussen wat je toetst (wat je vraagt) en wat je in je onderwijs wilt overbrengen. De toets moet behoorlijk kunnen functioneren in de afspraken die de onderwijsinstelling met de student maakt, zoals de afspraak welke rol de toetsresultaten voor examenbeslissingen zullen spelen. Een en ander laat zich goed illustreren aan de problematiek van laten zakken of slagen: waar moet de zak-slaaggrens, de cesuur, gelegd worden? De aanwijzing van de zak-slaaggrens kan niet gebeuren op louter toetstechnische gronden, op grond van de 'meetkwaliteiten' van de toets. De plaats van de zak-slaaggrens zal wel iets te maken moeten hebben met de doelstellingen zoals die voor groepen studenten als de onderhavige haalbaar blijken. Maar vooral is de zak-slaaggrens te zien als essentiëel onderdeel van de (eenzijdige) afspraak met de student: scoor je tenminste gelijk aan deze cesuur dan wordt je prestatie voldoende beoordeeld. Uiteraard wordt tevoren bekend gemaakt waar de grens zal liggen, zodat de student tevoren weet welke prestatie een voldoende oplevert en hij zijn voorbereiding daarnaar kan inrichten. De problematiek van het kiezen van de zak-slaaggrens is dan nog wel iets gedetailleerder in te vullen dan hier gesuggereerd lijkt te worden. Daar is zelfs zoveel over te zeggen dat een afzonderlijk hoofdstuk in deze cursus daar niet toereikend voor zal zijn: er is een afzonderlijke cursus Cesuurbepaling beschikbaar (Wilbrink 1980 html).
Een ander belangrijk onderwerp dat hier maar zijdelings aangeraakt wordt, betreft de wijze waarop de student zich voor kan bereiden op het binnen halen van de door hem verlangde resultaten: daar wordt in de cursus Studiestrategieën (Wilbrink 1978 html) uitgebreid op ingegaan.
Aan de leerstofkant wordt volstaan met de veronderstelling dat een opsomming van te behandelen onderwerpen die stof ook goed kan beschrijven. Ligt er in tegenstelling tot die aanname een zwaar accent op onderlinge relaties tussen die onderwerpen, op de structuur van teksten, dan is voor het in kaart brengen van die leerstof de cursus met diezelfde titel (Breuker, 1979) aangewezen.
Is het maken van toetsvragen een kunst? Je zou het wel zeggen wanneer je in het ene handboek na het andere ontboezemingen tegenkomt in de trant van 'je moet het maar in de vingers hebben', je moet over de nodige 'inspiratie' kunnen beschikken, het bedenken van goede vragen is een kunst, inderdaad, en 'je moet altijd open staan voor de creatieve inval' onder het afwassen, op weg naar je werk, or what not. Aan de andere kant zijn daar de vele ervaringen van het snel opgedroogd zijn, na enkele keren een toets in elkaar gezet te hebben, van de 'ideënstroom' die aan de vraagconstructie ten grond lag, zodat de steeds grotere moeite bij het bedenken van telkens weer nieuwe vragen over dezelfde stof leidt tot vragen van steeds trivialer karakter, minder over hoofdzaken en meer over bijzaken van de stof. Wie dan verdere inspiratie zoekt bij literatuur over het maken van studietoetsen komt teleurgesteld uit, hem worden stenen voor brood geboden: opsommingen van fouten die je bij het formuleren van vragen zou moeten vermijden, maar geen regels hoe je om te beginnen goede vragen over de stof zou kunnen formuleren.
Welnu, deze leemte wil ik graag opvullen in dit en het volgende hoofdstuk, waarin ik zal proberen een fors aantal vuistregels te geven die het mogelijk maken om niet alleen binnen korte tijd een groot aantal vragen over een stukje leerstof te construeren, maar bovendien dat vragen laten zijn die een redelijk hoge mate van laten we maar zeggen onderwijskundige 'zin' hebben. Deze cursus is de eerste presentatie van wat ik in het vervolg 'heuristieken voor het construeren van vragen', of vraagheuristieken zal noemen, en ik vlij mezelf niet met de gedachte dat ik in deze wonderschone opzet op stel en sprong ook volledig zou kunnen slagen. Ook moet ik in zoverre bescheiden zijn, dat ik steun op werk dat anderen voor mij verricht hebben, waarbij ik hier speciaal wil noemen het werk van Klausmeier en zijn medewerkers die in hun research naar de ontwikkeling van het begripsmatige denken bij kinderen toetsingsinstrumenten ontwikkelden langs ongeveer dezelfde lijn als hier door mij gepresenteerd.
Ik ga er in het volgende van uit dat de te toetsen leerstof zich laat opdelen in daarin afzonderlijk, zij het ook niet zonder relatie tot elkaar, behandelde onderwerpen. In plaats van over 'onderwerpen' zal ik verder over 'begrippen' spreken, en ik gebruik dat als een soort verzamelterm voor 'wetten', 'modellen', 'technieken', 'klassen', etc.:
------------------------------------------------------------------------
'begrippen' zijn: regels ziektebeelden
(in ruime zin) wetten klassen
modellen taxa
theorieën procedures
paradigma's technieken
begrippen (in enge zin)
etcetera.
------------------------------------------------------------------------
De reden om begrippen als organiserend principe te kiezen is dat de menselijke wijze van omgaan met de wereld om hem heen bij uitstek een begripsmatige is. Onze greep op de wereld, niet alleen de materiële maar bijvoorbeeld ook de sociale, wordt vergroot door een betere begripsmatige kijk er op, die ons bevrijdt van het verloren raken in een baaierd van onnozele details. Dat geldt al voor de kleinste peuters, die er een genoegen in scheppen alles wat vier poten, twee oren en een staart heeft, geen poes is, en 'woef' zegt 'hond' te noemen. Dat is ook zo voor de wetenschapper die bepaalde verschijnselen probeert te 'determineren' omdat ze dan voor hem een stuk begrijpelijker zijn, hij er andere relevante kennis ook op van toepassing weet.
Dingen of gebeurtenissen die onder een en hetzelfde begrip vallen, voorbeelden van datzelfde begrip zijn, hebben een aantal typische eigenschappen met elkaar gemeen. Lukt het om een gebeurtenis correct te benoemen of te labelen, dan weet je daarmee ook welke eigenschappen de gebeurtenis nog meer heeft dan degene die je direct al had waargenomen, tenminste voorzover het eigenschappen zijn die kenmerkend zijn voor gebeurtenissen die tot dezelfde klasse behoren, onder hetzelfde begrip vallen. Vanuit de wetenschap dat iets valt onder klasse of begrip zus-en-zo kun je bepaalde voorspellingen over eigenschappen of gedrag van dat 'iets' doen vanuit je kennis over eigenschappen van alle onder dat bepaalde begrip thuis horende zaken. Ik zal hier verder niet over uitweiden, en verwijs de belangstellende lezer verder naar bijvoorbeeld Wickelgren's 'Cognitive Psychology' en Klausmeier en Allen's 'Cognitive development of children and youth.'
De intellectuele vaardigheden bij dit begripsmatig met de wereld omgaan zijn dan ook het correct thuis kunnen brengen van dingen of gebeurtenissen; het kunnen gebruiken van (kenmerkende) eigenschappen van het begrip waar het om gaat, bijvoorbeeld om er voorspellingen op te baseren; het zelf kunnen maken of aanwijzen van dingen die onder een genoemd begrip vallen, etcetera. De open peuterschool Sesamstraat, loopt over van de heel alledaagse voorbeelden van wat ik hier bedoel. Ook bij de leerstof die je je studenten aanbiedt moet het dan gaan om begripsmatige beheersing van die stof, een beheersing die de student in staat stelt effectiever met de wereld om te gaan, geen beheersing die maar tot beperkt doel heeft uit boeken opgedane kennis in als het kan letterlijk bijna dezelfde vorm op ander papier te kunnen reproduceren. Toetsvragen moeten deze begripsmatige beheersing aanboren, geen beroep doen op uit het hoofd geleerde weetjes die o zo snel weer vervaagd zullen zijn. Meestal zal het een kleine moeite zijn een lijst te maken van alle begrippen die in de aangeboden leerstof aan de orde komen, of waarover de toets zal gaan. Ik geef een voorbeeld uit Veldkamp's Inleiding tot de analyse (1957), de begrippen die in het eerste hoofdstuk, over de reële getallen, behandeld worden:
verzameling faculteit
afbeelding volledige induktie
natuurlijke -,
gehele , en en drie met name genoemde stellingen:
rationele getallen
afbeelding op de de ongelijkheid van Bernouilly
getallenrechte het binomium van Newton
interval en omgeving de driehoeksongelijkheid
som en product
nest van segmenten.
Het gegeven lijstje is ongeveer gelijk aan de inhoudsopgave.
Dat ik een wiskunde tekst als voorbeeld heb genomen is misschien een beetje oneerlijk. Wiskunde is een door en door gestructureerd vak, terwijl in de leerboeken weinig motiverende tekst gegeven pleegt te worden. Neem je daartegenover Samuelson's Economics, dan valt op dat erg veel ruimte door motiverende tekst in beslag wordt genomen, op veel plaatsen zelfs ontaardend in pleidooien voor 'The american way of life', terwijl in de lay-out van de tekst heel slecht naar voren komt over welk begrip iedere passage nu eigenlijk handelt. Van zo'n handboek een begrippenlijst maken is een hele klus juist door de ongestructureerdheid van de tekst. Zo'n tekst als van Samuelson kan didactisch best goed zijn, de student enthousiast maken voor het vak, maar het is geen tekst die toegeschreven is op het leren omgaan met nieuwe begrippen op een wijze die zinvol toetsbaar is.
Ik ga ervan uit dat de vakdocent, ook wanneer de behandelde literatuur wollig en mistig is, zonder veel moeite een opsomming van daarin behandelde begrippen kan maken.
Nu is het uitgesloten om alles wat over een bepaald begrip weetbaar, bruikbaar of toepasbaar is ook in het onderwijs te behandelen, in de gegeven tekst te bespreken, of te toetsen. Keuzen, selecties, zullen altijd gemaakt moeten worden. Abstract bekeken ziet een lijstje 'weetbaarheden' over een bepaald begrip er ongeveer als volgt uit:
naam definitie(s) beschrijving eigenschappen voorbeelden en niet-voorbeelden relaties met andere begrippen deelbegrippen waaruit het opgebouwd is toepassingen.
Ik ga het rijtje even kort langs, en kom er bij de te behandelen vraagheuristieken uitgebreider op terug.
Het is handig wanneer het onderwerp dat je behandelt een naam heeft. Absoluut nodig is het niet, het is best mogelijk om vaardigheden te onderwijzen (of te leren) zonder daar ooit een naam aan gegeven te hebben. Kinderen kunnen grammaticaal correcte zinnen spreken zonder de grammaticale regels te kunnen noemen.
Definities zijn ook niet voor alle leerstof even onmisbaar. In de wiskunde moet je er goed mee kunnen werken. bij andere vakken kan een nadruk op definities juist een begripsmatige beheersing in de weg staan. Zo neemt Wickelgren in zijn al genoemde boek geen lijst van termen met definities op, om niet het naieve en onjuiste idee te bekrachtigen dat je al heel wat over een begrip zou weten wanneer je een definitie van een of twee zinnen kent. Een definitie kan natuurlijk een identificatiefunctie hebben: je kunt hem gebruiken om te bepalen of iets wel of niet onder het betreffende begrip valt. Je hebt aan de andere kant ook begrippen waar geen definitie voor te geven valt, zoals 'zwaartekracht' en 'intelligentie', hoewel sommige auteurs in zo'n geval dan maar pragmatische definities geven zoals 'intelligentie is datgene wat een intelligentietest meet', waar je ook weinig wijzer van wordt. Moeilijk te definiëren begrippen, je weet wel: die begrippen waar iedere auteur zijn eigen definitie voor heeft, kun je misschien beter ook maar ongedefinieerd laten.
Bij beschrijvingen komt het op de eigen bewoordingen van de docent aan, bewoordingen die als het even kan didactisch handig gekozen moeten zijn. Enige plooibaarheid ten toon gespreid bij het beschrijven in eigen woorden kan wijzen op een redelijke althans verbale beheersing van het begrip door de student.
Eigenschappen van een begrip hoeven niet per se ook definiërende eigenschappen te zijn.
Een voorbeeld van voorbeelden: voorbeelden van ecosystemen zijn de vijver, de wei, het terrarium, een ruimteschip. Begrippen waar geen voorbeelden van te geven zijn zouden wel eens zinledig kunnen zijn. Voorbeelden kunnen ook een definiërende functie bekleden: samen met gegeven niet-voorbeelden bakenen zij af wat (nog) wel en wat niet (meer) onder het bedoelde begrip valt.
Relaties met andere begrippen kunnen een wetmatig karakter hebben, en daarmee op zich ook weer een 'begrip' vormen.
Toepassingen zijn eigenlijk een bepaald soort voorbeelden. Of anders gezegd: er zijn begrippen waar het er niet zozeer om gaat om er voorbeelden van te kunnen geven of herkennen, maar er toepassingen van te kunnen geven of herkennen.
Dit alles is wel erg kortaf gezegd, maar ik wilde de lezer niet onnodig langer afhouden van het eigenlijke onderwerp van dit hoofdstuk, vraagheuristieken. Ik kom er toch al niet onder uit in een extra paragraaf eerst nog iets over de relatie tussen leerstof en vraagvorm (meerkeuze, open-eind, essay) te zeggen.
In het volgende zal ik bij iedere heuristiek kort aangeven of deze zich in het bijzonder leent tot een bepaalde vraagvorm: voor essayvragen, meerkeuzevragen, of open-eindvragen. Welke vraagvorm je kiest hangt dan ook in de eerste plaats af van wat je wilt vragen. Dat is een ander uitgangspunt dan het tot nu toe gebruikelijke: dat je eerst een te gebruiken vraagvorm kiest op grond van vermeende algemene voor- en nadelen van de verschillende overwogen vraagvormen, en je dan ook aan die ene vraagvorm houdt. Bijvoorbeeld formuleren Stanley en Hopkins (1972) dat als volgt:
De verleiding bij het lezen van dergelijke teksten is groot om op basis van die algemene aanprijzingen de keuze te bepalen op bijvoorbeeld meerkeuzevragen als enige te gebruiken vraagvorm. Dan zit je vervolgens met het probleem hoe je relevante vragen over je leerstof in dat eenmaal gekozen procrustusbed moet wringen: er zal nogal eens stevig gekapt moeten worden. Lang niet alle zinvolle vragen over de leerstof zijn even goed in meerkeuzevorm als in openeindvorm te vragen. De voorbeelden daarvan liggen voor het opscheppen, en zal ik in het vervolg ook in zij het algemene termen, proberen te geven.
Wat dan wel de juiste weg is? Bekijk iedere te stellen vraag afzonderlijk, en ga na of bij deze bepaalde vraag een bepaalde vraagvorm het best past, en kies dan ook die vraagvorm als dat maar enigszins mogelijk is. Bepaalde vragen laten zich bijna vanzelfsprekend in het meerkeuzejasje gieten, terwijl andere vragen over misschien hetzelfde onderwerp zich bij uitstek lenen voor het korte essay type. Is het van belang dat de student bepaalde fouten heeft leren vermijden, dan kan het zinvol zijn hem meerkeuzevragen voor te leggen waarin de afleiders corresponderen aan resultaten of oplossingen die verkregen worden wanneer deze bepaalde karakteristieke fouten gemaakt worden. Gaat het om woordenkennis, dan ligt de openeindvorm voor de hand waarin de student het Nederlandse (of vreemde taal-) equivalent opschrijft. Eenvoudige rekenopgaven giet je natuurlijk niet in de vorm van meerkeuzevragen, maar geef je de openeindvorm: de student geeft het antwoord. Vraag je om bewijsvoeringen, dan kies je de essayvorm. Vraag je een werkstuk te maken, dan kun je dat ook als een essay-opgave beschouwen. Het correct aan kunnen geven of gegeven voorbeelden al dan niet tot een bepaald begrip behoren kun je uitstekend in de meerkeuzevorm doen, waar de alternatieven bestaan uit een opsomming van voorbeeld(en) en niet-voorbeelden.
Heel vaak zal zich de situatie voordoen dat er maar een klein aantal mogelijke antwoorden is waar de student in feite uit kiest bij het beantwoorden van een bepaalde vraag. Je kunt in zo'n geval dan ook de meerkeuzevorm gebruiken, waarin de afleiders bestaan uit die alternatieven. De raadkans die de student dan heeft zou hij ook hebben wanneer de openeindvorm gebruikt wordt, omdat ook dan er uit een klein aantal mogelijkheden gekozen wordt. Een triviaal voorbeeld is de vraag naar de hoofdstad van Gelderland, de ontdekker van de penicilline, de diagnose bij een gegeven ziektebeeld.
Ik behandel hier niet de voordelen en nadelen die bepaalde vraagvormen in het algemeen hebben, afgezien van de stof die terug gevraagd wordt (zie daarvoor elders in deze cursus). Wel geef ik een kort overzicht van de meest gebruikte vraagvormen.
| essay, casus, werkstuk, | Iedere vraag wordt beantwoordt met een uiteenzetting; die kan lang zijn (het opstel), of korter (de toets bestaat uit een aantal essayvragen of opgaven). |
| open-eind, ook wel kort antwoord vragen, soms invul vragen | vragen die met een enkel woord, getal, of met een korte zin te beantwoorden zijn (en ook moeten worden). |
| juist/onjuist, of ja/nee vragen | aangegeven moet worden of de uitspraak die in de vraagstelling gedaan wordt juist of onjuist is. |
| meerkeuze vragen | bestaan uit de vraagstelling, ook wel de stam van de vraag of van het item genoemd, en twee of meer alternatieven waarvan het meest juiste aangestreept moet worden, of de juiste gekozen moet of moeten worden (er zijn vele varianten mogelijk, waarbij er voor te zorgen is dat de student goed ingespeeld is op het soort te stellen meerkeuzevragen). |
De vragen uit een schriftelijke toets zijn in dezelfde vorm natuurlijk ook mondeling te stellen; of een toets mondeling of schriftelijk wordt afgenomen hoeft dan ook in dit opzicht niet noodzakelijk verschil uit te maken. In de praktijk worden vragen voor mondeling echter niet tevoren opgesteld, laat staan dat er een gedetailleerd draaiboek van tevoren is vastgelegd voor de gesprekken, zodat dit meer ongestructureerde mondeling zo zijn eigen bijzondere problemen kent, waarop ik elders in deze cursus nog verder zal ingaan.
Deze benadering, de te kiezen vraagvorm af laten hangen van de specifieke te stellen vraag, kan ertoe leiden dat een toets bestaat uit verschillende vraagvormen naast elkaar. Daar hoeft geen bezwaar tegen te bestaan, als je er maar voor zorgt dat de presentatie overzichtelijk is, dat de meerkeuzevragen bij elkaar staan, evenals de open-eindvragen, de essayvragen. Praktische probleempjes kunnen zich natuurlijk wel voordoen, maar zijn ook eenvoudig op te lossen: bijvoorbeeld wanneer de keuzeantwoorden automatisch gescoord worden, en de essay antwoorden door meerdere beoordelaars afzonderlijk na te kijken zijn. Over de puntentelling voor vragen van verschillende vorm zijn tevoren natuurlijk duidelijke afspraken met de studenten gemaakt.
Nu kan het zijn dat de praktijk sterker is dan de leer, dat het aantal studenten zo groot is dat bij voorkeur van geautomatiseerde toetsverwerking gebruik gemaakt wordt, en er dus meerkeuzevragen gebruikt worden. Dat mag dan zo zijn, dan is het toch raadzaam bij de leerstofanalyse en een eerste aanzet tot vraagformulering te beginnen met de vragen te formuleren in de vorm die als vanzelfsprekend bij de stof en de bedoeling van de vraag past, om later eventueel te proberen het compromis te construeren waartoe de omstandigheden van de toetsing soms kunnen dwingen. Wetend dat het gebruik van meerkeuzevragen een praktisch compromis is, is het beter mogelijk om al te onzinnige formuleringen te voorkomen. Juist bij het zoeken naar 'afleiders', foute alternatieven, voor zijn meerkeuzevragen loopt de docent het gevaar dat de student keuzes worden gevraagd die in het onderwijs helemaal niet aan de orde zijn geweest, en eigelijk ook niet tot de doelstellingen horen.
Het idee studenten 'af te leiden' is een vorm van didactiekpathologie. In deze cursus zal ik het woord 'afleider' niet vervangen door 'fout antwoord' of iets dergelijks, ik zal deze zonde uit 1979 niet verbloemen. In de in 2006 begonnen herziening 'Toetsvragen ontwerpen' komt het woord 'afleider' maar een enkele keer voor: om voor dit misbruik te waarschuwen. Ik wijs er nadrukkelijk op dat het hier niet gaat om alleen maar een fijnzinnige nuance: het is dit soort misbruik van vertrouwen van studenten dat toetsen en examens bij hen in een kwaad daglicht stelt.
Vrijwel ieder begrip dat de moeite van het onderwijzen waard is, is rijk aan inhoud: vaak kunnen talloze voorbeelden of toepassingen bedacht worden. Dat heeft als prettige bijkomstigheid dat een vraag over een bepaald begrip waarin een voorbeeld of toepassing van dat begrip aan de orde is, zich makkelijk laat herformuleren tot een nieuwe vraag door alleen maar een ander voorbeeld of een andere toepassing te kiezen.
Het aantal gehele getallen onder de 10 is maar beperkt. Wanneer je echter een optelvraag construeert waarin de leerling twee getallen onder de tien bij elkaar op moet tellen, dan zijn er 36 varianten op deze zelfde vraag mogelijk door de in te vullen getallen (voorbeelden van het begrip 'gehele getallen onder de 10)' te variëren. Dat lijkt een beetje een al te simpel voorbeeld, maar toch geeft het de bedoeling heel erg goed weer. Een dergelijke vraag zonder concrete getallen (zonder concrete voorbeelden) wordt in de toetsliteratuur ook wel een item form genoemd.
Ook bij ingewikkelder begrippen, wetten, technieken, etcetera kan de item form gebruikt worden.
Op deze wijze kan bij iedere vraag die bij een bepaald begrip geconstrueerd wordt, wanneer toepassingen of voorbeelden daarin een rol spelen, een aanzienlijke reeks nieuwe vragen met weinig moeite gemaakt worden door alleen maar de toepassingen of voorbeelden te variëren.
Wat doe je nu met een reeks vragen die allemaal hetzelfde zijn behalve het daarin concreet ingevulde voorbeeld of de gegeven toepassing?
Ik heb tot nog toe een beetje impliciet gelaten wat ik nu duidelijk wil stellen: de vragen in een toets op te nemen zullen meestal nieuwe vragen moeten zijn, vragen die de student in precies deze vorm of aankleding niet eerder onder ogen heeft gehad. De idee hierbij is dat begripsmatig leren moet betekenen dat de student in situaties die hij niet eerder gezien heeft met het geleerde begrip moet kunnen werken. Of negatief geformuleerd: het kan als regel niet de bedoeling zijn dat de student leerstof (en vragen over die stof) louter uit het hoofd leert; het kan ook niet de bedoeling zijn dat toetsvragen letterlijk de stof terugvragen, of letterlijk gelijk zijn aan in het onderwijs besproken en geoefende vragen.
De vraag is dan: hoeveel verschil is genoeg verschil om van een 'nieuwe' of onbekende vraag te kunnen spreken? Bloom en de zijnen in hun oorspronkelijke werk over een cognitieve taxonomie voor onderwijsdoelstellingen (1956, blz. 125) hielden zich ook met die vraag bezig, en kwamen na het afstrepen van enkele minder reële mogelijkheden tot de formulering dat in de toets een goede (toepassings) vraag een probleem moet behelzen dat als zodanig aan de student bekend kan zijn, maar dat stelt op een manier waar de student waarschijnlijk nog niet eerder aan gedacht zal hebben ('a problem known to the student but a new slant that he is unlikely to have thought of previously). Bloom c.s. konden hier kennelijk nog niet tot klaarheid komen, hun formulering blijft vaag, en ook in de door hen gegeven voorbeelden is op generlei wijze iets van de item-forms-benadering al te herkennen. Want zo moet je 'bekende problemen vanuit een nieuwe invalshoek, zien: de aard en eventueel ook de formulering van de vraag blijft hetzelfde, wat verandert is het voorbeeld of de toepassing die in die formulering genoemd wordt.
In de literatuur is de item-forms-aanpak bij uitstek geprobeerd door onderzoekers die zich interesseerden in automatisering van de toetsvragen constructie, de vraag of je computerprogramma's zou kunnen opstellen die een grote hoeveelheid vragen op basis van gespecificeerde item forms zouden kunnen genereren. Nu is dat, behalve in enkele speciale en eenvoudige gevallen, nog niet gelukt, maar dat betekent niet dat deze zelfde item-forms-aanpak voor de docent die zijn eigen toetsvragen jaarin jaaruit moet maken niet bijzonder handig zou zijn (zie o.a. Smal 1977 en Hamaker en Wouters 1975 m.b.t. automatiseringspogingen).
Item forms zijn dus een bijzonder krachtig hulpmiddel bij het snel en efficiënt maken van vragen met een tot in hoge mate gecontroleerde kwaliteit. Het grote probleem is natuurlijk hoe je in de eerste plaats aan de formulering van het item form zelf komt, en daarvoor wil ik de heuristieken hierna en in het volgende hoofdstuk gegeven, van harte aanbevelen.
Ik heb de te behandelen heuristieken geordend rond wat er in de stam van de vraag als gegeven is opgenomen, en wat er van de student gevraagd wordt. Bijvoorbeeld kan in de stam van de vraag het betreffende begrip genoemd worden en van de student een illustratie of toepassing daarvan gevraagd worden:
Het begrip dat in de stam van de vraag genoemd wordt is de 'kwadratuur van de cirkel'. En dat is ook wat van de student gevraagd wordt: de methode daarvoor aan te geven. Het voorbeeld is een strikvraag, en daar moet je studenten niet mee plagen in een toets.
Het gaat hier om het thuis kunnen brengen, identificeren, herkennen van voorbeelden van een met name genoemd begrip, en dus ook het als zodanig kunnen 'ontmaskeren' van niet-voorbeelden van dat begrip.
Het begrip waar het in het voorbeeld om gaat is 'genetisch evenwicht,' waarvan a) t/m f) een aantal voorbeelden en niet-voorbeelden zijn; de student streept alleen de voorbeelden aan. Het voorbeeld is een meerkeuzevraag, met een wat groter aantal alternatieven dan gebruikelijk, waarbij bovendien meerdere alternatieven als 'juist' aangestreept kunnen (moeten) worden.
Niet altijd zal het onderscheid tussen wat nog wel, en wat niet meer als voorbeeld bij een bepaald begrip past even duidelijk of even makkelijk te trekken zijn. Ik zal op de hiermee samenhangende problematiek ingaan in paragraaf 3.1
Deze heuristiek 2.3.1 staat erg dicht bij de leerstof, erg dicht ook bij de wijze waarop begrippen in het onderwijs behandeld, geoefend, bestudeerd zullen zijn. Het zullen veelal 'makkelijke' vragen blijken te zijn, die daarom niet minder relevant hoeven te zijn. Of voor uw eigen vak dit soort heuristiek goed van pas komt? Dat hoeft zeker niet altijd het geval te zijn, de beslissing is aan u zelf.
Vanzelfsprekend worden nieuwe, in literatuur en onderwijs niet behandelde, voorbeelden en niet-voorbeelden, als alternatieven gekozen. Daar zit hem juist de crux van het onderwijs: begrippen leren hanteren in nieuwe situaties, situaties die als zodanig niet in het onderwijs zijn behandeld, maar waar de begrippen op passen. Ik geef nog enkele voorbeelden.
De beide laatste voorbeelden zijn vragen waarbij de student weet dat precies één alternatief (het meest) juist is. Je kunt aan deze vorm van meerkeuzevraag gebonden zijn omdat anders de antwoordformulieren niet automatisch te scoren zijn, maar het is dan toch wel erg inefficiënt: gebruik dan liever de ja-nee-vorm, dat scheelt de tijd nodig om al die extra alternatieven te lezen en daarover na te denken.
Ik heb overigens bij het nakijken van verschillende tekstboeken maar weinig vragen kunnen vinden die op deze heuristiek passen. Misschien komt dat doordat bij de behandeling van de leerstof (te) weinig accenten gelegd worden op een goede afbakening van de behandelde begrippen, misschien wordt wat al te makkelijk aangenomen dat alleen een definitie van besproken begrippen voldoende is om de student ook in bijvoorbeeld toepassingsproblemen met deze begrippen uit de voeten te kunnen laten komen. Ik kom daar straks nog op terug. Het kan ook zijn dat vragen naar deze heuristiek geconstrueerd relatief 'makkelijk' blijken te zijn, en daarom (overigens niet vanzelfsprekend terecht) uit de toetsing worden weggelaten.
Er is een grote verwantschap tussen deze heuristiek en de heuristiek in de laatste paragraaf besproken. Was daar het te maken onderscheid dat tussen voorbeelden en niet-voorbeelden, hier gaat het om het kunnen herkennen van juiste en onjuiste toepassingen, of om het kunnen vermijden van bepaalde karakteristieke fouten bij toepassing van een genoemde regel, techniek, wet, formule. Meestal zal de toepassing in een ook in de vraag aangegeven situatie moeten gebeuren, of met aangegeven materialen, of met gebruik van gegeven cijfers. Deze verdere gegevens moeten misschien eerst door de student nog bewerkt, geordend of geanalyseerd worden voordat ze 'toepassingsrijp' zijn, in welk geval de vraag moeilijker zal zijn dan wanneer die extra activiteit niet gevraagd wordt. Heuristiek 2.3.2 lijkt vooral van belang voor leerstof waar het er om gaat het inadequate gedrag van de student te vervangen door correct gedrag, voor vraagstukken waar de slecht geïnformeerde student geneigd is verkeerde technieken op toe te passen, en leerstof die nogal tegenintuïtief van karakter is (waar leek en deskundige anders of zelfs tegengesteld tegenaan kijken).
De voor de hand liggende vraagvorm is hier de meerkeuzevraag, waar in de stam van de vraag de regel, formule, wet, techniek, etcetera met name genoemd wordt, eventueel de toepassingssituatie beschreven wordt, en de alternatieven bestaan uit één juist (eventueel meerdere juiste wanneer meerdere oplossingen juist kunnen zijn) alternatief, en de overige alternatieven de oplossingen zijn die verkregen worden wanneer de student een bepaalde karakteristieke fout maakt (die hij juist in het voorafgaande onderwijs heeft leren vermijden, als het goed is).
Dit voorbeeld heeft erg veel weg van het in de vorige paragraaf gegeven voorbeeld over 'genetisch evenwicht'. Dat is een klein beetje met opzet, als demonstratie van het meer graduele dan categorische verschil tussen 'voorbeelden' en 'toepassingen'.
Dit voorbeeld betreft een open-eindvraag; er wordt van de student een kort geformuleerd antwoord verwacht. De toegepaste techniek die hier 'getoetst' wordt is de variantieanalyse, en niet de wijze waarop homogeniteit van varianties onderzocht wordt. Je ziet dat in dit voorbeeld meerdere 'begrippen' tegelijk aan de orde zijn, in hun specifieke onderlinge relatie; dat het accent ligt op het onderkennen van een manco in de uitvoering van de variantieanalyse, maar dat tegelijk dat manco ook met name door de student genoemd moet kunnen worden.
Het laatste voorbeeld is in hoge mate toegesneden op hetgeen ook later in studie zowel als beroep van belang is: het als vanzelfsprekend kritisch beschouwen van gerapporteerde data-analyses, waar auteurs met naam en toenaam de gebruikte techniek specificeren maar het aan de lezer is om af te checken of de techniek ook correct is toegepast. De heuristiek kan dan ook niet alleen het herkennen van goede toepassingen betreffen, maar ook het aangeven van omissies of het identificeren van gemaakte fouten.
Het gaat hier om gevraagde (nieuwe) toepassingen van een met name genoemde techniek, wet, regel, etcetera
Het zal bij dit soort vragen vaak gaan om een hint, een concrete aanwijzing op welke wijze het gegeven probleem opgelost kan worden. Dat bespaart de student het zoeken naar de te gebruiken techniek of wetmatigheid. Dat spitst de aard van de vraag toe op de vaardigheid in het toepassen van de betreffende techniek of wet of regel. Het gaat er niet om dat de student kan onderkennen dat hij in het gegeven probleem deze bepaalde techniek moet aanwenden. Het kan ook zijn dat het gaat om een beperking, een randvoorwaarde of een handicap die bij de oplossing van het gegeven probleem in acht genomen moet worden. Terwijl het hierboven gegeven voorbeeld om niets méér vraagt dan regelrechte toepassing van een techniek.
Het gaat hier om een zinvolle en bruikbare soort vraagstelling. Het ligt voor de hand om open-eindvragen te gebruiken, eventueel kort essay. Werkstukken hebben van nature al een essay karakter.
Ook hier geldt weer dat misschien van belang is dat de student bepaalde karakteristieke fouten heeft leren vermijden, in welk geval ook meerkeuzevragen bruikbaar zouden kunnen zijn; het gaat dan om vragen met als alternatieven de uitkomsten verkregen onder correcte toepassing van de gegeven regel of techniek, en uitkomsten verkregen wanneer bepaalde karakteristieke fouten gemaakt zouden zijn. Dan blijft de meerkeuzevraagvorm nog een compromiskarakter behouden: kennelijk gaat het hier om objectief scoorbare antwoorden (bij rekenopgaven bijvoorbeeld), dus waarom zou je dan meerkeuzevragen gaan gebruiken, met de daaraan inherente raadkansen voor studenten met op dat specifieke leerstof onderdeel een achterblijvende beheersing?
Bij de meeste toepassingen zul je te maken hebben met een situatie waarin of waarop de toepassing plaats moet vinden, met gegevens waarvan gebruik gemaakt moet (of eventueel kan) worden, met materialen die gebruikt moeten of mogen worden. Van belang voor de moeilijkheid van de vraagstelling is dan de aard van de gegevens, te gebruiken materialen, situatiebeschrijving e.d.
Zo is het mogelijk de student de gegevens die hij in de formule heeft in te vullen op een presenteerblaadje aan te reiken, maar je zou ook een verhaal kunnen geven waaruit de student moet zien de relevante gegevens te halen, of te vertalen. Voorbeelden daarvan zijn ingeklede vergelijkingen of redactiesommen.
Redactiesommen zijn in de geschiedenis van de wiskunde, overal ter wereld, altijd uitbundig gebruikt, maar in de 20e eeuw ook stevig onder vuur komen te liggen. In mijn herziening 'Toetsvragen ontwerpen' is er meer aandacht voor de ontsporingen bij redactiesommen. Een markante didactische ontsporing is dat leerlingen ervan leren dat je 'iets' met de gegeven getallen moet doen, ook wanneer dat evident niet tot een gepast antwoord op de gestelde vraag leidt. (Een schip heeft 25 koeien en 10 geiten aan boord. Hoe oud is de kapitein?)
Deze vraagvorm staat heel dicht bij de vorige: los op met behulp van, demonstreer, e.d. Wil deze vraagvorm enige zin hebben, dan moet het kunnen geven of genereren van nieuwe eigen voorbeelden een relevante wijze van omgaan met het betreffende begrip zijn. En dan blijven we eigenlijk in de toepassingssfeer zitten: vragen van het type: maak ... , speel ... , construeer ... , bedenk ... , teken ... . Of, wat minder stroef geformuleerd, moet de student het bedenken van nieuwe voorbeelden op kunnen vatten als een relevante bezigheid.
De vraagsoort is hier nogal strikt beperkt tot open eind en essay; meerkeuzevragen komen niet in aanmerking omdat door het voorgeprogrammeerde karakter van deze vraagsoort er geen ruimte is voor het zelf bedenken van nieuwe voorbeelden.
Deze vraagvorm is een beetje riskant, omdat je vaak niet kunt weten of het antwoord van de student echt door hem op het moment van de toetsing bedacht is: misschien heeft hij zich goed op de toets voorbereid en thuis al nieuwe voorbeelden bedacht die hij nu eenvoudig uitschrijft; misschien heeft hij zich breder in de literatuur georiënteerd dan alleen in het opgegeven tekstboek en kan hij daaruit putten naar nieuwe voorbeelden. Het lijkt me dat in nogal wat praktische situaties de docent dit risico best kan aanvaarden. Wil hij dat niet, dan is deze vraagvorm waarschijnlijk toch bruikbaar voor oefening, practicumopgaven, of eventueel take-home-toetsen. In de laatste gevallen gaat het dan minder om 'toetsing' als wel om 'oefening.'
De voorbeelden liggen voor het oprapen. De student rechten zou casus kunnen bedenken die mogelijk passen bij een gegeven rechtsregel; de student statistiek kan concrete problemen bedenken die met een gegeven techniek aangepakt kunnen worden; nieuwe illustraties, eventueel voorbeelden uit het dagelijks leven, van een gegeven natuurwet; etcetera.
Alleen begrippen die uit een klein aantal 'leden' bestaan lenen zich minder voor deze vraagvorm. Ik denk daarbij aan bovengeschikte categorieën waarvan alledaagse voorbeelden zijn: meubels, fruit, voertuigen. De opsomming van categorieën die hieronder vallen is al gauw min of meer volledig: stoelen, tafels, banken, kasten, putten de categorie 'meubels' al aardig uit, en nog meer voorbeelden vragen is meer een vorm van intelligentietesterij (slimmigheid) dan het toetsen van het weten om te gaan met het begrip 'meubel.' (Zie ook Rosch en Mervis, 1975).
Het gaat hier om de variaties op 'gegeven deze naam (van bepaald begrip), geef een andere naam.' Geconcretiseerd wordt dat dan: geef een ander woord voor .... ; geef vertaling van .... ; geef technische term voor .... .
Deze heuristiek kan van belang zijn voor onderwijs waar de beheersing van een basisvocabulaire van vreemde taal of van technische terminologie gewenst is. Daarbij gaat het om vrijwel perfecte vaardigheid in het hanteren van synoniemen, vertalingen, etcetera, althans in het kunnen omgaan met het woordenboek.
De verdere toepasbaarheid van deze heuristiek is gering. Het gaat om nogal primitieve associatieve kennis, van het makkelijk in het hoofd te stampen, maar o zo snel weer vergeten soort. Het kan soms nodig zijn dat de student over dit soort associatieve kennis beschikt om daarmee andere studieopgaven te vergemakkelijken. Dan zou je tussentoetsjes kunnen hebben waarin deze vraagsoort voorkomt. Voor eindtoetsen, waar alleen de einddoelstellingen van het onderwijs aan de orde zijn, zal deze vraagsoort slechts zelden een terechte plaats hebben.
Voorbeelden zijn vanzelfsprekend genoeg om ze hier weg te kunnen laten. De voor de hand liggende vraagvorm is open-eind; afwijken daarvan ten gunste van de meerkeuzevorm geeft al snel wanstaltige vragen, waarvan twee voorbeelden:
Let ook op het onzinnige alternatief d) in het eerste voorbeeld, kennelijk gekozen om ondanks het niet kunnen bedenken van een behoorlijk alternatief toch aan het vierkeuze schema te kunnen voldoen.
Er zijn gevallen waarin de meerkeuzevorm wel bruikbaar kan zijn, wanneer karakteristieke fouten in het onderwijs zijn behandeld, en de leerling die heeft leren vermijden. In dat geval kun je dergelijke 'fouten' als 'afleiders' in meerkeuzevragen gebruiken. Denk aan 'Schwere Wörter', 'Mots et tournures difficiles.'
Hoe belangrijk definities (of formules) ook mogen zijn, het is meestal zinloos deze uit het hoofd te kennen, maar niet in staat te zijn in reële situaties met het begrip, de wet, etcetera om te gaan. Wordt bij toetsing gevraagd definities, formules, uit het hoofd te kennen dan wordt een premie gezet op het uit het hoofd leren daarvan ten koste van misschien belangrijker andere vaardigheden.
Ook in disciplines waar definities of formules een belangrijke rol spelen gaat het om het kunnen-werken-met-definities of formules, en is de toetsvraag ook op dat kunnen-werken-met af te stemmen.
Sommige definities, zoals waarschijnlijk ook die uit het gegeven voorbeeld, kunnen door studenten heel goed toegepast worden zonder dat zij eerst de definitie hoeven na te slaan. Het is zelfs niet ondenkbaar dat studenten die de toepassing vrijwel perfect beheersen in verwarring gebracht zouden worden door de vraag om de definitie (of de formule) te reproduceren. Andere definities of formules zijn complexer, en de student die bij toepassingen zeker van zijn zaak wil zijn zal, als het even kan, niet afgaan op zijn geheugen, maar de definitie of de formule opzoeken in boek, syllabus, aantekeningen, glossarium, of de bij de toets verstrekte hand-out. Het is wenselijk om de student bij het afleggen van de toets in de gelegenheid te stellen deze informatie snel na te slaan, al was het alleen maar om te vermijden dat belangrijke opgaven fout gemaakt worden door op zich makkelijk te vergeven vergissingen bij het zich herinneren van daarbij nodige definities of formules.
Het is zelden zinvol dat de student goede definities kan onderscheiden van foutieve definities. Vraag daar dan ook niet naar, hoe groot de verleiding misschien ook is om een hierop gerichte meerkeuzevraag te construeren (want dat gaat heel erg makkelijk).
Gaat het om begrippen waar ongeveer evenveel definities van in omloop zijn als er auteurs van studieboeken zijn, dan kan ik niet anders dan uitspreken dat het kennen van de definitie papegaaienkennis is, en het leren ervan verkwiste tijd.
In het algemeen is deze vraagsoort dus te vermijden.
Het vragen van een beschrijving in eigen woorden is voor een eindtoets geen zinvolle vraagstelling. Bij mondelinge ondervraging zou zo'n vraag gebruikt kunnen worden om het gesprek op gang te helpen.
De bezwaren zijn gedeeltelijk dezelfde als die tegen het vragen van definities. Daarbij komt nog dat, waar er ruimte is voor het in eigen woorden formuleren, er ook ruimte is voor subjectieve beoordeling van die gegeven beschrijving-in-eigen-woorden.
Bij het bestuderen van de stof is het verstandig om voor jezelf die stof nog eens te herformuleren. Hoe verstandig ook, toch is dat een studiegewoonte die enig risico in zich kan bergen, afhankelijk van de wijze waarop de docent de stof 'terug vraagt'. In een onderzoek in vier studierichtingen in Leiden vonden Crombag, Gaff, en Chang (1976) dat de gewoonte leerstof in eigen woorden te formuleren vaker voorkwam bij zwakkere (blijkens de studieresultaten) studenten. Het gaat hier om &én schaaltje uit een studiegewoontenvragenlijst, het enige schaaltje ook waarop (statistisch significant) verschillend gescoord werd door studenten die geslaagd, respectievelijk gezakt waren voor het propedeutisch examen. De onderzoekers merken hierbij op:
De voorgaande vraagvormen hebben met elkaar gemeen dat in de vraagformulering of in de stam van de vraag aangegeven wordt om welk begrip het gaat, welke techniek of formule toe te passen is, en dergelijke. Lang niet altijd hoeft met naam en toenaam aangegeven te worden welke techniek de student kan toepassen om het probleem op te lossen, omdat op andere manieren het de student duidelijk kan zijn om welke techniek, begrip etcetera het hier kennelijk gaat. Denk alleen maar eens aan het toetsje dat een klein onderdeel van de stof, een bepaalde paragraaf van het boek, afsluit: de opgaven gaan evident over technieken die in dat stukje stof behandeld zijn.
De laatste observatie is ook om een andere reden van belang. Wanneer de stof opgedeeld wordt in kleinere, ook afzonderlijk getoetste onderdelen, wordt er een sterke koppeling gelegd tussen de vragen en het voorafgaande stukje stof. De student hoeft niet lang te zoeken naar de geschikte methode of techniek om een gesteld probleem te lijf te kunnen: die kan hij vinden in de zojuist door hem bestudeerde stof. Dat betekent dat de vragen in zo'n deeltoets relatief makkelijk zullen zijn. En dat je mag verwachten dat dergelijke vragen in de eindtoets moeilijker kunnen zijn, doordat nu de directe koppeling met bepaalde gedeelten van de stof verbroken is, de student wat meer zal moeten zoeken en daarbij het risico loopt niet te zullen vinden.
Het is eenvoudig in te zien dat opgaven in een eindtoets al gauw erg moeilijk kunnen worden wanneer van de student gevraagd wordt om meerdere begrippen of technieken in combinatie te hanteren om het gestelde probleem op te lossen, zonder dat expliciet aangegeven wordt welke technieken etcetera hij kan of moet gebruiken.
Tenslotte kan door oefening er een dermate sterk associatief verband gelegd worden tussen bepaalde soorten probleemstelling en de daarbij te gebruiken technieken, dat het noemen van de te gebruiken techniek rustig achterwege kan blijven zonder daardoor de opgave moeilijker te maken.
Het gaat hier nog niet om determineren, classificeren en dergelijke, waar voorbeelden van verschillende begrippen uit elkaar gehouden moeten kunnen worden (zie hoofdstuk 3 daarvoor).
Hebben we te doen met voorbeelden van toepassingen, dan gaat het om vragen als:
Gaat het niet zozeer om geïllustreerde toepassingen maar meer om gegeven objecten of gebeurtenissen, dan wordt deze vraagvorm wat lastiger doordat ze al makkelijk ambigu van karakter kan worden. Mogelijk geeft de student andere antwoorden dan de docent bedoelde, maar toch antwoorden die op zich niet fout hoeven te zijn. De meeste objecten en gebeurtenissen horen namelijk tot meerdere begrippen of categorieeën. Een voorbeeld is het begrip 'ecosysteem', waar een vijver toe behoort, een wei, tuinkas, en dergelijke. Vraag je nu omgekeerd tot welke bovengeschikte categorie een vijver behoort, dan kun je vele verschillende antwoorden verwachten, die waarschijnlijk alle als goed aangemerkt moeten worden, en misschien wordt het bedoelde 'ecosysteem' dan maar weinig genoemd. Een mogelijke oplossing voor het gesignaleerde probleem ligt voor de hand: geef meerdere voorbeelden, en vraag naar het hoger geordende begrip, de bovengeschikte categorie, of hoe dat ook maar genoemd mag worden.
Een andere manier om de ambiguïteit te vermijden is in de stam van de vraag min of meer te omschrijven welk antwoord je verwacht:
De vraagsoort die hier op goede wijze bij past, is die van de open-eindvraag, of de kort-antwoordvraag. Bij het scoren van de antwoorden is het wél zaak te letten op antwoorden die mogelijk goed te rekenen zijn, hoewel de docent het antwoord niet in het scoringsvoorschrift had opgenomen (eenvoudig niet aan gedacht). Meerkeuzevragen zullen veelal niet geschikt zijn. Ik geef daar een voorbeeld van.
Een onzinnig item, rare alternatieven. Het is bij deze vraagvorm nu eenmaal moeilijk om onjuiste alternatieven te vinden die niet onnatuurlijk zijn, er met de haren bij gesleept, of van de vraag geen strikvraag maken. Het gegeven voorbeeld illustreert nog een ander gevaar, een sluipend gevaar dat de niet gewaarschuwde docent voortdurend bedreigt: in plaats van een behoorlijke omschrijving van een levensecht voorbeeld, of tenminste iets dat best levensecht zou kunnen zijn, staat er in de stam van de vraag een algemene beschrijving die past op alle voorbeelden, je zou kunnen zeggen: het meest algemeen geformuleerde voorbeeld. Of gewoon: een beschrijving van het bedoelde begrip. De vraag toetst niet meer of de student een voorbeeld van het bedoelde begrip kan herkennen, maar of hij de beschrijving van het begrip herkent. En dat is iets heel anders. Dat is een verbaal kunstje, dat betekent niets, dat is vervelend en demotiverend. Het vervelende is nu dat veel toetsvragen, de meeste toetsvragen, waarschijnlijk onbedoeld verwaterd zijn tot dergelijke geestelijke manipulaties met verbaal materiaal, waar de leerstof toch in eerste instantie wel degelijk over reële, concrete, waarneembare objecten en verschijnselen gaat. Bekijk je een boek als dat van Mouly en Walton, waar het gegeven voorbeeld uit afkomstig is, dan zie je dat vrijwel alle items zich bevinden op dat niveau van abstract verbaal van alles en nog wat 'weten', maar nergens de koppeling met de realiteit, de observaties, de dingen, de gebeurtenissen nog aanwezig is.
Over juiste formulering van definities, over meer en minder correcte beschrijvingen van begrippen, en dergelijke vallen heel wat aardige vragen te bedenken, die echter onderwijskundig, om dat lelijke woord maar weer eens te gebruiken, te verfoeien zijn.
| uitspraak | voorwaarde |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Het bovenstaande is een mooi voorbeeld van een wat onconventioneel soort meerkeuzevraag, maar daar houdt de lovende commentaar dan ook wel op. Dit zijn gymnastische taaloefeningen die van de student gevraagd worden, dat heeft weinig of niets met natuurkunde te maken zou ik zeggen. De student die dit soort vraagstelling goed weet te beantwoorden kan nog met de mond vol tanden staan wanneer hij in een alledaags probleempje eens in de gelegenheid zou zijn het 'geleerde' 'toe te passen', gesteld al dat hij in staat zou zijn in dat alledaagse probleempje het algemene beginsel te herkennen dat hij zo fraai uit de boekjes geleerd had. Goed, ik chargeer, beste lezer. Maar het is ook wel bedroevend, vooral ook omdat dit voorbeeld verre van het enige in zijn soort is.
Tenslotte de belangrijke categorie vragen waar de student een opgave gesteld wordt, en hem gevraagd wordt om de juiste techniek, regel, wet, etcetera voor dit probleem te vinden en te gebruiken voor het bereiken van het gevraagde resultaat. Welke techniek, regel, of wet te gebruiken ligt niet direct voor de hand, is niet 'impliciet gegeven'. Wil de student met succes deze vragen te lijf kunnen, dan zal zijn beheersing van de gevraagde technieken etcetera van dusdanige kwaliteit zijn dat hij in staat is opgave en bruikbare techniek aan elkaar te koppelen. Hij moet de techniek, formule, wet, etcetera voldoende beschikbaar hebben in zijn geheugen, hij moet zelf op het idee kunnen komen de gevraagde techniek ook te proberen. Het is duidelijk dat dit soort opgaven meer of minder 'moeilijk' worden naarmate de stof die door de toets bestreken wordt meer of minder uitgebreid is, veel of juist weinig verschillende technieken, formules etcetera bevat.
Het geven van voorbeelden is hier overbodig vanwege de grote vanzelfsprekendheid.
Niet helemaal vanzelfsprekend is welke vraagsoorten hier overwogen kunnen worden. In veel gevallen zal de open-eindvraagvorm, of het korte essay geschikt zijn. Gaat het om te fabriceren werkstukken dan is er geen keus: die hebben altijd een essay-karakter. Gaat het om rekenopgaven en dergelijke, dan zou je wanneer dat om andere redenen dringend gewenst is de meerkeuzevraagvorm kunnen gebruiken: gebruik dan wat willekeurige getallen als 'foute alternatieven', tenzij wederom in het onderwijs het leren vermijden van bepaalde fouten een belangrijk punt is, in welk geval uitkomsten die door dergelijke fouten verkregen worden als fout alternatief te gebruiken zijn. Het nadeel van meerkeuzevragen blijft dan dat er een raadkans geïntroduceerd wordt die anders, bij de open-eindvorm, vrijwel afwezig is, en dat de student in staat wordt gesteld door terugrekenen het juiste antwoord te lokaliseren en dat kan wel eens in niet al te zuivere verhouding tot de doelstellingen van je onderwijs staan.
Het zal in het onderwijs niet zelden gaan over intellectuele vaardigheden die te maken hebben met het kunnen hanteren van meerdere begrippen tegelijkertijd. Ik herhaal nog even wat ik in brede zin met 'begrippen' aanduid:
------------------------------------------------------------------------
'begrippen' zijn: regels ziektebeelden
(in ruime zin) wetten klassen
modellen taxa
theorieën procedures
paradigma's technieken
begrippen (in enge zin)
etcetera.
------------------------------------------------------------------------
Na het leren van, of oefening in, afzonderlijke begrippen zal het er nog al eens op aan komen dat de student vervolgens leert om deze verschillende begrippen van elkaar te onderscheiden, dan wel ze in combinatie met elkaar te gebruiken, voor het oplossen van problemen die hem in onderwijs- of beroepssituatie gesteld kunnen worden. Bij sommige disciplines zal daarbij eerder het accent komen te liggen op de snelheid waarmee de student dat kan, dan op de juistheid (wanneer de laatste als vanzelfsprekend wordt beschouwd), in andere vakken kan de nadruk veeleer liggen op het al dan niet vinden van een correcte oplossing, al is voor dat laatste misschien wat meer tijd en enig uitproberen nodig.
Onderscheiden of combineren van begrippen lijken twee geheel verschillende vaardigheden te zijn, zodat ik beide in afzonderlijke paragrafen zal behandelen.
Snelheid of correctheid (speed or power) is veel minder een essentieel als wel een praktisch onderscheid. Het hangt sterk van de aard van de leerstof en de daarover gestelde doelen af of het gaat om eenvoudige opgaven die vrijwel altijd goed gemaakt kunnen worden maar waarbij het er juist om gaat dat dan ook snel te kunnen, of dat je te maken hebt met moeilijke opgaven die niet altijd correct opgelost zullen kunnen worden en waar ruim tijd voor beschikbaar wordt gesteld. Het spreekt vanzelf dat snelheid of correctheid ook zijn stempel zal drukken op de aard van de toetsing: een sterk accent op snelheid kan ertoe leiden dat bij toetsing het in de eerste plaats van belang is hoeveel vragen de student in de beschikbare tijd heeft geprobeerd (en meestal ook goed gemaakt); meestal zal correctheid van voldoende belang zijn om er voor te zorgen dat de beschikbare tijd ruim genoeg bemeten is dat vrijwel alle studenten het opgegeven werk ook af kunnen maken.
Wie een aantal min of meer verwante ziektebeelden afzonderlijk heeft bestudeerd, de bijbehorende symptomen kent, en goed in staat is om bij een gegeven geval aan te geven of het een voorbeeld van een bepaald ziektebeeld is of niet, kan in grote moeilijkheden raken wanneer hij zonder 'hints' aan de hand van symptomen die hij in een bepaald geval waarneemt moet zien te geraken tot een correcte diagnose. In de wiskundige analyse doet zich iets dergelijks voor bij het evalueren van integralen: de student heeft een aantal afzonderlijke technieken bestudeerd en geoefend, en wordt vervolgens geconfronteerd met het omgekeerde geval waarin hij moet ontdekken welke techniek mogelijk bruikbaar is voor het evalueren van de hem voorgelegde integraal. (keuze van een 'verkeerde' techniek leidt vaak niet tot een oplossing). Het tweede voorbeeld is ook bedoeld om aan te geven dat zelfs in geformaliseerde disciplines onderscheidingsproblemen een belangrijke rol kunnen spelen. Scheidslijnen zullen niet altijd scherp te trekken zijn: een bepaalde techniek leidt tot een snelle en elegante oplossing, enkele andere zijn ook bruikbaar maar vragen veel werk, de overige leiden waarschijnlijk niet tot oplossingen.
Dat scheidslijnen tussen verschillende ziektebeelden niet altijd even duidelijk te trekken zijn, zal ook buiten medische kringen ruimschoots bekend zijn. Vage scheidslijnen zijn in het algemeen een kenmerk van natuurlijke categorieën, en veel disciplines hebben nu juist deze natuurlijke categorieën als hun object van studie, en daarmee ook als object van het onderwijs.
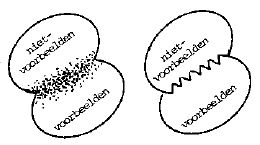
Deze vaagheid van natuurlijke categorieën is uiteraard ook al een probleem waar het gaat om het correct thuisbrengen van voorbeelden en niet-voorbeelden van een enkel begrip. Ik heb dat in figuur la aangegeven door een gestippeld scheidingsgebied in plaats van een scherpe lijn. Het kan zijn dat zo'n vaag of fuzzy overgangsgebied zich alleen maar voordoet in de ogen van de nog ongeoefende student: is dat het geval dan bestaat er kennelijk wel een duidelijke demarkatielijn maar kost het de nodige training om die te leren zien. Ik heb het laatste aangegeven door de zaagtand lijn in figuur 1b.

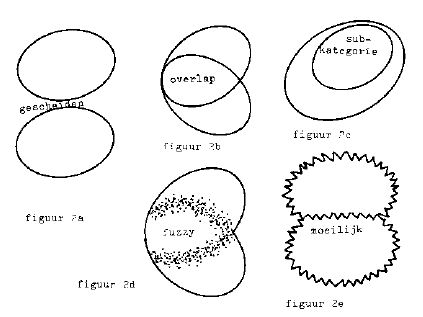
Heb je te maken met meerdere begrippen, dan kunnen deze om te beginnen *) van elkaar gescheiden zijn (figuur 2a), **) elkaar overlappen (2b), ***) of de een kan een subcategorie of speciale categorie van de ander zijn (2c). Ook in die gevallen kunnen scheidslijnen meer of minder fuzzy (2d) of moeilijk (2e) zijn.
Zie voor een recent overzicht: James A. Hampton (2007). Typicality, graded membership, and vagueness. Cognitive Science, 31, 355-384.
Zie voor filosofie en logica van vaag afgegrensde begrippen: Keefe, Rosanna, & Peter Smith (1996). Vagueness: A reader. The M.I.T. Press.
Voor de constructie van toetsvragen is het van belang om met dergelijke 'fuzzy' scheidingen tussen begrippen terdege rekening te houden. Al naar het belang dat aan het bestaan van die fuzzyness in het onderwijs wordt toegekend zal dat verschillend uitwerken. In het onderwijs zal benadrukt worden dat bepaalde onderscheidingen niet altijd scherp te maken zijn; dat niet altijd alle objecten, situaties, of gebeurtenissen éénduidig te classificeren zijn; dat sommige objecten etcetera méér prototypisch zijn voor een bepaald begrip dan andere objecten etcetera dat zijn; dat er op belangrijke punten soms moeilijk of geen overeenstemming tussen deskundigen te verkrijgen is over de betekenis van eenzelfde verschijnsel of onderzoekresultaat.
Juist vanwege dat gebrek aan eenduidigheid, ook in de beoordeling van vakdeskundigen, is het af te raden om in de toetsing vragen op te nemen die opereren in dergelijke fuzzy grensgebieden. Tenzij natuurlijk het kunnen werken met die fuzzyness tot de doelstellingen van je onderwijs behoort, denk aan gevallen waarin het van belang is die fuzzyness te leren onderkennen, en er mee te leren werken, bijvoorbeeld het stellen van een diagnose waarbij sterk rekening gehouden wordt met een alternatief dat niet uit te sluiten blijkt. Bij toetsvragen die opereren in fuzzy grensgebieden is het moeilijk om gegeven antwoorden op behoorlijke wijze als 'juist' of 'onjuist' te kwalificeren. Tenzij, zoals juist al aangeduid, van de student gevraagd wordt juist die fuzzyness aan te geven of te karakteriseren. In alle andere gevallen moet je vermijden onderscheidingen te vragen waar de ene beoordelaar van mening kan verschillen met de andere beoordelaar over de juistheid van beantwoording. Verschillen van inzicht zijn niet voorbehouden aan de deskundige beoordelaars, maar zijn ook de student toegestaan. Omdat de vraagconstructeur zich niet altijd even bewust zal zijn van de mate waarin zijn vragen zich in zo'n fuzzy grensgebied begeven, is het nodig om collega's bij de kwaliteitscontrole van de vragen nog voordat ze worden afgenomen, in te schakelen (zie ook hoofdstuk 5).
Het geschetste bijzondere karakter van natuurlijke categorieën, hun inherente vaagheid, krijgt pas de laatste jaren ook enige aandacht binnen de leerpsychologie (cognitieve psychologie). Studies op dit gebied zullen van belang zijn voor beantwoording van vragen hoe de natuurlijke categorieën uit dit vak op effectieve wijze in het onderwijs behandeld kunnen worden, en welke toetsingsvormen daarbij vooral geschikt zijn. Ik wijs op onderzoek van Norman en Bobrow (1979), Rosch (1973), Rosch en Mervis (1975), Klausmeier en Allen (1978), McCloskey en Glucksberg (1979), en het overzicht van Gagné (1978). In veel disciplines vindt met name ook onderzoek plaats gericht op het vinden van scheidslijnen, het afbakenen van categorieën, technieken voor classificatie en diagnose. bijvoorbeeld Lusted: Introduction to medical decision making (Springfield, Ill.: Thomas, 1968); Gregson: Psychometrics of similarity (London: Academie Press, 1975); Sneath en Sokal: Numerical taxonomy, the principles and practice of numerical classification (San Francisco: Freeman, 1973). De lezer zal het zelf aan kunnen vullen met relevante literatuur zijn eigen vakgebied betreffende. Deze complexere onderscheidingsproblematiek is bij de hier te behandelen heuristieken voor het construeren van toetsvragen natuurlijk niet direct aan de orde.
Bij dit soort opgaven moet de student correct kunnen classificeren, determineren, identificeren, etcetera, maar wordt het hem gemakkelijker gemaakt doordat aangegeven wordt uit welke alternatieven hij heeft te kiezen. Algemeen geformuleerde voorbeelden zijn:
In de praktijk wordt er nogal eens grof op papier bezuinigd door niet een concreet voorbeeld of een concrete situatie te geven, maar de probleemstelling in algemene termen te abstraheren. Dat is riskant, werkt uit het hoofd leren van teksten in de hand, vervreemdt de student van de stof, en bewerkt dat studenten die de stof verbaal goed beheersen later met concrete problemen niet goed uit de voeten kunnen. Hetzelfde verhaal geldt natuurlijk evenzeer voor vragen rond een enkel begrip, hoofdstuk 2. Ik leg er hier nog eens de nadruk op omdat ik bij het zoeken naar vraagvoorbeelden in met name onderwijskundige literatuur (Bloom et al 1956, Bloom et al. 1971, Mayer 1968, De Groot, Van Naerssen et al. 1975) geconstateerd heb dat meestal vragen in algemene termen gesteld worden, in plaats van op het concrete niveau waarin in studie en beroep de vragen op de student af zullen komen.
Het voorbeeld op de vorige bladzijde geeft een meerkeuzevraag, de vraagvorm waarop je onvermijdelijk uitkomt wanneer de alternatieven expliciet genoemd worden. Het kan zijn dat in bepaalde situaties de alternatieven waaruit gekozen moet worden impliciet gegeven zijn (bijvoorbeeld alle in een bepaald hoofdstuk behandelde technieken, classen, etc.), dan kan de open-eindvorm gebruikt worden; tegen de meerkeuzevorm bestaat dan echter geen enkel bezwaar, tenzij misschien het van belang is om deelnemers aan de toets die het onderwijs niet gevolgd hebben de wind uit de zeilen te nemen m.b.t. raadkansen. Wie de meerkeuzevorm wat magertjes vindt, kan uitbreiding zoeken in bijvoorbeeld een extra set alternatieven waar naar argumenten voor de gemaakte keuze(s) wordt gevraagd, zoals in het gegeven voorbeeld een aantal open-eindvragen werden toegevoegd.
Merk op dat in het gegeven voorbeeld alleen gevraagd wordt de correcte toets(en) aan te geven, niet om deze ook uit te voeren (waarvoor de precieze data in de probleemstelling ook ontbreken). Wie wil nagaan of de student een bepaalde toets correct kan uitvoeren, kan beter gebruik maken van een speciaal daarop toegesneden vraag, en een van de vraagsoorten uit hoofdstuk 2 gebruiken. Dat neemt niet weg dat het van belang is er voor te zorgen dat de student voldoende vertrouwd is met ieder van deze technieken afzonderlijk om vragen als deze niet te laten ontaarden in een woordenspelletje.
In het gegeven voorbeeld gaat het er om of de student de juiste alternatieven weet aan te geven, en is de snelheid waarmee hij dat kan van ondergeschikt belang.
Een voorbeeld waarin het wat meer op de snelheid van werken aankomt, waar iedere afzonderlijke techniek vrijwel perfect beheerst wordt en het er op aan komt trefzeker de juiste technieken voor het voorhanden liggende probleem te kiezen:
Evalueer met behulp van limiet stellingen
Dit is een open-eindvraag (drie open-eindvragen eigenlijk), de limietstellingen zijn impliciet gegeven, en behoren de student ook goed bekend te zijn. Eigenlijk is dit voorbeeld al een stap in de richting van de in paragraaf 3.2.2 te behandelen vraagvormen. Dat demonstreert nog weer eens dat de indeling in vraagvormen die ik hier geef niet formalistisch opgevat moet worden.
Dit is een variant op 3.1.1: de aangeboden probleemstelling bevat niet alle nodige informatie om de keuze tussen de aangeboden alternatieve diagnoses, categorieën etcetera te kunnen maken, en het is juist de bedoeling dat de student kan aangeven welke extra informatie voor die keuze nog nodig is. In algemene termen hebben we hier dan de volgende vraagvormen:
De vraagvorm genoemd bij het derde punt zou een dubbele meerkeuze kunnen zijn, of een open eind wat het eerste deel van de vraag (welke extra veronderstelling), en meerkeuze wat het tweede deel van de vraag (welke van de genoemde toetsen) betreft.
Niet altijd zal gevraagd worden dan ook de diagnose te stellen, tussen de categorieën te kiezen, etc.: in de regel heb je daar immers ook dat extra gegeven voor nodig, de uitslag van de extra test, etcetera Bij ingenieuze toetsprocedures zou je die extra informatie inderdaad tijdens de toetsafname kunnen verschaffen. Methoden daarvoor liggen voor de hand wanneer de toetsing plaats vindt aan de computerterminal. Is de toetsing schriftelijk, dan kan met speciale inkten gewerkt worden, die resultaten van door de student gevraagde tests en dergelijke zichtbaar maken. Ook geschikt is de 'tab item' techniek, waar de student plakkers verwijdert om extra informatie te verkrijgen, of verf wegkrabt. Voor beschrijving van deze tab-itemtechniek zie Fitzpatrick en Morrison, in Thorndike (1971) p. 248-250. Een voorbeeld van werken met speciale inkt die bij bewerking met een daarvoor meegeleverde viltstift het gedrukte zichtbaar laat worden, geeft het boek 'Clinical simulations; selected problems in patient management' van McGuire, Solomon en Forman (Appleton-Century-Crofts, 1976)
Wil deze vraagvorm zinvol, niet gekunsteld, zijn dan moet de hier gevraagde vaardigheid in onderwijs en beroepsuitoefening ook relevant zijn. Een waarschuwing die natuurlijk ook voor de andere vraagvormen geldt.
De problemen waar deze wereld ons mee confronteert plegen niet in voorgebakken vorm op ons bordje gelegd te worden. Er moet vaak eerst opgeruimd, geanalyseerd, geformaliseerd, geherformuleerd, geordend, voorbewerkt worden om vervolgens aan oplossingen, classificeren, behandelen, etcetera te kunnen gaan denken.
Hoe de vragen precies ingericht worden zal ook hier weer sterk van de aard van de stof afhangen. Gaat het om eenvoudige of routinematige bewerkingen van het aangeboden materiaal dan kun je misschien volstaan met te vragen de juiste alternatieven aan te geven (het best passende alternatief aan te geven). Gaat het om tamelijk uitvoerige bewerking van het aangeboden materiaal of probleem, dan ligt het voor de hand om de student ook die door hem uitgevoerde bewerking in te laten leveren (al is het alleen maar het kladpapier waarop de nodige berekeningen staan aangegeven, terwijl op het antwoordformulier alleen de uitkomst, de gekozen alternatieven, vermeld worden). In bepaalde gevallen zal de kwaliteit van de 'materiaalbewerking' zelf ter beoordeling zijn (naast het uiteindelijk resultaat), dan gaat het om wat uitvoeriger essays, werkstukken. In andere gevallen gaat het misschien om een selectie uit aangeboden informatie die op zich ook in meerkeuzevraagvorm gegoten kan worden: dan ontstaat weer een dubbele meerkeuzevraag waarin zowel een keuze uit aangeboden alternatieve categorieën, diagnoses, en dergelijke gedaan moet worden, als aangegeven moet worden op grond van welke informatie die keuze(n) werd(en) gemaakt.
Bijzondere zorgvuldigheid is ook met deze vraagsoort weer geboden: de overbodige of vuile informatie die je in het gegeven probleem stopt kan als 'afleider' werken, en dat lijkt alleen te verdedigen wanneer de student zich ook heeft geoefend om verleidelijke maar irrelevante informatie te negeren, zich daardoor niet op het verkeerde been te laten zetten. Je kunt daarbij denken aan gevallen van onjuiste diagnosestelling waartegen de arts zich heeft te wapenen. Het gaat natuurlijk niet aan om strikvragen te bedenken die verder in de betreffende discipline van geen enkel belang zijn.
Dit is de meer algemene vorm van de onder 3.1.1 behandelde vraagvorm. De student krijgt nu geen aanwijzingen meer tussen welke alternatieven hij moet beslissen. Ook zijn die alternatieven niet impliciet gegeven, althans niet wanneer het maar om een klein aantal zou gaan, want dan zijn we immers helemaal terug bij vraagvorm 3.1.1. Verdere toelichting is hier dan ook nauwelijks nodig. Uiteraard is de meerkeuzevraag hier niet meer te gebruiken. Deze vraagvorm is een stuk moeilijker dan 3.1.1: de student moet hier op eigen kompas de alternatieven zien te vinden waartussen de beslissing in feite te maken is.
Om dit soort vragen redelijk te kunnen beantwoorden zal de student de betreffende begrippen (categorieën, diagnoses, classen, technieken etc) tenminste voldoende paraat moeten hebben om ze bij de gegeven situatie te kunnen passen, op het gegeven voorbeeld te kunnen matchen. Naar die 'paraatheid' van het begrippenapparaat moet in het voorafgaande onderwijs dan ook toe gewerkt zijn. De student moet deze begrippen niet alleen beschikbaar weten, weten te 'adresseren', hij moet ze ook weten te hanteren.
Dit is de meer algemene vorm van de onder 31.2 behandelde vraagvorm. Het gaat nu om het zelfstandig kunnen uitvoeren van anamnese en stellen van diagnose; het maken van een experimenteel ontwerp, uitvoeren van het onderzoek, en bewerken en interpreteren van gegevens, bijvoorbeeld.
Dit is de meer algemene vorm van de onder 3.1.3 behandelde vraagvorm. Het gaat hier om het 'gewoon' zelfstandig toe kunnen passen van technieken in daartoe geschikt te maken omstandigheden; het hanteren van oplossingstechnieken in daartoe eerst geanalyseerde en gestructureerde problemen; etcetera.
Hier worden problemen opgelost, werkstukken gemaakt, opgaven uitgevoerd, en dergelijke waarbij de student bepaalde begrippen, technieken, wetten etcetera in combinatie met elkaar moet kunnen gebruiken. In het bijzonder gaat het dan om combinaties die nieuw zijn, niet als zodanig eerder door de student geoefend. Veel van dergelijke combinaties komen zo vaak voor dat ze een eigen naam verworven hebben, en als zodanig ook uitgebreid in het onderwijs ter sprake komen en geoefend worden. Vragen over dergelijke combinaties worden hier dan ook niet bedoeld, daar kan ik voor naar hoofdstuk 2 terug verwijzen.
Een bijzonder geval vormen problemen waarbij bepaalde oplossings-algoritmen toegepast moeten of kunnen worden, algoritmen die als zodanig ook weer aan de student bekend zijn, en door hem geoefend. Het problematische is dan niet de keuze van het algoritme, die keuze zal min of meer vanzelfsprekend zijn. De moeilijkheid zit hem dan in de juiste invulling van het algoritme, de keuze van de correcte begrippen, technieken, en dergelijke in iedere afzonderlijke stap van het algoritme.
Crombag, de Wijkerslooth, en van Tuyll van Serooskerken (1972) geven een algoritme voor het oplossen van casusposities, waarvan een enigszins primitieve vorm is:
Het algoritme als zodanig is de student goed bekend, staat misschien zelfs op de toetsformulieren nog eens expliciet vermeld. Waar het dan om gaat, is de juiste keuze van rechtsregels, juridische vertaling van casus, en toepassing van rechtsregels.
Dergelijke algoritmen spelen in vele disciplines een belangrijke rol. Zie bijvoorbeeld ook Mettes, Pilot en Roossink 'Het leren oplossen van problemen in de thermodynamika', T.H. Twente 1979. Landa (1974) geeft een globaal overzicht van zijn research over de plaats van algoritmen bij het onderwijs en in het leren, terwijl in het algemeen in de cognitieve psychologie grote belangstelling voor de rol van algoritmen bij probleemoplossen bestaat (Newell en Simon 1972, als bijzondere exponent daarvan, kan hier niet ongenoemd blijven).
Het wordt de student hier makkelijk gemaakt: hij moet het probleem oplossen door een juiste combinatie of sequentie te kiezen uit de begrippen, technieken, wetten, regels etcetera die bij de opgave genoemd worden. Zo'n opgave kan ook met die handreiking nog moeilijk genoeg zijn, en zonder die handreiking voor veel of alle studenten misschien zelfs onoplosbaar. Dat hangt van de aard van de leerstof af.
Varianten zijn dan (inclusief 3.2.2 en 3.2.3):
de te gebruiken begrippen, hulpmiddelen moeten gekozen worden uit een wat groter aantal genoemde begrippen, hulpmiddelen. Dat levert een kruising op tussen vraagvorm 3.1.1 en deze 3.2.1 zou je kunnen zeggen: de student moet dan ook de bruikbaarheid van ieder van de genoemde begrippen, hulpmiddelen tevoren kunnen beoordelen, wil hij tenminste snel enige voortgang maken met de oplossing.
In het juridische voorbeeld op de voorgaande bladzijde is dat de 2e stap, de juridische vertaling van de feiten zoals die in het casus gegeven worden.
Dit soort vragen draagt van nature een nogal open karakter: dat worden open-eindvragen, meestal essayvragen, of er wordt van de student een compleet werkstuk gevraagd, een opstel, etcetera
Is alleen het uiteindelijke antwoord van belang, dan kan op het antwoordformulier daar een passende kleine ruimte voor aangegeven worden. Wie ook belang stelt in de stappen die de student gevolgd heeft om tot de oplossing te komen, zal de volledige uitwerking moeten vragen, althans een afschrift van het kladpapier van de student beschikbaar willen hebben.
Stel je belang in de redenen waarom de student voor een bepaalde combinatie kiest, dan moet je daar ook expliciet naar vragen. Het laatste zou je ook kunnen doen in de vorm van een toegevoegde meerkeuzevraag waarin de student in de opsomming van mogelijke argumenten aanstreept welke hij gebruikt heeft.
Het gaat er hier om problemen op te lossen, opgaven uit te voeren, werkstukken te maken en dergelijke, waarbij begrippen, regels, of technieken etcetera, in combinatie toegepast moeten worden, en de student er zelf achter moet zien te komen welke begrippen, technieken daarbij nodig zijn. Zou het de student op enigerlei wijze impliciet bekend zijn uit welke set begrippen etcetera hij moet kiezen, dan is er eerder sprake van de onder 3.2.1 besproken vraagsoort.
Voorwaarde is hier weer dat de student de benodigde technieken, begrippen, wetten, regels, goed kent, ze voldoende paraat heeft (kan adresseren), en dat hij aan de gegeven probleemschets of -situatie ook kan herkennen welke begrippen, etcetera, voor de oplossing relevant zouden kunnen zijn. Vanzelfsprekend is dat ieder begrip, iedere techniek afzonderlijk door de student probleemloos beheerst wordt.
Varianten zijn dan:
vgl. 3.1.5 en 3.2.2
vgl. 3.1.6 en 3.2.3
Vanzelfsprekend gaat het hier vrijwel altijd om open vragen of essayvragen, of om werkstukken. Er is onmiskenbare verwantschap tussen deze vraagsoorten 3.2.4 t/m 3.2.6 en de doelstellingen in de categorie 'Synthese' van Bloom et al. 1956. (Ik zie ervan af hier de verschillen met Bloom et al. aan te geven: de lezer zal die verschillen op eenvoudige wijze zelf constateren bij lezing van de tekst van Bloom et al.).
In 1983 neem ik afstand van de psychologiserende benadering van Bloom en de zijnen. Wie een echt scherpe kritiek op Bloom c.s. wil lezen, raadpleegt Carl Bereiter (2002). Education and Mind in the Knowledge Age. Erlbaum. questia
Is niet alleen het eindproduct van belang, maar ook de wijze waarop de student naar dat resultaat heeft toegewerkt, en eventueel op welke gronden hij zijn keuze voor bepaalde technieken, of voor een bepaalde handelings volgorde heeft gedaan, dan kan daar ook naar gevraagd worden, of de docent kan zorgen dat hij over alle materiaal of waarnemingen beschikt zodat hij deze extra informatie ook binnenhaalt.
Zoals bij de aanvang van deze paragraaf opgemerkt, gaat het bij deze vragen om combinaties die nieuw zijn, waarvan aangenomen mag worden dat de meeste studenten die bepaalde combinatie niet eerder hebben geleerd, geoefend, of in de literatuur ontmoet. Daarmee hebben we nog niet direct met creatief probleemoplossen te maken. Ook waar het gaat om het vinden van combinaties kan het gaan om een vaardigheid die geoefend is, of om toepassing van redeneringsvaardigheden op basis waarvan gezochte combinaties geconstrueerd of gevonden kunnen worden.
_____________________________________________________________________
een enkel | het begrip is gegeven | het begrip is niet gegeven
begrip | (expliciet of |
| impliciet) |
------------------------------------------------------------------
voorbeelden | voorbeeld | voorbeeld
| herkennen | benoemen
| |
| voorbeeld |
| geven |
------------------------------------------------------------------
toepas- | toepassingen |
singen | herkennen |
| |
| probleemoplossen, | probleemoplossen
| toepassen | toepassen
====================================================================
meerdere | de begrippen zijn | de begrippen zijn niet gegeven
begrippen | gegeven (expliciet |
| of impliciet) |
--------------------------------------------------------------------
discrimi- | voorbeeld | idem
neren | benoemen |
| |
| informatie zoeken | idem
| voor benoeming |
| |
| informatie selecteren | idem
| voor benoeming |
-------------------------------------------------------------------
combineren | probleemoplossen met | idem
| gegeven informatie |
| |
| probleemoplossen met | idem
| gezochte informatie |
| |
| probleemoplossen met | idem
| geselecteerde |
| informatie |
_____________________________________________________________________
OVERZICHT VRAAGHEURISTIEKEN
[noot lay-out: de tabel gebruiken met een niet-proportionele letter zoals courier of monaco]
Goede bedoelingen alleen zijn niet voldoende om tot goede toetsen te geraken. Ook wie zijn vragen geformuleerd heeft met behulp van de heuristieken in hoofdstuk 2 en 3 zal vervolgens nog moeten checken of de vragen wel handig geformuleerd zijn, door de student goed begrepen worden, door zijn collega's op dezelfde wijze beantwoord, etcetera. Met andere woorden: er moeten empirische gegevens verzameld worden om de vraag te kunnen beantwoorden of de vragen metterdaad aan de bedoelingen voldoen. En die gegevens kun je al verzamelen nog voordat de toets afgenomen wordt, en je kijkt ook nà afname van de toets of de dan verkregen extra informatie misschien een ongunstig licht werpt op de kwaliteit van een enkele in die toets opgenomen vraag. controle vooraf, en controle achteraf dus, met mogelijk iets andere procedures.
Ik zal hier een aantal verschillende mogelijkheden bespreken, die niet altijd allemaal naast elkaar gebruikt hoeven te worden. Het is aan de docent om uit te maken of de moeite van een bepaalde check opweegt tegen het belang dat er mee gediend is, of de vruchten die het af kan werpen. Bedenk dat ook hier het betere de vijand van het goede kan zijn: een overmaat aan voorzichtigheid kan leiden tot overbelasting of irritatie, en weigeringen om verder nog mee te werken.
De controle begint al op het moment dat de vraag bedacht of geconstrueerd wordt. Niet iedere formulering van de vraag is even handig. Probeer al bij het formuleren zoveel mogelijk om dubbelzinnigheden te vermijden, duidelijk te zijn in wat je bedoelt dat de student als antwoord geeft, feitelijk correct te zijn etcetera Een aantal algemene aanwijzingen in het schrijfstadium zijn:
Voor open-eind vragen (kort antwoord vragen):
Voor ja-nee of juist-onjuist-vragen:
Voor meerkeuzevragen:
Gebruik de meerkeuzevraagvorm zo spaarzaam mogelijk, alleen waar de aard van doelstelling en leerstof in overeenstemming is met deze vraagvorm, en de meerkeuzevorm dan meer voordelen dan nadelen heeft boven de altijd bruikbare open-eindvraagvorm. Deze aanbeveling is niet nieuw, hoewel in deze cursus consequenter aangehouden dan in de literatuur gebruikelijk. Vergelijk bijvoorbeeld:
Na zorgvuldige constructie van vragen en bijbehorende zaken als scoringsvoorschrift en -alternatieven, eventueel fouten analyses, is het wensleijk om nog een enkele extra controle uit te voeren voordat de vragen in de af te nemen toets worden opgenomen. Het meest voor de hand liggend, en organisatorisch ook het eenvoudigst, is om jezelf als extra controle te gebruiken. Daarvoor is nodig:
Een eventuele nummering of andere rubricering van de vragen kan onbedoelde aanwijzingen bevatten waar bij het beantwoorden gebruik van gemaakt kan worden. Dat moet voorkomen worden, bijvoorbeeld door een nummering die 'toevallig' is (geen relatie heeft tot gedeelten uit de leerstof), door nummering op de achterzijde van de vraagformulieren te zetten (maar dan wel echt onleesbaar).
Probeer om vragen die met elkaar te maken hebben, waar in de stam van de ene vraag informatie gegeven wordt die in de andere vraag juist gevraagd wordt, niet in dezelfde controlebeurt samen met elkaar op te nemen. Houd daar bij het construeren van de vragen al rekening mee door dat in een code aan te geven, in aparte kaartenbakjes van elkaar bijtende vragen te zetten, of iets dergelijks
Dat leidt er dan allemaal toe dat er een paar uurtjes vrij gemaakt moeten worden om (een deel van) de vragen op geconcentreerde wijze onder het mes te nemen: eerst zelf proberen te beantwoorden, uiteraard onder dezelfde condities als waaronder de student straks moet werken (met of zonder woordenboeken, literatuur, glossarium, hand-out met formules of moeilijk idioom), daarna de andere punten uit het controlelijstje op de volgende bladzijde afwerkend (telkens per vraag, of eerst alle vragen beantwoorden en daarna per vraag de andere controlepunten).
Dat controle lijstje kan voorgedrukt worden, met bij ieder punt voldoende ruimte voor beantwoording, om tot een overzichtelijke verwerking van het materiaal te komen. Het is maar wat in jouw geval het handigst uitkomt.
------------------------------------------------------------------------
* geef het 'beste' antwoord op de vraag, zonder raadplegen van de
literatuur wanneer dat de studenten evenmin toegestaan is
* noteer de tijd nodig voor deze 'beste' beantwoording
* bedenk welke andere antwoorden ook goed zouden zijn
* geef aan welke karakteristieke fouten te verwachten zijn over
* is de redactie van de vraag OK? Wanneer je er niet tevreden over
bent, loop dan even het lijstje uit par. 4." 1 langs over
welk(e) begrip(pen) handelt de vraag
* wat is de bedoelde vraagsoort (volgens het schema van
vraagheuristieken bij hoofdstuk 2 en 3)
voor essayvragen of werkstukken:
* geef een antwoord waarin alle wezenlijke punten voorkomen, en zo
mogelijk niet meer dan die
voor meerkeuzevragen:
* beantwoord de vraag zowel als open-eindvraag, als in de meerkeuzevorm
(maar zo mogelijk niet al te kort na elkaar)
* beantwoord eventueel nogmaals de vraag over welk(e) begrip(pen) de
vraag als meerkeuzevraag handelt
* let op de redactie van de alternatieven, in aansluiting op de stam
------------------------------------------------------------------------
Het voorgaande is even hard werken, maar dan komt ook het leuke deel van de controlebeurt: het vergelijken van de gegeven antwoorden met de 'bedoelde' antwoorden, en het vergelijken van de resultaten op de andere controlepunten met wat je ten tijde van het construeren van de vraag er mee bedoeld hebt. De 'vondsten' die je hierbij doet wijzen vanzelf de weg naar remedial actions, eventueel het naar de prullenbak verwijzen van vragen.
Tenslotte: wanneer het niet om geheel nieuwe vragen gaat, maar slechts om oude vragen die met een nieuw 'voorbeeld' of iets dergelijks ingevuld worden, ofwel dezelfde item form maar in een nieuw jasje, dan kan heel deze controlebeurt een stuk bekort of vereenvoudigd worden, en misschien ook wel overgeslagen worden (het laatste hangt van de bij eerdere afnamen van het itemform opgedane ervaringen af).
Zijn er collega's die met deze leerstof vertrouwd zijn, bijvoorbeeld omdat zij deel uit maken van hetzelfde team dat dit onderwijs verzorgt, dan is het bijna vanzelfsprekend dat zij als controle fungeren voor de vragen door een andere collega gemaakt. De procedure is vrijwel gelijk aan de in paragraaf 4.1.2 geschetste voor controle door de maker zelf, inclusief gebruik van het controle lijstje uit figuur 4.1. Let er in het bijzonder op dat bij deze vraagcontrole de collega's onafhankelijk van elkaar werken: niet tijdens het beantwoorden van de vragen daar met elkaar al over van gedachten wisselen. Een belangrijk doel is immers het opsporen van ambiguïteiten, antwoorden waarover collega's met elkaar van mening verschillen en dergelijke, reden om te vermijden dat collega's te vroeg hun mening aan elkaar 'toetsen' en bijstellen. Dat laatste houdt met name ook in dat bespreking van voorgestelde vragen in de groep collega's af te raden is, zolang onafhankelijk door hen gegeven antwoorden op die vragen niet beschikbaar zijn. In dergelijke gesprekken dreigt een snel wegsmelten van verschillen in opvatting op te treden, waardoor juist bestaande dubbelzinnigheden en mogelijke alternatieve interpretaties verdoezeld in plaats van gesignaleerd worden. Dat gevaar wordt in de hand gewerkt door de eis bij gebruik van meerkeuzevragen het met elkaar eens te worden over het 'beste' alternatief. Natuurlijk kun je niet bij onderling fiat het beste alternatief bepalen, dat levert pseudo-objectiviteit op, of frozen subjectivity (Stanley en Hopkins 1972, p. 253).
De verwerking van de 'resultaten' van de controle ligt ook hier weer voor de hand, en zal menig moment van vrolijkheid opleveren, naast af en toe een pijnlijke miskleun. Maar wat nu te doen met gebleken verschillen in beantwoording? De vragenmaker die zichzelf controleert en ontdekt dat hij nu over het beste antwoord op een vraag anders denkt dan twee weken geleden kan zonder blikken of blozen de vraag naar de prullenbak verwijzen (wanneer het gesignaleerde probleem niet door een betere vraagformulering te verhelpen is). Maar wat doe je wanneer collega's verschillende antwoorden hebben gegeven?
Verschillen van 'inzicht' kunnen zich vooral voordoen bij het beoordelen van wat uitgebreidere antwoorden, essays en werkstukken. Dan wordt nogal eens 'gemiddeld' over de verschillende gegeven oordelen (bij twee of meer onafhankelijk van elkaar werkende beoordelaars). Dat is mijns inziens een strikt te vermijden procedure: wanneer beoordelaars met elkaar van mening verschillen over interpretatie of waardering behoort de student het voordeel van die onenigheid te krijgen. Wanneer tenminste één deskundige het met jouw antwoord eens is (of daar de hoogste waardering voor heeft gegeven), dan valt niet in te zien dat de student op dat voor hem beste oordeel geen recht zou hebben. Bij toetsen en examens waar inderdaad nogal eens verschillend gecijferd wordt door de beoordelaars zal dat leiden tot een lichte gemiddelde stijging in toegekende puntenaantallen, niets om je enige zorg over te maken.
Gaat het om het toekennen van een prijs voor de meest originele scriptie in het jaar, of iets dergelijks, dan gebeurt die toekenning door commissies en raden, en in die gevallen hoeft tegen 'middeling' van oordelen geen bezwaar te bestaan.
Overigens: bij mondelinge tentamens die door twee of meer docenten worden afgenomen is het erg lastig om een dergelijke 'middeling van het oordeel' tegen te gaan omdat zoiets al impliciet tijdens de ondervraging aan het gebeuren is. Ook bestaat bij deze vorm van mondeling toetsen het risico dat collega's al te snel instemmen met de antwoorden zoals de ondervragende docent die geeft, waar zij bij onafhankelijke controle zonder oogcontact of ruggespraak met elkaar misschien tot afwijkende antwoorden zouden komen. Overeenstemming tussen docenten bij mondelinge toetsing kan dan ook voor een deel schijn zijn, wat gedeeltelijk te ondervangen is door de vragen voor te bereiden via procedures als hier en in de vorige paragraaf beschreven.
Controle vooraf garandeert nog niet dat ambiguë en andere gemankeerde vragen alle door de mand gevallen zijn. Docenten zullen de vragen altijd door hun eigen vaak wat bijzonder geslepen bril bekijken, al was dat alleen maar door de brede vakmatige achtergrond kennis waarover studenten (nog) niet beschikken. Hoe deze koekjes van eigen deeg smaken zal pas duidelijk worden wanneer de studenten ze geproefd hebben. Ofwel: uit de resultaten, individuele of over groepen genomen, zal nog kunnen blijken dat bepaalde vragen het niet gedaan hebben zoals de bedoeling was.
Bedenk dat studenten op hun eigen wijze ook een deskundige mening over de toetsvragen zullen hebben. Zij zullen vaak beter dan de docent weten welke stof in de opgegeven literatuur voorkomt, en welke niet; of kennis die verondersteld wordt in voorafgaand onderwijs opgedaan te zijn dat ook is; etcetera
Het is altijd verstandig het communicatiekanaal van de student naar de docent zo wijd mogelijk open te houden, en door studenten gegeven feedback serieus te bekijken ook al is je eerste reactie er een van afwijzing, verveling, of ergernis. De belangen van studenten liggen anders dan die van jou als docent; dat betekent niet alleen dat je mag verwachten het nimmer op alle punten met elkaar volstrekt eens te worden, maar vooral dat je moet proberen het standpunt van studenten een eerlijke kans te geven, van invloed te laten zijn op te volgen procedures en dergelijke. In de ene situatie kan dat wat makkelijker geregeld worden dan de andere; dat kan meer of minder geformaliseerd worden, zelfs in wederzijdse contracten vastgelegd (Cohen, 1978).
tijdens de toetsafname. Er kunnen soms ernstige fouten in vraagformuleringen voorkomen, zoals een notatie die afwijkt van die waarmee studenten vertrouwd zijn, een stukje veronderstelde kennis waarover studenten niet beschikken, een ambigue vraagformulering waardoor de student niet weet of hij zijn korte antwoord nog moet motiveren of niet. Omdat dergelijke blunders niet met zekerheid te voorkomen zijn, is een goede strategie de student tijdens de toetsafname in de gelegenheid te stellen vragen en opmerkingen aan een surveillant door te spelen, die daarover vervolgens contact opneemt met de verantwoordelijke docent. Ziet de docent aanleiding in een opmerking om een correctie aan te brengen, dan kan dat nog redelijk tijdig aan alle deelnemende studenten meegedeeld worden. Hopelijk zal maar weinig studenten de ervaring van deze auteur deelachtig worden: tijdens een en dezelfde toets op deze wijze drie maal de docent te moeten verbeteren. [Helaas, anno 2007 kan ik mij dit voorval niet meer herinneren, mogelijk is het gebeurd in mijn afgebroken studie econometrie begin zeventiger jaren. b.w.] De docent moet dan ook tijdens de toetsafname aanwezig zijn, of tenminste bereikbaar, en het is handig wanneer hij de voor deze toets opgegeven literatuur ook bij de hand heeft.
schriftelijk tijdens of na toetsafname. Geef expliciet gelegenheid om
op en aanmerkingen bij de toetsvragen te maken, ofwel op het toetsformulier, of op een afzonderlijk, daartoe uitgereikt, papier. Spreek wel af dat dergelijke opmerkingen niet kunnen leiden tot extra puntentoekenning, eventueel wél tot niet meerekenen van bepaalde vragen.
Wie er wat meer werk van wil maken kan overwegen deze schriftelijke commentaar wat meer te structureren door een lijstje met suggesties te geven:
direct na de toetsafname. Wanneer je er voor zorgt dat direct na de toets de student de beschikking krijgt over de juiste antwoorden, kan hij zijn vragen nakijken, en problematische dingen die daarbij blijken kunnen meteen
mondeling of schriftelijk aan de docent doorgespeeld worden.
Bij meerkeuze toetsing is het van belang dat de scoringssleutel aan de studenten bekend gemaakt wordt. Zorg ervoor dat de bekend te maken sleutel exact gelijk is aan de sleutel die bij geautomatiseerde scoring gebruikt wordt: zouden er in die sleutel fouten zijn blijven zitten, dan kan dat direct na de toetsafname blijken, wanneer studenten hun eigen antwoorden nakijken en scoren. Het komt echt nogal eens voor dat er in zo'n scoringssleutel een foutje zit!
nabespreking van het tentamen. Wordt de toets nabesproken, met uitwerking van goede antwoorden, en aangeven waarom andere antwoorden fout zijn, dan wordt vanzelfsprekend goed gelet op commentaar die door studenten tijdens die bespreking gegeven wordt.
intensief doorspreken met klein groepje studenten. Bespreek met een klein groepje studenten (vrijwilligers, of een afvaardiging) intensief alle toetsvragen door, met inbegrip van de afstemming van de vragen op de doelstellingen, de scoringsvoorschriften die gehanteerd zijn, de puntentelling, bij meerkeuzevragen waarom voor bepaalde afleiders gekozen is, voor essayvragen en werkstukken de ervaringen die bij het nakijken en beoordelen zijn opgedaan.
Voorzover kommentaren van studenten geleid hebben tot bepaalde maatregelen (uit de toets verwijderen van bepaalde vragen, verlagen van de aftestgrens, en dergelijke) worden zij daar ook over geïnformeerd, dat spreekt vanzelf.
De toetsresultaten kunnen per vraag geanalyseerd worden. Wordt de (meerkeuze)toets automatisch gescoord, dan krijg je per vraag een aantal gegevens in de schoot geworpen. In andere gevallen kun je, wanneer daar tenminste uitgesproken behoefte aan bestaat, deze gegevens zelf berekenen.
--------------------------------------------------------------------------
vraagnr., goede alternatief, per alternatief a., b., c., d.: aantal, proportie , RAT
------ a ------ ----- b ------ ----- c ------ ----- d ------
1 2 149 .464 -.262 144 .449 .404 21 .065 -.168 7 .022 -.196
2 2 26 .081 .007 138 .430 .371 43 .134 .145 114 .355 .284
3 2 49 .153 -.068 160 .490 .324 72 .224 .222 39 .121 .129
4 2 92 .287 -.174 158 .492 .398 45 .140 .215 26 .081 -.168
5 1 56 .174 .136 3 .009 -.087 251 .782 -.042 11 .034 -.142
--------------------------------------------------------------------------
De moeilijkheid of p-waarde van een vraag is (per traditie) de proportie van de studenten die de vraag goed beantwoordde. Op een computeruitdraai wordt meestal, zoals in figuur 4.2, voor ieder alternatief aangegeven de proportie studenten die dat alternatief koos; de moeilijkheid van de vraag is dan de proportie die het als 'juist' gesleutelde alternatief koos. Deze p-waarden zijn met de hand snel te vinden door te turven (handig in het laatste geval is een lay-out van het antwoordformulier zodat alle kolommen met antwoorden naast elkaar gelegd kunnen worden, zodat het aantal 'goed' per rij snel te turven is).
Voor essays en werkstukken gaat het niet om p-waarden, maar bereken je gemiddeld behaalde scores over de groep studenten.
Wat doe je vervolgens met dergelijke p-waarden? Niet veel. Het probleem is dat de moeilijkheid van vragen door docenten vooraf vaak niet goed te schatten blijkt, en dan weet je achteraf ook niet of je lage p-waarde 'te' laag is of niet. Ook zijn deze p-waarden vatbaar voor toevalligheden, zeker wanneer de groep studenten niet al te groot is. Merk je 'verrassende' p-waarden op, trek je conclusies dan met de nodige voorzichtigheid, en liefst alleen in die gevallen waar er uit andere bron ook informatie komt dat er met deze vraag 'iets aan de hand is'.
Je komt hier en daar wel aanwijzingen tegen dat p-waarden voor meerkeuzetoetsen zo tussen 0,6 en 0,7 zouden moeten liggen, en voor open-eindvragen rond de 0,5. Dat zijn aanwijzingen die stammen uit de testtheorie. Toetsing in het onderwijs is er echter, grof gezegd, voor bedoeld na te gaan of de student datgene in het onderwijs heeft opgestoken dat van hem verwacht wordt. Anderson (1972): als het doel van de toets is om het niveau van stofbeheersing van de student te bepalen, dan heeft het vanzelfsprekend geen zin om het moeilijkheidsniveau van de vragen tevoren vast te leggen. Hij waarschuwt er voor dat het streven naar p-waarden van 0,5 kan leiden tot vragen over voetnoten en details. Omgekeerd zouden ook vragen over belangrijke onderwerpen ten onrechte verworpen kunnen worden omdat ze 'te moeilijk' zijn.
Wees dus terughoudend in het verwijderen van vragen uit de toets omdat ze te moeilijk of te makkelijk zouden zijn, daardoor kan de zin en de validiteit van de toetsing aangetast worden. Bedenk ook dat het hanteren van de vraagheuristieken uit de hoofdstukken 2 en 3 in veel gevallen zal leiden tot toetsen met naast elkaar nogal 'moeilijke' en nogal 'makkelijke' vragen.
Vragen die door alle studenten onveranderlijk goed (respectievelijk fout) gemaakt worden, hebben geen 'informatieve' waarde, en zou je om die reden in de toekomst uit de toets kunnen houden. Let er dan wel op of het niet meer 'toetsen' van de betrokken vaardigheid of kennis er niet toe leidt dat studenten dit onderdeeltje gaan verwaarlozen. Hoewel altijd goed gemaakte vragen, of vragen met zeer hoge p-waarden, weinig informatief zijn, kan het opnemen van dergelijke vragen in de toets dus wel degelijk een functie hebben, en kan het schrappen van dergelijke vragen een self-defeating aanpak zijn.
Met de r-bis wordt bedoeld de mate waarin studenten die een bepaalde vraag goed maken, ook de toets als geheel goed maken. Op een computeruitdraai zijn dat de als r-bis,r-it of RIT aangeduide waarden, of voor ieder alternatief afzonderlijke RAT-waarden in welk geval je de RAT-waarde van het juiste alternatief moet hebben. Deze r-bis variëren tussen -1 en +1. Ze zijn met de hand te berekenen, maar dat zal zelden de moeite lonen (zie voor formules De Groot en Van Naerssen 1975).
Is zo'n r-bis negatief (en niet zo'n klein beetje), dan wil dat zeggen dat studenten die deze vraag goed beantwoorden op de toets in z'n geheel tot de minder goede scoorders behoren, door de bank genomen. Zoiets komt uiteraard zelden voor, en kan een teken zijn van ambiguïteit in de vraagformulering, of het gevolg van een fout in de scoringssleutel. Behalve in dit soort heel duidelijke gevallen kun je met dat r-bis-gegeven weinig doen.
Lage r-bis-waarden, in de buurt van 0,0 of zelfs iets negatief zijn volkomen aceptabel. Het is voor toetsen op dit niveau van onderwijs nu eenmaal zo dat de vragen erg uiteenlopend van aard zullen zijn (heterogeen), en ieder voor zich zeker niet hetzelfde meten wat de toets als geheel meet. Daarom is het af te raden om alleen afgaande op hun r-bis-waarde bepaalde vragen uit de toets te verwijderen(vanwege een 'te lage' r-bis). Zou je dat doen, dan houd je vragen over met hogere r-bis-waarden. Anderson (1972): studenten die het op de toets in zijn geheel goed doen zullen een hogere verbale intelligentie, ability. hebben dan zij die het slechter doen. Vragen die een hoge r-bis hebben, die dus onderscheiden tussen beide groepen studenten, zullen vaker moeilijk vocabulaire bevatten of denkstappen vragen die niet direct te maken hebben met de eigenlijk te toetsen beheersing van de leerstof.
Maak je dus geen zorgen over r-bis: het is mooi wanneer ze voor je berekend zijn (zie figuur 4.2), kijk er dan ook naar, maar neem alleen maatregelen als ook andere informatie naast de r-bis in de richting wijst van gemankeerdheid van de vraag.
Het construeren van vragen, en het uit een vragenverzameling samenstellen van een toets. zijn verschillende zaken. Bij het componeren van de toets gaat het om de kwaliteit van het geheel, de wijze waarop de toets als geheel de leerstof dekt, en ook om een wijze van toetssamenstelling waarop de student voldoende zicht heeft om er zijn studie naar te richten.
Begin met het beschrijven van de leerstof. Maak een lijst van alle begrippen (wetten, regels, theorieën, technieken en dergelijke.) uit de leerstof die belangrijk genoeg zijn om in enigerlei vorm (eventueel) te toetsen. Splits als dat handiger is zo'n lijst uit naar met elkaar samenhangende begrippen. Probeer in eerste instantie zo'n opsomming niet te gedetailleerd te maken. Figuur 5.1 geeft een illustratie uit de praktijk.
-------------------------------------------------------
- domain sampling en paralleltest model 9
verbale definitie ware score en betrouw
baarheid, bronnen meetfouten, schattingen
betrouwbaarheid 9
schattingen ware scores 5
standaardmeetfout 6
Kuder-Richardson 20 3
precisie betrouwbaarheidsschattingen 5
SpearmanBrown 3
correctie voor attenuatie 6
betrouwbaarheid lineaire combinaties 4
----------
totaal 50
-------------------------------------------------------
Niet ieder onderwerp is even belangrijk of even uitgebreid. Druk het relatieve belang van ieder onderwerp uit in het aantal vragen dat daarover in de toets zal worden opgenomen, zoals in figuur 5.1 gedemonstreerd. Het gaat om relatieve gewichten, zodat een bevredigende gewichtstoekenning met wat proberen en wijzigen gevonden kan worden, waarbij de totale som van de gewichten gelijk genomen kan worden aan het aantal vragen waaruit de toets zal bestaan, of druk de gewichten uit in proporties (die sommeren tot l).
Druk je het belang van een onderwerp uit in het aantal daarover te verwachten toetsvragen, dan kun je voor kleinere onderwerpen afspreken dat getallen kleiner dan 1 de kans aangeven dat in een bepaalde toets over dat onderwerp een vraag wordt opgenomen.
Uit zo'n lijstje als figuur 5.1 kan de student aflezen hoeveel 'punten' ieder onderwerp waard is, of: wat een goede beheersing van een bepaald onderwerp op kan leveren, of: hoeveel inspanning een bepaald onderwerp waard is. De student doet er verstandig aan zijn studie-inspanning in ongeveer diezelfde verhouding over de onderwerpen te verdelen als in het lijstje aangegeven. Het loont altijd de moeite om tenminste iets van ieder onderwerp af te weten: beheers je bepaalde onderwerpen heel goed, dan kun je gebruik maken van het compensatorische karakter dat de toets heeft door andere onderwerpen wat 'minder' te doen, maar het zou bijzonder onhandig zijn om die andere onderwerpen helemaal niet te bestuderen.
Zou blijken dat de studenten als groep bepaalde onderwerpen verwaarlozen of vermijden, dan moet je als docent zorgvuldig nagaan wat daar de reden van kan zijn, om vervolgens zonodig maatregelen te treffen.
Vergroot je het aantal vragen over een bepaald onderwerp, dan valt het aantal te verdienen 'punten' over dat onderwerp gunstiger uit en loont het de moeite er wat meer aandacht aan te besteden dan de student anders gedaan zou hebben. Dat is het eenvoudige mechanisme waarmee je corrigeert op de 'weging' in je onderwerpen lijstje. Maar houd het bij kleine correcties tegelijk, om niet het risico te lopen van toets op toets een bepaald 'gewicht' dan weer eens fors te verhogen, dan weer te verlagen. De toetsresultaten op grond waarvan je dergelijke correcties aanbrengt zijn trouwens ook zelden sterk genoeg om grotere wijzigingen te rechtvaardigen.
Kun je voor ieder onderwerp ook aangeven dat er maar &én of twee vraagsoorten over gesteld zullen worden, dan ben je klaar met die vraagsoorten ook per onderwerp te omschrijven.
In de meeste gevallen zal de docent wel de vrijheid willen houden voor bepaalde onderwerpen zijn keus te doen uit het hele scala van vraagsoorten (zie het schema op blz. 46), hoewel een zelfopgelegde beperking in het aantal verschillende vraagsoorten de doorzichtigheid van de toetsing wel eens ten goede zou kunnen komen. Het laatste hangt natuurlijk sterk van de aard van de leerstof af. Is er een diversiteit in vraagsoorten die in de toets opgenomen kunnen worden, dan is ook daar een specificatielijstje over te maken.
------------------------------------------------------------------------
- voorbeeld of toepassing herkennen 3
- voorbeeld benoemen 5
- probleemoplossen of toepassen, begrip gegeven 3
- idem, begrip niet gegeven 9
- voorbeeld benoemen, meerdere begrippen gegeven 5
- idem, begrippen zijn niet gegeven 5
- informatie zoeken voor benoeming, begrippen gegeven -
- idem, begrippen niet gegeven 2
- informatie selecteren voor benoeming, begrippen gegeven -
- idem, begrippen niet gegeven 3
- probleemoplossen met gegeven informatie, begrippen gegeven 5
- idem, begrippen niet gegeven 5
- probleemoplossen met gezochte informatie, begrippen gegeven -
- idem, begrippen zijn niet gegeven 2
- probleemoplossen met geselecteerde informatie,
begrippen gegeven -
- idem, begrippen niet gegeven 3
---------
totaal 50
------------------------------------------------------------------------
Zou de getalsmatige invulling in figuur 5.2 reëel zijn, dan gaat het kennelijk om probleemoplossen dat door de student die zich redelijk heeft voorbereid snel en efficiënt kan gebeuren: anders zou een toets van 50 vragen veel te zwaar zijn.
Slechts zelden zullen alle vraagsoorten relevant genoeg zijn om in onderwijs en toetsing op te nemen, zodat meestal met een veel korter lijstje dan figuur 5,2 volstaan kan worden. Grotere overzichtelijkheid is ook te bereiken door van een eventuele clustering van onderwerpen en vraagsoorten gebruik te maken door afzonderlijke vraagsoortenlijstjes bij deellijstjes van onderwerpen te maken.
Het laatste is al een stap in de richting van eem matrijs van onderwerpen tegen vraagsoorten. Het maken van zo'n matrijs, die bij een wat groter aantal onderwerpen en vraagsoorten nogal omvangrijk kan worden, kan de moeite waard zijn omdat je daarmee een goed hulpmiddel krijgt om aan de hand daarvan een gebalanceerd aantal toetsvragen te maken (of te selecteren). 'Gebalanceerd' naar de doelstellingen die je met je onderwijs nastreeft, doelstellingen die expliciet geformuleerd kunnen zijn, maar tenminste blijken uit de concrete getalsmatige invullling van zo'n onderwerpen bij vraagsoorten matrijs. Voorbeelden van dergelijke matrijzen zijn o.a. te vinden in Bloom, Hastings en Madaus (1971). Ook het Centraal Instituut voor Toets Ontwikkeling maakt wel van dergelijke matrijzen gebruik. Door hun vaak grote gedetailleerdheid zijn dergelijke matrijzen minder geschikt om naar de studenten toe de toetsing doorzichtig te maken. Probeer daarom in ieder geval om zo'n gedetailleerde matrijs desnoods wat globaal samen te vatten op de wijze zoals hierboven eerder beschreven, dat geeft de student wat beter houvast in zijn voorbereiding op de toetsing. Hoe een en ander in jouw specifieke geval het beste op papier gezet kan worden wijst zich vanzelf.
Moet je nu de toets van 50 vragen volgens beide specificaties (figuur 5.1 en 5.2) in elkaar zetten, dan kan het nog lastig blijken om daar precies aan te voldoen. Het lijkt dan ook verstandig om kleine afwijkingen voor te behouden. Daardoor hoeft de doorzichtigheid voor de student niet te lijden, en zal zijn studiestrategie (zie cursus Studiestrategieën) niet gewijzigd hoeven worden.
Dat maken van lijstjes is toch vooral een hoop gedoe. Het risico is bovendien groot dat het gebruikmaken ervan leidt tot verdere bureaucratisering. Het is belangrijker om kwalitatief hoogwaardige vragen te ontwerpen, dan ze ook nog volgens dit soort schema's te ontwerpen.
Uiteenlopende vraagsoorten in een en dezelfde toets opnemen leidt er ook toe dat die toets gaat bestaan uit vragen met een mogelijk nogal uiteenlopende moeilijkheid (p-waarde, ofwel de proportie van de deelnemers die een bepaalde vraag 'goed' maakt). Dat hoeft op geen enkele wijze bezwaarlijk te zijn. Er is voor de gewone onderwijstoets niet zoiets als een 'gewenst' of zelfs 'voorgeschreven' moeilijkheidsniveau (wat niet wegneemt dat bepaalde vragen veel te moeilijk, of veel te makkelijk, kunnen blijken te zijn).
Kun je moeilijke vragen een hoger gewicht of een groter punten aantal toekennen dan makkelijke vragen in dezelfde toets? Jazeker kan dat wel. Denk bijvoorbeeld aan de soms gebruikte combinatie van meerkeuzevragen en essayvragen, bijvoorbeeld 40 meerkeuze-, en 3 essayvragen, waarbij met een essayvraag bijvoorbeeld 5 keer zoveel 'punten' gescoord kunnen worden als met een meerkeuzevraag. Vandaar is het maar een kleine stap naar een extra puntentoekenning voor meerkeuzevragen die naar verhouding moeilijk zijn en meer oplostijd vragen.
Gebruik je inderdaad een verschillende puntentelling voor moeilijke en makkelijke vragen, of voor meerkeuze- en open-eindvragen, en dergelijke, dan is het wel van belang:
De laatste aanbeveling is niet alleen bedoeld om de doorzichtigheid van het toetsgebeuren zo groot mogelijk te houden door met zo weinig mogelijk verschillende wegingen te werken, maar berust ook op de herhaalde waarneming dat subtiele wegingen geen praktisch verschil maken, en dan ook beter achterwege kunnen blijven.
Niettemin wordt er in de literatuur nogal eens een strikt niveau van moeilijkheid aangeraden, p-waarden (gecorrigeerd voor raden) van rond 0,5. Enige relativering daarop werd o.a. aangebracht door Lans en Mellenbergh (1973), maar ook over dàt standpunt valt nog wel iets meer te zeggen:
ad a.) Het is maar net wat je beheersing van de stof noemt. Gaat het om basisvaardigheden, en heb je toetsjes die direct op kleinere stukjes onderwijs aansluiten, dan zul je veelal een hoge mate van beheersing, hoge p waarden, verwachten, en ook verlangen. Gaat het daarentegen over probleemoplossen en dergelijke, en bestrijkt de toetsing een groot stuk leerstof, dan mag je van studenten die hun zaakjes goed beheersen geen hoge mate van succes verwachten, en volgens je doelstellingen zul je dat veelal ook niet verlangen. Ook bij vakken waar in de beroepsuitoefening een zeer hoge mate van beheersing wordt vereist zal in de opleidingsfase nogal eens met heel wat minder genoegen kunnen worden genomen, zeker wanneer die uiteindelijke hoge beheersing alleen in die beroepsuitoefening zelf te verwerven is.
ad b.) Het is op zich nimmer de bedoeling van een onderwijstoets om tussen betere en slechtere studenten te onderscheiden (laten we zeggen dat dat studenten zijn die de stof beter of slechter beheersen, hoe dat dan ook verder veroorzaakt mag zijn). Verschillen in stofbeheersing moeten op de toets tot uitdrukking kunnen komen wanneer ze aanwezig zijn, anders kun je beter maar helemaal niet toetsen. Maar let er goed op dat dergelijke verschillen niet vanzelfsprekend ook altijd zullen bestaan, en al helemaal niet wanneer het onderwijs goed functioneert, de toetsing goed doorzichtig is, en er over de waardering van de individuele toetsresultaten naar de studenten toe goede afspraken zijn gemaakt. Als 'slechtere leerlingen' niet aan de toets deelnemen is het heel goed mogelijk dat goed differentiërende toetsvragen hoge p-waarden hebben, p-waarden die een forse duikeling naar beneden zouden maken wanneer 'slechtere leerlingen' wel aan de toets deelgenomen zouden hebben. Zo zie je maar weer dat het uit de toets weglaten van vragen met hoge p-waarden omdat die niet zouden differentiëren alleen maar te verdedigen valt wanneer er aanwijsbaar grote verschillen in stofbeheersing bestaan tussen de deelnemende studenten. 'Grote verschillen' natuurlijk geïnterpreteerd naar de maatstaven die in je onderwijsdoelen t.a.v. beheersing zijn aangelegd.
Je kunt voor iedere af te nemen toets telkens de nodige vragen construeren. Dat is de gangbare procedure. Je kunt ook, en dat is het andere uiterste, eens en voor al een grote verzameling van vragen maken, en daaruit iedere keer een toets samenstellen. Of stel de toets gedeeltelijk uit nieuw te maken vragen samen, gedeeltelijk uit vragen die uit zo'n vragenverzameling gekozen worden.
telkens nieuwe vragen construeren. Daarbij kun je te werk gaan volgens de matrijs van onderwerpen bij vraagsoorten, wat je garandeert dat de verschillende onderwerpen ook in de bedoelde verhouding in de toets voor zullen komen. Het is nu eenmaal altijd verleidelijk bij voorkeur de wat makkelijker te formuleren vragen voor toets gebruik te nemen, maar daardoor kan al snel scheefgroei in de op deze toets gerepresenteerde onderwerpen ontstaan. Wanneer de oorspronkelijke specificatie van onderwerpen bij vraagsoorten nog veel ruimte laat voor uiteenlopende soorten vragen, dan is te overwegen een wat fijnere matrijsspecificatie te maken, om te voorkomen dat van de ene toetsing naar de andere er een zekere verschuiving in de aard van de vragen optreedt. Waarom is dat laatste belangrijk? Probeer je voor iedere toets weer een nieuwe set vragen te bedenken, dan loop je zonder ondersteuning van een goede matrijsspecificatie het risico iedere keer meer moeite te hebben nog weer 'nieuwe' vragen te bedenken. Het gevolg kan zijn dat je vragen steeds meer over onbelangrijke details gaan, steeds moeijker worden bovendien, en voor studenten ondoorzichtiger. Het laatste brengt met zich mee dat studenten vervallen in slechte studiegewoonten omdat ze steeds minder inzicht hebben in de vragen die ze kunnen verwachten. Daardoor zullen ze geneigd zijn hogere zakrisico's te nemen. Een en ander is niet bevorderlijk voor de motivatie voor het vak.
Goed. ik schilder het een beetje zwart af om het belang van een goede vragenspecificatie te onderstrepen. In de toetsliteratuur komen we dat wel tegen onder de naam domeinspecificatie. Een wel heel uitgebreide specificatie werd als voorbeeld gegeven door Hambleton, Eignor, en Rovinelli (1979):
De beschrijving gaat op die manier nog een tijdje door. Ook wordt beschreven dat het gaat om meerkeuzevragen, waarbij de student telkens uit 5 alternatieven de best passende moet kiezen, en waarbij die vijf alternatieven gekozen zijn uit een lijst van 8 mogelijke betrouwbaarheidscoëfficiënten zodanig dat de gekozen vijf uit deze acht het best passen bij de gegeven situatie.
Zo gedetailleerd is zeker overdreven. De achtergrond van dergelijke overgespecificeerde vraagsjablonen (item-forms) bij amerikaanse auteurs is het verlangen om zo objectief te formuleren dat verschillende vraagconstructeurs onafhankelijk van elkaar met zo'n sjabloon werkend tot toetsvragen komen die dezelfde eigenschappen bezitten. Dat streven hoeven we niet over te nemen. Het betere is hier weer eens de vijand van het goede.
vragen kiezen uit een grote verzameling. Heb je voor een groot aantal toetsen telkens nieuwe vragen geconstrueerd, dan beschik je tenslotte over een waarschijnlijk voldoende grote verzameling van vragen, om daar voortaan voor iedere nieuwe toets je vragen uit te kunnen trekken, tenminste een gedeelte van de benodigde vragen uit te trekken. Voordat je gaat 'trekken' controleer je of de samen stelling van de verzameling in overeenstemming is met je matrijsspecificatie. Is de verzameling qua samenstelling in overeenstemming met de matrijsspecificatie van onderwerpen tegen vraagsoorten, dan kun je iedere volgende toets samenstellen door de vragen toevallig te trekken: er voor te zorgen dat iedere vraag in de verzameling dezelfde kans heeft om in de toets opgenomen te worden als iedere andere vraag. Zo kun je het doen, maar zo hoeft het niet. Tenslotte kan op deze manier een toets uit vragen blijken te bestaan die niet al te best in overeenstemming zijn met de aan studenten gegeven lijstjes van onderwerpen en vraagsoorten, vanwege toevalsfluctuaties ontstaan door dat toevallig trekken. Dreigt dat gevaar, dan zou je in plaats van toevallig trekken uit de hele verzameling over kunnen gaan op toevallig trekken uit onderdelen van de verzameling (gestratificeerd trekken), waardoor de onderlinge verhouding van onderwerpen, en van vraagsoorten, beter gewaarborgd blijft.
Toevallig trekken kan op verschillende manieren: uit een grabbelton waarin alle (op kaartjes geschreven) vragen; of door de vragen op nummer te trekken met behulp van een tabel van willekeurige getallen. U ziet maar. Het is niet handig om vragen op een meer 'systematische' manier voor opname in de toets aan de beurt te laten komen, omdat daar het risico aan vast zit dat het 'systeem' uitlekt, waardoor sommige studenten een unfaire voorsprong op andere studenten zouden kunnen krijgen.
Voor de individuele student maakt het al heel weinig uit of de vragen iedere keer speciaal gemaakt worden, dan wel telkens getrokken uit een grote verzameling: de toets zal er voor hem 'gelijk' uit zien, voor hem ziet de toets er altijd uit als via 'toevallige trekking' samengesteld. Dat feit kan hij uitbuiten door er bij zijn studiestrategie rekening mee te houden (zie cursus Studiestrategieën, Wilbrink 1978 html).
Bestaat de verzameling uit vragen die al eens eerder in een toets gebruikt zijn, dan wordt er vanzelfsprekend voor gezorgd dat de vragenverzameling ook voor de student beschikbaar is. Hij kan met dat materiaal zich goed oefenen op de leerstof, op een wijze die ook direct relevant is voor de toetsing. Het dient dan ook bij uitstek de doorzichtigheid van de toetsing. N.B.: vragen geheim houden na afloop van de toets is er niet bij: dat is een daad van onbehoorlijk bestuur jegens de deelnemers, zie ook hoofdstuk 6 over algemene beginselen van behoorlijk bestuur.
Het werken met bekend gemaakte vragenverzamelingen waaruit ook nieuwe toetsen worden samengesteld is door een aantal docenten beproefd (Van Naerssen en Wouters, 1971). Daarbij is wel eens de ervaring opgedaan dat studenten een uitgekiende strategie volgden waarbij maar een deel van de vragen (uit het hoofd) geleerd hoefde te worden: bijvoorbeeld bij ja/nee vragen alleen de met 'ja' gesleutelde vragen [lezen en bij herkenning met 'ja' antwoorden]. Wees daar attent op, zeker wanneer je vragenverzameling nog maar klein is. Gebruik zo nodig in de toets niet letterlijk dezelfde vragen (en stel daar studenten dan ook tijdig van op de hoogte). Zou je de vragenverzameling niet bekend maken, dan zit je met het probleem dat sommige studenten niet, andere wel over delen van die vragenverzameling zullen kunnen beschikken, ook al zou je aan mogen nemen dat je de vragenverzameling voldoende tegen diefstal hebt beschermd. Wilmink (1977):
In hetzelfde artikel laat Wilmink overigens ook zien dat je niet gauw bang hoeft te zijn dat studenten door uit het hoofd leren van een (klein) deel van zo'n vragenverzameling voor een toets kunnen slagen zonder essentiële delen van de leerstof bestudeerd te hebben. Vanzelfsprekend is er wél voor gezorgd dat alle belangrijke onderwerpen uit de leerstof ook op de juiste manier in de vragenverzameling gerepresenteerd zijn, zodat je al helemaal geen angst hoeft te hebben dat studenten die de onhandige weg van maken van alle vragen verkiezen boven bestuderen van de stof daarmee een tekort aan inzicht op zouden doen.
Vergeet niet iedere keer weer te controleren of de voor de toets gekozen vragen wel samen gebruikt kunnen worden. Wordt bij de ene vraag een stukje informatie gegeven waar bij een andere nu juist naar gevraagd wordt, dan is dat op z'n minst onhandig. Haal een vraag van zo'n koppel tijdig uit de toets. Maak je gebruik van een programma zodat toevallige samenstelling van de toets door de computer kan gebeuren, neem dan het soort voorzorgsmaatregel als door Van Naerssen en Wouters (1975) beschreven: zet vragen die niet samen in één toets opgenomen mogen worden in groepjes bij elkaar, en programmeer zo dat uit een dergelijk groepje niet meer dan één vraag voor de toets getrokken wordt. Als je dat eenvoudig kunt vermijdeng neem dan ook geen vragen op waarbij de ene vraag voortbouwt op het antwoord van een andere vraag.
Meerdere vragen over hetzelfde onderwerp kun je natuurlijk wel, met de nodige voorzorg, in een toets opnemen. Denk aan een eenvoudige toets over optellen van telkens twee getallen onder de 100; zo'n toets bestaat uit vragen over telkens hetzelfde onderwerp, maar toch zal de beantwoording van iedere vraag afzonderlijk alleen afhankelijk zijn van de stofbeheersing van de leerling, en niet van het feit of hij àndere vragen al dan niet goed heeft kunnen beantwoorden.
tenslotte. Of een toets die op deze wijze in elkaar gezet is ook een kwalitatief goede toets is, dat is nu nog een open vraag. Kwaliteit kan met de procedures uit dit hoofdstuk niet gegarandeerd worden, maar wordt er uiteraard wel door bevorderd. Het kan zijn dat de toets die nu in elkaar gezet is niet helemaal aan zijn doel beantwoordt: dat validiteitsvraagstuk wordt in hoofdstuk 6 besproken.
Kwaliteit van de toets, en van de afnameprocedure, is het onderwerp van dit hoofdstuk. Tegenover de toetsdeelnemers is de docent verplicht tot een in alle opzichten behoorlijke procedure: zijn handelen is in juridische termen gebonden aan wat heet de Algemene Beginselen van Behoorlijk Bestuur. Daarnaast is de docent gehouden aan een vakbekwame werkwijze bij het opstellen van de toets, het afnemen van de toets, het interpreteren van toetsresultaten en rapporteren daarvan, en bij het nemen van beslissingen op basis van die toetsresultaten. Leidraad bij een en ander zouden de Richtlijnen voor ontwikkeling en gebruik van psychologische tests en studietoetsen kunnen zijn, ware het niet dat die tekst nogal is toegeschreven naar gestandaardiseerde, en niet in de eerste plaats door de docent zelf opgestelde toetsen.
Door de docent zelf opgesteld of niet, aan de eisen van behoorlijkheid doet dat niets af. Wat ik in 1979 bedoelde is dat de Richtlijnen sterk in het jargon van de psychologische test spreken. Voor de herziening van de Richtlijnen, uitgebracht in 1988, ben ik in de gelegenheid geweest om aanvullingen op de concept-tekst te geven, specifiek voor toetsen in het onderwijs.
Daaraan vooraf behandel ik de vraagstelling in hoeverre de toets functioneert zoals bedoeld, de vraag naar de validiteit van de toets. Over het functioneren van de toets kom je pas iets te weten door onderzoek, waarvoor enkele suggesties gegeven worden. Reden voor een achterblijvende validiteit kan soms een tekort aan betrouwbaarheid van de toets zijn, ook een veel gehanteerd begrip, een nogal overschat begrip ook, waarin de lezer zich voor zijn eigen toetspraktijk enig inzicht moet verschaffen.
Onderzoek naar het functioneren van de toets betrekt zich in welke vorm dan ook tenminste altijd op de toetsresultaten zelf, in samenhang tot andere relevant geachte gegevens over individuele studenten of bepaalde deelgroepen van studenten. Waar je dan vooral naar uitziet zijn oorzakelijke samenhangen, bijvoorbeeld tussen vooropleiding en studieresultaten, of tussen tijdbesteding en studieresultaten. Enig inzicht in dergelijke samenhangen geeft je meer houvast bij het interpreteren van je toetsresultaten (en dus ook de resultaten van je onderwijs!). Ik zal een heuristisch schema voor oorzakelijke verbanden achter studieresultaten presenteren, en daarna de praktische maatregelen bespreken die erdoor gesuggereerd worden.
Allereerst en vanzelfsprekend hangen intellectuele capaciteiten samen met studieresultaten. Daar bedoel ik mee dat studenten die van elkaar verschillen in intellectuele capaciteiten, maar overigens 'vergelijkbaar' zijn, ook zullen verschillen in de hoogte van de studieresultaten. De voorwaarde 'overigens vergelijkbaar' is niet in overeenstemming met de werkelijkheid, maar is handig bij het opzetten van deze logica. Weet je iets over de intellectuele capaciteiten van een student, dan kun je in bepaalde mate zijn studieresultaten voorspellen. Zou je in werkelijkheid die voorspelbaarheid onderzoeken, dan zul je tot teleurstellende resultaten komen. Daardoor hoef je je niet uit het veld te laten slaan: kennelijk zijn er nog enkele andere vanraibelen van invloed op studieresultaten.
(Verschillen in) intellectuele capaciteiten veroorzaken (verschillen) in studieresultaten, als alle andere omstandigheden gelijk zijn. Het oorzakelijke verband is niet omgekeerd, je mag aannemen dat studieresultaten die een enkele toets betreffen niet van invloed zijn op de intellectuele capaciteiten van iemand.
Zo zijn er meer eigenschappen van studenten te noemen die mogelijk van invloed zijn op de studieresultaten; eigenschappen bovendien die niet door dat studieresultaat belnvloed worden. Dergelijke eigenschappen heten in jargon exogene variabelen. Het is moeilijk in je onderwijs invloed op dergelijke variabelen uit te oefenen (hoewel dat soms wel eens geprobeerd wordt), het zijn veelal gegevenheden waar je maar zo goed mogelijk mee moet zien te werken.
EXOGENE intellectuele capaciteiten
VARIABELEN studiemotivatie ('intrinsieke' motivatie)
prestatiemotivatie ('extrinsieke' motivatie)
persoonlijkheidsvariabelen, biografische variabelen
vooropleiding, of nauwer: voorkennis
sexe
activiteiten buiten de studie
Studenten die van elkaar verschillen in termen van deze exogene variabelen zullen, ceteris paribus, verschillende toetsresultaten behalen. Met uitzondering van elkaar compenserende verschillen, zoals bijvoorbeeld studiemotivatie en prestatiemotivatie elkaar kunnen compenseren in deze zin dat een student hoog op de ene en laag op de andere tot dezelfde studieresultaten kan komen als de student die laag op de ene en hoog op de andere motivatie variabele 'zit'.
Naast deze exogene variabelen zijn er twee meer door de situatie bepaalde variabelen die op dat studieresultaat van invloed zijn: het streefniveau van de student, of hij mikt op hoge, redelijke, of juist nog aceptabele resultaten, en de tijdbesteding in de voorbereiding op de toets. Studenten verschillen van elkaar in het 'cijfer' waarop ze mikken; of in het risico dat ze willen nemen om voor de toets een onvoldoende te halen; of in de mate waarin ze de leerstof willen beheersen. Of hoe je dat 'streefniveau' verder ook maar wilt beschrijven. Het is evident dat sommige exogene variabelen van invloed zijn op de hoogte van het gekozen streefniveau: er zal zeker een oorzakelijk verband van exogene variabelen op streefniveau zijn. Ceteris paribus zal een hoger streefniveau leiden tot hogere studieprestaties.
Dat meer of minder tijd besteden aan de voorbereiding een oorzakelijk verband heeft met behaalde studieresultaten hoeft niet aan enige twijfel onderhevig te zijn (een tegenovergestelde conclusie van Crombag, Gaff en Chang, 1976, is te wijten aan een ingrijpende methodologische vergissing van deze auteurs). Ook deze variabele zal onder invloed staan van exogene variabelen, en bovendien van het gekozen streefniveau.
Geef je een oorzakelijk verband weer met een pijl, dan is het voorgaande samen te vatten tot de volgende figuur 6.1. Technisch gesproken is deze figuur een weergave van een 'fully recursive structural equation model', zie Tromp en Wilbrink (1977 html) en Duncan (1975). Dat model zou je om kunnen zetten in een model voor empirisch onderzoek, maar dat is een weg die hier afgeraden wordt omdat het aantal te schatten parameters in dit model te groot is, het daarvoor benodigde aantal waarnemingen in de praktijk niet bijeen te krijgen is (en al helemaal niet door de docent zelf). Met excuus voor al dit vakbargoens.
Wat kunnen we hier nu mee doen? Laat ik om te beginnen eens de tijdbesteding bespreken. Het streven is om de koppeling tussen tijdbesteding en studieresultaten zo strak mogelijk te maken, dat wil zeggen dat je er voor zorgt dat de studenten goed geïnformeerd zijn over het soort kennis en inzicht dat de toets hen vraagt te demonstreren, en over de onderwerpen die ter toetsing staan (zie hoofdstuk 5). Daardoor zal de studie immers gerichter, efficiënter, kunnen zijn. Dat betekent nog niet dat studenten die langer over de voorbereiding op de toets doen dan ook hogere scores zullen boeken dan studenten die minder tijd hebben besteed. De andere variabelen uit het schema 6.1 kunnen zelfs zo'n invloed hebben dat precies het omgekeerde gevonden wordt, of helemaal geen verband. Wil je dat uitzoeken, dan zul je studenten naar hun tijdbesteding moeten vragen, wat bijvoorbeeld kan (direct voorafgaand aan de toetsafname) op deze manier (Cohen-Schotanus 1979):
Kunt u schatten hoeveel voorbereidingstijd u in het tentamen pathologie hebt geïnvesteerd? Probeer de berekening zo nauwkeurig mogelijk te maken. Een goede manier is eerst te schatten hoeveel uur u gemiddeld per dag studeerde voor pathologie; vermenigvuldig dat vervolgens met het aantal dagen dat u met pathologie bezig bent geweest. Laat de collegetijd buiten beschouwing.
Andere formuleringen kunnen gekozen worden. De lay-out van de vraag of vragen pas je aan bij die van de toetsvragen. Je kunt het houden bij een globale vraag, zoals het gegeven voorbeeld. Wanneer je nauwkeuriger informatie wilt hebben kun je aanwijzingen bedenken die de student helpen een betere schatting te maken. bijvoorbeeld door de vraag te herhalen voor verschillende onderdelen uit de literatuur voor de toets, door aan te geven hoe groot de spreiding in het opgegeven aantal uren kan zijn, en dergelijke. Maak duidelijk dat dit gegeven over zijn tijdbesteding op geen enkele wijze de beoordeling van zijn resultaten zal beinvloeden. Bevorder dat door antwoorden op deze vraag gescheiden te houden van de toets beantwoording (bijvoorbeeld: zamel deze antwoorden in voordat de toets uitgedeeld wordt). Leg uit dat het gewenst is dat de student zijn naam vermeldt, maar dat wie daar bezwaar tegen heeft natuurlijk niet daaraan mee hoeft te werken.
In de tachtiger jaren heb ik op deze wijze tijdbestedingsgegevens verzameld in de propedeuse van de studies tandheelkunde en rechten aan de UvA. Dat eenvoudige tijdbestedingsgegevens werkelijk iets meten dat relevant is, is ondere in een in 1992 gepresenteerde studie aangetoond, waarin een model van James Coleman is gecombineerd met een multi-trait-multi-method analyse (1992a html). Overigens was al bij eenvoudige analyses duidelijk dat deze tijdbestedingsgegevens op het niveau van de groep valide zijn (1992bhtml.)
Cohen-Schotanus (1979) vond in haar onderzoek dat studenten die slaagden voor een tentamen daar gemiddeld meer voorbereidingstijd in gestoken hadden dan studenten die zakten. Dat was een opvallend resultaat, omdat doorgaans bij dit soort onderzoek geen duidelijke samenhangen gevonden worden. Het ging hier om tentamens met onbeperkte herkansingsmogelijkheden, zodat je zou kunnen veronderstellen dat er een sterk verband is tussen streefniveau (in dit geval de slaagkans waarop de student mikt) en bestede tijd, en wel in deze zin dat studenten nogal verschillen in de mate waarin zij het willen laten aankomen op een herkansing.
Wil je uitzoeken of deze veronderstelling juist is, dan zul je de studenten ook moeten vragen naar het resultaat waarop zij in de voorbereiding gemikt hebben, cijfer, score of slaagkans. Ga er van uit dat studenten met een minimale studiestrategie daarvoor gekozen hebben, dat het geen ongelukje is. Vraag dus naar de achtergronden van die keuze, en niet in de eerste plaats, en al helemaal niet met uitsluiting van andere en meer rationele motieven, of korte tijdbesteding te wijten is aan 'te laat met de studie begonnen zijn' 'de zwaarte van het vak onderschat hebben' 'ziek geweest zijn', en dergelijke. In een enkel geval kunnen dergelijke pathologische omstandigheden een rol spelen, maar meestal zal de student voor zijn minimale studiestrategie zijn goede redenen hebben, al mag de docent die redenen ook wat minder waarderen.
-------------
*) noot. complexere technieken voor tijdbestedingsonderzoek worden gegeven door o.a. Crombag, Meuwese en Roskam (1973) en Everwijn en Muggen (1973). Het gaat in 'traditioneel' tijdbestedingsonderzoek om het schatten van door de gemiddelde student bestede studietijd, als het even kan in klokuren. Het streven in dit hoofdstuk is echter een andere, en levert ook veel rijkere informatie op: per individuele student bestede tijd koppelen aan behaald resultaat en eventuele andere variabelen, en nagaan hoe studenten daarin van elkaar verschillen. Kun je vervolgens ook nog effecten van onderwijsveranderingen op deze relaties signaleren, dan heb je gegevens in handen voor een gericht onderwijsbeleid.
Vraag naar de slaagkans waarop de student heeft gemikt, en of hij denkt daar ook in geslaagd te zijn. Vraag niet of de student denkt voor de toets een voldoende te zullen behalen, omdat het antwoord op deze vraag, een simpel 'ja' of 'nee', te weinig informatief is. Wil je het de student wat makkelijker maken om met zijn lage slaagkans voor de dag te komen, dan kun je de vraag in de meerkeuzevorm gieten, waarbij ook lage slaagkansen aangegeven worden.
Maakt de toets onderdeel uit van een compensatorische examenregeling, wordt met andere woorden het resultaat niet als 'voldoende' of 'onvoldoende' beoordeeld, dan vraag je niet naar de slaagkans maar naar de score of het cijfer waarop gemikt is.
Hoe je de gegevens die dit soort onderzoeksvragen opleveren moet of kunt interpreteren is sterk afhankelijk van de betreffende onderwijssituatie, en de doelen die daarin nagestreefd worden. De docent die wat meer werk van het onderzoek naar de validiteit van zijn toets wil maken wordt dan ook sterk aangeraden daar advies voor te vragen bij het onderwijsresearchbureau van zijn of haar onderwijsinstelling. Wie op eigen kracht aan het onderzoeken slaat heeft zich in ieder geval te hoeden voor de verleiding om pas als de gegevens al binnen zijn aan het interpreteren te slaan: formuleer zo nauwkeurig mogelijk wat je wilt weten en wat je verwacht te vinden nog voordat je met je onderzoek begint, maar in ieder geval voordat je enige inzage in de resultaten hebt gehad. Hoe zo'n validerings onderzoek voor een toets er uit zou kunnen zien wordt getoond in Van der Vleugel en anderen (1973), waarin enkele tevoren opgestelde vraagstellingen en veronderstellingen ten aanzien van het functioneren van de toets en de toetsprocedure empirisch werden onderzocht.
Exogene variabelen zijn altijd bijzonder scherp op de korrel te nemen. Om te beginnen moet je van je toets verlangen dat studenten die aan het onderwijs hebben deelgenomen er duidelijk hoger op scoren dan studenten die er (nog) niet of nog maar gedeeltelijk aan hebben deelgenomen. Vermoed je problemen in dit opzicht, dan kun je dat onderzoeken door de toets ook op zo'n bijzondere groep af te nemen (bijvoorbeeld studenten die net aan je cursus beginnen).
Voor bepaalde exogene variabelen is het verstandig om ze te controleren: studenten die op enigerlei wijze een bijzondere positie innemen ten opzichte van de groep 'normaal' studerenden wil je bij voorkeur signaleren, en qua studieresultaten ook afzonderlijk bekijken. Bijvoorbeeld de groep studenten die de toets al eens eerder heeft afgelegd. Of zij die voor de tweede maal aan de propedeuse deelnemen. Of degenen met een afwijkende of onvoldoende vooropleiding. Verzamel dergelijke informatie, en gebruik ze om deze speciale deelgroepen van studenten apart te nemen. Niet met de bedoeling om ze op een speciale manier te beoordelen (zorg dat bij het nakijken van antwoordformulieren bijzondere informatie over de persoon niet van invloed kan zijn), maar om effectiever te kunnen onderzoeken of de toets functioneert zoals bedoeld.
Enkele suggesties voor 'exogene variabelen' die je daarbij zou kunnen betrekken:
De beide laatste categorieën studenten 'blijken' pas later Wanneer de toetsresultaten binnen zijn kunnen sommige studenten dermate achterblijvende prestaties geleverd hebben dat je mag concluderen dat het deelnemen aan de toets niet serieus bedoeld was maar misschien om eens 'droog te zwemmen'. Studenten die later de studie gestaakt blijken te hebben vormen een bijzondere groep, waarvan misschien aan te nemen valt dat hun studiemotivatie al geruime tijd eerder op een laag pitje was geraakt. In sommige gevallen, maar dat zal ook weer van je vraagstelling afhangen, kun je je gegevens nog eens heranalyseren zonder de groep studiestakers.
Het aardige van het rekening houden met allerlei bijzondere groepen studenten is dat de resultaten van je onderwijs veel duidelijker zullen blijken. Immers, studenten die om bijzondere redenen, zoals ziekte of andere persoonlijke omstandigheden, of omdat zij het eerste studiejaar gebruiken om kennis te maken met deze studierichting en ondertussen een eveneens aantrekkelijk alternatief in hun achterhoofd hebben, achterblijven in hun studieresultaten vertroebelen de relatie tussen de kwaliteit van het geboden onderwijs en de bereikte resultaten. Neem je deze groep apart, dan zou het plaatje van je onderwijs best eens sterk op kunnen klaren. Ik zal een voorbeeld geven uit de praktijk, waarbij ik de naam van de faculteit heb gewijzigd.
bijzondere situaties. Iedere docent zal met zijn toets wel bepaalde bepaalde bedoelingen hebben die specifiek voor zijn toets of cursus zijn. Sommige toetsen zullen daarin opmerkelijker zijn dan andere. Ik ben van alle opmerkelijkheden niet op de hoogte, en volsta hier met er twee te noemen: Maastrichtse evaluatie, en participatie controle.
Maastrichtse evaluatie. Aan de medische faculteit Maastricht wordt geëxperimenteerd met een opmerkelijk toetssysteem waarbij studenten van meet af aan toetsen krijgen voorgelegd met vragen zoals die in het artsexamen zouden kunnen voorkomen. Ook de eerstejaars krijgen deze toetsen te maken! De staf in Maastricht heeft dan ook heel bijzondere bedoelingen met deze vorm van toetsing, en de evaluatie (validering zou je kunnen zeggen) is nog in volle gang. Zie Imbos en Verwijnen (1978) en Greep (1979).
Dit systeem van voortgangstoetsen is in 2007 nog steeds in gebruik. Enkele decennia lang zijn er ja-nee-vragen voor gebruikt, sinds kort is die dogmatiek verlaten.
participatiecontrole. Hofstee (1973) introduceerde het participatieprincipe:
Wil je zo'n toets op validiteit onderzoeken, of ze beantwoordt aan het beschreven doel, dan moet nagegaan worden of deze 'eenvoudige vragen' inderdaad door 'deelnemers' aan het onderwijs in redelijke mate goed beantwoord worden, en tegelijk door studenten die aan het onderwijs (nog) niet hebben deelgenomen slecht of helemaal niet beantwoord kunnen worden. Dat is het principe van het onderzoek, maar in de praktijk kunnen daar nog wel eens wat haken en ogen aan zitten.
Bij de ene cursus zal deze vorm van toetsing beter passen dan bij de andere. Is er veel literatuur te bestuderen of door te nemen, dan ligt deze vorm van toetsing al erg voor de hand. Maar ook voor vakken waarvan je het op het eerste gezicht niet zou denken is deze Hofstee variant te overwegen. Bijvoorbeeld is het bij wiskunde al heel simpel om vraagstukken te maken die studenten die het onderwijs gevolgd hebben vrijwel perfect zullen kunnen beantwoorden, terwijl andere studenten hun antwoordvel leeg moeten laten. In dit geval komt de docent bovendien niet in de verleiding opgaven te bedenken die veeleer wiskundige genialiteit dan behoorlijke studie-inzet 'meten'.
Een hier en daar wel gehanteerde vorm van participatiecontrole is het uitgebreide literatuurtentamen dat mondeling wordt afgenomen, en waarbij het gesprek plaats vindt aan de hand van een korte literatuurscriptie die door de student enige tijd daarvoor is ingeleverd. De scriptie is bedoeld als blijk van het kennis genomen hebben van de opgegeven literatuur; acepteert de docent de scriptie, dan kan daarna het 'gesprek' plaats vinden onder de garantie dat de student in ieder geval een 'voldoende' beoordeling zal krijgen. Een vorm van mondelinge toetsing waarbij op een elegante manier de druk van de ketel genomen is.
tenslotte. In de literatuur worden vele soorten validiteit onderscheiden; ik heb daar de lezer niet mee willen vermoeien. Wel is te bedenken dat het volgen van de procedure in hoofdstukken 4 en 5 essentiëel is voor het (kunnen) bereiken van wat het doel van de toetsing in jouw geval is.
Het heeft weinig zin om op traditionele wijze 'betrouwbaarheid' te beschrijven als de mate waarin de toets iets 'meet', omdat toetsen in het onderwijs niet in de eerste plaats 'meten' is. In het eerste hoofdstuk heb ik erop gewezen dat de toetsing in het onderwijs heel bepaalde functies heeft; dat het juist de bedoeling is dat studenten zich zo 'optimaal' mogelijk op de toetsing voorbereiden in tegenstelling tot bij psychologische tests waar een dergelijke voorbereiding zoveel mogelijk uitgesloten zal worden; dat een toets meer een mijlpaal dan een meetlat is, meer focus voor de studie-inspanning dan de peilstok ervoor. De toetsing heeft een heel bepaalde plaats in de afspraak die de onderwijs instelling met de student aangaat. Bijvoorbeeld: dat je slaagt voor de opleiding door voor de afzonderlijke vakken te 'slagen' (conjunctieve examenregeling). Of: je slaagt voor het examen door tenminste een bepaald gemiddelde te behalen (compensatorisch). Met vele mogelijke tussenvormen, die vooral bij propedeuseregelingen voorkomen (zie ook Studiestrategieën hoofdstuk 9, Wilbrink 1978 html). Hoe de afspraken er ook precies uit mogen zien, het is voor de student van belang dat hij op de toets een resultaat kan boeken dat niet al te ver afwijkt van wat hij 'verdient' gezien zijn ware beheersing (als je die ware beheersing zou weten). Het gaat er maar om dat de altijd aanwezige invloed van allerlei toevalligheden binnen aanvaardbare perken gehouden wordt.
De docent heeft er al evenzeer belang bij dat toetssscores een goede aanwijzing geven van de 'ware beheersing' van studenten, dat allerlei toevalligheden zoveel mogelijk uitgesloten worden. Voor dat laatste heeft hij een aantal maatregelen tot zijn beschikking.
Welke zijn nu die mogelijke invloeden van 'het toeval'? Stanley (1971) geeft er een tamelijk volledig overzicht van, waarin hij ook variabelen meeneemt waarvan het uitdrukkelijk niet de bedoeling is dat zij de toetsscore beïnvloeden:
eigenschappen van de individuele student
- exogene variabelen, zoals in vorige paragraaf genoemd
- speciale handigheid in het maken van toetsen (test wiseness,
stijl bij essay toetsen, innemendheid bij mondeling)
- het algemene vermogen om instructies goed te begrijpen.
- gezondheid
- vermoeidheid
toetsomstandigheden
- duidelijkheid van instructies aan de student
- tijdlimiet
- afleidingen
- licht, temperatuur, lucht
- persoon en rol van supervisor bij de toetsing
- onbetrouwbaarheid van de beoordeling (scoring, sleutel)
op niveau van afzonderlijke vragen
- het toevalselement of de student het onderwerp van een
bepaalde vraag goed bestudeerd heeft of niet
- fluctuaties in aandacht en nauwkeurigheid
andere
- tijdelijk afgeleid zijn
- geluk bij raden van antwoorden
Ieder punt uit dit lijstje vraagt om zijn eigen maatregelen om de invloed ervan uit te schakelen of terug te dringen. Op een aantal punten wil ik hier even ingaan.
Toetshandigheid, waardoor de ene student een voordeeltje zou hebben ten opzichte van de andere student, is binnen de perken te houden door goede voorlichting over de aard van de te verwachten toetsvragen, oefening in het maken van dergelijke vragen, duidelijke aanwijzingen bij de toetsafname, bij essays de 'stijl' van de beantwoording niet bij het oordeel te betrekken (eventueel wel afzonderlijk te laten scoren), ingewikkelde vraagvormen achterwege te laten (dubbele juist-onjuist-vragen, zekerheidsscoring).
Een juiste instelling tegenover het toetsgebeuren brengt met zich mee dat studenten die om gezondheidsredenen niet volwaardig aan de toets mee zouden kunnen doen, in de gelegenheid worden gesteld op een ander tijdstip tentamen af te leggen.
Voorkom vermoeidheid, waar de ene student nu eenmaal vatbaarder voor is dan de andere, door niet te lang achtereen te toetsen (geen toetsweek, geen 4 of 5 uur onafgebroken, en dergelijke).
Zorg voor een tijdslimiet waarbinnen iedereen (vrijwel iedereen) met zijn werk klaar kan komen. Verleng daartoe desnoods de van tevoren afgesproken tijd wanneer de toets onverwacht veel tijd vraagt. Voorkom liever het laatste soort verrassing door bij de vraagcontrole vooraf (hoofdstuk 4) te letten op de tijd nodig voor het goed beantwoorden van opgaven.
Zorg voor een ongestoorde ruimte, goede verlichting, een werkbaar klimaat, een absoluut rookverbod.
Wordt er gesuperviseerd bij de toetsafname, laat dat dan doen door personen met een welwillende houding tegenover de toetsdeelnemers (geen autoritaire stijl van aanwijzingen geven, geen overbodige strengheid, studenten alle gelegenheid gevend met hun problemen bij de surveillant aan te komen, voor vergeetachtige lieden pennen en potloden bij de hand hebbend).
Zorg dat de toets de stof goed dekt, door procedures als in hoofdstuk 5 te hanteren. Kom je daarmee nog niet goed uit, dan kun je proberen het aantal vragen uit te breiden (wanneer daar nog 'tijd' voor beschikbaar is). Misschien vraag je teveel berekeningen of teveel schrijfwerk waar je het even goed zonder zou kunnen doen: verbeteren van de vragen in dat opzicht geeft je gelegenheid om meer afzonderlijke vragen in de toets op te nemen. Op deze manieren kan het lukken deze speciale rol van het toeval, of de gevraagde onderwerpen behoren tot die stukken van de literatuur die de student wat beter of misschien juist wat minder goed bestudeerd heeft, terug te dringen.
Geluk of pech bij het raden van antwoorden is te vermijden door geen meerkeuzevragen te gebruiken wanneer dat niet door andere factoren (extreem grote aantallen deelnemers) opgelegd wordt. Voor raden kan nimmer gecorrigeerd worden, ook al suggereren talrijke in omloop zijnde procedures voor dergelijke correcties het omgekeerde. Dergelijke correctieformules geven een gemiddelde correctie, en dat is volstrekt oninformatief en kun je net zo goed helemaal achterwege laten.
Wordt er op grote schaal geraden, en is dat niet te voorkomen door andere vraagvormen te gebruiken, dan worden je toetsresultaten door die speciale vorm van het 'toeval' lelijk beïnvloed, waardoor de informatieve waarde vermindert. Je zou kunnen overwegen dat tegen te gaan met procedures die je in staat stellen vragen waarop de student het antwoord niet weet, er zelfs geen 'educated guess' naar weet te doen, ook als zodanig te identificeren. Het zou naief zijn om de student te vragen aan te geven op welke vragen hij maar een beetje heeft zitten gokken. Maar je zou het hem wel aantrekkelijk kunnen maken vragen waar hij het antwoord niet op weet dan ook maar helemaal niet in te vullen: gaat het om vierkeuze vragen dan zou je op het niet invullen van de vraag een bonus van punt kunnen zetten. Er is echter een nadeel aan dit handeltje verbonden: sommige studenten zullen er eerder toe neigen de 'bonus' te pakken dan andere, wat misschien als unfair zou kunnen worden gezien.
Wie De Groot en Van Naerssen (1969) er nog eens zorgvuldig op naleest, vindt er (p. 17) toch de aanbeveling om open gelaten keuzevragen altijd met een bonus te honoreren.
Belangrijke tests in de VS bieden tegenwoordig nadrukkelijk de mogelijkheid om keuzevragen open te laten. Er zijn twee methoden om daar bij het scoren van de vragen rekening mee te houden: ofwel een bonus toekennen, ofwel voor fout gemaakte vragen een punt aftrekken.
De stelling is verdedigbaar dat het niet ethisch verantwoord is om leerlingen te dwingen om toch te raden op vragen die zij niet weten, een gewoonte die in Nederland nog steeds wijdverbreid is. Al kan het meestal geen kwaad, er zijn juist rond de grens zakken-slagen vervelende complicaties denkbaar waar gedwongen raden een niet te verwaarlozen kans om te zakken oplevert, waar die anders niet zou bestaan.
Voor details over al dit gedoe rond raadkansen, zie hoofdstuk 2 van de herziene tekst Toetsvragen ontwerpen html.
Betrouwbaarheid is een begrip dat alles met deze toevalsinvloeden te maken heeft. De invloed van het toeval zorgt ervoor dat de score die de student op vergelijkbare toetsen, of op twee toetshelften krijgt zal variëren. Voor twee studenten zul je soms waarnemen dat de ene keer de ene, de andere keer de andere student de hogere score heeft. De mate waarin scores op deze wijze inconsistent zijn wordt de onbetrouwbaarheid van de toets genoemd. Zie ook bijlage A.
Neem je op basis van toetsscores zak-slaag-beslissingen, dan ken je in feite maar twee verschillende scores aan studenten toe: voldoendes en onvoldoendes. Betrouwbaarheid van de toets zou je dan op kunnen vatten als de mate waarin (bijvoorbeeld) vergelijkbare toetsen leiden tot dezelfde oordelen voldoende of onvoldoende.
Nu is het niet ongebruikelijk om als maat (schatting, of ondergrens) voor de betrouwbaarheid een index te gebruiken die eigenlijk helemaal geen betrouwbaarheidsindex is: de welbekende KR-20 geheten (Kuder-Richardson 1937, formule 20), bij computer-gescoorde toetsen als regel op de uitdraai vermeld. Ik geef de formule van deze KR-20 niet, de belangstellende lezer kan daarop naslaan: Gulliksen (1951), Van Naerssen (1975), Stanley (1971), Lord en Novick (1968), of het hoofdstuk betrouwbaarheid in de reader van Mehrens en Ebel (1967), waarin ook andere betrouwbaarheidscoëfficiënten behandeld worden.
Bestaat de leerstof nu uit niet al te zeer onsamenhangende onderdelen, dan wordt deze KR-20 als 'betrouwbaarheidscoëfficiënt' gebruikt, en dan wordt wel de vraag gesteld hoe hoog de waarde van KR-20 dan bij voorkeur zou moeten zijn. Van Naerssen (1975, blz. 263) suggereert dat de docent tevreden mag zijn met een coëfficiënt in de buurt van 0,8 (het maximum is l,0), en voegt daaraan toe:
Omdat het in het onderwijs niet gaat om het rangschikken van personen ten opzichte van elkaar is dat deel van Van Naerssen's uitspraak eenvoudig niet van toepassing. Blijft over: kun je beslissingen nemen op basis van toetsscores waarvan de KR-20 'laag' is?
Bij traditionele examenregelingen is het de student erom te doen boven de cesuur te scoren, te 'slagen' voor de toets. Hij moet tevoren goed in kunnen schatten wat zijn kans om te slagen is, gegeven wat hij denkt dat zijn beheersing van de stof is. De student die zijn slaagkans niet groot genoeg vindt, zal nog even doorgaan met de voorbereiding op de toets, totdat hij denkt een voldoend grote slaagkans te hebben.
Voor de docent zijn dit soort overwegingen bij de student ook van belang: immers, verlaagt hij de cesuur dan zullen studenten eerder het punt bereiken waarop ze denken wel een voldoende slaagkans te hebben. Misschien nemen studenten dan ook genoegen met een wat kleinere slaagkans, of wordt juist een hogere slaagkans aantrekkelijk (dat is door onderzoek uit te maken). Door het verschuiven van de cesuur (maar ook door verbeteren van de toetskwaliteit) beïnvloedt de docent het gedrag van de studenten, en daarmee het gemiddeld niveau van stofbeheersing dat studenten voor zijn vak bereiken.
Welnu, noch bij de overwegingen van de student, noch bij die van de docent speelt de betrouwbaarheidscoëfficiënt KR-20 enige rol van betekenis. Zie verder ook bijlage A, figuur A.l.
Voor de student is van belang de nauwkeurigheid waarmee hij zijn ware stofbeheersing kan schatten, en de nauwkeurigheid waarmee hij vervolgens zijn te verwachten toetsscore kan schatten. De eerste is afhankelijk van informatie en oefening vooraf, de tweede is afhankelijk van het aantal vragen in de toets. In jargon: hier gaat het om de standaardmeetfout voor de gegeven student (zie hoofdstuk 8).
Voor de docent gaat het om de nauwkeurigheid waarmee hij de ware stofbeheersing van de student (beter: de groep studenten) kan schatten op basis van de toetsscores. Of die schatting bevredigend zal zijn of niet heeft op zich niets met de hoogte van KR-20 te maken. Zie ook hier het in hoofdstuk 8 behandelde.
Het gaat hier niet om revolutionaire inzichten. Ik citeer de Richtlijnen (1978):
Heb je de keuze tussen twee toetsen die even valide, maar ongelijk in betrouwbaarheid zijn, dan zal vaak de minder betrouwbare toets de voorkeur hebben: deze levert bij verlenging waarschijnlijk de grootste 'winst' in extra validiteit. Zie ook Stanley (1971).
Laat je nimmer in de verleiding brengen gebruik te maken van de opties die sommige computerprogramma's bieden: de waarde van KR-20 te verhogen door bepaalde items uit de toets te verwijderen. Ten eerste is het streven naar een hogere KR-20-waarde op zich al een twijfelachtige zaak. Ten tweede worden items 'verwijderd' die misschien louter toevallig een p-waarde of een r-bis-waarde hebben beneden de willekeurig door de maker van het programma vastgestelde grens. Ten derde is die hogere KR-20-waarde gedeeltelijk 'fake', en zul je na moeten gaan op een groep andere studenten of KR-20 met de nu verkorte toets (eventueel aangevuld met nieuwe vragen) inderdaad hoger is (Zie ook Cureton 1950 op dit punt). Tenslotte zijn de 'afwijkende' vragen die verwijderd worden nogal eens precies die vragen die je juist bedacht had om te toetsen of de student zijn inzichten ook in wat meer complexe of ongestructureerde problemen kan toepassen; weglaten van deze vragen zou de heterogeniteit van de toetsvragen verminderen, daardoor KR-20 verhogen ... en een minder valide toets opleveren vanwege verminking van de representatie van je onderwijsdoelen in de toets.
Vooral in Nederlandse literatuur wordt het gebruiken van meerkeuzevragen nogal eens aangeraden als wapen in de strijd tegen subjectiviteit van beoordelen, tegen toevalsinvloeden, tegen onbetrouwbaarheid. Meerkeuzevragen zouden de ideale eigenschap hebben 'objectief' te zijn. Hoera, dus, deze vraagvorm zou ons kunnen verlossen van het spook van de subjectieve beoordeling, van de ene docent die het met de andere niet eens is, de docent die er vandaag nog zus, morgen misschien zo over denkt?
Niets is minder waar. Meerkeuzevragen zijn al even subjectief als open-eindvragen, invulvragen, kort-antwoordvragen of hoe u ze ook mag noemen: al die vragen waarbij de student het antwoord moet produceren, en dat antwoord vervolgens door een beoordelaar gescoord wordt.
O zeker, meerkeuzevragen hebben het gemak dat antwoordformulieren aan de computer gevoerd kunnen worden, en die zal in 999 van de 1000 gevallen de antwoorden exact scoren zoals de scoringssleutel voorschrijft. Maar wie maakt die scoringssleutel? Precies, de scoringssleutel is ook maar een menselijk product, en eenmaal vastgesteld zou je kunnen zeggen dat de 'objectiviteit' van de scoringssleutel niets meer is dan de bevroren subjectiviteit van de opsteller ervan.
Automatische scoring is op zich geen enkele waarborg tegen slechte vragen, tegen ambigue vragen, tegen vragen met meerdere juiste alternatieve in plaats van die ene in de sleutel, en biedt zelfs geen waarborg tegen fouten in de sleutel zelf. In principe kun je de mate van 'subjectiviteit' van een meerkeuzetoets onderzoeken met behulp van de procedures in hoofdstuk 4 aangegeven. Wanneer je de meerkeuzevraag aan collega's voorlegt als open-eindvraag, zou wel eens kunnen blijken dat die collega's meerdere juiste antwoorden weten te produceren. Zou je ondanks dat feit het item als meerkeuzevraag handhaven met maar één van die mogelijke goede antwoorden als het juiste alternatief, dan heb je een evident subjectief item. Andere mogelijkheden waarop zo'n meerkeuzevraag subjectief kan zijn laten zich makkelijk raden.
Een heel ander gevaar dat juist bij meerkeuzevragen dreigt is dat dit meerkeuze-keurslijf niet voor alle (delen van je) leerstof geschikt is. Past de meerkeuzevraagvorm niet goed bij de stof en dat wat je er over zou willen vragen, dan kan dat leiden tot vergaand gekunstelde vragen, waar van de student intellectuele capriolen worden gevraagd waarop hij zich nimmer heeft kunnen voorbereiden. De docent kan de nattigheid meestal wel voelen wanneer hij moeite heeft met het vinden van goede afleiders, foute alternatieven. Ik verwijs terug naar hoofdstukken 2 en 3.
Meerkeuzevragen zijn dus niet 'objectiever' dan open-eindvragen. En inderdaad zien we dat amerikaanse auteurs het woordje 'objectief' zo gebruiken dat beide vraagvormen eronder vallen, die daarme gecontrasteerd worden met de meer subjectieve essayvragen. Misschien hebben Nederlandse schrijvers een wat bredere opvatting van wat 'subjectief' is: dat de beoordelaar zich mede zou laten leiden door wat hij overigens meent te weten over het kennen en kunnen van de student van wie hij het werk nakijkt. Tenslotte hebben we hier nog niet zo lang de tijd achter ons dat het mondeling de dominante wijze van toetsen was, met de uitwassen die daaraan inherent schenen te zijn, of dat althans in de geruchtvorming onder studenten waren.
Op grond van toetsscores worden soms beslissingen genomen die voor de student ernstige gevolgen kunnen hebben. Denk aan zakken voor een examen op grond van die ene onvoldoende, verlies van een studiebeurs door een enkel tegenvallend toetsresultaat, verlies van de vacantie door de verplichting die onvoldoende te herkansen, en dergelijke. Dat werpt dan ook de vraag op welke maatregelen de docent heeft te treffen om toetsing en daarop te nemen beslissingen op verantwoorde wijze te laten verlopen, en welke mogelijkheden de student heeft om tegen een als onjuist of onrechtvaardig ondervonden behandeling in verweer te komen. Nicolai (Folia Civitatis 11 mei 1974):
Welke mogelijkheden staan de student ter beschikking om beroep aan te tekenen tegen over hem genomen beslissingen, of om te protesteren tegen de bij de beoordeling gevolgde werkwijze? Cohen (1978):
Gaat het echter om beslissingen op grond van tentamens waartegen de student beroep aantekent, dan kan de student gebruik maken van artikel 40 van de Wet Universitaire Bestuurshervorming 1970:
Op deze formulering zijn talrijke varianten in omloop bij bijzondere universiteiten waarvoor art. 40 WUB niet geldt, en in facultaire reglementen. Zie voor de juridische aspecten ook Verpaalen (1978). Hoe moet het verder wanneer de student tegen de uitspraak van zo'n geschillen kommissie bezwaar wil aantekenen? Cohen (1978):
Job Cohen is later op dit onderwerp gepromoveerd: M. J. Cohen (1981). Studierechten in het wetenschappelijk onderwijs. Zwolle: Tjeenk Willink.
Het is duidelijk dat een en ander vooral speelt waar het om zak-slaag-beslissingen gaat, daarvoor verwijs ik naar de cursus Cesuurbepaling html. Maar er zijn ook bij het samenstellen van de toets, en de inrichting van het onderwijs waarvan de toets de afsluiting vormt, een aantal zaken waar de docent speciaal op heeft te letten waar het gaat om behoorlijk bestuur, de rechten van de student.
Vanuit onderwijskundig, en niet vanuit juridisch, standpunt bekeken wil ik hier een aantal aanbevelingen doen, gekoppeld aan een aantal van die Algemene Beginselen van Behoorlijk Bestuur, de ongeschreven rechtsbeginselen waarnaar men zich bij het bestuurlijk handelen te richten heeft. Zie voor een inleiding op deze Beginselen Van Wijk en Konijnenbelt (1976).
Het is inherent aan 'in het algemeen rechtsbewustzijn levende beginselen van behoorlijk bestuur' dat die niet veranderen wanneer nieuwe wetgeving de oude vervangt. Dat laatste is in latere jaren natuurlijk gebeurd. Het recht van beroep bij een College van Beroep voor de Examens, een CoBEx, is blijven bestaan voor universitaire instellingen; in het HBO bestaat meen ik een overeenkomstige regeling, terwijl in het voortgezet onderwijs er meestal volgens het leerlingenstatuut een klachtencommissie zal zijn die bezwaren in behandeling kan nemen (maar gebeurt dat ook? Ik hoor dat graag).
fair play. Door overigens formeel-wettelijk correct te handelen, zou de overheid de burger mogelijkheden om voor zijn belang op te komen kunnen ontnemen. Het beginsel van fair play houdt in dat zo'n handelwijze niet toelaatbaar is.
Het belang van de student is o.a. dat hij in staat gesteld wordt in beroep te gaan tegen de toetsuitslag, en daarvoor moet hij over alle relevante gegevens beschikken: de gestelde vragen, de scoringssleutel, de door hem gegeven antwoorden, de wijze waarop deze gescoord zijn. Zou de docent de vragen ook na de toetsing geheim willen houden, dan ontneemt hij de student een belangrijke mogelijkheid om tegen een mogelijk onjuiste uitslag bezwaar aan te tekenen, omdat de student niet in staat is de juistheid van de uitslag te controleren.
In ik meen 1980 heeft het College van Bestuur van de Universiteit van Amsterdam besloten dat tentamenwerk door de student moet kunnen worden ingezien. De formulering was waarschijnlijk een iets andere: dat oude tentamenvragen openbaar gemaakt moeten worden. Dat laatste gaat verder dan wat 'fair play' strikt genomen vraagt, de motivering daarvoor is dat het recht op inzage een strikte geheimhouding van oude vragen onmogelijk maakt, en dan is het beter om ongelijke informatie vaan studenten te voorkomen door oude vragen gewoon voor iedereen toegankelijk te maken. Een en ander was zeer tot verdriet van docenten die met een klein aantal 'geheim' veronderstelde toetsvragen werkten: zij moesten nu echt telkens een nieuwe set vragen ontwerpen. Vandaar dat de verdere uitwerking van deze cursus Toetsen uitliep op een op het ontwerpen van toetsvragen toegespitste onderwijndige Aula 809, in 1983.
zorgvuldigheid. Het gaat om de 'zorgvuldige voorbereiding van de beschikking en het in aanmerking nemen van alle factoren en omstandigheden die van belang kunnen zijn'. Naar het onderwijs en de toetsing vertaald gaat het er dan om dat de kwaliteit van de toets als geheel en van de afzonderlijke vragen op voldoende niveau staat, daar door de docent de nodige zorg aan is besteed (par. 6.5 richtlijnen).
zuiverheid van oogmerk. Het bestuur mag een bevoegdheid alleen gebruiken voor het doel waarvoor die bevoegdheid is gegeven. Dat betekent heel concreet dat je niet door bepaalde maatregelen rond de toetsing het bezoeken van je college mag proberen op te vijzelen (in de toets opnemen van vragen die alleen door trouwe collegebezoekers te beantwoorden zijn, omdat de nodige informatie niet in de syllabus werd opgenomen). Ook kun je van de docent verlangen dat hij geen vragen in de toets opneemt die niet de voor die toets opgegeven leerstof bestrijken (geen intelligentietest-achtige vragen in de toets opnemen dus). Het afwijzen van studenten, niet op grond van gebleken ongeschiktheid, maar om het aantal studenten terug te dringen; niet meer studenten te laten slagen dan het vervolgonderwijs (een practicum bijvoorbeeld) direct kan opnemen, en dergelijke is handelen in strijd met dit beginsel.
vertrouwen. Gewekte verwachtingen worden gehonoreerd. Gemaakte afspraken, gedane toezeggingen worden nagekomen. In de toetsing en de wijze van beslissen worden niet onaangekondigd ingrijpende veranderingen aangebracht. Gebleken fouten en tekortkomingen in de toets of afzonderlijke vraagformuleringen worden de student niet toegerekend. Wanneer bij een serie toetsen tussentijds resultaten aan de docent bekend zijn, maakt hij ze ook aan de studenten bekend. De aan de student te geven informatie vooraf over de aard van de toetsing dient in alle opzichten correct te zijn.
De toenemende invloed van het overheidshandelen op het dagelijks leven van de burger leidde tot het recht waarin de juist besproken algemene beginselen van behoorlijk bestuur een belangrijke plaats zijn gaan innemen. Iets dergelijks deed zich voor bij het steeds grootschaliger test- en toetsgebruik. Ook hier groeide de behoefte aan waarborgen voor toetskwaliteit, en explicitering van de zorgvuldigheid die bij het beslissen over personen in acht is te nemen.
Commissies uit beroepsorganisaties van psychologen en onderwijskundigen in de verenigde staten brachten de belangrijkste normen voor toetsconstructie, toetsafname, en gebruik van toetsresultaten bij het beslissen over personen, bijeen in de brochure Standards for Educational and Psychological Tests, waarvan de derde editie, voorzien van een extra hoofdstuk over het gebruik van tests en toetsen, in 1974 uitgebracht werd. Het Nederlands Instituut van Psychologen verzorgde er een bewerking van: Richtlijnen voor ontwikkeling en gebruik van psychologische tests en studietoetsen.
Aan deze Richtlijnen zijn niet alleen psychologen en onderwijskundigen gebonden, maar [in beginsel] ook docenten die op welke wijze dan ook bij de beoordeling van (het werk van) studenten zijn betrokken.
Het oordeel of in bepaalde gevallen de toetsing op correcte en rechtvaardige wijze is uitgevoerd zal zich in veel gevallen niet tot een strikt juridische beschouwing kunnen beperken, omdat vaak ook toetstechnische zaken in het geding zullen zijn. Dan stelt zich de vraag naar de technische eisen die je ten aanzien van de kwaliteit van de toetsing mag stellen, en waar de docent de verantwoording voor draagt dat er aan voldaan is. In de verenigde staten baseert het Supreme Court zich meer en meer op de Standards als autoriteitsmaatstaf waar dergelijke technische vraagstukken in het geding zijn (Lerner, 1978). In ons land is de aandacht voor een behoorlijke wijze van toetsen nog aan het groeien, en zal het weinig verbazen dat in de discussie over artikel 40 WUB uitsluitend juridische (Verpaalen 1978) en nog nauwelijks toetstechnische problemen (maar zie De Groot 1970) een rol spelen.
In het volgende zal ik die richtlijnen parafraseren die vooral van belang zijn voor de docent die zijn eigen toets maakt, afneemt, en analyseert. (nummers verwijzen naar de betreffende aanwijzing in zowel Standards als Richtlijnen).
Concreet betekent dat, dat de docent het materiaal in een cursus als deze, en in het bijzonder dat in hoofdstuk 8, in zijn intellectuele bagage moet hebben. Met name moet hij inzicht hebben in wat meetfouten zijn, hij moet verkregen scores kunnen interpreteren (zie hoofdstuk 8), hij moet beseffen dat een bepaalde score mogelijk op verschillende manieren bereikt kan worden, wat voor de interpretatie van belang is (zie ook paragraaf 6.1). Een cursus over toetsen zoals de onderhavige is voor de docent geen facultatief nummer, hij is aanspreekbaar op beheersing van dit materiaal.
Zo is het geenszins vanzelfsprekend dat je ieder stuk onderwijs ook met een toetsing afsluit. De relatie tussen de vaardigheden die je toetst en hetgeen je onderwezen hebt moet duidelijk zijn. In het bijzonder geldt een en ander ook voor het gebruik van zak-slaag grenzen, ofwel cesuren:
Het geven van een rechtvaardiging voor een bepaalde cesuur is geen sinecure. Het is niet voldoende te zeggen dat je een bepaalde methode gebruikt hebt om tot de cesuur te geraken (kernitem-methode, methode-Wijnen, en dergelijke), dat stelt je vervolgens voor de opgave te beargumenteren waarom je voor een bepaalde methode gekozen hebt, en dat de gekozen methode ook werkelijk functioneert zoals bedoeld (en het laatste kan bijvoorbeeld bij die kernitem-methode wel eens onmogelijk blijken). Het is mogelijk een en ander kort te sluiten door over de plaats van de cesuur een afspraak met de studenten te maken. Ik verwijs verder naar de cursus Cesuurbepaling (Wilbrink, 1980).
Dat betekent dat de docent ervoor zorgt dat de toetsvragen niet tevoren uitlekken, waardoor sommige studenten een voordeeltje zouden hebben dat andere niet hebben. Hij houdt achteraf de toetsvragen niet geheim met het doel ze later nog eens te kunnen gebruiken, omdat ook daardoor sommige studenten (die wél over die oude vragen weten te beschikken) een voordeel zouden verkrijgen over andere studenten. In paragraaf 6.2 is gewezen op de omstandigheden die een goede prestatie van de deelnemers aan de toets bevorderen.
Ook wanneer het nakijken gedelegeerd is aan assistenten, of wanneer scoring per computer gebeurt, heeft de docent er voor te zorgen dat er geen fouten gemaakt worden; dat betekent dat de scoring per automaat gecontroleerd moet worden door een steekproef uit de antwoordvellen te nemen en die met de hand te scoren. Handig en verstandig is het altijd om studenten alle informatie te geven die nodig is om het eigen werk te kunnen nakijken en scoren, zodat de student eventuele scoringsfouten ook zelf kan signaleren.
Bij opstellen, werkstukbeoordeling, mondeling en dergelijke, moet de docent aannemelijk kunnen maken dat verschillende beoordelaars het in redelijke mate met elkaar eens zijn, althans dat een procedure is gevolgd waarbij de student het voordeel van de twijfel krijgt. Zie ook hoofdstuk 7.
Dat betekent: geen mondeling afnemen met daarbij de kaart met de studiegegevens van de student op tafel. De score voor deze toets behoort uitsluitend door de op die toets verkregen gegevens bepaald te worden. Dat neemt niet weg dat een examenbeslissing natuurlijk op overwegingen betreffende alle behaalde toetsresultaten gebaseerd is. Er is discussie mogelijk over hoe ver je moet gaan, mag gaan: mag je bijvoorbeeld de resultaten van de groep gebruiken om tot een gewijzigd (beter?) oordeel voor het individuele geval te komen? Dergelijke procedures, als ze al gevolgd worden, zullen tenminste goed beargumenteerd moeten worden. Bij die argumentatie zullen de kosten en baten van de procedure, zowel voor de instelling als voor de betrokken individuele personen (en de samenleving) betrokken moeten worden. Dit punt speelt met name ook daar waar cesuren op basis van groepsgegevens bepaald worden, dus ook bij criterium gerefereerde toetsing bijvoorbeeld.
Maak je geen gebruik van objectieve vraagvormen, zoals open-eindvragen of meerkeuzevragen, dan word je geconfronteerd met een aantal bijzondere problemen waar het de beoordeling betreft. Spectaculaire resultaten rollen nogal eens uit onderzoek naar de mate waarin verschillende beoordelaars het met elkaar oneens zijn. Wat minder opvallend, maar voor de onderwijspraktijk misschien van groter belang, is het feit dat je met enkele essayvragen meestal maar een deel van de leerstof kunt bestrijken, zodat de toevallige keuze van onderwerpen nogal wat invloed kan hebben op de score van de individuele student.
Een indruk van de problemen die zich kunnen voordoen bij de beoordeling van essays of werkstukken, en zeker ook bij mondelinge toetsing, geven de 'retrospecties' die Mellenbergh vroeg aan een aantal beoordelaars (Mellenbergh 1971):
Beoordelaars verschillen nogal in hun opvattingen over hoe je essayistische antwoorden kunt, mag, of moet waarderen. Daarnaast zal de ene beoordelaar strenger zijn dan de andere, meer gebruik maken van de héle beschikbare scoreschaal of cijferschaal. Dat houdt risico's in zich van een unfaire beoordeling van (sommige) studenten, risico's waartegen je je kunt wapenen door bepaalde, zorgvuldige procedures bij die beoordeling te volgen.
Dezelfde problemen bij het beoordelen doen zich uiteraard ook voor wanneer het om werkstukken gaat. Ik ontleen aan Tromp (1979) de gegevens in tabel 7.1: drie instructeurs beoordeelden onafhankelijk van elkaar de werkstukken van studenten in een tandheelkundig practicum. Daarbij werden 15 criteria gehanteerd, de score is het aantal criteria waaraan het werkstuk voldoet. (De gegevens van Tromp zijn uitgebreider dan wat ik er hier bij wijze van illustratie van weergeef).
---------------------------------------------------------- werkstuk: 1 2 3 4 5 6 7 8 9 10 --------------------------------------------------------- instructeur a 8 11 14 7 10 11 7 14 9 10 instructeur b 8 14 9 9 11 14 12 9 9 12 instructeur c 6 9 6 13 10 14 13 8 11 9 --------------------------------------------------------- hoogste oordeel 8 14 14 13 11 14 13 14 11 12 laagste oordeel 6 9 6 7 10 11 7 8 9 9 ----------------------------------------------------------
Dit soort beoordelingsproblemen doen zich niet alleen voor bij toetsing, maar bijvoorbeeld ook in de medische en psychologische diagnostiek. Ook de exacte wetenschappen zijn er niet van verschoond. Een bekend geval uit de astronomie was dat waarnemers stelselmatig konden verschillen in hun tijdmetingen. Opgemerkt door de koninklijke astronoom, de heer Maskelyne, in Greenwhich in 1795, leidde dat in eerste instantie tot ontslag van zijn 'afwijkende' medewerker Kinnebrook (verschil: bijna een seconde), in tweede aanleg tot verder onderzoek door Bessel, en een voortdurende belangstelling voor dit probleem in de vorige eeuw. De astronomische waarneming betrof het tijdstip waarop een hemellichaam een bepaalde lijn in het gezichtsveld van de man achter de teleskoop kruist. Verschillen bij die meting bleken voor dezelfde waarnemer tamelijk constant te zijn, zodat je er enigszins voor kon corrigeren. Beter zou het zijn om de waarneming te objectiveren, onafhankelijk van de menselijke waarneming te maken, wat inderdaad spoedig lukte. Eenzelfde probleem doet zich vandaag de dag op andere onderzoekgebieden ook nog wel voor, zie bijvoorbeeld Draper en Guttman (1975).
Er zitten voldoende nadelen vast aan deze essaytoetsing om het de moeite waard te maken te zoeken naar mogelijkheden om op meer objectieve toetsingsvormen over te gaan. Dan moet de aard van de leerstof en de doelstellingen van je onderwijs dat wel mogelijk maken. Een voorbeeld van een essayvraag die goed door objectieve vragen te vervangen bleek geeft Ebel (1979). De vraag stamt uit een cursus prothetische tandheelkunde:
De verantwoordelijke docent schreef een modelantwoord van bijna 500 woorden uit, waarin ook nogal wat motivatie opgenomen was (waarom een bepaalde handeling wel, andere niet), en te vermijden fouten en risico's genoemd werden. De hierin beschreven handelingen konden beter afzonderlijk gevraagd worden in open-eind- of meerkeuzevragen, waarvan Ebel (p. 139) er een aantal laat zien (het jargon maakt ze wat minder illustratief).
In andere disciplines ligt een mogelijke objectivering misschien wat minder voor de hand. Hoe zou je dat bijvoorbeeld kunnen doen met casus zoals die de rechten student voorgelegd worden? Crombag en anderen (1972) hebben geprobeerd op die bijzondere problematiek greep te krijgen. Zij waren in staat het oplosproces in een aantal specifieke deelstappen op te splitsen, waarmee in beginsel de mogelijkheid gegeven is om casus op te splitsen in een aantal objectieve (bijvoorbeeld open-eind-) vragen. In dit geval zou je als alternatief kunnen overwegen om studenten te oefenen in het deelstapsgewijze oplosproces, het algoritme, zodat zij betere casusoplossers worden. Zo'n algoritmisering kan voor veel vakken zijn nut hebben, zie ook Landa (1976). Het vinden van dergelijke algoritmen is niet altijd even makkelijk, zoals het verslag van Crombag et al. ook laat zien. De schakende docent zou in dit verband het werk van De Groot (1978) over denkprocessen bij schakers er eens op na kunnen slaan. Voor ieder vak zal het nodige ontwikkelingswerk telkens afzonderlijk verricht moeten worden.
Er is nogal wat speurwerk verricht naar de vraag of je met essay toetsen hetzelfde meet als met objectieve toetsen. Zonder eenduidige resultaten, zoals Mellenbergh (1972) in een overzicht laat zien. En daar hoeven we ons niet over te verbazen: beide vormen van toetsen zijn nu eenmaal niet even geschikt voor eenzelfde soort leerstof. Leerstof die zich bij uitstek leent voor een bepaaldde toetsingsvorm ga je niet in het keurslijf van een ongeschikte vorm persen. Zie ook het besprokene in hoofdstukken 2 en 3. De vraag of je met essays en met objectieve vragen hetzelfde meet kan alleen maar interssant zijn wanneer jouw leerstof zich voor beide even goed leent, en je bovendien mag verwachten van de specifieke nadelen van essay toetsing niet al te veel last te hebben. En dat zal zelden voorkomen, zodat ik me ontslagen acht van de noodzaak dat onderzoek hier te bespreken. Met één uitzondering:
Het overwegende bezwaar tegen indirecte toetsing is dat het inherent ondoorzichtig is. Studenten kunnen zich er moeilijk effectief op voorbereiden. Het zal studenten ook lastig uit te leggen zijn dat je met zo'n indirecte toetsing hetzelfde meet als bij directe toetsing (of beoordeling), en ook docenten zullen dat vaak niet inzien, zoals ik het ook niet inzie, ook al zouden de onderzoekcijfers wel in die richting wijzen. Het is maar de vraag hoe studenten in hun studiegedrag zullen reageren op dergelijke gecastreerde toetsingsbenaderingen. Het voordeel van indirecte toetsing, hogere scoringsbetrouwbaarheid (maar wat is dat waard?), wordt overigens waarschijnlijk gekocht tegen de prijs van een lagere, althans niet hogere, validiteit van de toets (Coffman, 1966).
Helemaal te gek wordt het wanneer het scoren van essays aan de computer gedelegeerd wordt, die let dan op 'objectieve kenmerken' van essays die gecorreleerd blijken te zijn (= samenhangen met) de kwaliteit zoals beoordelaars die inschatten. Dan worden punten en comma's geteld, het gebruik van cijfers en eigennamen, etcetera. Mellenbergh (1971, p. 25) bespreekt zo'n onderzoek waarin de computer het even goed of zelfs beter dan 'menselijke' beoordelaars blijkt te doen. Dit is niet de richting waarin we het moeten zoeken.
Valt er niet aan essayvragen te ontkomen, dan zorg je er voor dat de toetsing zo doorzichtig mogelijk is, dat studenten zich er effectief op voor kunnen bereiden. Bedenk dat de grootste bron van troebelheid ligt in de uiteenlopende opvattingen die de verschillende beoordelaars er op na kunnen houden over wat nu de kwaliteiten van een 'goed' essay zijn. Ik wil dat nog eens illustreren aan de onderzoeksresultaten van Linn, Klein en Hart (1972) die de beoordeling van een juridische casus door 17 docenten onderzochten:
De implicatie van de commentaar van Linn e.a. is dat de studenten niet op de hoogte waren van de wijze waarop hun werk beoordeeld zou worden. Daar komt bij dat ook de beoordelaars zich er niet goed rekenschap van blijken te geven op welke aspecten zij een werkstuk plegen te beoordelen. Wat het laatste betreft is het aan te raden beoordelaars om een schriftelijk verslag te vragen over de wijze waarop zij in het algemeen het werk hebben nagekeken, ongeveer zoals de retrospecties waar Mellenbergh (1971) de beoordelaars naar vroeg.
Het effect van het vragen naar retrospekties is tweeledig. De opdracht alleen al zal er de beoordelaar op attent maken dat hij misschien een speciale stijl van beoordelen heeft. Het schriftelijk verslag geeft de docenten gezamenlijk de gelegenheid vat te krijgen op de beoordeling: bepaalde beoordelingsaspecten kunnen benaderukt worden, andere expliciet achterwege gelaten. Zo is een vaak terugkerend punt dat gelet wordt op de 'netheid', op taal en stijlfouten, structuur van de presentatie. Dat mogen op zich geen onbelangrijke zaken zijn, ze kunnen echter alleen voor beoordeling in aanmerking komen wanneer een en ander tot de doelstellingen van het onderwijs hoort. Zoals bij het gebruik van vakterminologie van de student een correcte spelling verwacht mag worden. De vormgeving van het essay, de structuur en geordendheid van de presentatie, staan niet ter beoordeling tenzij het gaat om vormaspecten die ook onderwezen zijn. In het andere geval doe je namelijk sommige studenten onrecht, omdat het hier gaat om verschillen tussen studenten in het vermogen zich verbaal uit te drukken: veeleer een persoonlijke eigenschap dan het resultaat van een correcte studie-inspanning.
Eén van de beoordelaars van Mellenbergh (1971) had veel waardering voor studenten die de structuur van het antwoord goed op kunnen zetten. Maar diezelfde docent heeft vrijwel zeker geen onderwijs daarin gegeven, en dan is het onrechtvaardig tegenover andere studenten die weliswaar correct antwoorden, maar er niet die structuur in hebben gebouwd die deze docent zo aanspreekt. Ik druk me met opzet oneerbiedig uit, want het gaat hier nu precies om het soort subjectiviteit dat we proberen terug te dringen door naar zo objectief mogelijke toetsingsvormen te zoeken.
Het is van belang al die beoordelingscriteria uit te wieden die op zich niets met de doelstellingen van je onderwijs te maken hebben. Juist bij essays, omdat nogal eens gemeend wordt dat je die op algemene maatstaven zou moeten beoordelen, in plaats van specifiek op het gegeven onderwijs betrokken criteria. Op gevaar af de lezer te gaan vervelen geef ik hier nog een citaat waarin het belang van dit adagium overduidelijk gedemonstreerd wordt in de opsomming van redenen waarom beoordelaars zo kunnen verschillen in hun scoring. Bhushan en Ginther (1968):
En dat geldt zowel voor het opstel in de eigen taal, als voor de wijze waarop wiskundige bewijzen geleverd of opgaven gemaakt worden: ook daar is er ruimte voor subjectiviteit in de beoordeling, of de oplossing meer of minder elegant is, of er heuristische shortcuts gevonden zijn dan wel moeizame algoritmische uitwerkingen, of er overzichtelijk gewerkt is dan wel een chaotisch volgeschreven pak papier ingeleverd wordt.
Zijn essayvragen de enige passende toetsingsvorm bij jouw leerstof, zorg er dan voor dat de vragen kwalitatief goed in elkaar zitten (hoofdstuk 4), en besteed grote zorg aan nakijken en waardering van de essay antwoorden.
Stel voor iedere vraag een modelantwoord op, met daarin alle inhoudelijke punten die voor een volledige of een goede beantwoording vermeld moeten worden. Houd rekening met alternatieve antwoorden die ook (gedeeltelijk) goed zijn. Al naar gelang daaraan behoefte is, vermeld je speciale punten zoals bepaalde fouten die in ieder geval niet door de student gemaakt zouden mogen worden, of een onderscheid naar kernpunten en bijzaken.
Vraag bij het vooraf controleren van de essayvragen aan je collega's om hun antwoord te geven in de vorm van zo'n modelantwoord.
Het is niet moeilijk om vragen te bedenken die meer (schrijf)tijd vragen dan de student straks krijgt. Let daar in het bijzonder op bij de controle-vooraf op.
Bekijk ook mogelijkheden om de vraag zo te formuleren dat de beantwoording korter kan zijn. Dat heeft het voordeel dat de tijdwinst die daaruit resulteert gebruikt kan worden om meer vragen te stellen, waardoor de score van de student minder afhankelijk,wordt van de toevalligheden die voortvloeien uit een klein aantal onderwerpen waarop de toetsing plaats vindt.
Verschillen in wetenschappelijk inzicht laten zich niet 'middelen'. Evenmin is het terecht om dat te doen met beoordelings verschillen die te maken hebben met verschillende opvattingen van de betrokken beoordelaars.
Het nakijken van essay antwoorden bestaat uit twee te onderscheiden stappen: het beoordelen van de mate van volledigheid van het antwoord, en het vervolgens waarderen van dat antwoord. Het hangt van de opzet van het modelantwoord af hoe de eerste beoordeling uitgevoerd kan worden. Bestaat het uit een opsomming van onderwerpen die tenminste genoemd moeten zijn, dan kun je op een scoringsformulier aangeven welke ook door de student genoemd zijn.
Dan is deze inhoudelijke beoordeling of scoring nog om te zetten in een waardering, of in een aantal toe te kennen punten. Stel daar zo eenvoudig mogelijke regels voor op, als het even kan door gewoon tellen van aantal genoemde onderwerpen uit het modelantwoord. Is het ene onderwerp belangrijker dan het andere, dan kan daar een simpele weging voor gebruikt worden (bijvoorbeeld 2 punten voor meer, 1 punt voor minder belangrijke of kernachtige onderwerpen). Zo is voor ieder essayantwoord de puntenwaardering toe te kennen.
Essayvragen verschillen nogal eens van elkaar in omvang en tijdbeslag. Ook dat wil je in de puntentelling tot uitdrukking brengen door de ene vraag zwaarder te wegen dan de andere. Vind je zoiets nodig, beperk je dan tot een eenvoudige weging, probeer niet om daar subtiel in te zijn.
Controleer achteraf hoe de beoordelaars met modelantwoorden en waarderingsvoorschriften hebben gewerkt, en breng aan de hand van deze bevindingen eventueel correcties in puntentoekenningen aan.
Latere ontwikkelingen naar meer bureaucratisering van de beoordeling hebben het gebruiken van modelantwoorden verabsoluteerd. Het middel is daarmee erger geworden dan de kwaal. Zoals uit tal van hierboven gegeven citaten mag blijken, gaat het er bij de eerlijkheid van de beoordeling van essayvragen niet zozeer om of detail A en X wel in het antwoord voorkomen, maar of de ene beoordeelaar bepaalde stijlaspecten in het oordeel betrekt, een andere weer andere, etcetera.
Een enorme misvatting die ik ten onrechte in deze paragraaf niet heb gesignaleerd, is het volgende. Een gedetailleerd antwoordmodel is op zichzelf nog geen waarborg van objectiviteit, omdat het een specifieke opvatting of uitwerking tot norm kan verklaren. Dat is precies hetzelfde probleem dat eerder bij het bepalen van de sleutel voor keuzevragen is besproken: dat heet frozen subjectivity.'
Inherent aan veel modelantwoorden is dat punten worden toegekend voor deelkennis. Het is niet vanzelfsprekend dat dit een verstandige manier van beoordelen is: het kan oppervlakkig bestuderen van de stof uitlokken, ook waar het de bedoeling is dat meer complexe vraagstukken in hun geheel goed aangepakt en uitgewerkt kunnen worden. Voor modelvorming: zie mijn 1998.
Ook bij in alle opzichten zorgvuldige procedures zullen verschillende beoordelaars tot afwijkende resultaten komen. Soms tot behoorlijk afwijkende resultaten. Op zich hoeft dat niet erg te zijn, het kan zelfs kenmerkend voor het vak in kwestie zijn dat er nogal enig verschil van inzicht bestaat tussen vakdeskundigen. Maar dat neemt niet weg dat je er naar moet streven ondanks dergelijke beoordelingsverschillen het werk van de student eerlijk te waarderen.
In de praktijk wordt als regel al de procedure gehanteerd ieder werkstuk door tenminste twee beoordelaars na te laten kijken. Het spreekt vanzelf dat de eerste beoordelaar geen aantekeningen op het werk maakt, om de tweede beoordelaar ook de kans op een onafhankelijke scoring en waardering van hetzelfde werk te geven. Al even vanzelfsprekend is dat beoordelaars onafhankelijk van elkaar werken, en tijdens het werk niet met elkaar daarover overleggen.
Spreek van tevoren af hoe de puntentoekenning zal zijn in die gevallen waarin beoordelaars op verschillende puntentallen uitkomen. Geef bij voorkeur de student het voordeel van de deskundige onenigheid, en ken het hoogste gegeven puntental toe.
Het middelen van punten van verschillende beoordelaars is meestal niet gerechtvaardigd. Het is slechts verdedigbaar in die gevallen waarvan je aannemelijk kunt maken dat de beoordelaars slechts op toevallige gronden van elkaar verschillen (kleine foutjes, vergissingen, verslappen van aandacht, afgeleid zijn door irrelevante zaken als een minder leesbaar handschrift, en dergelijke, zie ook par. 6.2).
Er bestaat een subtiele variant op het direct middelen van punten. Dat is het docentenoverleg waarin geprobeerd wordt om verschillen van mening bij te leggen, tot unanieme oordelen te komen, om bepaalde antwoorden bij fiat 'goed', en andere bij fiat 'fout' te rekenen. Verschillen van opvatting moet je juist zoveel mogelijk voor het voetlicht proberen te halen, in plaats van ze in de coulissen weg te werken. Daar hoeft ook niemand gezichtsverlies bij te lijden.
Dan blijft nog over de nieuwsgierigheid van de beoordelaars zèlf naar de mate waarin zij verschillende opvattingen over de kwaliteit van de werkstukken hebben. Wat eenvoudig cijferwerk kan aan het licht brengen hoe groot de verschillen in strengheid tussen de beoordelaars zijn: bereken daarvoor de puntentotalen per beoordelaar (zoals in tabel 7.1 laatste kolom), of de gemiddelden van de toegekende waarderingen. Verschil in de mate waarin van het hele scorebereik gebruik gemaakt wordt kan blijken uit de per beoordelaar berekende standaarddeviatie (zie paragraaf 8.6). Of maak per beoordelaar een frequentieverdeling van de door hem of haar toegekende waarderingen (zoals figuur 8.3).
Zouden de resultaten tot droefenis stemmen, of zouden met andere woorden de gevonden verschillen niet aceptabel zijn, dan is het zaak uit te pluizen waarin die verschillen hun oorzaak vinden, waarna het misschien mogelijk is een korte training van de beoordelaars op te zetten waardoor die verschillen verkleind worden. Het laatste heeft alleen zin wanneer de bron van die verschillen niet bij de inhoudelijke beoordeling, dus buiten de vakdeskundigheden van de beoordelaars, ligt.
Een bijzonder puntje bij de controle op de consistentie van de beoordelingen is een eventueel verloop in strengheid, bijvoorbeeld van het eerst nagekeken werk naar het laatst nagekeken werk. Zou zich dat voordoen, wat op voor de hand liggende wijze is na te gaan, dan zou je ter voorkoming er voor kunnen zorgen dat de antwoorden per vraag, en niet per hele toets, worden nagekeken zo dat voor iedere student sommige van zijn antwoorden voorin de keu staan, andere meer naar achteren. Je kunt ook achteraf corrigeren door de puntentoekenning voor de strenger beoordeelde werkstukken naar boven toe bij te stellen.
Voor wat minder oppervlakkig onderzoek naar de mate van overeenstemming tussen beoordelaars zijn tegenwoordig vele technieken beschikbaar, zie bijvoorbeeld Stanley (1971), De Gruyter (1977), Mellenbergh (1972). De vraag is echter of dergelijk onderzoek, waarvoor in de regel deskundigen ingeschakeld moeten worden, resultaten op kan leveren die de moeite van die inspanning waard zijn. In de kleinschalige situatie waar de docent in werkt kan deze vraag zeker ontkennend beantwoord worden. De moeite van het uitvoeren van sophisticated onderzoek naar de mate van overeenstemming tussen beoordelaars is beter te investeren in maatregelen die het kwaad, als dat zou bestaan, bij de wortel bestrijden. Deze cursus bevat aanwijzingen en technieken die dat nu juist mogelijk maken.
De mondelinge ondervraging is niet meer, en niet minder, dan één van de mogelijkheden om je toetsing vorm te geven. Voor het mondeling gelden onverminderd alle regels, voorschriften en normen zoals die op alle toetsing betrekking hebben (hoofdstuk 6). Het zal alleen heel wat moeilijker zijn om dat mondeling zodanig vorm te geven dat de procedure de toets der kritiek kan doorstaan. In paragraaf 6.1 heb ik aangegeven hoe het mondeling ingericht kan worden wanneer participatiecontrole de bedoeling is. Op basis van het gesprek worden in het laatste geval geen zwaarwegende beslissingen meer genomen.
Omdat allerlei maatregelen die een verantwoorde toetsing kunnen bevorderen in het geval van mondelinge ondervraging moeilijk te treffen zijn, moet je in de eerste plaats zoeken naar mogelijkheden om over te gaan op een of andere vorm van schriftelijke toetsing (of het concreet laten maken van werkstukken, tonen van de bereikte vaardigheden).
Is het mondeling de enige goede mogelijkheid voor toetsing, dan is het kennelijk niet mogelijk de ondervraging van te voren behoorlijk te structureren (anders zou je waarschijnlijk ook schriftelijk kunnen toetsen). Maar juist in die gevallen waarin het moeilijk is anders dan mondeling te toetsen zit je met datzelfde mondeling dik in de problemen omdat het dan ook erg ongestructureerd zal zijn. Je kunt natuurlijk proberen een en ander een beetje op te vangen, bijvoorbeeld door de ondervraging en/of waardering door meer personen te laten doen. Maar....
Het zal bij het mondeling moeilijk of onmogelijk zijn de verschillende beoordelaars onafhankelijk van elkaar te laten oordelen. Tijdens het gesprek zien zij elkaars reacties op de vragen en antwoorden, waarbij de werkwijze van degene die ondervraagt het oordeel van de anderen zeker zal beïnvloeden. Er is als het ware tijdens het gesprek een voortdurend stil overleg gaande tussen de ondervrager en de andere beoordelaars. Dat leidt tot hoge onderlinge overeenstemming tussen de beoordelaars, een overeenstemming die wel eens voor een aanzienlijk deel fake zou kunnen zijn. Het laatste nog even afgezien van de mogelijkheid dat beoordelaars het met elkaar eens kunnen zijn op grond van een gemeenschappelijk vooroordeel.
Tenslotte wil ik hier een speciaal puntje van toetsingsethiek aanstippen. Het komt wel eens voor dat vooral bij mondeling examineren de examinandus ook gewaardeerd wordt naar maatstaven zoals die aangelegd zouden worden wanneer hij zou solliciteren naar een baan op zijn vakgebied. Het hoeft geen nadere toelichting dat zoiets volstrekt ontoelaatbaar is, tenzij er expliciet een (overtuigende) rechtvaardiging voor gegeven wordt. De examinator mag zich nimmer laten verleiden tot koffiedikkijkerij als 'zie ik deze juffrouw of knaap in het bedrijf, de school, de wijk, ook effectief als X-onoom of Y-oloog functioneren?' Het examen is afsluiting van een opleiding. Straks zullen anderen oordelen of zij de kersvers afgestudeerde Kees, Klaas of Keetje in dienst nemen.
Dit is ook na bijna dertig jaar nog steeds een bijzonder hoofdstuk, omdat het een aantal mogelijkheden voor de analyse van toetsresultaten laat zien, die in de literatuur zelden zijn te vinden. Dat ligt niet aan de gebruikte statistische modellen, die zijn tamelijk elementair van aard . Het gaat meer om een andere manier van analyseren dan overigens gebruikelijk is voor psychologische tests. Dat hoeft niet vreemd te zijn: toetsen in het onderwijs is wezenlijk iets anders dan het afnemen van psychologische tests: op toetsen bereiden studenten zich voor, terwijl bij psychologische tests de veronderstelling juist is dat kandidaten zich daar niet gericht op hebben kunnen voorbereiden. Dit hoofdstuk 8 is in zekere zin complementair aan de modellen voor studiestrategieën zoals in de gelijknamige cursus in 1978 behandeld, en in deze 21e eeuw veel verder uitgewerkt in de vorm van het model voor Strategic Preparation for Achievement Testing (het SPA-model) hier, dat bestaat uit een reeks modulen met bijbehorende applets die alle op deze website toegankelijk zijn.
De tekst van dit hoofdstuk stelt hoge eisen aan de omzetting van een scan naar correcte html-tekst. Op 7 mei 2007 is de controle op de juistheid van de tekst, de formules en de berekeningen afgerond. Een garantie dat alles nu foutloos is, kan ik niet geven. Mail mij bij onzekerheid.
In dit hoofdstuk geef ik een beknopte inleiding op de mogelijkheden en technieken bij het interpreteren van toetsresultaten, zowel ten aanzien van individuele personen, als waar het gaat om groepen studenten. Met uitzondering van interpretaties die betrekking hebben op de cesuurproblematiek: die komen in de cursus Cesuurbepaling ter sprake.
Inhoudelijk is het hier gepresenteerde in de eerste plaats bedoeld voor een kennismaking, in de tweede plaats om het een en ander te kunnen naslaan op het moment dat de vraag naar interpretatie van toetsresultaten zich voordoet. Ik raad dan ook aan om bij eerste lezing niet tezeer op details en eventuele subtiele formuleringen te letten.
Bij de hier gepresenteerde 'leerstof' wordt een groot aantal toetsvragen gegeven, als illustratiemateriaal bij de voorgaande hoofdstukken. Voorbeelden van toetsvragen zijn alleen zinvol te geven wanneer ook de leerstof waar ze naar terug verwijzen gegeven wordt, en eventueel de doelstellingen van de docent. Bekijk de voorbeelden dan ook in relatie tot de hier gegeven 'leerstof', en ga ervanuit dat de gegeven toetsvragen in overeenstemming zijn met de doelstellingen van de docent, doelstellingen die hij weliswaar niet expliciet geformuleerd hoeft te hebben, maar waarover hij voldoende duidelijke gedachten moet hebben om althans bij iedere toetsvraag aan te kunnen geven of die vraag binnen zijn (impliciete) doelstellingen past.
In volgende edities van deze cursus kan hopelijk voorbeeldenmateriaal uit verschillende disciplines gegeven worden, waartoe de medewerking van docenten wordt gevraagd.
De beheersing die een student over de leerstof heeft wordt aangegeven door de vragen die hij wel, respectievelijk de vragen die hij niet kan beantwoorden. Daarbij gaat het alleen om die toetsvragen die onder de doelstellingen van de docent vallen, alle andere mogelijke en misschien heel aardige toetsvragen vallen hier buiten.
Het is handig om de stofbeheersing van de student uit te drukken als de proportie van alle mogelijke vragen, die tevens binnen de doelsteling vallen, die hij kan beantwoorden. Een concreet voorbeeld is de vragenverzameling van 3000 vragen die docent I. Know heeft opgesteld, een vragenverzameling die nog best uit te breiden zou zijn maar slechts door variaties van marginale betekenis. De student die daarvan 2100 vragen goed weet te beantwoorden heeft een stofbeheersing van 0,7.
Een toets van 3000 vragen is praktisch uitgesloten, de beantwoording zou te veel tijd vergen. Misschien volstaat docent Know met een toets van 100 vragen, gekozen als een willekeurige steekproef uit zijn verzameling van 3000 vragen. Toch blijven we dan de beheersing van de student definiëren op de volledige verzameling van 3000 vragen, en zullen dat ook wel de ware beheersing noemen. Het is duidelijk dat in het algemeen de proportie goed gemaakte vragen van de toets niet gelijk is aan de ware beheersing van de leerstof, maar daar een meer of minder sterke aanwijzing voor geeft [goede schatting van is].
Het begrip steekproef behoeft geen verdere toelichting. Met willekeurig wordt bedoeld dat iedere vraag uit de verzameling evenveel kans heeft in de toets (de steekproef) opgenomen te worden als iedere andere vraag uit de verzameling. Dat is in de praktijk te realiseren door alle vragen in de verzameling te nummeren, dan een aantal getallen te trekken uit bijvoorbeeld een tabel van willekeurige getallen of de computer een serie willekeurige getallen te laten genereren.
Helemaal 'willekeurig' zal de docent in de praktijk niet kunnen werken, omdat bepaalde vragen niet met elkaar in een en dezelfde toets voor mogen komen, omdat de ene vraag informatie verschaft die juist voor het beantwoorden van een andere vraag nodig kan zijn. Dergelijke praktische maatregelen hoeven aan het beginsel van de willekeurigheid geen afbreuk te doen.
Het komt zelden voor dat de student een volledige vragenverzameling als toets voorgelegd krijgt. Het komt ook niet vaak voor dat de docent concreet de beschikking heeft over zo'n uitgebreide vragenverzameling. Er is misschien wel een kleine, onvolledige, verzameling, waarvan ook gebruik gemaakt wordt door er een gedeelte van de vragen voor de toets op willekeurige wijze uit te trekken. De ontbrekende toetsvragen worden voor de gelegenheid gemaakt, en zijn strikt genomen dan ook niet als willekeurig getrokken op te vatten. Wanneer dergelijke nieuwe vragen volgens een goed gedefinieerd voorschrift, een 'item form', gemaakt worden dan is er geen bezwaar tegen om ze te beschouwen als willekeurige vragen uit de denkbeeldige verzameling van vragen die correspondeert aan dat voorschrift, die 'item form'. Een simpel voorbeeld van zo'n voorschrift is 'horizontaal optellen van twee getallen onder de 100'. Vragen: 21+34= .. 75+86= .. etcetera.
Ook wanneer een volledige vragenverzameling in feite niet bestaat, is het mogelijk om te blijven spreken over de ware beheersing van de student, gedefinieerd op de vragenverzameling zoals die er uit zou zien wanneer wel alle vragen, zo mogelijk via de opgestelde vraagvoorschriften of item forms, gemaakt zouden zijn. In de onderwijspraktijk zal niemand de ware beheersing van de student kennen, ook de student zelf niet, maar dat betekent nog niet dat het niet nuttig zou zijn om met dit begrip 'ware beheersing' te werken.
De resultaten die de student op de toets boekt geven een aanwijzing over zijn ware beheersing van de stof. De kwaliteit van die aanwijzing is beter naarmate de wijze waarop de toets is samengesteld beter voldoet aan de eis van willekeurigheid, omdat afwijkingen van die willekeurigheid leiden tot vertekeningen waarvoor niet eenvoudig gecorrigeerd kan worden.
Het is mogelijk om met de gegeven begrippen te werken ook wanneer de vragen erg heterogeen zijn, zoals nogal uiteenlopende vraagsoorten over heel verschillende onderwerpen. Wie dat doet moet, als het even kan, ook vasthouden aan het willekeurig trekken van toetsvragen uit deze verzameling. Wie tegen het laatste bezwaar heeft, omdat gevreesd wordt voor een toets die dan misschien niet goed de behandelde onderwerpen dekt, te veel moeilijke vragen kan bevatten of iets dergelijks, die kan de vragenverzameling opdelen in een aantal deelverzamelingen, en voor iedere deelverzameling de geschetste werkwijze volgen. De ware beheersing van de student is dan ook per deelverzameling gedefinieerd. Wie daar behoefte aan heeft kan vervolgens de ware beheersing definiëren als het (eventueel gewogen) gemiddelde van deze deelbeheersingen.
Vragen die door raden goed te beantwoorden zijn, zoals tweekeuze- en meerkeuzevragen, hoeven geen bijzondere problemen op te leveren zolang ook door raden goed beantwoorde vragen onder de definitie van ware beheersing vallen. Zie ook Lord (1957).
Over bovenstaand stuk tekst zijn heel wat toetsvragen te formuleren. Met name is het erg makkelijk om vragen te maken waarin niet veel anders gedaan wordt dan terugvragen van informatie die in deze tekst gegeven wordt. Maar het is niet interessant of de lezer stukjes informatie uit deze tekst kan reproduceren, of herkennen. Wel van belang is dat hij inzicht heeft in het steekproefkarakter van iedere toets, met name de rol van het begrip 'willekeurig' daarbij: dat hij aan kan geven welke samenstellingsprocedures voor de toets daaraan voldoen, en welke niet. Ook is van belang dat hij weet wat wel en wat niet onder 'ware beheersing' van de stof verstaan wordt. Beide globaal aangeduide doelstellingen leiden tot (bijvoorbeeld) de volgende mogelijke toetsvragen.
Bij controle op de formulering van deze vragen zal waarschijnlijk gesignaleerd worden dat in de stam van de vraag (boven aan deze bladzijde) vermeld moet worden dat met 'willekeurige steekproef' het in de tekst gedefinieerde begrip bedoeld wordt. Er zou in dit geval ook geen bezwaar tegen hoeven bestaan om die definitie in de stam van de vraag op te nemen: het gaat er niet om of de definitie gekend wordt, maar of er mee gewerkt kan worden.
Interpretatie van toetsresultaten kan twee kanten op gebeuren, die beide voor docent en student interessant zijn. De ene soort interpretatie is van waargenomen toetsscore naar de mogelijke achterliggende ware beheersing, de andere is van gegeven ware beheersing naar de dan te verwachten toetsscore. Ik begin met de tweede, om technische en didactische redenen.
Bekend is de frequentieverdeling van toetsscores voor de groep studenten (zie fig 8.3), waar voor iedere mogelijke toetsscore geturfd is hoeveel studenten die score hebben, en van die aantallen een grafiek is gemaakt. In deze paragraaf wordt een techniek gegeven om een dergelijke frequentieverdeling te maken voor de toetsscore die een student die de eigen ware beheersing zou kennen, mag verwachten.
Zoals we weten uit de voorgaande paragraaf is de ware beheersing van de individuele student meestal niet bekend, maar zouden we hem in beginsel wel te weten kunnen komen door een verzameling van alle mogelijke vragen over de stof te maken (die ook binnen de doelstellingen vallen), en hem die te laten beantwoorden. Ook wanneer dat omvangrijke karwei niet gedaan wordt, kan het zinvol zijn om over zoiets als de 'ware beheersing' van de student te spreken. Je kunt die ware beheersing voor een bepaalde student algebraïsch aanduiden met de letter p, eventueel p(i) om aan te geven dat de ware beheersing van student i bedoeld wordt. Deze p kan waarden aannemen tussen 0 en 1 inclusief, waarmee aangegeven wordt de proportie vragen uit de denkbare vragenverzameling die deze student goed zou beantwoorden als hij ze voorgelegd zou krijgen.
Wordt een toets op willekeurige wijze (zie par. 8.1) uit de denkbare vragenverzameling samengesteld, dan geldt voor iedere vraag in deze toets dat de kans dat een student met ware beheersing p de vraag goed kan beantwoorden eveneens gelijk aan p is. Dat volgt uit de definities van 'willekeurige steekproef' en 'ware beheersing'.
Kansen kun je nabootsen met een roulettewiel: markeer op de cirkel het stuk p zo dat dit stuk de even grote proportie van de cirkel is als de ware beheersing. Is de ware beheersing p = 0,8, markeer dan een stuk gelijk aan het 4/5e deel van de cirkelomtrek; is de cirkel in 36 gelijke stukjes opgedeeld, laat dan de eerste 28 het stuk p voorstellen, en laat het 36e stukje geheel buiten beschouwing (opnieuw draaien wanneer het balletje daarop zou vallen).
Met dat roulettewiel kun je een toetsuitslag nabootsen van een student met ware beheersing p = 0,8, door voor iedere vraag die de toets telt één keer te 'spelen', en 'goed' te noteren als het balletje blijft liggen in het als 'p' aangeduide stuk.
Wie één toetsuitslag kan nabootsen, kan er meerdere nabootsen. Je zou bijvoorbeeld een serie uitslagen kunnen nabootsen voor een toets die bestaat uit 25 vragen, telkens voor dezelfde student met p = 0,8. Of, wat op hetzelfde neerkomt, je zou voor een groep studenten met allen dezelfde ware beheersing p = 0,8 de toeisuitslagen op deze wijze kunnen nabootsen.
Dat draaien aan het wiel is erg omslachtig, zeker wanneer je een erg groot aantal toetsuitslagen zou willen nabootsen, bijvoorbeeld om eens na te gaan of de frequentieverdeling van toetsuitslagen die je dan krijgt een bepaalde stabiele vorm gaat krijgen. Ook zonder al die moeite te doen is het mogelijk aan te tonen dat het laatste inderdaad gebeurt, en dat de verdeling die je krijgt bij een naar oneindig oplopend aantal nabootsingen de theoretische frequentieverdeling is die bekend staat onder de naam
(1) binomiaalverdeling ƒ(x|p) = { n! / ((n-x)! x!) } × p x (1-p) n - x
waarbij
ƒ(x|p) = kans op toetsscore x, gegeven p
n = aantal vragen in de toets
x = toetsscore = aantal vragen goed
x! spreek uit: 'x faculteit'
= x × (x-l ) × (x-2) × .... × (3) × (2) × (1).
Deze binomiaalverdeling is de theoretische frequentieverdeling voor de toetsscore wanneer een student met ware beheersing p een groot aantal keren een telkens opnieuw willekeurig getrokken toets zou maken. Maakt de student de toets maar één keer, dan kan met behulp van deze theoretische frequentieverdeling de kans op een bepaalde toetsscore berekend worden, of de kans dat de toetsscore tenminste gelijk aan een bepaald getal zal zijn (bijvoorbeeld tenminste gelijk aan de cesuur).
Voor een toets met n=10 vragen, en een student met ware beheersing p=0,8, is de kans op toetsscore 8 te berekenen als:
{10! / (2! × 8!) } 0,8 8 × 0,2 2 = 45 × 0,16778 × 0,04 = 0,30.
Evenzo de kans op toetsscore 9 als ƒ(9|p)=10×0,13422×0,1 = 0,13 en ƒ(10|p) = 0,11 (de lezer kan dat narekenen).
De kans op een toetsscore van tenminste 8 is 0,30+0,13+0,11=0,54.
Met een zakrekenmachine die faculteiten berekent zijn dergelijke kansen snel te berekenen, mits n niet te groot is. Er bestaan tabellen voor de cumulatieve binomiaalverdeling, die de kansen op tenminste een bepaalde score geven.
Merk op dat voor de vragen 8 t/m 16 met drie verschillende vraagvoorschriften (item forms) gewerkt wordt:
Verschillende vragen zijn dan te genereren door verschillende getallen in te vullen, een karweitje dat eventueel ook met behulp van de computer geautomatiseerd kan worden. Zeer goede doorzichtigheid van de toetsing is dan te verkrijgen door de student te informeren dat alleen deze drie vraagsoorten over deze paragraaf gesteld zullen worden.
Nu we voor iedere toetsscore de kans kunnen berekenen dat een student met ware beheersing p deze score behaalt, is het mogelijk voor een concreet geval de hele theoretische frequentieverdeling te berekenen en te tekenen: figuur 8.1
[noot 2002. De oorspronkelijk getekende verdelingen voor ware beheersing 0,25 0,5 0,75 en 0,9 zijn hier vervangen door verdelingen voor ware beheersing 0,25 0,6 en 0,9, geplot vanuit het programma voor het Algemeen ToetsModel (nu voor gebruik beschikbaar: SPA moduul 1). De plot is nu een histogram, wat correcter is dan het lijndiagram in de oorspronkelijke wijze van afbeelden, hoewel die voor dit kleine aantal vragen een duidelijker plaatje opleverde; vandaar nu de beperking tot slechts 3 verdelingen.]
Merk op uit figuur 8.1 dat het zelfs met deze korte toets van maar 20 vragen mogelijk is om studenten met ware beheersing van respectievelijk 0,25 en 0,75 bijna perfect van elkaar te onderscheiden. Daarvoor hoeven we verdere eigenschappen van de toets, zoals zijn betrouwbaarheid, niet eens te weten.
Wie dergelijke theoretische frequentieverdelingen berekenen wil, kan het rekenwerk vereenvoudigen door de functiewaarde voor iedere volgende toetsscore uit de laatste te berekenen:
(2) ƒ(x+1|p) = {(n-x)/(x+1) } × { p/(1-p) } × ƒ(x|p)
Voor grotere waarden van n kan de normaalverdeling als benadering gebruikt worden (mits p niet te groot of te klein is, in welk geval de poissonverdeling als benadering gebruikt moet worden). Voor details verwijs ik naar de statistische literatuur.
Met behulp van het theoretische model uit de vorige paragraaf kunnen er uitspraken gedaan worden over te verwachten toetsscores voor studenten met gegeven (bekende) ware beheersing. Als het gaat om het voorspellen van toetsscores is dat niet erg zinvol, omdat niemand, ook de student zelf niet, die ware beheersing kent.
Toch is er wel enige informatie over hoe goed de stof beheerst wordt. De student maakt opgaven van hetzelfde soort als ook in de toets gebruikt zullen worden, en weet ongeveer wel hoe goed hij is in het beantwoorden van dergelijke vragen. Misschien organiseert de docent een proeftoetsgelegenheid enige tijd voor de eigenlijke toets; wordt zo'n proeftoets op dezelfde wijze samengesteld als de toets, door willekeurige trekking uit de (denkbare) vragenverzameling, dan geeft het proeftoetsresultaat een mooie aanwijzing voor de eigen ware beheersing. Een aanwijzing die nog heel wat onzekerheden kan bevatten.
Het is mogelijk op grond van verkregen informatie, bijvoorbeeld een proeftoetsresultaat, een theoretische frequentieverdeling voor de ware beheersing op te stellen, ook wel kansverdeling of waarschijnlijkheidsverdeling voor de ware beheersing p genoemd. Voor dit doel is bruikbaar de
(3) bètaverdeling ƒ(p) = { (a+b-1)! / ((a-1)!(b-1)!) } p a-1 (1p) b-1
Wordt de schatting alleen gebaseerd op een pioeftoetsresultaat dan kun je voor de som (a+b) het aantal vragen in die proeftoets + 2 nemen, en voor a het aantal vragen goed + 1 nemen (respectievelijk voor b het aantal vragen fout + 1). Zie voor verdere details over dit gebruik van deze bètaverdeling o.a. Novick en Jackson (1974), en de cursus Examenregeling deel A: Studiestrategieën, hoofdstuk 3 en bijlage A daarin. Figuur 3.3 en 3.4 in genoemde cursus laten een aantal van dergelijke verdelingen zien.
Een bron van voortdurende verwarring is de conventie in de statistische literatuur om voor de bètaverdeling de formule (3) te gebruiken, en niet de meer voor de hand liggende formule met a' en b', waar a' = a-1 en b'=b-1, zodat a' eenvoudig het aantal goed, en b' het aantal fout is.
Hoe dat ook zij, in 1979 heb ik het in bovenstaande alinea precies verkeerd aangegeven, zonder de nu vetgedrukte optellingen. De fout kon destijds verborgen blijven, omdat niet de formule, maar de interpretatie ervan verkeerd is: de talrijke berekeningen in de opgaven in dit hoofdstuk zijn correct. Voor de bètaverdeling is een geheugensteuntje dat dat die voor een toets met twee vragen, waarvan 1 goed gemaakt, ook nog bestaat. De 'verkeerde' interpretatie dat a = 1 zou zijn, zou dan tot een deling door nul leiden! Hetzelfde bruggetje is te gebruiken bij de formule (4) voor de negatief-hypergeometrische verdeling. Want vervolgkwestie is, natuurlijk, dat de parametrisering voor de betabinomiaalverdeling, in deze cursus consequent overal de negatief-hypergeometrische verdeling genoemd, in overeenstemming moet zijn met de voor de bètaverdeling gekozen parametrisering.
Over deze paragraaf geen opgaven; het gepresenteerde materiaal is nodig voor de volgende paragraaf. Houd in gedachten dat in de praktijk niemand ooit exacte waarden van de ware beheersing p kent, dat p door de student voorafgaand aan de toets benaderd kan worden met een theoretische frequentieverdeling, waarvoor een bètaverdeling bruikbaar is. De student kan dat in principe inderdaad doen, maar in de praktijk zal hij dat niet kunnen, niet begrijpen, of er geen belangstelling voor hebben.
Een theoretische frequentieverdeling voor de toetsscore waarbij de ware beheersing niet meer bekend verondersteld wordt, maar waarbij wel de ware beheersing gespecificeerd is in de vorm van een bètaverdeling (formule 3), is de
(4) negatief-hypergeometrische verdeling
ƒ(x) = {n!/(n-x)! x!} × {(a+b-1)!/(a-1)!(b-1)!} × {(a+x-1)! (b+n-x-1)!/(a+b+n-1)!}
De formule ziet er afschrikwekkend uit, maar is rechttoe rechtaan uit te rekenen. De afleiding is o.a. te vinden in bijlage A van de cursus Studiestrategieën.
Wordt uitgegaan van het resultaat op een proeftoets behaald, dan kan voor a - 1 het aantal goed op de proeftoets worden genomen, respectievelijk voor - 1 het aantal fout op de proeftoets behaald. Is geen proeftoets afgenomen dan zou je kunnen werken met de schatting die de student geeft van het meest waarschijnlijke aantal goed dat hij zou maken op een toets die bijvoorbeeld evenveel vragen bevat als de af te nemen toets, of minder (dat pseudoaantal toetsvragen geeft als het ware het vertrouwen aan dat de student in zijn schatting heeft, en moet daarom niet al te hoog worden genomen).
Let op, a - 1 is het aantal goed op de proeftoets, niet a zelf, zoals verkeerd geschreven in 1979. Idem b - 1, in plaats van alleen b, voor het aantal fout.
Een vervelende eigenschap van deze verdeling ƒ(x) is dat de faculteiten die er in voorkomen al snel zo groot worden dat ze niet op een zakrekenmachine te bepalen zijn. De volledige verdeling is daarentegen eenvoudig term voor term te berekenen gebruik makend van de relatie
(5) ƒ(x-1) = { x / (n-x+1) } × { (b+n-x) / (a+x-1) } × ƒ(x)
eventueel ook eenvoudig te programmeren op bijvoorbeeld de Texas Instruments 58 of 59 zakrekenmachines.
Voorbeeld. a=10 b=5 n=20
Voor x=20 valt de eerste term in (4) weg (die is gelijk 1). Dan
ƒ(20) = (14! / 9!×4! ) × (29!×4! / 34! ) = 14×13×12×11×10 / 34×33×32×31×30 = 0,00719481.
Gebruik voor de verdere berekeningen alle decimalen die uw zakrekenmachine heeft! Rond pas af op 2 of 3 decimalen nadat alle berekeningen gemaakt zijn.
ƒ(19) = {20/(20-20+1)}×{(5+20-20)/(10+20-1)}× ƒ(20) = 20 ×(5/29)× 0,00719481 = 0,0248096
ƒ(18) = (19/2) (6/28) × ƒ(19) = 0,0505052
ƒ(17) = (18/3) (7/27)× ƒ(18) = 0,0785636 etcetera.
ƒ(20) = 0,0071948 = 0,007
ƒ(19) = 0,0248096 = 0,025
ƒ(18) = 0,0505052 = 0,051
ƒ(17) = 0,0785636 = 0,079
ƒ(16) = 17/4 × 8/26 ƒ(17) = 0,1027370 = 0,103
ƒ(15) = 16/5 × 9/25 ƒ(16) = 091183530 = 0,118
ƒ(14) = 15/6 × 10/24 ƒ(15) = 0,1232843 = 0,123
ƒ(13) = 14/7 × 11/23 ƒ(14) = 0,1179241 = 09118
ƒ(12) = 13/8 × 12/22 ƒ(13) = 0,1045236 = 0,105
ƒ(11) = 12/9 × 13/21 ƒ(12) = 0,0862734 = 0,086
ƒ(10) = 11/10 × 14/20 ƒ(11) = 0,0664305 = 0,066
ƒ(9) = 10/11 × 15/19 ƒ(10) = 0,0476773 = 0,048
ƒ(8) = 9/12 × 16/18 ƒ(9) = 0,0317848 = 0,032
f{7) = 8/13 × 17/17 ƒ(8) = 0,0195598 = 0,020
f 6) = 7/14 × 18/16 ƒ(7) = 0,0110023 = 0,011
ƒ(5) = 6/15 × 19/15 ƒ(6) = 0,0055745 = 0,006
ƒ(4) = 5/16 × 20/14 ƒ(5) = 0,0024887 = 0,002
ƒ(3) = 4/17 × 21113 ƒ(4) = 0,0011711 = 0,001
ƒ(2) = 3/18 × 22/12 ƒ(3) = 0,0003578 = 0,000
ƒ(1) = 2/19 × 23/11 ƒ(2) = 0,0000768 = 0,000
ƒ(0) = 1/20 × 24/10 ƒ(1) = 0,0000095 = 0,000
------
1,001
De kansen moeten sommeren tot 1, op een afrondingsfoutje na, wat tevens een controle op de berekening is. Merk op dat de breuken in de achtereenvolgende berekeningen snel achter elkaar uit te schrijven zijn. Wanneer iedere uitkomst in de rekenmachine blijft staan, kan alleen de op drie decimalen afgeronde kans opgeschreven worden.
Dit soort berekeningen doe je natuurlijk niet moeiteloos, van de student zou je mogen verwachten dat hij in staat is aan de hand van de formule snel ƒ(n) te berekenen, dat hij snel ƒ(x-l) kan berekenen wanneer ƒ(x) gegeven is, dat hij de kans op tenminste de toetsscore x kan vinden door alle nodige termen te berekenen en de kansen te sommeren.
Opgave 17 moet zijn proeftoets 10 vragen, waarop 8 goed. In 1979 per abuis: 12 vragen, 9 goed.
Ook deze vraag is op te vatten als een vraagvoorschrift, waar door invulling van in dit geval andere getalswaarden telkens nieuwe concrete vragen uit gemaakt kunnen worden.
Er zijn ook een aantal variaties in de formulering mogelijk, waar de student mee overweg moet kunnen. Bijvoorbeeld:
Er zijn nu 3 theoretische frequentieverdelingen besproken, en de student (de lezer) zou moeten weten welke verdeling te gebruiken is bij welke vraagstelling.
De varianten op vragen 19 en 20 liggen voor de hand. Wanneer in dezelfde toets ook toepassingen gevraagd worden, is het waarschijnlijk niet handig vragen zoals 19 of 20 ook daarin op te nemen.
Dan zijn er nog mooie opgaven te bedenken die te uitgebreid zijn om in de toetsing op te nemen, maar in het onderwijs een rol kunnen spelen, zoals:
Het voorgaande gaf een stukje basistheorie die van belang is voor studenten die een rationele studiestrategie willen hanteren. De cursus Cesuurbepaling laat zien dat deze theoretische beginselen dan ook weer door de docent te gebruiken zijn wanneer hij door verschuiven van de cesuur op zijn toets het studiegedrag van studenten wil beïnvloeden.
Dan is nu de beurt aan de docent die een toetsscore wil interpreteren in termen van de waarschijnlijke ware beheersing van de student die deze score behaalde. Zou hij een toets van 10 vragen gebruikt hebben, dan is uit figuur 8.2 voor iedere toetsscore af te lezen tussen welke waarden de ware beheersing in 90 % van de gevallen ligt.
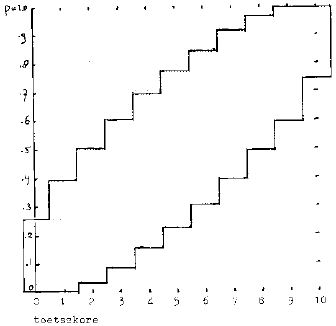
Het verticale gedeelte binnen de gordel en boven de waargenoinen toetsscore bevat in 90 % van de gevallen de ware beheersing van de betreffende student. Bijvoorbeeld: een student scoort 8, dan ligt zijn ware beheersing met waarschijnlijkheid van 90 % binnen de grenzen p=0,50 en p=0,96, inclusief 0,50 en 0,96 zelf. De tabel is op een honderdste nauwkeurig.
Verondersteld wordt ook hier weer dat de toets samengesteld is door willekeurig trekken uit de (denkbare) vragenverzameling waar ook de ware beheersing op gedefinieerd is.
De waarschijnlijkheid van 90 % betekent dat de docent in een groot aantal individuele gevallen waarin hij op deze manier een uitspraak doet over de grenzen waartussen de ware beheersing van de betrokken studenten ligt, op de lange duur in 90 % van de gevallen gelijk zal hebben. Ik wijs er hier al vast op dat het niet waar hoeft te zijn dat van alle studenten met een bepaalde toetsscore er 90 % een ware beheersing hebben die binnen het bijbehorende 90 % betrouwbaarheids interval ligt. Lord en Novick wijzen er op dat voor een groep personen met dezelfde toetsscore het niet uitgesloten hoeft te zijn dat geen enkele persoon een ware beheersing heeft die in dat interval ligt. Ook is een belangrijk detail dat strikt genomen de docent over meerdere studenten alleen maar dit soort uitspraak mag doen wanneer iedere student een speciaal voor hem willekeurig getrokken toets heeft afgelegd.
Merk op dat over de waarschijnlijke ware beheersing van een enkele student op deze wijze stellige uitspraken gedaan kunnen worden, ook al zou deze student de enige zijn die de toets heeft afgelegd.
Hoe is die betrouwbaarheidsgordel in figuur 8.2 geconstrueerd? Met de binomiaalverdeling kan voor iedere gekozen p een theoretische frequentieverdeling geconstrueerd worden, waarvan er in figuur 8.1 enkele als voorbeeld gegeven werden. Bij zo'n verdeling kun je de toetsscores zoeken waarbinnen de score op de toets van deze student met waarschijnlijkheid van 90 % zal vallen (of iets meer dan 90 %, omdat precies uitkomen op die 90 % er meestal niet bij is). Doe dat door de hoogste toetsscore in de theoretische frequentieverdeling te zoeken waarvoor geldt dat de kans op deze of een lagere score nog kleiner is dan 5% en evenzo de laagste score waarvoor geldt dat de kans op deze of een hogere score nog kleiner is dan 5%.
Voor een verdeling van de schaal voor ware beheersing in honderdsten zou dat een heel werk zijn, maar het karwei kan vereenvoudigd worden door een uitgebreide tabel voor de binomiaalverdeling te gebruiken waaruit de bedoelde scores direct zijn af te lezen. In figuur 8.2 zijn al deze scores voor 101 waarden van p getekend als verticale lijntjes. Daarna werden deze lijntjes aan elkaar verbonden met de horizontale lijnen. Omdat het gebied tussen de beide zo geconstrueerde lijnen in 90% van de gevallen de ware beheersing van de student zal bevatten, wat deze ware beheersing in werkelijkheid ook mag zijn, zullen we ook in 90% van de gevallen gelijk hebben wanneer we zeggen dat zijn ware beheersing in deze betrouwbaarheidsgordel valt. Wanneer zijn toetsscore bekend is, komt dat er op neer dat we in 90% van de gevallen gelijk zullen hebben wanneer we zeggen dat zijn ware beheersing in het verticaal aan de toetsscore corresponderende betrouwbaarheidsinterval ligt.
Zie ook Lord en Novick (1968, par. 23,3) en Kendall en Stuart vol. 2 (19679 voorbeeld 20.2).
In bijlage B van deze cursus worden betrouwbaarheidsgordels gegeven voor toetsen van 10, 20, 30, 40 en 50 vragen.
Bij de volgende opgaven kan zonodig van de ter beschikking gestelde tabellen of grafieken gebruik gemaakt worden.
Vroeger of later, en eerder vroeg dan laat, stuit je bij het interpreteren van toetsresultaten op begrippen als 'gemiddelde', 'standaarddeviatie', 'standaardmeetfout', en 'variantie.'
Het gemiddelde van een n aantal scores is de som van die scores gedeeld door hun aantal n. Dit is het rekenkundig gemiddelde, er zijn andere gemiddelden te definiëren, zoals meetkundig gemiddelde, harmonisch gemiddelde, modus en mediaan, waarvan voor ons de modus nog wel eens van pas komt. De modus van een aantal waarnemingen is de waarneming (de toetsscore) die het vaakst voorkomt.
De standaarddeviatie van een aantal van n getallen is een maat voor de spreiding van de getallen, voor de gemiddelde afstand tot hun gemiddelde zou je losjes kunnen zeggen, maar dan een verkregen door eerst alle afstanden te kwadrateren, vervolgens bij elkaar op te tellen, deze som door n te delen, en daar de wortel van te nemen.
(6) m = (1/n) Σ xi
(7) s = √ {(1/n) Σ (x i - m)2 } xi
sommering over i=1 tot n
m = gemiddelde
s = standaarddeviatie
xi = score van persoon i
n = aantal personen (observaties)
Σ = sommeringsteken : tel op voor alle personen i
Je hóeft het niet zo te doen, het kan ook anders. Er zijn verschillende formules mogelijk. Zeker wanneer het op berekenen aankomt hoeven formules (6) en (7) nu niet direct de meest efficiënte te zijn. Over de toetsgegevens vermeld in figuur 8.3 zal de berekening van gemiddelde en standaarddeviatie geïllustreerd worden in tabel 8.1; daarbij wordt gebruik gemaakt van berekeningsformules (8) en (9).
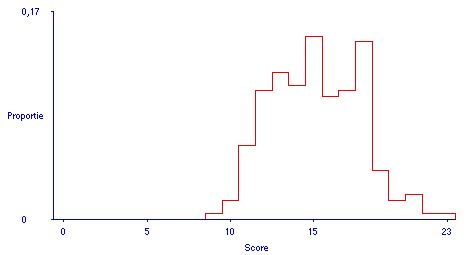
[De plot is gemaakt met de programmatuur van het Algemene Toetsmodel, door een invoerfile te construeren met de frequenties zoals in de tabel weergegeven.]
----------------------------
toets f u uf u²f
score
----------------------------
9 1 6 6 36 m = c m(u) + x(0)
10 3 5 15 75
11 12 4 48 192 = 33/200 + 15 = 15,165
12 21 3 63 189
13 24 2 48 96
14 22 1 22 22 s = c √{(Σ u(i)² × ƒ(i))/k - m(u)²}
15 30 0 0 0
16 20 1 20 20 = √(1435/200 - 0,0272)
17 21 2 42 84
18 29 3 87 261 = 2,6735
20 3 5 15 75
21 4 6 24 144
22 1 7 7 49 (in dit voorbeeld is c=l)
23 1 8 8 64
--- + --- + ---- +
200 33 1435
----------------------------
Voor het berekenen van gemiddelde en standaarddeviatie over gegroepeerde scores, waar we bij toetsen vaak mee te maken zullen hebben, zijn de beide volgende formules goed bruikbaar (voor de afleiding van deze formules zie bijvoorbeeld Hoel (1962):
(8) m = cmu + x0
waarbij
mu = (1/k) Σ ui fi (sommatie over alle toetsscores i)
(9) s = c √ {((Σ ui2×fi) / k) - mu2}
c = interval tussen toetsscores
u = nieuwe variabele die gedefinieerd is door xi = c ui + x0
x0 = toetsscore waarvoor ui = 0 gekozen wordt
xi = toetsscore i, i = 0, 1, 2, .... , n
n = aantal toetsvragen
fi = aantal personen (observaties) met toetsscore xi
k = totaal aantal personen (of observaties).
Het lijkt ingewikkeld, maar het loont de moeite wanneer het aantal studenten groot is om deze berekeningsformules te hanteren. Kies de x0 ergens in het midden van de scorerange, dat vergemakkelijkt de berekening enigszins; let er dan wel op dat de u-waarden voor de score kleiner dan x0 het negatief teken krijgen (op die conventie zijn de gegeven formules gebaseerd).
Zou je met gegroepeerde data werken (telkens drie naastliggende toetsscores tot één klasse bijeengenomen bijvoorbeeld), dan is c niet gelijk aan 1 (in het genoemde voorbeeld zou c gelijk 3 zijn), maar gelijk aan de klassebreedte zoals dat dan heet.
Over empirische frequentieverdelingen kun je m en s berekenen uit de data. Theoretische frequentieverdelingen hebben ook een gemiddelde en standaarddeviatie (hoewel daar uitzonderingen op zijn, voor ons niet van belang), en die worden uit formules berekend die specifiek voor de betreffende verdeling zijn. Met de wijze waarop dergelijke formules verkregen worden zullen we ons hier niet bezig houden.
(10) binomiaalverdeling
gemiddelde = n × p
standaarddeviatie = √ { np (1 - p )}
(11) bètaverdeling
gemiddelde = a / ( a + b )
standaarddeviatie = √ { a b / ((a+b)2 (a+b+1)) }
(12) negatief-hypergeometrische verdeling [of bètabinomiaalverdeling]
gemiddelde = na /( a + b )
standaarddeviatie = √ { nab (n+a+b) / ((a+b)2 (a+b+1)) }
Het gemiddelde van een theoretische frequentieverdeling wordt ook wel de verwachte waarde genoemd.
Voor een bepaalde student heeft de standaarddeviatie voor de verwachte scoreverdeling gegeven zijn ware beheersing p de speciale naam standaardmeetfout voor een bepaalde student:
(13) s.m.i = √ { np (1 - p ) } standaardmeetfout voor student i.
De ware beheersing p is in de praktijk natuurlijk niet bekend, we hebben ons dan te behelpen met de score die de student op de toets'behaalt, waaruit zijn standaardmeetfout geschat wordt:
(14) s.m.i ≅ √ { xi (n - xi ) / ( n - 1) } standaardmeetfout voor student i.
xi = toetsscore van student i.
(zie Lord 1957). De formule (14) levert een uitkomst die maar bij benadering waar is, en dat is aangeduid met het slangetje boven het gelijk teken. Lord (1957) geeft de techniek om voor de 'ware' s.m.(i) een betrouwbaarheidsgordel te construeren, zoals in de voorgaande paragraaf voor de ware beheersing gedaan werd.
In plaats van de standaarddeviatie alsmaat voor de spreiding wordt vaak de variantie gehanteerd, het kwadraat van de standaarddeviatie.
Met gemiddelde en variantie als gegeven kun je vaak erg veel doen. Ook waar het om theoretische frequentieverdelingen gaat. Zo is de binomiaalverdeling volledig door zijn gemiddelde en variantie bepaald, wat betekent dat met gemiddelde en variantie als gegeven de binomiaalverdeling te construeren is. Hetzelfde geldt voor de bètaverdeling, en voor een verdeling die we later nog zullen ontmoeten: de normaalverdeling. Voor de negatief-hypergeometrische verdeling geldt dat ook de waarde van n bekend moet zijn (of van een van de beide andere parameters van deze verdeling) naast zijn gemiddelde en standaarddeviatie. Hier ligt een van de redenen voor het belang van gemiddelde en variantie.
Naast gemiddelde en variantie van theoretische frequentieverdelingen wordt vaak gesproken over gemiddelde en variantie van
Let met name op het mogelijke voorkomen van het gemiddelde van gemiddelden. Denk bijvoorbeeld aan de gemiddelde score op een willekeurig getrokken toets: wanneer dezelfde groep studenten een aantal van dergelijke willekeurig getrokken toetsen krijgt voorgelegd, dan is er gelegenheid om het gemiddelde over de toetsgemiddelden te berekenen. Ook al zou je niet in werkelijkheid meerdere van dergelijke toetsen bij dezelfde groep studenten afnemen, dan is het nog wel denkbaar dat je zoiets zou doen, en kun je je voorstellen dat je dan een bepaalde verdeling van toetsgemiddelden zou krijgen waar je het gemiddelde over zou kunnen nemen. Of de variantie van bepalen. Op dezelfde wijze kun je het gemiddelde van een aantal berekende varianties bepalen, of de variantie over een empirische frequentieverdeling van toetsvarianties. Dit alles vraagt om enige soepelheid in het kunnen omgaan met deze begrippen.
vragen studenten: JAN ELS JOS BEN DIK ANS 1 0 1 1 0 0 0 2 1 0 1 1 1 1 3 1 0 1 1 0 0 4 0 1 0 1 0 0 5 0 1 1 0 0 1
-------------------------------------------------------------- score 10 11 12 13 14 15 16 17 18 19 20 21 22 23 aantal 2 1 6 10 18 16 27 27 35 13 20 12 12 1 --------------------------------------------------------------
Zoals figuur 8.3 al liet zien, kan een empirische frequentieverdeling er nogal grillig uitzien. In de globale vorm van de verdeling kun je wel enig vertrouwen hebben, maar de sprongen omlaag en omhoog zijn waarschijnlijk aan het toeval te wijten. De vraag is dan of het mogelijk is zo'n empirische frequentieverdeling glad te strijken, en daarmee een beter beeld te verkrijgen over de aard van de toetsscoreverdeling voor groepen studenten zoals die waarover deze empirische gegevens verzameld zijn. Die vraag kan bevestigend beantwoord worden. Tukey (1977) geeft mooie vereffeningstechnieken (smoothing techniques) voor gevallen waarin verder niets over de aard van de verdeling bekend is.
Hebben we te maken met toetsscores, waarbij de score gelijk is aan het aantal vragen goed, dan weten we wel iets over de aard van de verdeling, en kunnen van die kennis gebruik maken door een sterkere vereffeningstechniek te gebruiken. (Wat we 'weten', weten we strikt genomen alleen bij veronderstelling, en zullen we bij twijfel aan de juistheid van de veronderstelling eerst op grond van (een deel van) de empirische gegevens de moeten zien te toetsen). Een sterke vereffening wordt verkregen door een theoretische frequentieverdeling te fitten op de empirische frequentieverdeling. De verdeling die zich bij uitstek leent voor het vereffenen van toetsscoreverdelingen is de negatief-hypergeometrische verdeling, die ik al eerder ten tonele heb gevoerd. Alles wat voor dat fitten nodig is, is het gemiddelde en de variantie van de empirische frequentieverdeling. De best passende negatief-hypergeometrische verdeling is de verdeling met gemiddelde en variantie gelijk aan die van de empirische verdeling. Op de gegevens uit figuur 8.3 of tabel 8.1 vinden we dan:
m = 15,165; gemiddelde negatief-hypergeometrische verdeling is
= na / (a+b).
s2 = 7,1; variantie negatief-hypergeometrische verdeling is
= nab (n+a+b) / ((a+b)2 (a+b+1)).
n = 23
Hieruit zijn a en b op te lossen. Eenvoudiger is het om gebruik te maken van de volgende relaties (Lord en Novick 1968 par. 23.6):
(17a) R = (n / (n-1)) × (1-m(n-m) / (n2))
(17b) a = (m/R) - m
(17c) b = (n/R) - n - a
Waaruit voor het voorbeeld volgt
R = (23 / 22) (1 - 15,165×(23 - 15,165) / (23 - 7,148) = 0,290.
a = (15,165 / 0,290) - 15,165 = 37,13 afgerond op geheel getal 37.
b = (23 / 0,290) - 23 - 37,13 = 19,18 afgerond op geheel getal 19.
De negatief-hypergeometrische verdeling met a=37, b=19, n=23 kunnen we dan volgens de constructieregels uit paragraaf 8.5 in elkaar zetten.
De eerste term ƒ(23) is dan als volgt te berekenen (formule 4)
n! (a+b-1)! (a+x-1)! (b+n-x-1)!
ƒ(23) -------- ------------ -----------------
(n-x)!x! (a-1)!(b-1)! (a+b+n-1)!
55! 23! 59! 18! 55! 59!
= ------- ------ ------- = --------- ( 0! = 0 per definitie)
36!×18! 0!×23! 78! 36!×78!
55.54.53.52.51.50.49.48.47.46.45.44.43.42.41.40.39.38.37
= ---------------------------------------------------------
78.77.76.75.74.73.72.71.70.69.68.67.66.65.64.63.62.61.60
= 3,41307 × (10(macht 31) / 8,16558) × 10(macht 34) = 0,00041798.
De berekening ziet er een beetje omslachtig uit, maar omdat zelfs zakrekenmachines die n! berekenen het zullen vertikken wanneer n groter dan 68 wordt, is dit alternatief dan te gebruiken. Worden de aantallen ook na vereenvoudiging nog zo groot dat op deze directe wijze moeilijk te werken is, dan kan een benaderingsformule gebruikt wordeng zoals deze:
(18a) Stirling's formule n! ≅ {√(2π)} en nn+½
π = 3,141592 ....
e = 2,718281 ....
Een preciezere variant is met e(n-1/12n) in plaats van e-n, en wie nog nauwkeuriger wil zijn kan te rade bij Kendall en Stuart volume 1 (1969, formule 3.64).
Voor het gebruik van (18a) hoeft n geen geheel getal te zijn, dus ook a en b hoeven daarvoor niet per se op gehele getallen afgerond te worden.
Evenwel, als n echt groot is, is (18a) niet in die vorm te gebruiken. Bereken
dan eerst de logaritme van n!, volgens:
(18b) log n! = ½ log(2π) - n × log e + (n + ½) × log n
waarbij tenslotte n! gevonden wordt door n! = 10 log n!.
Terug nu naar de verdere berekening van de te 'fitten' negatief-hypergeometrische verdeling. Met behulp van formule (5) vinden we
ƒ(22) = 23/1 × 19/59 × 0,00041798 = 0,00309588
ƒ(21) = 22/2 × 20/58 × ƒ(22) = 0,0117429
ƒ(20) = 21/3 × 21/57 × ƒ(21) = .....
etcetera.
Het resultaat staat in de volgende tabel, naast de empirische frequentieverdeling.
ƒ(23) = 0,000 empirisch: 0,005
22 0,003 0,005
21 0,012 0,020
20 0,030 0,015
19 0,059 0,040
18 0,095 0,145
17 0,126 0,105
16 0,144 0,100
15 0,144 0,150
14 0,127 0,110
13 0,100 0,120
12 0,070 0,105
11 0,044 0,060
10 0,024 0,015
9 0,012 0,005
8 0,005 0,000
7 0,002 0,000
6 0,001 0,000
------ + ----- +
0,998 1,000
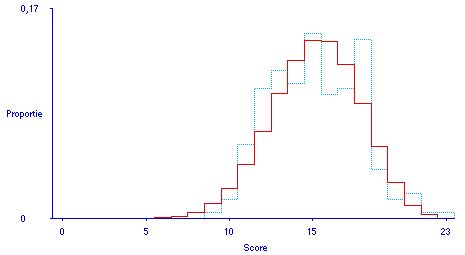
[noot 2002: de beide verdelingen nu geplot met programmatuur Algemeen ToetsModel: rood getrokken de gefitte, blauw gestippeld de empirische verdeling. Die programmatuur maakt alle gereken met de hand overbodig. Omdat het om frequentieverdelingen gaat is plotten als histogram de correcte methode. Het computerprogramma is nu voor gebruik onder uw browser beschikbaar: SPA moduul 3
score 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 aantal 1 2 4 6 3 5 8 11 9 21 22 18 13 15 10 9 7 12 12 5 5 1 1
In de praktijk neem je in een toets alleen deelvragen op, waarbij de daarbij noodzakelijke gegevens ook als gegeven vermeld worden.
Voor iedere docent is het van belang een goede indruk te krijgen van wat de studenten van zijn onderwijs hebben opgestoken, van de mate waarin hij met zijn onderwijs de gestelde doelen ook heeft bereikt, met andere woorden dus van de mate waarin de studenten als groep de stof beheersen ('ware beheersing').
Het zal niet verbazen dat we voor deze verdeling van de ware beheersing in de groep studenten een theoretische frequentieverdeling zoeken. En wel in het bijzonder een verdeling die goed past bij de theoretische frequentieverdeling die in de voorgaande paragraaf 'gefit' werd bij de empirische frequentieverdeling van de toetsresultaten.
Wanneer voor iedere student de theoretische verdeling voor zijn toetsscore, gegeven zijn ware beheersing, de binomiale verdeling is (wanneer het binomiale foutenmodel gehanteerd wordt, zo heet dat in jargon), en de verdeling van de ware beheersing in de groep studenten zou een bètaverdeling zijn, dan is aan te tonen dat de toetsresultaten de negatief-hypergeometrische verdeling hebben. Dit geval is helemaal analoog aan dat van de individuele student, waarvoor een bètaverdeling voor zijn ware beheersing gespecificeerd werd, waaruit onder het binomiale foutenmodel voor zijn toetsscore de negatief-hypergeometrische verdeling af te leiden was (par. 8.2 t/m 8.4), hoewel die afleiding daar niet expliciet gegeven werd (zie daarvoor bijlage A cursus Studiestrategieën).
Voor onze praktische doeleinden kan ook aangenomen worden dat het omgekeerde eveneens van toepassing is: wanneer de empirische scoreverdeling als negatief-hypergeometrisch beschouwd kan worden, is de theoretische frequentieverdeling voor de ware beheersing de bètaverdeling (met corresponderende waarden voor de parameters a en b). (Zie Lord en Novick 1968, paragraaf 23.7 en 23.8).
Voor het voorbeeld in figuur 8.4, waar de negatief-hypergeometrische verdeling met parameters a=37 en b=19 'gefit' werd bij toetsresultaten van 200 studenten op een toets van 23 vragen, kunnen we als theoretische frequentieverdeling voor de ware beheersing voor deze groep studenten de bètaverdeling met eveneens a=37 en b=19 hanteren:
(19) bètaverdeling ƒ(p) = {(a+b-1)!/((a-1)! (b-l)!)} p a-1 (1-p) b-1 = 55! / 36! × 18! = p 36 (1-p) 18
Zijn we tevreden met globale interpretaties verkregen uit inspektie van een getekende verdeling, dan kan de volgende techniek gebruikt worden om deze bètaverdeling grafisch uit te zetten.
Het gemiddelde van de bètaverdeling is 37/56 = 0,67. Kies p hier dicht bij, bijvoorbeeld p = 0,7, en bereken
0,7 36 × 0,3 18 = 2,65173 × 10-6 × 3,87420 × 10-10 = 1,02733 × 10-15
Definieer een nieuwe functie g(p) = 1015 p36 (1-p)18. Deze g(p) verschilt slechts in een constante schaalfactor van de bètaverdeling (19), en heeft dezelfde vorm als (19). Bereken een aantal waarden van g(p) zodat de functie geschetst kan worden.
Afronden op een decimaal is voor ons doel nauwkeurig genoeg. Dan vinden we achtereenvolgens
g(0,70) = 10 (macht 15) × 1,02733 × 10 (macht -15) = 1,03.
g(0,69) = 10 (macht 15) × 1,10430 × 10 (macht -15) = 1,10.
En verder:
g(0,68) = 1,16 g(0,60) = 0,71 g(0,52) = 0,11 g(0,76) = 0,36
g(0,66) = 1,17 g(0,58) = 0,50 g(0,50) = 0,05 g(0,78) = 0,19
g(0,64) = 1,09 g(0,56) = 0,33 g(0,72) = 0,82 g(0,80) = 0,09
g(0,62) = 0,92 g(O,54) = 0,20 g(0,74) = 0,58 g(0,82) = 0,03
Hier is op simpele wijze de theoretische frequentieverdeling uit te construeren, als in figuur 8.5 getekend.
Omdat het hier om een continue verdeling gaat wordt door de gevonden punten een vloeiende doorgaande lijn getrokken (op het oog en met de hand, of op het oog en langs een gummilineaal). (noot 2002; of plotten via een geschikt computerprogramma, zoals het Algemene Toetsmodel moduul 2).
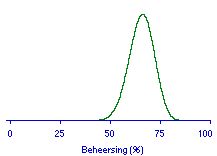
noot 2002: oorspronkelijke tekening vevangen door plot gemaakt met programma Algemeen ToetsModel. Het computerprogramma is nu voor gebruik onder uw browser beschikbaar: SPA moduul 2
Het hoogste punt van de verdeling, de modus, is te vinden uit
(20) modus van de bètaverdeling is (a-1) / (a+b-2) (Novick & Jackson1974).
In het voorbeeld figuur 8.5 ligt de modus bij p= 36/54 = 2/3.
Kwantitatieve uitspraken zijn aan de hand van figuur 8,5 niet mogelijk, want dan moeten we oppervlakken onder de verdeling berekenen. Uit de figuur valt echter wel op te maken dat de ware beheersing van deze groep studenten zich bevindt tussen ongeveer 0,5 en 0,8. Zou deze toets toevallig een beetje moeilijk uitgevallen zijn, dan is de verdeling iets naar rechts te schuiven; voor een makkelijk uitgevallen toets geeft deze verdeling een te rooskleurig beeld, en zou ze naar links op moeten schuiven.
De variantie van deze bètaverdeling is volgens formule (11)
ab / ((a+b)2 (a+b+l)) = s2 = 0,00393. De standaarddeviatie is de wortel daaruit, s = 0,06271.
Deze getallen zijn op de schaal van ware beheersing, van 0 tot 1.
Voor verdere kwantitatieve uitspraken over de ware beheersing van deze groep studenten moeten we over stukjes van deze verdeling de integraal kunnen evalueren. Aangezien dat een heidens karwei is voor de bètaverdeling, en voor grote waarden van de parameters a en b ook geen tabellen gebruikt kunnen worden waar het werk al voor ons gedaan is, is het zoeken naar een wél praktische mogelijkheid. Misschien is de bètaverdeling te benaderen met een andere theoretische frequentieverdeling die wé1 eenvoudig te evalueren is, of waarvoor tabellen bestaan. Novick en Jackson (1974) wijden een heel hoofdstuk aan verschillende mogelijke benaderingen voor de bètaverdeling (hoofdstuk 10).
Uit het fraaie symmetrische karakter van de verdeling in figuur 8.5 zal een enkele lezer al begrepen hebben dat het gebruik van een normaalverdeling voor grote waarden van de parameters a en b voor de hand ligt. De te kiezen verdeling is die met zelfde gemiddelde en variantie als de te benaderen bètaverdeling.
Bij de verdeling in figuur 8.5 is de normaalverdeling met gemiddelde 37/56 = 0,66 en variantie 0,00393 als benadering te kiezen.
Het werken met een normaalverdeling, en bijbehorende tabellen, is een techniek die in iedere inleiding in de statistiek te vinden is, zodat ik in verband met de beperkte doelstelling van dit hoofdstuk graag naar die literatuur verwijs.
Ik wil daar één uitzondering op maken. Ik geeft hier een korte tabel met de proportie van (het oppervlak onder) de verdeling dat ligt tussen gemiddelde ± ½, 1, 1½, 2, 2½, 3 standaarddeviaties.
proportie van (opp. onder) de verdeling
in het aangegeven gebied:
m ± ½ s 0,38292
m ± 1 s 0,68268
m ± 1½ s 0,86638
m ± 2 s 0,95450
m ± 2½ s 0,98758
m ± 3 s 0,99730
Voorbeeld: voor mp = 0,66 en s= 0,063 is de proportie van de verdeling in het gebied 0,66 + 0,063 gelijk aan 0,68, oftewel ongeveer 68 % van de studenten heeft een ware beheersing tussen 0,60 en 0,72.
In paragraaf 8.5 werd een methode gegeven om uitspraken te kunnen doen over de ware beheersing van een enkele student, ook al zou hij de enige zijn die de toets had afgelegd. In de praktijk is er altijd een groep van enige omvang die de toets aflegt, en in de voorgaande paragraaf heb ik laten zien dat er met redelijke nauwkeurigheid aangegeven kan worden hoe de ware beheersing in zo'n groep studenten verdeeld is.
Kiezen we nu willekeurig uit zo'n groep één persoon uit, dan moet het mogelijk zijn om een nauwkeuriger schatting voor zijn ware beheersing te maken dan met de techniek van de betrouwbaarheidsgordel uit paragraaf 8.5 bereikt werd. Het is dan immers bekend dat hij tot een bepaalde groep hoort, waarvan de verdeling van ware scores te schatten is. Van die informatie, extra informatie naast het gegeven van de door deze persoon behaalde toetsscore, kan dan ook goed gebruik gemaakt worden.
De vraag is dan, kun je uitgaande van de groepsresultaten een theoretische frequentieverdeling vinden voor de ware beheersing van een persoon met een gegeven toetsscore? Dat kan.
Wanneer bij de scoreverdeling over studenten een negatief-hypergeometrische verdeling gefit kan worden, en het binomiale foutenmodel gebruikt wordt, is aan te tonen dat de theoretische frequentieverdeling voor de ware beheersing van een student met gegeven toetsscore x een bètaverdeling is.
Wanneer bij de toetsresultaten van de groep de negatief-hypergeometrische verdeling met parameters a, b, en n gefit is, heeft deze bètaverdeling voor een enkele student de parameters v=a+x en w=b+nx:
(21) theoretische frequentieverdeling voor ware beheersing gegeven de toetsscore
ƒ(p|x) = {(a+b+n-1)! / ((a+x-1)! (b+n-x-1)!)} × p a+x-1 × (1-p) b+n-x-1}
De verwachte waarde voor de ware beheersing is het gemiddelde van deze verdelingg volgens formule (11), maar nu met parameters v=a+x en w=b+n-x
(22) verwachte waarde voor ware beheersing v / (v+w) = (a+x) / (a+b+n)
(23) variantie voor ware beheersing vw / {(v+w)2 × ( v+w+l)}
= {(a+x) × (b+nx)} / {(a+b+n)2 × (a+b+n+1)}
Terug naar het voorbeeld uit de voorgaande paragraaf, waar voor de beide parameters gevonden werd a=37 en b=19, wordt voor een student met toetsscore x=20 berekend
verwachte waarde ware beheersing 57/79 = 0,71
variantie ware beheersing 57 × 22 / (792 × 80)= 0,002512
De parameters v en w hebben grote waarden, zodat de normaalverdeling als benadering voor deze bètaverdeling gebruikt kan worden.
Hetzelfde bereken ik voor een student met score x=12 verwachte waarde ware beheersing 49/79 = 0,62.
In onderstaande figuur 8.6 zijn op de horizontale as de toetsscores afgezet, op de verticale as de ware beheersing. De beide berekende resultaten zijn in het vlak ingevuld (snijpunt van de lijnen x = 20 en p = 0,71, en x = 12 en p = 0,62 respectievelijk). Door beide zo gevonden punten is een rechte lijn getrokken die in staat stelt voor ieder toetsscore x de 'bijbehorende' verwachte waarde voor de ware beheersing p te vinden (zoals door de pijlen weergegeven).
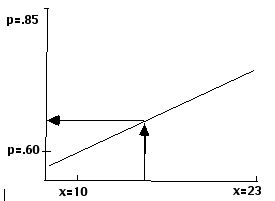
Lord en Novick (1968, par. 23.6) laten zien dat onder dit model de regressie van ware beheersing op waargenomen score lineair is, zodat de in figuur 8.6 geconstrueerde lijn gelijk aan de regressielijn is. De vergelijking voor de regressielijn heeft de algemene vorm
(24) regressielijn V(p|x) = m/n + R × (x-m) / n
V(p|x) = verwachte ware beheersing bij gegeven score x.
R = regressiecoëfficiënt.
Aangetoond kan worden dat in het hier gehanteerde model
(25) R = {n / (n-1)} (1 - m(n-m) / nsx2 ) (Lord en Novick 1968 formule 23.6.14)
Met behulp van formules (25) en (24) is voor iedere score x de verwachte ware beheersing te berekenen. (De uitkomst daarvan moet gelijk zijn, in ons voorbeeld, aan de uitkomst verkregen met behulp van figuur 8 .6).
De theoretische frequentieverdeling voor de ware beheersing van de student, gegeven zijn toetsscore x, is een bètaverdeling volgens formule (21), waarvan de variantie gegeven is door formule (23). Wanneer deze bètaverdeling benaderd wordt door de normaalverdeling met hetzelfde gemiddelde en dezelfde variantie, kan van tabellen voor de normaal verdeling gebruik gemaakt worden om betrouwbaarheids intervallen voor de ware beheersing te construeren. Onderstaande tabel geeft enkele gebruikelijke intervallen (het 99% interval is slecht bruikbaar omdat de normaal verdeling in de staart een slechte benadering voor de bètaverdeling is).
betrouwbaarheids- proportie van (opp. onder) de verdeling interval binnen het interval
^p ± 0,97 s 0,67 ^p ± 1,15 s 0,75 ^p ± 1,645 s 0,90 ^p ± 1,96 s 0,95
Zodat in het voorbeeld het 90 % betrouwbaarheidsinterval voor de student met score 20 gelijk is aan 0,71 ± 0,082, De uitspraak dat de ware beheersing van deze student in dit interval ligt is waar òf niet waar. Het is niet zo dat de kans 90 % dat dit interval de ware beheersing inderdaad bevat. Over een groot aantal van dergelijke uitspraken echter geldt dat in 90 % van de gevallen de uitspraak dat de ware beheersing in het 90 % betrouwbaarheidsinterval ligt, waar is.
Nog even terugkomend op formule (25) voor de regressiecoëfficiënt: deze formule is gelijk aan de Kuder-Richardson formule 21 uit de klassieke testheorie. Het verband tussen het binomiale foutenmodel en de klassieke testtheorie wordt verder uitgewerkt in Lord en Novick (1968, paragraaf 23.9), en is voor het doel van deze cursus niet van direct belang.
Wie R toch berekend heeft, kan met behulp daarvan ook de parameters a en b voor de negatief-hypergeometrische verdeling die als benadering voor de empirische frequentieverdeling gebruikt wordt berekenen met behulp van:
(26) a = (m/R) - m
(27) b = (n/R) - n - a (Lord en Novick, 1968, par. 23.6).
De resultaten in de voorgaande paragrafen gepresenteerd moeten met enige voorzichtigheid gebruikt worden wanneer de praktijk niet in overeenstemming is met de belangrijke veronderstelling dat voor iedere student afzonderlijk een toets samengesteld wordt (willekeurig getrokken uit de vragenverzameling). Dat er in feite geen vragenverzameling bestaat waaruit door willekeurig trekken toetsen samengesteld worden, is een schending van de veronderstelling waar met een klein beetje zorg heel goed mee te leven valt (zie ook de ontboezeming daarover van Lord en Novick, 1968, par. 11.1). Wat vervelender is dat meestal alle studenten dezelfde toets voorgelegd krijgen, en dan is strikt genomen het binomiale foutenmodel niet op de groep studenten van toepassing. Hoe robuust het binomiale foutenmodel tegen schending van deze veronderstelling is, is niet nagegaan, voorzover mij bekend. Het hangt er ook van af welk gebruik er van de toetsresultaten gemaakt wordt: zou schending van deze veronderstelling een belangrijke invloed op beslissingen op basis van deze resultaten kunnen hebben, dan is het zeker af te raden dit model te gebruiken wanneer daar tenminste wél bruikbare alternatieven voor bestaan. Wordt het binomiale foutenmodel gebruikt bij een analyse zoals in paragraaf 8.8, om een indruk te krijgen van de mate waarin de groep studenten zich de leerstof heeft eigen gemaakt, dan lijkt er weinig bezwaar tegen hanteren van het modelte bestaan, mits er rekening mee wordt gehouden dat deze toets wel eens iets makkelijker of moeilijker zou kunnen zijn uitgevallen dan andere willekeurig getrokken toetsen zouden zijn.
Het laatste wat verder uitwerkend: de mate waarin verschillende willekeurig getrokken toetsen van n vragen in moeilijkheid verschillen kun je uitdrukken in de variantie van de toetsgemiddelden (gemiddelde / n is gelijk de moeilijkheid). Een schatting voor die variantie is te krijgen uit de variantie van de vraagmoeilijkheden in de afgenomen toets:
(28) (^sm)2 = ((N-n) / N) (sp)2 / (n-1)
(sm)2 = variantie van de moeilijkheid van verschillende willekeurig getrokken toetsen van n vragen
(sp)2 = variantie van de moeilijkheid (p-waarden) van de vragen in de afgenomen toets
N = aantal vragen in de vragenverzameling waaruit getrokken wordt.
Zie verder Lord en Novick (1968, par. 11.11).
Bij deze laatste paragraaf geen opgaven. In plaats daarvan enkele algemene opmerkingen.
De opgaven aan het eind van iedere paragraaf slaan evident op het in die paragraaf gepresenteerde materiaal. Door die impliciete verwijzing naar een heel bepaald stuk tekst zijn dergelijke opgaven heel wat gemakkelijker te maken dan wanneer een dergelijke tekstverwijzing minder voor de hand ligt. En dat laatste zal typisch het geval zijn bij een afsluitende toetsing, waarin vragen over alle behandelde stof voorkomen. Bij de afsluitende toetsing moet de student 'zoeken' op welk deel van de stof de vraag slaat; hij loopt dan ook het risico al bij de start te verdwalen. Je mag dan ook verwachten dat vragen die door studenten heel bevredigend beantwoord konden worden in deeltoetsjes aan het eind van iedere paragraaf, heel wat moeilijker blijken wanneer ze in een eindtoets opgenomen zijn.
Om ook de student op dat verschijnsel voor te bereiden zijn verschillende wegen te bewandelen. Een mogelijkheid is een 'toetsvragenboek' samen te stellen, waarin de vragen niet naar paragraaf geordend voorkomen, maar ongeveer zoals ze ook in een afsluitende toets samen voor kunnen komen. Dan is de impliciete verwijzing naar een bepaalde paragraaf uit de leerstof verdwenen, en is het oefenen op dergelijke vragen voor de student informatiever. Een andere mogelijkheid is om bij tussentijdse deeltoetsen ook telkens vragen uit al eerder behandelde stof op te nemen. Nog verder gaande stap, een stap die voor een deel van de stof ook min of meer vanzelfsprekend zal zijn, is dat bij opgaven over een deel van de stof ook kennis en inzicht uit eerder behandelde stof aanwezig moet zijn om de opgaven te kunnen maken.
Veel van de in dit hoofdstuk gepresenteerde opgaven zijn 'sommen,' die zich als zodanig lenen voor schier eindeloze variatie door de keuze van andere getallen, waarbij de aard van de opgave telkens hetzelfde blijft, en met name de afstemming op de onderwijsdoelen niet verandert. Hetzelfde geldt naar mijn mening ook voor meer 'verbale' stof, waar meestal als 'voorbeeld' voor een bepaald begrip of een bepaalde wetmatigheid etcetera, gekozen kan worden uit een tamelijk grote en hopelijk goed af te grenzen verzameling van concrete voorbeelden.
Tenslotte: de aard van de gestelde vragen is heel nauw toegesneden op de belangrijkste 'boodschappen' uit de teksten. Zonder veel moeite zou je allerlei andere vragen kunnen bedenken, die door een minder directe relatie tot de doelstellingen niet geschikt zijn om in de toets te worden opgenomen. Voornaamste reden van dat laatste is dat studenten minder of in het geheel niet in de gelegenheid zijn geweest zich op dergelijke (misschien veel ingenieuzer en creatiever vragen) door oefening voor te bereiden. En om die oefening gaat het uiteindelijk zolang het om onderwijs gaat.
(1) Ja. De vraag is echter niet duidelijk geformuleerd. Je zou ook met 'Nee' kunnen antwoorden, met als motivatie dat je het begrip 'willekeurige steekproef' uitbreidt in die zin dat (sommige) studenten geen voorkennis m.b.t. in de toets opgenomen vragen mogen hebben die hen ten onrechte bevoordeelt, ofwel: waardoor de toets geen juiste aanwijzing omtrent hun ware beheersing meer geeft.
(2) Ja.
(3) Nee. De aard van de vragen verandert stelselmatig, waardoor achtereenvolgende toetsen niet als getrokken uit dezelfde vragenverzameling zijn te beschouwen. Er zit echter een dubbelzinnigheid in de vraag, waardoor ook het antwoord 'Ja' te verdedigen is: hoewel de aard van de vragen van toets tot toets verschilt, is iedere toets nog wel als willekeurige steekproef op te vatten, maar niet als willekeurige steekproef uit telkens dezelfde vragenverzameling.
(4) Ja. De verwijderde vragen horen namelijk in de vragenverzameling niet thuis; verwijderen van dergelijke vragen tast het steekproefkarakter van de toets niet aan.
(5) Nee. Welke vragen de student zal beantwoorden bepaalt hij niet door het toeval, maar op grond van zijn oordeel of hij het antwoord op de vraag kan geven of niet, en dat is zeker geen willekeurige selectie uit de 75 vragen.
(6) Nee. Of een bepaalde vraag tot de vragenverzameling behoort wordt niet door zijn statistische eigenschappen bepaald. In het algemeen zullen dergelijke verwijderde vragen wel degelijk tot de vragenverzameling behoren. De toets die overblijft na verwijdering van deze vragen is dan niet meer als willekeurige steekproef op te vatten. Vergelijk vraag (4). De conclusie is inderdaad dat deze optie van bepaalde computerprogramma's vermeden moet worden omdat de toets er door beschadigd wordt.
(7) Ja. Hoewel ook het andere antwoord te verdedigen is. Formele toepassing van de definitie zou tot 'Nee' leiden, terwijl beschouwing van de gegeven procedure in het licht van wat de bedoeling van het toetsen is, tot het antwoord 'Ja' leidt. Zie ook de commentaar gegeven bij vraag (1).
(1-7) Er zijn nogal wat dubbelzinnigheden in deze vragen verstopt. Voor gebruik als ja-neevragen in een toets moeten die er zeker uit gehaald worden. Zouden bovengegeven antwoorden die van een collega-docent zijn, dan beschik je al over aardig wat informatie over de zwakke punten uit de vragen.
Een andere mogelijkheid is om de vragen tot kort-antwoordvragen te maken, door de student te vragen zijn antwoord te motiveren. Of dat een goed alternatief is, hangt er weer van af of het op dergelijke wijze met deze vraagstellingen om kunnen gaan tot de doelstellingen voor de stof in deze paragraaf gerekend wordt (en de studenten daar ook oefening in hebben gekregen).
(8) ƒ(45|0,9) = (50!/(5! 45!)) × 0,9 45 × 0,1 5
= ((50×49×48×47×46) / (5×4×3×2×1)) × 8,728 × 10 -8 = 0,185
(9) ƒ(30|0,4) = 0,00199 (n = 50)
(10) ƒ(25|0,9) = 0,00132 (n = 35)
(11) ƒ(25|0,5) = 0,00534 (n = 35)
(12) ƒ(x ≥ 7|0,75) = ƒ(10|0,75) + ƒ(9|0,75) + ƒ(8|0,75) + ƒ(7|0,75)
= 0,0563 + 0,1877 + 0,2816 + 0,2503 = 0,776
(13) ƒ(x ≥ 7|0,25) = 0,0000009537 + 0,00002861 + 0,0003862 + 0,003090 = 0,00351
(14) ƒ(x ≤ 6|0,8) = ƒ(6|0,8) + ƒ(5|0,8)+etcetera
= 0,05315 + 0,01550 + 0,00332 + 0,00052 + 0,00006
+ beide laatste termen, maar die zijn verwaarloosbaar,
= 09073
(15) ƒ(x ≤ 6|0,7) = 0,07925 + 0,02911 + 0,00780 + 0,001485 + 0,000212
+ beide laatste termen, maar die zijn verwaarloosbaar
= 0,118
(16) ƒ(x ≥ 7|0,6) = 0,002177 + 0,01741 + 0,06385 + 0,14189 +
0,21284 + 0,22703
= 0,665
(17) De bètaverdeling heeft parameters a=8+1=9 en b=2+1=3. De theoretische frequentieverdeling voor zijn toetsscore is de negatief-hypergeometrische verdeling met dezelfde parameters a=9 en b=3 en bovendien de parameter n=20. Gevraagd is ƒ(x ≥ 18), dat is gelijk aan de som van ƒ(20), ƒ(19) en ƒ(18).
ƒ(20) = (11! / (8!×2)) × ((28!×2)/31!) = (11×10×9/2) × (2 / (31×30×29)) = 990/26970 = 0,0367074
ƒ(19) = 20 × (3/28) × ƒ(20) = 0,0786587
ƒ(18) = (19/2) × (4/27) × ƒ(19) = 0,1107048
ƒ(x ≥ 18) = 0,0367074 + 0,0786587 + 0,1107048 = 0,226
(18) De vraag is met nogal wat overbodige omhaal van woorden geformuleerd, dat kost maar extra leestijd. De theoretische frequentieverdeling voor de toetsscore van deze student is de negatief-hypergeometrische met parameters a=15, b=5 en n=50.
ƒ(50) = (19!/14! 4!) × (64! 4!/69!)
= (19×18×17×16×15) / (69×69×68×67×66×65)
= 1395360 / (1,34862 × 109) = 0,00103
(19) b
(20) a
(21) Voor het berekenen van alle waarden van een binomiaalverdeling maken we gebruik van een recursie formule:
ƒ(x-1) = (x / (n-x+1)) × ((1-p)/p) × ƒ(x) recursieformule voor de binomiaal.
binomiaal n=20 en p=0,5 :
ƒ(20) = 0,520 = 9,53674 × 10-7
ƒ(19) = (20/1) × 1 × ƒ(20) = 1,90734 × 10-5
etcetera
binomiaal voor n=20 en p=0,8
ƒ(20) = 0,820 = 0,0115292 = 0,012
ƒ(19) = (20/1) × 0,25 × ƒ(20) = 0,058
etc.
noot 2002: de overige termen in deze tabel weggelaten, het cursusboek geeft ze allemaal. Omdat nu het programma ATM, applet moduul 1, de binomiaal als uitvoerfile kan geven, is het moeizame berekenen verleden tijd. Hetzelfde geldt voor de negatief-hypergeometrische verdelingen, ofwel de voorspellende toetsscoreverdelingen, applet moduul 3
negatief-hypergeometrische verdeling (bèta-binomiaalverdeling) a=10, b=10, n=20
ƒ(20)= (19! / (9! 9!)) × (29! 9!)/39!)) = 1,45306 × 10-4
ƒ(19)= (20/1) × (10/29) × ƒ(20) = 0,001
etc
negatief-hypergeometrische verdeling (bèta-binomiaalverdeling) a=16, b=4, n=20
ƒ(20)= (19! / (15! 3!)) × (35! 3!)/39!) = 0,047124
ƒ(19)= (20/1) × (4/35) × ƒ(20) = 0,108
etcetera
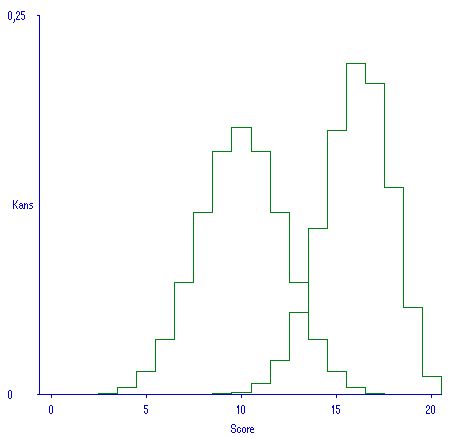
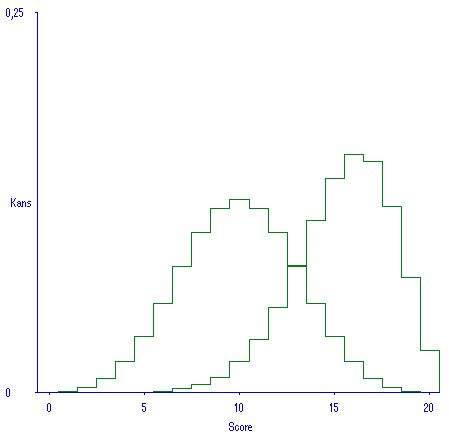
noot 2002: plot mbv programma ATM. Het SPA-applet moduul 3 kunt u meteen in uw browser gebruiken.
Bespreking van de figuur. De eigen onzekerheid van de student over zijn ware beheersing heeft belangrijke gevolgen voor de verwachting die hij over zijn toetsscore heeft. Hoe zekerder hij is over zijn ware beheersing, des te kleiner de kans is dat de toetsscore extreem laag of hoog uitvalt, de voorspelling van zijn toetsscore wordt dan nauwkeuriger, komt dichter in de buurt van de binomiaalverdeling te liggen (welke laatste op 'zekerheid' m.b.t. die ware beheersing gebaseerd is).
Een toets van 20 vragen kan het onderscheid tussen studenten met een beheersing van 0,5 respectievelijk 0,8 behoorlijk goed maken.
(22) De negatief-hypergeometrische verdeling voor de toets van 20 vragen werd in opgave 21 al berekend. Voor de toets van 40 vragen, a=16 en b=4 is te berekenen:
19! 55! 3! 19×18×17×16
ƒ(40) = ______ × ______ ×___________ = 8,51632 × 10(macht -3) = 0,009
15! 3! 59! = 59×58×57×56
ƒ(39) = 40/1×4/55׃(40) = 0,025
etc 39/2×5/54׃(39) = 0,045
38/3×6/53 0,064
37/4×7/52 0,080
36/5×8/51 09090
35/6×9/50 0,095
34/7×10/49 0,094
33/8×11/48 0,089
32/9×12/47 0,081
31/10×13/46 0,071
30/11×14/45 0,060
29/12×15/44 0,049
28/13×16/43 0,040
27/14×17/42 0,031
26/15×18/41 0,023
25/16×19/40 0,017
24/17×20/39 0,013
23/18×21/38 0,009
22/19×22/37 0,006
21/20×23/36 0,004
20/21×24/35 0,003
19/22×25/34 0,002
18/23×26/33 0,001
17/24×27/32 0,001
16/25×28/31 0,000
-------- +
1,002
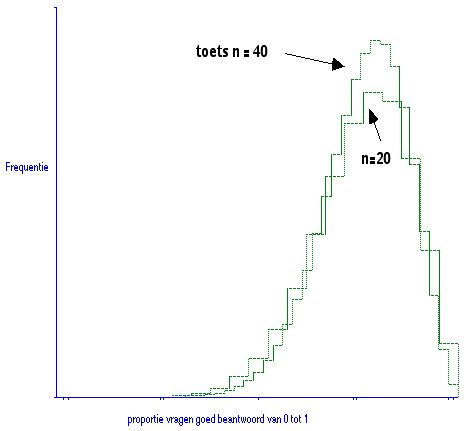
[noot 2002: voor plot is prgramma ATM gebruikt: 16 goed uit 20, toetslengte resp, 20 en 40.]
(23) Het 90 % betrouwbaarheidsinterval voor de ware beheersing van Zomaar is 0,59 - 0,83. Dat is zo te interpreteren dat bij meerdere van dergelijke uitspraken over het 90 % betrouwbaarheids interval voor de ware beheersing van studenten op den lange duur deze uitspraken in 90 % van de gevallen juist zullen zijn, of dat in 90 % van de gevallen het betrouwbaarheidsinterval de ware beheersing bevat.
(24) b
(25a) gemiddelde is 0,5; variantie is 0,25
(25b) gemiddelde is (2+3+4+3+1+2)/6 = 295
variantie is (0,25 + 0,25 + 2,25 + 0,25 + 2,25 + 0,25) / 6 = 0,917
(25c) gemiddelde (2/6 + 5/6 + 3/6 + 2/6 + 3/6) / 5 = 0,5
(opmerking: in het algemeen geldt inderdaad dat gemiddelde moeilijkheid van de vragen in de toets gelijk is aan het gemiddelde van alle vragen, of het gemiddelde van de totaal scores van de studenten gedeeld door het aantal vragen in de toets)
variantie (1/36+ 4/36+ 0+ 1/36+ 0) / 5 = 1/30
(25d) gemiddelde is 1/3
variantie (1/9+ 4/9+ 4/9+ 1/9+ 1/9+ 1/9) / 6 = 2/9
(25e) gemiddelde is 3/5
variantie is (9/25 + 4/25 + 4/25 + 4/25 + 9/25) / 5 = 6/25
(26)
-------------------------------
toets- f u uf u²f gem(u) = -168 / 200 = -0,84 c=1
score
-------------------------------
10 2 -8 -16 128 gem(x) = c gem(u) + x(0) = 18 - 0,84 = 17,16
11 1 -7 -7 49
12 6 -6 -36 216 s² = 1628 / 200 - 0,7056 = 7,4344
13 10 -5 -50 250
14 18 -4 -72 288 s = 2,7266
15 16 -3 -48 144
16 27 -2 -54 108
17 27 -1 -27 27
18 35 0 0 0
19 13 1 13 13
20 20 2 40 80
21 12 3 36 108
22 12 4 48 192
23 1 5 5 25
--- + ---- +
-168 1628
-------------------------------
(27) De theoretische frequentieverdeling voor de ware beheersing is een bètaverdeling, in dit geval met parameters a = 18+1 = 19 en b = 23 - 18 + 1 = 6. Gemiddelde van deze bètaverdeling is 0,76 standaarddeviatie is 0,0838.
Dit antwoord is een correctie op het antwoord gegeven in 1979, dat berustte op de eerder aangeduide 'verkeerde' interpretatie van de parameters a en b.
(28) De theoretische frequentieverdeling voor de ware beheersing is de bètaverdeling met parameters a = 18+1 en b = 30-18+1 = 12+1. De theoretische frequentieverdeling voor de te behalen toets score is de negatief-hypergeometrische verdeling.met dezelfde parameters a = 18+1 en b = 12+1, en parameter n=50. Gemiddelde van deze negatief-hypergeometrische verdeling is 29.687, standaarddeviatie is 5,474.
Dit antwoord is een correctie op het antwoord gegeven in 1979, dat berustte op de eerder aangeduide 'verkeerde' interpretatie van de parameters a en b.
(29) n=50, p=0,5 s.m.(i) = 3,536
n=50, p=0,7 s.m.(i) = 3,240
n=50, p=0,9 s.m.(i) = 2,121
n=50, p=0,99 s.m.(i) = 0,704
(30) n=50 x(i)=25 s.m.(i) ≅ 3,571
n=50 x(i)=35 s.m.(i) ≅ 3,273
n=50 x(i)=45 s.m.(i) ≅ 2,143
n=50 x(i)=49 s.m.(i) ≅ 1,000
(31) n=25 p=0,8 s.m.(i) = 2,000
n=40 p=098 s.m.(i) = 2,530
n=75 p=0,8 s.m.(i) = 3,464
(32) n=40 x(i) = 30 s.m.(i) ≅ 2,774
n=60 x(i) = 45 s.m.(i) ≅ 3,382
n=100 x(i) = 75 s.m.(i) ≅ 4,352
(33) gemiddelde is (15,165 + 17,160) / 2 = 16,1625
standaarddeviatie ((15,165 - 16,1625 )2 + (17,160 - 16,1625)2) / 2 = 0,995.
gemiddelde van de varianties (7,148 + 7,434) / 2 = 7,291
standaarddeviatie van de varianties (7,148 - 7,291)2+ (7,434 - 7,291)2) / 2 = 0,020
(34a)
--------------------------------
toets f u uf u²f gem(u) = 65/200 = 0,325 c=1
score
--------------------------------
43 1 11 11 121
42 1 10 10 100
41 5 9 45 405 gem(x) = 32 + 0,325 = 32,325
40 5 8 40 320
39 12 7 84 588 s² = 4367/200 - 0,105625
38 12 6 72 432 = 21,7294
37 7 5 35 175
36 9 4 36 144 s = 4,6615
35 10 3 30 90
34 15 2 30 60
33 15 1 13 13
32 18 0 0 0
31 22 1 -22 22
30 21 2 -42 84
29 9 3 -27 81
28 11 4 -44 176
27 8 5 -40 200
26 5 6 -32 180
25 3 7 -21 147
24 6 8 -48 384
23 4 9 -36 324
22 2 10 -20 200
21 1 11 -11 121
--- + --- + --- +
200 65 4360
--------------------------------
(34b)
R = (46 / 45) × (1 - (32,325 × 13,675) / (14 × 21,7294) = 0,570
a = (0,325 / 0,57) - 32,325 = 24,386 ≅ 24
b = (46 / 0,57) - 46 - 24,386 = 10,316 ≅ 10
(34c)
33! 69! 9! 33×32×31×30×29×28×27×26×25×24
ƒ(46) = _____ × _____ = _______________________________ = 6,42477 × 10(macht -5)
23 !9! 79! 79×78×77×76×75×74×73×72×71×70
(34d)
ƒ(45)=(46/1).(10/69).ƒ(46)= 0,000 ƒ(44)=(45/2).(11/68).ƒ(47)= 0,002 ƒ(21)=0,006 ƒ(43)=0,004 ƒ(20)=0,004 ƒ(42)=0,008 ƒ(35)=0,079 ƒ(28)=0,049 ƒ(19)=0,002 ƒ(41)=0,016 ƒ(34)=0,083 ƒ(27)=0,040 ƒ(18)=0,001 ƒ(40)=0,025 ƒ(33)=0,084 ƒ(26)=0,031 ƒ(17)=0,001 ƒ(39)=0,036 ƒ(32)=0,081 ƒ(25)=0,024 ƒ(16)=0,000 ƒ(38)=0,049 ƒ(31)=0,076 ƒ(24)=0,017 ƒ(15)=0,000 ƒ(37)=0,061 ƒ(30)=0,068 ƒ(23)=0,012 ƒ(14)=0,000 ƒ(36)=0,071 ƒ(29)=0,059 ƒ(22)=0,008 ƒ(13)=0,000
(34e) en
(34g)
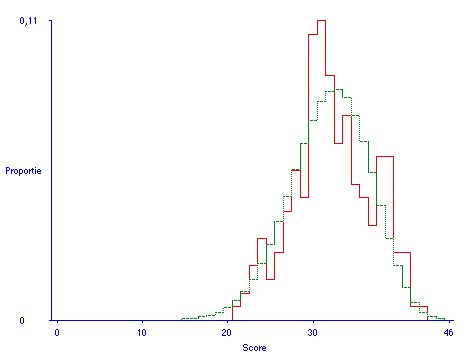
noot 2002. Plot gemaakt met programma Algemeen Toetsmodel, invoerfile met de empirische data voor de empirische verdeling, ptoeftoets 24 goed uit 34 voor de theoretische. De plto als histogram komt beter overeen met het karakter van de verdelingen als frequentieverdeling, dan de oorspronkelijke afbeelding in het cursusboek. Rood; empirisch; groen: theoretisch
(34f)
empirische running
frequentie medians
0,00 0,005 0,090 0,090
0,010 0,010 0,065 0,075
0,020 0,020 0,075 0,065
0,030 0,020 0,050 0,050
0,015 0,025 0,045 0,045
0,025 0,025 01035 0,045
0,040 0,040 0,060 0,060
0,055 0,045 0,060 0,060
0,045 0,055 0,025 0,025
0,105 0,105 0,025 0,025
0,110 0,105 0,005 0,005
0,005 0,005
(35a) De theoretische frequentieverdeling voor de ware beheersing van de studenten is de bètaverdeling met parameters a=24, b=10.
ƒ(p) = (33! / (23! 9!)) × p23 (1-p)9
gem(p) = a / (a+b) = 24/34 = 0,706
(sp)2 = 24×10 / (342×35) = 0,00593
sp = 0,077
(35b) Voor p=0,7 is ƒ(0,7)= 9,2561 × 108 × 2,7369 × 10-4 × 1,9683 × 10-5 = 4,986.
(omdat het quotiënt van de faculteiten in dit geval eenvoudig is te berekenen hoeft de bijzondere techniek in de tekst gepresenteerd niet gebruikt te worden).
ƒ(0,73)=5,07 ƒ(0,70)=4,99 ƒ(0,52)=0,37 ƒ(0,76)=4,44 ƒ(0,67)=4,29 ƒ(0,49)=0,16 ƒ(0,79)=3,25 ƒ(0,64)=3,28 de modus is (a-1)/(a+b²)= 0,719 ƒ(0,82)=1,91 ƒ(0,61)=2,23 ƒ(0,85)=0,85 ƒ(0,58)=1,36 ƒ(0,719)=5,12 ƒ(0,88)=0,25 ƒ(0,55)=0,75
noot 2002: figuur geplot mbv programma Algemeen Toetsmodel als aannemelijkheid voor de ware beheersing gegeven proeftoetsscore van 24 uit 34 ( corresponderend met a = 24 en b = 10; de lengte van de toets speelt hierbij geen rol).
(35c)
68% heeft ware beheersing tussen 0,629 en 0,783
95% ,, ,, ,, ,, 0,552 en 0,860.
(36a) ƒ(p|xi = 40 ) = (79! / (63! 15!)) × p63 × (1-p)15 [gebruik formule 21]
(36b) gemiddelde van deze verdeling is 64/80 = 0,8
variantie van deze verdeling is 64 × 16 / (802 × 81) = 0,0019753
standaarddeviatie van deze verdeling is 0,04444
(36c)
ƒ(0,8|xi = 40) = 3945065 × 1017 × 7,84637 × 10-7 × 3,2768 × 10-11 = 8,87
ƒ(0,83|.) =7,88 ƒ(0,77|.)=6,50 modus is 63/78 = 0,608 ƒ(0,86|.) =4,01 ƒ(0,74|.)=3,34 ƒ(0,808|.) = 9,00 ƒ(0,89|.) =0,93 ƒ(0,71|.)=1,27 ƒ(0,92|.) =0,06 ƒ(0,68|.)=0,37 ƒ(0,95|.) =0,00 ƒ(0,65|.)=0,08

noot 2002: figuur geplot mbv programma Algemeen Toetsmodel als aannemelijkheid voor de ware beheersing gegeven proeftoetsscore van 40 uit 46.
(36d) 67% betrouwbaarheidsinterval ware beheersing student i:
0,8 ± 0,97 × 0,04444 = 0,76 tot 0,84.
90% betrouwbaarheidsinterval ware beheersing student i is:
0,8 ± 1,645 × 0,04444 = 0,73 tot 0,87.
(36e) ƒ(p|x=25) = (79! / (48!×30!)) × p48 × (1-p)30
(36f) gemiddelde van deze verdeling is 49/80 = 0,6125
variantie van deze verdeling is 49.31/(80² × 81) = 0,002930
standaarddeviatie van deze verdeling is 0,05413
(36g) 67% betrouwbaarheidsinterval is 0,56 tot 0,67
90% betrouwbaarheidsinterval is 0,52 tot 0,70.
(36h) regressielijn
V(p|x)= (m / n) + R(x-m) / n = 32,325/46 + 0,570 × (x - 32,325) / 46
wat eventueel te vereenvoudigen is tot 0,0124 × x + 0,302.
(36i) V(p|25) = 0,0124 × 25 + 0,302 = 0,61
V(P|40) = 0,0124 × 40 + 0,302 = 0,80.
Een betrouwbaarheidsinterval geeft de waarschijnlijkheid dat op de lange duur voor deze uitspraken geldt dat de ware beheersing in het aangegeven interval ligt (of: een docent die vaak met dergelijke betrouwbaarheidsintervallen werkt zal op de lange duur in het aangegeven percentage van de gevallen een juiste uitspraak hebben gedaan).
In het voorafgaande cursusmateriaal is het begrip 'betrouwbaarheid' slechts zijdelings aan de orde gesteld. De reden daarvoor is dat 'betrouwbaarheid' in klassieke opvatting slechts marginaal van belang is voor in het onderwijs gebruikte toetsing van de bereikte stofbeheersing. Een uitspraak die lijnrecht in tegenstelling staat tot de belangrijke plaats die in vrijwel ieder boek over toetsen aan 'betrouwbaarheid' van de toetsen toegekend wordt, vandaar een toelichting in deze bijlage.
Van Naerssen ziet de betrouwbaarheidscoeuml;fficieuml;nt als een bruikbare maat voor de waarde of het nut van een toets, en omschrijft hem als volgt:
Wat niet in de definitie staat, maar als vanzelfsprekend wordt beschouwd, is dat de variantie over personen wordt genomen.
De betrouwbaarheid is gelijk aan de correlatie tussen paralleltests, waarbij 'paralleltest' de klassieke betekenis heeft, zie bijvoorbeeld Van Naerssen (1975, par. 15.3). Te onderscheiden zijn dan (Van Naerssen 1975):
Merk op dat zo'n stabiliteitscoëfficiënt niet afhankelijk is van verschillen in gemiddelde score tussen beide afgenomen toetsen. Zou de gemeten stofbeheersing voor alle studenten in de tussenliggende periode ongeveer in gelijke mate gedaald zijn, dan komt dat niet in de stabiliteitscoëfficiënt tot uitdrukking.
Gebruikelijk is om een homogeniteitscoëfficiënt gebaseerd op een splitsing van de toets in de afzonderlijke items, in plaats van een splitsing in twee willekeurige helften, te gebruiken: coëfficiënt alpha, of de variant daarvan die bij 0-1 gescoorde vragen hoort: KR 20, op te vatten als 'een soort gemiddelde homogeniteitscoëfficiënt. Deze laatste worden in de praktijk gehanteerd als aanwijzingen (ondergrenzen) voor de 'betrouwbaarheid' van de toets, wat men veronderstelt of definieert te zijn: 'de mate waarin de toets werkelijk iets meet.' De kwaliteit van de toets wordt dan verondersteld afhankelijk te zijn van deze betrouwbaarheid, en dat is precies het punt dat ik in het volgende kritisch wil bespreken.
Maar eerst nog enkele citaten uit de literatuur over het begrip 'betrouwbaarheid'. De Groot (1970):
Het 'ontbreken van betrouwbaarheid' betekent dat scores over personen niet met elkaar gecorreleerd zijn over replicaties van de toets. Dat hoeft dan nog in het geheel niet te betekenen dat de toets voor deze groep personen een nutteloos en betekenisloos instrument is. Denk aan de 'normale' onderwijsdoelstelling dat alle studenten tot een omschreven niveau van stofbeheersing te brengen zijn. Zou dat lukken, dan wordt de ware-scorevariantie over studenten klein ten opzichte van de foutenvariantie: de betrouwbaarheid is dan gering. Toch kan zo'n toets misschien perfect onderscheiden tussen studenten die het onderwijs gevolgd hebben, en studenten die het niet gevolgd hebben. Dààr vinden we dan een perfecte 'betrouwbaarheid,' hoewel we nog niet weten of het verschil tussen beide groepen ook toe te schrijven is aan het gegeven onderwijs (het laatste is de vraag naar de validiteit van het verschil tussen beide groepen studenten). Het is dus zaak zich terdege te realiseren in welke meetvraag je eigenlijk geinteresseerd bent, voordat je begint met bepaalde 'betrouwbaarheidscoëfficiënten' uit te rekenen. Ook voor de betrouwbaarheid geldt wat overigens voor de validiteitsvraag meer gemeengoed is: in de regel zul je antwoorden op je vraag slechts door experimenteren, door onderzoek, kunnen verkrijgen.
Voor toetsen zoals die in het onderwijs gebruikt worden, zal zo'n betrouwbaarheidsexperiment dan ook vaak de vorm kunnen hebben van een toetsafname aan deelgroepen studenten die op bekende wijze verschillen in de mate waarin zij aan het onderwijs hebben deelgenomen. Althans, dat is het uitgangspunt, waarna er nog heel wat moeilijkheden te overwinnen zijn voordat het experiment zèlf een voldoende mate van betrouwbaarheid en validiteit heeft verkregen om goede antwoorden te kunnen leveren. Cronbach, Gleser, Nanda en Rajaratnam hebben de nodige statistische werktuigen hiervoor aangedragen (Cronbach et al. 1972). Dan is het nog maar de vraag of alle moeite wel in goede verhouding staat tot de waarde van de resultaten die dergelijk onderzoek naar verwachting op zal leveren.
Er is nog een andere voor de hand liggende parallel met de validiteitsproblematiek, een parallel die scherp onderstreept om welk specifiek probleem het gaat. Het is een bekend verschijnsel dat een voorspellende toets voor gebruik bij bijvoorbeeld personeelsselectie bij validerings onderzoek op ongeselecteerde (althans niet op de onderhavige test geselecteerde) personen een hoge voorspellende waarde kan bezitten, maar die in later jaren wanneer de test operationeel is ogenschijnlijk verloren lijkt te hebben: binnen de groep op deze test geselecteerde personen is de voorspellende waarde gering geworden. Het punt is natuurlijk dat de validiteit van deze test niet op de groep geselecteerden, maar op de te selecteren groep betrekking heeft. Zo ook met toetsen in het onderwijs: wie toetsen gebruikt om er verschillen tussen studenten in hun mate van stofbeheersing mee vast te stellen, zal er bij onderzoek naar de betrouwbaarheid van de toets in dit opzicht ook voor moeten zorgen dat om te beginnen de groep studenten die de toets aflegt ook door belangrijke verschillen in dat opzicht gekenmerkt is. Verschillen die er niet zijn kan een toets nimmer aantonen, het is de vraag of de toets gevoelig genoeg is om verschillen die er wèl zijn ook in de scores tot uitdrukking te brengen. Naief gebruik van betrouwbaarheidscoëfficiënten, zoals door vele tekstboekschrijvers jammer genoeg aangeraden, gaat er stilzwijgend vanuit dat in iedere groep personen die een toets aflegt belangrijke verschillen tussen personen aanwezig zijn. Heb je reden om te veronderstellen dat inderdaad belangrijke verschillen tussen personen aanwezig zijn (verschillen in stofbeheersing), ja, dan zal je toets tenminste ook betrouwbaar moeten zijn. Maar heb je om te beginnen geen reden om die veronderstelling aan te hangen, dan is iedere interesse in 'betrouwbaarheid' van de toets misplaatst.
Ebel (1962) construeerde een aardige figuur, waarmee hij heel dicht in de buurt van bovenstaand inzicht kwam (figuur A.1 is een reconstructie). Ebel:
[nb 2002: de plotjes zijn niet exact, daarvoor ontbreken ook de nodige aanvullende gegevens zoals groepssamenstelling en dergelijke, die mede van invloed zijn op de betrouwbaarheid).
De essaytoets van Ebel mag dan relatief onbetrouwbaar zijn, wanneer je als docent er allereerst in geïnteresseerd bent of je studenten boven de 'passing score' van 80 uit komen, dan kun je met dergelijke toetsresultaten bijzonder tevreden zijn. Zou bij verder onderzoek blijken dat studenten die het onderwijs niet gevolgd hebben essays maken die niet boven die 80 punten uit komen, dan is de toets perfect 'betrouwbaar' in het maken van het onderscheid tussen studenten die het onderwijs wél, en die het niet gevolgd hebben. Kijk je naar de scoreverdeling over de meerkeuze toets, dan zie je onmiddellijk dat met deze toets het maken van een goed onderscheid tussen die twee groepen studenten niet mogelijk is, omdat voor de groep die het onderwijs niet gevolgd heeft de toetsscores verdeeld zullen zijn rond de kansscore, en aanzienlijk zullen overlappen met de scores in het lage gebied, van studenten die het onderwijs wel volgden. Fraaier illustratie van het onnut van deze klassieke betrouwbaarheid had Ebel moeilijk kunnen bedenken.
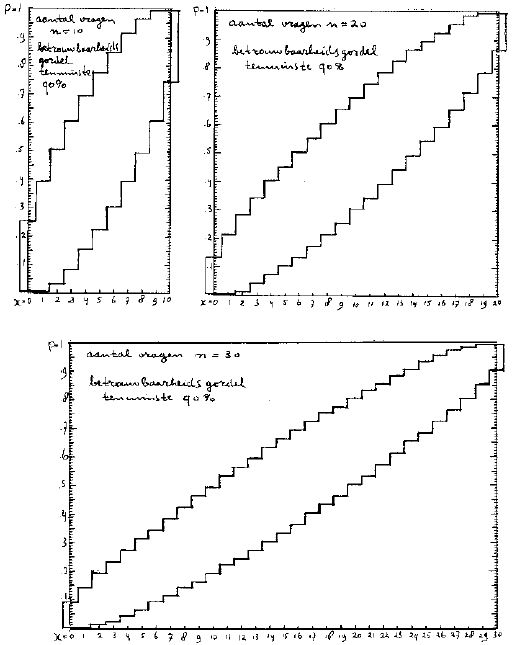
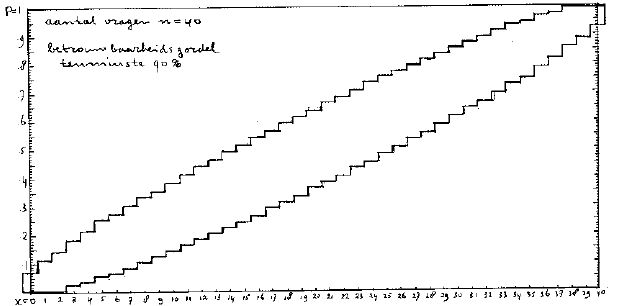
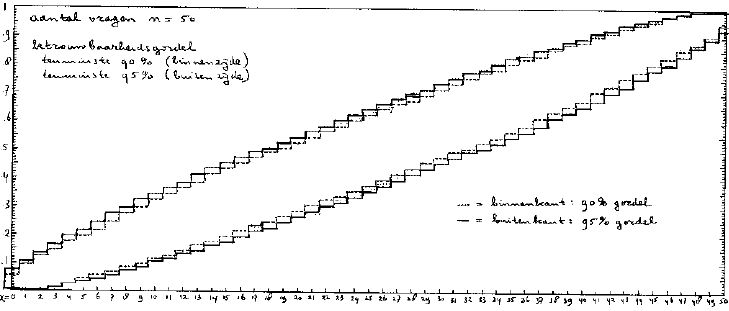
ANDERSON, R.C., How to construct achievement tests to assess comprehension. Review of Educational Research, 1972, 42, 145-170.
BLOOM, B.S. (Editor) Taxonomy of educational objectives: cognitive domain. 1956. Longman (17e druk).
BLOOM, B.S., HASTINGS, J.T. en MADAUS, G.F. Handbook on formative and summative evaluation of student learning. London: McGraw Hill, 1971.
BHUSHAN, V. en GINTHER,J.R. Discriminitating between a good and a poor essay. Behavioral Science, 1968, 13, 417420.
BORING, E.G., A historp of experimental psychology. New York: Appleton CenturyCrofts, 1957.
BRACHT, G.H., HOPKINS, K.D., en STANLEY, J.C., Perspectives in educational and psychological measurement. London: Prentice Hall, 1972.
BRELAND, H.M., en GAYNOR, J.L., A comparison of direct and indirect assessments of writing skill. Journal of Educational Measurement, 1979, 16, 119-128.
BREUKER, J. In kaart brengen van leerstof. C.O.W.O., U.v.A., 1979.
COHEN, M.J., Contracten in het hoger onderwijs. In Crombag en Chang (red) 1978.
COHENSCHOTANUS, J. Hoe langer hoe beter. De relatie tussen voorbereidingstijd en tentamenresultaat bij medische studenten te Groningen,0.R.D., 1979. Buro Onderwijs Ontwikkeling Geneeskunde, Groningen.
COFFMAN, W.E., Essay toetsen. In Vroon en Everwijn (red) deel 4.
COFFMAN, W.E., On the validity of essay tests of achievement. Journal of Educational Measurement. 1966, 3, 151 156. Herdrukt in Bracht, Hopkins en Stanley, 1972.
CROMBAG, H.F., en CHANG, T.M. Een kleine zoölogie van het onàerwijs. Leiden. Universitaire Pers, 1978.
CROMBAG, H.F., GAFF, J.G., en CHANG, T.M., Study behavior and academic performance. Tijdschrift voor onderwijsresearch, 1976, 1, 3-14.
CROMBAG, H.F.M., ROSKAM, E.E.Ch.I., en MEUWESE, W.A.T.,. Het meten van studiebelasting. In Van Woerden et al. (1973).
CROMBAG, H.F.M., DE WIJKERSLOOTH, J.L. en VAN TUYLL VAN SEROOSKERKEN, E.H.,Over het oplossen van casusposities.Groningen: Tjeenk Willink, 1972.
CURETON, E.E., Validity, reliability, and baloney. Educational and Psychological Measurement, 1950, 94-96. Herdrukt in Mehrens en Ebel (1967).
DRAPER, N. en GUTTMAN, I., Two simultaneous measurement procedures; a Bayesian approach. Journal of the American Statistics Association, 1975, 70, 43-46.
DUNCAN, O.D., Introduction to structural equation models. London, Academic Press, 1975.
EBEL, R.L., Measurement and the teacher. Educational Leadership, 1962, 20 (october 1962): 20-24, 43. Herdrukt in Mehrens, (1976).
EBEL, R.L.,Essentials of educational measurement. London: Prentice Hall, 1979.
EVERWIJN, S.E.M., en MUGGEN, G.,Methoden voor het meten van studietijd. In Van Woerden et al. (18-73).
GAGNÉ, E.D., Longterm retention of informmation following learning f rom prose. Review of Educational Research, 1978, 48, 629-665.
GAGNé, R.M., The conditions of learning. London: Holt, Rinehart and Winston, 1977.
GAGNé, R.M., en MERRILL, M.D., The content analysis of subject matter. Instructional Science, 1976, 5, 128.
GREEP, J.M, Het onderwijs aan de medische faculteit in Maastricht. Medisch Contact, 1979, nr. 35, 1107-1114.
GREGSON, R.A.M., Psychometrics of similarity. London: Academic Press, 1975.
GROOT, A.D. de, Thought and choice in chess. Den Haag: Mouton, 1978.
GROOT, A.D. de, Some badly needed nonstatistical concepts in applied psychometrics. Nederlands Tijdschrift voor de Psychologie, 1970, 25, 360-376. html
GROOT, A.D. de, en R.F. VAN,NAERSSEN (red.) Studietoetsen: construeren, afnemen, analyseren. Den Haag: Mouton, 1975. (deel I en II).
GRUYTER, D.N.M. Psychometrische aspecten van tentamens. proefschrift R.U. Leiden, 1977.
GULLIKSEN, H., Theory of mental tests, New York: Wiley, 1950.
Standards for educational and psychological tests, Washington, D.C.: American Psychological Association, 1974.
HAMAKER, C., en WOUTERS, L., The production of achievement test items by computer programs, Psychologisch laboratorium, Universiteit van Amsterdam, Weesperplein 8, Amsterdam
HAMBLETON, R.K., On the use of cutoff scores with criterionreferenced tests in instructional settings. Journal of Educational Measuronent, 1978, 15, 277-290.
HAMBLETON, R.K., EIGNOR,.D.R., en ROVINELLI, R.J., Toward better achievement tests and testscore interpretations in PSI courses. Journal of Personalized Instruction, 1978, 3, 180-186.
HARROW, A.J., A taxonomy of the psychomotor domain; a guide for developing behavioral objectives New York: McKay, 1972.
HOFSTEE, W.K.B., De betrouwbaarheid van zak-slaag beslissingen. Nederlande Tijdschrift voor de Psychologie, 1970, 25, 380-383.
HOFSTEE, W.K.B., Participatie controle door 'onbenullige' toetsitems. Nederlands Tijdschrift voor de Psychologie, 1973, 28, 189-198. Ook in Vroon en Everwijn (red.) deel 4.
HOEL, P.G., Introduction to mathematical statistics. London: Wiley, 1962.
IMBOS, Tj., en VERWIJNEN, M., Evaluatie aan de medische faculteit Maastricht. Metamedica, 1978, 57, 21-32.
KENDALL, M.G., en STUART, A., The advanced theory of statistics, volume II, London: Griffin, 1967.
KLAUSMEIER, H.J. en ALLEN, P.S., Cognitive development of children and youth; a longitudinal study. London: Academic Press, 1978
KLAUSMEIER, H.J., CHATALA, E.S., en FRAYER, D.A., Conceptual learning and development; a cognitive view. London: Academic Press, 1974.
KRATHWOHL, D.R., BLOOM, B.S., en MASIA, B.B., Taxonomy of educational objectives: the classification of educational goals, Handbook II: Affdctive domain. New York: Mc Kay, 1964.
KRATHWOHL, D.R., en PAYNE, D.A., Defining and assessing educational objectives. In Thorndike, R.L. (Editor)
KREVELD, D. VAN, De onbetrouwbaarheid van het oordeel over een open vraag. Nederlands Tijdschrift voor Psychologie, 1971, 26, 592-595. KUDER, G.F., EN RICHARDSON, M.W., The theory of the estimation of test reliability. Psychometrika, 1937, 2, 151160. Herdrukt in Mehrens en Ebel (1967).
LANDA, L.N., ALgorithmization in learning and instruction, Englewood Cliffs, N.J.: Educational Technology Publications, 1976.
LANDA, L.N., Instructional regulation and control. Cybernetics, algorithmization and heuristics in education. Englewood Cliffs, N.J.: Educational Technology Pyblications, 1976.
LANS, W. en MELLENBERGH, G.J., Constructie en beoordeling van items: formele aspecten. In De Groot en Van Naerssen (1975).
LERNER, B., The Supreme Court and the APA, AERA, NCME Test Standards: past references and future possibilities. American Psychologist, 1978, 33, 915-919.
LINDEN, W.J. VAN DER, Pretestposttest validatie van criterium georienteerde toetsen.Congresboek Onderwijs Research Dagen 1977, 129-134.
LINN, R.L., KLEIN, S.P., en HART, F.M., The nature and correlates of law school essay grades. Educational and Psychologicat measurement, 1972, 32, 267-279.
LORD, F.M., Do tests of the same length have the same standard error of measurement? Educational and Psychological Measurement, 1957, 17, 510-521. Herdrukt in Mehrens en Ebel (1967).
LORD, F.M. en NOVICK, M.R., Statistical theories of mental test scores. London: AddisonWesley, 1968.
LUSTED, L.B., Introduction to medical decision making. Springfield, Illinois: Thomas, 1968.
MAYER, R.W., Student guide to John P. de Cecco The psychology of learning and instruction: educational psychology. Englewood Cliffs, N.J.: Prentice Hall, 1968.
McCLOSKEY, M. en CLUCKSBERG, S., Decision processes in verifying category membership statements: implications for models of semantic memory. Cognitive Psychology, 1979, 11, 137.
WGUIRE, C.H., SOLOMDN, L.M., en FORMAN, P.M., Clinical simulations, selected problems in patient management. New York; Appleton Century Crofts, 1976.
MEHRENS, W.A. (editor), Reading in measurement and evaluation in education and psychology, London: Holt, Rinehart and Winston, 1976.
MEHRENS, W.A., en EBEL, R.L. (Editors) Principles of educational and psychological measurement. Chicago: Rand McNally, 1967.
MEHRENS, W.A., en LEHMANN, I.J., Measurement and evaluation in education and psychology. London: Holt, Rinehart and Winston, 1975.
MELLENBERGH, G.J., Studies in studietoetsen (proefschrift). Amsterdam; RITP, 1971.
MELLENBERGH, G.J., Een onderzoek naar het beoordelen van open vragen. Nederlands Tijdschrift voor de Psychologie. 1971, 26, 102-120.
METTES, C.T.C.W., PILOT, A. en ROOSSINK, H.J., Het leren oplossen van problemen in de thermodynamika. T.H. Twente, onderwijskundig centrum CDO/AVC no 38, 1979.
MOULY, G.J. en WALTON, L.E., Test items in education. (Schaum's outline series). New York: McGrawHill, 1962.
NAERSSEN, R.F. VAN , Betrouwbaarheid. In De Groot, A.D. en Van Naerssen, R.F. deel 11 (1975, 227-247).
NAERSSEN, R.F. VAN De interpretatie van indices. In De Groot, A.D., en Van Naerssen, R.F. deel 11 (1975, 260-274).
NEWELL, A. en SIMON, H.A., Human problem solving, London: PrenticeHall, 1972.
NORMAN, D.A. en BOBROW, D.G. , Descriptions: an intermediate stage in memeory retrieval. Cognitive Psychology, 1979, 107-123.
NOVICK, M.R., en JACKSON, P.H., Statistical methods for educational and psychological research. Düsseldorf: McGrawHill, 1974.
Richtlijnen Voor ontwikkeling en gebruik van psychologische tests en studietoetsen. Nederlands Instituut voor Psychologen, 1978.
ROSCH, E., On the internal structure of percepual and semantie categories. In T.E. Moore (cd.) Cognitive development and the acquisition oflanguage London: Academic Press, 1973.
ROSCH, E., en MERVIS, C.B.Jamily resemblances: studies in the internal structure of categories. Cognitive Psychologie, 1975, 7, 573-605.
SALOMON, G., Heuristic models of the generation of aptitudetreatment Wteraction hypotheses. Review of EducationaL Research, 1972, 42, 327-343.
SEDDON, G.M., The properties of Bloom's taxonomy of educational objectives for the cognitive domain. Review of Educational Research, 1978, 48, 303-323.
SMAL, J.A., Machinaal vervaardigen van toetsvragen,Onderzoek van Onderwijs, 1977, nr. 4, jaargang 6, 38.
SNEATH, P.H.A. en SOKAL, R.R., Numerical taxonamy, the principles and practice of numerical classification. San Francisco: Freeman, 1973.
Standards for educational and psychological tests. Washington, D.C.: American Psychological Association, 1974.
STANLEY, J.C., Reliability. In Thorndike, R.L. (1971), 356-442.
STANLEY, J.C. en HOPKINS, K.D., Educational and psychological measurement and evaluation. London: PrenticeHall, 1972.
STERN, C., Principles of human genetics, San Francisco: Freeman, 1973.
TROMP, D. en WILBRINK, B., Het meten van studietijd. Congresboek Onderwijs Research Dagen 1977, 186-189.
TROMP, D., Het oordeel van studenten in een individueel studie systeem.(IR.D. 1979.
TUKEY. J.W., Exploratory data analysis. London: AddisonWesley, 1977.
VERPAALEN, O.A.C., Beroep tegen examen en tentamen. artikel 40 WVB, Zwolle: Tjeenk Willink, 1978.
VLEUGEL, H. VAN DER , W.K.B. HOFSTEE, H. VAN DIJK, H.GROEN en J.COHEN SCHOTANUS, Begripsvalidatie van een studietoets. Nederlands tijdeehrift voor de Psychologie, 1973, 28, 237-347.
VROON, A.G., en EVERWIJN, S.E.M. (red.), Handboek voor de onderwijspraktijk Deventer: Van Loghum Slaterus, losbladig.
WICKELGREN , W.A., Cognitive Psychology, London: Prentice Hall, 1979. WILBRINK, B., Studiestrategieën, COWO, U.v.A., 1978
WILBRINK, B., Cesuurbepaling (2e versie). COWO, U.v.A., 1980. html
WILCOX, R.R.,Estimating true score in the compound binomial error model. Psyohometrika, 1978, 43, 245-258.
WILMINK, F.W., Publikatie van tentamenvragen en tentamenscore. Tijdschrift voor Onderwijs Research, 1977, 2, 157-164.
WOERDEN, W.M. VAN , CHANG, T.M., en VAN GEUNS-WIEGMAN, L.J.M., Onderwijs in de maak. Utrecht, het Spectrum, 1973.
WIJK, H.D. VMT ,en KONIJNENBELT, W., Hoofdstukken van administratief recht. 's Gravenhage, VUGA, 1976.
Ik heb geen poging gedaan deze lijst te actualiseren naar de 21e eeuw. In het algemeen is recente literatuur goed te vinden door auteur en titel van oude publicaties als zoektermen in bijvoorbeeld Google te gebruiken.
In de cursustekst zijn een aantal onderwerpen slechts zijdelings of in het geheel niet behandeld. Om dat enigszins goed te maken geef ik hier enkele titels op onderwerp, bedoeld als ingang tot de betreffende literatuur. Ook voor enkele andere onderwerpen wordt hier nog een enkele extra literatuurverwijzing gegeven.
Kortheidshalve zijn de meeste tijdschrift titels afgekort:
AERJ American Educational Research Journal
APM Applied Psychological Measurement
BrJMSP British Journal of Mathematical and Statistical
Psychology
EPM Educational and Psychological Measurement
JEM Journal of Educational Measurement
JEP Journal of Educational Psychology
NTvdP Nederlands Tijdschrift voor de Psychologie
PB Psychological Bulletin
Pm Psychometrika
RER Review of Educational Research
TOR Tijdschrift voor Onderwijsresearch
Thorndike 1971: Thorndike, R.L. (Editor) Educational Measurement. Washington, D.C.: American Council on Education, 1971. (een 'must' voor iedere geinteresseerde)
automatisering (zie ook toetsen: flexibele)
Baker, F.B. Automation of test scoring, reporting, and analysis. In Thorndike 1971.
Hamer, R. & Young, F.W. TESTER: A computer program to produce individualized multiple choice tests. EPM 1978, 38, 819-821.
Holtzman, W.H. (Ed.) Computerassisted instruction, testing, and guidance. London: Harper & Row, 1970.
Lippey, G. (Ed.) Computerassisted test construction. Englewood Cliffs, N.J.: Educational Technology Publications 1974.
beheersingsleren & toetsen (zie ook criteriumgerefereerd toetsen)
Block, J.H. & Burns, R.B. Mastery learning. In Shulman, L.S. (ed) Review of research in education volume 4. Itasca, Ill.: Peacock, 1977.
Hambleton, R.K. Testing and decisionmaking procedures for selected individualized instructional programs.RER 1974,44, 371-400.
Torshen, K.P. The mastery approach to competencybased education. London: Academic Press, 1977.
betrouwbaarheid (zie ook homogeniteit)
Cureton, E.E. The definition and estimation of test reliability. EPM 1958, 18, 715-738. Ook in Mehrens, W.A. & Ebel , R.L. (Eds.) Principles of educational and psychological measurement. Chicago: Rand McNally, 1967.
Hofstee, W.K.B. Toetsbetrouwbaarheid bij mastery learning. TOR 1975, 1, 43-45.
Lumsden, J. Person reliability. APM 1977, 1, 477-482.
Lumsden, J. Tests are perfectly reliable. BrJMSP 1978, 31, 1926.
Werts, C.E., Rock, D.R., Linn, R.L., & Vreskog, K.G. A general method of estimating the reliability of a composite. EPM 1978, 38, 933-938.
Williams, R.H. & Zimmerman, D.W. The reliability of difference scores when errors are correlated. EPM 1977, 37, 679-689.
Woodward, J.A. & Bentler, P.M. A statistical lower bound to population reliability. PB 1978, 85, 1323-1326.
Zwarts, M. Betrouwbaarheidsonderzoek met behulp van de generaliseerbaarheidstheorie. TOR 1978, 3, 61-73.
betrouwbaarheid van beoordelingen (overeenstemming) (zie ook persoonsbeoordeling)
Brennan, R.L. & Kane, M.T. An index of dependability for mastery tests. JEM 1977, 14, 277-289
Hubert, J.J. Comparison of sequences. PB 1979, 86, 1098-1106.
Kamp, L.J.Th van der Betrouwbaarheid van beoordelingen van open vragen: eenvoudige correlatietechnieken. NTvdP 1972, 27, 460-470.
Mitchell, S.K. Interobserver agreement, reliability, and generalizability of data collected in observational studies. PB 1979, 86, 376-390.
Shrout, P.E. & Fleiss, J.L. Intraclass correlations: uses in assessing rater reliability. PB 1979, 86, 420-428.
Singer, B. Distributionfree methods for nonparametric problems: a classified and selected bibliography. BrJMSP 1979, 32, 160 (esp. p. 5455 on agreement).
betrouwbaarheid van beslissingen
Hofstee, W.K.B. De betrouwbaarheid van zak-slaag beslissingen. NTvdP 1970, 25, 380-383.
Huynh, H. On the reliability of decisions in domain referenced testing. JEM 1976, 13, 265-276.
Huynh, H. Reliability of multiple classifications. Pm 1978, 43, 317-325.
Mellenbergh, G.J. & van der Linden, W.J. The internal and external optimality of decisions based on tests. APM 1979, 3, 257-273.
Naerssen, R.F. van Lokale betrouwbaarheid: begrip en operationalisatie. TOR 1977, 2, 111-119.
Naerssen, R.F. van Lokale discriminatie bij twee en vierkeuzetoetsen. TOR 1978, 3, 131-133.
Subkoviak, M.J. The reliability of mastery classification desicions. Unpublished paper, 1978.
betrouwbaarheid van profielen en samengestelde toetsen Conger, A.J. & Lipshitz, R. Measures of reliability for profiles and test batteries. Pm 1973, 38, 411-427.
Maxwell, A.E. Estimating true scores and their reliabilities in the case of composite psychological tests. BrJMSP 1971, 24, 195-204.
binomiaal foutenmodel
Wilcox, R.R. Estimating the likelihood of falsepositive and falsenegative decisions in mastery testing: an empirical Bayes approach. Journal of Educational Statisties 1977, 2, 289-307.
Wilcox, R.R. Estimating true score in the compound binomial error model. Pm 1978, 43, 245-258.
cesuurbepaling (zie ook krit. geref. toetsen en beheersings l.)
Glass, G.V. Standards and criteria. JEM 1978, 15, 236-261.
Cruijter, D.N.M. de A Bayesian approach to the passing score problem. TOR 1978, 3, 145-151.
Wilcox, R.R. A lower bound to the probability of choosing the optimal passing score for a mastery test when there is an external criterion. Pm 1979, 44, 245-249.
Wijnen, W.H.F.W. Onder of boven de maat. Een methode voor het bepalen van de grens voldoende/onvoldoende bij studietoetsen. Amsterdam: Swets & Zeitlinger, 1972.
Zegers, F.E., Hofstee, W.K.B. & Korbee, C.J.M. Een beleidsinstrument m.b.t. cesuurbepaling. Paper ORD 1978. R.U. Groningen, subfaculteit Psychologie, vakgroep persoonlijkheidsleer. (zie ook normhandhaving)
Angoff, W.H. Scales, norms, and equivalent scores. In Thorndike 1971.
Baird, L. & Feister, W.J. Grading standards: the relation of changes in average student ability to the average grades awarded. AERJ 1972, 9, 431-441.
Hewitt, B.N. & Jacobs, R. Student perseptions of grading practices in different major fields. JEM 1978, 15, 213-218.
Hills, J.R. Consistent college grading standards through equating. EPM 1972, 32, 137-146.
Hofstee, W.K.B. selectie van personen. Inaugurele rede. Assen: Van Gorcum, 1970.
Lewis, W.A., Dexter, H.G. & Smith, W.C. Grading procedures and test validation: a proposed new approach. JEM 1978, 15, 219-228.
Naerssen, R.F. van Het schalen van testscores. NTvdP 1972, 27, 471-485.
Nuttall, D.L., Backhouse, J.K. & Wilmott, A.S. Comparability of standards between subjects. Schools Council Examinations Bulletin 29, London: Evans/Methuen Educational, 1974.
Schoenfeldt, L.F. & Brush, D.H. Patterns of college grades across curricular areas: some implications for GPA as a eriterion. AERJ 1975, 12, 313-321.
essaytoetsen
Breuker, J. & van der Roest, W. Conceptual structure of texts: a study in the validity of scoring essay examinations. TOR 1978, 3, 10-21.
Draper, N. & Guttman, I. Two simultaneous measurement procedures: a Bayesian approach. Journal of the American Statistical Association 1975, 70, 43-46.
Kreeft, H. & Sanders, P. Correctiemodellen bij examens in open vraagvorm. Paper ORD 1979. Arnhem: CITO projekt Open Vragen 1979.
Paul, S.R. Models and estimation procedures for the calibration of examiners. BrJMSP 1979, 31, 242-251.
Tluanga, L.N. A scaling formula for bounded mark intervals. BrJMSP 1974, 27, 53-61.
ethische en juridische aspecten
Byham, W.C. & Spitzer, M.E. The law and personnel testing. American Management Association, 1971.
Holman, M.G. & Docter, R. Educational and psychological testing: a study of the industry and its practices. New York: Russell Sage, 1972.
Jackson, D.N. & Messick, S. (Eds) Problems in human assessment. London: McGrawHill, 1967. Esp. Part 9: The ethics of assessment.
Kirkland, M.C. The effects of tests on students and schools. RER 1971, 41, 303-350.
Kirp, D.L. & Yudof, M.G. Educational policy and the law. Berkeley, Calif.: McCutchan, 1974.
Strien, P.J. van (red.) Personeelsselectie in discussie. Meppel: Boom, 1976.
Tyler, R.W. & Wolf, R.M. (Eds) Crucial issues in testing. Berkeley, Calif.: McCutchan, 1974.
College Entrance Examination Board Report of the commission on tests. New York: CEEB, 1970. (two volumes).
examenvrees
Spielberger, Ch. D. et al. Examination stress and test anxiety. In Spielberger, Ch. D. & Sarason, I. G. (Eds) Stress and anxiety, volume 5. London: Wiley, 1978.
frequentie van toetsing
Gaynor, J. & Millham, J. Student performance and evaluation under variant testing methods in a large college course. JEP 1976, 68, 312-317.
homogeniteit (_&_KR_20)
Hartke, A.R. The use of latent partition analysis to identify homogeneity of an item population. JEM 1978, 15, 4348.
Lumsden, J. Tests are perfectly reliable. BrJMSP 1978, 31, 1926.
Terwilliger, J.S. & Lele, K. Same relationships azong internal consistency, reproducibility, and homogeneity. JEM 1979, 16, 101-108.
individuele verschillen (zie ook intelligentie)
Biggs, J.B. Individual and group differences in study processes. British Journal of Educational Psychology, 1978, 48, 266-279.
Carroll, J.B. How shall we study individual differences in cognitive abilities? methodological and theoretical perspectives. Intelligence, 1978, 2, 87-115.
Polachek, S.W., Kniesner, T.J. & Harwood, H.J. Educational production functions. Journal of Educational Statistics 1978, 3, 209-231.
Schmeck, R.R., Ribich, F. & Ramanaiah, N. Development of a selfreport inventory for assessing individual differences in learning processes. APM 1977, 1, 413-431
Sperry, L. (Ed.) Learning performance and individual differences. Glenview, Ill.: Scott, Foreman & Cy, 1972.
Willerman, L. The psychology of individual and group differences. San Francisco: Freeman, 1979.
instructie voor beantwoording (zie ook raadkans)
Clemans, W.V. Test administration. In Thorndike 1971.
Naerssen, R.F. van Correctie voor raden en ethiek. TOR 1979, 4, 90-91.
intellectuele capaciteiten
Cattell, R.B. Abilities: their structure, growth and action. New York: Houghton Mifflin, 1971.
Eysenck, H.J. (Ed.) The measurement of intelligence. Lancaster: MTP Medical and Technical Publishing Co., 1973.
Eysenck, H.J. The structure and measurement of intelligence. Heidelberg: Springer, 1979.
Green, D.R. (Ed.) The aptitudeachievement distinction. Monterey, Calif.: CTB/MeGrawHill, 1974.
Guilford, J.P. & Hoepfner, R. The analysis of intelligence. Düsseldorf: MeGrawHill, 1971.
Humphreys, L.G. The construct of general intelligenee. Intelligence 1979, 3, 105-120.
Pellegrino, J.W. & Lyon, D.R. The components of a componential analysis. Review of Sternberg's "Intelligence, information processing and analogical reasoning: the componential analysis of human abilities.'' Intelligence, 1979, 3, 169-186.
Royce, J.R. Multivariate analysis and psychological theory. The third Banff conference on theoretical psychology. London: Academic Press, 1973.
Sternberg, R.J. Intelligenee research at the interface between differential and cognitive psychology: prospects and proposals. Intelligence 1978, 2, 195-222.
Sternberg, R.J. The nature of mental abilities. American Psychologist 1979, 34, 214-230.
intelligentie tests (zie ook ethische en juridische aspecten)
Cronbach, L.J. Five decades of public controversy over mental testing. American Psychologist 1975, 30, 114.
interpretatie van toetsscores (zie ook toetsen)
Hashway, R.M. Objective mental measurement. Individual and program evaluation using the Rasch model. London: Praeger, 1978.
Linden, W.J. van der Het klassieke testmodel, latente trek modellen en evaluatieonderzoek. Vereniging voor Onderwijs Research publikatiereeks no 7 ongedateerd, ook uitgegeven door de Onderafdeling Toegepaste Onderwijskunde, T.H. Twente, juli 1978.
Lord, F.M. An interval estimate for making statistical inferences about true scores. Pm 1976, 41, 79-87.
Lord, F.M. Some item analysis and test theory for a system of camputer assisted test construction for individualized instruction. APM 1977, 1, 447-455.
Lord, F.M. Estimating truescore distributions in psychological testing (an empirical Bayes estimation problem). Pm 1969, 34, 259-299.
Hofstee, WK.B. Schatting van de true score met inachtneming van andere variabelen. TOR 1979, 4, 38-40.
Werts, C E. & Linn, R.L. Estimating true scores using group membership. EPM 1972, 32, 323-327.
item form (zie ook criterium gerefereerd toetsen)
Durnin, J.H. & Scandura, J.M. Algorithmic approach to assessing behavior potential: camparison with item forms. In Scandura, J.M. (Ed.) Problem solving. A structural/process approach with instructional implications.London: Academic Press, 1977.
keuzevragen (optional questions)
DuCette, J. & Wolk, S. Test performance and the use of optional questions. Journal of Experimental Education 1972, 40 no 3, 21-24
Willmott, A.S. & Hall, C.G.W. O-level examined: the effect of question choice. London: MacMillan Education, 1975
contracten
Yarber, W.L. Retention of knowledge: grade contract method campared to the traditional grading method. Journal of Experimental Education 1974, 43 no 1, 92-95.
criteriumgerefereerd toetsen (zie ook cesuurbepaling)
Hambleton, R.K., Swaminathan, H., Algina, J. & Coulson, D.B. Criterion referenced testing and measurement: a review of technical issues and developments. RER 1978, 48, 147.
Harris, C.W., Alkin, M.C. & Popham, W.J. (Eds.) Problems in criterionreferenced measurement. (CSE Monograph no 3). Los Angeles: Center for the study of evaluation, University of California, 1974.
Hively, W., Maxwell, G., Rabehl, G., Sension, D. & Lundin, S. Domain referenced curriculum evaluation: a technical handbook and a case study from the Minnemast project. (CSE monograph no l). Los Angeles: Center for the study of evaluation, University of California, 1973.
Popham, W.J. Criterionreferenced measurement. Englewood Cliffs, N.J.: PrenticeHall, 1978.
Wilbrink, B. Optimale criterium gerefereerde grensscores zijn eenvoudig te vinden. TOR 1980 in druk. html
Wilbrink, B. Enkele radikale oplossingen voor criterium gerefereerde grensscores. TOR 1980 in druk. html
Zwarts, M. Criterium toetsen, een overzicht. AP onderzoek, vakgroep onderwijskunde, R.U. Utrecht, Heidelberglaan 1. November 1979.
lay-out en productie
Thorndike, R.L. Reproducing the test. In Thorndike 1971.
lengte van de toets (zie ook betrouwbaarheid)
Novick, M.R. & Lewis, Ch. Prescribing test length for criterionreferenced measurement. In Harris, Alkin & Popham 1974, zie onder criterium gerefereerd toetsen.
Alker, H.A., Carlson, J.A. & Hermann, M.G. Multiplechoice questions and student characteristics. JEP 1969, 60, 231-243.
Brink, W.P. van den Het optimale aantal alternatieven per item. TOR 1979, 4, 151-158.
Frisbie, D.A. The effect of item format on reliability and validity: a study of multiple choice and truefalse achievement tests. EPM 1974, 34, 885-892.
Langerak, W.F. Herkennen vs herinneren, aftewel meerkeuze vs opstelvragen. TOR 1979, 4, 140-143.
Lord, F.M. Optimal number of choices per item a comparison of four approaches. JEM 1977, 14, 33-38.
Naerssen, R.F. van Discriminerend vermogen van toetsen met twee en met vierkeuze items. TOR 1976, 1, 269-272.
Naerssen, R.F. van - Optimal number of choices in parallel item tests. TOR 1979, 4, 145-130.
Traub, R.E. & Fisher, Ch.W. On the equivalence of constructedresponse and multiple choice tests. APM 1977, 1, 355369.
moeilijkheid
Gotts, E.E. Ability and test anxiety as factors in 'the influence of test difficulty upon study efforts and achievement'? AERJ 1971, 8, 576-579.
Marso, R.N. The influence of test difficulty upon study efforts and achievement. AERJ 1969, 6, 621-632.
Quereshi, M.Y. & Fisher, T.L. Logical versus empirical estimates of item difficulty. EPM 1977, 37, 91-100.
mondeling toetsen
Birkel, P. Mündliche PrUfungen. Zur objectivität und Validität der Leistungsbeurteilung. Bochum: Ferdinand Kamp, 1978.
motivatie
Atkinson, J.W., Lens, W. & O'Malley, P.M. Motivation and ability: interactive psychological determinants of intellective performance, educational achievement, and each other. In Sewell, W.H., Hauser, R.M. & Featherman, D.L. (Eds.) Schooling and achievement in american society. London: Academic Press, 1976.
Ball, S. (Ed.) Mbtivation in education. London: Academie Press, 1977.
Kuhl, J. & Blankenship, V. The dynamic theory of achievement motivation: from episodic to dynamic thinking. Psychological Review 1979, 86, 141-151.
Revelle, W. & Michaels, E.J. The theory of achievement motivation revisited: the implications of inertial tendencies. Psychological Review 1976, 83, 394-404.
nabootsen van toetsresultaten
Lehman, R.S. Computer simulation and modeling: an introduction. Hillsdale, N.J.: Lawrence Erlbaum Ass. 1977.
Marks, E. & Lindsay, C.A. Some results relating to test equating under relaxed test form equivalnece. JEM 1972, 9, 45-55.
McBride, J.R. Same properties of a Bayesian adaptive ability testing program. APM 1977, 1, 121-140.
Naerssen, R.F. van Computersimulatie bij het onderzoek van tentamenregelingen. TOR 1976, 1, 112-117.
Naerssen, R.F. van Een snel programma voor de simulatie van een gegeven test. TOR 1978, 3, 281-283.
Naerssen, R.F. van Absolute of relatieve aftestgrens een verkenning met simulaties. TOR 1979, 4, 817
Shoemaker, D.M. & Osburn, H.G. A simulation model for achievement testing. EPM 1970, 30, 267-272.
normhandhaving (zie ook cijfers)
Gruijter, D.N.M. de Het handhaven van normen bij studietoetsen door toetsvergelijking. NTvdP 1971, 26, 480-490.
Hofstee, W.K.B. Een alternatief voor normhandhaving bij toetsen. NTvdP 1973, 28, 215-227.
Lord, F.M. A survey of equating methods based on item characteristic curve theory. Research Bulletin RB7513, Educational Testing Service, Princeton, New Jersey. April 1975.
Marks, E. & Lindsay, C.A. Some results relating to test equating under relaxed test form equivalence. JEM 1972, 9, 45-55.
Solberg, J.W. Normhandhaving: een beschouwing naar aanleiding van een door Hofstee ontwikkeld alternatief. TOR 1976, 1, 59-67.
open boek toets
Krarup, N., Naeraa, N. & Olsen, C. Openbook tests in a university course. Higher Education 1974, 3, 157-164.
persoonsbeoordeling (zie ook betrouwbaarheid van beoordelingen)
Dawes, R.M. The robust beauty of improper linear models in decisionmaking. American Psychologist 1979, 34, 571-582.
Einhorn, H.J., Kleinmuntz, D.N. & Kleinmuntz, B. Linear regression and processtracing models of judgment. Psychological Review 1979, 86, 465-585.
Grossberg, J.M. & Grant, B.T. Clinical psychophysics: applications of ratio scaling and signal detection methods to research on pain, fear, drugs, and medical decision making. PB 1978, 85, 1154-1176.
Hofstee, W.K.B. Psychologische uitspraken over personen: beoordeling, voorspelling, advies, test. Deventer: Van Loghum Slaterus, 1974.
raadkans ( & correcties) (zie ook toetsen zelfscorende)
Abu-Sayf, F.K. The scoring of multiplechoice tests: a closer look. Educational Technology 1979, june, 515.
Bejar, I.I. & Weiss, D.J. A comparison of empirical differential option weighting scoring procedures as a function of interitem correlation. EPM 1977, 37, 335-340.
Borgesius, T.G. Een empirisch onderzoek naar het correctie voor raden scoringssysteem. Nijmegen, Instituut voor Onderzoek van het Wetenschappelijk Onderwijs, K.U. Nijmegen. 1978.
Claudy, J.G. Biserial weights: a new approach to test item option weighting. APM 1978, 2, 25-30.
Diamond, J. & Evans, W. The correction for guessing. RER 1973, 43, 181-192.
Duncan, G.T. & Milton, E.O. Multipleanswer multiplechoice test items: responding and scoring through Bayes and minimax strategies. Pm 1978, 43, 43-57.
Echternacht, G. The variances of empirically derived option scoring weights. EPM 1975, 35, 307-311.
Gibbons, J.D., Olkin, I. & Sobel, M. A subset selection technique for scoring items on a multiple choice test. Pm 1979, 44, 259-278.
Lord, F.M. Formula scoring and number right scoring. JEM 1975, 12, 7-12.
Molenaar, W. On Bayesian formula scores for random guessing in multipple choice tests. BrJMSP 1977, 30, 79-89.
Slakter, M.J., Crehan, K.D. & Koehler, R.A. Longitudinal studies on risk taking on objective examinations. EPM 1975, 35, 97-105.
Thorndike, R.L. The problem. of guessing. In Thorndike 1971, 59-61.
Wilcox, R.R. Achievement tests and latent structure models. BrJMSP 1979, 32, 61-71.
signaal/ruis ratio index
Brennan, R.L. & Kane, M.T. Signal/noise ratios for domainreferenced tests. Pm 1977, 42, 609-625.
Naerssen, R.F. van A signal/noise ratio index used for item selection in teachermade tests. In Ingenkamp, K. (Ed.) Developments in educational testing, volume 1. University of London Press, 1969.
standaardmeetfout
Cureton, E.E. at al. Length of test and standard error of measurement. EPM 1973, 33, 63-68.
Dudek, F.J. The continuing misinterpretation of the standard error of measurement. PB 1979, 86, 335-337.
Garvin, A.D. A simple, accurate approximation of the standard error of measurement. JEM 1976, 13, 101-106.
Kleinke , D.J. Systematic errors in approximations to the standard error of measurement and reliability. APM 1979, 3, 161-164.
steekproeftrekken (toevallig of willekeurig trekken)
Hamer, R. & Young, F.W. TESTER: a computer program to produce individualized multiple choice tests. EEM 1978, 38, 819-821.
Lord, F.M. Some item analysis and test theory for a system of computerassisted test construction for individualized instruction. APM 1977, 1, 447-455.
Myerberg, N.J. The effect of item stratification on the estimation of the mean and variance of universe scores in multiple matrix sampling. EPM 1979, 39, 57-68.
Shoemaker, D.M. Principles and procedures of multiple matrix sampling. Cambridge, Mass.: Ballinger, 1973.
Sirotnik, K.A. Introduction to matrix sampling for the practitioner. In Popham, W.J. (Ed.) Evaluation in education. Current applications. Berkeley, Calif.: McCutchan, 1974.
Sirotnik, K. & Wellington, R. Incidence sampling: an integrated theory for 'matrix sampling'. JEM 1977, 14, 343-400.
Wood, R. & Skurnik, L.S. Item banking. Slough, Bucks: National Foundation for Educational Research in England and Wales, 1969. (A method for producing schoolbased examinations and nationally comparable grades).
taalvaardigheidstoetsen
Bol, E. Het meten van leesvaardigheid door middel van vragen. TOR 1978, 3, 201-215.
Breland, H.M. & Gaynor, J.L. A comparison of direct and indirect assessments of writing skill. JEM 1979, 16, 119-128.
Jansen, C. & Woudstra, E. De clozeprocedure, een bruikbare maat voor schriftelijke taalvaardigheid? TOR 1978, 3, 87-89.
Kintsch& Vipond Reading comprehension and readability in educational practice and psychological theory. In Nilsson (ed) perspectives on memory research. Hillsdale, N.J.: Lawrence Erlbaum Ass, 1979.
Wijnstra, J.M., FloorGaastra, H., Buter, P. & Wesseling, H. Het radiospel: een toetsprocedure voor spreekvaardigheid. TOR 1978, 3, 124-130.
toetsen (zie ook interpretatie van toetsscores)
Glaser, R. & Nitko, A.J. Measurement in learning and instruction. In Thorndike 1971.
Jones, L.V. The nature of measurement. In Thorndike 1971.
Lumsden, J. Test theory. Annual Review of Psychology, 1976, 27, 251-280.
Miller, C.M.L. & Parlett, M. Up to the mark. A study of the examination game. London: Society for Research into Higher Education, 1974.
Nuy, M.J.G. Diagnostische toetsen. Functie in het onderwijsleerproces en wijze van constructie. 'sHertogenbosch: Malmberg, 1972.
Shoemaker, D.M. Toward a framework for achievement testing. RER 1975, 45, 127-147
Wilmott, A.S. & Fowles, D.E. The objective interpretation of test performance: the Rasch model applied. Windsor, Birks: National Foundation for Educational Research, 1974.
toetsen,_flexibele
Cliff, N. Complete orders from incomplete data: interactive ordering and tailored testing. PB 1975, 82, 289-302
Linn, RS., Rock, D.A. & Cleary, T.A. Sequential testing for dichomous decisions. EPM 1972, 32, 85-95.
Lord, F.M. Individualized testing and item characteristic curve theory. In Krantz, D.H., Atkinson, R.C., Luce, R.D. & Suppes, P. (Eds.) Contemporary developments in mathematical psychology, volume II. San Francisco: Freeman, 1974.
McBride, J.R. Some properties of a Bayesian adaptive ability testing program. APM 1977, 1, 121-140.
Spineti, J.P. & Hambleton, R.K. A computer simulation study of tailored testing strategies for objectivebased instructional programs. EPM 1977, 37, 139-158.
Wood, R. Responsecontingent testing. RER 1973, 43, 529-543.
Weiss, D.J. (Ed.) Proceedings of the 1977 computerized adaptive testing conference. Psychometrics Methods Program, department of Psychology, University of Minnesota, july 1978.
toetsen, zelfscorende_('stradaptive testing')
Gilman, D.A. & Ferry, P. Increasing test reliability through selfscoring procedures. JEM 1972, 9, 205-207.
Hanna, G.S. A study of the reliability and validity effects of total and partial immediate feedback in multiple choice testing. JEM 1977, 14, 18.
Kane, M. & Moloney, J. The effect of guessing on item reliability under answeruntilcorrect scoring. APM 1978, 2, 41-49.
Lord, F.M. The selfscoring flexilevel test. JEM 1971, 8, 147151. Prestwood, J.S. Knowledge of results and the proportion of positive feedback on tests of ability. APM 1979, 3, 155-160.
tijdbesteding en tijdmeting
Everwijn, S.E.M. Studietijdmetingen: problemen en oplossingen. TOR 1977, 2, 181-184.
Marso, R.N. The influence of test difficulty upon study efforts and achievements. AERJ 1969, 6, 621-632.
tijdlimiet (snelheid)
Iseler, A. Leistungsgeschwindigkeit und Leistungsgüte. Theoretische Analysen unter besonderer berAcksichtigung von Intelligenzleistungen. Berlin: Beltz, 1970.
Ven, A.H.G.S. van der The reliability of speed and precision in timelimit tests. TOR 1976, 1, 68-73.
Ven, A.H.G.S. van der An error score model for time limit tests. TOR 1976, 1, 215-226.
vaardigheden (skills)
Fitzpatrick, R. & Morrison, E.J. Performance and product evaluation. In Thorndike 1971.
Tromp, D. Cursus construeren van practica. Amsterdam: COWO, 1979.
validiteit (zie ook voorspellen)
Cronbach, L.J. Test validation. In Thorndike 1971.
Fenker, R.M. The organization of conceptual materials: a methodology for measuring ideal and actual cognitive structures. Instructional Science 1975, 4, 33-57.
Guion, R.M. Content validity the source of my discontent. AFM 1977, 1, 1-10.
McDonald, R.P. Generalizability in factorable domains: 'domain validity' and generalizability. EFM 1978, 38, 75-80.
Mosier, Ch.I. A critical examination of the concepts of face validity. EPM 1947, 7, 191-205. Ook in Mehrens, W.A. & Ebel, R.L. (Eds.) Principles of educational and psychological measurement. London: Rand McNally, 1967.
Rovinelli, R.J. & Hambleton, R.K. On the use of content specialists in the assessment of criterionreferenced testitem validity. TOR 1977, 2, 49-60.
Rozeboom, W.W. Domain validity why care? EPM 1978, 38, 81-90.
Shavelson, R.J. & Stanton, G.C. Construct validation: methodology and application to three measures of cognitive structure. JEM 1975, 12, 67-86.
voorspellen
Elshout, J. Predicting the validity of predietors of academic performance. TOR 1977, 2, 24-31.
Hills, J.R. Use of measurement in selection and placement. In Thorndike 1971.
Jansen, M.G.H. De voorspellende waarde van de eindtoets basisonderwijs. TOR 1979, 4, 239-244.
Wiggins, J.S. Personality and predietion. Principles of personality assessment. London: AddisonWesley, 1973.
vraagconstructie
Stommel, I.H.M. Handleiding voor het construeren van openvraag tentamens. Tilburg: Onderwijs Research Centrum K.H. Tilburg, 1978.
weging (voor weging van alternatieven bij meerkeuzevragen zie ook raadkans)
Rozeboom, W.W. Sensitivity of a linear composite of predietor items to differential item weighting. Pm 1979, 44, 289-296.
Stanley, J.C. & Wang, M.D. Weighting test items and testitem options, an overview of the analytical and empirical literature. EFM 1970,30,21-35.
zekerheidsaanduiding
Echternacht, G.J. The use of confidence testing in objective tests. RER 1972, 42, 217-236.
Hakstian, A.R. & Kansup, W. A comparison of several methods of assessing partial knowledge in multiplechoice tests: II testing procedures. JEM 1975, 12, 231-240.
Kansup, W. & Hakstian, A.R. A comparison of several methods of assessing partial knowledge in multiplechoice tests: I scoring procedures. JEM 1975, 12, 219-230
Linn, R.L. Response models and examinee behavior: a note on the lack of correspondence. EPM 1976, 36, 835-841.
Poizner, S.B., Nicewander, W.A. & Gettys, C.F. Alternative response and scoring methods for multiplechoice items: an empirical study of probabilistic and ordinal response modes. AFM 1978, 2, 83-96.
Sandbergen, S. Zekerheidsaanduiding bij het meten van studieprestaties. (proefschrift). Amsterdam: Stichting RITP, 1972.
Shuford, E. & Brown, T.A. Elicitation of personal probabilities and their assessment. Instructional Science 1975, 4, 137-188.
Sieber, J.E. Confidence estimates on the correctness of constructed and multiple choice responses. Contemporary Educational Psychology 1979, 4, 272-287.
De bladzijdenaanduiding in deze index slaat op de oorspronkelijke uitgave. De huidige lezer kan de zoekfunctie van de browser gebruiken.
abbb: algemene beginselen item form 16, 17, 51, 65, van behoorlijk bestuur 100, 105, 161 83-86, 160 itemstatistieken 56, 57 algoritmen 43, 91, 161 keuzevragen (optional automatisering 157 questions) 162 beheersingsleren 157 computergebruik zie auto beheersingstoetsen 157 matisering, en toetsen beroep 83-84 - flexibele bètaverdeling 106, 115, contract 77, 162 122-124 kort antwoord vragen zie betrouwbaarheid zie ook open-eindvragen homogeniteit 77-81, 105, KR 20, KR 21 7981, 160 143-146, 158. criterium gerefereerde betrouwbaarheid van beoor toetsen 162 delingen (overeenstem lay-out 162 ming) 53, 86-99, 158. lengte van de toets 80, 94, betrouwbaarheid van beslis 162 singen 79, 158 meerkeuzevragen 48, 49, 162 betrouwbaarheid van profie meerkeuzevragen: objectivi len en samengestelde teit 8182 toetsen 158 meerkeuze of essay? 146, 162 betrouwbaarheidsgordel meerkeuze of janee? 13, 14, 110-111, 147-149 19, 162 binomiaal foutenmodel 122, meerkeuze of open eind? 13, 130, 159 14, 32, 42, 82, 162 binomiaalverdeling 104, 115 meerkeuzevragen: sleutel voor cesuurbepaling 8, 80, 87, scoring 55, 771 81, 87 99, 159 moeilijkheid 28, 5657, 62 cijfers (cijfergeven, verge 63, 130, 163 lijkbaarheid van cijfers) mondeling toetsen 53, 76, 97, 159 163 definities 12, 26, 31 motivatie 163 doelstellingen 5, 69-76, 87, nabootsen van toetsresultaten 93, 99, 103, 163 domeinspecificatie 64 negatief-hypergeometrische doorzichtigheid 60, 62, 92 verdeling 107, 115, 118 94, 105 120, 122 essay toetsen 89-96, 159 normaalverdeling 124 ethiek 97, 160 normhandhaving 164 examenvrees 160 objectiviteit 52, 81-82 frequentie van toetsen 160 open boek toets 164 frequentieverdeling 103, open-eindvragen 14 113, 118 opstel zie essay toetsen homogeniteit 79-81, 143-146 participatiecontrole 76 160 persoonsbeoordeling 164 individuele verschillen 69 raadkans 14, 78, 79, 101, 164 74, 160 raadkans: correctie voor instructie voor beantwoording raden 79, 164 77, 87, 160 rbis (biseriële correlatie) intelligentie 161 57 intelligentietests 161 Richtlijnen 80, 8688, 160 interpretatie van toetsscores signaal/ruis ratio index 165 hoofdstuk 8, 161 scoren 79, 87 standaarddeviatie 113116 standaardmeetfout 80, 115, 165 steekproeftrekken 6467, 100, 165 studiestrategie 8, 72,73, 77, 80, 106, 107-108 taalvaardigheid 165 tab item techniek zie ook' toetsen: zelfscorende 40 testtheorie zie o.a. steek proeftrekken, toetsen toetsen 166 toetsen: flexibele 164 toetsen: zelfscorende 164 toevallig trekken (wille keurig trekken, of steekproeftrekken) 64-67, 100, 165 tijdbesteding 70-74, 166 tijdlimiet 33, 77, 78, 94, 167 vaardigheden (skills) 167 validiteit 69-76, 167 variantie 116-143 voorspellen 167 vragen: toetsen met bekende vragen 66 vragen: formulering 47-49 vragen: constructie 9-45, 64, 167 ware beheersing (ware score) 77, 80, 100-131 weging 59-61, 62, 168 zak-slaaggrens zie cesuur bepaling zekerheidsaanduiding 168
Er zijn voorgangers van het in deze cursus 'Toetsen' behandelde.
Een intern stuk uit 1976 'Toetsconstructie.'
ORD-presentatie 1977 over het opgeklopte voordeel van keuzetoetsen als zouden deze 'objectief' zijn. html
De cursus Cesuurbepaling' (1977) bevat ook materiaal. html
En er zijn opvolgers, vooral 'Toetsvragen schrijven' Aula 809, 1983. Een herziene versie hier is in de maak, de tekst uit 1983 is beschikbaar als 1.4 Mb pdf; hoewel in dat boek de formulering hier en daar bepaald beroerd is, staat de inhoud nog recht overeind, al is met de in gang gezette herziening al gebleken dat er belangrijke verdere ontwikkelingen mogelijk zijn.
[De workshop is meen ik alleen gehouden tijdens het congres in Eindhoven (1980), daar zijn ook de door de deelnemers ingevulde data nog van beschikbaar]
Dit materiaal is als html-pagina beschikbaar 79toetsen.workshop.cowo.htm
Centrum voor Onderzoek van het Wetenschappelijk Onderwijs
Universiteit van Amsterdam. december 1980
![]() http://www.benwilbrink.nl/publicaties/79toetsen.cowo.htm
http://www.benwilbrink.nl/publicaties/79toetsen.cowo.htm