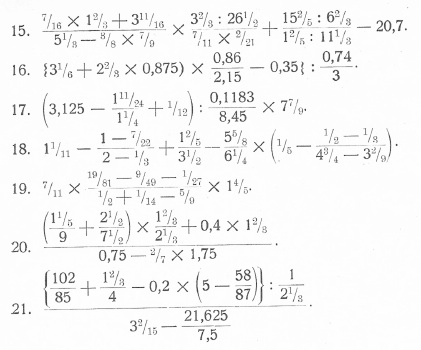
Key publication on teaching fractions.
De actuele problematiek van het breukenonderwijs is dat het deels is afgeschaft, zonder rekening te houden met de gevolgschade daarvan. Dat die gevolgschade er is, laat een recent artikel van Siegler cs. zien, zie enkele aantekeningen bij deze sleutelpublicatie hier
Jan van de Craats (website 20 maart 2008). Waarom Daan en Sanne niet kunnen rekenen. Zwartboek rekenonderwijs. pdf.
Ronald Keijzer (2003). Teaching formal mathematics in primary education . Fraction learning as mathematising process. Proefschrift Vrije Universiteit. CD-&zelig; Press. isbn 9073346525
Liesbeth van der Plas-Eskes (website). Minder bekende problemen van het Nederlandse wiskunde onderwijs. Een kleine analyse van het wiskunde onderwijs binnen twee generaties. pdf.
Het idee dat een rekenmachientje het vele oefenen onnodig heeft gemaakt, berust op een groot en fataal misverstand. Voordat je echt aan algebra kunt beginnen moet je eerst op de basisschool goed hebben leren optellen, aftrekken, vermenigvuldigen en delen, eerst gewoon, daarna met breuken. Zo niet, dan is algebra bij voorbaat al abracadabra.
De Cito-toets bevat geen echte breukensommen.
Om alle breukenvragen van de Cito-toets foutloos te kunnen beantwoorden hoeft een kind feitelijk alleen te weten wat 1/5 betekent en dat 1/5 taartpunt groter is dan 1/10 taartpunt. Gewoon de berekening laten zien van sommetjes zoals: 1 2/5 + 2 3/7 wordt niet gevraagd. Doordat de Cito-toets alleen meerkeuzevragen bevat worden berekeningen bij voorbaat al nooit verlangd, maar zelfs meerkeuzevragen over dit soort sommen ontbreken geheel. Zoals dat gaat met proefwerken in het algemeen en al helemaal bij een toets met zoveel impact als de Cito-toets, stelt de gemiddelde school zijn onderwijs hierop af. Bedoeld of onbedoeld, want de meest gebruikte schoolboeken bevatten ook veel te weinig oefenmateriaal.
N.B. In het origineel zijn de breuken met een horizontaal deelstreepje geschreven.
Samenvattend moet de leerling bij het verlaten van de basisschool de onderstaande vier feitjes weten over breuken voor een foutloze toets.
Zelfs zonder deze geringe breukenkennis mist een leerling slechts 10 van de 60 rekenvragen en kan hij nog met gemak naar het VWO.
We vergelijken dit voor de grap eens met iets heel anders. In het huis van mijn grootvader, ooit het hoofd van een lagere school in Noordwijk, vond ik op zolder het volgende boekje uit 1918:
’Mijn Examen, opgaven van de toelatings-examens voor hoogere burgerscholen en gymnasia’
Zie het stuk van Liesbeth voor de voorbeelden van complexe breuken in die examens. Die ingewikkeldheid is natuurlijk te gek voor woorden (zie ook het proefschrift van Leen: ik meen Wijdenes heeft er ernstige kritiek op geleverd, en gepleit voor de essentie, dus voor wegsnijden van de ballast). Maar Liesbeth heeft hier wel een punt. Dat er nu een generatie onderwijsontwikkelaars is die de breuk 1/3 al te hoog gegrepen vindt, duidt er m.i. ook op dat zij hun geschiedenis van het rekenonderwijs niet kennen.
Rond 1965 werd er een paar keer per week intensief geoefend met algebra. Door de nu volgende bladzijden uit het algebra brugklasboek goed te bekijken (inzoomen met het vergrootglas), zal duidelijk worden dat de moeders van nu aan het einde van de eerste klas al een zeer grote vaardigheid hadden opgebouwd in het rekenen met letters en een goed inzicht hadden verworven in het hoe en waarom van algebra.
Liesbeth heeft een groot aantal bladzijden van het algebraboekje gescand. Prachtig.
Van onschatbare waarde is ook dat men via de wiskunde leert denken in abstracties.
Tja, bedoelt Liesbeth misschien gewoon dat het van belang is dat leerlingen intensief kennis maken met het denken in abstracties? Of je dat ook ‘leert’, ja zou moeten leren, is in de geschiedenis van het wiskundeonderwijs een strijdpunt, en voor psychologen die langskomen meestal iets dat ze niet serieus kunnen nemen (van klassieke talen of schaken wordt dat ook gezegd: zou je wiskunde dan in kunnen ruilen voor schaken?)
Om dat belang van kennismaken met abstract redeneren te onderstrepen, wijst Liesbeth op de in dit opzicht ernstig tekortschietende huidige methoden: zie de zes punten die zij noemt. Dat lijkt inderdaad verdacht veel op verkwanseling van de wiskunde.
Liesbeth van der Plas: Breuken voor de Basisschool, Vmbo, Havo, VWO en Pabo. [oefen-dvd] oefen-dvd
Joost Hulshof (12 september 2011). Doorlopende leerlijnen breuken lopen niet door. Voordracht SLO, Enschede.
Hulshof wijst er onder andere op dat breuken met noemers anders dan veelvouden van twee en vijf uit het onderwijs dreigen te verdwijnen, onder invloed van bijvoorbeeld het referentiekader rekenen van de commissie-Meijerink, een kader dat is vastgelegd in de Wet op de referentieniveaus taal en rekenen.
G. Bruin-Muurling (2010). The development of proficiency in the fraction domain. Affordances and constraints in the curriculum. Technische Universiteit Eindhoven. open
Onderzoek dat het realistisch rekenen als uitgangspunt neemt. Anders dan de meeste proefschriften uit realistische hoek, begint dit proefschrift (p. 3) met signaleren dat realistisch rekenen controversieel is. Nee, niet in die woorden, maar Geeke geeft aan dat er een maatschappelijk debat over dat realistisch rekenen is, en dat vind ik al heel wat.
We found that problems in de fraction domain start already early in education and continue in later grades. Although the proficiency of the students developed considerably from grade 4, the students’ proficiency level at the end of grade six showed lack of deeper understanding of fractions. Corresponding to the textbooks, the teaching of fractions and fraction arithmetic in primary education, is directed towards procedural problem solving of standard tasks. The students did not develop deeper understanding of underlying concepts like unit, rational number and equivalence. Moreover, strategies that students did learn appeared to be number specific. The consequence of this unconnected knowledge might be that their proficiency level is unstable.
Bruin-Muurling 2010 p. 103, zie ook de conclusies p. 144
Onderwijs in breuken: in de lijn van de opvattingen van RR heeft Geeke Bruin-Muurling (2010) onderzocht hoe dit onderwijs in de praktijk reilt en zeilt. Als ik het in de gauwigheid goed heb gezien, geeft de passage in bovenstaande box de kern van haar resultaten weer. Ik kan daar niet uit afleiden dat het RR is geslaagd op zijn eigen doelen, en het valt dan te vermoeden dat de eenvoudige rekenvaardigheid met breuken verwaarloosd blijkt te zijn. Het lastige met dit onderzoek is dat het noodzakelijkerwijs alleen op RR-gebaseerd rekenonderwijs onderzoek berust (ander onderwijs was er immers niet of nauwelijks), zodat het ongewis blijft hoe de resultaten van het onderzoek zijn te duiden in termen van geslaagd zijn van de missie van het RR. In beginsel kan een onderzoek zoals dit wel degelijk inzichten in de effectiviteit van tal van varianten binnen het RR in de klas opleveren, ik ben dus wel benieuwd wat verdere lezing van dit proefschrift nog op gaat leveren.
K. P. E. Gravemeijer, G. Bruin-Muurling & M. van Eijck (2009). Aansluitingsproblemen tussen primair en voortgezet onderwijs — geen doorgaande lijn voor het vermenigvuldigen van breuken. Panam-Post pdf.
Het blijkt dat opgaven en voorbeelden in de basisschoolmethoden aansturen op verschillende rekenprocedures voor verschillende getalcombinaties, terwijl de havo/vwomethoden al snel starten met één algemene regel voor alle mogelijke gevallen (‘teller keer teller en noemer keer noemer’). Bovendien blijken de basisschoolprocedures sterk gebonden aan contexten, waardoor de leerlingen in het algemeen niet met breuken als onbenoemde, op zichzelf staande, getallen rekenen, maar met benoemde contextgebonden getallen. In het voortgezet onderwijs wordt echter al snel op het niveau van de on- benoemde getallen gerekend.
Ik denk toch dat dit zó moet worden gelezen dat het realistisch rekenonderwijs in de basisschool op een paar verkeerde paarden heeft gewed. Nee hoor, Gravemeijer c.s. vinden dat het VO zelf een aansluitingsprobleem heeft: het goede werk dat op de basisschool is gedaan, moet in het VO worden afgerond om een goede overgang naar de wiskunde te krijgen.
En ik maar denken dat hier staat dat de leerlingen bij de overgang van het rekenen van hun basisschool naar de wiskunde in het VO een paar verkeerde gewoonten weer moeten afleren.
M. Koopman, G. Bruin-Muurling, P.J. den Brok (2013). Ook bij breukenonderwijs maakt de leraar het verschil. Didactief, 43 #10, 44-45. [Heb ik dit artikel over het hoofd gezien?]
Ron Aharoni (2009). Kinderen leren rekenen. Boom.
Merlyn J. Behr, Richard Lesh, Thomas R. Post & Edward A. Silver: Rational-number concepts. in Richard Lesh & Marsha Landau (Eds.) (1983). Acquisition of Mathematics Concepts and Processes (91-126). Academic Press. pdf
Breuken, procenten, kommagetallen en verhoudingen - tussendoelen Annex Leerlijnen Bovenbouw Basisschool Noordhoff. isbn 9789001851064. [nog niet gezien, KB ter inzage]
S. Kuipers (2004). De leerlijn rekenen/breuken - voor groep 6 en hoger. cd-rom (is dit een boek of alleen een cd-rom?)(nog niet gezien)
Boomsma (). Resultaten van het onderwijs in breuken op de lagere school. Wolters (nog niet gezien)
Liesbeth van der Plas (2007). Wiskunde interactief - breuken voor de Basisschool, Vmbo, Havo/VWO en Pabo. Karakter Uitgevers. (nog niet gezien)
Hessel Pot (2005). Breuken, wat zijn dat eigenlijk voor dingen? Euclides, 82 #2 [inhoudsopgave Euclides 81; dit artikel niet online beschikbaar]
F. Goffree, A. A. Hiddink & J. M. Dijkshoorn (1970 4e). Rekenen en didactiek. Wolters-Noordhoff.
Breuken worden behandeld in hoofdstuk 6, kommagetallen in hoofdstuk 8, verhoudingen en evenredigheden in hoofdstuk 15, telkens met twee hoofdrekentoetsen.
15.B.6. Hoofdrekentest (zesde klas) Tijd: 5 min.
30 x 4 1⁄2 = 25 - 3⁄4 = 9 x 25 = 17 - 2⁄3 = 1⁄3 x 72 = 7 x 12,5 = 27 : 4 = 8 x 13,5 = 27 + 38 = 13 - 1⁄5 = 9 x 4,5 = 92 - 47 = 12 1⁄2 + 1 1⁄4 = 7 x 8,5 = 21 : 4 = 4 x 27,5 = 43 : 5 = 5⁄6 - 1⁄3 = 16 x 125 = 44 st. = .. gld. 28 rijksd. = ƒ . . . 36 kw = ƒ . . . 1/5 x 120 = 40 rijksd. = ƒ . . .
Voor een hoofdrekentoets zie 2.A.8. zie hier
Treffers, A. Treffers, L. Streefland & E. de Moor (1994). Proeve van een nationaal programma voor het reken-wiskundeonderwijs op de basisschool. Deel 3A. Breuken. Zwijsen. isbn 9027633398
Soo Jin Lee, Rachael Eriksen Brown & Chandra Hawley Orrill (2011): Mathematics Teachers' Reasoning About Fractions and Decimals Using Drawn Representations. Mathematical Thinking and Learning, 13, 198-220. abstract
Thomas P. Carpenter, Elizabeth Fennema & Thomas A. Romberg (Eds.) (1993). Rational Numbers. An Integration of Research. Erlbaum.
Amy Fleeger Hillen (2005). Examining Preservice Secondary Mathematics Teachers' Ability to Reason Proportionally prior to and upon Completion of a Practice-Based Mathematics Methods Course Focused on Proportional Reasoning. Dissertation University of Pittsburg. Approved by Ellen Ansell, Ellice Forman & Gaea Leinhardt. pdf.
Steven A. Hecht & Kevin J. Vagi (2010). Sources of Group and Individual Differences in Emerging Fraction Skills. Journal of Educational Psychology, 102, 843-859.
Darcy Hallett, Terezinha Nunes & Peter Bryant (2010). Individual Differences in Conceptual and Procedural Knowledge When Learning Fractions. Journal of Educational Psychology, 102, 395-406.
E. M. Meyers (1928). Vergelijkingen met breuken in middeleeuwse rechtsteksten. Mededelingen der Koninklijke Akademie van Wetenschappen, Afdeeling Letterkunde, Deel 66 Serie B, No. 6. 25 blz brochure
J. Versluys (1906). Deelbaarheid en repeteerende breuken. Amsterdam: A. Versluys.
L. Streefland (1988). Realistisch breukenonderwijs. Vakgroep Onderzoek Wiskundeonderwijs en Onderwijscomputercentrum, Rijksuniversiteit Utrecht. proefschrift RUU.
Nadrukkelijk op de ideologische grondslag van het realistisch rekenen.
Catherine Sophian (2007). The origins of mathematical knowledge in childhood. Lawrence Erlbaum.
Steven A. Hecht & Kevin J. Vagi (2010). Sources of Group and Individual Differences in Emerging Fraction Skills. Journal of Educational Psychology, 102, 843-859.
Darcy Hallett, Terezinha Nunes & Peter Bryant (2010). Individual Differences in Conceptual and Procedural Knowledge When Learning Fractions. Journal of Educational Psychology, 102, 395-406.
Kristie Jones Newton (2008). An extensive analysis of preservice elementary teachers' knowledge of fractions. American Educational Research Journal, 45, 1080-1110. abstract
R. S. Siegler, G. J. Duncan, P. E. Davis-Kean, K. Duckworth, A. Claessens, M. Engel, M. I. Susperreguy & M. Chen (2012). Early predictors of high school mathematics achievement. Psychological Science, 23, 691-697. pdf
“This view of fractions as occupying a central position within mathematical development differs substantially from other theories in the area, which focus on whole numbers and relegate fractions to secondary status. To the extent that such theories address development of understanding of fractions at all, it is usually to document ways in which learning about them is hindered by whole-number knowledge (e.g., Gelman & Williams, 1998; Wynn, 1995). Nothing in these theories suggests that early knowledge of fractions would uniquely predict later mathematics proficiency.
Consider some reasons, however, why elementary schoolstudents’ knowledge of fractions might be crucial for later mathematics—for example, algebra. If students do not understand fractions, they cannot estimate answers even to simple algebraic equations. For example, students who do not understand fractions will not know that in the equation 1/3X = 2/3Y, X must be twice as large as Y, or that for the equation 3/4X = 6, the value of X must be somewhat, but not greatly, larger than 6. Students who do not understand fraction magnitudes also would not be able to reject flawed equations by reasoning that the answers they yield are impossible. Consistent with this analysis, studies have shown that accurate estimation of fraction magnitudes is closely related to correct use of fractions arithmetic procedures (Hecht & Vagi, 2010; Siegler et al., 2011).”
Methode
Siegler c.s. maken gebruik van beschikbare data uit cohortstudies. In Nederland zou het onderzoek gerepliceerd kunnen worden met data uit de PRIMA en VOCL cohortstudies (tegenwoordig gefuseerd tot het COOL-cohort, beheerd door RION en ITS) (als daar voldoende gedetailleerde rekentoetsen zijn afgenomen; mogelijk is via onderwijsnummers tegenwoordig een koppeling te maken met Citotoets (het rekengedeelte daarvan is irrelevant voor dit onderzoek, helaas: dat is geen rekenen) en eindexamens).
Niet onbelangrijk is dat, althans in het VS-cohort, een testje voor omvang van het werkgeheugen meeliep.
Methode is adequaat. Dit is geen experimenteel onderzoek. Er zijn gegevens verzameld op twee tijdstippen die ver uit elkaar liggen. De uitdaging is dan om van die tijdsvolgorde gebruik te maken om diverse samenhangen in oorzakelijke zin te kunnen interpreteren. Op voorhand valt te speculeren dat positieve samenhangen veroorzaakt kunnen zijn door gemeenschappelijke factoren zoals sociale achtergrond, intelligentie, werkgeheugen: probeer dan die mogelijke verklaringen uit te schakelen door statistisch te corrigeren. Dat maakt het onderzoek niet experimenteel, dus het blijft behelpen, maar het is veel beter dan niets.
Als mogelijke gemeenschappelijke oorzaken zijn uitgeschakeld, en er blijft desondanks een aanzienlijk (en dus ook statistisch significant) verband over tussen beheersing van breuken en delen, en latere wiskundeprestaties, dan kan dat voorzichtig geponeerd worden een oorzakelijk verband te zijn: vroege beheersing van breuken en delen is een noodzakelijke voorwaarde voor latere prestaties in wiskunde (algebra).
Results
( . . . )
Early knowledge of whole-number division also was consistently related to later mathematics proficiency.
( . . . )
To the best of our knowledge, relations between elementaryschool children’s division knowledge and their mathematics proficiency in high school have not been documented previously.
( . . . )
The greater predictive power of knowledge of fractions and knowledge of division was not due to their generally predicting intellectual outcomes more accurately.
Discussion
( . . . )
Thus, the unique predictive value of early fractions and division knowledge seems to be due to many students not mastering fractions and division and to those operations being essential for more advanced mathematics, rather than simply to fractions and division being relatively difficult to master.
( . . . )
One likely reason for students’ limited mastery of fractions and division is that many U.S. teachers lack a firm conceptual understanding of fractions and division. In several studies, the majority of elementary and middle school teachers in the United States were unable to generate even a single explanation for why the invert-and-multiply algorithm (i.e., a /b : c /d = ad × bc ) is a legitimate way to solve division problems with fractions. In contrast, most teachers in Japan and China generated two or three explanations in response to the same question (Ma, 1999; Moseley, Okamoto, & Ishida, 2007).
These and the present results suggest that improved teaching of fractions and division could yield substantial improvements in students’ learning, not only of fractions and division but of more advanced mathematics as well.
De crux is: beheersing van breuken en delen is een voorwaarde voor latere wiskunde. Hoe dat precies zit, daar valt wel over te speculeren, wat de auteurs in hun discussie ook wel doen.
Bedenk bij dit alles dat het rekenonderwijs in de VS gemiddeld van bedroevende kwaliteit is, door tekortschietende vakkennis van leraren. Of dat in Engeland ook zo is, weet ik niet. In Nederland schiet de kennis van leraren ondertussen ook schromelijk tekort. Een vergelijkend onderzoek tussen leraren primair onderwijs in Nederland, de VS en Engeland zou niet misstaan.
Dit artikel is zeker een sleutelpublicatie waar het gaat om het belang van breuken en delen in het rekenonderwijs.
Merk op dat in dit artikel eigenlijk nergens sprake is van word problems, laat staan wat in Nederland onder contextopgaven (rekentoets, maar ook eindexamens wiskunde) wordt verstaan. Alleen ter illustratie van het bedroevende niveau van de gemiddelde high school leerling geven de auteurs een zeer simpel woordprobleem:
Joke Torbeyns, Michael Schneider, Ziqiang Xin & Robert S. Siegler (2014). Bridging the gap: Fraction understanding is central to mathematics achievement in students from three different continents. Learning and Instruction, 37, 5-13. pdf
Siegler, R., Carpenter, T., Fennell, F., Geary, D., Lewis, J., Okamoto, Y., Thompson, L., & Wray, J. (2010). Developing effective fractions instruction for kindergarten through 8th grade: A practice guide (NCEE #2010-4039). Washington, DC: National Center for Education Evaluation and Regional Assistance, Institute of Education Sciences, U.S. Department of Education. Retrieved from whatworks.ed.gov/ publications/practiceguides. pdf
Robert S. Siegler, Clarissa A. Thompson & Michael Schneider (2011). An integrated theory of whole number and fractions development. Cognitive Psychology. abstract en pdf
Siegler, R. S. & Lortie-Forgues, H. (in press 2015) Conceptual knowledge of fraction arithmetic. Journal of Educational Psychology. http://dx.doi.org/10.1037/edu0000025 concept
Daniel Willingham blogged Computational Competence Doesn't Guarantee Conceptual Understanding in Math. No, of course it doesn’t. What, then, is the point of the Siegler & Lortie-Forgues article?
Robert Siegler, of course, is a prolific reseacher on things mathematical in education. See Bryan Penfound's blog http://bryanpenfoundsmathblog.blogspot.ca/2015/04/more-time-in-mathematics-for-pre.html?m=1 on the importance of conceptual mastery of fracion arithmetic in education.
Laetitia Desmet, Jacques Grégoire & Christophe Mussolin (2010). Developmental changes in the comparison of decimal fractions. Learning and Instruction, 20, 521-532. abstract
Susanne Prediger (2008). The relevance of didactic categories for analysing obstacles in, conceptual change: Revisiting the case of multiplication of fractions. Learning and Instruction, 18, 3-17. pdf
Morris Kline (1980). Mathematics. The loss of certainty. Oxford University Press.
Linda Fisher (2007). Learning About Fractions from Assessment, by Linda Fisher In Alan H. Schoenfeld: Assessing mathematical proficiency. Cambridge University Press. pp 195-211 pdf
Susan B. Empson (1999). Equal Sharing and Shared Meaning: the Development of Fraction Concepts in a First-Grade Classroom. Cognition and Instruction, 17, 283-342. questia
Andrew Iszák (2011). Mathematical knowledge for teaching fraction multiplication. Cognition and Instruction, 26, 95-143.
Bárbara M. Brizuela (2006). Young children's notations for fractions. Educational Studies in Mathematics, 62, 281-305. pdf
T. W. Boyer, Levine, S. C., & Huttenlocher, J. (2008). Development of proportional reasoning: Where young children go wrong. Developmental Psychology, 44, 1478-1490.
Bright, G., Behr, M., Post, T., & Wachsmuth, I. (1988). Identifying fractions on number lines. Journal for Research in Mathematics Education, 19, 215-232.
Fujimura, N. (2001). Facilitating children’s proportional reasoning: A model of reasoning processes and effects of intervention on strategy change. Journal of Educational Psychology, 93, 589-603.abstract
Jitendra, A. K., Star, J. R., Starosta, K., Leh, J. M., Sood, S., Caskie, G., . . . Mack, T. R. (2009). Improving seventh grade students’ learning of ratio and proportion: The role of schema-based instruction. Contemporary Educational Psychology, 34, 250-264.
Susan B. Empson (1999). Equal sharing and shared meaning: The development of fraction concepts in a first-grade classroom. Cognition and Instruction, 17, 283-342. abstract
Geoffrey B. Saxe, Maryl Gearhart & Michael Seltzer (1999). Relations between classroom practices and student learning in th edomain of fractions. Cognition and Instruction, 17, 1-24. abstract
Hessel Pot (2009). Zijn breuken en verhoudingen nou wel of niet hetzelfde? Studiedag NVvW - 7 november 2009.abstract
Darcy Hallett, Terezinha Nunes & Peter Bryant (2010). Individual Differences in Conceptual and Procedural Knowledge When Learning Fractions. Journal of Educational Psychology, 102, 395-406.
Steven A. Hecht & Kevin J. Vagi (2010). Sources of Group and Individual Differences in Emerging Fraction Skills. Journal of Educational Psychology, 102, 843-859. abstract
Gerhard F. Steiner & Markus Stoecklin (1997). Fraction calculation — a didactic approach to constructing mathematical networks. Learning and Instruction, 7, 211-233. abstract
Yujing Ni & Yong-Di Zhou (2005): Teaching and Learning Fraction and Rational Numbers: The Origins and Implications of Whole Number Bias, Educational Psychologist, 40:1, 27-52 abstract
De afbeelding: enkele breukensommen voor de zesde klas, 1924, voor leerlingen die toelating voor mulo, hbs of gymnasium willen gaan doen.
P. Wijdenes (1924). Voorlooper op de rekenboeken voor de H.B.S en voor M.U.L.O., tevens slotstukje voor het rekenonderwijs op de lagere school. P. Noordhoff.
Lonneke Boels (2011). Breuken op de basisschool. Euclides, 86, 244. abstract
Hoe zit het met die breuken bij de overgang bo-vo, wat kunnen en kennen deze leerlingen? Zij noemt alleen enkele Nederlandse publicaties, geen empirisch onderzoek.
Hans Freudenthal heeft eind zeventiger jaren met veel moeite een opzet voor een cursus breuken gemaakt, daar is nooit iets mee gedaan, ook niet gepubliceerd als ik het goed heb
Tal-team (2005). Breuken, procenten, kommagetallen en verhoudingen. FI/Wolters/Noordhoff [niet in mijn bezit]
P. van den Brom-Snijders e.a. (2006). Gebroken getallen Reken/wiskundedidactiek. ThiemeMeulenhof [voor de Pabo; niet in mijn bezit]
P. M. van Hiele (1973). Begrip en inzicht. Werkboek van de wiskundedidactiek. Muusses. Zie ook de pagina met aantekeningen bij werk van Van Hiele html
Hoofdstuk 22. Zouden we het rekenen met breuken misschien kunnen afschaffen? Ik heb mij laten informeren dat dit hoofdstuk van Van Hiele gebazel is. Nog een citaat uit een ander hoofdstuk:
De voornaamste oorzaak van het mislukken van het onderwijs in breuken op de basisschool is, dat de leerlingen vrijwel niets met de breuken kunnen doen: de kennis van de breuken maakt hun leven niet rijker.
blz. 225
P. M. van Hiele (1973). Begrip en inzicht. Werkboek van de wiskundedidactiek. Muusses. Zie ook de pagina met aantekeningen bij werk van Van Hiele html
Hoofdstuk 1. Evenredigheden gaat over de evenredigheidsmatrix.
Men is gewoon een evenredigheid te lezen als een gelijkheid van quotiënten: 2 : 5 = 6 : 15. Deze evenredigheid is juist, want 2/5 = 6/15.
Deze beschouwingswijze maakt de leer der evenredigheden moeilijker dan wel nodig is. Breuken hebben twee nadelen: 1e het getal in de noemer kan niet gelijk zijn aan nul; 2e het rekenen met breuken is minder eenvoudig dan het rekeen met produkten.
Het kan heel gemakkelijk anders. Verschillende didaktici die zich bezig hielden met het rekenen in het basisonderwijs hebben al een lans gebroken voor het werken met ‘verhoudingsblokken’. Men treft deze gedachte o.a. aan bij Dreckhahn in zijn ‘Arbeitsbuch für den Rechenunterricht’ en bij Turkstra en Timmer in ‘Rekendidactiek, 1e deel’. Het komt erop neer, dat men twee rijtjes getallen onder elkaar zet:
2 4 7 12 -2 -5
6 12 21 36 -6 -15
Het tweede rijtje wordt uit het eerste verkregen door alle getallen met eenzelfde getal te vermenigvuldigen.
Het belangrijkste van deze metode is, dat er nergens een bewerkingsteken geplaatst is: de getallen staan in een rechthoekig blok, zij vormen een evenredigheidsmatrix.
blz. 1
Rainer Kaenders & Klaas Landsman (2010). Interview Chris Zaal. Wiskunde opstuwen in de vaart der volkeren. Nieuw Archief Wiskunde, 5/11 nr 1
“( .. ) Het hele probleem met het realistische wiskundeonderwijs zoals het FI dat maakt, is hun idee dat de abstractie wel vanzelf komt als je maar genoeg contexten aanbiedt. Almaar aansluiten bij de gedachtenwereld van de leerlingen. B-leerlingen vragen dan na een tijdje: ‘Waarom zeggen ze niet gewoon wat ze bedoelen?’ Dit zie je ook terug in de lespakketjes van het FI: daarin wordt eindeloos verkend, maar het gewenste einddoel blijft achter de horizon. De zogenaamde ‘didactische modellen’ maken het nog erger. Een ‘verhoudingstabel’ geeft de leerling in het begin steun, maar blokkeert uiteindelijk de wiskundige ontwikkeling omdat de vervolgstap van verhoudingstabel naar algebraïsch rekenen niet gemaakt wordt. Al heet het instituut naar Freudenthal met zijn Mathematik als pädagogische Aufgabe—het pedagogisch inzicht ontbreekt. Door de realistische didactiek blijft de ontwikkeling van de leerling in een initieel stadium steken.”
blz. 43
Robert A. Reeve and Philippa E. Pattison (1998). The Referential Adequacy of Students’ Visual Analogies of Fractions. Mathematical Cognition, 2, 137-169. pdf
Andrew Iszák, Erik Jacobsons, Sandra de Araujo & Chandra Hawley Orrill (2012). Measuring mathematical knowledge for teaching fractions with drawn quantities. Journal for Research in Mathematics Education, 43, 391-427. preview
Seems to be nonsense research, applying irt-modelling to data from a handful of teachers. Dumped my copy of the article.
Jimmy de la Torre (2009). A cognitive diagnosis model for cognitively based multiple-choice options. Applied Psychological Measurement, 33, 163-183. abstract
Het gebruikte voorbeeld is een breukenopgave 2 4/7 - 7/12. Het lijkt me wel interessant en van belang om te zien hoe dit ‘cognitief-psychologisch’ wordt geanalyseerd. De psychometrie van een en ander is meer arcaan van karakter, wat mij betreft met weinig realiteitswaarde.
Theo Thijssen (1941). In de ochtend van het leven. Jeugdherinneringen. Van Dishoeck.
Voor het rekenen had meester Wopkes een merkwaardig systeem: we maakten maar één model sommen: twee even getallen van vijf cijfers met elkaar vermenigvuldigen, en het product delen door de helft van het ene getal. De getallen mocht je zelf bedenken; als de som af was, moest je twee getallen nemen, die 26, of 36, of 48 hoger waren, dat hing er van af, welk getal de meester op het bord had gezet — en dan had je je tweede som.
Het begon al, als je ’s morgens de klas in kwam. [sic] voordat de bel van beginnen ging. Dan keek je, welk getal de meester op het bord had gezet, en je pakte je lei, en ging sommen maken, tot de lei vol was aan twee kanten. Dan moest je naar Krantz, dat was de jongen die door de meester als opzichter was aangesteld; en Kranz telde hoeveel sommen je gemaakt had, en keek of er ‘eerlijk’ nul uit was gekomen, en nam de natte bordspons, en veegde alles uit, en zette in een hoekje van je lei met krijt, hoeveel sommen je had ingeleverd. Eerst kon je dat cijfer van Kranz niet eens lezen, door de nattigheid, maar weldra trok dat bij, en hel-wit zag je dan staan, hoeveel je al af had gekregen. Wat er met die Kranz was, ik weet het niet; ik heb hem altijd aangezien voor iets als een neefje van de meester, maar hj liet zich nooit uithoren. Maar ondanks zijn drukke opzichterswerk maakte hij de meeste sommen van allemaal, en eerlijk want zijn sommen keek de meester zèlf na! ‘Klaar’ met je sommen was je, als Kranz in de hoek van je lei ‘25’ had gezet; dan mocht je een boek gaan lezen. Maar kranz zat dan al lang te lezen, die had zijn ‘25’ van de meester al te pakken. Ik probeerde tegen die Kranz te concusrreren; hij zat altijd te peuteren met een heel klein stukje griffel, en ik verbeeldde me, dat dààrin de vlugheid zat, en ging het ook met een klein peukje griffel, maar bij mij gleed dat telkens uit m’n vingers . . .
Aan het eind van de ‘rekenles’ ging Kranz rond met een lei, waarop de ‘lijst’ stond, en tekende aan, hoeveel sommen je had gemaakt. Zaterdags telde hij op, hoeveel je er in de hele week had klaar gekregen; bij veel jongens was dat over de twee honderd; de meester ging dan deftig aan z’n tafeltje zitten, met een schrift en schreef zorgvldig al de totalen op, die Kranz opnoemde; wij zaten daarbij in spanning te luisteren, en hoonden met gezichtentrekken de sukkels die maar weinig sommen hadden geproduceerd. M’n broertje Henk is natuurlijk later ook die zesde klas bij meester Mop doorgelopen, en heeft dezelfde reken-training ondergaan; hij heeft me daarover wel eens geweldige verhalen gedaan; over de streken die ze daarbij uithaalden; ze zetten maar cijfertjes, zonder iets uit te rekenen, en zorgden alleen maar, dat er de verplichte nul onderaan stond, en kwamen zo tot fantastische hoeveelheden op de lijst. Ik heb de mogelijkheid van dat bedrog toen verklaard door het feit, dat er in die klas geen Kranz zat; die Kranz van ons kon je zo iets niet lappen — dat is nu nòg mijn overtuiging — al kan ik met mijn tegenwoordige inzicht dat fenomeen Kranz niet verplaren!
Theo Thijssen (1941). In de ochtend van het leven. Van Dishoeck. blz. 68-70
Van het rekenen met breuken herinner ik me, dat we bij het optellen, en aftrekken ‘een galg’ moesten tekenen: een loodrechte streep achter de op te tellen of af te trekken getallen, en bovenaan een dwarsstreep. Boven die dwarsstreep zetten we dan de gemeenschappelijke noemer, die we nodig hadden om de breuken gelijknamig te maken.
Van enige poging, om iets begrijpelijk of aanschouwelijk te maken, was geen sprake: de meester deed vóór op het bord, hoe ’t moest. En we leerden perfekt, met breuken te werken. Ik heb later eens een onderwijzer gehad, die heeft getracht, me begrip bij te brengen van dat kunstjes-doen met breuken; ik moet eerlijk bekennen, dat hij me wanhopig maakte; ik was blij, als hij eindelijk ophield met zijn uitlegging, en ik weer met m’n heerlijke zekerheid de kunstjes mocht doén . . .
Theo Thijssen (1941). In de ochtend van het leven. Van Dishoeck. blz. 71
‘in de zesde klas’: Theo Thijssen zat op een lagere school (2e klasse, in Amsterdam) met 8 klassen van negen maanden
Welke zonde had ik begaan? Natuurlijk weet ik de getalletjes niet meer; maar wel de zonde. Ik moest iets uitrekenen als 11⁄2 + 21⁄3 + 11⁄4, en had geschreven: 11⁄2 + 21⁄3 = 35⁄6 + 11⁄4 = 51⁄12.
Daar stond de leugen: 11⁄2 + 21⁄3 = 35⁄6 + 11⁄4. Ik moest het toegeven. “Snor nou maar ’es uit, hoe je ’t wèl mag schrijven,” was daarna de opdracht.
Ik snorde ’t uit, en ik groeide.
Theo Thijssen (1941). In de ochtend van het leven. Van Dishoeck. blz. 148
Joh. H. Wansink (1957 8e). Reken- en stelkunde. Leerboek der algebra voor het middelbaar en voorbereidend hoger onderwijs. Deel I J. B. Wolters.
Hoofdstuk III: Deelbaarheid, merkwaardige produkten, ontbinding in factoren 82-116; Hoofdstuk IV: Het gebroken getal. 117-137; Hoofdstuk V: Evenredigheden 138-159
Van Steenbrugge, H., Valcke, M., Lesage, E., Desoete, A. & Burny, E. (2015). Preservice elementary school teachers’ knowledge of fractions: A mirror of students’ knowledge? Manuscript submitted for publication in Journal of curriculum studies abstract of hfdst 4 in deze pdf
Hendrik van Steenbrugge (2012). Teaching Fractions in Elementary School. Dissertation Gent. Promotor: Martin Valcke. Copromotor: Annemie Desoete. pdf
Hendrik Van Steenbrugge, Janine Remillard, Lieven Verschaffel, Martin Valcke and Annemie Desoete (2015). Teaching Fractions in Elementary School An Observational Study. The Elementary School Journal, 116, 49-75. abstract
from the abstract
Ad 1. Multiple solution pathways. Is there any evidence for effectivenes of stressing multiple solutions in education? Gearhart et al 1999 is mentioned here; it is research changingen a lot of things at the same time, however, without measurement of effects — it is an observational study. Another study, Kazemi and Stipek (2001, using 4 teachers as subject, only ‘suggested’ importance of, again among others, ‘understanding the relations among multiple stategies’. Another study Cramer et al 2002) is claimed to have demonstrated positive results compared to a control group of the Rational Numbers Project Curriculum. That’s all in terms of support mentioned in the research literature.
Anja Eichelmann · Susanne Narciss · Lenka Schnaubert · Erica Melis (2012). Typische Fehler bei der Addition und Subtraktion von Brüchen – Ein Review zu empirischen Fehleranalysen J Math Didakt (2012) 33:29–57 pdf
H. Wu (April 30, 1998). Teaching fractions in elementary school: A manual for teachers. (revised 2010) pdf
Ben Wilbrink (October 24 2015). Teaching fractions, or fractionated teaching? http://www.jstor.org/stable/10.1086/683111 5 myths taken seriously? Twitter
As far as I know none of these 5 instruction strategies has been proven to be superior to strategies based on learning psychology proper. Those strategies are approximately nine in number, as described by Stellan Ohlsson in his 2011 ‘Deep Learning’: Twitter + picture
Danny Beckers & Harm Jan Smid (1828/2003). Grondbeginselen der rekenkunde. Uitgegeven door het wiskundig genootschap, Onder de Zinspreuk Mathesis Scientiarum Genitrix, te Leyden. isbn 9065507442 abstract
Dit facsimile is het deeltje over breuken. Voor decimalebreuken waren immers gouden tijden aangebroken met het ingevoerde decimale stelsel.
Resnick, Ilyse; Jordan, Nancy C.; Hansen, Nicole; Rajan, Vinaya; Rodrigues, Jessica; Siegler, Robert S.; Fuchs, Lynn S. (May 2016). Developmental growth trajectories in understanding of fraction magnitude from fourth through sixth grade. Developmental Psychology, 52, 746-757. abstract [I haveno access]
Hugues Lortie-Forgues & Robert S. Siegler (2017). Conceptual knowledge of decimal arithmetic. Journal of Educational Psychology, Vol 109(3), Apr 2017, 374-386. http://dx.doi.org/10.1037/edu0000148 abstract & manuscript
Pooja Gupta Sidney, Martha Wagner Alibali (2017). Creating a Context for Learning: Activating Children’s Whole Number Knowledge Prepares Them to Understand Fraction Division Journal of Numerical Cognition open access
Fractions: Where It All Goes Wrong. Why do Americans have such trouble with fractions—and what can be done? By Robert S. Siegler on November 28, 2017 Scientific American open access
Braithwaite, D. W., & Siegler, R. S. (2018). Children learn spurious associations in their math textbooks: Examples from fraction arithmetic. Journal of Experimental Psychology: Learning, Memory, and Cognition. Advance online publication. http://dx.doi.org/10.1037/xlm0000546 abstract
FRACTIONS. A set of intertwined constructs. Cambridge Mathematics. pdf
a name="">
a name="">
a name="">
![]() http://www.benwilbrink.nl/projecten/breuken.htm
http://goo.gl/bsQjV
http://www.benwilbrink.nl/projecten/breuken.htm
http://goo.gl/bsQjV